Abstract
Continuous authentication enhances security by re-verifying a user’s validity during the active session. It utilizes data about users’ behavioral actions and contextual information to authenticate them continuously. Such data contain information about user-sensitive attributes such as gender, age, contextual information, and may also provide information about the user’s emotional states. The collection and processing of sensitive data cause privacy concerns. In this paper, we propose two efficient protocols that enable privacy-preserving continuous authentication. The contribution is to prevent the disclosure of user-sensitive attributes using partial homomorphic cryptographic primitives and reveal only the aggregated result without the explicit use of decryption. The protocols complete an authentication decision in a single unidirectional transmission and have very low communication and computation costs with no degradation in biometric performance.
1. Introduction
Computing technology is growing rapidly; mobile devices are now commonly used for different applications and services. The rapid advancement of technology also invites various security threats in different domains. Security breaches, including unauthorized access to user accounts, malware attacks, insider attacks, brute-force attacks, etc., are happening every day. Authentication is considered a fundamental aspect of digital security; it ensures whether the identity claimer is the right person or not. Verifying user identity with a weak authentication mechanism is one of the reasons for such security breaches. User authentication is usually accomplished in a static way, where the user is authenticated only once at the beginning of a session. Security problems likely occur when the PINs/passwords are stolen, or the device remains unattended for a while and somebody else uses it. To reduce security vulnerabilities, a second-factor authentication may be employed so that the user validity can be verified persistently. In this regard, continuous authentication may help to prevent unauthorized access by continuously authenticating the user during the session. It can be accomplished by collecting and monitoring user contextual information such as user physical location by GPS, logical location IP addresses, etc., or authenticating users using their behavioral traits.
Both behavioral biometrics and context-aware modalities offer passive and seamless authentication; therefore, they do not reduce usability. But, sometimes, they may face problems, and to address such problems, one should carefully choose the mode of continuous authentication. Different modalities solve different problems; for example, monitoring users by their location data, IP addresses, or other context-aware data only enhances security when an attacker tries to breach security from a different place with different devices, etc. Still, the limitation of this particular mechanism is that it gives no protection when the user leaves the device unattended and an imposter uses it. Behavioral biometric modalities may overcome this problem because users are authenticated based on the behavioral patterns they perform while using a device [1]. The limitation can be overcome because the imposter can be identified immediately. In this regard, keystroke dynamics or swipe gestures are the most suitable modes for continuous authentication.
Continuous authentication may have different applications, such as it can be used to secure mobile devices, financial services, IoT and smart homes, E-commerce, healthcare, cloud-based services, etc. Continuous authentication for such applications is also crucial because it requires outsourcing user data. Continuous authentication can be performed locally in the device, but devices have limited storage and computation resources, and there is a possibility of malicious or compromised client [2,3].
Continuous authentication modalities use user behavioral data such as keystroke patterns, swipe gestures, gait dynamics, and contextual data, including user location data, IP addresses, carrier data, user calendars, Bluetooth connectivity, or other personal data [1]. Such data are enormous and contain sensitive information about the user’s appearance, biometric information, and other user-sensitive and demographic information that may be induced from such features [4]. Outsourcing such personal data to a third party raises privacy concerns. These data contain biometric traits and contain identifiable and sensitive attributes. As per GDPR [5,6], these data must be stored and processed in a privacy-preserving manner.
Efficiency is another important concern in continuous authentication that requires attention. Continuous authentication works actively throughout the session; therefore, it requires low transmission overhead and efficient performance. The privacy-preserving continuous authentication protocols in the literature are either very inefficient [7,8] or proven insecure in [9]. For instance, in most cases, the authentication decision is made by performing many rounds of interaction between the client and the authentication server. This causes communication and computation overhead, as mentioned in the later Section 8.
Our contribution
To solve privacy and efficiency issues, this article makes the following contributions:
- Using the additive homomorphic encryption property, we propose two efficient protocols that protect the privacy of user behavioral features (enrollment vector and probe vector). Protocol 1 assumes an honest client and a malicious authentication server, and protocol 2 assumes a compromised client and malicious authentication server.
- Low communication and computation costs. Taking high communication and computation costs into consideration, we propose very efficient authentication protocols that avoid rounds of communication between the client and the authentication server; the protocols complete the authentication in a single unidirectional (client/server) transmission.
- The biometric performance (accuracy) of the proposed protocols is the same as is in the plaintext domain. In other words, there is no degradation in accuracy.
The rest of the paper is organized as follows: we discuss the related work in Section 2; the preliminaries are discussed in Section 3; the adversarial model is presented in Section 5; security requirements are discussed in Section 5.4; privacy-preserving protocol 1 is presented in Section 6; an extended protocol, taking a compromised client into account, is presented in Section 7; computation cost and communication is assessed in Section 8; a biometric evaluation is shown in Section 9; and Section 10 concludes the paper and discusses the future work.
2. Related Work
This section presents the literature review of privacy-preserving continuous authentication schemes. We only consider privacy-preserving solutions that utilize only cryptographic primitives to achieve privacy. Govindarajan et al. [7] proposed protocols for privacy-preserving continuous authentication. They use additive homomorphic encryption and computed encrypted Scaled Euclidean Distance (SED) and Scaled Manhattan Distance (SMD) to determine the dissimilarity between a reference template and a fresh input probe.
Safa et al. [10] proposed a generic implicit authentication scheme for contextual data. They used additive homomorphic encryption accompanied by order-preserving symmetric encryption. The final result is based on the dissimilarity scores of Average Absolute Deviation (AAD) between the enrollment and probe vector. Domingo-Ferrer et al. [11] presented an implicit authentication protocol using an additively homomorphic encryption primitive and computed a private set intersection between a set of enrollment features and a set of probes. Sitová et al. [8] used the idea of a fuzzy commitment scheme proposed by Juels and Wattenberg [12] to propose a touch dynamics-based authentication scheme. However, such techniques face certain limitations related to data reversibility and data distinguishability and do not achieve privacy [13]. Balagani et al. [14] presented privacy-preserving keystroke dynamics-based protocols for implicit authentication. Like Govindarajan et al., they also used additive homomorphic with a secure comparison protocol presented by Damgård et al. [15,16].
Acar et al. [17] proposed a second-factor hybrid privacy-preserving authentication protocol using keystroke dynamics. Their multi-factor authentication mechanism uses two types of cryptographic primitives: fully homomorphic encryption (FHE) [18] and fuzzy hashing [19].
Wei et al. [20] proposed a privacy-preserving continuous authentication protocol using the Paillier cryptosystem. The cosine similarity is used to determine the similarity between the encrypted reference template and the probe. The enrollment features are encrypted using the public key of the authentication server, and privacy is achieved using secret random numbers (secret key), such as each element is blinded with a secret blinding factor that is only known to the client. However, it is shown by Eskeland and Baig [9] that the Wei et al. scheme is insecure and not privacy preserving. They showed that the honest and curious authentication server obtains not only the plaintext of biometric features, but also the secret key vector. Moreover, they also showed that the Wei et al. scheme is vulnerable to active adversarial attacks.
Loya and Bana [21] used fully homomorphic encryption proposed by Cheon et al. [22] with differential privacy to propose a privacy-preserving protocol for keystroke analysis. Their solution trains neural networks utilizing differential privacy and evaluates the encrypted data.
Baig and Eskeland [23] proposed a privacy-preserving keystroke dynamics-based continuous authentication that computes penalty and reward functions defined by Bours [24]. Their privacy-preserving solution uses additive homomorphic encryption with a secure comparison protocol and completes authentication in five rounds.
Baig et al. [25] utilized an oblivious transfer protocol (OT) with homomorphic encryption to propose two privacy-preserving continuous authentication protocols. Their proposed protocols protect user biometric data and user activities and complete authentication in four rounds. Their proposed protocols provide communication efficiency as they compute similarity based on k actions and make interaction after k actions.
3. Preliminaries
This section discusses the building blocks.
Building Blocks
Our privacy-preserving continuous authentication protocols use the following building blocks:
(a) The Paillier cryptosystem [26,27] can be explained as follows: During a key generation phase, two large random prime numbers of equal length are selected and RSA product is computed.The public and private keys are generated, of which is the public key, where , and is the private key, where , respectively. Encryption is performed as , where r is chosen randomly in . Decryption is performed as , where L is a function .
Homomorphic encryption schemes enable the algebraic plaintext computations in the encrypted domain. The Paillier cryptosystem supports the following homomorphic properties: and scalar multiplication can be stated as , where notation represents the encryption of x. The notation is presented in Table 1.

Table 1.
Notation.
(b) The cosine similarity. Assume and are two vectors, where the cosine similarity between is defined as
The cosine similarity of 1 indicates that vector and vector are exactly similar, where 0 indicates complete dissimilarity between two vectors.
4. Generic Continuous Authentication Algorithm Based on Cosine Similarity
User authentication is accomplished in two phases: an enrollment phase and an authentication phase. A generic authentication scenario is presented in Algorithm 1. In the enrollment phase, biometric features are sampled, and in accordance with the cosine similarity, a reference feature vector (template) is created by computing , where , .
| Algorithm 1 |
| Enrollment phase , Authentication phase , if then Accept end if |
Authentication features are sampled in the authentication phase, where , , , are precomputed in the same way as stated above to construct the probe vector , where m indicates the total elements in a vector. The cosine similarity s between the template vector and the probe vector is computed as a dot product:
Finally, to make an authentication decision, s is compared to a predefined threshold . If is true, then the user is accepted.
5. Adversarial Model
Different types of adversaries are considered in biometric authentication systems, such as malicious parties, semi-honest parties, etc.; malicious parties are considered strong adversaries, whereas semi-honest parties follow the protocol honestly. The protocols presented in the later sections do not take external adversaries into account and assume that communication between the user and the server is secure and that external threats, such as replay attacks and other similar attacks, are mitigated by applying other security techniques. Note that the enrollment phase is completed in a trusted environment. The proposed authentication protocols consider the following adversaries.
5.1. Trusted Client
A trusted client in a biometric system is considered fully reliable and honest. In this regard, Protocol 1 assumes that the client’s device is secure and that the client is trusted and honestly follows the protocol, and the trusted client is not even curious about the protocol working.
5.2. Malicious Authentication Server
The malicious parties may deviate from the protocol and may act as an active adversary. We assume the authentication server is a malicious party and may deviate from the protocol. The goals of a malicious authentication server may include attempting to learn the stored enrollment data or authentication features by any means. The malicious may send false messages to the client to extract additional information [28].
5.3. Malicious Client
A malicious client is a type of adversary that may also deviate from the protocol. This type of adversary may try to learn enrollment data or may forge the biometric data and try to gain unauthorized access. In the extended protocol, protocol 2, we assume that the client is malicious and can deviate from the protocol [28].
5.4. Security Requirements
To preserve the privacy of biometric features, we assume that a privacy-preserving protocol fulfills the following privacy requirements (PR):
- PR1: The authentication server must not learn the reference features stored during the enrollment phase.
- PR2: The authentication server must not learn the probe during the authentication phase.
- PR3: The authentication server should only learn the outcome but nothing more.
- PR4: The identity claimer should not learn the enrollment feature vector.
6. The Novel Privacy-Preserving Authentication Protocol
In this section, we propose a novel privacy-preserving authentication protocol that protects the enrollment feature vector and the probe vector. It consists of three phases: A setup phase, an enrollment phase, and an authentication phase. The privacy-preserving protocol is shown in Figure 1.
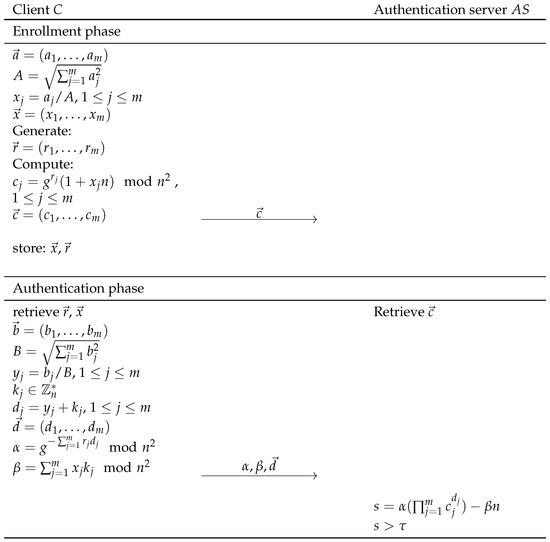
Figure 1.
Privacy-preserving authentication protocol.
6.1. Setup Phase
The authentication server generates a Paillier public key , that is shared with the client .
6.2. Enrollment Phase
During the enrollment phase, C is registered to by providing reference biometric features (template) in a privacy-preserving way.
This phase samples biometric features as and prepares the template vector , in accordance with the cosine similarity, as stated in Section 4. C randomly selects a vector and computes , where the secret encryption factor is an element in , . Note that the encryption factor is computed differently from the Paillier encryption scheme. The encryption factor is removed using and in the authentication phase without a private key while the enrollment features remain protected. C computes an encrypted reference template vector and sends to . stores the encrypted reference template , and C stores locally.
6.3. Authentication Phase
During the authentication phase, the similarity between the probe and the reference template is determined. The probe vector is sampled for each behavioral action, and C computes and , in accordance with the cosine similarity.
C randomly chooses for blinding the probe elements as , , where . C retrieves the reference enrollment template and secret vector , and computes
and
and are computed for subsequent elimination of the encryption factors of and of , such that obtains only the result of dot product s (Equation (2)), but learns nothing about , , , .
C sends an authentication request message to the for the authentication. Upon receiving from C, retrieves encrypted reference template and computes
The correctness can be verified as
Finally, the dot product is restored. checks . If this is true, then accepts the request.
6.4. Security Analysis
Note that protocol 1 does not deal with the malicious client (privacy requirement 4 ). The proposed protocol fulfills the privacy requirements mentioned in Section 5.4 as follows:
- . The authentication server must not learn the reference feature vector stored during the enrollment phase.
The client sends to the authentication server during the enrollment phase, and the elements of the reference template vector are created as , . Each element is protected with , which is randomly chosen. As and are unknown to the adversary, it is hard to determine .
has knowledge of . Since , , are aggregated values, they do not reveal information about the elements of .
- . The authentication server must not learn the probe vector during the authentication phase.
In the authentication phase, C blinds each element of the probe vector as , , with a secret random integer . Due to the blinding, it is impossible to determine or from . However, , , occur in the computation of the dot product . Thus, no information about from could be learned.
- . The authentication server should only learn the outcome but nothing more.
The reference template vector and probe vector are blinded by the mean of random secret elements , , which are canceled out by means of and in a privacy-persevering way. can only see the final result of the dot product, which is the cosine similarity between the probe and the reference template.
7. Extended Scheme w.r.t a Malicious Client
The privacy-preserving scheme in Section 6 requires that the enrollment template vector and the random vector are stored unprotected in the device. Considering that the client is a malicious adversary who can potentially obtain access to the enrollment template vector . To deal with this problem, we extend the previous protocol w.r.t protecting the enrollment template vector . The extended protocol is presented in Figure 2 and solves.

Figure 2.
Extended privacy-preserving authentication protocol.
7.1. Setup Phase
The authentication server shares the public key with the client C and keeps secret, as stated in Section 6.1.
7.2. Enrollment Phase
During this phase, C prepares an encrypted reference template in the same way as stated in Section 6.2. C randomly selects a vector , where is an element in and blinds each element of as . Note that the encryption factor is computed differently from the Paillier encryption scheme, as stated in protocol 1. C sends to . C stores locally in the device.
To protect the reference template , each element is encrypted using an public key in agreement with the Paillier cryptosystem. C randomly chooses and computes the Paillier encryption , and stores the encrypted vector locally.
7.3. Authentication Phase
The probe vector is sampled and C randomly chooses for blinding the probe elements as , , where , and computes in the same way as in Section 6.3. C computes , where is an element of random vector , which is also used in . C sends to the for the authentication.
Upon receiving the message from C, first decrypts in agreement with the Paillier cryptosystem by first computing
where , restores
which is same as , as stated in the Section 6.3,
After that, retrieves the encrypted template and computes
The correctness is in agreement with Equation (4).
The dot product is restored. verifies whether is true, then C is accepted.
7.4. Security Analysis
This section presents the security analysis of ; the rest of the privacy requirements ( and ) are in agreement with the security analysis presented in Section 6.4. Since both protocols do not send anything back to the client, the malicious cannot send any false messages to the client. Any message from will considered as a false message.
- . The identity claimer should not learn the enrollment feature vector.
The device stores the encrypted reference template vector by the public key of ; due to that, C cannot access the unencrypted reference template vector. Hence, if the device gets compromised, the adversary cannot access . Moreover, C sends the blinded probe to , where determines the similarity between the encrypted reference template and the blinded probe in a privacy-preserving way without a second interaction.
8. Computation Cost Analysis and Comparison
The computation and communication efficiency of the proposed protocol are determined by comparing them with the existing protocols proposed in a similar domain. We analyze the computation cost of encrypted operations, the number of rounds required to complete the authentication decision, and the transmitted encryptions in each transmission.
The proposed protocols complete an authentication decision in a single unidirectional transmission between the client and the authentication server . C blinds each element of the probe vector and sends it the . Using a homomorphic property, computes m scalar products.
The abbreviations used in Table 2 are denoted as SE: Symmetric encryption, PSI: Private set intersection, OPE: Order preserving encryption, and OT: Oblivious transfer protocol.

Table 2.
Complexity comparison.
The protocol proposed by Govindarajan et al. [7] completes the authentication decision by performing four round transmissions between the client and the server, whereas in the first transmission, a vector of the m encrypted element is transmitted to the client. Then, the client and the server invoke the privacy-preserving comparison protocol proposed by Damgård et al. [15,16] to compute the Scaled Manhattan Distance. Note that the Damgård et al. [15,16] protocol compares integers in privacy-preserving manners without compromising their confidentiality. They computed the Squared Euclidean distance based on the Erkin et al. protocol [29]. Due to computational and communication inefficiencies of the sub-protocol proposed by Damgård et al. [15,16], the Govindarajan et al. protocols [7,14] are very inefficient.
The Wei et al. protocol [20] completes an authentication decision by making three rounds of transmissions between the client and the server. In each interaction, m encrypted elements are transmitted. Each party computes m scalar multiplication in each interaction.
The Baig et al. [25] protocols complete the authentication decision for k activities in four rounds. Other means of continuous authentication, such as utilizing user physical location data, cookies, IP addresses, etc., proposed in [10,11,30], are also very inefficient. Domingo-Ferrer et al. [11] protocol takes two rounds, where each round sends an encryption of m elements. Similarly, Shahandashti et al. [30] protocol also takes three rounds to complete the authentication decision, and each round transmits m encryptions.
In comparison to the protocols in [7,20,23,25], our proposed protocols are very efficient in terms of computation cost and communication costs.
Considering the scenario of continuous authentication, the authentication decision is made periodically, such as instead of making the authentication decision based on a single behavioral action, it should be decided on the basis of more than one action, such as actions; for such scenarios, the protocols in [7,20] take , interactions, respectively. Meanwhile, for k actions, our protocols require only k round transmissions. The comparison is presented in Table 2.
9. Performance Evaluation
To analyze the performance of the proposed protocols, we perform the biometric analysis of the proposed protocols and determine the running time in milliseconds (ms).
9.1. Biometric Evaluation
Table 3 presents the biometric analysis of the proposed protocols. To determine the biometric performance of the proposed protocols, we used a publicly available dataset [4] (Available at: https://www.ms.sapientia.ro/~manyi/bioident.html, accessed on 15 June 2023) to evaluate the biometric performance. The touch gestures data are collected from 51 participants, 42 male and 9 female. A swipe gesture contains the following feature elements [4]:

Table 3.
Biometric evaluation of the proposed protocols.
“stroke-duration, start-x, start-y, stop-x, stop-y, direct-end-to-end-distance, mean-resultant-length, up-down-left-right-flag, direction-of-end-to-end line, largest-deviation-from-end-to-end-line, average-direction, length-of-trajectory, average-velocity, mid-stroke-pressure, mid-stroke-area”.
Each user provides l samples in different sessions and on different devices. The biometric performance is analyzed by determining the false match rate (FMR), false non-match rate (FNMR), and equal error rate (EER). We randomly select one sample and make it a reference template. For each user, a template is created by following the steps stated in the enrollment phase of proposed protocols; for example, we created 51 reference templates (one for each user). The rest of the samples are utilized for the testing. FNMR determines the similarity between the reference template and the remaining samples.
For FMR, we construct (l) imposter samples by choosing different samples from different users. FMR is determined by computing the similarity between the reference template of each user and the imposter samples. The similarity is computed by following steps mentioned in the proposed protocols.
The performance on the blinded features is the same as the performance of the baseline in the plaintext domain. We achieved different performances on different thresholds (T). The lower threshold gives lower FNMR but also gives high FMR. The highest FNMR of has been achieved on , whereas the lowest FNMR has been on . The best FNMR and FMR are achieved on . Note that the accuracy of the proposed protocols is the same as without privacy presented in Algorithm 1. Adding cryptography does not degrade the accuracy.
9.2. Running Time
The running time of the proposed protocols is measured on Intel(R) Core(TM) i5-7440 HQ CPU@2.80 GHz, 32 GB RAM in Python 3.10. The running time of the proposed protocols is tested on different security levels . The running time of the proposed protocol 1 is shown in Figure 3a.
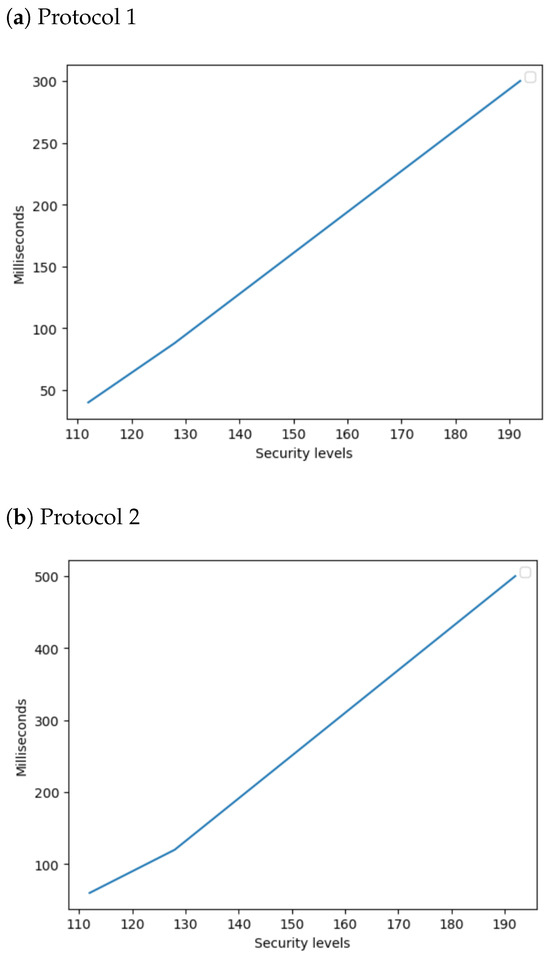
Figure 3.
Running time of the proposed protocols.
Figure 3b shows the running time of the proposed protocol, protocol 2; due to the decryption, protocol 2 has a slightly higher running time than protocol 1. This analysis does not include the communication costs.
10. Conclusions and Future Work
In this paper, we have proposed two efficient privacy-preserving continuous authentication protocols that protect user biometric features. The proposed protocol 1, provides privacy protection under the malicious authentication server and honest client, and the proposed protocol 2, considers malicious parties. The biometric evaluation on a publicly available dataset has shown that the proposed protocols have good performance. The privacy-preserving protocols provide the same accuracy as without encryption. The proposed protocols offer low communication and computation costs and complete authentication in a single uni-directional transmission. Low costs overhead and good biometric performance prove the practicality of the proposed protocols in real-life applications.
The proposed protocols can be utilized for continuous authentication as well as static authentication, such as authentication using any biometrics or contextual modalities.
In future work, we will consider making the final comparison in a privacy-preserving way.
Author Contributions
Conceptualization, A.F.B. and S.E.; Methodology, A.F.B. and B.Y.; Validation, A.F.B. and S.E.; Investigation, A.F.B., S.E. and B.Y.; Writing—original draft, A.F.B.; Writing—review & editing, A.F.B.; Supervision, S.E. and B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the Privacy Matters (PriMa) project. The PriMa project has received funding from European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 860315.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baig, A.F.; Eskeland, S. Security, Privacy, and Usability in Continuous Authentication: A Survey. Sensors 2021, 21, 5967. [Google Scholar] [CrossRef] [PubMed]
- Atanassov, N.; Chowdhury, M.M. Mobile device threat: Malware. In Proceedings of the 2021 IEEE International Conference on Electro Information Technology (EIT), Mt. Pleasant, MI, USA, 14–15 May 2021; pp. 7–13. [Google Scholar]
- Weichbroth, P.; Łysik, Ł. Mobile security: Threats and best practices. Mob. Inf. Syst. 2020, 2020, 8828078. [Google Scholar] [CrossRef]
- Antal, M.; Bokor, Z.; Szabó, L.Z. Information revealed from scrolling interactions on mobile devices. Pattern Recognit. Lett. 2015, 56, 7–13. [Google Scholar] [CrossRef]
- GDPR. Processing of Special Categories of Personal Data. 2021. Available online: https://gdpr-info.eu/art-9-gdpr/ (accessed on 3 March 2023).
- On the Protection of Natural Persons with Regard to the Processing of Personal Data and on the Free Movement of Such Data, and Repealing Directive 95/46/EC (General Data Protection Regulation). 2016. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A02016R0679-20160504 (accessed on 14 January 2024).
- Govindarajan, S.; Gasti, P.; Balagani, K.S. Secure privacy-preserving protocols for outsourcing continuous authentication of smartphone users with touch data. In Proceedings of the 2013 IEEE Sixth International Conference on Biometrics: Theory, Applications and Systems (BTAS), Arlington, VA, USA, 29 September–2 October 2013; pp. 1–8. [Google Scholar]
- Sitová, Z.; Šeděnka, J.; Yang, Q.; Peng, G.; Zhou, G.; Gasti, P.; Balagani, K.S. HMOG: New behavioral biometric features for continuous authentication of smartphone users. IEEE Trans. Inf. Forensics Secur. 2015, 11, 877–892. [Google Scholar] [CrossRef]
- Eskeland, S.; Baig, A.F. Cryptanalysis of a Privacy-preserving Behavior-oriented Authentication Scheme. In Proceedings of the 19th International Conference on Security and Cryptography—SECRYPT 2022, Lisbon, Portugal, 11–13 July 2022; pp. 299–304. [Google Scholar] [CrossRef]
- Safa, N.A.; Safavi-Naini, R.; Shahandashti, S.F. Privacy-preserving implicit authentication. In Proceedings of the IFIP International Information Security Conference, Marrakech, Morocco, 2–4 June 2014; pp. 471–484. [Google Scholar]
- Domingo-Ferrer, J.; Wu, Q.; Blanco-Justicia, A. Flexible and robust privacy-preserving implicit authentication. In Proceedings of the IFIP International Information Security and Privacy Conference, Hamburg, Germany, 26–28 May 2015; pp. 18–34. [Google Scholar]
- Juels, A.; Wattenberg, M. A fuzzy commitment scheme. In Proceedings of the 6th ACM Conference on Computer and Communications Security, Singapore, 1–4 November 1999; pp. 28–36. [Google Scholar]
- Bringer, J.; Chabanne, H.; Patey, A. Privacy-preserving biometric identification using secure multiparty computation: An overview and recent trends. IEEE Signal Process. Mag. 2013, 30, 42–52. [Google Scholar] [CrossRef]
- Balagani, K.S.; Gasti, P.; Elliott, A.; Richardson, A.; O’Neal, M. The impact of application context on privacy and performance of keystroke authentication systems. J. Comput. Secur. 2018, 26, 543–556. [Google Scholar] [CrossRef]
- Damgård, I.; Geisler, M.; Krøigaard, M. Efficient and secure comparison for on-line auctions. In Proceedings of the Australasian Conference on Information Security and Privacy, Townsville, Australia, 2–4 July 2007; pp. 416–430. [Google Scholar]
- Damgård, I.; Geisler, M.; Krøigard, M. A correction to ‘Efficient and secure comparison for on-line auctions’. Int. J. Appl. Cryptogr. 2009, 1, 323–324. [Google Scholar] [CrossRef]
- Acar, A.; Liu, W.; Beyah, R.; Akkaya, K.; Uluagac, A.S. A privacy-preserving multifactor authentication system. Secur. Priv. 2019, 2, e88. [Google Scholar]
- Gentry, C. A Fully Homomorphic Encryption Scheme; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Kornblum, J. Identifying almost identical files using context triggered piecewise hashing. Digit. Investig. 2006, 3, 91–97. [Google Scholar] [CrossRef]
- Wei, F.; Vijayakumar, P.; Kumar, N.; Zhang, R.; Cheng, Q. Privacy-Preserving Implicit Authentication Protocol Using Cosine Similarity for Internet of Things. IEEE Internet Things J. 2020, 8, 5599–5606. [Google Scholar] [CrossRef]
- Loya, J.; Bana, T. Privacy-Preserving Keystroke Analysis using Fully Homomorphic Encryption & Differential Privacy. In Proceedings of the 2021 International Conference on Cyberworlds (CW), Caen, France, 28–30 September 2021; pp. 291–294. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Advances in Cryptology–ASIACRYPT 2017, Proceedings of the 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Proceedings, Part I 23; Springer: Berlin/Heidelberg, Germany, 2017; pp. 409–437. [Google Scholar]
- Baig, A.F.; Eskeland, S. A Generic Privacy-Preserving Protocol For Keystroke Dynamics-Based Continuous Authentication. In Proceedings of the 19th International Conference on Security and Cryptography—SECRYPT 2022, Lisbon, Portugal, 11–13 July 2022; pp. 491–498. [Google Scholar] [CrossRef]
- Bours, P. Continuous keystroke dynamics: A different perspective towards biometric evaluation. Inf. Secur. Tech. Rep. 2012, 17, 36–43. [Google Scholar] [CrossRef]
- Baig, A.F.; Eskeland, S.; Yang, B. Privacy-preserving continuous authentication using behavioral biometrics. Int. J. Inf. Secur. 2023, 22, 1833–1847. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Damgård, I.; Jurik, M. A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In Public Key Cryptography, Proceedings of the 4th International Workshop on Practice and Theory in Public Key Cryptosystems, PKC 2001, Cheju Island, Republic of Korea, 13–15 February 2001; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2001; pp. 119–136. [Google Scholar]
- Simoens, K.; Bringer, J.; Chabanne, H.; Seys, S. A framework for analyzing template security and privacy in biometric authentication systems. IEEE Trans. Inf. Forensics Secur. 2012, 7, 833–841. [Google Scholar] [CrossRef]
- Erkin, Z.; Franz, M.; Guajardo, J.; Katzenbeisser, S.; Lagendijk, I.; Toft, T. Privacy-preserving face recognition. In Proceedings of the International Symposium on Privacy Enhancing Technologies Symposium, Seattle, WA, USA, 5–7 August 2009; pp. 235–253. [Google Scholar]
- Shahandashti, S.F.; Safavi-Naini, R.; Safa, N.A. Reconciling user privacy and implicit authentication for mobile devices. Comput. Secur. 2015, 53, 215–233. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).