Detecting Smart Contract Vulnerabilities with Combined Binary and Multiclass Classification
Abstract
1. Introduction
- 1.
- The research on and necessity of solutions, which can be applied in the real world, is an actual problem.
- 2.
- The possible solution demonstrates a general way to apply ML to increase distributed systems’ qualitative metrics.
- 3.
- Ethereum is one of the most popular platforms for creating decentralized applications, which is why the proposed solution will have practical value and can be compared with existing approaches for smart contract analysis in Ethereum. The quality dataset Ethereum [10] for designing and testing ML solutions is publicly available.
- We designed a two-phase ML-based framework that can detect vulnerable contracts and determine the type of vulnerability.
- Our system focuses on the vulnerable contracts by filtering the non-vulnerable ones, which can potentially save time and reduce computational load.
- After comparison with a single-phase classification, the proposed system has fewer false-negative detection samples.
- We have proved that instead of the traditional method of application, either multiclass or binary classification, it is possible to achieve better results using the two phases consequently.
2. Related Work
2.1. Tools for Analysis of Smart Contracts
2.2. ML for Smart Contract Analysis
2.3. Summary
3. Methodology
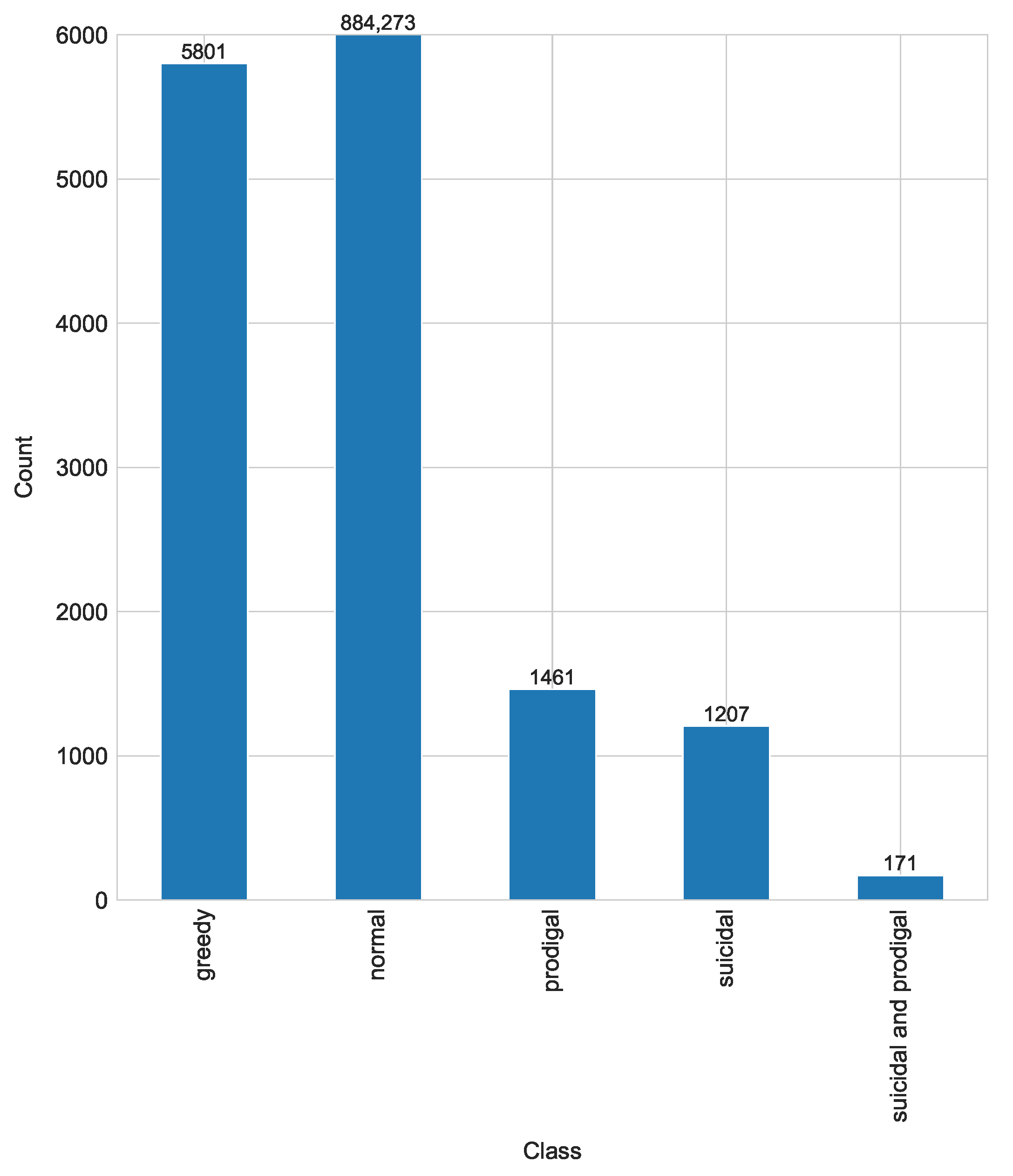
3.1. Dataset Description
- Normal contracts where no vulnerability is detected.
- Suicidal contract that can be killed arbitrarily. In spite of the ability of some contracts to kill themselves in emergency situations, in the case of improper implementation, this ability can be exploited by any arbitrary account by executing the “suicide” instruction [16].
- Prodigal contracts refund the funds to owners, in the case of attacks, to the addresses that have previously sent Ether or that present the specific solution. The contract is considered vulnerable when a contract distributes to an arbitrary address which does not belong to the owner, has never made a deposit of Ether in the contract, and has not provided any data, which is difficult to forge [16].
- Greedy contracts remain alive and indefinitely lock Ether, allowing it to be released without any conditions. Straightforward errors can occur in contracts which accept Ether but either entirely lack instructions to transfer Ether out or these instructions are unreachable [16].
- Suicidal and prodigal contracts have appeared after the cleaning and processing phases of dataset creation according to the description in [3]. The contracts were flagged as both classes.
3.2. Description of ML Methods for Analysis
- Decision tree predicts the target value using the sequence of simple rules.
- k-Nearest Neighbors (k-NN) assigns the class based on the most common class among neighbors.
- Support Vector Machine (SVM) transforms the classes into a higher dimensionality and searches the hyperplanes, which will separate the classes.
- Random forest is the decision trees ensemble.
- Multilayer Perceptron (MLP) is the perceptron where backpropagation is applied.
- Logistic regression is the statistical technique to find the relationships between independent variables and outcome values.
- Space for random forest:
- –
- Number or estimators: 1 to 10;
- –
- Number of features: 1 to 30;
- –
- Depth: 2 to 30;
- –
- Criterion: , .
- Space for the logistic regression:
- –
- C: to 10;
- –
- Solver: , , , ;
- –
- Iterations: 1 to 200.
- Space for the decision tree:
- –
- Max features: , , ;
- –
- Depth: 10 to 30;
- –
- Criterion: , .
- Space for MLP:
- –
- Solver: , , ;
- –
- Hidden layer size: 100 to 250;
- –
- Maximum iterations: 10 to 150.
- Space for k-NN:
- –
- Number of neighbors: 1 to 10;
- –
- Weights: , ;
- –
- Algorithm: , , , .
- Space for SVM:
- –
- to 10 with number of spaced samples 200;
- –
- Kernel: , .
3.3. Scenario 1
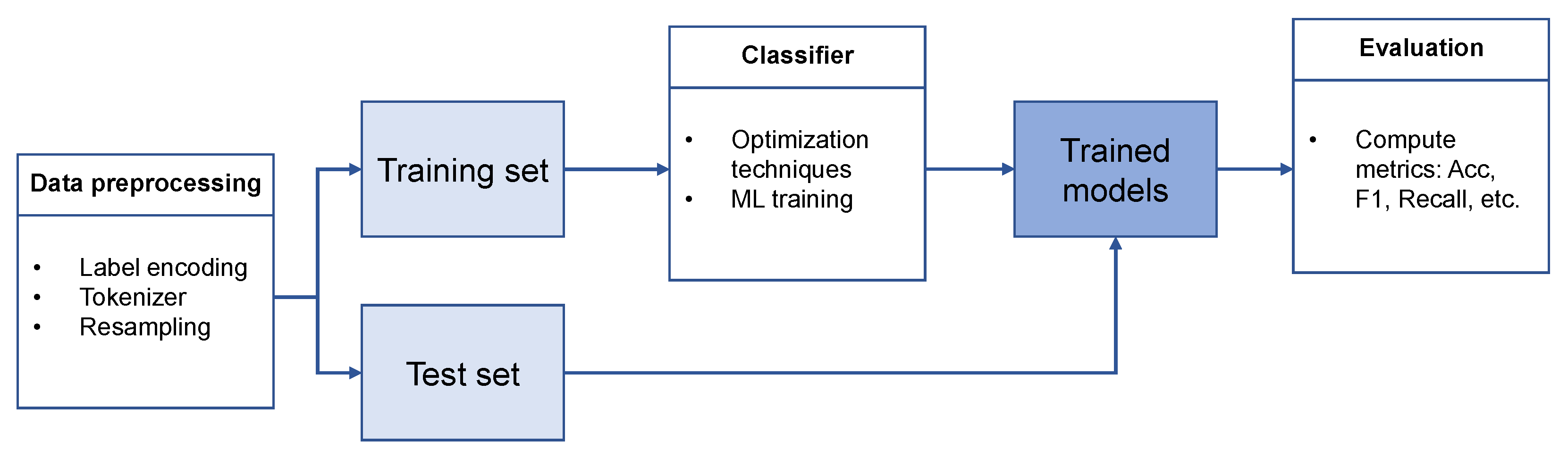
3.3.1. Data Preprocessing
3.3.2. Classification in One Step
- 1.
- Random forest: number of estimators: 9; max features: 26; max depth: 21; criterion: ;
- 2.
- Logistic regression: solver: ; max iterations: 178; C: ;
- 3.
- Decision tree: max depth: 25; criterion: ; features: ;
- 4.
- MLP: solver: ; max iterations: 65; hidden layer sizes: 234;
- 5.
- k-NN: weights: ; number of neighbours: 1; algorithm: ;
- 6.
- SVM: kernel: ; C: ;
3.4. Scenario 2
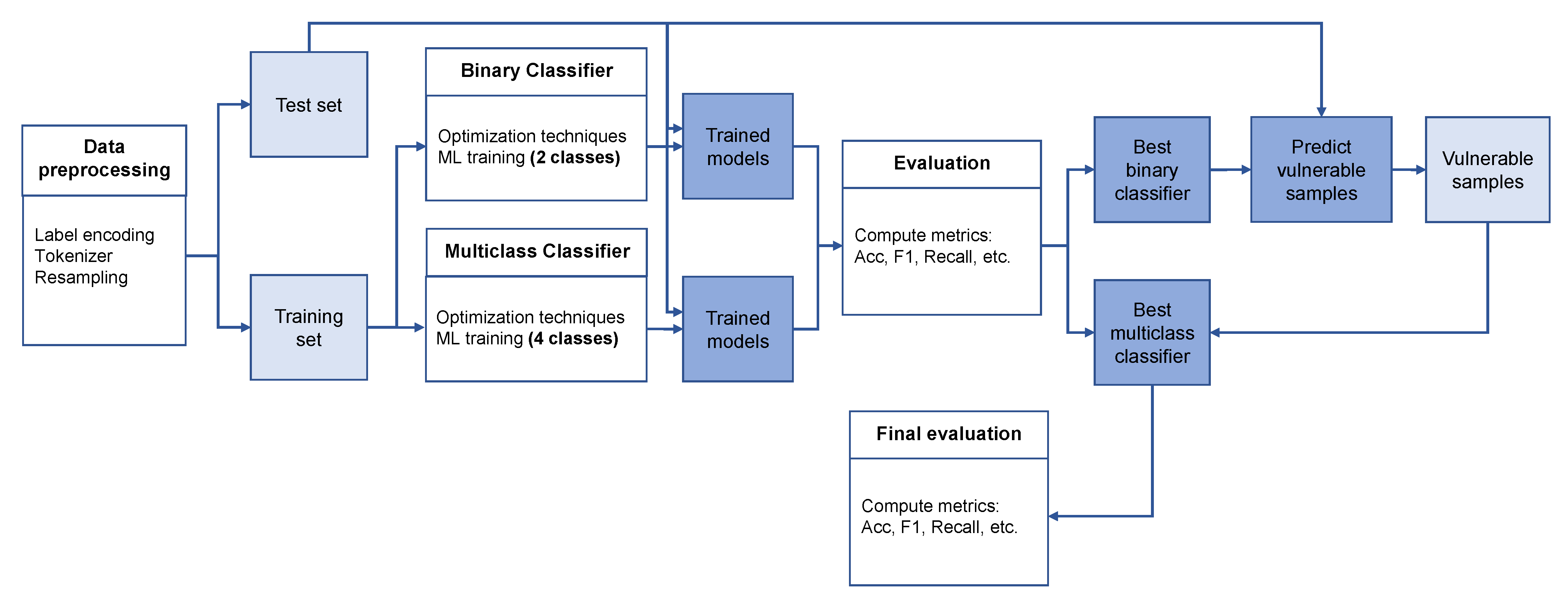
3.4.1. Data Preprocessing
3.4.2. Classification in Two Phases
- 1.
- Random forest: number of estimators: 7; max features: 12; max depth: 17; criterion: ;
- 2.
- Logistic regression: solver: ; max iterations: 144; C: ;
- 3.
- Decision tree: max depth: 25; criterion: ; max features: ;
- 4.
- MLP: solver: ; max iterations: 147; hidden layer sizes: 136;
- 5.
- k-NN: weights: ; number of neighbors: 3; algorithm: ;
- 6.
- SVM: kernel: ; C: ;
- 1.
- Random forest: number of estimators: 9; max features: 26; max depth: 21; criterion: ;
- 2.
- Logistic regression: solver: ; max iterations: 178; C: ;
- 3.
- Decision tree: max depth: 22; criterion: ; max features: ;
- 4.
- MLP solver: ; max iterations: 134; hidden layer sizes: 222;
- 5.
- k-NN weights: ; number of neighbors: 1; algorithm: ;
- 6.
- SVM kernel: ; C: ;
4. Evaluation and Results
4.1. Utilized Metrics
4.2. Results for Scenario 1
4.3. Results for Scenario 2
4.3.1. Classification into Two Classes
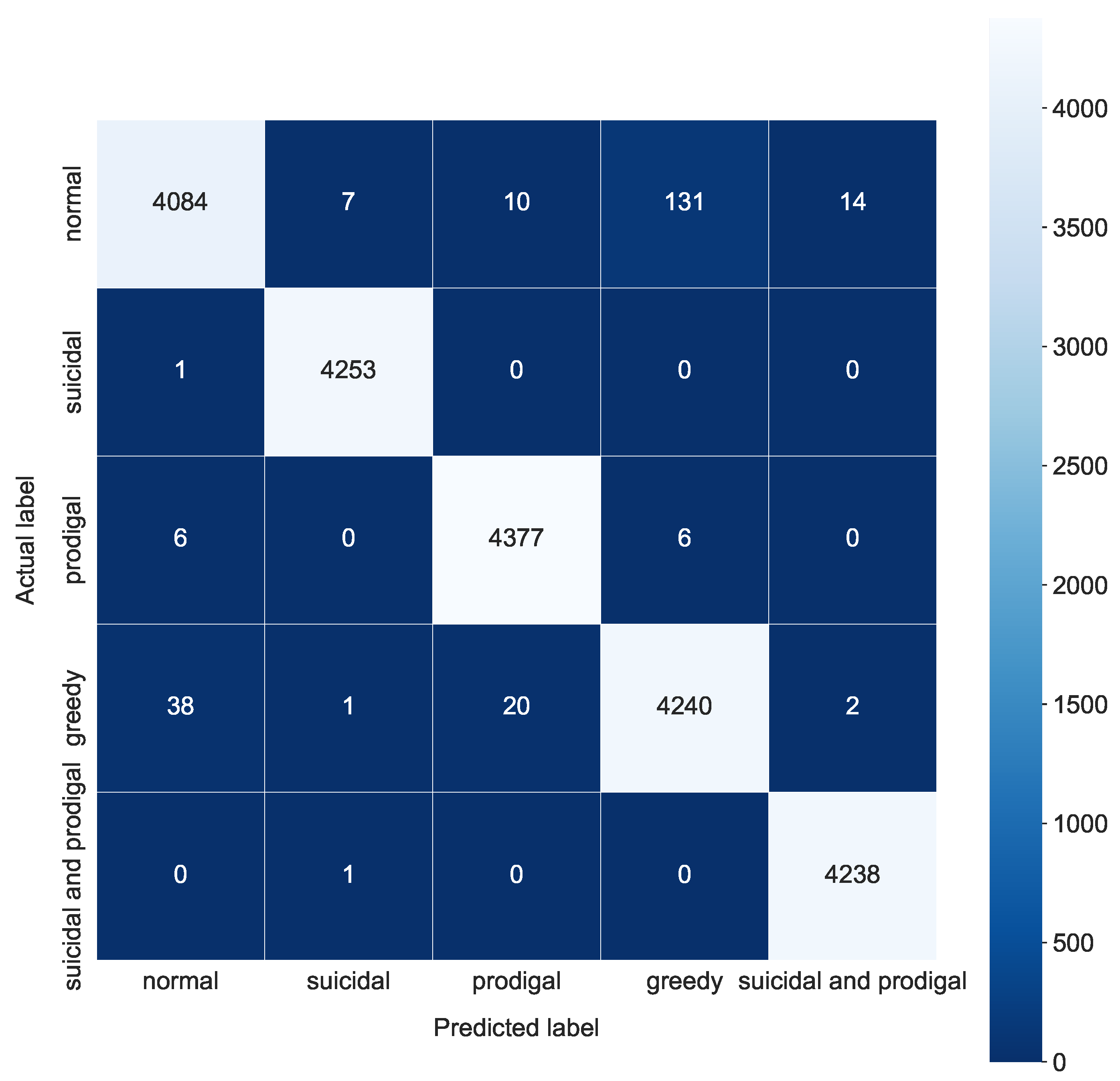
4.3.2. Classification into Four Classes
4.3.3. Final Results for Proposed System
5. Discussion
5.1. Numerical Perspectives
5.2. Future Perspectives
- Overall Network Operation: Exploits targeting vulnerable smart contracts can disrupt the Ethereum network’s operation and stability. Detecting and repairing vulnerabilities with ML on the fly contributes to a more resilient and reliable network infrastructure, lowering the likelihood of service disruptions, congestion, or cascading effects caused by breached contracts.
- Enhanced Security: The Ethereum ecosystem could be made more secure overall by identifying vulnerable smart contracts [22]. Malicious actors may use vulnerabilities to act unlawfully or affect the funds. The likelihood of such assaults can be greatly decreased by identifying and addressing vulnerabilities, safeguarding user assets, and upholding network trust.
- Protection of User Privacy: Certain smart contract flaws can reveal sensitive user data or transaction details [23]. Detecting these vulnerabilities enables immediate correction, limiting illegal access to personal information and protecting user privacy.
- Trust in the System’s Operation: Identifying and providing appropriate countermeasures to vulnerabilities in smart contracts contributes to the development of trust among Ethereum developers and consumers [24]. Increased trust in the security of smart contracts can lead to a greater adoption of Ethereum-based applications and services, supporting network innovation and growth beyond state-of-the-art versions.
- Evolution of Best Practices: Vulnerability detection provides significant insights into emerging threats in the smart contract world [24]. This knowledge can help the Ethereum community define best practices, code standards, and security recommendations. Sharing this information aids in the entire ecosystem’s maturation and develops a security-conscious development culture.
5.3. Integration Issues
- Limited Training Data: A large volume of labeled training data is needed to train ML models. Nevertheless, obtaining a significant and diversified collection of identified vulnerabilities in the case of vulnerable smart contracts remains close to impossible. The restricted availability of labeled data may hamper the capacity to train precise and reliable ML models.
- Evolving Attack Techniques: The landscape of smart contract flaws and attack methods constantly changes [25]. ML models naturally use historical data to find trends and predict future outcomes. Ethereum’s smart contract ecosystem is extensive and diverse, with many contract types and functionalities. If trained on a single set of contracts, ML algorithms might not generalize effectively to new contract kinds or vulnerabilities. Adapting models to different contract architectures and keeping them current with changing smart contract standards and practices can be challenging and time-consuming.
- “Back box” issue: It can be difficult to comprehend how ML models come to their conclusions because they frequently operate as black boxes when employed. In security-critical applications, explainability is essential to promote openness and confidence. It could be challenging for developers and integrators to comprehend the logic behind found vulnerabilities if a machine learning model cannot explain its predictions concisely.
- False Positives and False Negatives: ML models are prone to false positives, where they mistakenly identify a non-vulnerable contract as vulnerable, and false negatives, when they fail to recognize a contract as vulnerable. False positives can result in pointless audits or interventions, while false negatives can leave vulnerabilities and potential vulnerabilities undiscovered. It is still difficult to balance reducing false alarms and correctly identifying risks.
- Scalability: Applying ML techniques for smart contract vulnerability detection in real-life applications often requires significant computational resources and integration phases. Training complex models, deploying them in production, and maintaining them over time can be costly. Moreover, as the Ethereum network continues to grow, the volume of smart contracts increases, posing scalability challenges for machine learning-based detection approaches.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kushwaha, S.S.; Joshi, S.; Singh, D.; Kaur, M.; Lee, H.N. Systematic Review of Security Vulnerabilities in Ethereum Blockchain Smart Contract. IEEE Access 2022, 10, 6605–6621. [Google Scholar] [CrossRef]
- Gupta, R.; Patel, M.M.; Shukla, A.; Tanwar, S. Deep Learning-based Malicious Smart Contract Detection Scheme for Internet of Things Environment. Comput. Electr. Eng. 2022, 97, 107583. [Google Scholar] [CrossRef]
- Tann, W.J.W.; Han, X.J.; Gupta, S.S.; Ong, Y.S. Towards Safer Smart Contracts: A Sequence Learning Approach to Detecting Security Threats. arXiv 2018, arXiv:1811.06632. [Google Scholar]
- Mehar, M.I.; Shier, C.L.; Giambattista, A.; Gong, E.; Fletcher, G.; Sanayhie, R.; Kim, H.M.; Laskowski, M. Understanding a Revolutionary and Flawed Grand Experiment in Blockchain: The DAO Attack. J. Cases Inf. Technol. (JCIT) 2019, 21, 19–32. [Google Scholar] [CrossRef]
- Parity Technologies. A Postmortem on the Parity Multi-Sig Library Self-Destruct. Parity Technologies. 2023. Available online: https://parity.io/blog/a-postmortem-on-the-parity-multi-sig-library-self-destruct/ (accessed on 25 January 2023).
- Chen, T.; Cao, R.; Li, T.; Luo, X.; Gu, G.; Zhang, Y.; Liao, Z.; Zhu, H.; Chen, G.; He, Z.; et al. SODA: A Generic Online Detection Framework for Smart Contracts. In Proceedings of the Network and Distributed Systems Security (NDSS) Symposium 2020, San Diego, CA, USA, 23–26 February 2020. [Google Scholar]
- Zhou, H.; Milani Fard, A.; Makanju, A. The State of Ethereum Smart Contracts Security: Vulnerabilities, Countermeasures, and Tool Support. J. Cybersecur. Priv. 2022, 2, 358–378. [Google Scholar] [CrossRef]
- Vacca, A.; Di Sorbo, A.; Visaggio, C.A.; Canfora, G. A Systematic Literature Review of Blockchain and Smart Contract Development: Techniques, Tools, and Open Challenges. J. Syst. Softw. 2021, 174, 110891. [Google Scholar] [CrossRef]
- Liao, J.W.; Tsai, T.T.; He, C.K.; Tien, C.W. Soliaudit: Smart Contract Vulnerability Assessment Based on Machine Learning and Fuzz Testing. In Proceedings of the 6th International Conference on Internet of Things: Systems, Management and Security (IOTSMS), Granada, Spain, 22–25 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 458–465. [Google Scholar]
- Google BigQuery. Kaggle Dataset. Available online: https://www.kaggle.com/datasets/bigquery/ethereum-blockchain (accessed on 25 January 2023).
- Luu, L.; Chu, D.H.; Olickel, H.; Saxena, P.; Hobor, A. Making Smart Contracts Smarter. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 254–269. [Google Scholar]
- Qian, P.; Liu, Z.; He, Q.; Huang, B.; Tian, D.; Wang, X. Smart Contract Vulnerability Detection Technique: A Survey. arXiv 2022, arXiv:2209.05872. [Google Scholar]
- Grishchenko, I.; Maffei, M.; Schneidewind, C. A Semantic Framework for the Security Analysis of Ethereum Smart Contracts. In Proceedings of the International Conference on Principles of Security and Trust, Thessaloniki, Greece, 14–20 April 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 243–269. [Google Scholar]
- ConsenSys: Mythril. Mythril GitHub. Available online: https://github.com/ConsenSys/mythril/ (accessed on 25 January 2023).
- Tsankov, P.; Dan, A.; Drachsler-Cohen, D.; Gervais, A.; Buenzli, F.; Vechev, M. Securify: Practical Security Analysis of Smart Contracts. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 67–82. [Google Scholar]
- Nikolić, I.; Kolluri, A.; Sergey, I.; Saxena, P.; Hobor, A. Finding the Greedy, Prodigal, and Suicidal Contracts at Scale. In Proceedings of the 34th Annual Computer Security Applications Conference, San Juan, PR, USA, 3–7 December 2018; pp. 653–663. [Google Scholar]
- Xing, C.; Chen, Z.; Chen, L.; Guo, X.; Zheng, Z.; Li, J. A New Scheme of Vulnerability Analysis in Smart Contract with Machine Learning. Wirel. Netw. 2020, 1–10. [Google Scholar] [CrossRef]
- Hwang, S.J.; Choi, S.H.; Shin, J.; Choi, Y.H. CodeNet: Code-targeted Convolutional Neural Network Architecture for Smart Contract Vulnerability Detection. IEEE Access 2022, 10, 32595–32607. [Google Scholar] [CrossRef]
- Liu, Z.; Qian, P.; Wang, X.; Zhuang, Y.; Qiu, L.; Wang, X. Combining Graph Neural Networks with Expert Knowledge for Smart Contract Vulnerability Detection. IEEE Trans. Knowl. Data Eng. 2021, 35, 1296–1310. [Google Scholar] [CrossRef]
- Wang, W.; Song, J.; Xu, G.; Li, Y.; Wang, H.; Su, C. Contractward: Automated Vulnerability Detection Models for Ethereum Smart Contracts. IEEE Trans. Netw. Sci. Eng. 2020, 8, 1133–1144. [Google Scholar] [CrossRef]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Ren, M.; Ma, F.; Yin, Z.; Fu, Y.; Li, H.; Chang, W.; Jiang, Y. Making Smart Contract Development More Secure and Easier. In Proceedings of the 29th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Athens, Greece, 23–28 August 2021; pp. 1360–1370. [Google Scholar]
- Bhardwaj, A.; Shah, S.B.H.; Shankar, A.; Alazab, M.; Kumar, M.; Gadekallu, T.R. Penetration Testing Framework for Smart Contract Blockchain. Peer Peer Netw. Appl. 2021, 14, 2635–2650. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Lin, S.W.; Ma, L.; Liu, Y. Vultron: Catching Vulnerable Smart Contracts Once and for All. In Proceedings of the IEEE/ACM 41st International Conference on Software Engineering: New Ideas and Emerging Results (ICSE-NIER), Montreal, QC, Canada, 25–31 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Atzei, N.; Bartoletti, M.; Cimoli, T. A Survey of Attacks on Ethereum Smart Contracts (SOK). In Proceedings of the Principles of Security and Trust: 6th International Conference, POST 2017, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2017, Uppsala, Sweden, 22–29 April 2017; Proceedings 6. Springer: Berlin/Heidelberg, Germany, 2017; pp. 164–186. [Google Scholar]
- Krichen, M.; Lahami, M.; Al-Haija, Q.A. Formal Methods for the Verification of Smart Contracts: A Review. In Proceedings of the 15th International Conference on Security of Information and Networks (SIN), Sousse, Tunisia, 11–13 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Abdellatif, T.; Brousmiche, K.L. Formal Verification of Smart Contracts based on Users and Blockchain Behaviors Models. In Proceedings of the 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Paris, France, 26–28 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Zhidanov, K.; Bezzateev, S.; Afanasyeva, A.; Sayfullin, M.; Vanurin, S.; Bardinova, Y.; Ometov, A. Blockchain Technology for Smartphones and Constrained IoT Devices: A Future Perspective and Implementation. In Proceedings of the IEEE 21st Conference on Business Informatics (CBI), Moscow, Russia, 15–17 July 2019; IEEE: Piscataway, NJ, USA, 2019. Volume 2. pp. 20–27. [Google Scholar]





| Model | NCA | SCA | PCA | GCA | SPCA | FNP |
|---|---|---|---|---|---|---|
| Random forest | 0.9910 | 0.9946 | 0.9709 | 0.9564 | 0.9863 | 0.0090 |
| Logistic regression | 0.8873 | 0.9029 | 0.8789 | 0.7317 | 0.8190 | 0.0236 |
| Decision tree | 0.9612 | 0.9779 | 0.9511 | 0.9296 | 0.9669 | 0.0099 |
| MLP | 0.9850 | 0.9956 | 0.9943 | 0.9666 | 0.9937 | 0.0082 |
| k-NN | 0.9958 | 0.9951 | 0.9772 | 0.9732 | 0.9911 | 0.0106 |
| SVM | 0.9614 | 0.9998 | 0.9973 | 0.9858 | 0.9998 | 0.0021 |
| Method | Accuracy | F1 | Precision | Recall | Time, ms |
|---|---|---|---|---|---|
| One-phase scenario | |||||
| 5 classes | |||||
| Random forest | 0.9796 | 0.9795 | 0.9797 | 0.9796 | 0.000863 |
| Logistic regression | 0.8433 | 0.8433 | 0.8439 | 0.8433 | 0.000327 |
| Decision tree | 0.9573 | 0.9572 | 0.9572 | 0.9573 | 0.000373 |
| MLP | 0.9870 | 0.9870 | 0.9870 | 0.9870 | 0.00126 |
| k-NN | 0.9862 | 0.9862 | 0.9864 | 0.9862 | 2.707967 |
| SVM | 0.9888 | 0.9888 | 0.9889 | 0.9888 | 0.312428 |
| Two-phase scenario | |||||
| 2 classes | |||||
| Random forest | 0.9732 | 0.9735 | 0.9569 | 0.9906 | 0.000939 |
| Logistic regression | 0.9189 | 0.9189 | 0.9143 | 0.9235 | 0.0007 |
| Decision tree | 0.9670 | 0.9668 | 0.9667 | 0.9669 | 0.00082 |
| MLP | 0.9713 | 0.9713 | 0.9665 | 0.9761 | 0.000931 |
| k-NN | 0.9732 | 0.9736 | 0.9528 | 0.9953 | 0.18213 |
| SVM | 0.9724 | 0.9726 | 0.9589 | 0.9866 | 0.151349 |
| 4 classes | |||||
| Random forest | 0.9698 | 0.9697 | 0.9698 | 0.9698 | 0.001005 |
| Logistic regression | 0.8374 | 0.8370 | 0.8368 | 0.8374 | 0.000503 |
| Decision tree | 0.9500 | 0.9499 | 0.9499 | 0.9500 | 0.000431 |
| MLP | 0.9838 | 0.9837 | 0.9839 | 0.9838 | 0.001292 |
| k-NN | 0.9767 | 0.9764 | 0.9774 | 0.9767 | 0.133743 |
| SVM | 0.9899 | 0.9899 | 0.9900 | 0.9899 | 0.17381 |
| Potential example solution | |||||
| k-NN+SVM | 0.9921 | 0.9902 | 0.9883 | 0.9921 | 0.329363 |
| Model | SCA | PCA | GCA | SPCA |
|---|---|---|---|---|
| Random forest | 0.9805 | 0.9581 | 0.9691 | 0.9715 |
| Logistic regression | 0.8961 | 0.8771 | 0.7613 | 0.8132 |
| Decision tree | 0.9675 | 0.9436 | 0.9358 | 0.9527 |
| MLP | 0.9931 | 0.9688 | 0.9899 | 0.9836 |
| k-NN | 0.9803 | 0.9587 | 0.9981 | 0.9721 |
| SVM | 0.9937 | 0.9777 | 0.9930 | 0.9954 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mezina, A.; Ometov, A. Detecting Smart Contract Vulnerabilities with Combined Binary and Multiclass Classification. Cryptography 2023, 7, 34. https://doi.org/10.3390/cryptography7030034
Mezina A, Ometov A. Detecting Smart Contract Vulnerabilities with Combined Binary and Multiclass Classification. Cryptography. 2023; 7(3):34. https://doi.org/10.3390/cryptography7030034
Chicago/Turabian StyleMezina, Anzhelika, and Aleksandr Ometov. 2023. "Detecting Smart Contract Vulnerabilities with Combined Binary and Multiclass Classification" Cryptography 7, no. 3: 34. https://doi.org/10.3390/cryptography7030034
APA StyleMezina, A., & Ometov, A. (2023). Detecting Smart Contract Vulnerabilities with Combined Binary and Multiclass Classification. Cryptography, 7(3), 34. https://doi.org/10.3390/cryptography7030034







