1. Introduction
Cryptography refers to a communication technique of altering a message using mathematical concepts in a way that only allows the receiver to have access to its original content. Modern day cryptography aims to encrypt digital information. The idea behind encrypting schemes is related to a field of mathematics called “number theory” and more specifically “large number factoring” [
1]. This is because it has been proven that computers cannot find the prime factors of a number efficiently, making these schemes secure and thus suitable for commercial use nowadays.
Over the last few decades, researchers have been trying to build quantum computers with limited success. Their work has motivated other scientists to investigate the capabilities of such computers. This has led Peter Shor, an American mathematician, to prove that number factorization becomes trivial for quantum computers using an algorithm that takes advantage of certain quantum phenomena, inevitably breaking current encryption mechanisms [
2]. It is therefore necessary to develop an encryption technique that is unbreakable both for classical and quantum computers, and to migrate to it before the completion of the development of the first quantum computer. Otherwise, having access to a quantum computer would immediately imply having access to any encrypted information that exists online such as bank transfers, emails, passwords, and messages. The National Institute of Standards and Technology (NIST) has held a competition which aimed to identify and standardize the best quantum-safe encryption scheme [
3]. Many ideas were put on the table, but the winner of the competition was Kyber [
4], which will be shortly standardized. This means that every online data transmission will be encrypted using Kyber. The following paper will be focused on how to increase Kyber’s security using error correction.
Error correction refers to the ability to detect and correct errors that emerge when a message is transmitted through a noisy channel. There has been extensive research on this field, and researchers have developed many error correcting codes (ECC). The efficiency of such codes is measured with the Shannon capacity [
5]. Polar Codes are a type of ECC, were introduced by Arıkan in [
6], and have been proven to be as efficient as possible by reaching the theoretical maximum that was set by Shannon. This makes it very attractive for commercial use, and that is why these codes are used in new technologies such as the 5G. Moreover, Polar Codes can be implemented in quasilinear time complexity
O(
Nlog
N), giving them a comparative advantage over other ECCs such as low-density parity check (LDPC) or Bose–Chaudhuri–Hocquenghem (BCH) codes. Having such an outstanding performance, Polar Codes made the best candidate for this paper.
The idea is to alter the parameters of Kyber in order to achieve a more secure scheme. This increase in security comes at the cost of an increase in the decryption failure rate (DFR). Although this is straightforward, one must also take into consideration that the DFR has to be below the bound set by the NIST (2
) in order to be safe against decryption failure attacks [
7]. That is why Polar Codes are introduced, in order to decrease the DFR and to take advantage of this excess DFR in order to be used to increase the security.
A similar approach has been taken for Ring LWE schemes in [
8] where Polar Codes where used to increase the security of NewHope [
9]. In that paper, the security of the specified scheme was increased by 9.4%. Moreover, in [
10], BCH and LDPC codes as well as a combination of the two have been applied to NewHope, enhancing the security by 31.76%. It is mentioned that these types of ECC can be applied to Kyber as well. Although, at first glance, the latter method achieves better performance, it should be mentioned that the results are based on an “independence assumption”, which is not proven in the paper. Finally, it should be mentioned that no previous research has focused on applying ECC to Kyber, and given that it is a matter of time until this scheme becomes the global standard for Public Key Encryption, it is sensible to explore how to make it more secure.
2. Preliminary
2.1. Kyber
As mentioned before, modern cryptography is based on arithmetic operations, which cannot guarantee security in the post quantum era. Scientists have turned their attention to Lattices and more specifically Lattice cryptography. Lattice cryptography is a field in mathematics that uses sets of points in the
n-dimensional space in order to create difficult problems that can be used to encrypt information. One such problem that is widely used in post quantum cryptography is the learning with errors (LWE) problem introduced in [
11]. It has been proven that the average case of an LWE problem is as difficult as its worst case, and its difficulty is based on several lattice problems such as the shortest vector problem (SVP) which has been proven to be hard. Moreover, the advantage that sets LWE apart from the rest when it comes to cryptosystems is that there are some variations such as the Ring-LWE (RLWE) and the Module-LWE (MLWE) that make LWE time- and space-efficient for real life applications while keeping the problems of the variations relatively difficult. Kyber is based on MLWE. Before explaining how Kyber works, it is useful to introduce the following notions:
is the polynomial ring ;
is the binomial distribution: , centered around 0;
Decompress;
Compress;
“←” will be interpreted as “sampled from”.
Kyber’s three steps (key generation, encryption, and decryption) for secure data transmission are as follows:
A, s,e,
Public Key: t = , Secret Key: ;
r,
u = r + e, v = tr+e + Decompress
Transmit Compress(u, d), Compress(v,d);
m = Compress(Decompress(v, d) −sDecompress(u, 1),d).
All of these parameters determine Kyber’s security. The parameters suggested by the development team are shown in
Table 1:
2.2. Polar Codes
Now, let us introduce error correcting codes. In communications, channels are used to send data which might be corrupted during transmission due to the noisy nature of the channel. In order to prevent this from happening, one could encode the data that are sent in a clever way, such that in the case where a bit is inverted while transmitting, it would be obvious to the receiver and could thus be corrected. This error controlling mechanism is called error correction. To perform error correction, we use error correcting codes (ECC). There are several types of ECC, but the main idea behind all of them is that before transmitting the data, one encodes it using redundant information, which will then help the receiver detect and correct inverted (flawed) bits without needing to retransmit the whole message. Error correction is, thus, essential for efficient communication. The maximum performance limit of such codes was set by Shannon and can be achieved by a few ECCs. In this paper, we focus on one of them, namely Polar Codes, but similarly to our research, other ECCs are expected to achieve analogous results. The extent to which other ECCs can perform alongside Kyber is a field that could be further explored in the future.
A Polar Code is an error correction code that uses a linear block of length . It was introduced by Arikan and has been proven to achieve Shannon capacity for binary discrete memoryless symmetric (BDMS) channels. To measure the performance of Polar Codes, one can use mutual information and the Bhattacharyya parameter of BDMS channels. These two are defined as follows:
Definition 1. Mutual information () is a measure of the rate at which information can be transmitted. and is given by the following equation:A larger indicates a better transmission rate. Definition 2. The Bhattacharyya parameter () is a measure of reliability of the channel. and is given by the following equation:A smaller indicates a more reliable channel and is preferred. The idea behind Polar Codes is to split a noisy channel into sub-channels and to polarize them, resulting in some channels having and some others having . Then, use the more reliable channels () in order to transmit a message without much interference. Then, decide how to decode the received bit (after the effect of noise), based on some likelihoods that will indicate the bit that was sent. The better the channel, the more obvious it would be to decode the received bits by observing the likelihoods.
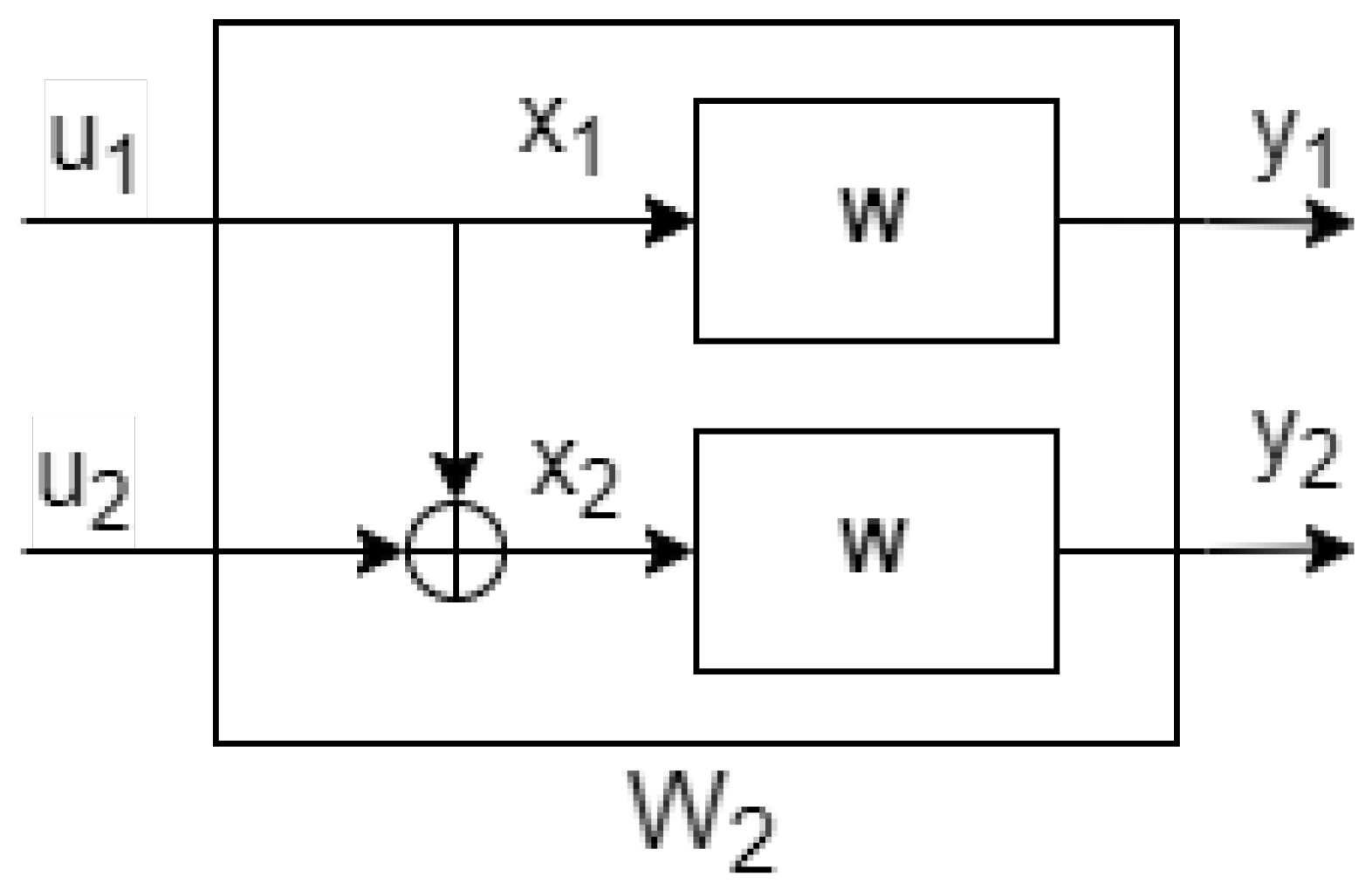
For the base case, where n = 1, there are N = 2 channels, as shown below.
Suppose that there are two independent inputs and , which are random variables of a discrete distribution:
The output
shown in
Figure 1 of the channel
is given by the following:
which, using matrices, can be written as follows:
For a larger n = 2 (N = 4), one should expect the following matrix:
To achieve larger
N, smaller channels are used recursively, resulting in the following formula.
where ⊗ represents the Kronecker product defined as follows:
where
n =
logN,
N = number of channels.
As shown by Arıkan in [
6], as
N , the
N channels are split into two categories:
Channels where ;
Channels where
This proves that, for a larger
N, a fraction of the channels are reliable (
) and the rest are unreliable (
). In the two cases introduced, for
W,
u would be the reliable one and
u is the unreliable one. For
W,
u and
u are the most reliable, whereas
u and
u are the least reliable. The list of channels sorted from most reliable to least reliable is called reliability sequence and has been found for every N experimentally through simulations [
12], and it is thus beyond the scope of the paper to investigate any further.
2.3. Security against Side Channel Attacks
In this section, we prove why wrapping Kyber with Polar Codes is safe against side channel attacks (SCAs). As explained in [
13,
14], Polar Coding does not leak any sensitive information to the attacker. To prove this, we must look at encoding and decoding separately.
For encoding, it is sufficient to say that the number of logic XOR gates used to perform encoding is constant, independent of input, and is equal to , where n = block length.
Decoding needs a three part proof. Firstly, calculating the transition probabilities W does not leak sensitive information as exactly floating point operations take place. Secondly, the time needed for the comparison between the likelihoods is only dependent on how close the two floating numbers that we are comparing are, but that does not give information about the output of the comparison. Finally, the amount of XOR operations used to decode is identical to this to perform encoding, and as explained before, it is independent of the plaintext input.
4. Results
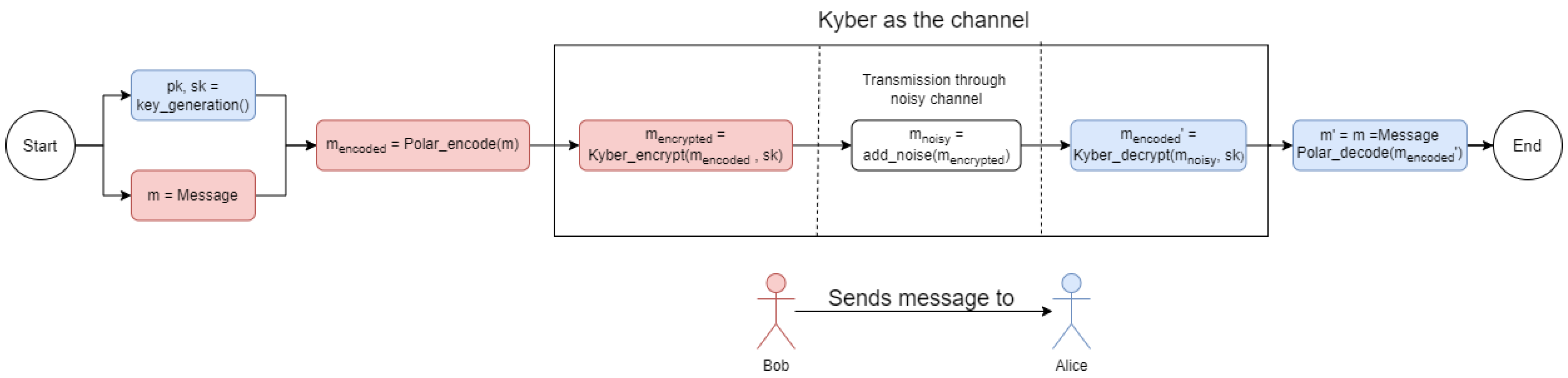
In order to analyse the results, we must first understand how the changes in Kyber parameters affect them. First, security comes solely from the Kyber parameters as Polar Codes do not affect it at all but are used to ensure that the DFR is below the boundary. Moreover, increasing the security by changing some Kyber parameters comes at the cost of an increased DFR, thus reaching values that surpass the upper bound set by the NIST (2
). By applying Polar Codes to Kyber, we can calculate the block error rate (BLER), which in this case, is the same as the DFR of the scheme. To achieve this, we treat Kyber as the channel, and thus, Kyber’s parameters correspond to a certain SNR value, which is used to calculate the upper bound of the DFR by finding the sum of the Bhattacharya parameters, as suggested in [
6]. To alter the security, we first use the security parameter
k, as suggested by the CRYSTALS development team in [
15]. The security estimates for different values of
k when
are presented in
Table 3.
In
Table 3, DFR refers to the decryption failure rate that the Kyber has without including Polar Codes, whereas BLER refers to the probability that a message is incorrectly received after decoding. This is the same as the DFR of the new scheme (Kyber with Polar Codes). The BLER estimates were obtained by the FERestimate variable in
https://github.com/mcba1n/polar-codes/tree/master/polarcodes (accessed on 30 June 2022), which is the sum of the Bhattacharya parameters . The security estimates were obtained by the script provided by the CRYSTALS team, which is available at
https://github.com/pq-crystals/security-estimates/blob/master/Kyber.py (accessed on 5 November 2022). In this script, there are some functions that find the best possible quantum attack for the given MLWE parameter set, both for primal and dual attacks, and return the security in bits. The same script was used by the CRYSTALS team to calculate Kyber’s security in [
4].
The values obtained for BLER are extremely small, but we need to keep in mind that, by viewing Kyber as the channel, we end up with a very large SNR, and given that the code rate is 0.5, meaning that we only use the best 50% of the subchannels created, we can expect that the probability of too many bits being inverted through the addition of Kyber’s error terms (e, e, etc.), making Polar decoding unable to detect them, is extremely small. Note also that these are estimates, not exact values, and testing is only indicative of the scheme working, as finding a case where a message would fail to decode is practically impossible.
As we can see, increasing k leads to better security but, at the same time, the time per transmission is also increased. Although the software is not optimized and the time to complete every transmission is largely depending on the hardware used, the percentage increase in time is indicative of the number of polynomial multiplications increasing linearly as k increases. Moreover, a security above 300 quantum bits is considered overkill, thus suggesting that a value of k above 6 is not sensible, but is just given as an indication for possible future needs and will not be explored any further.
Even though the results obtained are satisfactory, we can achieve better by introducing a new method of increasing the security, that is, to change the binomial parameter . This method’s most important benefit is that security can be strengthen without the need for more calculations. In the specification, it is not recommended that be used to enhance the security because there is a strong relationship between that and the DFR. This is because the variance of the noise term increases and, thus, decryption becomes more likely to fail. In our case, where Kyber is the channel, this increase in is reflected by a decrease in SNR, but the increase in BLER does not exceed the bounds. It is thus possible to use it in combination with a higher k to achieve better results.
From
Table 4, one can observe that, by increasing
, the classical bit security for primal attacks for the case where
k = 4 can be increased from 256 to 281 bits (10% increase) while keeping the transmission time constant. Although theoretically, this idea can be extrapolated until the DFR hits the boundaries set by the NIST, it is safer to leave a generous gap between the predicted value and that boundary. It is also not sensible to try to further increase the security as even the base case, which is 164 qubits secure, is considered safe for the time being.
In summary, in this section, we have shown that the introduction of Polar Codes around Kyber gives us the flexibility to use higher security parameters (k). The problem with that is that increasing k comes at the expense of more mathematical operations. To avoid this extra complexity, changing another parameter which was not mentioned by Kyber’s development team, namely , can lead to a security increase without an increase in time. We suggest a combination of these two methods and, thus, propose the following new parameters:
The parameters presented in
Table 5 can obtain a classical bit security of 281, which compared to the initial security, which was 182, is a 54.4% increase in security.
5. Discussion
Now that the results have been presented, it is time to talk about their influence to the future of post-quantum cryptography. Although quantum computers that are reliable and capable of breaking modern day encryption schemes are still under development, it is never too early to develop tools that give us flexibility in terms of increasing security. This paper has thoroughly presented one such tool and opens the way for further investigation on the effect of other error correcting codes such as low-density parity checks (LDPC) and BCH codes. It is also straightforward to apply this technique to other MLWE cryptosystems by leaving out the error terms in the noise that arise from compressing and decompressing values.
Moreover, this research motivates researchers to develop hardware-efficient implementation of Kyber with Polar Codes that could be beneficial for real-time communication. Similar to [
16,
17], where FPGAs were used to improve Kyber key generation, encryption and decryption time, one can implement an FPGA solution that performs Polar encoding and decoding steps as well, in order to get the best of both worlds.
It should also be noted that, if one wants to decrease the key size of Kyber, our findings can be used to keep the security at a safe level by altering the parameters appropriately.
Since this field is relatively new, there has not been any previous research that focuses on Kyber. A similar approach to post-quantum encryption was taken in [
8] where Polar Codes were applied to RLWE schemes with NewHope [
9] in mind. The results on that research are compliant with those found here.
Before concluding this paper, it is essential to discuss the limitations of the proposed solution. As shown by the results, increasing the value of the security parameter k as a negative effect in time per transmission, which is not desirable for real life communications. Moreover, this increase in transmission time will be further increased by the Polar encoding and decoding steps that have been added. In order though to draw more accurate solutions, software/hardware-optimised versions of the suggested solution must be implemented to be compared with plain Kyber.