1. Introduction
Sidechains (SCs) were first proposed in [
1] and quickly became a universal and very comfortable tool in blockchain technology, while [
1] proposed sidechains with a “classical” proof-of-work (PoW) protocol for usage in Bitcoin blockchain, the next article [
2] builds secure proof-of-stake (PoS) sidechains, and articles [
3,
4] create a special type of sidechain consensus, the Latus protocol, which is secure for both PoW and PoS sidechains. They may be considered as an additional construction bound to blockchain (called mainchain (MC)) with the aim to provide some additional functionalities. SCs should be bound to an MC, as described in mentioned articles, to provide stronger security guarantees using blockchain properties, such as liveness and persistence [
5]. Binding means that SCs also should send some information to the MC to guarantee the fairness of transformations in the SC [
3].
In Latus, this information contains a series of recursive zk-SNARK-proofs [
6,
7] to establish decentralized and verifiable cross-chain transfers. Such an approach is similar to the ones proposed in [
8] (
Mina) and [
9] (
zkSync Era), but with additional features that allow its secure usage in sidechains. Latus introduces a special dispatching scheme that assigns the generation of proofs randomly to interested parties, who then implement these tasks in parallel and submit generated proofs to the blockchain. An incentive scheme provides a reward for each accepted proof.
There are a variety of purposes to use SCs in different blockchains: for making smart-grid systems scalable and adaptable [
10]; for secure data isolation in scalable consortium blockchain architecture based on world-state collaborative storage methods [
11]; for secure parallel computation [
12]; and for creating an exchange platform that allows the ability to trade tokens issued from different sidechains [
13].
SCs may be based on various consensus protocols (such as PoW [
14], PoS [
15], etc.).
In this paper, we assume that SC uses the Latus protocol [
4], which is a hybrid PoS based on Ouroboros Praos [
16]. However, as SCs may be based on various consensuses, our main results may be applied for other consensus protocols (such as proof of work, proof of stake, etc.) with similar properties, allowing distributed proof generation and recursive SNARKs.
Following the modern trends in blockchain investigations, we use SNARKs to prove the correct functioning of SCs (detailed survey about different types of SNARKs used in blockchain can be found in [
17]). These cause some modifications of the Merkle tree, which we call the “proof tree”.
Distributed proof generation for block creation is the basic feature of Latus consensus. In brief, the procedure of block creation is as follows. A block forger—an entity that creates the block—shares a list of transactions to be included into the block. Then, other entities, called provers, construct SNARK-proofs for these transactions and also for each node of the corresponding proof trees built on these transactions.
Each prover, who creates a SNARK-proof, sets the prices for their proofs, according to the pricing policy of the current epoch. In the case of collisions, when there are several proofs for some node of the binary tree, the block forger chooses the cheapest one. Proofs that were included into the block are paid by the block forger from the corresponding transaction fees.
Our previous papers [
18,
19,
20] considered only issues related to a single block creation. We used probabilistic and game-theoretic approaches to answer the questions on the optimal choice of SC parameters (e.g., a recommended number of transactions per block and a recommended value of incentives chosen). The model in which we obtain our results is very close to realistic with only one simplifying assumption: splitting of the block construction process into a fixed number of similar steps. Such assumption can be justified by the fact that the network synchronization time is essentially smaller than the proof generation time.
In this paper, unlike the previous ones, we consider algorithms related to simultaneous construction of trees by different block forgers. The sequence of such trees forms a linearly ordered forest. When the following block is published, the most left tree is included into it, and the remaining ones are regarded as a buffer for further block generation. The base assumptions used in this paper is almost the same as in the our previous papers, with the following modification: In practice, blockchain’s sequences of transitions are proved using base SNARK for certifying single state transitions (in leaves) and merge SNARK for merging two proofs (in other vertices) ([
21], Section 4.1.1). We consider the scheme that replaces each base proof for a transaction by merged proofs for pair of leaves from the new additional level. So, we obtain a mathematically equivalent model where trees are one level higher and a pair of fresh leaves correspond to each transaction; therefore, we obtain more succinct algorithms.
The paper is organized as follows. The necessary basic preliminary results on binary trees are presented in
Section 2. For us it is convenient to consider the sets of strict binary trees and of non-strict binary trees as specific realizations of the free magma
with a single generator. In
Section 2.2, we introduce agreed monoid structures on infinite sequences of strict binary trees and positive numbers. The background of these constructions is explained in
Appendix A. In
Section 2.3, we introduce the concept of perfect forest necessary for description of the main algorithm.
Section 3 presents the general scheme for
algorithms corresponding to the prover’s behavior: deterministic (mutually consistent) or stochastic (independent), and shapes of generated trees: strict binary or perfect binary. It works with a potentially infinite sequence of trees
t called a buffer. In the external for-loop, the first element is removed from the buffer and published as the following block. Block generation is divided into a fixed number of steps, each of which calls the OneStep() procedure. In all
cases each of suitable subsequent pairs of trees is merged into a single tree. Selection of such suitable pairs, deterministic or stochastic, is the unique difference among
cases (see Table 1). Its result can be encoded as a sequence
of trees with the height
. After this, the result of OneStep() procedure can be described as a function
, acting on the buffer
t via the product defined in
Section 2.2. Iteration of
f over all steps and then a removal of the first tree from the buffer determines a function
describing transformation of the buffer during block generation. In
Section 3.1, we consider a reduction of the above scheme, where only the number of leaves of each tree is taken into account. This is sufficient to study the throughput parameters of the blockchain(s). This reduction is possible due to the homomorphism of monoids described in
Section 2.2.
In
Section 4, we consider the case when behavior is deterministic. We prove that a sequence
of buffer states takes a finite number of values and, hence, this sequence and the sequence of published trees are ultimately periodic. In
Section 4.1, deterministic generation of strict binary trees is considered. The sequences of buffer states and published blocks are ultimately periodic with a period of length 1. This follows from the fact that transformation of the buffer after each block publishing is a weak contraction with respect to the Hamming distance. Under some natural assumption the height of the tree published over the period is the sum of (the integer part of) the binary logarithm of the number of provers and of the number of steps. An explicit formula for the fixed point is obtained in terms of the product on infinite sequences of binary trees. In
Section 4.2, deterministic generation of perfect binary trees is considered. It is observed that the period of the sequence of published trees consists of perfect trees of two heights
and
. The total efficiency is independent of shapes of generated trees and can be expressed by an explicit formula and admits natural asymptotics. Explicit results are obtained in the cases of a singe prover of a single step.
In
Section 5, we consider the case when behavior is stochastic. In
Section 5.1, it is shown that the placement of provers into suitable positions at each stage can be described by the classical occupancy distribution. In the deterministic case, the total number of generated proofs is the product of numbers of published blocks, of steps in a block and of provers. In the stochastic case, we define the total efficiency (respectively the block publishing efficiency) as the total number of generated proofs (respectively the number of proofs embodied in published blocks) divided by the above product. Thus, both efficiencies are numbers in the interval
. They are convenient to compare the cases of various shapes and various values of integer parameters. The total efficiency is independent of shapes of generated trees and is expressed by an explicit formula and admits natural asymptotics. In
Section 5.2, average values of the block publishing efficiency are calculated using a simulation model. We compare two cases when the shape of trees is binary strict or perfect. The maxima of these values as functions of numbers of positions are investigated. In
Section 5.3 for generation of strict binary trees in a stochastic case we investigate an analog of the deterministic Formula (
22) for heights of trees. Using the least squares method, we find the best approximation of the expected height of generated trees linear on the number of steps and logarithmic on the number of provers.
In
Appendix A, we recall the concept of a non-symmetric operad and construction of the corresponding PRO. As the following step, one can obtain a monoid structure of infinite sequences of operations. The non-symmetric magma operad and the non-symmetric semi-group operad as its factor come from corresponding free objects with a single generator. The corresponding monoids of infinite sequences of strict binary trees and its factor-monoid given by taking the number of leaves of each tree are considered in
Section 2.2.
In
Appendix B, we describe the software implementation of our algorithms and explain how they are used in the main text.
2. Preliminaries: Binary Trees and Forests
2.1. Binary Trees and Free Magmas
Trees, as a part of Graph Theory, are used in mathematics ([
22], Chapter 5) and computer science, (see the classical volume [
23]). In this subsection, we give some necessary definitions related to various types of binary rooted trees and forests, as there is no precise description convenient for our purposes and there might exist a confusion in terminology.
Rooted trees can be defined either (1) recursively, or as (2) partially ordered sets, or as (3) special types of graphs. All of these points of view are useful in their respective contexts.
A tree is defined as a connected acyclic undirected graph. Choosing a vertex in a tree as a root determines the natural direction for all edges (towards the root). However, usually it is not shown explicitly.
A rooted tree is a directed graph with a distinguished vertex called the root such that there exists a unique path from each vertex to the root. Thus, the set of vertices is equipped with a natural partial order: if there exists a path from v to w. In addition, the rooted tree itself becomes the Hasse diagram for this partial order (being drawn root up). If is an edge in a directed rooted tree, we say that v is a child of w, and w is a parent of v. A vertex that has no child is called a leaf. Let us denote as the height of the tree t, i.e., the maximal length of the path from a leaf to the root. Thus, leaves are minimal elements, and the root is the greatest element in the corresponding partially ordered set.
Each tree can be embedded in the plane. For a rooted tree all such embeddings are classified by linear orderings for the children of each vertex. Thus, if all such orderings are fixed, we say they are an ordered rooted tree (or a plane rooted tree).
Here, we mainly consider strict binary plane rooted trees (Instead of the term “strict binary tree”, the terms “complete binary trees” and “full binary trees” are also used.), where “strict binary” means that every vertex is either a leaf or has exactly two children (left and right). In this case, for each non-leaf vertex, its left child vertex and its right child vertex are roots of maximal binary subtrees called, respectively, a left child tree and a right child tree.
Notation 1. Let us denote as the number of vertices, as the number of internal vertices and as the number of leaves in a rooted tree t.
In a strict binary tree
t these numbers satisfy the identities
A
magma is a set equipped with a binary operation ★ without any additional properties Chapter 1 [
23], ([
24], 0.2). The free magma
with a single generator ∗ (up to isomorphism) is described recursively as
of recursively described subsets:
Thus, an element of
is a bracketing of a string of
symbols ∗, i.e., the insertion of
n left parentheses and
n right parentheses defining the order of an
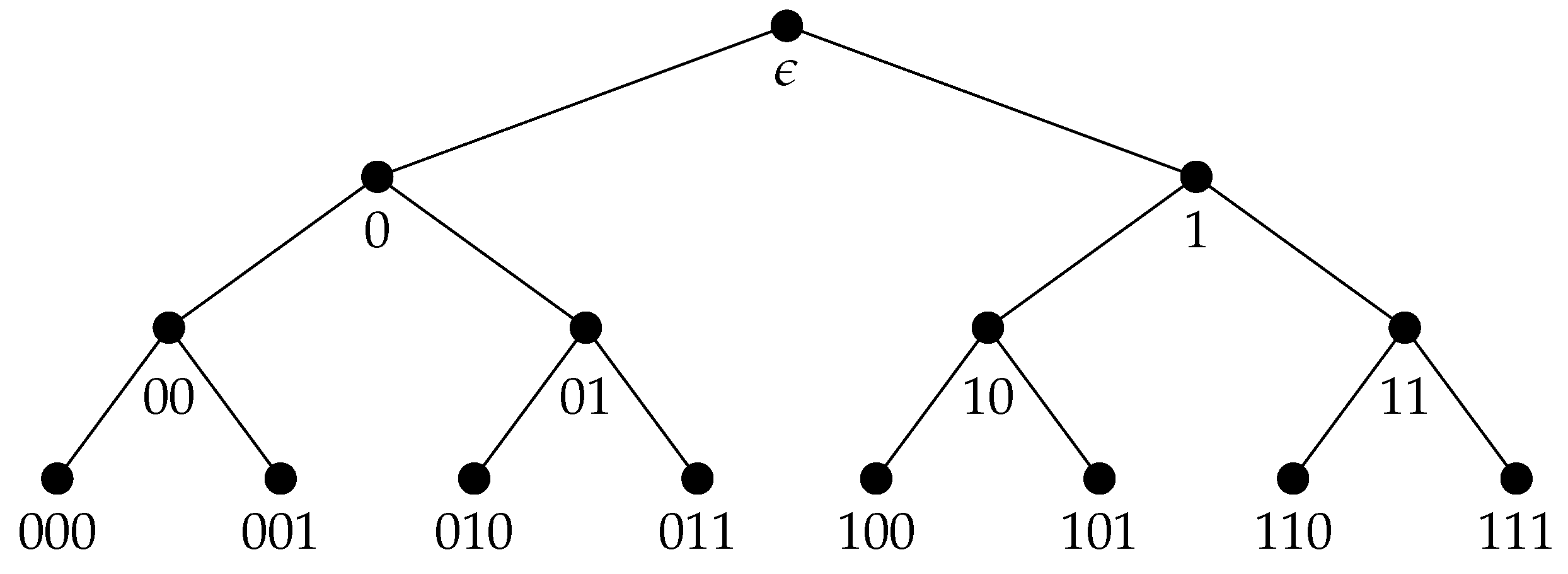
n-fold application of the binary operation, e.g., five elements of
are presented in
Figure 1a (with the outer brackets removed). Cardinality of
is counted by Catalan number
. Various kinds of objects that are counted using Catalan numbers are called Catalan families. The Stanley’s book [
25] presents 214 Catalan families including various types of trees.
Strict binary trees are mentioned in Exercise 2.5 [
25]. The generator of the free magma of strict binary trees is the zero height tree • whose single vertex is the root. For two binary trees
, the binary tree
is a binary tree with a new root, whose left child tree is
and the right child tree is
. Strict binary trees with four leaves corresponding to elements of
are presented in
Figure 1c.
Non-strict binary trees (often in computer science literature just “binary trees”) obtain yet another example of Catalan family Exercise 2.4 [
25]. Thus, they can be defined recursively in the same way as strict binary trees, with the only difference that their free magma generator is the empty tree. A non-empty non-strict binary tree can be represented by a plane rooted tree, where each vertex has 0, 1 or 2 children, but with additional structure, every single child must be labeled “left” or “right”. Such trees with three vertices corresponding to elements of
are presented in
Figure 1b. Note that a non-strict binary tree is obtained from the corresponding strict binary by removing all its leaves.
2.2. Monoid of Sequences of Strict Binary Trees
Here, we consider composition of infinite sequences of strict binary trees given by the gluing of subsequent leaves in t with subsequent roots in , and composition of infinite sequences of positive integers corresponding to the numbers of leaves in a tree.
First, for a strict binary tree t with n leaves and strict binary trees , we define the composition obtained by gluing together the i-th leaf in t with the root of for .
This obtains the a non-symmetric operad structure on strict binary trees. Then one can apply the construction from
Appendix A to obtain the monoidal structures described below. The details of the
Appendix A are not necessary to understand the remainder of the material.
Let
be a set of sequences
of strict binary trees with only a finite number of non-zero height trees, equipped with a binary operation
, where
i.e., each
is successively applied in the sense of (
A1) to the first not yet used
elements of
.
Let
be a set of sequences
of positive integers with only a finite number of elements
, equipped with a binary operation
, where
i.e., successively each
is the sum of the first not yet used
elements of
.
Corollary 1. The above binary operations turn both and into monoids. The units are and . The map , is a morphism of monoids.
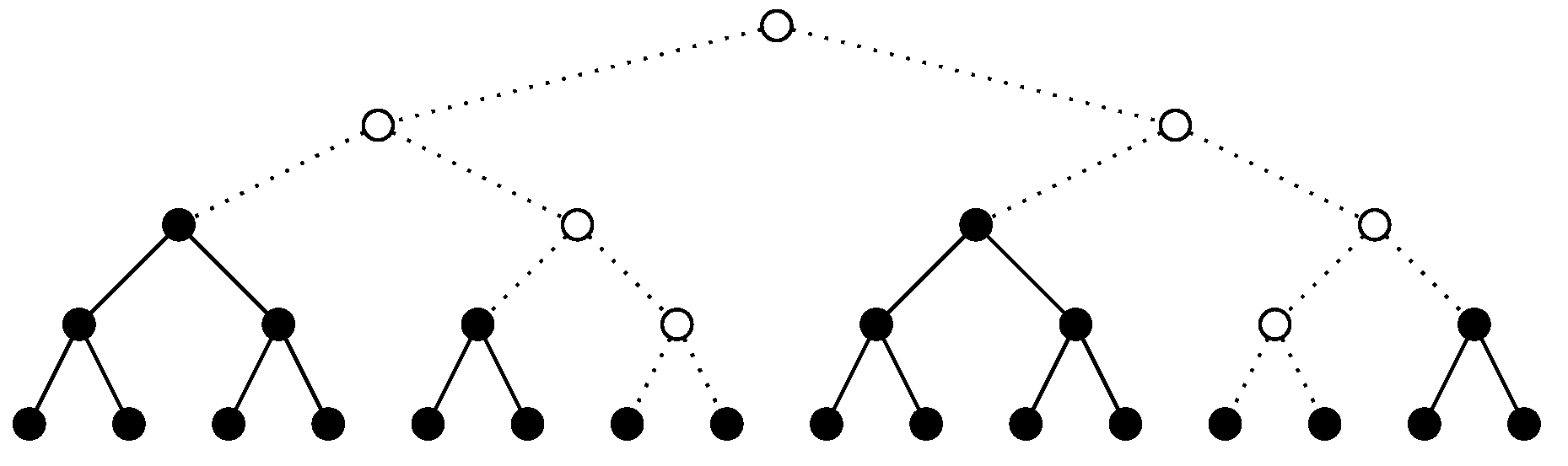
2.3. Perfect Binary Trees and Forests
A rooted tree is called perfect (“complete” by some authors) if all leaves are of the same distance to the root (that equals to the height h of the tree).
Notation 2. For each non-negative integer h, the unique perfect binary tree of height h is denoted as .
The perfect binary tree
has
leaves; moreover,
vertices are on the distance
d from the root (they can be subsequently indexed with
, whose binary string representation has length
d), and
vertices in total. See
Figure 2.
Note that a non-strict binary tree can be obtained from the corresponding strict binary tree by removing all its leaves.
All perfect binary trees are built recursively using magma square:
Perfect binary trees are most convenient to store a maximal number of leaves (that correspond to transactions).
A forest (respectively plane forest) f is a co-product (disconnected disjoint union) of a family of trees (respectively plane trees) . In both cases, the set of components I is unordered.
Let us recall that a subset in a poset P is called a down-set (respectively up-set) if, for each and with (respectively ), we have . Note that a subset is a down-set if its complement is an up-set.
Lemma 1. For a finite sequence of strict binary trees, the following conditions are equivalent:
- 1.
There exists a bracketing, i.e., an element of the free magma , such that, after the corresponding application of magma operations ★, a perfect binary tree is obtained;
- 2.
is a down-set of some perfect binary tree containing all its leaves with components ordered from left to right;
- 3.
(a) Each tree in the family is perfect,
(b) For each i, divides ;
(c) The total sum is an power of 2.
Proof. : For a down-set in the perfect binary tree containing all its leaves, its complement is the non-strict binary tree corresponding to the appropriate bracketing.
: (a) and (c) are obvious; to prove (b), let be a subtree of height in a perfect tree t of height h such that each leaf in is a leaf in t. Then, there exists a subforest in t that consists of perfect trees of height h including .
: Split the leaves of f into equal left and right halves. If there is a tree in our forest whose leaves are in both halves, then, from 3(c), we conclude that the forest consists of this unique tree. Otherwise, we can represent as a co-product of two forests satisfying condition 3, so we suppose and repeat the above choice for and . □
Definition 1. A finite sequence of binary trees satisfying conditions of the above lemma is called a perfect binary forest.
Figure 3 shows an example of a perfect binary forest and the corresponding perfect binary tree
.
In what follows, we use (potentially) infinite sequences of proof trees with only a finite number of non-zero height trees as a buffer of proofs.
Definition 2. An infinite sequences of binary trees with only a finite number of non-zero height trees is called perfect if some its initial fragment , containing all non-zero height trees, is perfect.
Proposition 1. A sequence is perfect if there exists such that is a sequence that consists of a single perfect tree followed by zero-height trees.
Definition 3. A pair of subsequent trees in a perfect sequence is called a perfect, if the new sequence with the pair replaced with the product remains perfect.
Note that the binary operation between two strict binary trees can be written as
, where ∧ is the strict binary tree of the height 1. Thus, to replace
with the product
is the same as to take the composition
in the sense of (
2), where
.
According to Lemma 1 a pair is perfect if and divides .
Equivalently, suppose that the vertices of the whole perfect tree are labeled as in
Figure 2. A pair
of neighboring trees in its down-set is perfect if their roots are labeled by strings ’
’ and ’
’ respectively for some
.
Obviously, two different perfect pairs cannot intersect. Thus, perfect pairs in a perfect sequence form an infinite sequence.
3. The General Scheme
A special feature of Algorithm 1 considered in this paper is a simultaneous construction of several trees forming a linear ordered forest, rather than a single tree. Periodically, the leftmost tree is included into the published block, and the remainder are considered as a buffer for further block generation.
| Algorithm 1: The general scheme of blocks generation |
![Cryptography 07 00014 i001 Cryptography 07 00014 i001]() |
Input parameters are:
Dichotomous regulates behavior of provers, deterministic (mutually consistent) or stochastic (independent);
Dichotomous describes the shape of generated trees, only perfect binary trees or arbitrary strict binary trees;
is the number of blocks published during the epoch;
is the number of steps for one block generation;
is the number of provers;
is the number of positions allocated for proof.
During the work of the algorithm, a potentially infinite sequence of binary trees arises that we call a buffer. It describes the state of the system and is used in the further block generation.
The output is the sequence of binary trees included into published blocks (one tree per block).
The published list is initialized with the empty list . Theoretically, we assume that at the beginning is a potentially infinite sequence of zero height trees. In practice, we initialize t with an empty list and put zero-height trees there as needed.
Remark 1. In a specific implementation, instead of two lists of binary trees, one can work with a single list, and an integer pointer p; trees with indexes are considered as published, and trees with indexes form a buffer. Block publishing in these terms is just an increment of the pointer .
The external for-loop of Algorithm 1 runs over all blocks in the epoch. The body of this loop consists of the internal for-loop that runs over steps in the block and the block publishing directives. The body of the internal loop consists of Procedure OneStep.
| Procedure OneStep(bbehavior, bshape, npr, npos) |
![Cryptography 07 00014 i002 Cryptography 07 00014 i002]() |
This procedure presents the general scheme for different cases corresponding to combinations of two dichotomous parameters and . It acts on the buffer: some subsequent pairs of trees are replaced with their magma product , and these pairs essentially depend on dichotomous parameters and .
In the case “ is deterministic”, the number of such pairs coincides with the number of provers ; then, for the case that “ is strict”, these pairs are first subsequent pairs of the trees in the buffer: ; for the case that is perfect, we use first perfect pairs in the buffer. In the case “ is stochastic”, first subsequent/perfect positions are reserved for the random choice. Each prover independently with equal probability selects one of these positions. For positions selected by at least one prover, the corresponding pair of trees is replaced with its magma product.
For fixed input parameters , , , , , the following functions (deterministic or random) together with their domains and codomains are defined. Let us denote
the set of (i.e., strict/perfect) binary trees;
the set of sequences of binary trees with finitely many non-zero height trees;
be the sequence obtained by the shift, i.e.,
for
.
Here, the function (
4) is determined by Procedure OneStep. It can be described as a product (
2) with the sequence
of trees of height
. The internal for-loop of Algorithm 1 means the
-th iteration of this function. Then, block publishing determines the map (6), and the state of the buffer after each block publishing is changed according to the map (5).
Table 1 shows the whole scheme. This four cases are also implemented in software described in
Appendix B.
The Algorithm in Terms of Numbers of Leaves
Let us recall that a perfect tree is completely determined by its height, but there are
strict binary trees with
leaves. However, the exact shape of trees is not important for the blockchain(’s) throughput parameters’ study. Thus, we can collect information about the number of leaves (and, therefore, (
1) about the number of vertices) and optionally about heights of trees. Thus, instead of the sequence of trees
, one can consider the sequence of integers
, where
is the number of leaves of the corresponding tree. The initial state is described as
. The magma operation ★ on strict trees corresponds to addition of the numbers of leaves:
.
A pair of numbers
in a perfect sequence
is perfect (i.e., corresponds to the perfect pair of trees) if
If, moreover, the sequence
is non-increasing, the condition (
7) takes the equivalent form
Let us denote by
a set of sequences
of positive integers with only a finite number of elements
, in the case that
is perfect. For a version of Algorithm 1 in terms of numbers of leaves, one considers the functions corresponding to (
4)–(6). We keep the same names for the functions. Different (co)domains avoid ambiguity:
where in (
9),
is the sequence of 1 or 2.
Functionality of the transition from trees to their numbers of leaves is expressed by the commutative squares
Here, means .
Let us define the sequences of sequences (of elements of
) as
Elements of the double sequence
are naturally linearly ordered, lexicographically on the pairs
. In this sequence,
The
length of the sequence
is defined as follows:
4. Deterministic Case
In this section, we consider only the case of Algorithm 1 when
is deterministic. We consider sequences
for an arbitrary
n that corresponds to the limiting case
of an infinite outer for-loop. One can also consider the infinite sequence
of the number of leaves of published trees with elements
Lemma 2. In the case, is deterministic, and the function preserves a property of a sequence to be non-increasing.
Proof. In the case
is perfect, take into account (
8). □
Corollary 2. In the case that is deterministic, the sequences from (12) are non-increasing for all and . Let us denote as a set of non-increasing sequences from .
For a non-increasing sequence
(e.g., for all
when
is deterministic), the Formula (
14) can be simplified:
For
, the sum
has only finite non-zero summands and, according to (
1), can be interpreted as the total numbers of internal vertices. Independently on
, for
, we have the identities
Lemma 3. In the case “ is deterministic”, for fixed , the total number of internal vertices (and, hence, the length and all elements) of all are bounded together, i.e.,: Proof. In the case “ is strict”, and . This follows from the observation that implies .
In the case that “ is perfect”, the number of the same non-zero height trees in the buffer is bounded by . See (27) for more accurate estimates.
Then, we can estimate from above the total number of internal vertices:
In the second case, we use the fact that all
are powers of 2. For
and
, the function
is monotone increasing and, hence, invertible. Let
. Then,
and, by (
16), we have
. Thus,
. □
Definition 4. The sequence is called ultimately periodic
if there exists and such that, if , then . In this case, we write The minimal preperiod is the minimal r satisfying the above condition. The minimal period is the minimal s for minimal r satisfying the above condition.
Given a function and an element , the sequence is ultimately periodic, whenever X is finite. Lemma 3 implies that the set is finite.
Corollary 3. In the case that " is deterministic", the sequences of buffer states and of published trees are ultimately periodic.
Lemma 4. If is a period of , then Proof. The identity (
17) is the result of the summing of (
16) over a period, i.e., for
. □
4.1. Generation of Strict Binary Trees
In this subsection, we consider the case “
is deterministic” and “
is strict”. In this case, one-step functions (
4) and (
9) are
Let us consider the
Hamming distance for
:
Lemma 6. In the case that " is deterministic and is strict", the transformation F is a weak contraction on : Corollary 4. The sequence of buffer states is stabilized at the fixed point of F. Thus, this sequence and the sequence of published blocks are ultimately periodic with a period of length 1. The tree published in the period has leaves.
The following lemma shows that, if , then the length of pre-period .
Lemma 7. If , then If , then Proof. In both cases, we use the observation: for , if , then . □
Thus, if
, then the period of the sequence of published trees consists of a single tree
. According to (
17), this is a tree with
leaves.
Proposition 2. For , the height of the tree published in the period is the following Proof. Both parts of (
22) equal to
. □
Example 1. Let and ; then, the period of the buffers consists of the single sequence (21) of perfect trees Let us consider a semi-infinite matrix, where rows are given by (
21) for
, and the corresponding matrix, where each tree is replaced by the number of its leaves. Elements
are removed after the shift. The matrix is lower triangular in the sense that
for
.
Proposition 3. Let us denote the sequence of trees of length for .
- 1.
For each , the following sequence can be presented as the concatenation - 2.
Proof. For each
, the sequence (
23) is the concatenation over all positive integers
k of sequences consisting of
copies of
and then compositions
for
p from 1 to
. (Note that
.) The tree
appears in the positions
, or, equivalently,
. The tree
appears in the position
, or, equivalently,
. □
Corollary 5. For each ,is a sequence of positive integers with inserted additional copies of for each . 4.2. Generation of Perfect Binary Trees
Let us recall that the perfect tree is completely determined by its height. Thus, in this subsection, we consider the sequences of heights of perfect trees instead of perfect trees itself: . Buffer states and published trees are characterized by the sequences of heights and with and .
According to Lemma 2, at each moment, the sequence of heights of perfect trees in the buffer is non-increasing. By Lemma 3, the heights of trees are bounded by the constant , the same for all buffer states.
Let
be the number of perfect trees in the buffer of positive height
h, i.e., the buffer at each step has the form
where
.
The following Lemma describes these parameters for a fixed number of provers and number of steps .
Lemma 8. The map f corresponding to one step is given by the formulaHere is the parity of p. Proof. The inequality (
26) is proved by induction. Let
. Then
and
.
The inequality (
27) and the formula (
28) are proved together. If (
27) is satisfied, then the quantity of provers is sufficient to build all possible non-zero height perfect trees and, hence, we obtain (
28). Now, suppose that
; then, at the next step, by (
28),
where the last inequality follows from the fact that the number of non-zero summands in (
27) is not greater than
. □
Remark 2. The above lemma allows for constructing an optimized implementation of OneStep() procedure according to formula (28), and then to obtain a (pre-)reduced form of according to Definition 5. The remainder of the results in this subsection essentially use this implementation. Let be the sequence of heights of trees in generated blocks. According to Corollary 3, it is ultimately periodic.
Hypothesis 1. Moreover, after block publishing.
Hypothesis 2. A period of consists of perfect trees of heights and in some order.
Corollary 6. Let a (respectively b) be the number of perfect trees of height (respectively ). Then, the length of the period isfor some , where is the multiplicity of 2 in prime factorization of , and Remark 3. The difference can be arbitrarily large: Definition 5. The presentation of the sequence (of heights) of published trees with the smallest pre-period and period is called the reduced form of .
If is the presentation of the sequence of buffer states with the smallest pre-period and period, then the corresponding presentation of the sequence (of heights) of published trees is called the pre-reduced form of .
Remark 4. The pre-reduced and reduced forms of can be different as in the following cases: Hypothesis 3. The pre-period of the reduced form of is a non-decreasing sequence.
Remark 5. The above hypothesis is not true for the pre-reduced form of as we can see in (29) and (30). 4.2.1. The Case of a Single Prover
In the case of a single prover Conjectures 1 and 2 are obvious, moreover explicit description is obtained.
Proposition 4. Let . In the case of a single prover , the sequence can be determined recursively together with an auxiliary sequence g that calculates the number of generated proofs in the buffer Corollary 7. In the case of a single prover , the sequence is periodic.
Let and . Then, the periods of reduced forms of and are obtained each from the other with order reversing and replacement .
Proof. The sequence of the buffer state is periodic because at each step the increment of the number of generated proofs in the buffer is constant k by module .
If
is the period of the sequence of the number of generated proofs in the buffer for
k steps, then
is the period of the sequence of the number of generated proofs in the buffer for
steps. Equation (
31) for the first data implies the same equations for the second data. □
Example 2. The cases of and are closed to . The following presentations are special cases (31): , , , , , if
4.2.2. The Case of a Single Step
Hypothesis 4. Let and . Then the periods of reduced forms of and are obtained each from the other by order reversing and replacement .
Example 3. The cases of and closed to agree with the above hypothesis:
, , , ,
6. Discussion
Latus consensus, proposed in [
3,
4], provides secure and stable sidechain operation, even under the complete distrust assumption in sidechains, and even when all participants in the sidechain consensus are malicious. We assume that the adversary in the sidechain may try to sensor the transactions of other participants inside the SC, or from the MC to the SC, or try to steal tokens in the SC, hide the state of the SC, or stop block production in the SC, but these actions must not be successful. For reliable operation under such assumptions, Latus consensus needs uninterruptible zk-SNARK-proof generation, which, in turn, demands essential computational power and cannot be performed by a single regular participant with commodity hardware. Projects Coda [
8] or Polygon [
28] implicitly involve a semi-trusted participant with powerful computational capabilities (such as cloud computation) to solve this task on time, but this approach may lead to a single failure point. To eliminate this problem we propose a new approach for efficient decentralization proof generation. According to our approach, decentralized generation is applied not only to blocks in the whole epoch but even to each block. Thus, proofs are generated with the involvement of a large number of independent participants, which are called provers. This provides a decentralization of the zk-SNARK sidechain operation in secure and reliable way.
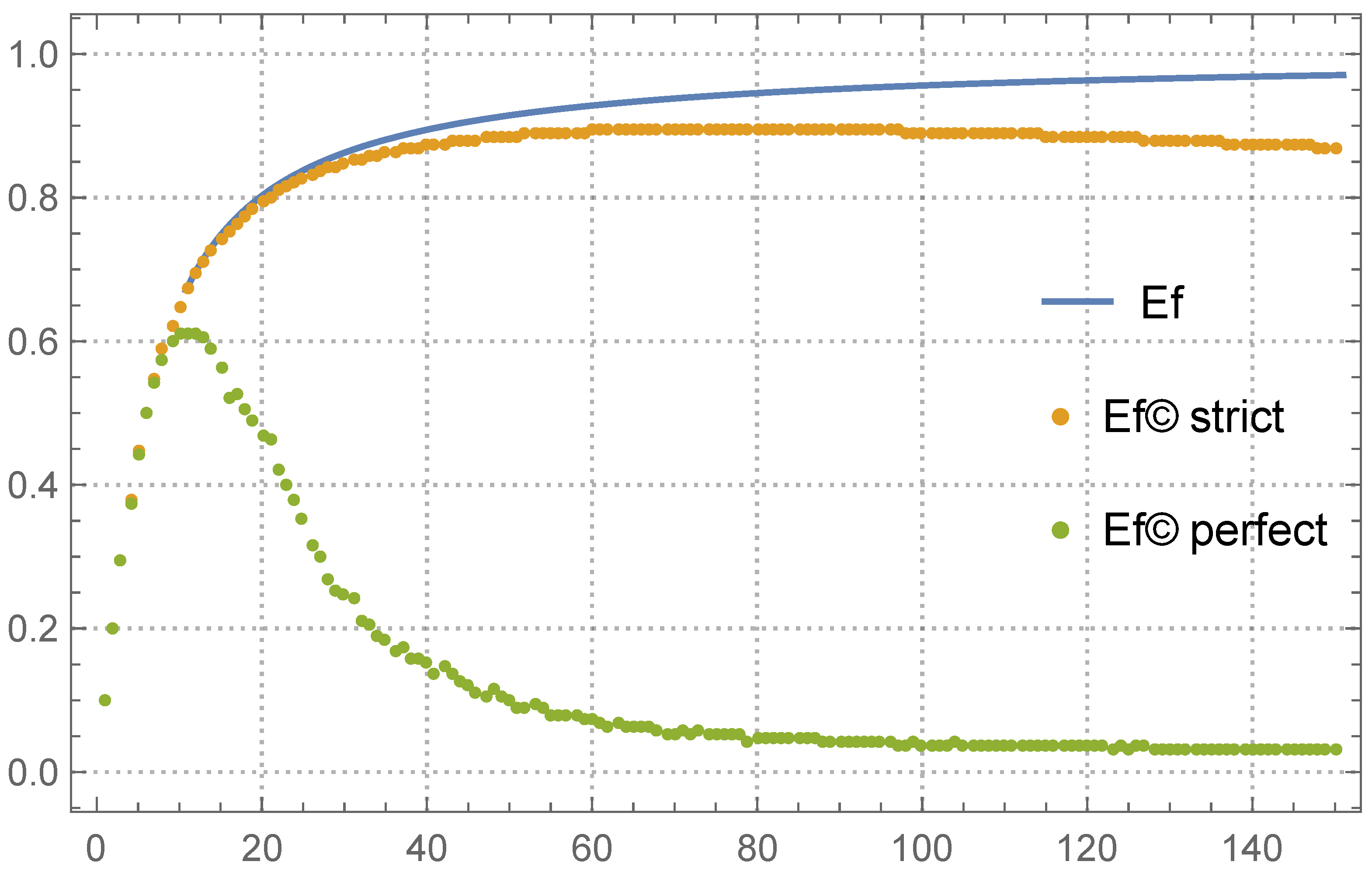
In this article, we introduced the properties of this process as proof generation efficiency Ef and proof publishing efficiency
, which are investigated in
Section 5.1.
For the generation of a single block considered in [
18], the block forger initially selects the number of levels
ℓ of a perfect binary tree that will be included into a block. In [
18] (
Table 1), we find what number of provers is needed to build the perfect binary tree with
levels during
steps with probability
. In this limit case, the role of the efficiency garnered from this article results in the ratio of the number of useful proofs, which is the number of internal vertices
in the built tree to the total number of proofs
produced by all provers during the block publishing process
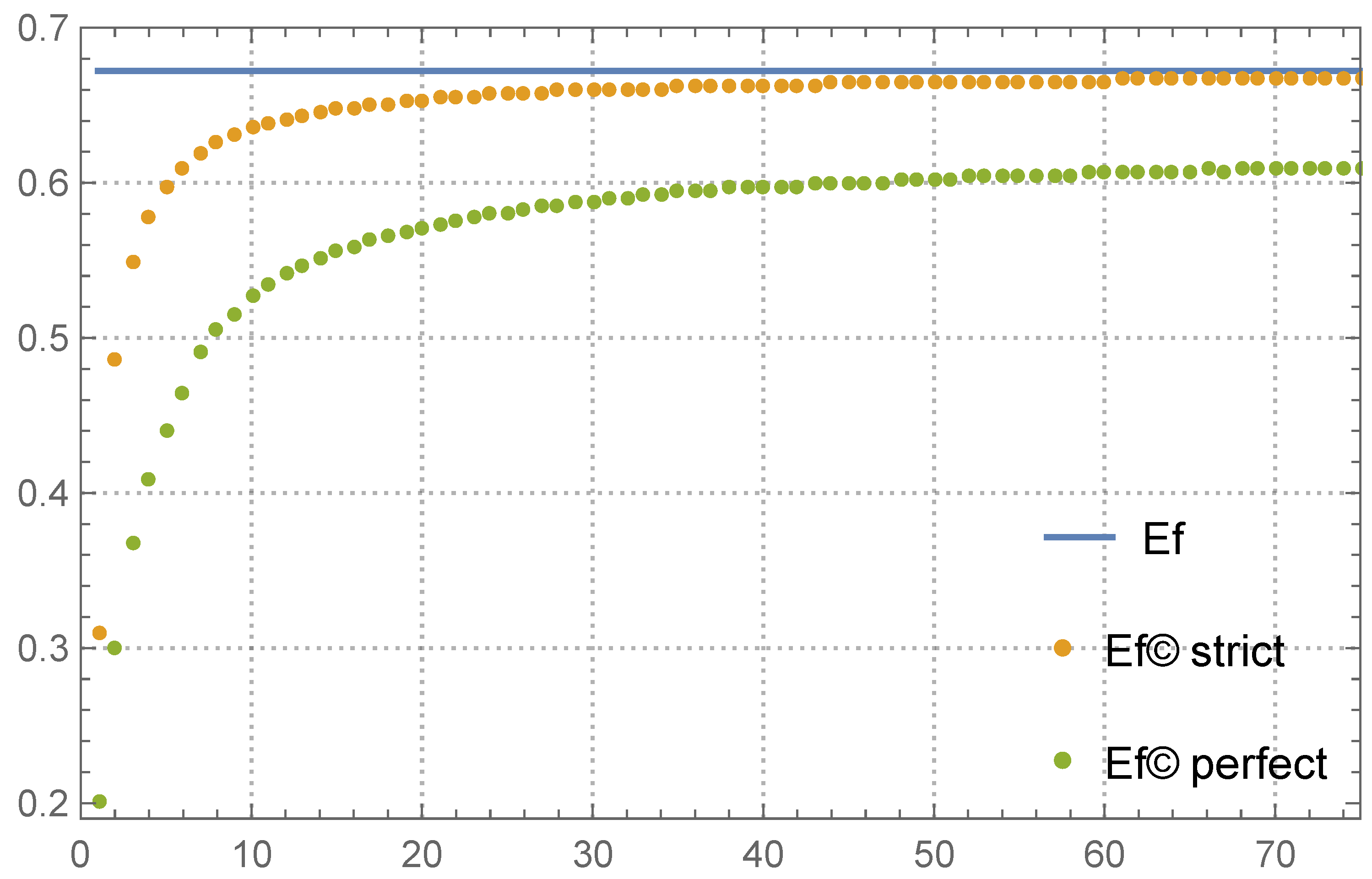
In
Table 5, we compare the values of
from (
37) with the efficiencies
obtained by the emulation procedure when
is perfect in three cases:
,
and
, and when
is strict and
(denoted
and
, respectively). The value of Ef calculated from (
34) is the limit for both
and
at
.
So, one can see
/
as the average. In the top half of
Table 5, the values of
are closed to the best possible limit Ef. At the bottom, when the number of provers becomes extreme,
still obtains an increment with respect to
; however, both values are too small. The convergence
is slow and a very big buffer size is required in this situation. However,
remains closed to Ef.
7. Conclusions
We investigated characteristics of blocks and characteristics of a SC in a whole under various parameters of a SC, such as the number of blocks in an epoch, number of provers, number of available transactions, time of block creation, etc. We obtained theoretical results for a model with additional restrictions on provers’ behavior and various experimental results for an extended model without such restrictions. These results are helpful when determining the parameters of a sidechain, such as epoch length, block creation time, proof incentives, etc. We show that in deterministic cases the sequences of published trees are ultimately periodic and ensure the highest possible efficiency of the proof creation process, because in this case there are no collisions in proof creation.
In stochastic cases, we obtain a universal measure of prover efficiencies taking values in the interval [0,1] and given by the explicit formula in one case, calculated by simulation models in other cases.
In the sense of efficiency defined, the optimal number of allowed prover positions for a step can be proposed for various sidechain parameters, such as number of provers, number of steps in a block, and so on. We also considered non-perfect binary tree utilization in a blockchain, and described benefits and restrictions for such trees’ use. It turns out that we can achieve large efficiency using these very trees.
Our algorithm for the strict binary trees gives the following differences (compared with the case of perfect binary trees):
The buffer size is smaller;
Block publishing efficiency is higher;
The average height of the generated perfect binary trees is proportional to . The average height of the generated strict binary trees has a similar linear dependence on the logarithm of the number of provers , but a different linear dependence to the number of steps (not ). So, we can consider the case of strict binary trees practically interesting only if the number of steps is small.
All results from [
18,
19,
20] and the present paper are related and, put together, give a comprehensive description of SC behavior under our chosen parameters, allowing us to find the optimal sets of parameters that help to optimize functioning, in particular increasing throughput.
One of the most interesting results in this article shows that, under the condition of quick synchronization among block forgers, the throughput increases up to three times in practical settings and can be increased even more for extreme settings cases.
One topic of future research is the investigation of the efficiency of Verkle tree [
29] and Curve tree structures [
30], which can be used for creating proof trees instead of using different variants of Merkle trees.