Improving User Privacy in Identity-Based Encryption Environments
Abstract
1. Introduction
2. Materials and Methods
2.1. Digital Credentials
2.2. Elliptic Curves
2.3. Bilinear Maps
- Bilinear: and
- Non-degenerate: ∀ non-trivial points ,
- Computable: is efficiently computable.
2.4. Identity-Based Encryption
An Example IBE Instantiation
- Compute
- Choose
- Compute
- Compute
- Compute ciphertext
- Obtain her private key from the PKG (To do this, she will prove to the PKG that she validly owns the e-mail address “alice@gmail.com” and the PKG will compute Alice’s identity from this address, compute , and give to Alice as her private key).
- Compute . (Note that
- Compute
- If , return . Otherwise, return invalid.
3. Results
3.1. The Private Key Generator (PKG)
3.2. Threat Model and Security Goal
3.3. Previous Proposals to Reduce Trust in the PKG
3.3.1. Threshold Techniques
3.3.2. Separation Techniques
4. Our Proposal
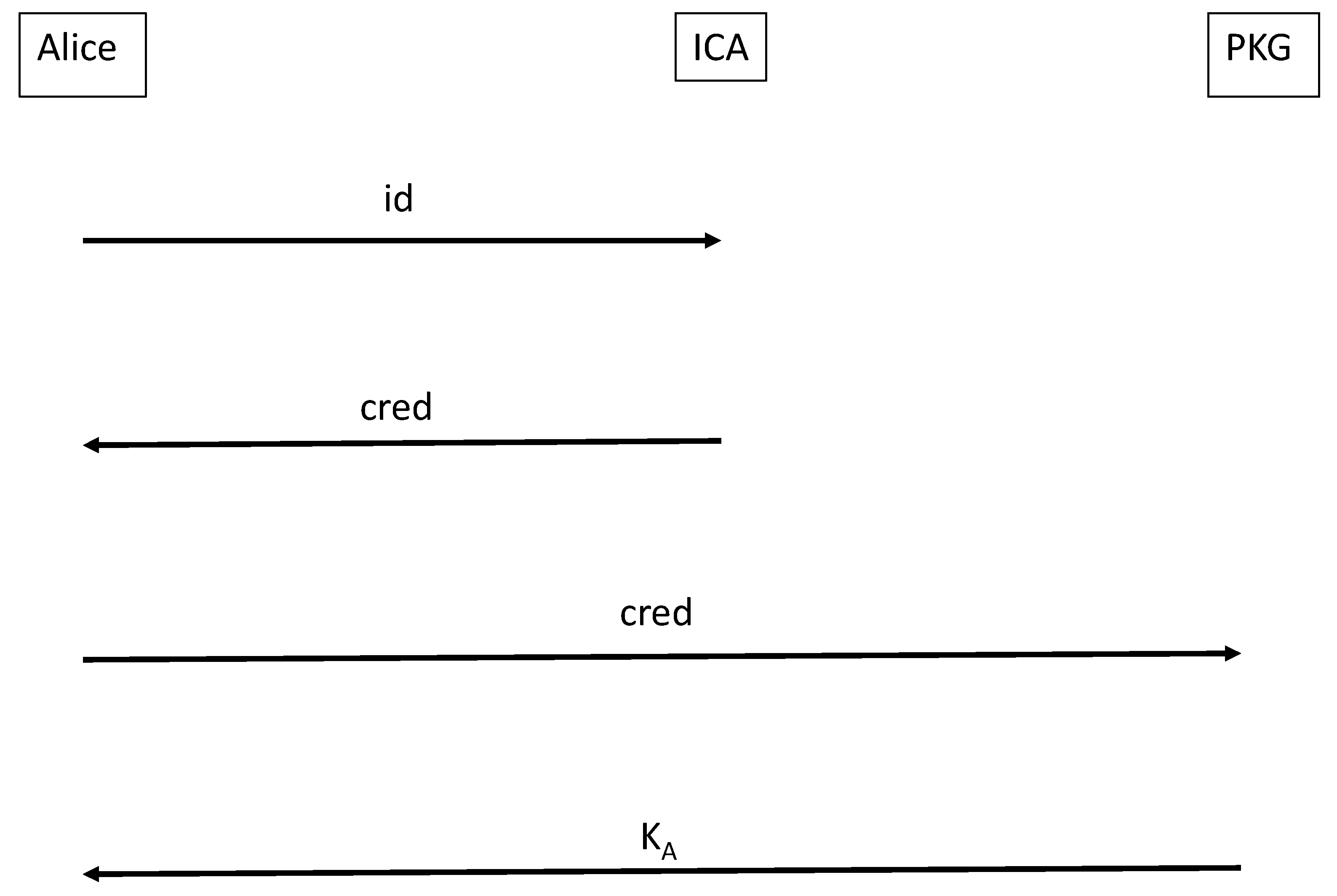
4.1. Basic Scheme
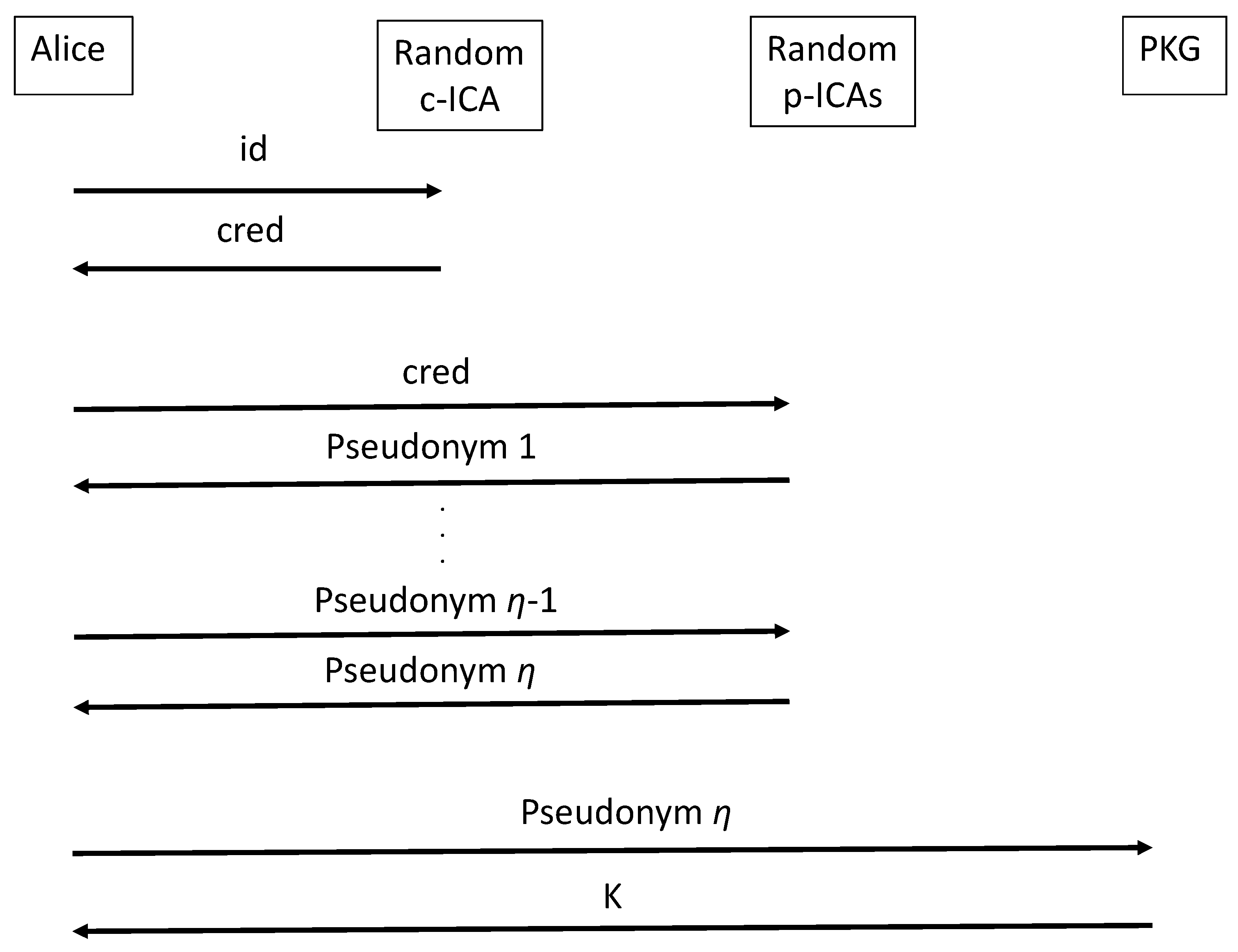
4.2. Augmented Scheme
5. Discussion
- The scheme by Bendlin, et al. [5], is a threshold scheme over lattices in which out of n PKGs are required to compute Alice’s private key, and the protocol will remain correct and secure even if up to of the PKGs deviate from the protocol adversarially (for fixed system parameters and ). Alice must interact with PKGs to obtain her private key shares, but the (very minor) computation she requires is simply to combine the shares into her private key. Alice’s privacy is lost if any PKGs are malicious (because they can collude to learn her private key).
- The scheme by Chow [4] is a separation scheme involving a PKG and an ICA. Alice receives a (blinded) certificate from the ICA and submits this to the PKG to acquire a blinded key. She then needs to unblind this value to obtain her private key.
- The scheme by Emura, et al. [6], is also a separation scheme involving a PKG and an ICA. Alice receives a (blinded) certificate from the ICA and submits this to the PKG to acquire a blinded key. She then needs to unblind this value to obtain her private key.
- Our basic scheme (Section 3 above) requires Alice to obtain a credential from the ICA, but then she can submit this credential and an elliptic curve point to the PKG without further computation.
- Our augmented scheme (Section 3 above) requires Alice to obtain a number of pseudonyms prior to contacting the PKG: there will be pseudonyms and each pseudonym will have ICA signatures (the system administrator will choose for the environment, but Alice can choose the value to reflect her desired level of privacy). Alice needs to be involved in all this computation, as well as in the unblinding of her private key from the PKG.
5.1. Fully-Automated Services
5.2. Smart Contract Instantiation
5.3. Potential Ubiquity
5.4. Formalism and Security Analysis
5.5. Limitations: Additional Computation and Revocation Needs
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Advances in Cryptology—Proceedings of Crypto ’84, LNCS; Springer: Berlin/Heidelberg, Germany, 1985; Volume 196, pp. 47–53. [Google Scholar] [CrossRef]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing (extended abstract). In Advances in Cryptology: Proceedings of Crypto 2001, LNCS; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2139, pp. 229–231. Available online: http://eprint.iacr.org/2001/090/ (accessed on 3 November 2022).
- Boneh, D.; Franklin, M. Identity-Based Encryption from the Weil Pairing. SIAM J. Comput. 2003, 32, 586–615. [Google Scholar] [CrossRef]
- Chow, S.S.M. Removing Escrow from Identity-Based Encryption: New Security Notions and Key Management Techniques. In Public Key Cryptography—PKC 2009, LNCS; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5443, pp. 256–276. [Google Scholar] [CrossRef]
- Bendlin, R.; Krehbiel, S.; Peikert, C. How to Share a Lattice Trapdoor: Threshold Protocols for Signatures and (H)IBE. In Applied Cryptography and Network Security, LNCS; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7954, pp. 218–236. [Google Scholar] [CrossRef]
- Emura, K.; Katsumata, S.; Watanabe, Y. Identity-based encryption with security against the KGC: A formal model and its instantiations. In Theoretical Computer Science; Elsevier: Amsterdam, The Netherlands, 2022; Volume 900, pp. 97–119. Available online: https://www.sciencedirect.com/science/article/pii/S030439752100699X (accessed on 3 November 2022).
- The Tor Project. Available online: https://www.torproject.org/ (accessed on 3 November 2022).
- Brands, S. Rethinking Public Key Infrastructure and Digital Certificates: Building in Privacy; The MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Brands, S. A Technical Overview of Digital Credentials. Credentica Paper, 20 February 2002. Available online: http://www.credentica.com/overview.pdf (accessed on 3 November 2022).
- Koblitz, N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48, 203–209. Available online: https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf (accessed on 3 November 2022). [CrossRef]
- Miller, V. Use of elliptic curves in cryptography. In Advances in Cryptology—Proceedings of Crypto 1985, LNCS; Springer: Berlin/Heidelberg, Germany, 1986; Volume 218, pp. 417–426. [Google Scholar] [CrossRef]
- Galbraith, S.; Harrison, K.; Soldera, D. Implementing the Tate pairing. In International Algorithmic Number Theory Symposium; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2369, pp. 324–337. [Google Scholar] [CrossRef]
- Miller, V. The Weil pairing, and its efficient calculation. J. Cryptol. 2004, 17, 235–261. [Google Scholar] [CrossRef]
- Barreto, P.S.L.M.; Costello, C.; Misoczki, R.; Naehrig, M.; Pereira, G.C.C.F.; Zanon, G. Subgroup Security in Pairing-Based Cryptography. In Progress in Cryptology—LATINCRYPT 2015, LNCS 9230; Springer: Berlin/Heidelberg, Germany, 2015; pp. 245–265. [Google Scholar] [CrossRef]
- Adams, C.; Lloyd, S. Understanding PKI: Concepts, Standards, and Deployment Considerations, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2003. [Google Scholar]
- Housley, R.; Polk, T. Planning for PKI: Best Practices Guide for Deploying Public Key Infrastructure; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Boneh, D.; Boyen, X. Secure Identity Based Encryption Without Random Oracles. In Advances in Cryptology—Proceedings of Crypto 2004. LNCS; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3152, pp. 443–459. [Google Scholar] [CrossRef]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for Hard Lattices and New Cryptographic Constructions. Cryptology ePrint Archive, Paper 2007/432 (2007). Available online: https://eprint.iacr.org/2007/432 (accessed on 3 November 2022).
- Gemmell, P. An introduction to threshold cryptography. In CryptoBytes, a Technical Newsletter of RSA Laboratories; RSA Laboratories: Redwood City, CA, USA, 1997; Volume 2, pp. 7–12. [Google Scholar]
- Evans, D.; Kolesnikov, V.; Rosulek, M. A Pragmatic Introduction to Secure Multi-Party Computation; NOW Publishers: Delft, The Netherlands, 2018; Available online: https://www.cs.virginia.edu/~evans/pragmaticmpc/pragmaticmpc.pdf (accessed on 3 November 2022).
- Gennaro, R.; Jarecki, S.; Krawczyk, H.; Rabin, T. Secure Distributed Key Generation for Discrete-Log Based Cryptosystems. J. Cryptol. 2007, 20, 51–83. [Google Scholar] [CrossRef]
- Szabo, N. Smart Contracts: Building Blocks for Digital Markets. 1996. Available online: https://www.fon.hum.uva.nl/rob/Courses/InformationInSpeech/CDROM/Literature/LOTwinterschool2006/szabo.best.vwh.net/smart_contracts_2.html (accessed on 3 November 2022).
- Levi, S.D.; Lipton, A.B. An Introduction to Smart Contracts and Their Potential and Inherent Limitations, Harvard Law School Forum on Corporate Governance. 2018. Available online: https://corpgov.law.harvard.edu/2018/05/26/an-introduction-to-smart-contracts-and-their-potential-and-inherent-limitations/ (accessed on 3 November 2022).
- Adams, C. Security Analysis of a Privacy-Preserving Identity-Based Encryption Architecture. J. Inf. Secur. (Spec. Issue Cryptogr. Netw. Secur.) 2022, 13, 323–336. [Google Scholar] [CrossRef]
- Boldyreva, A.; Goyal, V.; Kumar, V. Identity-based encryption with efficient revocation. In Proceedings of the 15th ACM Conference on Computer and Communications Security—CCS ’08, Alexandria, VA, USA, 27–31 October 2008; p. 417. [Google Scholar] [CrossRef]
- Elashry, I.; Mu, Y.; Susilo, W. Generic Mediated Encryption. In Security and Privacy in Communication Networks; Zia, T., Zomaya, A., Varadharajan, V., Mao, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; Volume 127, pp. 154–168. [Google Scholar] [CrossRef]
- Seo, J.H.; Emura, K. Revocable hierarchical identity-based encryption. Theor. Comput. Sci. 2014, 542, 44–62. [Google Scholar] [CrossRef]
| Proposal | Setting | Computation by Alice to Obtain | Privacy Breach |
|---|---|---|---|
| Boneh [2] | single PKG | none | PKG is HbC or malicious |
| Bendlin [5] | many PKGs (threshold scheme) | combining private key shares | PKGs are malicious (for fixed ) |
| Chow [4] | single PKG, single ICA (separation scheme) | unblinding step | ICA & PKG are malicious |
| Emura [6] | single PKG, single ICA (separation scheme) | unblinding step | ICA & PKG are malicious |
| Basic scheme (this paper) | single PKG, single ICA (separation scheme) | credential signing | ICA & PKG are malicious |
| Augmented scheme | single PKG, many ICAs | credential signing, pseudonymizations, | () ICAs and PKG are |
| (this paper) | (separation | signatures per pseudonym | all malicious |
| scheme) | unblinding step | (for fixed , user-chosen ) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adams, C. Improving User Privacy in Identity-Based Encryption Environments. Cryptography 2022, 6, 55. https://doi.org/10.3390/cryptography6040055
Adams C. Improving User Privacy in Identity-Based Encryption Environments. Cryptography. 2022; 6(4):55. https://doi.org/10.3390/cryptography6040055
Chicago/Turabian StyleAdams, Carlisle. 2022. "Improving User Privacy in Identity-Based Encryption Environments" Cryptography 6, no. 4: 55. https://doi.org/10.3390/cryptography6040055
APA StyleAdams, C. (2022). Improving User Privacy in Identity-Based Encryption Environments. Cryptography, 6(4), 55. https://doi.org/10.3390/cryptography6040055






