Abstract
The ever-increasing need for securing computing systems using cryptographic algorithms is spurring interest in the efficient implementation of common algorithms. While the algorithms can be implemented in software using base instruction sets, there is considerable potential to reduce memory cost and improve speed using specialized instructions and associated hardware. However, there is a need to assess the benefits and costs of software implementations and new instructions that implement key cryptographic algorithms in fewer cycles. The primary aim of this paper is to improve the understanding of the performance and cost of implementing cryptographic algorithms for the RISC-V instruction set architecture (ISA) in two cases: software implementations of the algorithms using the rv32i instruction set and using cryptographic instructions supported by dedicated hardware in additional functional units. For both cases, we describe a RISC-V processor with cryptography hardware extensions and hand-optimized RISC-V assembly language implementations of eleven cryptographic algorithms. Compared to implementations with only the rv32i instruction set, implementations with the cryptography set extension provide a 1.5× to 8.6× faster execution speed and 1.2× to 5.8× less program memory for five of the eleven algorithms. Based on our performance analyses, a new instruction is proposed to increase the implementation efficiency of the algorithms.
1. Introduction
The ever-increasing need for securing computing systems using cryptographic algorithms is spurring interest in the efficient implementation of common algorithms. While the algorithms can be implemented in software using the base instruction set of processors, there is considerable potential to reduce memory cost and improve speed using specialized instructions and associated hardware. However, there is a need to assess the relative benefits and costs of software implementations and new instructions that implement key cryptographic algorithms in fewer cycles. With the growing popularity of the extensible RISC-V ISA, there is a need to improve the understanding of the cost of implementing cryptographic algorithms for both implementations of the algorithms in software using the rv32i instruction set and with the implementation of instructions as hardware in additional functional units.
RISC-V is an open-source RISC ISA, which was developed starting in 2010 at UC-Berkeley [1]. In 2011, the team published Volume 1 of the RISC-V ISA manual [2]. In 2015, the RISC-V International Foundation [3] was founded to build a RISC-V ISA community. RISC-V has 32-bit and 64-bit versions, and currently, it has eight ratified instruction set extensions (-M, -A, -F, -D, -Q, -C, -Zicsr, -Zifencei) and the base instruction set (-I) [4]. However, there are several upcoming extensions.
One of these upcoming extensions is the RISC-V cryptography extension (-crypto), which has two sets of instructions—Scalar & Entropy Source [5] and Vector [6]. The scalar extension has groups of instructions. The first group includes instructions that are borrowed from the upcoming bitmanip extension [7], and five other groups are designed to accelerate particular cryptography algorithms: AES [8], SHA-256 [9], SHA-512 [9], SM3 [10], and SM4 [11]. The scalar extension provides both 32-bit and 64-bit versions of the instructions. Similarly, the vector cryptography extension provides vector versions of some of the bitmanip instructions and vector instructions to accelerate the AES and the SHA2 [9] algorithms. The RISC-V cryptography extension task group published version v1.0.0-rc6 of the RISC-V Cryptography Extensions Volume 1—Scalar & Entropy Source Instructions [5]. There is a slight difference between the instructions explained in version v1.0.0-rc6 and the instructions that are evaluated in this work. In this work, we implemented grev[i], shlf[i], and unshlf[i], which were removed from the cryptography extension in version 0.7.2 [12]. These instructions are replaced with brev8, rev8, zip, and unzip instructions, which are simplified versions of grev[i], shlf[i], and unshlf[i].
This work presents software-only algorithms for eleven cryptographic algorithms using the RISC-V rv32i ISA and compares the performance of these algorithms to the performance of a RISC-V processor with additional hardware modules that implement specialized instructions for single-cycle execution of cryptographic primitives.
In our study, we have not implemented any of the cryptographic algorithms fully in hardware. Instead, we wanted to observe their software performance without and with the aid of hardware acceleration via application-specific instruction set extensions. The only hardware modules we implemented are those added into the processor datapath in order to realize those additional instructions.
On the other hand, our software implementations reflect a balanced approach between execution speed and code size, with a greater emphasis on execution speed. To this end, we used loop unrolling where it was most effective and did not increase the program memory significantly. Furthermore, all SBOX tables were pre-computed and stored in memory rather than being calculated on the fly unless there is a specialized instruction that calculates the SBOX value. We obtained the clock cycle count, program memory, and static memory requirements of the software implementations and performed the comparison.
We grouped the cryptography instructions based on their structure and designed each group as a hardware module. The modular approach allows integration of any subset of modules with the RISC-V processor that we also implemented. Since each algorithm uses only a subset of the 32-bit scalar cryptography instructions, to ensure a valid performance comparison, we determined the module usage of each of the algorithms and evaluated the implementation cost accordingly.
1.1. Previous and Related Work
RISC-V ISA cryptography extensions have been the subject of several recent studies. In [13], two new cryptography instructions are proposed for the RISC-V ISA. The instructions accelerate the AES and SM4 block ciphers. Using the AES instructions, one round of AES can be implemented using only 16 instructions instead of 80. The instructions lead to a similar reduction for the SM4 algorithm. An efficient way to implement these instructions in hardware is proposed in [14]. An ISE [15] for RISC-V is proposed to accelerate a stream-cipher called ChaCha [16]. Compared to OpenSSL baseline and ISA-based optimized implementations, ISE-assisted ChaCha speeds up at least 5.4× and 3.4×, respectively.
The core building block of ASCON is implemented as an instruction extension for RISC-V ISA [17]. Comparing the results with efficient C implementations, the accelerator sped up the implementations by about a factor of 50 for ASCON and 80 for ASCON-HASH. Furthermore, the extensions lead to significant binary size reduction.
A set of hardware accelerators and 29 new instructions for lattice-based cryptography are proposed in [18], with implementations of a RISC-V-based processor with the proposed accelerators and instructions in ASIC and FPGA. Compared to pure software implementations, accelerators and the instructions lead to a speed-up factor of 11.4 for NewHope, 9.6 for Kyber, and 2.7 for Saber. On the other hand, the cell count of the CPU is increased by a factor of 1.6 compared to the original RISC-V design due to additional instructions and accelerators.
An energy-efficient crypto-coprocessor is designed for the AES, ECC, and SHA-256 algorithms and integrated with an open-source RISC-V core in [19], using a conditionally charged flip-flop to implement the crypto-coprocessor. The pipelined design achieved a 10.3% power reduction on average for cryptography tasks. Reference [20] developed an optimized RISC-V assembly the implementation of the table-based AES, bitsliced-AES, ChaCha, and Keccak-f[1600] algorithms.
The RISC-V cryptography extensions task group published RISC-V Cryptography Extensions Volume 1—Scalar & Entropy Source Instructions version v1.0.0-RC6 [5]. The extension provides details about the cryptography instructions; however, it does not analyze software implementations using these instructions. Although an increase in software implementation efficiency using the extension is expected, the possible gain is not provided.
A versatile RISC-V Galois Field ISA extension is proposed in [21]. The researchers achieved 5X acceleration for AES, Reed–Solomon codes, and Classic McEliece by increasing the logic utilization by 1.27%.
The performance of the AES, RC6, Twofish, SPECK128, and ChaCha20-Poly1305 algorithms is presented in [22]. The researchers included execution time, throughput, and power consumption as performance parameters. Based on the obtained performance parameters, the researchers decided that ChaCha20-Poly is a very good option for resource-constrained devices, along with SPECK128 and LEA.
1.2. Objectives
In this paper, we implement 11 cryptographic algorithms in both RISC-V assembly code using the 32-bit base RISC-V instructions (rv32i) and using the 32-bit scalar cryptography instruction set in addition to base instructions (rv32i+crypto). We analyze the performance of the two approaches using clock cycle count, program memory, and static memory requirements and extract area requirements of the hardware implementations. We then use these results to analyze the benefit vs. cost in terms of the acceleration of execution times as a function of the additional hardware cost relative to that for the rv32i datapath implementation. Finally, based on our results, we propose a new instruction to increase the software implementation efficiency of the cryptographic algorithms and analyze its benefits and costs.
2. Materials and Methods
We implemented eight ISO standard symmetric-key block ciphers and three NIST standard hash functions. Five of the block ciphers (TDEA [23], MISTY1 [24], CAST-128 [25], HIGHT [26], PRESENT [27]) have a 64-bit block size, and the remaining three (AES-128, CAMELLIA [28], SEED [29]) have a 128-bit block size. PRESENT is the only lightweight cipher among these eight block ciphers, specified in the ISO/IEC 29192-2:2019 standard. The other seven ciphers are specified in the ISO/IEC 18033-3:2010 standard. The hash algorithms are SHA-256 [9], SHA-512 [9], and SHA3-256 [30]. SHA3-256 is specified in the NIST FIPS-202 [30], and two other hash functions are specified in NIST FIPS-180 [9].
We implemented a simple assembly language simulator for RISC-V, which allowed us to easily modify the simulator to display the required outputs (clock cycle count, program memory, static memory). We also built a simple assembler in the Python programming language to convert RISC-V assembly language code to machine code. We developed de novo a 32-bit RISC-V processor and cryptography instruction modules using Verilog HDL. Designs were simulated on Xilinx’s Vivado Design Suite. The Yosys [31] open-source framework for Verilog RTL synthesis was used to extract the hardware area requirements for the different implementations.
3. Cryptographic Algorithms
This section summarizes the eleven implemented cryptographic algorithms: eight symmetric block ciphers and three hash functions. All of the algorithms are standardized algorithms. Table 1 and Table 2 list the block ciphers and hash functions, respectively. To limit the scope while retaining the ability to develop insights, we implemented only one key size of the listed block ciphers.

Table 1.
Symmetric block ciphers.

Table 2.
Hash functions.
4. Software Implementations
This section summarizes the software implementation process. In order to have a flexible development environment, we implemented a RISC-V assembly language simulator using MATLAB and implemented the algorithms using this simulator. First, the algorithms were implemented by only using the 32-bit RISC-V integer instructions, and then, the cryptography instructions were used to accelerate them. The following sections will give more details about how the cryptography instructions are used to accelerate the initial implementations.
4.1. Software Implementation of AES
In this study, we implemented the AES-128 encryption algorithm using the T-table approach [34]. We used the T-table approach because the AES instructions are designed according to this approach [13]. The T-table approach accelerates the software implementation by pre-calculating the “SubBytes” and “MixColumns” layers. The approach is explained in detail below.
Figure 1 shows the state matrices of the AES-128 encryption algorithm after the “SubBytes” (S(i)), “ShiftRows”, and “MixColumns” layers. The “MixColumns” layer multiplies each column of matrix B to calculate matrix C.
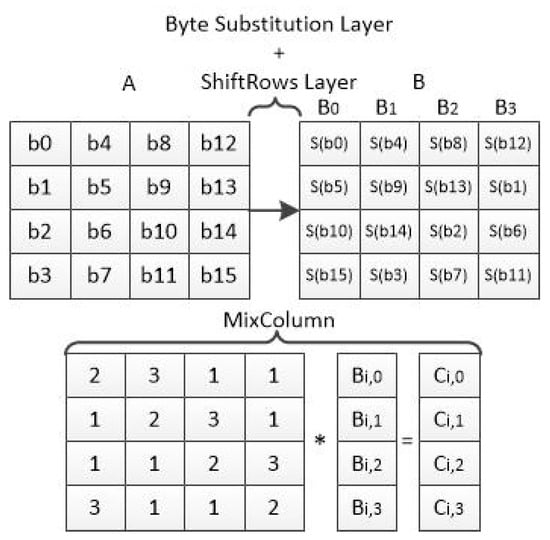
Figure 1.
AES state matrices.
Figure 2 shows the formulas used in the “MixColumns” layer to calculate matrix C. If we re-arrange the formulas, we can use the 32-bit ak (k = 1, 2, ⋯, 15) values to calculate matrix C as shown in Figure 2.

Figure 2.
AES-128 round state matrix calculation.
The T-table implementation pre-calculates and stores the 32-bit ak values for every possible 8-bit b value. Therefore, it is possible to calculate matrix C directly using matrix A. Figure 3 shows the four T-tables used for the implementation. It is also possible to store only one T-table and calculate the other three T-tables using logical rotate operations.

Figure 3.
T-tables.
We can use the aes32esmi instruction to calculate the 32-bit ak values and XOR it with the rs1 to implement the “MixColumns” layer [13]. The aes32esi instruction is used to perform AES SBOX transformation for key scheduling and the last round of the algorithm.
4.2. Software Implementation of Seed
The function F and function G use modular addition and subtraction. These functions are explained in the SEED documentation [29]. These operations can be implemented using ADD[I] and SUB instructions, respectively. The RISC-V ISA does not have a carry flag, so the carry bit should be calculated when needed.
SEED provides two versions of the algorithm. Both versions generate the same output when the same input is given. The only difference is that Version 1 is slower than Version 2. However, Version 1 uses less data memory space for SBOX table storage than Version 2. Version 1 and Version 2 use two 8 × 8 SBOX tables and four 8×32 SBOX tables, respectively. Version 2 of the algorithm accelerates the G function implementation by sacrificing data memory space (explained in [29]).
One of the most time-consuming operations for the block ciphers is to read the SBOX table from memory. For simplicity, the SBOX tables are stored into the memory such that the SBOX value of the input x is stored into the memory location (x + offset), where the offset is zero in our implementation. Assembly code for memory address calculation of the Version 1 SBOX table is shown in Figure 4. The state values are stored in 32-bit registers, but the SBOX transformation is applied for each individual byte for the state value. Therefore, we shift the input byte to the least significant position and mask it. Then, we add the offset address to the masked value. The RD3 register has the 32-bit memory address of the SBOX table value.
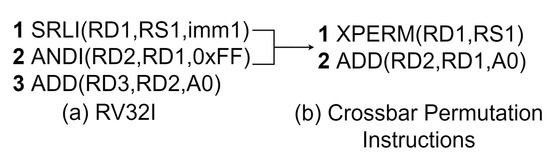
Figure 4.
Memory address calculation for 8 × 8 SBOX table.
To accelerate this operation, we can use one of the crossbar permutation instructions (xperm4 or xperm8). The RS1 register holds the required value to shift the desired byte to the least significant byte position.
4.3. Software Implementation of CAMELLIA
In this work, we implemented CAMELLIA-128. The CAMELLIA key scheduling uses 128-bit logical left rotation (⋘). A 128-bit value is stored in four 32-bit registers. Therefore, to perform the 128-bit rotate operation, we need to modify all four registers (RS1, RS2, RS3, RS4), as shown by the assembly code in Figure 5. The imm values are calculated based on the rotation amount, and the new results are stored in the registers T1, T2, T3, and T4. For each 128-bit rotate operation, we need 12 instructions.

Figure 5.
Assembly code for 128-bit rotation using rv32i.
The algorithm has two versions according to the SBOX tables. Version 1 stores four 8 × 8 SBOX tables in the memory. Version 2 calculates three of these tables using Equations (1)–(3). Therefore, Version 1 of the algorithm computes the result faster by sacrificing data memory space.
Version 2 of the algorithm uses 8-bit rotation to calculate the SBOX tables using the equations above. The 8-bit left rotation is performed as shown by the assembly code in Figure 6. Suppose RS1 stores a zero-extended 8-bit value. The imm1 value is the rotate amount, where imm2 is equal to 8 minus imm1. The FL and invFL functions contain 32-bit left rotate operations, which can be accelerated using the rotate instructions. The FL and invFL functions are described in the CAMELLIA documentation [28].

Figure 6.
Assembly code for 8-bit rotation using rv32i.
4.4. Software Implementation of CAST
Compared to the other block ciphers in this thesis, CAST-128 has the biggest SBOX tables that occupy 8KB memory space. The algorithm has eight 8 × 32 SBOX tables. The rv32i provides byte-addressed 32-bit address space. Therefore, we need to leave the most significant two bits of the address zero when we read the 32-bit value with the rv32i LW instruction. Figure 7 shows the assembly codes of the address calculation operation for the 8 × 32 SBOX table.

Figure 7.
Memory address calculation for 8 × 32 SBOX table using rv32i.
4.5. Software Implementation of SHA-256 and SHA-512
The RISC-V cryptography instruction set extension has specific instructions that are designed to accelerate SHA-256 and SHA-512. The instructions implement the SIGMA and SUM transformation functions (explained in [9]) of these algorithms. The following section will describe the benefits of using the cryptography extension instructions.
Each transformation function of SHA-256 is implemented as a single instruction in the cryptography extension. Figure 8 shows the three different software implementations of the SHA-256 0 (SIGMA0) function. All three implementations receive the register x as the input and store the 32-bit result into the register RD.
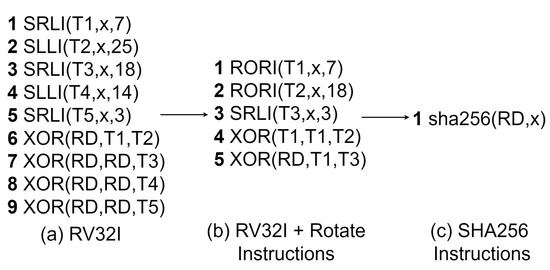
Figure 8.
SHA-256 0 function software implementation.
The SHA-512 transformation functions receive a 64-bit input and generate a 64-bit result. Therefore, each transformation function takes two SHA-512 instructions to calculate in a 32-bit RISC-V processor, and it is not possible to use 32-bit rotate instructions to perform a 64-bit rotate operation. Figure 9 shows the software implementations of the SHA-512 1 (SIGMA1) function.
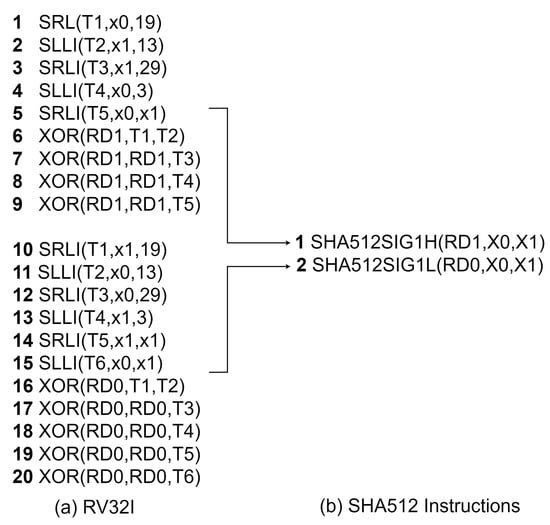
Figure 9.
SHA-512 1 function software implementation.
4.6. Software Implementation of TDEA
The algorithm has several bit permutations. The assembly code, shown in Figure 10, shows a basic way to perform single-bit permutation using rv32i. First, we shift a bit of the RS1 to the least significant bit position and mask it. Then, we shift the bit to its new position. It is possible to perform any bit permutation just by repeating these four assembly instructions.

Figure 10.
Single-bit permutation using rv32i.
4.7. Software Implementation of MISTY1
MISTY1 [24,32] is a 64-bit block cipher with a 128-bit key. The algorithm has a variable number of rounds, but the eight-round version of the algorithm is recommended. The algorithm uses two SBOX tables named S7 and S9, which are 7 × 7 and 9 × 9 SBOX tables, respectively. The MISTY1 key scheduling algorithm (Algorithm 1) uses the primary key (K) to generate 16-bit round keys (EK). Each element of K (K[i]) holds a byte of the key.
| Algorithm 1: MISTY1 key scheduling. |
| 1.35 Date: 128-bit Main Key(K) Result: Array of 16-bit round keys for i = 0 to 7 { EK[i] = K[i×2]×256 XOR K[i×2 + 1]; } for i = 0 to 7 { EK[i + 8] = FI(EK[i], EK[(i + 1)%8]); EK[i + 16] = EK[i + 8] & 0x1ff; EK[i + 24] = EK[i + 8] 9; } |
Figure 11 shows the assembly implementation of the Misty FI and FL functions. The functions are described in [24].

Figure 11.
MISTY1 FI and FL functions using the PACK instruction.
4.8. Software Implementation of HIGHT
HIGHT [26,32] is a 64-bit block cipher with a 128-bit key size. The algorithm uses 32 rounds with no SBOX table. Algorithm 2 describes the HIGHT key scheduling algorithm. The 128-bit subkeys are generated at each round.
| Algorithm 2 HIGHT key scheduling. |
| Date: s0 = 0, s1 = 1, s2 = 0, s3 = 1, s4 = 1, s5 = 0, s6 = 1 d0 = s6 s5 s4 s3 s2 s1 s0 Result: Subkey Array SK for i = 1 to 127{ di = s(i + 6) s(i + 5) s(i + 4) s(i + 3) s(i + 2) s(i + 1) si } for i = 0 to 7 { for i = 0 to 7 { SK(16×i + j) = K(j − i mod 8) [+] d(16×i + j) } } for j = 0 to 7 { SK(16×i + j + 8) = K((j − i mod 8) + 8) [+] d(16×i + j + 8) } |
HIGHT takes the 64-bit plaintext (P) block as the input and generates the 64-bit ciphertext (C). Figure 12 shows the structure of HIGHT. The algorithm uses 8-bit operations, which require additional operations on a 32-bit system. For example, the modulo addition and subtraction operations require masking on a 32-bit system. Furthermore, the algorithm uses 8-bit rotate operations, which require three instructions using rv32i.
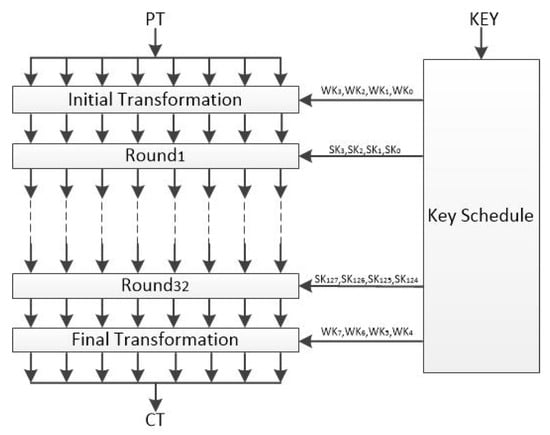
Figure 12.
HIGHT encryption.
4.9. Software Implementation of PRESENT
PRESENT is a 64-bit block cipher that uses a substitution–permutation network of 31 rounds. “sBoxLayer” and “pLayer” are the two key parts of this algorithm. The assembly code in Figure 13 shows the “SBoxLayer” implementation with crossbar permutation instructions. The code performs the PRESENT SBOX transformation on each nibble of the registers S0 and S1.

Figure 13.
PRESENT “sBoxLayer” using crossbar permutation instructions.
We used the lower part of SBOX (B1 register) to transform each nibble using the xperm4 instruction. If a nibble is greater than seven, the corresponding nibble will be zero in register T0. Then, we used a masking value (B2 = 88,888,888) to flip the most significant bit of each nibble and transform the nibbles using the upper part of the PRESENT SBOX table and save the result to T1. Then, we XORed T0 and T1 to obtain the result that holds the transformed version of nibbles in register S0. The same operation is applied to S1, and the result is saved to Y1.
The “pLayer” of the algorithm performs bit permutation defined by the “pLayer” table in [27]. Figure 14 shows the assembly code that implements the PRESENT “pLayer” using shuffle instructions.

Figure 14.
PRESENT “pLayer” using generalized shuffle instructions.
5. Hardware Implementations
This section describes the hardware module designs that are implemented in this project. The hardware design contains eight modules:
- 1.
- RISC-V Core
- 2.
- Bit Re-positioning Instructions
- 3.
- Carry-Less Multiply Instructions
- 4.
- Crossbar Permutation Instructions
- 5.
- Logic With Negate Instructions
- 6.
- Packing Instructions
- 7.
- Hash Instructions
- 8.
- AES and SM4 Instructions
The first module is a 32-bit 5-stage pipelined RISC-V processor that only supports base integer instructions. The remaining seven modules implement cryptography extension instructions. The instruction extension modules share logic to optimize the hardware area. Any combination of the seven extension modules can be used to extend the processor. The following sections will explain some of the hardware design highlights we used to reduce the area of the modules. All the modules are designed as fully combinational to allow one clock cycle execution.
5.1. Hardware Architecture of Bit Re-Positioning Instructions
The bit re-positioning instructions re-position the bits of the register RS1 based on the value of the register RS2 and save the result to the register RD. The bit re-positioning instructions are rotate (ROR[I], ROL), generalized reverse (GREV[I]), and shuffle (SHFL[I], UNSHFL[I]). Figure 15 shows the hardware block diagram of the bit re-positioning instructions.
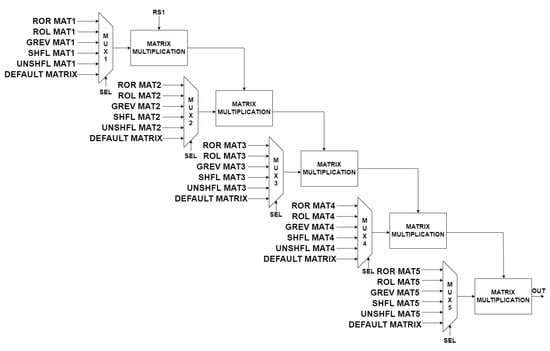
Figure 15.
Hardware architecture of re-positioning instructions.
We used matrix multiplication for the hardware design of these instructions. To clarify the bit re-positioning with matrix multiplication, see Figure 16, which demonstrates a 4-bit matrix multiplication. It is possible to choose a matrix B such that when we multiply it with matrix A, matrix C will have the bits of A in the desired position. For example, if we set b03, b12, b21, and b30 to 1 and the rest of the B matrix elements to 0, we reverse the A matrix elements’ order and save the result to the C matrix.
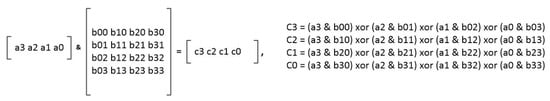
Figure 16.
The 4-bit matrix multiplication in GF(2).
The architecture contains five multiplexers and five 32-bit matrix multipliers. Each multiplexer chooses one of the six 32 × 32 B matrices based on the instruction and rs2. Then multipliers perform the matrix multiplication to re-position the bits of rs1. Finally, the output of the fifth matrix multiplier gives the result.
5.2. Hardware Architecture of Carry-Less Multiply Instructions
The carry-less multiplication is multiplication in . The carry-less multiplication can be implemented with logical AND (&) and XOR gates. Figure 17a demonstrates 4-bit carry-less multiplication.

Figure 17.
Carry-less multiplication.
The method of performing the multiplication in a fully combinational circuit is to calculate the result directly as shown in Figure 17a. In this case, we will have a logic circuit (circuit1, ..., circuit8) for each of the eight bits, where circuit8 is hardwired to zero. Instead of using all eight circuits, we used the similarity between lower (circuit0, ...,circuit3) and upper (circuit4, ..., circuit6) parts of the logic circuits to reduce the circuit area. It is possible to use only the lower part of the circuits to calculate both the lower (c0, ..., c3) and higher (c4, ..., c7) halves of the result. It is necessary to change the inputs of the circuits as shown in Figure 17b in order to calculate the higher order half of the result.
In this study, we implemented 32-bit carry-less multiplication. The hardware architecture takes advantage of the similarity between the upper and lower part of the full carry-less multiplication circuit to reduce the area cost of the circuit, as explained above. Figure 18 shows the block diagram of the hardware architecture of the carry-less multiplication circuit. The multiplexers are used to select the correct input for CLMULH and CLMUL. The “Shift Left” block performs a logical 1-bit left shift. The “Multiplication Unit” contains the lower part of the full 32-bit carry-less multiplication circuit. The “Reverse Order” blocks reverse the order of the 32-bit values.
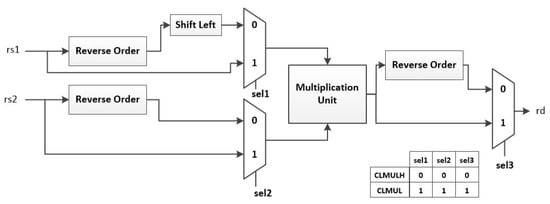
Figure 18.
Hardware architecture of carry-less multiply instructions.
6. Hardware Architecture of 32-bit Algorithm Specific Cryptography Instructions
This section describes the hardware architecture of the algorithm-specific cryptography instructions. The instructions are described in the RISC-V cryptography extension [5].
6.1. Hardware Architecture of Hash Instructions
The SHA-256 and sm3 instructions consist of 32-bit bitwise rotate and logical XOR operations. Each bit of the result is obtained by XORing a subset of bits of rs1. This operation can be implemented by a matrix multiplication, described in Figure 16. In the case of SHA-512 instructions, each bit is calculated by XORing a subset of bits of rs1 and rs2. In this case, two matrix multiplications and a 32-bit XOR operation are needed for the calculation.
Figure 19 describes the hardware architecture of the hash instructions. The multiplexers choose two matrices to be multiplied with rs1 and rs2 and the results are XORed to generate the output.
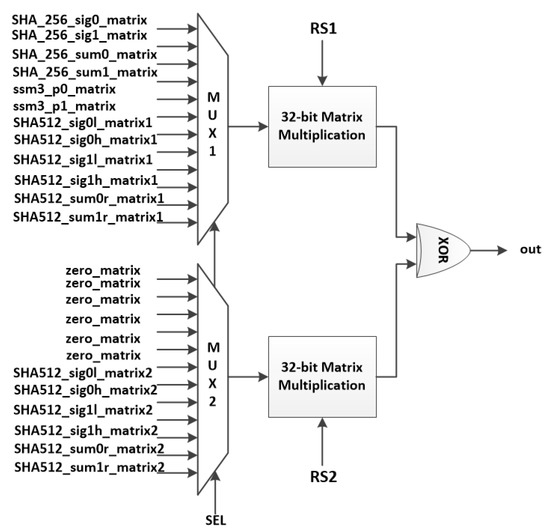
Figure 19.
Hardware implementation of hash instructions.
6.2. Hardware Implementation of AES and SM4 Instructions
This Section describes the hardware architecture of the AES and SM4 instructions. The instructions are described in RISC-V cryptography extension [5].
Figure 20 demonstrates the overall architecture of the AES and SM4 instructions. Multiplexer 1 chooses one of the four bytes of rs1 as the SBOX module input. The selection value bs is a 2-bit value specified in the instruction encoding. The SBOX module, described in detail later on in this section, performs a one-to-one transformation. The module performs the AES encryption (AES), AES decryption () or SM4 algorithm SBOX transformation based on the selection bits. The following multiplier performs the forward or inverse mixcolumn multiplication of the AES. The SM4 operations module, described in Figure 21, calculates the sm4_ed and sm4_ks values. After that, multiplexers three, four, and five choose one of the values and send the result to the rotate modules. After the value is rotated according to the bs value, the result is XORed with rs1 to generate rd. Figure 21 shows the hardware architecture of the “SM4 operations module”.
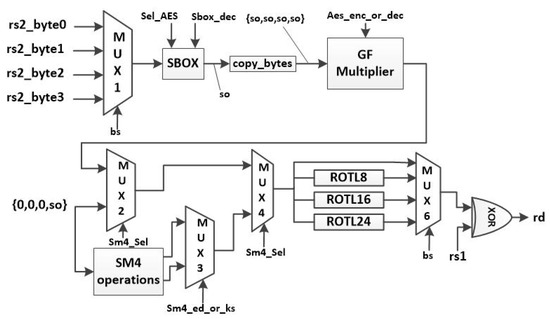
Figure 20.
Hardware implementation of AES and SM4 instructions.
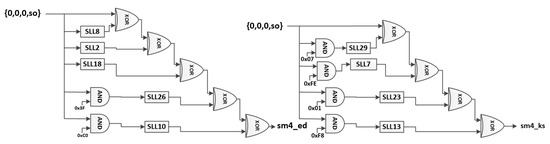
Figure 21.
SM4 operations module.
The SBOX transformations of the algorithms can be performed using finite field arithmetic. The SBOX transformation of AES, , and SM4 algorithms are defined by (4), (5), and (6), respectively. The SBOX module chooses one of these three equations to calculate its output. The equations use affine transformations and require inverse operation in GF() ( ). The affine transformations for the AES, AES , and SM4 algorithms are shown in Figure 22 and Figure 23. In the affine transformation, the B matrix is multiplied with an 8 × 8 matrix, and the result is added to the C matrix. The AES and SM4 algorithms use the irreducible polynomials (7) and (8) for the inverse operation, respectively.
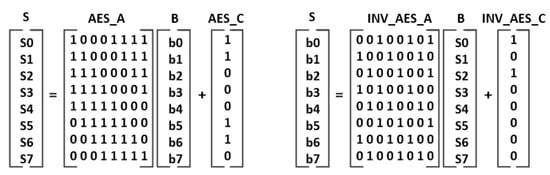
Figure 22.
AES forward and inverse SBOX affine transformations.
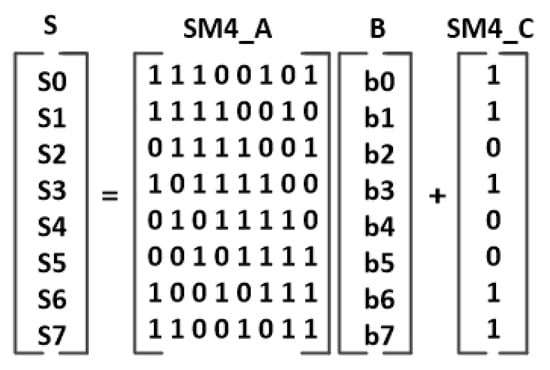
Figure 23.
SM4 affine transformation.
Calculating the inverse of a seventh-degree polynomial modulo an eighth-degree polynomial in GF() is not easy. Therefore, we used the composite field approach to simplify the operations.
Two fields {GF(), + } and {GF(), + } are called a composite field if GF() is constructed from GF(2) by and GF() is constructed from GF() by . A field GF() is isomorphic to the field GF(), therefore mapping between fields is possible using an isomorphic transformation [35]. In our case, we mapped the field GF() to the field GF(), where + x + 9 and + y + 1. After the the mapping, it is possible to perform the operations in GF() and re-map the composite field to the field GF().
The isomorphic transformation is a single matrix multiplication. In our case, the 8-bit element in GF() is multiplied by an 8 × 8 matrix and the result is an 8-bit element in GF().
Although the same mapping, GF() to GF() with and , is performed for both algorithms, we use different ISO matrices for AES and SM4 because they require irreducible polynomials. Since there are no calculated ISO matrices for this operation, we used an algorithm to determine the binary ISO matrices.
Figure 24 and Figure 25 show the binary ISO matrices of the AES and the SM4 algorithms, respectively. To find the ISO matrices, we used the algorithm described in Section 2.2 of [35].

Figure 24.
AES binary matrices for forward and inverse ISO transformation.
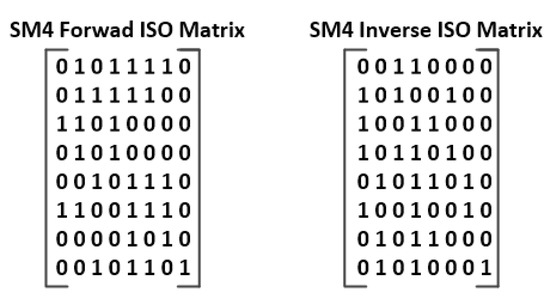
Figure 25.
SM4 binary matrices for forward and inverse ISO transformation.
Figure 26 demonstrates the hardware architecture of the SBOX module shown in Figure 20. The architecture implements the SBOX transformations of the algorithms shown in (4)–(6). Although it implements three SBOX transformations (AES, , SM4), the architecture uses a single inverse module with selection of the appropriate input, reducing the hardware area cost.
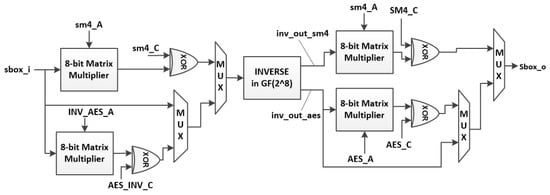
Figure 26.
SBOX module.
Figure 27 demonstrates the inverse in the GF() module. As explained before, the inverse operation is performed in the composite field, GF(). First, the elements in GF() are mapped to the composite field, then the inverse operation is performed in GF(), and finally, the elements are mapped back to GF().
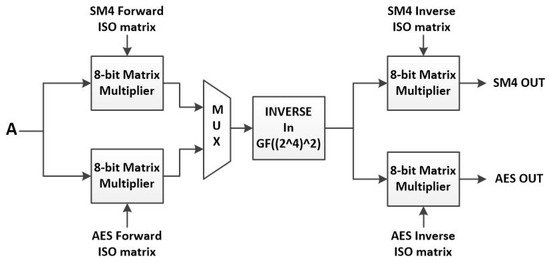
Figure 27.
Hardware architecture of “inverse in ” module.
Equation (9) [36] shows the inversion in GF(), where and are the lower and upper 4 bits of the 8-bit input , respectively. is constant nine due to .
Figure 28 shows the hardware architecture of the inverse operation in GF(). The architecture implements (9). All the operations are performed in GF(), modulo , where . The operations are described below.
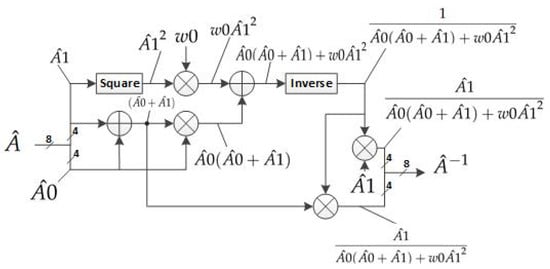
Figure 28.
Hardware architecture of “inverse in GF(” module.
- Multiplication in GF():
Multiplication is implemented as polynomial multiplication mod . We implement the modulus operation by replacing every occurrence of with .
- Square in GF():
To square a number in GF(), we multiply the polynomial of degree four by itself and apply the mod operation. When we take the square of the polynomial A, (Equation (10)), we find the polynomial , (Equation (11)).
- Addition in GF():
The addition operation is implemented as a logical XOR operation.
- Inverse in GF():
The inverse of each element in GF() is calculated by applying modulus to (i = 0 to 15). By doing this, we find the 16 elements listed in Table 3. The inverse of each element is , where . If we multiply a polynomial with its multiplicative inverse, the product is 1.

Table 3.
Inverse of Elements in GF().
7. Results
In this section, we analyze the software and the hardware implementation results and propose an instruction to improve performance. We evaluated the performance of the eleven cryptography algorithms described in Section 3. The algorithms are implemented first using the 32-bit base integer instruction set (rv32i) and then the extended base instruction set (rv32i+crypto). From now on, the “rv32i” and “rv32i+crypto” implementations will be called base and crypto software implementations, respectively. The base software implementations use only the base instruction set [4]. The crypto software implementations use the base instruction set and also a subset of the cryptography instructions. The crypto instructions used for each of the crypto software implementations are specified. The analysis includes clock cycle count (CC), program memory, and static memory requirements.
Using these results, we analyze the gain in performance as a function of the hardware cost for the rv32i+crypto hardware, measured as the acceleration vs. hardware cost for the processor with the cryptography instructions and the new proposed instruction relative to the rv32i hardware. Finally, based on the performance of the software and hardware implementations, we propose a new instruction.
7.1. Clock Cycle Count
The clock cycle count is the total number of clock cycles required to process one block of data with each algorithm on the 5-stage RISC-V processor. The processor is a single-issue, in-order processor and the execution stage requires one cycle for all instructions. Therefore, the clock cycle count is almost equal to the total number of executed instructions. Table 4, Table 5 and Table 6 show the clock cycle count count and the acceleration for the software implementations. The acceleration is computed as the ratio of CC for the base and crypto software implementations. Figure 29 and Figure 30 graphically compare the CC for the block ciphers and hash algorithms, respectively. The results show that the TDEA algorithm requires the highest, and MISTY1 requires the lowest CC among block ciphers. PRESENT has the highest acceleration. MISTY1, CAST-128, HIGHT, and CAMELLIA V1 have almost no acceleration. Some of the algorithms do not have a crypto implementation because the cryptography instructions could not be used to accelerate the algorithms. Clock cycle count and acceleration for these algorithms are stated as NC (Not Calculated).

Table 4.
Clock cycle count of 64-bit block ciphers.

Table 5.
Clock cycle count of 128-bit block ciphers.

Table 6.
Clock cycle count of hash functions.
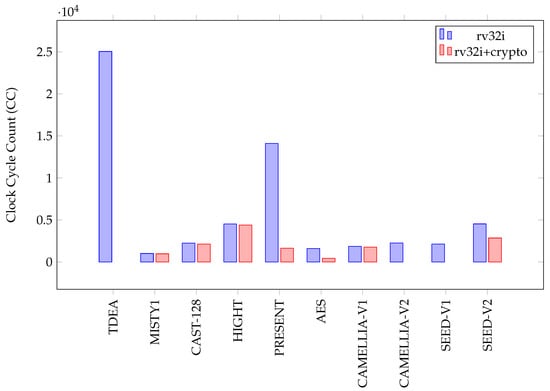
Figure 29.
Clock cycle count of block ciphers.
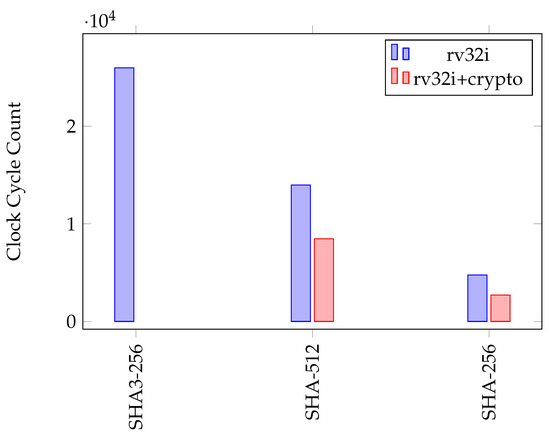
Figure 30.
Clock cycle count of hash functions.
Table 6 shows that SHA3-256 has the highest CC among hash functions.
Table 7 shows the CC of the SBOX address calculation for the SEED implementations. Version-1 and Version-2 of the algorithm use 8 × 8 and 8 × 32 SBOX tables, respectively. Section 4.2 shows how we used the xperm4 instruction to accelerate the address calculation for 8 × 8 SBOX tables. We did not implement the crypto implementation for the 8 × 32 SBOX address calculation. The CC of the address calculation occupies 38% and 18% of the CC of the Version-1 and Version-2 base software implementation of the algorithm, respectively, with a corresponding significant reduction in executed instructions.

Table 7.
Clock cycle count for SEED SBOX address calculation.
The CAMELLIA block cipher contains several rotate operations and address calculation for the 8 × 8 SBOX table. Section 4.3 explains the software implementations of the rotate operations. Table 8 shows the CC for the rotate and address calculation operations for the CAMELLIA-128 encryption algorithm. The clock cycle count of the address calculation occupies 24% and 20% of the CC of Version-1 and Version-2 base software implementations of the algorithm, respectively.

Table 8.
Clock cycle count of CAMELLIA-128 rotate operations.
The CAST-128 block cipher reads the SBOX table 384 times for encrypting one block of data. Address calculation for each of the SBOX read operations requires three instructions in the base software implementation. Section 4.4 explains the SBOX table address calculation for CAST-128. The algorithm uses an 8 × 32 SBOX table, so the address calculation is not accelerated using crypto instructions. Table 9 shows the instruction counts for 32-bit rotate and SBOX address calculations for CAST-128.

Table 9.
Clock cycle count of CAST-128 operations.
One of the key operations for the HIGHT block cipher is the 8-bit rotation. Section 4.3 explains the software implementation of 8-bit rotation. The rv32i+crypto implementation requires 9% fewer instructions (Table 10).

Table 10.
Clock cycle count of HIGHT operations.
Table 11 displays the CC of key operations in TDEA. The CC of the SBOX table read operation includes address calculation and the load instructions that are used to read the data memory. The clock cycle count of the SBOX table read operation occupies 22% of the TDEA base software implementation. It is costly to implement the bit permutation operations with a 32-bit architecture; the clock cycle count of the permutation operations occupies 73% of the TDEA base software implementation.

Table 11.
Clock cycle count of TDEA operations.
Finally, as shown in Table 12, the rv32i+cypto instruction set greatly reduces the CC for the sBoxLayer and pLayer of the PRESENT block cipher.

Table 12.
Clock cycle count of PRESENT operations.
7.2. Program Memory
Table 13 and Table 14 provide program memory requirements of the software implementations of the block ciphers, where the the ratio of program memory requirement of the base software implementation to that for the rv32i+crypto software implementation is shown as Reduction. The program memory is calculated by multiplying the number of instructions in the assembly language program by four (since each instruction is four bytes), with verification by examining the output of the RISC-V GNU Compiler Toolchain. CAMELLIA and SEED-V1 respectively have the highest and lowest program memory requirement. With the rv32i+crypto implementations, PRESENT and AES have low program memory requirements and hence a high reduction ratio compared to the other block ciphers. SHA3-256 requires 6.3 times more program memory than SHA-256, although they generate the same size message digest, as shown in Table 15.

Table 13.
Program memory requirement of 64-bit block ciphers in bytes.

Table 14.
Program memory requirement of 128-bit block ciphers in bytes.

Table 15.
Program memory requirement of hash functions in bytes.
7.3. Static Memory
The static memory required by an implementation is another important factor, especially for embedded applications where memory size is limited. A program’s static memory is allocated at compile time, unlike dynamic memory, which is allocated during execution. In our analyses, the static memory used is calculated by adding up the memory required to store constant values, including, but not limited to, SBOX tables and initialization vectors. The static memory requirement for an algorithm can change based on the implementation. In this study, the AES-128 is implemented with T-tables as described Section 4.1. This approach provides significant acceleration for the algorithm by sacrificing static memory. In general, we attempted to minimize the CC of of the software implementation. Note that the rv32i+crypto implementations do not provide a reduction in static memory requirements: the same constant values are required regardless of the ISA used. Table 16, Table 17 and Table 18 provide the static memory requirements of the algorithms. Due to its 8KB SBOX table, CAST-128 has the largest static memory requirement, while HIGHT and PRESENT have the lowest static memory requirements.

Table 16.
Static memory requirement of 64-bit block ciphers in bytes.

Table 17.
Static memory requirement of 128-bit block ciphers in bytes.

Table 18.
Static memory requirement of SHA algorithms in bytes.
7.4. Analysis for Cryptography Instructions
In Section 5, we grouped the cryptography instructions and described the hardware architecture of each group. Each group of instructions is designed as a separate hardware module, and modules can be added to the RISC-V core in any combination. Table 19 lists the hardware modules with their gate equivalent (GE) area.

Table 19.
Area (GE) of hardware modules.
Table 20 shows the cryptography instructions used for each crypto implementation. The AES, SHA-256, and SHA-512 crypto implementations only use the algorithm-specific instructions. The rest of the implementations use only a subset of the 32-bit cryptography bitmanip instructions. The rightmost column of the table shows the cryptography instruction modules that are used by the crypto implementations. The table shows that some of the cryptography instructions are not used by any crypto implementation. This does not mean that these instructions are not used in other cryptography applications; for example, Shay and Micheal [37] show the usage of a Carry-Less multiply instruction for computing AES in GCM mode.

Table 20.
Cryptography instruction and instruction module extension usage of crypto implementations.
The benefit vs. cost of the additional specialized hardware for rv32i+crypto can be visualized by plotting the acceleration (reduction in clock cycle count) against the relative hardware cost. The relative hardware cost is the area of extended RISC-V core divided by the RISC-V core area. The extended RISC-V core includes modules that are needed by the crypto implementation, specified in Table 20. To calculate the implementations’ hardware cost, we summed the gate equivalent area of each module used in each implementation. For example, to calculate the hardware cost of the AES crypto implementation, we added gate equivalent area of the RISC-V core and the modules for AES and SM4 Instructions. The hardware cost of the base software implementations includes only the area of the RISC-V core module. Figure 31 shows the acceleration vs. the relative hardware cost of the crypto implementations. Compared to implementations with only the base rv32i instruction set, implementations with the cryptography set extension provide 1.5× to 8.6× faster execution speed, at additional hardware cost of less than 9%.
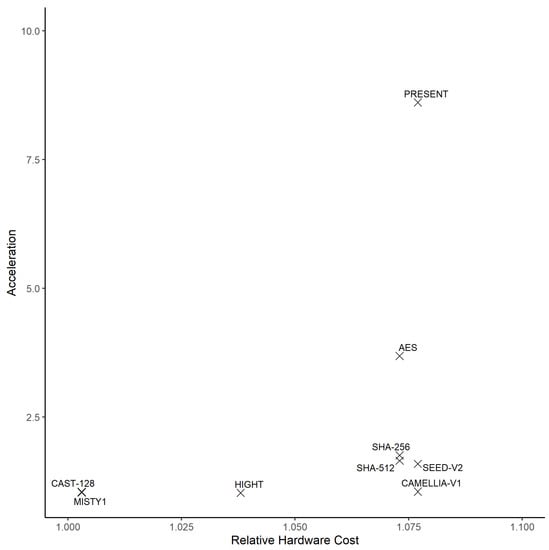
Figure 31.
Acceleration vs. hardware cost of implementation of crypto implementations.
7.5. Proposed New Instruction for SBOX Address Calculation
Section 7.1 shows that address calculation for data memory to read SBOX values is one of the most time-consuming operations. Therefore, we developed an instruction to accelerate the address calculation for 8-bit input SBOX tables. Figure 32 shows the assembly code for the address calculation of 8-bit input SBOX tables using rv32i instructions, where one of the 4 bytes of the 32-bit RS1 register is the SBOX input byte, and the input byte bx is stored in the memory location (bx + offset). The new instruction performs the address calculation operation. Therefore, instead of three instructions, implementation with the new instruction uses one. The implementation with the new instruction (rv32i+PI) uses the 32-bit base integer instructions and the new instruction only. Figure 33 shows the hardware architecture of the address calculation instruction. Similar to the assembly language implementation, the architecture selects one of the four bytes, zero extends the byte and shifts the result left before adding the offset. Table 21 shows the GE area of the architecture.

Figure 32.
Assembly code for address calculation of 8-bit input SBOX tables.
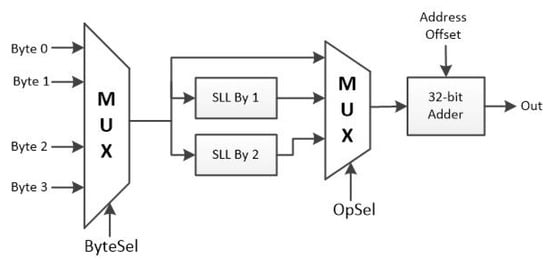
Figure 33.
Hardware architecture of address calculation instruction.

Table 21.
Area (GE) of address calculation instruction hardware module.
Figure 34 compares the clock cycle count for the five software implementations that are implemented with the three different instruction sets. Figure 35 shows the cost-benefit analysis of five software implementations that use the new address calculation instruction. The instruction provides a 1.2× to 1.6× faster execution time for the implementations with an incremental hardware cost of <1.5%.
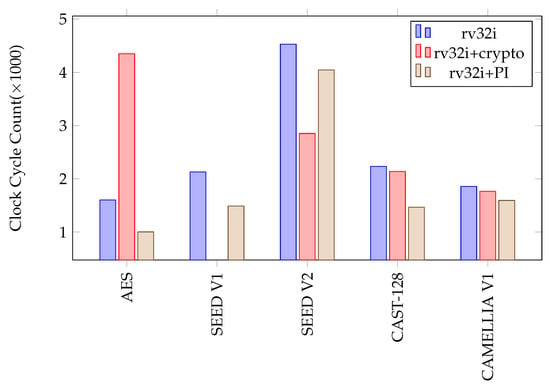
Figure 34.
Clock cycle count comparison.
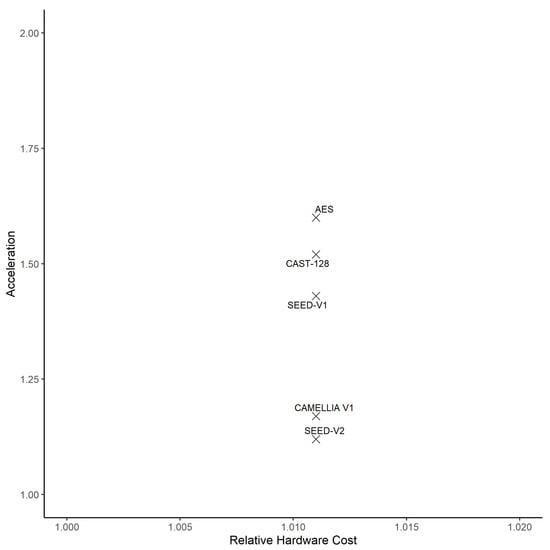
Figure 35.
Acceleration vs. hardware cost of crypto implementations with new address calculation instruction.
In summary, our results show that additional, application-specific hardware for cryptographic primitives can significantly improve execution time performance at a small additional areal cost. We also grouped the cryptographic instructions into modules that enable precise matching of capability to specific sets of algorithms. Moreover, we have demonstrated that just one additional instruction can provide significant improvement based on a careful analysis of algorithmic requirements.
7.6. Conclusion
In this work, we developed software-only algorithms for eleven key cryptographic algorithms using the RISC-V rv32i ISA, and compared the performance of these algorithms to the performance of a RISC-V processor with additional hardware modules that implement specialized instructions for single-cycle execution of cryptographic primitives. Our software implementations reflect a balanced approach between execution speed and code size, with a greater emphasis on execution speed. To this end, we used loop unrolling where it was most effective and did not increase the program memory significantly. Furthermore, all SBOX tables were pre-computed and stored memory rather than calculated on the fly unless there is a specialized instruction that calculates the SBOX value.
For the RISC-V processor augmented with cryptographic hardware, the cryptography instructions were grouped based on their structure, with each group designed as a hardware module. The modular approach allows integration of any subset of modules with the processor. Since each algorithm uses only a subset of the 32-bit scalar cryptography instructions, to assure a valid performance comparison, we determined the module usage of each of the algorithms and evaluated the implementation cost accordingly.
The key technical contributions of this work are:
- Compared to implementations using only the base rv32i instruction set, implementations with the cryptography set extension provide 1.5× to 8.6× faster execution speed and 1.2× to 5.8× less program memory for five of the eleven algorithms. For the remaining six algorithms, the increase in execution speed and reduction in program memory requirement is less than 6%.
- The hardware crypto implementations have an additional hardware complexity of 0.3% to 7.7% over the software implementations using the rv32i ISA.
- The benefit-cost analysis in Figure 31 graphically shows the acceleration of execution time as a function of the relative hardware cost, summarizing the gains in execution time as a function of the costs in terms of hardware complexity for each algorithm. As one illustration of the benefit vs. cost, we see that for the SHA algorithms, we achieve an acceleration of approximately 1.7× at a hardware cost increase of less than 7.5%.
- Based on our analysis of execution times, we proposed a new instruction to accelerate the memory address calculation operations for the 8-bit input SBOX table, which is dominant in the execution time for four of the eleven algorithms. This new instruction provided a 1.2× to 1.6× faster execution time for the four algorithms with only a 1.1% additional hardware cost, as shown in Figure 35.
Our work differs from the previous studies done on cryptographic hardware acceleration support for RISC-V in mainly its completeness. Instead of implementing support for only cryptographic algorithms as in [38], we have implemented support also for permutation instructions, thereby providing a more complete solution for the implementation of any cryptographic algorithm. This approach allows software support and hardware acceleration not only for any symmetric cryptographic algorithm including future standards, but also asymmetric algorithms. The additional cost for permutation instructions is only 4K GE, which is only 8% higher than the area cost of 3.7K GE required for cryptographic instruction support (see Table 19). In comparison, a synthesis of the solution proposed in [38], would require close to 5K GE for cryptographic instructions alone.
The eleven cryptographic algorithms evaluated here have similar structures. For example, none of the algorithms use multiply/divide instructions or floating-point instructions. Some of the cryptography instructions are not used for any of the implementations. However, this does not mean that these instructions are not helpful for other cryptographic algorithms and applications. Therefore, future research should investigate the usability of these instructions for cryptographic algorithms not considered here. Future efforts could also examine implementations of different ISAs for the same set of algorithms, revealing the pros and cons of the RISC-V ISA compared to other ISAs.
Author Contributions
Conceptualization, G.N., P.G.F. and T.Y.; methodology, G.N. and T.Y.; software, G.N.; validation, G.N.; formal analysis, G.N.; investigation, G.N.; resources, G.N, P.G.F. and T.Y.; data curation, G.N. and T.Y.; writing—original draft preparation, G.N.; writing—review and editing, P.G.F. and T.Y.; visualization, G.N.; supervision, P.G.F. and T.Y.; project administration, P.G.F.; funding acquisition, P.G.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by U.S. Air Force Research Laboratory Contract FA8750-19-2-0503.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AES | Advanced Encryption Standard |
| SHA | Secure Hash Algorithm |
| FPGA | Field Programmable Gate Array |
| ISE | Instruction Set Extension |
| ISA | Instruction Set Architecture |
| HDL | Hardware Description Language |
| RTL | Register Transfer Level |
| GF | Galois Field |
| RISC | Reduced Instruction Set Computer |
| PI | Proposed Instruction |
| GE | Gate Equivalent |
| NC | Not Calculated |
References
- History-RISC-V International. Available online: https://riscv.org/about/history/ (accessed on 26 March 2021).
- Waterman, A.; Lee, Y.; Patterson, D.A.; Asanovic, K. UCB/EECS-2011-62; The RISC-V Instruction Set Manual, Volume i Base User-Level Isa; EECS Department: Berkeley, CA, USA, 2011; Volume 116. [Google Scholar]
- RISC-V INTERNATIONAL. Available online: https://riscv.org/ (accessed on 26 March 2021).
- The RISC-V Instruction Set Manual Volume I: Unprivileged ISA 2019, volume 1. Available online: https://riscv.org/wp-content/uploads/2019/12/riscv-spec-20191213.pdf (accessed on 3 August 2022).
- Zeh, A.; Glew, A.; Spinney, B.; Marshall, B.; Page, D.; Atkins, D.; Dockser, K.; Saarinen, M.-J.O.; Menhorn, N.; Deutsch, L.P.; et al. RISC-V Cryptographic Extension Proposals Volume I: Scalar & Entropy Source Instructions Version v1.0.0-rc6. 2021. Available online: https://github.com/riscv/riscv-crypto/releases/tag/v1.0.0-rc6-scalar (accessed on 20 July 2022).
- Zeh, A.; Glew, A.; Spinney, B.; Marshall, B.; Page, D.; Atkins, D.; Dockser, K.; Saarinen, M.J.O.; Menhorn, N.; Newell, R.; et al. RISC-V Cryptographic Extension Proposals Volume II: Vector Instructions. 2020. Available online: https://github.com/riscv/riscv-crypto/releases/tag/v0.7.0 (accessed on 20 July 2022).
- RISC-V Bitmanip Extension Document Version 0.94 Draft. Available online: https://github.com/riscv/riscv-bitmanip/blob/main-history/bitmanip-draft.pdf (accessed on 24 July 2022).
- Pub, N.F. FIPS 197: Advanced Encryption Standard (AES), FIPS PUB 197, US Department of Commerce/NIST, November 2001. 2001. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf (accessed on 3 August 2022).
- Dang, Q. Changes in Federal Information Processing Standard (FIPS) 180-4, Secure Hash Standard. Cryptologia 2013, 37, 69–73. [Google Scholar] [CrossRef]
- Specification of SM3 Cryptographic Hash Function. 2010. Organization of State Commercial Administration of China. Available online: https://www.chinesestandard.net/PDF.aspx/GBT32905-2016 (accessed on 3 August 2022).
- Diffie, W.; Translators, G.L. SMS4 Encryption Algorithm for Wireless Networks. Cryptology ePrint Archive. Paper 2008/329. 2008. Available online: https://eprint.iacr.org/2008/329 (accessed on 3 August 2022).
- Zeh, A.; Glew, A.; Spinney, B.; Marshall, B.; Page, D.; Atkins, D.; Dockser, K.; Saarinen, M.J.O.; Menhorn, N.; Newell, R. RISC-V Cryptographic Extension Proposals Volume I: Scalar & Entropy Source Instructions Version 0.7.2. 2021. Available online: https://github.com/riscv/riscv-crypto/releases/tag/v0.7.2-scalar (accessed on 3 August 2022).
- Saarinen, M.J.O. A Lightweight ISA Extension for AES and SM4. arXiv 2020. arXiv.2002.07041. [Google Scholar]
- Marshall, B.; Newell, G.R.; Page, D.; Saarinen, M.J.O.; Wolf, C. The Design of Scalar AES Instruction Set Extensions for RISC-V. Cryptology ePrint Archive. Paper 2020/930. 2020. Available online: https://eprint.iacr.org/2020/930 (accessed on 3 August 2022).
- Marshall, B.; Page, D.; Hung Pham, T. A lightweight ISE for ChaCha on RISC-V. In Proceedings of the 2021 IEEE 32nd International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Virtual, 7–9 July 2021; pp. 25–32. [Google Scholar]
- Bernstein, D.J. ChaCha, a Variant of Salsa20. In Workshop Record of SASC; University of Illinois: Chicago, IL, USA, 2008; Volume 8, pp. 3–5. Available online: http://cr.yp.to/chacha/chacha-20080120.pdf (accessed on 3 August 2022).
- Steinegger, S.; Primas, R. A Fast and Compact Accelerator for Ascon and Friends. IACR Cryptol. ePrint Arch. 2020, 2020, 1083. [Google Scholar]
- Fritzmann, T.; Sigl, G.; Sepúlveda, J. RISQ-V: Tightly Coupled RISC-V Accelerators for Post-Quantum Cryptography. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 239–280. [Google Scholar] [CrossRef]
- Wang, W.; Han, J.; Cheng, X.; Zeng, X. An energy-efficient crypto-extension design for RISC-V. Microelectron. J. 2021, 115, 105165. [Google Scholar] [CrossRef]
- Stoffelen, K. Efficient Cryptography on the RISC-V Architecture. In Progress in Cryptology–LATINCRYPT 2019; Schwabe, P., Thériault, N., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 323–340. [Google Scholar] [CrossRef]
- Kuo, Y.M.; Garcia-Herrero, F.; Ruano, O.; Maestro, J.A. RISC-V Galois Field ISA Extension for Non-Binary Error-Correction Codes and Classical and Post-Quantum Cryptography. IEEE Trans. Comput. 2022. [Google Scholar] [CrossRef]
- Saraiva, D.A.F.; Leithardt, V.R.Q.; de Paula, D.; Sales Mendes, A.; González, G.V.; Crocker, P. PRISEC: Comparison of Symmetric Key Algorithms for IoT Devices. Sensors 2019, 19, 4312. [Google Scholar] [CrossRef] [PubMed]
- Barker, E.; Mouha, N. Recommendation for the Triple Data Encryption Algorithm (TDEA) Block Cipher; NIST Special Publication 800-67 Revision 2; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017. [Google Scholar] [CrossRef]
- Matsui, M. New block encryption algorithm MISTY. In Fast Software Encryption; Biham, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 54–68. [Google Scholar] [CrossRef]
- Adams, C. The CAST-128 Encryption Algorithm. Available online: https://www.ietf.org/rfc/rfc2144.txt (accessed on 3 August 2022).
- Hong, D.; Sung, J.; Hong, S.; Lim, J.; Lee, S.; Koo, B.S.; Lee, C.; Chang, D.; Lee, J.; Jeong, K.; et al. HIGHT: A New Block Cipher Suitable for Low-Resource Device. In Cryptographic Hardware and Embedded Systems-CHES 2006; Goubin, L., Matsui, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 46–59. (accessed on 3 August 2022). [Google Scholar] [CrossRef]
- Bogdanov, A.; Knudsen, L.R.; Leander, G.; Paar, C.; Poschmann, A.; Robshaw, M.J.B.; Seurin, Y.; Vikkelsoe, C. PRESENT: An Ultra-Lightweight Block Cipher. In Cryptographic Hardware and Embedded Systems-CHES 2007; Paillier, P., Verbauwhede, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 450–466. (accessed on 24 July 2022). [Google Scholar] [CrossRef]
- Aoki, K.; Ichikawa, T.; Kanda, M.; Matsui, M.; Moriai, S.; Nakajima, J.; Tokita, T. Camellia: A 128-Bit Block Cipher Suitable for Multiple Platforms—Design andAnalysis. In Selected Areas in Cryptography; Stinson, D.R., Tavares, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 39–56. (accessed on 20 July 2022). [Google Scholar] [CrossRef]
- Lee, S.; Yoon, J.; Cheon, D.H.; Lee, J.; Lee, H. The SEED Encryption Algorithm. RFC 4269. 2005. Available online: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.374.1600 (accessed on 24 July 2022). [CrossRef]
- Dworkin, M. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; FIPS PUB 202. Federal Information Processing Standards Publication. Information Technology Laboratory National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. Available online: https://www.nist.gov/publications/sha-3-standard-permutation-based-hash-and-extendable-output-functions (accessed on 3 August 2022). [CrossRef]
- Wolf, C.; Glaser, J.; Kepler, J. Yosys-a free Verilog synthesis suite. In Proceedings of the 21st Austrian Workshop on Microelectronics (Austrochip), Linz, Austria, 10 October 2013. [Google Scholar]
- ISO/IEC 18033-3:2010; Information Security—Lightweight Cryptography—Part 3: Block Ciphers. ISO: London, UK, 2010.
- ISO/IEC 29192-2:2019; Information security—Lightweight Cryptography—Part 2: Block Ciphers. ISO: London, UK, 2019.
- Daemen, J.; Rijmen, V. AES Proposal: Rijndael 1999. AES Submission Document on Rijndael. Available online: https://csrc.nist.gov/csrc/media/projects/cryptographic-standards-and-guidelines/documents/aes-development/rijndael-ammended.pdf (accessed on 3 August 2022).
- Paar, C. Efficient VLSI Architectures for Bit-Parallel Computation in Galois Fields. PhD Thesis, Institute for Experimental Mathematics, University of Duisburg-Essen, Essen, Germany, 1994. [Google Scholar]
- Canright, D. A Very Compact S-Box for AES. In Cryptographic Hardware and Embedded Systems–CHES 2005; Rao, J.R., Sunar, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 441–455. [Google Scholar] [CrossRef]
- Gueron, S.; Kounavis, M.E. Intel® Carry-Less Multiplication Instruction and Its Usage for Computing the GCM Mode. White Paper, April 2014. Revision 2.02. Available online: https://www.intel.com/content/dam/develop/external/us/en/documents/clmul-wp-rev-2-02-2014-04-20.pdf (accessed on 3 August 2022).
- RISC-V Cryptography Extensions Standardisation Work. 2022. Available online: https://github.com/riscv/riscv-crypto (accessed on 24 July 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).