Abstract
The influx of wearable sensor devices has influenced a new paradigm termed wearable health crowd-sensing (WHCS). WHCS enables wearable data collection through active sensing to provide health monitoring to users. Wearable sensing devices capture data and transmit it to the cloud for data processing and analytics. However, data sent to the cloud is vulnerable to on-path attacks. The bandwidth limitation issue is also another major problem during large data transfers. Moreover, the WHCS faces several anonymization issues. In light of this, this article presents a batch processing method to solve the identified issues in WHCS. The proposed batch processing method provides an aggregate authentication and verification approach to resolve bandwidth limitation issues in WHCS. The security of our scheme shows its resistance to forgery and replay attacks, as proved in the random oracle (ROM), while offering anonymity to users. Our performance analysis shows that the proposed scheme achieves a lower computational and communication cost with a reduction in the storage overhead compared to other existing schemes. Finally, the proposed method is more energy-efficient, demonstrating that it is suitable for the WHCS system.
1. Introduction
The evolution of mobile technology has enabled continuous physiological data collection in a vital-sign monitoring system, lowering healthcare expenses and improving disease management. The cost-effectiveness of vital-sign monitoring systems for the collective wellbeing of the populace has triggered a new health phenomenon known as wearable health crowd-sensing (WHCS) [1]. WHCS is an approach involving a broader group of dispersed audience that utilizes wearable devices with embedded health sensors to provide continuous monitoring with the extraction of personal health data to promote data sharing and analysis. WHCS has numerous advantages in terms of minimizing data acquisition costs, making it possible for researchers and businesses to obtain data for analysis without investing large sums of money. Cloud computing for WHCS is an intriguing solution for data storage and analysis. It provides lower data storage and maintenance costs with constant availability of computing resources, enabling users to access cloud resources at their leisure. Considering the scenario presented in Figure 1, sensors are deployed on a patient to collect vital signs. The gateway transmits the collected data from the sensors to the aggregator. The gateway is a transmission medium that transfers wearable data using wireless technology such as WIFI, cellular communication, and the Bluetooth technology. The gateway in the scenario can be a mobile device with storage, battery, and network capabilities that can serve as a communication link between the wearable devices and the aggregator. The aggregator garners the wearable data from the gateway and processes it into batches before releasing it to the cloud. The cloud acts as a repository for data storage as well as the provision of data analytics. As the cloud server is semi-trusted and susceptible to cyber-attacks, what is the guarantee that the data received from the cloud server will be the original data obtained directly from the wearable sensors? Despite the efficient functionality of cloud-based WHCS, it is not without drawbacks. First and foremost, the transfer of large amounts of generated wearable data is limited by low bandwidth in network-constrained domains. As a result, pending wearable data may be abandoned due to network congestion. Moreover, wearable devices cannot conduct high-level programming tasks on the massive amounts of generated data due to their tiny size and lack of computational resources. In addition, on-path attackers, such as man-in-the-middle (MITM) and man-in-the-mobile (MITMO) attacks, may intercept and modify transmitted data from wearable devices to the cloud. Typically, these attackers capture host devices to filter user data and redirect the filtered information to the attacker’s web server. The Zeus malware is a prime example. Again, crowd-sensing systems face anonymization issues whereby the private information of a user is extracted from the collected data before it reaches the cloud. The extracted confidential information includes the user’s name, location, and IP address. In this case, the private information can be traced to identify the legitimate data owner, causing a breach of privacy [2].
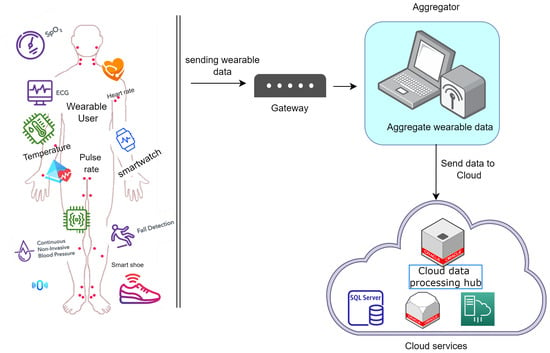
Figure 1.
Wearable health crowd-sensing platform.
Even though public-key infrastructure (PKI) can provide WHCS with data security benefits, it is not without security issues. PKI offers the benefits of confidentiality, integrity, and authenticity. Nevertheless, identity and certificate management issues affect the traditional PKIs [3] thereby leading to an increase communication overhead. Additionally, a certificate authority can compromise the private key of a user. Consequently, Boneh and Franklin [4] introduced Identity-Based Cryptography (IBC) to address the shortcomings of traditional PKIs. With IBC, a private key generator (PKG) derives the complete private keys for users based on the PKG’s master secret key. However, the dependence of PKGs on user-generated private keys introduces the inherent key escrow problem. Thus, a malicious PKG can compromise the user’s identity due to its exclusive ability to generate private keys. Al-Riyami and Patterson [5] proposed certificateless cryptography (CLC) to address the inherent key escrow problems in IBC and resolve certificate management issues in traditional PKI. The concept arose from searching for public-key schemes that do not rely on certificates and lack the key escrow feature of identity-based cryptography (IBC). CLC provides security for WHCS by bridging the gap between traditional PKI and IBC. Using the CLC method, the PKG and the system user jointly generate private and public keys. Thus, the PKG does not possess the complete private key of the user, but generates a partial private key that is sent to the user. The user, therefore, derives their private key through self-selected security parameters and the partial private key obtained from the PKG. CLC [5] being a variant of IBC, offers non-repudiation, and supports lightweight infrastructures, such as wearable systems. Moreover, the CLC is highly desirable for deployment in situations with low bandwidth. Motivated by the addressed concerns, the main contributions of the proposed article is outlined as follows:
- Firstly, this article proposes a batch processing technique based on certificateless cryptography for the wearable health crowd-sensing (WHCS) system. The batch processing technique uses aggregate authentication and verification procedure to improve bandwidth limitation issues in large data transfers.
- Secondly, the proposed scheme provides anonymity by obscuring users’ identities during data transmission. In obscuring the user’s identity, the wearable device and the aggregator perform anonymous computation on the user’s identity to derive anonymity tuples before sending the user’s wearable data to the cloud.
- The formal security analysis proves the scheme is resistant to forgery and replay attacks, assuming that the Computational Diffie-Hellman (CDH) problem is hard to solve by a probabilistic polynomial-time (PPT) attacker in the random oracle model (ROM).
- Additionally, results from our performance evaluation have shown the proposed method to be more efficient than other existing batch processing schemes, reducing computational and communication costs while achieving less storage overhead.
- Results from our power consumption analysis prove the proposed scheme to be energy efficient, making it suitable for network bandwidth environments.
The article’s organization is as follows: Section 2 summarises existing research in wearable health crowd-sensing. Section 3 focuses on the preliminaries and definitions of the underlying basic syntax. Section 4 presents the system architecture, the design objectives and the scheme construction. Section 5 examines the security proofs of the proposed scheme. Section 6 highlights the performance evaluation of the scheme. Section 7 contains the discussion, while Section 8 concludes the work.
Motivation
Considering the global pandemic crisis, many people cannot live normal lives due to the restrictive nature of COVID-19 rules. Most governments have enforced rigorous rules to curb the spread of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Even though most individuals were forced to work from home, some governments imposed lockdowns while initiating a social distancing strategy on the general populace. As such, most advanced nations, such as China, the United States, et cetera, have established mass-testing procedures to prevent the spread of the virus to identify infected people. While mass testing has proven to be an effective method, there are some concerns: for example, the movement of health professionals during mass testing becomes costly in terms of logistics, and occasionally, there is a lack of health professionals to participate in the mass testing exercise. So, using a crowd-sensing strategy to identify citizen complaints is an excellent way to discover possible emergencies and solutions. Moreover, using wearable smart devices for pre-symptomatic detection [6] and contact tracing [7] can help crowd-sensing methods to obtain data so that governments can make informed decisions on epidemic control [1]. Although prior studies on public-key cryptography have shown the practicability of WHCS, there are still existing issues that need to be addressed. Either the existing solutions are too computationally intensive, introducing extra communication overhead for wearable devices, or the security of anonymity is overlooked. As a result, this article presents a batch processing scheme based on certificateless cryptography (CLC). CLC is an ideal PKC primitive that is designed to support lightweight infrastructure [5]. Constructing a batch processing scheme using certificateless cryptography is an ideal solution for bandwidth issues during large data transfers. Consequently, the CLC method is suited for low-power smart devices such as wearable systems. Meanwhile, the provision of anonymity is not left out. The proposed batch solution performs anonymous calculations to users’ identities before relaying the collected data to the cloud for storage and analysis. Another significant advantage is eliminating the inherent key escrow since private key generation is not solely left on the key generation server (KGS). However, the user is responsible for deriving their full private keys from their identity and the partial private key produced by the KGS. Lastly, the batch processing method can protect users against forgery and replay attacks initiated by cyber adversaries.
2. Summary of Existing Research
Wearable health crowd-sensing (WHCS) has been inspired by the incorporation of artificial intelligence (AI) analytical capabilities into wearable devices, whereby users generate a substantial amount of wearable data utilizing monitoring sensors. The generated data is sent to the cloud for processing and analysis, enabling enterprises to make more informed decisions by detecting customer demands and determining how to satisfy them. Several existing works tackle crowd-sensing paradigm-related concerns.
The survey presented by Liu et al. [8] examined crowd-sensing strategies on mobile networks. In the mobile crowd-sensing IoT, the observed resource utilization concerns, precisely bandwidth issues resulting from the generation of vast amounts of data. Cecilia et al. [1] also described how crowd-sensing approaches were applied in Spain to detect COVID-19 early warning indications. In addition, Owoh et al. [9] provided a security study for crowd-sensing networks that rely on end-to-end encryption. His scheme design was based on a symmetric method but he did not demonstrate how the scheme could ensure user security. As security and confidentiality are essential in wireless communications, Daojing et al. [2] highlighted anonymization issues in crowd-sensing networks. The paper considered how an organization (PEPSI) uses an Identity-Based Encryption (IBE) method to encrypt a user’s information before sending the information to the service provider. One major flaw of this approach is the inherent key escrow in IBE. Kamil et al. [10] introduced a lightweight aggregation certificateless signature strategy for crowd-sensing that is more resistant to possible attacks such as replay, MITM, and impersonation attacks. Pius et al. [11] also presented a security framework for mobile crowd-sensing applications. However, the authors in [11] did not provide a security proof to demonstrate the security of their scheme. The scheme does not solve the pertinent crowd-sensing issues of bandwidth, anonymization, and other security problems. Although their scheme was constructed using encryption, it required more heavy computational operations with an extra communication overhead. Li et al. [12] also presented a de-duplication protocol to identify and remove duplicates for edge-assisted crowd-sensing services. Their protocol prevents the leakage of linked, duplicated data.
Ni et al. [13] also proposed a robust privacy-preserving crowd-sensing called SPOON. In SPOON, the service providers recruit mobile users based on their locations and select appropriate sensing reports depending on their trust levels without compromising user privacy. Sensing tasks are protected with proxy re-encryption and BBS+ signature to prevent privacy leakage.
The authors in [14] examined a security flaw in an existing scheme and designed a certificateless signature scheme (CLS) without map-to-point (MTP) and Random Oracle (ROM) to address data authenticity issues at the same time providing data crowd-sensing security for cloud-assisted Industrial Internet of Things (IIoT) applications. Shim et al. [15] proposed an obfuscatable anonymous authentication model to address device capture attacks when mobile devices are misplaced. The authors created an obfuscated authentication procedure to transform the authentication request algorithm into an unintelligible form. Their method provides users with authenticity and unlinkability by applying encrypted group signature and linear encryption.
Although Certificateless Cryptography (CLC) methods are well-suited for low-resource devices and low-bandwidth applications, several aggregate CLC algorithms do not support complete batch processing. For instance, Kumar et al. [16] presented a certificateless aggregate signature scheme for healthcare wireless sensor networks (CASS-HWSN). The proposed approach is energy efficient in the healthcare wireless sensor networks (HWSN). However, the scheme only satisfies partial batch processing. Their scheme also incurred extra verification costs as the number of participants in the network grows making it unfeasible for healthcare wireless sensor networks. Similarly, Asari et al. [17], proposed hierarchical anonymous certificateless authentication protocol (HACA) to achieve anonymity. Their protocol maps distinct identities to various pseudonyms. However, their analysis presented the aggregate verification feature but excluded the aggregate authentication method, which does not satisfy the complete batch processing procedure.
3. Preliminaries
3.1. Bilinear Pairings
The concept of bilinear pairings was originally introduced by Joux [18] in his proposal of a pairing-based three-party key-exchange protocol. As used in the scheme construction, this subsection defines the underlying concept of bilinear pairing. A pairing (also known as Bilinear pairing) is bilinear map of where denotes an additive cyclic group and denotes a multiplicative cyclic group both of prime order q having a generator [19]. The bilinear map is an admissible map if it satisfies the following properties:
- Bilinearity: and , then . where (a times) and (b times) where are scalar multiplication in the additive group [4].
- Non-degeneracy: a bilinear pairing is non-degenerate if all the pairs in do not map to the pairs in where is the identity element of .
- The algorithm should be efficiently computed, such that , there exists an efficient algorithm to compute that . Such a mapping is called a bilinear mapping which can be constructed using the Weil or Tate Pairings [20].
3.2. Hardness Assumption
The hardness of the proposed algorithm is based on the following assumption:
Computational Diffie–Hellman Assumption (CDH) in Given for some unknown , the goal of the adversary is to compute . The success probability of any probabilistic polynomial time algorithm in solving the CDH problem is defined as where .
3.3. Formal Definition of a Certificateless Signature Scheme (CLS)
We present the construction of the proposed scheme based on the generic model of a CLS scheme in [5]. The mathematical symbols used in the CLS are shown in Table 1. The CLS model consists of two entities, the KGS (key Generation Server) and the User (U), who execute the CLS algorithm. The algorithm consists of Setup, Partial-Private Key Extract, Set-secret value, Set-private key, Set-public key, Sign, Verify.

Table 1.
Notations and description of abbreviated text.
- Setup ]: The KGC takes a security parameter and runs the setup algorithm to return params and . It keeps secret and publicly publishes .
- Partial-Private-Key extract ]: The KGC takes , and the identity of as input. It returns a partial private key value and sends it to the user through a secure channel.
- Set-Secret-Value ]: The user (U) runs this algorithm by taking its identity and . It returns as its secret value.
- Set-Private-Key ]: the user (U) takes , , as inputs, and generates a private key as .
- Set-Public-Key ]: the user (U) takes , , as inputs, and returns as public key.
- Sign ]: The user (U) signs a message m by taking identity ,a private key as inputs and generates a valid signature as . It sends the signature value to the KGS through a secure channel.
- Verify ]: The KGS receives and performs the verification algorithm by taking the user’s identity , public key to obtain the message m. It checks if received from the user is a valid signature. It returns true for a valid signature and returns false for an invalid signature. It therefore rejects the message if the signature is invalid.
3.4. Security Model
The hardness of our scheme is based on the security model of a certificateless cryptography (CLC) addressed in [5,21] which considers two adversaries: modeled as a Type 1 adversary and modeled as a Type 2 adversary capable of forging the signature.
- Adversary depicts a dishonest user who does not have access to the master secret key , but may request public keys and replace public keys of its choice, extract partial private keys, extract private keys and make forge queries on signatures of identities of its choice.
- Adversary represents a mistrusted KGS, which has, access to the master key but does not perform public key replacement. It has the ability to compute partial private keys having the master secret key. However, it is restricted not to replace public keys and make private key extraction queries.
3.4.1. Game 1
In Game 1, adversary makes queries to the hash oracles, queries to extract Partial Private Key, makes Private Key queries, performs public key replacement and forge queries to the sign oracle. The challenger runs the Setup, Attack and Forgery algorithms as follows:
- Setup: The challenger takes a security parameter as input, and runs the setup algorithm to obtain the master secret key and generate the system parameters . The challenger keeps secret, and sends to .
- Attack: The adversary challenges the oracle by making the following queries:
- Create User: If an identity has already been created, then there is nothing to be done. Otherwise the oracle runs the Private-key extract, Set-secret value, Set-public key algorithm to obtain a secret value , a partial private key and returns the as the public key.
- Hash Queries: the adversary make hash queries to the hash oracles.
- Extract partial private key queries: The adversary makes a request on the partial private key on chosen identity . The oracle runs the query and returns , if has been created, otherwise it returns a null ∅.
- Set Secret value: The adversary makes a request on a chosen . The oracle returns as the secret value if the identity has been created. Otherwise it returns a null ∅.
- Private-key-Extraction: On input of an arbitrary identity it returns to the adversary if has been created. Otherwise it returns a null ∅.
- Replace public key: the oracle runs this query and replaces the public key on the requested identity .
- Sign: Adversary makes a query on a chosen identity , a message m and .
- If has been created, it outputs a signature such that .
- If has not been created, it returns an ∅.
- Forgery: Adversary outputs a forgery on and wins the game if =, has never been queried or has never been submitted to the Partial private key oracle.
Definition 1.
Let be the advantage of a Type I adversary adaptively winning chosen messages and chosen identities attack in the above security game, where coin tosses are made by the challenger. We say a certificateless signature scheme is secure against Type I adversary in the random oracle model (ROM), if, for all probabilistic polynomial-time (PPT) adversary , the success probability of is negligible.
3.4.2. Game 2
Similarly in Game 2, adversary makes queries to the hash oracles, makes Private Key queries, performs public key replacement and forge queries to the sign oracle. The challenger runs the Setup, Attack and Forgery algorithms as follows:
- Setup: The challenger takes as input a security parameter , and runs the setup algorithm to obtain the master secret key and the system parameters . The challenger keeps secret, and sends to .
- Attack: Adversary makes similar queries defined in Game 1 in Section 3.4.1 but does not query the partial private key extract.
- Sign: makes a query on a chosen identity , a message m and and returns a signature as in the sign phase of Game 1 in Section 3.4.1.
- Forgery: adversary outputs a forgery on and wins the game if , has never been queried or has never been submitted to the Partial private key oracle.
Definition 2.
Let be the advantage of a Type II adversary adaptively winning the chosen messages and chosen identities attack in the above security game, where the challenger tosses a coin. We say a certificateless signature scheme is secure against Type II adversary in the random oracle model (ROM), if, for all probabilistic polynomial-time (PPT) adversary , the success probability of is negligible.
3.5. System Requirements
To achieve secure data transmission in WHCS system, the following security requirements must be achieved:
- Non-repudiation: it is noteworthy that the entities existing within the wearable health crowd-sensing(WHCS) system do not deny accessing the system resources for authentication to share wearable data.
- Resistance to forgery attacks: this feature requires the inability of any known adversary of forging valid individual and aggregate signatures from the wearable data.
- Resistance to Replay attacks: the feature prevents an adversary from replaying a message during message interception to modify the wearable data.
- Data Privacy: although our scheme requires the user to submit its identity for authentication, we assume the medical cloud server cannot leak the private information of the user.
- Anonymity: it requires that the identity of user is not revealed during message transfer from the wearable device onto the medical cloud server.
- Aggregate Authentication and verification: The medical cloud server is able to authenticate large wearable sensor data simultaneously. Likewise, aggregate message–signature pair can be verified through aggregate verification.
4. System Architecture
This section provides an overview of the system architecture of the proposed scheme. It first introduces the entities and describes their respective roles in the system. Secondly, it discusses the design objectives and finally presents the scheme description.
4.1. Entity Roles
According to Figure 2, the system entities consist of a wearable device (WD), a user (U), an aggregation unit (AU), and a medical cloud server (MCS). We give a brief description of their roles in the system.
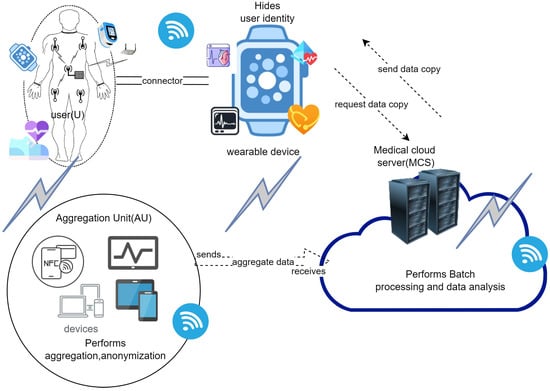
Figure 2.
Wearable health crowd-sensing system architecture.
- Wearable device (WD): The wearable device is equipped with micro-sensors to monitor and detect the user’s physiological data. It performs sensing functions such as monitoring heartbeat and detecting health abnormalities such as COVID-19 symptoms. It serves as the collection point to collect all the captured wearable sensor data. It performs anonymity computations to hide the user’s identity before submitting the wearable data to the aggregation unit.
- User (U): The user represents the device owner who wears the wearable device for daily personal health monitoring. The user can request a copy of their data from the medical cloud server.
- Aggregation unit (AU): The aggregation unit consists of the user’s mobile devices that aggregates all the received wearable sensor data from the wearable device. Since the mobile device is computationally powerful than the wearable device, it is designated to perform aggregation functions. It also performs anonymous computation to generate an anonymity tuple, which conceals the user’s identity before transferring the wearable sensor data to the medical cloud server.
- Medical cloud server (MCS): The medical cloud server represents the trusted cloud model. It receives the aggregated wearable sensor data from the aggregation unit and performs batch processing functions on the received data. It also stores and analyzes the received wearable sensor data. It sends a copy of the user’s data based on the user’s request.
Design Objectives
A wearable health crowd-sensing (WHCS) system provides constant health monitoring to wearable device users in remote environments. The system tracks a user’s health by using a wearable device to capture the physiological data of the user’s daily activities. It facilitates the early detection of health abnormalities, prompting health responders to provide a quick diagnosis. The wearable device collects the captured wearable sensor data and transmits the data to the aggregation unit. The aggregation unit then gathers all the captured data from the wearable devices, performs anonymization algorithms on the user’s identity, and sends it to the medical cloud server for data processing and storage. Notably, the aggregation unit comprises mobile devices (such as smartphones, tablets, and iPads). In addition, current mobile devices are computationally equipped to perform edge computing tasks, which is why they are adopted to perform aggregate authentication functions in the WHCS. In the WHCS, the wearable device cannot process massive physiological data due to its resource-constrained nature. Similarly, the lack of computational power prevents them from processing extensive data. More so, transmitted data is constantly vulnerable to various adversarial attacks. Finally, the massive wearable sensor data transfer creates bandwidth constraints in the WHCS network environment. The constructive batch processing method, which relies on certificateless cryptography (CLC), is adopted to address these concerns and resolve the bandwidth limitation issues during data transfer. In order to provide anonymity to users, the wearable device obscures the user’s identity before transmitting the wearable data to the aggregation unit. The aggregation unit also hides the user’s data for the second time before finally relaying the wearable data onto the medical cloud server. Consequently, the CLC method is designed to suit light portable systems such as wearable devices.
4.2. Scheme Construction
This subsection describes the scheme generation according to Figure 3. According to [5], a certificateless signature consists of five stages, namely: setup, partial-private key derivative, key generation, signing, and verification. The proposed batch processing wearable health crowd-sensing scheme consists of seven stages, namely: setup, partial-private key derivative, key generation, aggregation unit registration, anonymity computation, signing, verification, and batch processing. The anonymity computation is executed by both the wearable device and the aggregation unit. The batch processing comprises both aggregate authentication and aggregate verification.
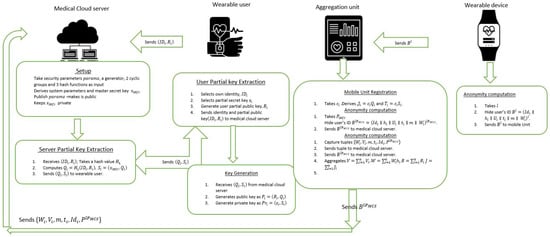
Figure 3.
The process flow of system architecture.
- Setup : The medical cloud server (MCS) executes the setup algorithm by taking a security parameter as input. The MCS defines two cyclic groups and where is an additive group and is a multiplicative group of prime order q. With P as a generator, MCS constructs a bilinear pairing . It selects as its master secret key and derives its corresponding master public key as . It returns a master private/public key pair as . It chooses three one-way hash functions and generates system parameters as . It publicly publishes and keeps private. Refer to (Algorithm 1).
- Partial-Private Key Derivative: This algorithm comprises of two steps.
- (a)
- In the first step, the user(U) chooses and computes . It sets the partial public parameters as and sends it to the medical cloud server as seen in (Algorithm 2).
- (b)
- The medical cloud server(MCS) receives from the user and calculates the partial private key for the user as , where .It sends through a secure channel to the user(U). Refer (Algorithm 3).
- Key Generation: The user(U) executes the key generation algorithm by generating its full public/private key pair where and after obtaining from the MCS. From (Algorithm 4).
- Aggregation unit Registration: The aggregation unit (which comprises of the user’s mobile devices) randomly selects , and registers itself to the medical cloud server (MCS) by computing where and . Reference (Algorithm 5).
- Anonymity Computation: The wearable device initially hides the user’s identity by computing, and sends to the aggregation unit (AU). The aggregation unit (AU) in turn computes to hide the user’s identity for the second time. The aggregation unit(AU) sends the tuple to medical cloud server (MCS). Reference (Algorithms 6 and 7).
- Signing: The user takes its private key , and signs its wearable sensor data m, by taking a nonce , applying a timestamp , and signs the wearable sensor data as in Algorithm 8). It returns a signature value and sends to the medical cloud server (MCS). Reference in (Algorithm 8).
- Verification: The medical cloud server(MCS) receives both and the signature .
- (a)
- After receiving the tuple from the AU, the checks the validity of the tuple through the timestamp, . If the timestamp has elapsed, that means the tuple is invalid and hence rejects it. Else, it accepts the tuple and computes it as .
- (b)
- It also verifies signature and checks the equation: . It accepts the signature, if it is valid. Otherwise it rejects it. Refer to (Algorithm 9).
- Batch Processing: The aggregate authentication and verification occur at this stage. In the aggregate authentication, the identities of the individual users, with their corresponding public keys and generated signature values, are aggregated by their respective aggregation units and sent to the medical cloud server for verification.
- (a)
- Aggregate authentication: The respective aggregation units aggregates all messages from the respective users n having identities with corresponding public keys . It then transmits them onto the medical cloud server (MCS).
- (b)
- Aggregate Verification: the medical cloud server (MCS) performs the aggregate verification algorithm to verify the received accumulated tuples and the received wearable sensor data from the aggregation units.
The scheme algorithm is described below:
| Algorithm 1: Setup (Run by Medical cloud Server) |
|
| Algorithm 2: Partial-Key Extraction Algorithm Part 1 (Executed by U) |
|
| Algorithm 3: Partial-Key Extraction Algorithm Part 2 (Executed by MCS) |
|
| Algorithm 4: Key Generation Algorithm (Run by user) |
|
| Algorithm 5: Aggregation unit Registration (Run by aggregation unit) |
|
| Algorithm 6: Anonymity (performed by Wearable device) |
|
| Algorithm 7: Anonymity (Performed by Aggregation Unit) |
|
| Algorithm 8: Signing (Run by user(U)) |
|
The medical cloud server (MCS) checks for correctness by computing the following:
| Algorithm 9: Verification (Run by Medical cloud Server) |
 |
Batch Processing
The batch processing methods performs both aggregate authentication and aggregate verification by aggregating all the captured wearable sensor data from different wearable devices as follows:
- Aggregate Authentication:The medical cloud server (MCS) receives of each user. Suppose there are n number of users with identities having public keys of with generated signatures as . The authenticated signature values are aggregated as follows:
- (a)
- (b)
- (c)
- (d)
The aggregated values are sent to the MCS for aggregate verification. - Aggregate Verification:After receiving the aggregated signature values, the MCS checks the validity of aggregate signatures by verifying if and performs the correctness equation as follows:
5. Security Proofs and Analysis
5.1. Security Proofs
Theorem 1.
The proposed scheme is existentially unforgeable in the random oracle (ROM) against adversaries and against adaptive chosen-message attack under the CDH problem with the assumption that the CDH problem is hard to solve.
In the random oracle, is an adversary (a probabilistic Turing machine) who can forge the signature in a response–attack game having a running time t and making hash queries to the hash oracles for executing partial private key queries , making private key queries as and signature queries . The Adversary has the advantage of winning the game if it is able to solve the following:
With running time .
Proof of Theorem 1.
Let . The goal is to compute from the tuple with the assumption that there exists an adversary of Type 1 capable of computing the CDH problem. The Adversary cooperates with the Challenger, , in the following ways.
- Setup: The challenger performs a system setup by randomly picking a security parameter , and establishes the system parameters as and sets Before executing the query, maintains a list . A challenged identity is selected at random by the challenger and answer queries made by the adversary based on the following oracles .
- Query: initially creates an empty list containing the tuples . A query is made on and flips a . If , then , else if , and updates the tuples with in both cases. If then chooses and sets but if , then it sets . It finally returns and updates the list
- Query: A query is made on to the oracle. scans the list and checks if the tuple exists. If it exists, returns as answer. Otherwise, picks and returns as answer and updates the list with the tuple .
- Query: A query is made on . checks if the tuple exists in the list . If it exists, is returned to . Otherwise, it picks and returns as a new hash value of and sends to and updates the list with the tuple
- Reveal-Partial-Private-Key makes a query on . flips a coin . If , outputs a failure. Else, if , and contains , checks if . If , returns to . Otherwise, if , recovers from the list and selects , and defines . computes and returns as answer and adds an element to the tuple . It finally updates the list If , and the list does not contain the tuple , then sets , and computes . C adds an element to the tuple and inserts it to and returns as an answer.
- Public-key Queries: A request is made on an identity . On receiving the query, a public key request is selected from the list and checks the tuple if it exists in . checks if . If it holds, selects and sets , and updates the list with . Otherwise, returns to . If is not in , let , then selects and sets . inserts into the tuple and returns as a reply to .
- Secret-key Queries: makes a query on a chosen identity . On receiving a query, checks if and if . If they hold, selects and returns and updates the list . Otherwise, if , sends as a response to
- Query on Public key Replacement: When the adversary submits a query to replace the public key . checks the tuple if the tuple exists in the list and sets and . It updates the list with the tuple If the tuple does not exist in , sets and , it then updates the list with the tuple .
- Sign queries: makes a sign query on an identity with ), searches the tuple from the list . If the list contains , checks whether . If , makes a public-key Query to generate and sets . Otherwise, if the tuple is empty makes a public key query to generate and sets and adds to the list, . It computes the following:
- (a)
- .
- (b)
- .
- (c)
- .
- (d)
- .
and returns as a signature on the message m. - Forgery: Applying the forking lemma, outputs two signatures and where . Therefore, and . tosses a coin , if , outputs a failure and aborts the simulation. Otherwise, computesFrom Equations (3) and (4)Notice that, and .Therefore,Hence, . □
From the above proof, it is computationally hard for a polynomial time-bounded adversary of Type 1, having the probability of solving the CDH problem. Hence, the proposed scheme has proven to be existentially unforgeable against adaptive chosen message attack of the Type 1 adversary in the random oracle under the CDH assumption.
Theorem 2.
The proposed scheme is existentially unforgeable in the random oracle (ROM) against adversaries and against adaptive chosen-message attack under the CDH problem with the assumption that the CDH problem is hard to solve. For the Type 2 adversary , the proposed scheme is existentially unforgeable against adaptive chosen message attacks in the random oracle with the assumption that the CDH problem is hard to solve. For a polynomial time-bounded adversary having an advantage ε of forging the signature of the proposed is negligible after making the following queries to the random oracle, to the hash oracles for executing partial private key queries , making private key queries as and signature queries . The Adversary has the advantage of winning the game if it is able to solve the following:
With running time .
The proof of Theorem 2 is similar to the proof of Theorem 1.
5.2. Analysis
- denotes an event in which the adversary queries the partial private key which results in the probability of . The success probability of occurring is .
- denotes an event in which the adversary makes sign queries .
- indicates an event in which the adversary has queries to the private keys =. The success probability of occurring is . The success probability of winning the game is
5.3. Security Requirements Analysis
- Non-Repudiation: The proposed scheme satisfies non-repudiation since the wearable user cannot deny signing its wearable sensor data to the medical cloud server. Neither can the medical cloud server deny verifying the user’s data. Therefore, in case of any denial, the identity of the wearable user can serve as proof.
- Anonymity: The scheme ensures that the user’s (device owner) identity is not revealed during the transfer of data. The wearable device firstly computes to conceal the wearable user’s identity before transmitting to the aggregation unit. subsequently, the aggregation unit also computes before transmitting it to the medical cloud server. Consequently, both wearable device and aggregation unit do not reveal the user’s identity during the data transfer process.
- Resistance to forgery Attacks: According to the random oracle of theorem 1, the probability of a polynomial adversary forging a valid signature is negligible under the assumption that the ability to solve the CDH problem is hard. Hence, the scheme can resist forgery attacks.
- Resistance to replay attacks: Timestamps provide the precise time or period during which the user signed their wearable sensor data. It prevents an adversary from replaying a message if the timestamp validity of the corresponding signature is expired.
- Aggregate authentication: The proposed scheme ensures batch authentication of n messages from n group of users. Consequently, the medical cloud server is able to authenticate an individual user by computing .
- Aggregate Verification: the proposed scheme extends the batch processing to verify aggregated message-signature pairs from a large group of users to improve bandwidth efficiency during batch data transfer.
6. Performance Evaluation
This section discusses the performance evaluation of the batch processing method presented in this paper. Based on Certificateless cryptography, the batch processing approach is categorized into aggregate authentication and aggregate verification. The evaluation of the proposed scheme is compared with schemes in [22,23,24] and ref. [17] in terms of functional analysis, computation and communication cost.
6.1. Background of Comparative Schemes
Authors in [22] presented an aggregated signature for SaaS authentication (SecAuth-SaaS) for cloud computing that works as a collaborative service attestation to provide authentication and non-repudiation for software as a service (SaaS). Similarly, Wang et al. [23] also performed a batch verification Cryptanalysis for a mobile healthcare crowd-sensing (CABV-MHCS) that is secure against forgery, identity, and security attacks.
A novel Certificateless aggregate signature scheme for healthcare multimedia social network (CASS-HMSN) was suggested by [24] to fix the security flaws identified in [16] for cloud environments. Asari et al. [17] also proposed the Hierarchical Anonymous Certificateless Authentication (HACA-ADS (B)) that preserves conditional privacy for the Automatic Dependent Surveillance-Broadcast (ADS-B) environment.
Finally, the presented scheme also proposed a batch processing technique based on Certificateless cryptography to resolve bandwidth limitations of large data transfers from wearable health crowd-sensing. The proposed method also provides anonymity to users’ identity during data transmission.
6.2. Functionality Analysis
In functional analysis, we compare Batch Processing (aggregating authentication and verification), Forgery Attack, Non-Repudiation, Anonymity, Replay Attack, and Bandwidth improvement. The schemes for comparison use CLC method. According to Table 2, all the schemes showed to be resilient against forgery attacks (especially Type 1 and Type 2 adversaries). For batch processing, schemes that showed both aggregate authentication and aggregate verification are considered to satisfy batch processing. As shown in Table 2, all schemes demonstrated both aggregate authentication and aggregate verification with the exception of HACA-ADs-B [17] that fulfilled partial batch processing since their scheme considered only aggregate verification. The proposed scheme, HACA-ADS-B [17], CABV-MHCS [23], satisfies non-repudiation; nevertheless, CASS-HMSN [24] did not explicitly demonstrate the non-repudiation feature in their work. Regarding anonymity, HACA-ADS-B [17] uses short pseudonyms to preserve anonymity. Consequently, the scheme in CABV-MHCS [23] allows a client to encrypt its identity before submitting it to a data center. In case of message interception, an adversary in CABV-MHCS [23] cannot reveal the client’s identity without knowing the secret key of the data center. Similarly, the proposed scheme fulfils the anonymity requirement since the wearable device and the aggregation unit perform anonymization algorithms to conceal user’s identity before sending the wearable sensor data. Schemes in CABV-MHCS [23] and the proposed scheme are secure against any replay attacks due to the presence of timestamps validity in the scheme. Thus, an adversary cannot replay a message if the timestamp is invalid. All schemes facilitate batch verification in bandwidth-constrained contexts.

Table 2.
Functional Analysis.
6.3. Computational Cost
For fair analysis, we implement the MIRACL library on a Raspberry Pi with an ARMv7 processor of 1GB memory on Ubuntu 18.04 operating system. For our client-side, the Raspberry Pi acts as the wearable client while the Lenovo laptop acts as the server. We perform the experiments and test the running times on the existing and proposed schemes. The experiment uses a PBC library of Type A elliptic curve with a 512-bit prime field with a group order of 160-bit on a Lenovo laptop with an 8GB RAM, 64 bits of an I5 Intel Processor. For each operation, we represent the timely cost of a scalar multiplication as , Pairing operation as , and point addition operation as . A total of 100 executions of each operation were run, and the total results were averaged. The cost of scalar multiplication () is 0.093 s, pairing operation () is 4.054 s, and the cost of point addition () is 0.014 s. For evaluation purposes we compare the the computational costs and the running times of the proposed scheme with existing schemes namely SecAuth-SaaS [22], CABV-MHCS [23], CASS-HMSN [24], and HACA-ADS-B [17]. We also compare the efficiency of the proposed schemes with the existing schemes. In computing the batch processing, we assume the number of users owning wearable devices to be 100 (n = 100) and perform the batch processing as the total of aggregate sign and aggregate verify.
According to Table 3 and Table 4, scheme SecAuth-SaaS [22] generates a signature of ≈ 0.335 s and takes ≈ 24.324 s in verifying the signature. In performing batch processing, the signer executes to sign n generated data from n users. It verifies the generated signature by requiring to verify the signed n group of data. It takes a total time of 40.819 s to complete both signing and verification processes of a single message. In performing the batch process of 100 users, it requires to complete the batch operation in 1226 s.

Table 3.
Computational Complexity.

Table 4.
Analysis of computational cost.
Likewise, CABV-MHCS [23] scheme takes ≈ 0.121 s and ≈ 12.269 s to finish signing and verifying a single message, respectively. In requires a total of 12.627 s. The signer takes to generate n data whilst the verifier execute in verifying n aggregated data. Moreover, it executes to perform both aggregation signature and verification process requiring a total time of 1225.5 s on n given data.
Similarly, to compute an individual signature in CASS-HMSN [24] scheme requires s and s to complete a verification process. It requires a total time of 12.762 s to complete a signing and verification process of a single message. Additionally, to perform a batch processing of n messages, CASS-HMSN [24] requires to complete a batch operation with a finishing time of 1274.8 s. To complete a signing process in HACA-ADS-B [17]’s scheme, the signer requires s to sign an individual message and needs + s to verify the individual signature. It takes 12.534 s to complete the whole signing and verification process of an individual data. Furthermore, is needed to sign n aggregated messages and to complete a verification process of n aggregated messages. In total it spends 1225.5 s to compute .
Comparatively, the proposed scheme requires s for the user to sign a single wearable sensor data and requires s for the medical cloud server to verify the single wearable message. The proposed scheme needs a total of 8.694 s to complete the signing and verification of a single wearable message. Moreover, in performing a batch process of n generated data from n users, it needs to execute requiring a total finishing time of 820.1 s, assuming the number of users is 10. In computing the batch processing, it executes for aggregate signing and for aggregate verification.
Table 4 shows that the proposed scheme achieved a better computing cost than the existing schemes. In Figure 4, it is evident that the signing process of all schemes takes less time than the verifying process. However, the signing cost of the proposed scheme is higher than CABV-MHCS [23] and HACA-ADS-B [17] since the algorithm generation in the signing phase is high. However, the proposed scheme achieved a lower verification time than all the existing schemes, which shows that the medical cloud server does not require extra time to complete the verification of a single data.
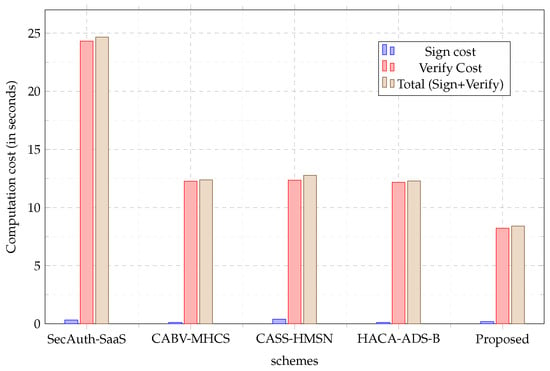
Figure 4.
Computational Cost.
We test the efficiency of the proposed scheme with the existing schemes by using the formulae in [25], which is computed as follows:
The improvement of the proposed scheme with respect to the total signing and verification costs of a single message with reference to scheme is SecAuth-SaaS [22]
The suggested technique is 78.7% more efficient than SecAuthSaas [22] for single message sign and verify and 33% better for batch processing. Similarly, the proposed scheme outperformed the CABV-MHCS [23] scheme by 31.14% in signing and verifying a single message and 33% better in performing aggregation sign and aggregation verification together. The proposed scheme is 31.88% more efficient than CASS-HMSN [24] in signing and verifying a single message, at the same time 33% efficient in performing batch processing. Similar to HACA-ADS-B [17], the proposed achieved better efficiency of 30.64% in single sign and verify, and 33% in batch processing.
The graph in Figure 5 illustrates that the proposed approach has the least batch processing time for an increased number of users. By this reasoning, the proposed batch processing approach fits WHCS in bandwidth situations.
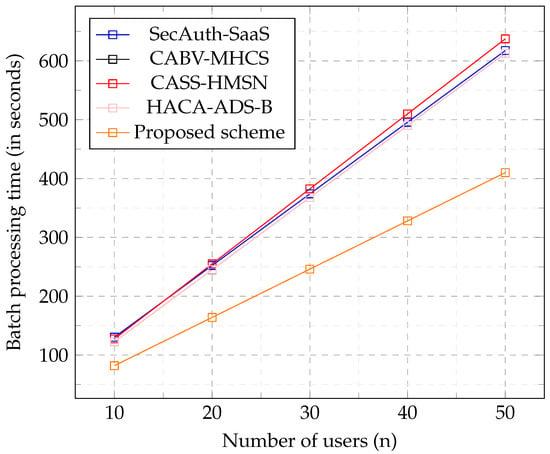
Figure 5.
Batch processing cost of n users.
6.4. Communication and Overhead Cost
We analyze the communication cost of the related schemes [17,22,23,24] and the proposed scheme. We apply a bilinear pairing of Type A curve of over the field for some prime . At 80 bit security level, the length of a group element bytes where is an additive group. The size of a field element bits equivalent to 64 bytes.
By applying the stated parameters, we determine the signature size of a single message and the aggregated messages of the existing schemes and compare them with the proposed scheme. From Table 5, the proposed scheme consists of with a communication cost of 128 bytes. The proposed scheme achieved the lowest communication cost compared to the existing schemes. It costs 128n bytes to send an aggregate signature and 128 bytes to send a single signature. Identically, the CABV-MHCS scheme [23] and CASS-HMSN [24] scheme incurred a communication cost of 320 bytes in generating single-size signature and 320n bytes in sending n signatures. Finally, the HACA-ADS-B [17] scheme incurred a communication cost of 256 bytes in generating a single message and 256n bytes for signing n messages. According to Figure 6, increasing the number of participants to 100, showed a reduction in communication cost for all scheme with the proposed scheme achieving the least communication cost.

Table 5.
Comparison of Communication cost.
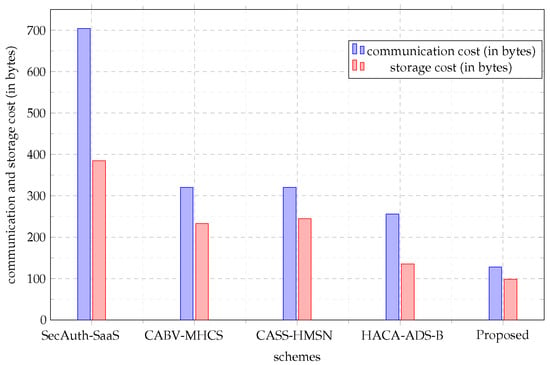
Figure 6.
Communication and overhead cost.
In determining the efficiency of the proposed scheme with respect to (w.r.t) communication cost, we apply the efficiency methodology in Equation (5), and presented the results as follows: the proposed scheme achieved better efficiency by surpassing SecAUth-SaaS [22] by 81.8%, and also outperformed HACA-ADS-B [17] by 50%. Similarly, the proposed scheme is 60% more efficient than CABV-MHCS [23] and CASS-HMSN [24], respectively.
In the WHCS system, when the medical cloud server (MCS) receives the tuple within the valid time, it stores the received tuple from different users. The storage overhead of the proposed scheme considers the size of the signature , the timestamp , the identity of the user , the message m and the anonymity value . The MCS keeps the whole tuple in the cloud storage as . At 80 bit security level, we assume bits, bits, bits, the size of bits, bits and assume bits. Applying the standard compression technique in [15,26], the size of is reduced to 65 bytes. The storage overhead for the tuple in the proposed scheme results in bytes. The storage overhead for the rest of the schemes are as follows:
- (a)
- The storage overhead of SecAuth-SaaS [22] is bytes.
- (b)
- The storage overhead of CABV-MHCS [23] is bytes.
- (c)
- The storage overhead of CASS-HMSN [24] is bytes.
- (d)
- The storage overhead of HACA-ADS-B [17] is bytes.
6.5. Energy Consumption
This subsection determines the energy efficiency of schemes in terms of energy consumption. Energy consumption is computed as the , where P represents utilization power and represents scheme execution time. To measure the energy, we connected an fitness band to the Raspberry Pi, and a measurement of 1293 mW (1.293 W) was recorded. Using the measurement, the energy for sign, verify and batch processing operations are evaluated all the schemes and the results are presented in Table 6.

Table 6.
Comparison of Energy Consumption (in mJ).
From the graph in Figure 7, the energy consumption results are lower in the single signing phase across all schemes. By contrast, the energy consumption in the verification phase is higher for single-message verification. Figure 7 also shows that the proposed scheme has the least energy consumption in both signing and verification phases. Considerably, in Figure 8, the amount of energy consumed by an increasing number of wearable users lowers in the proposed scheme. By reasoning, energy is more optimized in the proposed method than in the rest of the schemes. Therefore, the proposed method is suitable for deployment in WHCS.
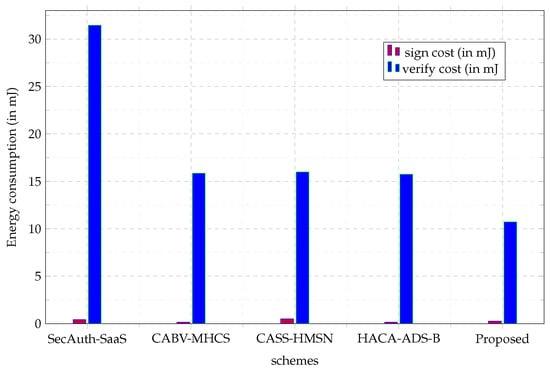
Figure 7.
Energy Consumption of schemes.
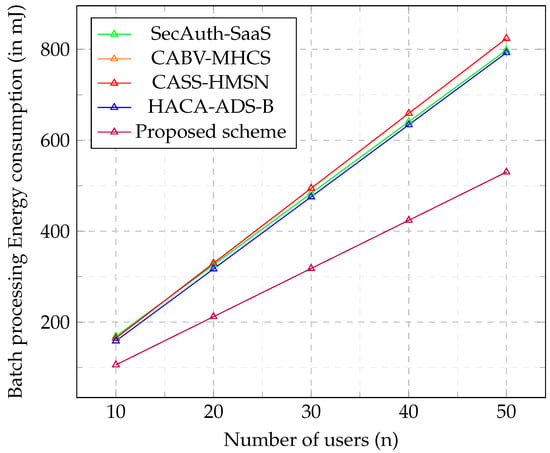
Figure 8.
Batch processing energy consumption (in mJ).
7. Discussion
The inception of cloud-based wearable health crowd-sensing (WHCS) has immensely impacted decision analytics through the collection of wearable sensor data. Owing to the batch processing for WHCS applications, the proposed method is shown to be a good fit for WHCS. The computational cost resulting from the intensive programming task and high computational processing is significantly reduced in the proposed method. In terms of signing and verifying an individual message, the proposed scheme outperforms SecAuthSaas [22] by 78.7%, 31.14% better than CABV-MHCS [23], 31.88% efficient than CASS-HMSN [24], and 30.64% better than HACA-ADS-B [17]. Comparatively, in terms of computational cost for batch processing, the proposed scheme is 33% efficient than all the existing schemes in [17,22,23,24].
With reference to communication cost comparison, results from the analysis shows that the proposed scheme achieves the least communication cost of 128 bytes with a lower storage overhead of 98 bytes compared to the existing schemes. As power consumption is essential in WHCS, energy is optimised in the proposed scheme with the increasing number of participants (users) from 10 users to 50 users; hence, the proposed scheme incurs less energy cost.
8. Conclusions
This paper introduced a batch processing scheme for the wearable health crowd-sensing system (WHCS). We discussed the issues existing in the WHCS system. In batch processing, we perform aggregation and aggregation verification to resolve the bandwidth situations in WHCS. More so, the scheme allows entities such as wearable devices and aggregation units to perform anonymity to obscure the identity of a user before sending the collected data to the cloud. Security analysis has shown the scheme to be secure against replay and forgery attacks and on-path attacks (such as man-in-the-mobile attacks) during large data transfers. Results from performance analysis have shown to achieve lower computation and communication costs with less storage overhead. To conclude, the performance analysis has shown the proposed scheme to be energy efficient and fit for the wearable health crowd-sensing (WHCS) system.
Author Contributions
Conceptualization, A.A.A. and Q.L.; methodology, A.A.A. and I.O.A.; software, A.A.A.; validation, A.A.A., Q.L. and J.H.; formal analysis, A.A.A.; resources, Q.L.; writing—original draft preparation, A.A.A. and I.O.A.; writing—review and editing, A.A.A. and I.O.A.; visualization, J.H. and Q.L.; supervision, Q.L.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the 4th project “Research on the Key Technology of Endogenous Security Switches” (2020YFB1804604) of the National Key R&D Program “New Network Equipment Based on Independent Programmable Chips” (2020YFB1804600), the 2020 Industrial Internet Innovation and Development Project from Ministry of Industry and Information Technology of China, 2018 Jiangsu Province Major Technical Research Project “Information Security Simulation System”, the Fundamental Research Fund for the Central Universities (30918012204, 30920041112), the 2019 Industrial Internet Innovation and Development Project from Ministry of Industry and Information Technology of China, Jiangsu Province Modern Education Technology Research Project (84365); National Vocational Education Teacher Enterprise Practice Base “Integration of Industry and Education” Special Project (Study on Evaluation Standard of Artificial Intelligence Vocational Skilled Level).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The library used in the simulation of the computational cost was based on the charm crypto library https://github.com/blynn/pbc accessed on 15 February 2022.
Conflicts of Interest
The authors have all agreed to the publication of this manuscript and therefore have declared no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AP | Application Provider |
| AU | Aggregation Unit |
| C | Client |
| CLC | Certificateless Cryptography |
| CDH | Computational Diffie-Hellman |
| CL-PKC | Certificateless Public Key Cryptography |
| COVID-19 | Coronavirus Disease 2019 |
| HACA | Hierarchical Anonymous Certificateless Authentication |
| HWSN | Healthcare wireless sensor networks |
| IBC | Identity based Cryptography |
| IoT | Internet of Things |
| KGS | Key Generation Server |
| MCS | Medical Cloud Server |
| MITM | Man-in-the-middle attack |
| MITMO | Man-in-the-mobile attack |
| params | Public System parameters |
| PKG | Public Key Generator |
| PKI | Public Key Infrastructure |
| U | User |
| WBAN | Wireless Body Area Networks |
| WD | Wearable Device |
| WHCS | Wearable Health Crowd-Sensing |
References
- Cecilia, J.M.; Cano, J.C.; Hernández-Orallo, E.; Calafate, C.T.; Manzoni, P. Mobile crowdsensing approaches to address the COVID-19 pandemic in Spain. IET Smart Cities 2020, 2, 58–63. [Google Scholar] [CrossRef]
- He, D.; Chan, S.; Guizani, M. User privacy and data trustworthiness in mobile crowd sensing. IEEE Wirel. Commun. 2015, 22, 28–34. [Google Scholar] [CrossRef]
- Gutmann, P. PKI: It’s not dead, just resting. Computer 2002, 35, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; Springer: Berlin, Heidelberg/Germany, 2001; pp. 213–229. [Google Scholar]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless public key cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 3 November–4 December 2003; Springer: Berlin, Heidelberg/Germany, 2003; pp. 452–473. [Google Scholar]
- Ates, H.C.; Yetisen, A.K.; Güder, F.; Dincer, C. Wearable devices for the detection of COVID-19. Nat. Electron. 2021, 4, 13–14. [Google Scholar] [CrossRef]
- Channa, A.; Popescu, N.; Skibinska, J.; Burget, R. The rise of wearable devices during the COVID-19 pandemic: A systematic review. Sensors 2021, 21, 5787. [Google Scholar] [CrossRef]
- Liu, J.; Shen, H.; Narman, H.S.; Chung, W.; Lin, Z. A survey of mobile crowdsensing techniques: A critical component for the internet of things. ACM Trans. Cyber-Phys. Syst. 2018, 2, 1–26. [Google Scholar] [CrossRef]
- Owoh, N.P.; Singh, M.M. Security analysis of mobile crowd sensing applications. Appl. Comput. Inform. 2020, 18, 2–21. [Google Scholar] [CrossRef]
- Kamil, I.A.; Ogundoyin, S.O. A lightweight CLAS scheme with complete aggregation for healthcare mobile crowdsensing. Comput. Commun. 2019, 147, 209–224. [Google Scholar] [CrossRef]
- Pius Owoh, N.; Mahinderjit Singh, M. SenseCrypt: A security framework for mobile crowd sensing applications. Sensors 2020, 20, 3280. [Google Scholar] [CrossRef]
- Li, J.; Su, Z.; Guo, D.; Choo, K.K.R.; Ji, Y.; Pu, H. Secure data deduplication protocol for edge-assisted mobile crowdsensing services. IEEE Trans. Veh. Technol. 2020, 70, 742–753. [Google Scholar] [CrossRef]
- Ni, J.; Zhang, K.; Xia, Q.; Lin, X.; Shen, X.S. Enabling strong privacy preservation and accurate task allocation for mobile crowdsensing. IEEE Trans. Mob. Comput. 2019, 19, 1317–1331. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Deng, R.H.; Zheng, D.; Li, J.; Wu, P.; Cao, J. Efficient and robust certificateless signature for data crowdsensing in cloud-assisted industrial IoT. IEEE Trans. Ind. Inform. 2019, 15, 5099–5108. [Google Scholar] [CrossRef]
- Shim, K.A.; Lee, Y.R.; Park, C.M. EIBAS: An efficient identity-based broadcast authentication scheme in wireless sensor networks. Ad. Hoc. Netw. 2013, 11, 182–189. [Google Scholar] [CrossRef]
- Kumar, P.; Kumari, S.; Sharma, V.; Sangaiah, A.K.; Wei, J.; Li, X. A certificateless aggregate signature scheme for healthcare wireless sensor network. Sustain. Comput. Inform. Syst. 2018, 18, 80–89. [Google Scholar] [CrossRef]
- Asari, A.; Alagheband, M.R.; Bayat, M.; Asaar, M.R. A new provable hierarchical anonymous certificateless authentication protocol with aggregate verification in ADS-B systems. Comput. Netw. 2021, 185, 107599. [Google Scholar] [CrossRef]
- Joux, A. A one round protocol for tripartite Diffie–Hellman. J. Cryptol. 2004, 17, 263–276. [Google Scholar] [CrossRef]
- Karantaidou, I.; Halkidis, S.T.; Petridou, S.; Mamatas, L.; Stephanides, G. Pairing-based cryptography on the Internet of Things: A feasibility study. In Proceedings of the International Conference on Wired/Wireless Internet Communication, Boston, MA, USA, 18–20 June 2018; Springer: Berlin, Heidelberg/Germany, 2018; pp. 219–230. [Google Scholar]
- Miller, V.S. The Weil pairing, and its efficient calculation. J. Cryptol. 2004, 17, 235–261. [Google Scholar] [CrossRef]
- Tso, R.; Huang, X.; Susilo, W. Strongly secure certificateless short signatures. J. Syst. Softw. 2012, 85, 1409–1417. [Google Scholar] [CrossRef]
- Tiwari, D.; Gangadharan, G. SecAuth-SaaS: A hierarchical certificateless aggregate signature for secure collaborative SaaS authentication in cloud computing. J. Ambient Intell. Humaniz. Comput. 2021, 12, 10539–10563. [Google Scholar] [CrossRef]
- Wang, W.; Huang, H.; Wu, Y.; Huang, Q. Cryptanalysis and improvement of an anonymous batch verification scheme for mobile healthcare crowd sensing. IEEE Access 2019, 7, 165842–165851. [Google Scholar] [CrossRef]
- Wu, L.; Xu, Z.; He, D.; Wang, X. New certificateless aggregate signature scheme for healthcare multimedia social network on cloud environment. Secur. Commun. Netw. 2018, 2018, 2595273. [Google Scholar] [CrossRef]
- Ullah, I.; Amin, N.U.; Khan, M.A.; Khattak, H.; Kumari, S. An efficient and provable secure certificate-based combined signature, encryption and signcryption scheme for internet of things (IoT) in mobile health (M-health) system. J. Med. Syst. 2021, 45, 1–14. [Google Scholar] [CrossRef]
- Li, F.; Hong, J. Efficient certificateless access control for wireless body area networks. IEEE Sens. J. 2016, 16, 5389–5396. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).