The Cost of a True Random Bit—On the Electronic Cost Gain of ASIC Time-Domain-Based TRNGs
Abstract
1. Introduction
1.1. Contributions
- Providing an evaluation of the robustness and reliability issues of efficient TRNGs implemented over FPGA platforms. In particular, we demonstrate its sensitivity to physical properties, such as routing, and device placement, in terms of the amount of effort required to make a design robust, and the degree of complexity of non-standard FPGAs flows.
- Proposing an ASIC-based implementation of the TRNG, along with the optimization steps, to enhance its characteristics that lead to significant performance-entropy improvement.
- Discussing the quantitative question of how much gain in electronic cost factors can be expected over ASIC TRNGs, and the cost Per Bit/Source. To facilitate easy extrapolation for security architects and designers, we exemplify a TRNG versus PRNG ASIC test-case feeding a lightweight encryption core.
Paper Organization and Roadmap
2. Tools and Theory
2.1. Entropy Evaluation and Efficiency Criteria
2.2. Time-Domain Efficient TRNG
3. On the Variability of FPGA-Based Implementation
3.1. Circuit Level Implementation
3.2. Platform Dependent Sensitivities
3.2.1. Oscillator Ratio ()
3.2.2. Tapped-Delay Characteristics
3.3. FPGA Unknowns and the Hard TRNG Design Cycle
4. ASIC Technology Implementation and Optimization
4.1. Throughput and Entropy
4.2. Area and Power
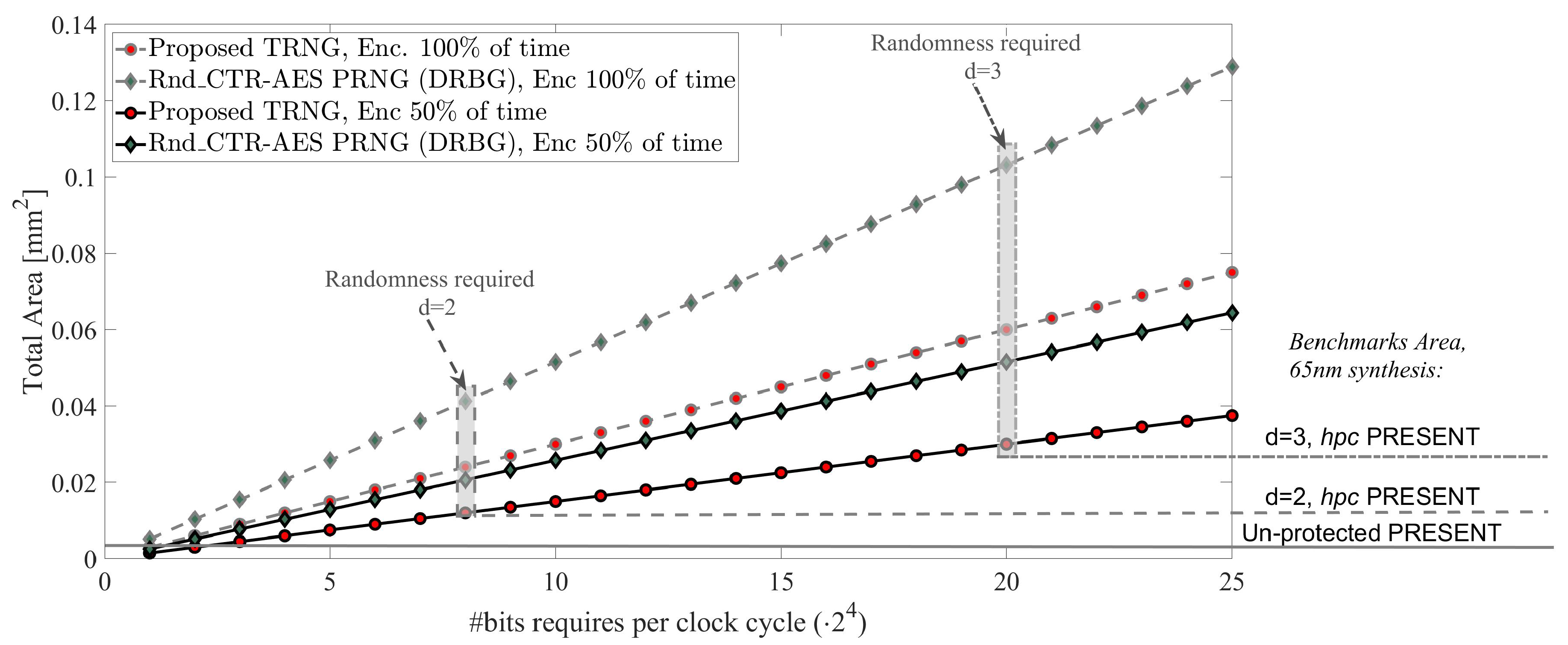
5. Discussion and a Test Case Analysis
Analysis: Example of a TRNG vs. a PRNG Feeding a Lightweight Encryption Core
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panda, A.K.; Rajput, P.; Shukla, B. FPGA implementation of 8, 16 and 32 bit LFSR with maximum length feedback polynomial using VHDL. In Proceedings of the 2012 International Conference on Communication Systems and Network Technologies, Rajkot, India, 11–13 May 2012; pp. 769–773. [Google Scholar]
- Tuncer, T.; Avaroğlu, E. Random number generation with LFSR based stream cipher algorithms. In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 22–26 May 2017; pp. 171–175. [Google Scholar]
- Parker, R.J. Entropy justification for metastability based nondeterministic random bit generator. In Proceedings of the 2017 IEEE 2nd International Verification and Security Workshop (IVSW), Thessaloniki, Greece, 3–5 July 2017; pp. 25–30. [Google Scholar]
- Vasyltsov, I.; Hambardzumyan, E.; Kim, Y.S.; Karpinskyy, B. Fast digital TRNG based on metastable ring oscillator. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 164–180. [Google Scholar]
- Suresh, V.B.; Burleson, W.P. Entropy extraction in metastability-based TRNG. In Proceedings of the 2010 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Anaheim, CA, USA, 13–14 June 2010; pp. 135–140. [Google Scholar]
- Wieczorek, P.Z.; Gołofit, K. Dual-metastability time-competitive true random number generator. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 61, 134–145. [Google Scholar] [CrossRef]
- Tokunaga, C.; Blaauw, D.; Mudge, T. True random number generator with a metastability-based quality control. IEEE J. Solid-State Circuits 2008, 43, 78–85. [Google Scholar] [CrossRef]
- Srinivasan, S.; Mathew, S.; Ramanarayanan, R.; Sheikh, F.; Anders, M.; Kaul, H.; Erraguntla, V.; Krishnamurthy, R.; Taylor, G. 2.4 GHz 7mW all-digital PVT-variation tolerant true random number generator in 45nm CMOS. In Proceedings of the 2010 Symposium on VLSI Circuits, Honolulu, HI, USA, 16–18 June 2010; pp. 203–204. [Google Scholar]
- Mathew, S.K.; Johnston, D.; Satpathy, S.; Suresh, V.; Newman, P.; Anders, M.A.; Kaul, H.; Agarwal, A.; Hsu, S.K.; Chen, G.; et al. μ RNG: A 300–950 mV, 323 Gbps/W All-Digital Full-Entropy True Random Number Generator in 14 nm FinFET CMOS. IEEE J. Solid-State Circuits 2016, 51, 1695–1704. [Google Scholar] [CrossRef]
- Bucci, M.; Luzzi, R. Design of testable random bit generators. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 147–156. [Google Scholar]
- Sunar, B.; Martin, W.J.; Stinson, D.R. A provably secure true random number generator with built-in tolerance to active attacks. IEEE Trans. Comput. 2006, 56, 109–119. [Google Scholar] [CrossRef]
- Wold, K.; Petrović, S. Behavioral model of TRNG based on oscillator rings implemented in FPGA. In Proceedings of the 14th IEEE International Symposium on Design and Diagnostics of Electronic Circuits and Systems, Cottbus, Germany, 13–15 April 2011; pp. 163–166. [Google Scholar]
- Haddad, P.; Fischer, V.; Bernard, F.; Nicolai, J. A physical approach for stochastic modeling of TERO-based TRNG. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 357–372. [Google Scholar]
- Callegari, S.; Rovatti, R.; Setti, G. Embeddable ADC-based true random number generator for cryptographic applications exploiting nonlinear signal processing and chaos. IEEE Trans. Signal Process. 2005, 53, 793–805. [Google Scholar] [CrossRef]
- Cherkaoui, A.; Fischer, V.; Fesquet, L.; Aubert, A. A very high speed true random number generator with entropy assessment. In International Conference on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 179–196. [Google Scholar]
- Fischer, V.; Drutarovskỳ, M. True random number generator embedded in reconfigurable hardware. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2002; pp. 415–430. [Google Scholar]
- Yang, B.; Rožic, V.; Grujic, M.; Mentens, N.; Verbauwhede, I. ES-TRNG: A high-throughput, low-area true random number generator based on edge sampling. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 2018, 267–292. [Google Scholar] [CrossRef]
- Petrie, C.S.; Connelly, J.A. A noise-based IC random number generator for applications in cryptography. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 615–621. [Google Scholar] [CrossRef]
- Bucci, M.; Germani, L.; Luzzi, R.; Tommasino, P.; Trifiletti, A.; Varanonuovo, M. A high-speed IC random-number source for smartcard microcontrollers. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 1373–1380. [Google Scholar] [CrossRef]
- Brederlow, R.; Prakash, R.; Paulus, C.; Thewes, R. A low-power true random number generator using random telegraph noise of single oxide-traps. In Proceedings of the 2006 IEEE International Solid State Circuits Conference-Digest of Technical Papers, San Francisco, CA, USA, 6–9 February 2006; pp. 1666–1675. [Google Scholar]
- Matsumoto, M.; Yasuda, S.; Ohba, R.; Ikegami, K.; Tanamoto, T.; Fujita, S. 1200 μm 2 physical random-number generators based on SiN MOSFET for secure smart-card application. In Proceedings of the 2008 IEEE International Solid-State Circuits Conference-Digest of Technical Papers, San Francisco, CA, USA, 3–7 February 2008; pp. 414–624. [Google Scholar]
- Pareschi, F.; Setti, G.; Rovatti, R. A fast chaos-based true random number generator for cryptographic applications. In Proceedings of the 2006 Proceedings of the 32nd European Solid-State Circuits Conference, Montreaux, Switzerland, 19–21 September 2006; pp. 130–133.
- Bucci, M.; Germani, L.; Luzzi, R.; Trifiletti, A.; Varanonuovo, M. A high-speed oscillator-based truly random number source for cryptographic applications on a smart card IC. IEEE Trans. Comput. 2003, 52, 403–409. [Google Scholar] [CrossRef]
- Bucci, M.; Luzzi, R. Fully digital random bit generators for cryptographic applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 861–875. [Google Scholar] [CrossRef]
- De Roover, C.; Steyaert, M. A 500 mV 650 pW random number generator in 130 nm CMOS for a UWB localization system. In Proceedings of the 2010 Proceedings of ESSCIRC, Seville, Spain, 14–16 September 2010; pp. 278–281.
- Liu, N.; Pinckney, N.; Hanson, S.; Sylvester, D.; Blaauw, D. A true random number generator using time-dependent dielectric breakdown. In Proceedings of the 2011 Symposium on VLSI Circuits-Digest of Technical Papers, Kyoto, Japan, 15–17 June 2011; pp. 216–217. [Google Scholar]
- Amaki, T.; Hashimoto, M.; Onoye, T. A process and temperature tolerant oscillator-based true random number generator with dynamic 0/1 bias correction. In Proceedings of the 2013 IEEE Asian Solid-State Circuits Conference (A-SSCC), Singapore, 11–13 November 2013; pp. 133–136. [Google Scholar]
- Holleman, J.; Bridges, S.; Otis, B.P.; Diorio, C. A 3 μ W CMOS True Random Number Generator With Adaptive Floating-Gate Offset Cancellation. IEEE J. Solid-State Circuits 2008, 43, 1324–1336. [Google Scholar] [CrossRef]
- Mathew, S.K.; Srinivasan, S.; Anders, M.A.; Kaul, H.; Hsu, S.K.; Sheikh, F.; Agarwal, A.; Satpathy, S.; Krishnamurthy, R.K. 2.4 Gbps, 7 mW all-digital PVT-variation tolerant true random number generator for 45 nm CMOS high-performance microprocessors. IEEE J. Solid-State Circuits 2012, 47, 2807–2821. [Google Scholar] [CrossRef]
- Kokubo, H.; Yamamoto, D.; Takenaka, M.; Itoh, K.; Torii, N. Evaluation of ASIC implementation of physical random number generators using RS latches. In International Conference on Smart Card Research and Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–15. [Google Scholar]
- Torii, N.; Kokubo, H.; Yamamoto, D.; Itoh, K.; Takenaka, M.; Matsumoto, T. ASIC implementation of random number generators using SR latches and its evaluation. EURASIP J. Inf. Secur. 2016, 2016, 1–12. [Google Scholar] [CrossRef][Green Version]
- Torii, N.; Yamamoto, D.; Matsumoto, T. Evaluation of latch-based physical random number generator implementation on 40 nm ASICs. In Proceedings of the 6th International Workshop on Trustworthy Embedded Devices, Vienna, Austria, 28 October 2016; pp. 23–30. [Google Scholar]
- Sỳs, M.; Říha, Z. Faster randomness testing with the NIST statistical test suite. In International Conference on Security, Privacy, and Applied Cryptography Engineering; Springer: Berlin/Heidelberg, Germany, 2014; pp. 272–284. [Google Scholar]
- Petura, O.; Mureddu, U.; Bochard, N.; Fischer, V.; Bossuet, L. A survey of AIS-20/31 compliant TRNG cores suitable for FPGA devices. In Proceedings of the 2016 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Switzerland, 29 August–2 September 2016; pp. 1–10. [Google Scholar]
- Schellekens, D.; Preneel, B.; Verbauwhede, I. FPGA vendor agnostic true random number generator. In Proceedings of the 2006 International Conference on Field Programmable Logic and Applications, Madrid, Spain, 28–30 August 2006; pp. 1–6. [Google Scholar]
- Varchola, M.; Drutarovsky, M. New high entropy element for FPGA based true random number generators. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 351–365. [Google Scholar]
- Cassiers, G.; Grégoire, B.; Levi, I.; Standaert, F.X. Hardware private circuits: From trivial composition to full verification. IEEE Trans. Comput. 2020, 70, 1677–1690. [Google Scholar] [CrossRef]
- Levi, I.; Bellizia, D.; Bol, D.; Standaert, F.X. Ask Less, Get More: Side-Channel Signal Hiding, Revisited. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4904–4917. [Google Scholar] [CrossRef]
- Levi, I.; Bellizia, D.; Standaert, F.X. Beyond algorithmic noise or how to shuffle parallel implementations? Int. J. Circuit Theory Appl. Wiley Online Libr. 2020, 48, 674–695. [Google Scholar] [CrossRef]
- Levi, I.; Fish, A.; Keren, O. Low-cost pseudoasynchronous circuit design style with reduced exploitable side information. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 26, 82–95. [Google Scholar] [CrossRef]
- Levi, I.; Rudin, Y.; Fish, A.; Keren, O. Embedded randomness and data dependencies design paradigm: Advantages and challenges. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 395–400. [Google Scholar]


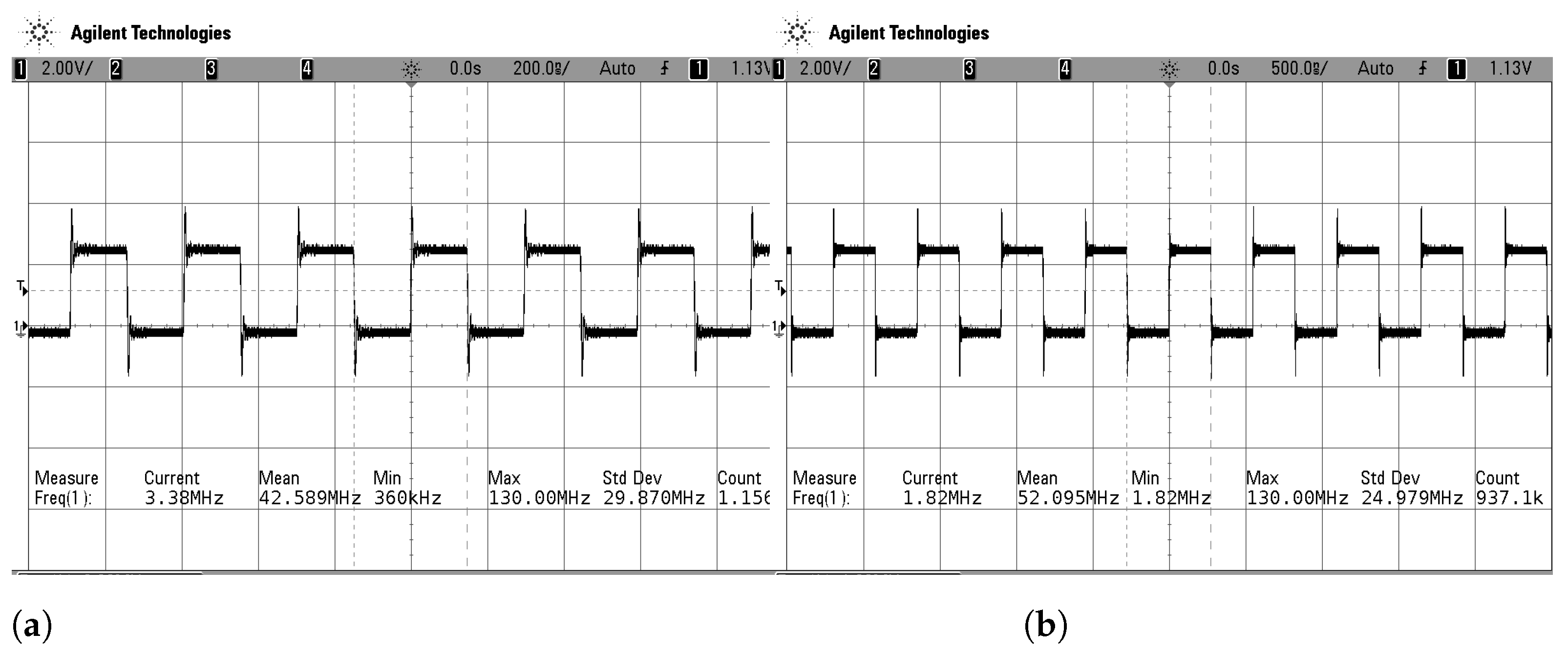

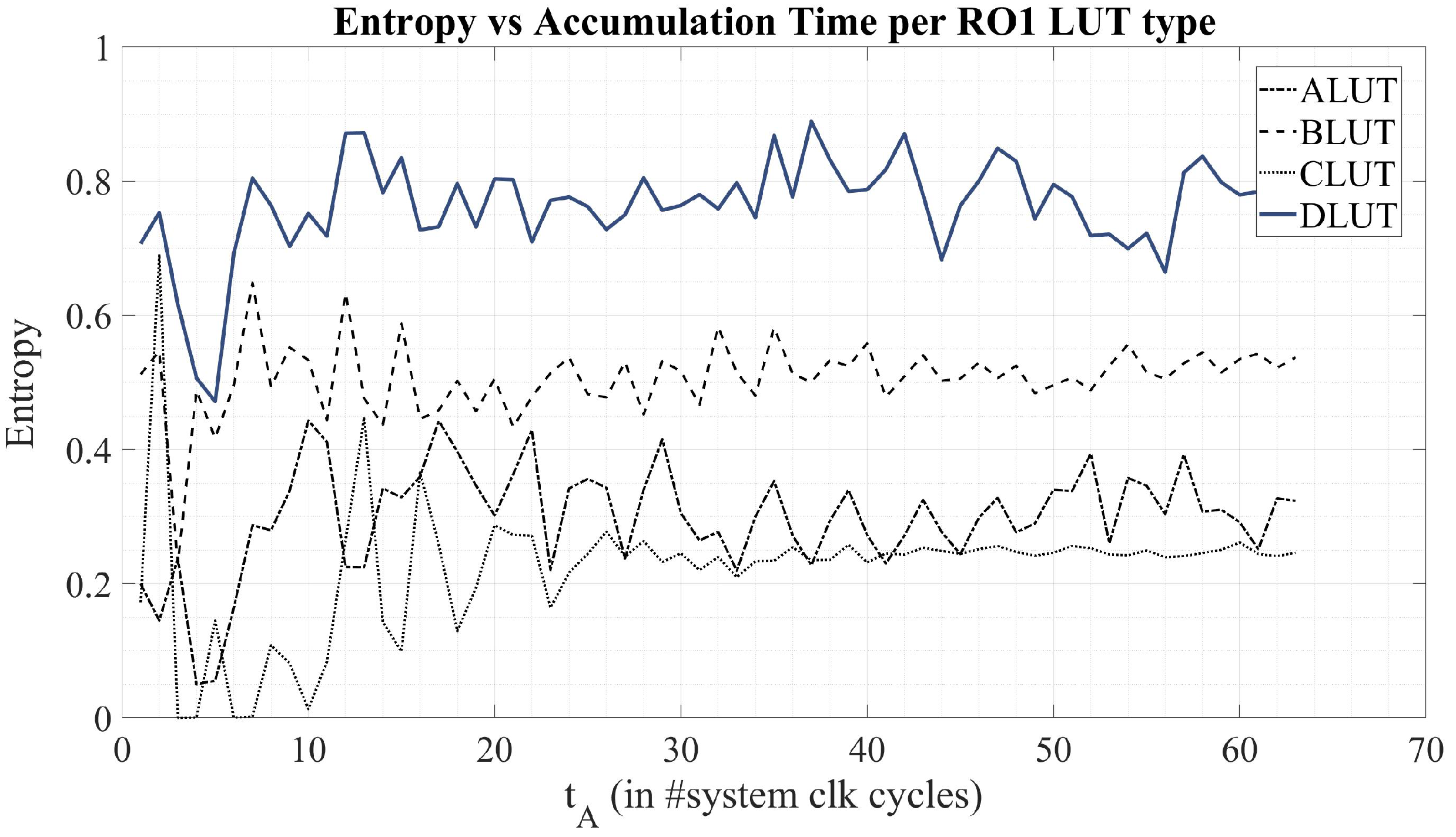
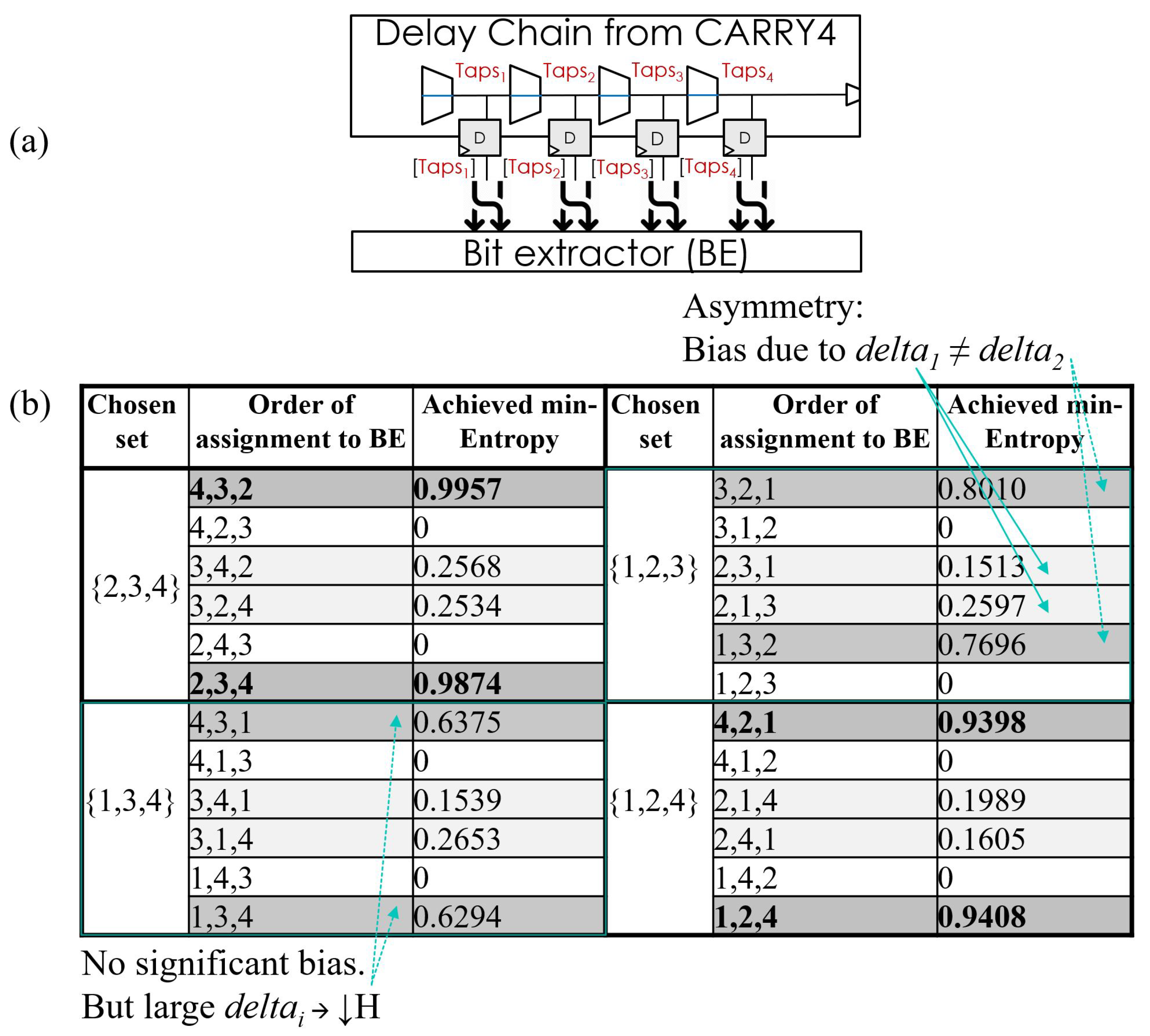
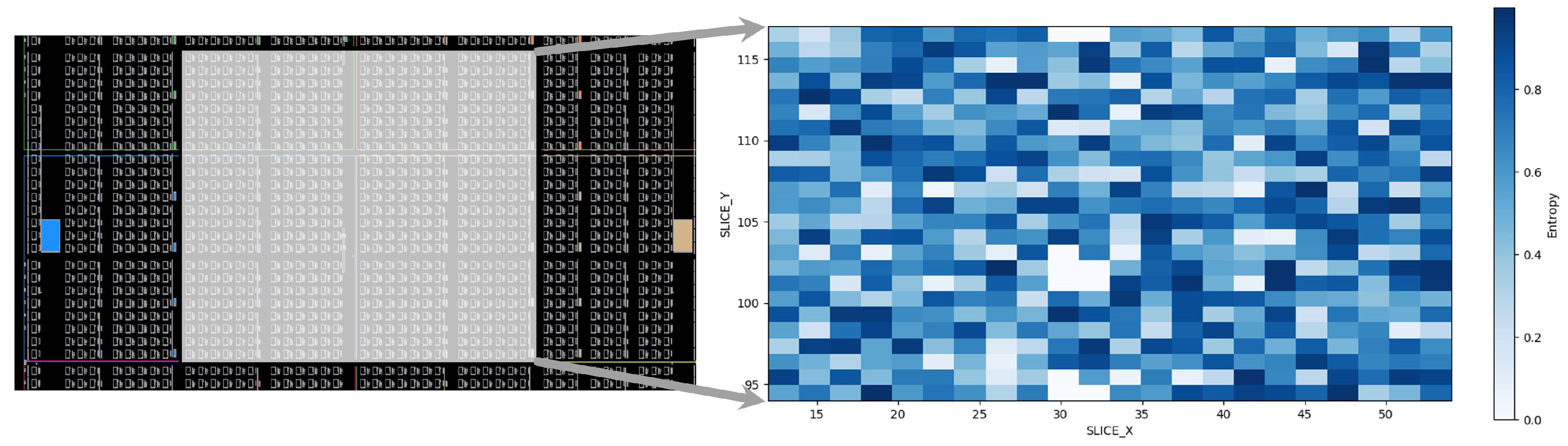


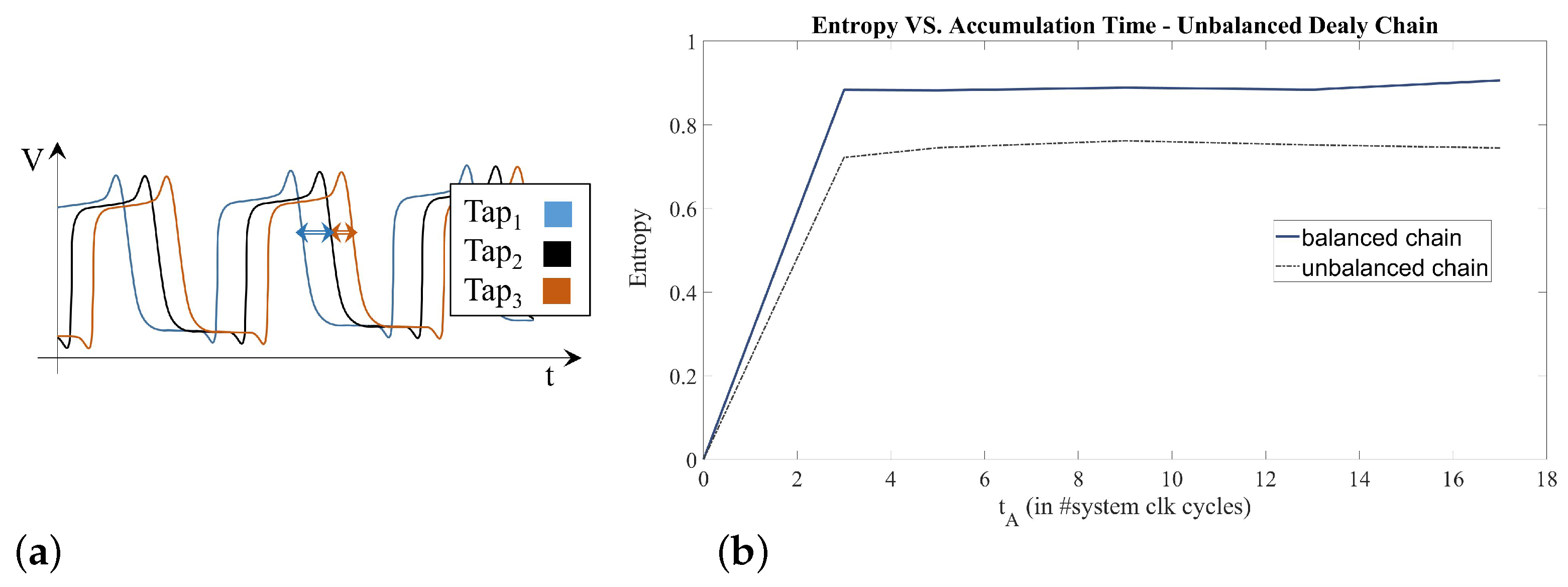
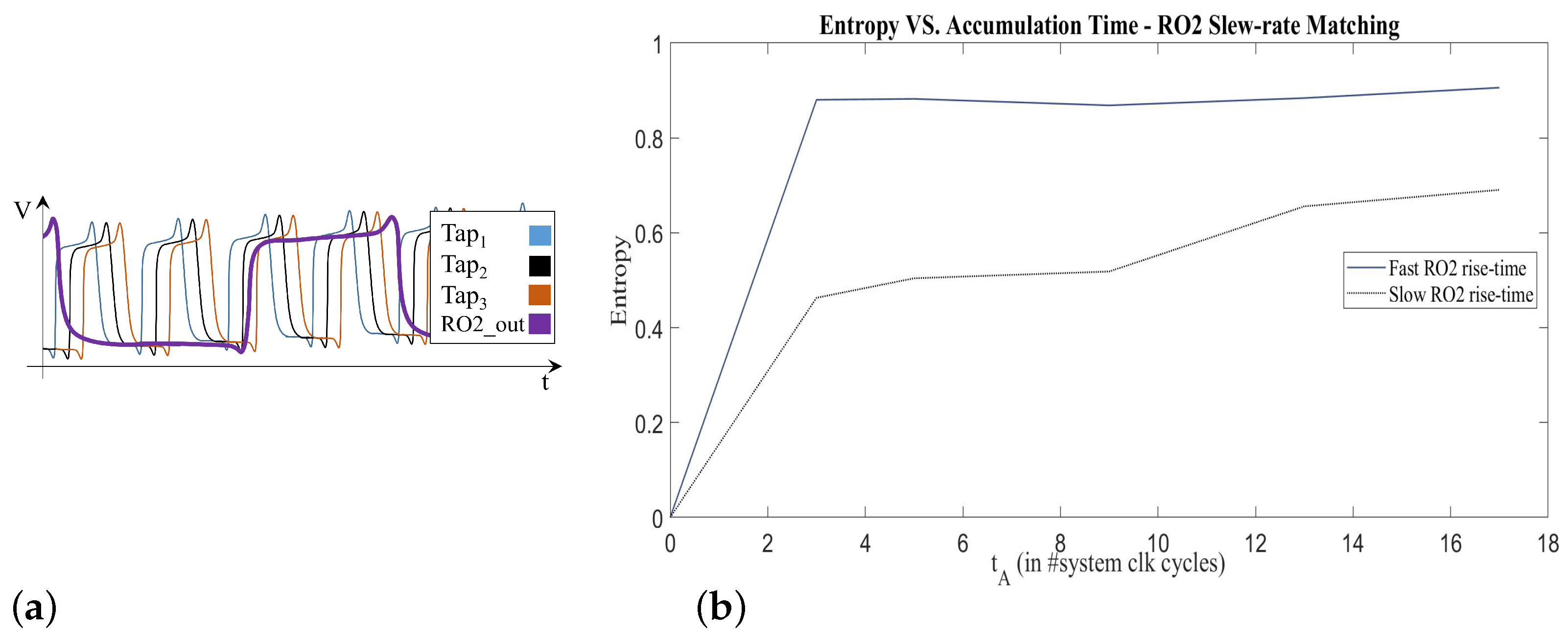
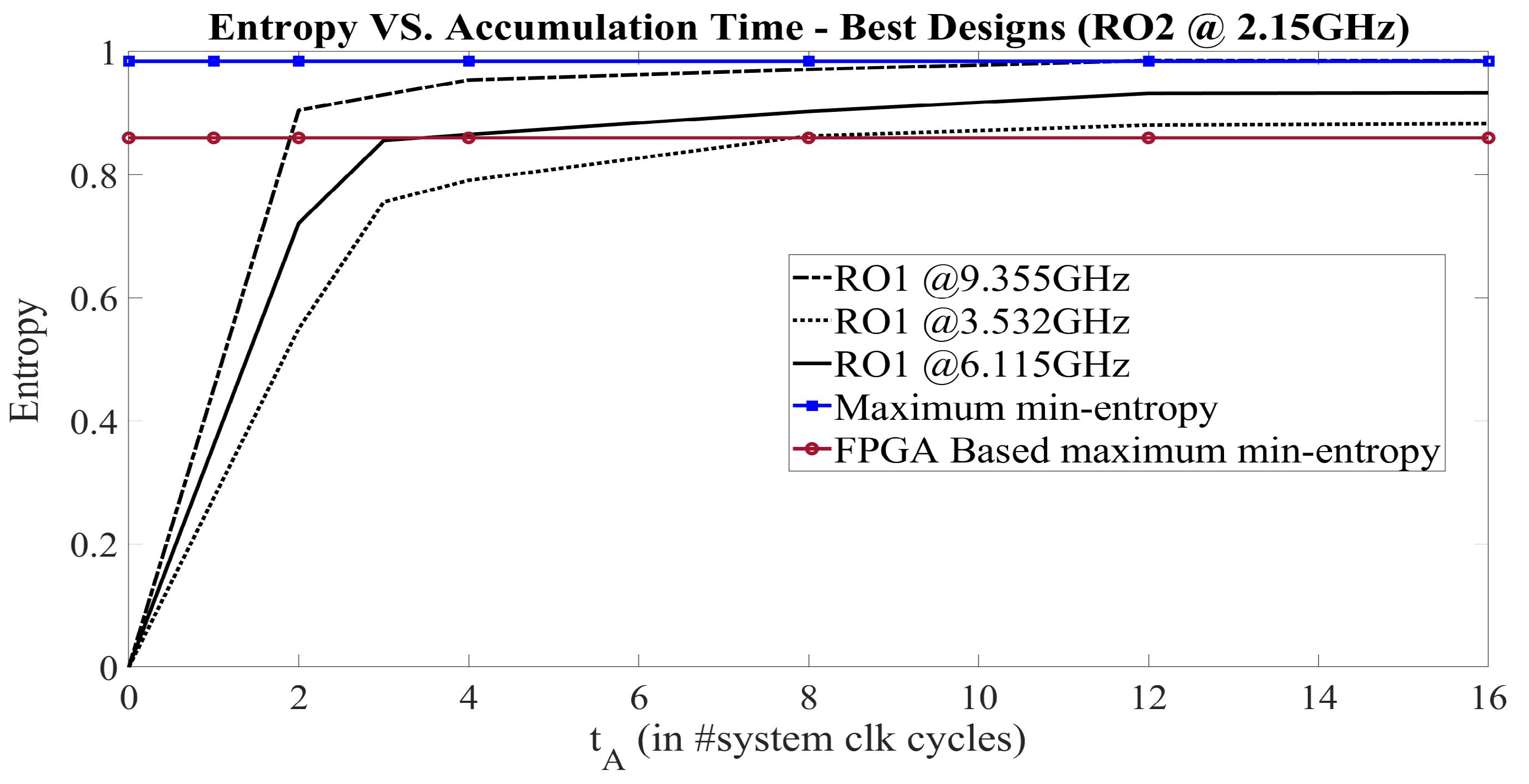

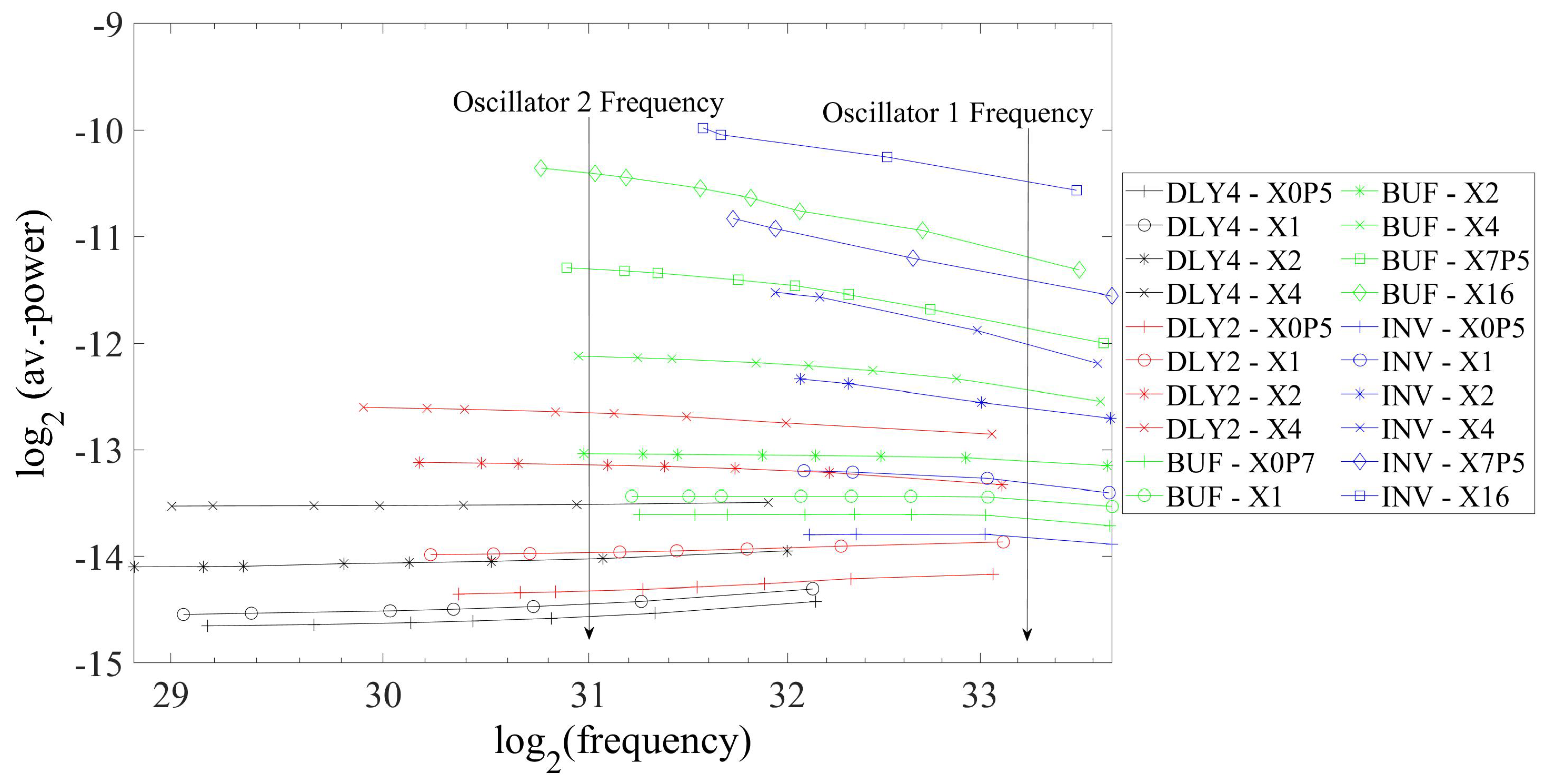


| Entropy | Throughput [Mbit/s] | Area [mm] | Av.-Power [mW/Source] |
|---|---|---|---|
| -na-(Smallest known [26] 65 nm) | 0.011 | 0.0012 | 2 |
| -na-(Max. Throughput [29] 45 nm) | 2400 | 0.004 | 7 |
| 0.86 prior art-FPGA [17] | 1.15 | * | * |
| (Proposed) 0.86 | 47.8 | 0.000252 | 0.1 |
| (Proposed) 0.985 | 8.27 | 1.06 |
| TRNG | FPGA Device | AREA (LUT/Reg/CARRY4) | Bit Rate [Mbits/s] | Entropy/bit | Entropy·Bit Rate | MHz | MHz | MHz | |
|---|---|---|---|---|---|---|---|---|---|
| ES-TRNG (Implemented) | Spartan 6 | 7/6/1 (controller): 4/9/0 | 10 | 0.815 (Raw) | 8.15 | 9 | 603.1 | 453.3 | 100 |
| ES-TRNG (prior-art) | Spartan 6 Cyclone V | 10/5/1 (controller): 6/6/0 10/6/1 (controller): 6/6/0 | 4 (no post-processing) 4.34 (no post-processing) | 0.746 (Raw) 0.746 (Raw) | 2.984 3.237 | 25 23 | 460.4 572.8 | 364.9 331.1 | 100 |
| ERO [34] | Spartan 6 Cyclone V SmartFusion 2 | 46/19/X 34/20/X 45/19/X | 0.0042 0.0027 0.014 | 0.999 0.990 0.980 | 0.004 0.003 0.013 | ||||
| COSO [34] | Spartan 6 Cyclone V SmartFusion 2 | 18/3/X 13/3/X 23/3/X | 0.54 1.44 0.328 | 0.999 0.999 0.999 | 0.539 1.438 0.327 | ||||
| MURO [11,34,35] | Spartan 6 Cyclone V SmartFusion 2 | 521/131/X 525/130/X 545/130/X | 2.57 2.2 3.62 | 0.999 0.999 0.999 | 2.567 2.197 3.616 | ||||
| PLL [34] | Spartan 6 Cyclone V SmartFusion 2 | 34/14/X 24/14/X 30/15/X | 0.44 0.6 0.37 | 0.981 0.986 0.921 | 0.431 0.592 0.340 | ||||
| TERO [34,36] | Spartan 6 Cyclone V SmartFusion 2 | 39/12/X 46/12/X 46/12/X | 0.625 1 1 | 0.999 0.987 0.999 | 0.624 0.985 0.999 | ||||
| STR [15,34] | Spartan 6 Cyclone V SmartFusion 2 | 346/256/X 352/256/X 350/256/X | 154 245 188 | 0.998 0.999 0.999 | 154.121 244.755 188.522 | ||||
| Entropy Source | Reference | Tech. | Area | Power | Throughput | Post-Proc. | Evaluation |
|---|---|---|---|---|---|---|---|
| Amplitude Noise | [18] | 2 µm | * 1.5 mm | 3.9 mW | 1.4 Mbps | - | FIPS140-1, DIEHARD |
| [19] | 0.18 µm | 0.025 mm | 2.3 mW | 5 Mbps | XOR decorr. | FIPS140-1, Knuth 2nd ed. | |
| [20] | 0.12 µm | 0.009 mm | 0.05 mW | 200 Kbps | V.Neumann | Entropy dist | |
| [21] | 0.25 µm | 0.0012 mm | 1.9 mW | 2 Mbps | - | FIPS140-2 | |
| [22] | 0.35 µm | 0.52 mm | 30 mW | 40 Mbps | - | SP800-22 | |
| Time-domain | [23] | 0.18 µm | 0.0016 mm | 2.3 mW | 10 Mbps | - | FIPS140-1, Knuth 2nd ed. |
| [24] | 90 nm | 0.006 mm | 0.24 mW | 1.74 Mbps | LFSR | AIS31, Entropy dist | |
| [25] | 130 nm | 0.2465 mm | 0.00065 mW | 25 bps | 6 bit LFSR | SP800-22 Basic | |
| [26] | 65 nm | 0.0012 mm | 2 mW | 11 Kbps | - | SP800-22 | |
| [27] | 65 nm | 0.00667 mm | - | 7.5 Mbps | - | SP800-22 Basic, DIEHARD | |
| This work (1) | 65nm | 0.00025 mm2 | 0.1 mW | 47.8 Mbps | - | SP800-90B | |
| This work (2) | 1.06 mW | 8.27 Mbps | |||||
| Metastable | [7] | 0.13 µm | 0.145 mm | 1 mW | 40 Kbps | 5:1 decimation | SP800-22 Basic |
| [28] | 0.35 µm | 0.031 mm | 0.0094 mW | 5 Kbps | NFSR | SP800-22 Basic | |
| [29] | 45 nm | 0.004 mm | 7 mW | 2.4 Gbps | - | SP800-22 | |
| [30,31] | 0.18 µm | ** 0.0018 mm | 0.27 mW | 2.5 Mbps | - | SP800-90B & -22, AIS20/31 | |
| [32] | 40 nm | 0.0188 mW | 2.5 Mbps | - | SP800-90B, AIS20/31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klein, N.; Harel, E.; Levi, I. The Cost of a True Random Bit—On the Electronic Cost Gain of ASIC Time-Domain-Based TRNGs. Cryptography 2021, 5, 25. https://doi.org/10.3390/cryptography5030025
Klein N, Harel E, Levi I. The Cost of a True Random Bit—On the Electronic Cost Gain of ASIC Time-Domain-Based TRNGs. Cryptography. 2021; 5(3):25. https://doi.org/10.3390/cryptography5030025
Chicago/Turabian StyleKlein, Netanel, Eyal Harel, and Itamar Levi. 2021. "The Cost of a True Random Bit—On the Electronic Cost Gain of ASIC Time-Domain-Based TRNGs" Cryptography 5, no. 3: 25. https://doi.org/10.3390/cryptography5030025
APA StyleKlein, N., Harel, E., & Levi, I. (2021). The Cost of a True Random Bit—On the Electronic Cost Gain of ASIC Time-Domain-Based TRNGs. Cryptography, 5(3), 25. https://doi.org/10.3390/cryptography5030025







