Abstract
In recent years, data-enabled technologies have intensified the rate and scale at which organisations collect and analyse data. Data mining techniques are applied to realise the full potential of large-scale data analysis. These techniques are highly efficient in sifting through big data to extract hidden knowledge and assist evidence-based decisions, offering significant benefits to their adopters. However, this capability is constrained by important legal, ethical and reputational concerns. These concerns arise because they can be exploited to allow inferences to be made on sensitive data, thus posing severe threats to individuals’ privacy. Studies have shown Privacy-Preserving Data Mining (PPDM) can adequately address this privacy risk and permit knowledge extraction in mining processes. Several published works in this area have utilised clustering techniques to enforce anonymisation models on private data, which work by grouping the data into clusters using a quality measure and generalising the data in each group separately to achieve an anonymisation threshold. However, existing approaches do not work well with high-dimensional data, since it is difficult to develop good groupings without incurring excessive information loss. Our work aims to complement this balancing act by optimising utility in PPDM processes. To illustrate this, we propose a hybrid approach, that combines self-organising maps with conventional privacy-based clustering algorithms. We demonstrate through experimental evaluation, that results from our approach produce more utility for data mining tasks and outperforms conventional privacy-based clustering algorithms. This approach can significantly enable large-scale analysis of data in a privacy-preserving and trustworthy manner.
1. Introduction
Advances in Information and Communication Technology (ICT) have enabled public and private service solutions to increasingly adopt technologies that collect, process, store and distribute data. This development is proliferated by strategies that permit the extraction of implicit and useful information from big data. The approach of knowledge extraction that mainly focuses on data analysis and modelling for prediction is known as data mining. Data mining techniques are programmed to sift through data automatically, seeking patterns that will likely generalise to make evidence-based decisions or accurate predictions that hold in data collections [1]. Although this emerging technology facilitates inferencing and enjoys intense commercial attention, there is a growing concern that data mining results could potentially be exploited to infer sensitive information, therefore potentially breaching individual privacy in a variety of ways [2].
In response to privacy concerns, Privacy Preserving Data Mining (PPDM) has been proposed by a number of studies [3,4,5,6,7] as an effective method for accommodating privacy concerns during mining processes to address the risk of re-identification. PPDM aims to provide a trade-off between data utility on one side and data privacy on the other side, by enforcing a certain degree of privacy without relinquishing the purposefulness of the data [8]. The evolving role of PPDM is to ensure that the benefits of data mining are enjoyed while guaranteeing the privacy of data subjects, thus providing the legal and ethical grounds for organisations to access and use data safely. It has remained the most successful solution to the significant challenge of privacy in data mining [9]. PPDM techniques depend on a definition of anonymity, which preserves the underlying information in the original data and protects it from either direct or indirect disclosures [10]. There are several measures of anonymity such as k-anonymity l-diversity and t-closeness, each with varying goals in preventing disclosure of sensitive information. Although all measures are effective in mitigating risks, k-anonymity receives considerable attention and persistent uptake in PPDM approaches [10]. The motivating factor behind this is due to its effectiveness in reducing the granularity of representation of the data while also maximising utility of the data better than other measures [11]. Several published works [12,13,14,15,16] in this area have proposed different clustering techniques to enforce anonymity measures on private data. These techniques work by grouping the data into clusters using a quality measure and then generalising the data in each group separately to achieve an anonymisation threshold [17]. These studies have illustrated that clustering-based methods are capable of assuring anonymity measures and permitting mining of data with less concern about privacy violations. Despite this breakthrough, conventional approaches primarily apply a transformation which reduces the effectiveness of the underlying data when it is subjected to data mining methods or algorithms. Furthermore, the trade-off between privacy and utility is always affected by the clustering algorithm used for privacy preservation. Finally, most approaches optimise privacy over utility, thus cannot guarantee an adequate balance between the two properties [13,18,19].
This work aims to address this key issue of maintaining maximum utility of the data without compromising the underlying privacy constraints. To achieve this, we apply dimensionality reduction techniques in conjunction with conventional clustering techniques to transform original data into an anonymised version of the data. The goal of this hybrid strategy is to maximise data utility in PPDM techniques and show it can produce a more desirable balance than existing techniques. To illustrate this point, we apply our proposed method to the Adult dataset [20]. First, we partition the dataset into two distinct parts based on their categorisation and several other measures. Second, we apply heuristic clustering algorithms to anonymise one partition of the dataset. In this instance, the clustering algorithms model the k-anonymity property for privacy-preservation. Third, a dimensionality reduction technique is used to map features of the other partition to a 1-dimensional set of neurons. In other studies [6,12], these features are dropped due to inaccurate categorisation. Four, the anonymised results of the first partition are united with the discretisized results of the second partition. Five, the newly derived dataset is subjected to several classification techniques that are typically employed on the original Adult dataset for prediction tasks. Lastly, we compare the accuracy of performing this prediction task with our anonymised version of the dataset and several other versions derived from conventional clustering techniques. This will give us valuable insight on which approach suffers less information loss (in terms of loss of precision and completeness) as a result of the transformation caused by the algorithm and hence maximises utility.
This paper significantly extends a preliminary investigation in [21] by utilising additional anonymisation techniques for benchmark comparisons with conventional clustering techniques. Also additional classification metrics are used for evaluating the machine learning models applied on all versions of the dataset. The main contributions of our work are:
- An implementation of Self-Organizing Maps in conjunction with clustering-based k-anonymisation algorithms to derive more data utility.
- A comprehensive comparison of k-anonymisation algorithms in terms of effectiveness for data mining tasks.
- An extensive analysis of the effects of the privacy parameters and some aspects of the datasets on the anonymisation process.
The purpose of this research is to optimise utility in data anonymisation processes. Our work demonstrates how using self-organising maps in conjunction with clustering-based k-anonymisation can produce more accurate results for data mining. Our comparative analysis using numerous metrics provides an extensive understanding of PPDM techniques and their performance. Our findings could serve as guidelines to data practitioners for finding more suitable techniques in scenarios where the need for higher data utility supersedes the need for higher data privacy, particularly if there are no privacy costs associated with the desire for more data utility. Therefore, the results obtained with the application of this strategy justify its use. The remainder of the paper is organised as follows: Section 2 presents a brief bibliographical review about privacy preserving data mining algorithms, and Section 3 describes the main aspects of dimensionality techniques, more specifically Self-Organizing Maps and its advantages over other techniques. Section 4 describes the Adult data set and its properties, while Section 5 presents the strategy and the methodology for conducting the experiments. Section 6 presents the outcomes of the proposed strategy, comparing it with results obtained from conventional approaches. Section 7 highlights some of the limitations of our work and provides some directions for future work. Finally, Section 8 draws some conclusions.
2. Anonymisation
Anonymisation is a process of information sanitisation on data collections with the intent of privacy protection. The process requires the data to undergo a transformation procedure by applying masking techniques to minimise the probability of identity disclosure [22]. Anonymisation models have been a key component of various data governance frameworks in different domains e.g., healthcare, finance, governance and corporate. They remain the most prevailing methods of privacy preservation both in scientific research and in privacy related legislation. k-anonymity is the primal anonymisation model which was first introduced by Samarati and Sweeney [23] in an attempt to prevent possible re-identification of user information from published microdata. This concept requires that each combination of quasi-identifier (see Section 4) values in a released table must be indistinctly matched to at least k respondents [24]. For example, a table is said to satisfy k-anonymity if each quasi-identifier associated with the values maps to at least k records in a transformed version of the table . denotes a k-anonymised version of the original table D. More formally, k is the largest number such that the magnitude of each equivalence class in table D is at least k. The k-anonymity requirement is typically enforced through generalisation, suppression and deletion techniques. Generalisation replaces real values with “less specific but semantically consistent value” [25]. Numerical values are typically specified by a range of values, while categorical values are combined into a set of distinct values based on a hierarchical tree of the data attribute domain. Suppression is also applied in conjunction with generalisation to obtain k-anonymity by replacing tuple values with a special symbol like a “*”. An example of tuple suppression is demonstrated in Table 2 and Figure 2. Whereas, deletion removes an entire attribute from a dataset.
2.1. k-Anonymity Example
Table 1 below shows an example of a released medical record with the following attributes: direct identifier (Name), quasi-identifiers (Age, Sex, Zipcode) and sensitive attribute (Disease).

Table 1.
Released medical data.
Table 2 illustrates the three techniques of anonymisation in practice (suppression, generalisation and deletion) in order to satisfy 2-anonymity and preserve the original table. Therefore, for any combination of attributes found in the table there are always at least two rows with those exact attributes. Generalisation is applied to the Age attribute by replacing the values with an age range rather than an exact value. Suppression is applied to mask values of the Zip-code attribute. Deletion is expressed in the removal of the entire Name attribute.

Table 2.
2-Anonymised medical data.
2.2. Data Utility
Data utility is a measure of a data’s analytical completeness and its analytical validity. Data utility is paramount in PPDM where the ultimate goal is to provide optimal utility whilst enforcing a certain degree of privacy without relinquishing the purposefulness of the data. In these scenarios, techniques that produce the highest data utility are more desirable. Data quality metrics for measuring utility mostly assess the degradation of the quality of the data as a result of anonymisation. These metrics are often referred to as functionality loss metrics. The main method of satisfying these metrics is by comparing the results of a function over two data sets, the original and the transformed data. Data quality metrics can be categorised into two types, result and data metrics [26]. The former measures the aggregate results of a PPDM task as defined in Equations (8)–(11), whereas the latter evaluates data quality after the enforcement of anonymisation on a dataset as defined in Equations (5)–(7) in Section 5.
2.3. k-Anonymity Approaches
The specific goal of all anonymisation algorithms is to satisfy the privacy requirements of a specific privacy model. These algorithms use a data transformation process where varying masking techniques are applied to generate privacy preserved data. This is typically a less precise and less complete version of the original data. This effect is termed as information loss. Minimising information loss is vital in order to preserve data utility, otherwise the usefulness of the protected data will be significantly diminished. Data owners try to maintain this balance between privacy and utility by ensuring that the applied algorithm satisfies certain constraints based on their privacy and utility objectives. All anonymisation algorithms differ in their approaches to transform data because they employ different heuristic strategies. Consequently, their results are different even if they are satisfying the requirements of the same anonymisation model. Generalisation algorithms are conceptually simple however the computational complexity of finding an optimal solution for the k-anonymity problem has been shown to be NP-hard [27]. Thus, these techniques generally restrict the possibility of maintaining maximum utility on the anonymised data as generalisations are limited by the imposed hierarchical tree [28]. Whereas, suppression and deletion techniques inadvertently exclude essential features of the data that may be useful for data mining, which ultimately limits the significance of the results [10]. In addition to this, data mining operations may violate the privacy of the protected data, therefore this approach is unable to guarantee a privacy protected output. An example of this is the Mondrian anonymisation algorithm which anonymises data in a two step process: first, multidimensional regions are defined that cover the domain space; second, recoding functions are constructed using summary statistics from each region [29]. Generalisation algorithms like Mondrian lead to higher-quality anonymisation because they aim to obtain uniform occupancy through median-partitioning. However, median-partitioning cannot be performed effectively for attributes affected by outliers, leading to high information loss whenever the data is skewed [30]. Thus, techniques like mondrian are inadequate for producing any output suitable for mining purposes due to excess anonymisation, as we will see in the experiments in Section 6.
To overcome these challenges, several PPDM approaches have viewed anonymisation as a clustering problem [6,12,14,15,16]. Clustering-based anonymisation works by partitioning datasets into clusters using a quality measure and generalising the data for each cluster to ensure that they contain at least k records [31]. This method produces high data quality because it reduces data distortion, making the results suitable for further analysis, mining, or publishing purposes. In addition, it is a unified approach, which gives it the benefit of simplicity, unlike the combination of suppression and generalisation techniques in traditional k-anonymity approaches [17]. Several published works in this area have proposed different clustering techniques to enforce anonymisation measures on private data.
For instance, Byun et al. in [12] proposed a greedy algorithm for k-member clustering where each cluster must contain at least k records and the sum of all intra-cluster distances is minimised. Although this is shown to be efficient, it is impractical in cases involving categorical attributes which cannot be enumerated in any specific order. Loukides and Shao in [17] improve the greedy clustering algorithm by introducing measures that capture usefulness and protection in k-anonymisation. Thus, they are able to produce better clusters by ensuring a balance between usefulness and protection. However, this approach suffers from the same drawbacks as its predecessor. In [6], Lin et al propose a new clustering anonymisation method known as One-pass k-means Algorithm. Unlike the conventional k-means clustering, this only runs for one iteration and proceeds in two phases. In the first phase, all records are sorted by their quasi-identifier. Then k records are randomly selected as the seeds (centroids) to build clusters. The nearest records are assigned to a cluster, and the centroid is subsequently updated. In the second phase, formed clusters are adjusted by removing records from clusters with more than k records and adding them to ones with less than k records. Although this algorithm outperforms the k-member algorithm, the whole process is restricted to one iteration, thus prohibiting the possibility of finding more optimal clustering solutions. The most current modification of the k-member clustering is an improved approach proposed in [32], referred to as k-member Co-clustering. This approach is adjusted to work in conjunction with maximising the aggregate degree of clustering so that each cluster is composed of records which are mutually related. Despite this, it only performs better than the conventional k-member clustering for high anonymity levels, where , and has so far been only applied on numerical attributes. Thus, its true performance against other clustering approaches is yet to be fully determined.
So far, clustering approaches have proven to be successful in providing a trade-off between data utility on one side and data privacy on the other side by enforcing a certain degree of privacy without relinquishing the purposefulness of the data. There still remains myriad ways of improving the state of the art through hybrid approaches that can sufficiently reduce the risks of inferences while still maintaining maximal data utility with reasonable computational costs.
3. Dimensionality Reduction
Dimensionality Reduction (DR) summarises a large set of features into a smaller set by removing irrelevant and noisy information. The DR problem can be formally defined as: given a d-dimensional variable the goal is to find a lower-dimensional representation of where is the reduced dimensionality, with no or less redundancy [33]. As a result of its effectiveness in mitigating the curse of dimensionality, a wide selection of its methods enjoy wide application in scenarios where high-dimensional data are typically encountered. This includes, but is not limited to image processing, multivariate data analysis and data mining. Another important application of its techniques is data visualisation, which is the process of visually representing the compressed high dimensional data into a 2- or 3-dimensional space. This new representation is effective in exploratory data analysis as important properties in the original data space are preserved. DR can also be applied as an intermediate step to facilitate other analyses as it reduces the number of explicitly used features in the original dataset which enables the observation of patterns more clearly [34].
DR methods can be classified between linear or nonlinear models. Linear methods are generally less powerful than nonlinear ones because they generate a much richer connection between the latent variables and the observed ones [34]. The best known technique for liner models is Principal Component Analysis (PCA). PCA is highly efficient in reducing dimensionality without much loss. Its estimated variables can also be used to perfectly reconstruct the observed variable. However, it cannot retrieve exactly the true latent variables if they are nonlinear. In addition, it relies on assumptions that are too restrictive, particularly in the case of latent variable separation. Extending PCA to nonlinear models remains an appealing challenge. As for nonlinear models, methods like Self-Organising Maps (SOM) are best applicable to this class. This method is more effective on a complex dataset and naturally outperforms traditional linear methods on artificial datasets [33].
3.1. Self-Organising Maps
SOM is a variation of the competitive-learning approach in which the goal is to generate a low-dimensional discretized representation of high-dimensional data while preserving its topological and metric relationships [35]. The basic idea in competitive learning is not to map inputs to outputs in order to correct errors or to have output and input layers with the same dimensionality, as in autoencoders. Rather an input layer and output layer are connected to adjacent neurons based on predefined neighbourhood relationships, forming a topographic map [36]. Neurons are tuned to various input patterns until a winning neuron is determined, where the neuron best matches the input vector, more commonly known as the Best Matching Unit (BMU). The BMU for one input pattern can be formally defined by:
where is the measure of distance.
The closer a node is to the BMU, the more its weights get altered, and the farther away the neighbour is from the BMU, the less it learns. The broad idea of the training occurs in a similar manner to k-means clustering where a winning centroid moves by a small distance towards the training instance once a point is assigned to it at the end of each iteration. SOM allows some variation of this framework, albeit in a different way because it cannot guarantee assigning the same number of instances to each class. Despite this, SOM is an excellent tool that can be used for unsupervised applications like clustering and information compression.Several frameworks for combining SOM with clustering techniques to improve the solutions of data mining have been proposed in [37,38,39].
3.2. Significance to PPDM
As stated earlier, DR can serve as an intermediary process for further data analysis due to multiple reasons: first it produces lower-dimensional projections of the original data, leading to less computation and training time; second its lower-dimensional variables still capture the interesting characteristics of the initial set, making it valuable for further analysis; third it eliminates any redundancy in the dataset, which allows observation of patterns more clearly. In PPDM studies, it is standard practice to drop variables due to multiple reasons, for example, certain variables may be considered irrelevant due to little or no correlation with the overall dataset. Inaccurate classification of variables as sensitive values or quasi-identifiers may lead to their discardment. Likewise, high correlated variables can be removed to reduce disclosure risks. This arises when an adversary uses a protected dataset to ascertain confidential information on a data subject in the original dataset V [40].
However, dependencies between variables in big data can be very complex, thus reducing the size of a dataset by discarding some of its features can be costly in terms of the overall utility that can be derived from that dataset. Despite reducing the chances of disclosure, the retention of interesting characteristics in the deleted set may be lost completely. DR offers a way out this impasse, by enabling the transformation of unwanted variables with some well-defined properties. This process does not only reserve the interesting characteristics of the unwanted features, but also represents it in a different form, which can potentially reduce the risk of inferences. Therefore DR techniques like self-organising map stand as ideal candidates for enabling the derivation of more useful results from unwanted features, without revealing their true form.
4. Adult Dataset
The Adult dataset [20] is used in a variety of studies on data privacy [12,41,42,43] and is considered the de facto benchmark for experimenting and evaluating anonymisation techniques and PPDM algorithms. It is an extract of the 1994 U.S. census database and comprises 48,842 entries with 15 different attributes, of which 8 are categorical and 7 numerical. Table 3 presents all features of the dataset, categorised by their attribute types and their attribute set. 9 features of the dataset have been classified as quasi-identifiers, 5 other features as sensitive attributes, and 1 feature as a non-sensitive attribute. The dataset does not contain any value which can directly identify an individual on its own, thus the lack of an identifier attribute. This data classification can be defined as follows:

Table 3.
Adult dataset.
- Identifiers: a data attribute that explicitly declares the identity of an individual e.g., name, social security number, ID number, biometric record.
- Quasi-Identifiers: a data attribute that is inadequate to reveal individual identities independently, however, if combined with other publicly available information (quasi-identifiers), they can explicitly reveal the identity of a data subject e.g., date of birth, postcode, gender, address, phone number.
- Sensitive Attributes: a data attribute that reveals personal information about an individual that they may be unwilling to share publicly. These attributes can implicitly reveal confidential information about individuals when combined with quasi-identifiers and are likely to cause harm e.g., medical diagnosis, financial records, criminal records.
- Non-Sensitive Attributes: a data attribute that may not explicitly or implicitly declare any sensitive information about individuals. These records need to be associated with identifiers, quasi-identifiers or sensitive attributes to determine a respondent’s behaviour or action e.g., cookie IDs.
The goal of the Adult dataset is for income prediction tasks, it is generally applied to predict whether an individual’s annual income exceeds using traditional statistical modeling and machine learning techniques. To perform this task we utilised seven classification models which are detailed in Section 6.
Table 3 also presents the quality of each feature in the Adult dataset using 3 measures: correlation, id-ness, and stability.
- Correlation: We utilise linear correlation to measure the relationship between each feature and the label feature Income, this is derived as a value between 1 and as shown in Figure 1. This allows us to detect linear dependencies and make informed choices on which features to use for DR.
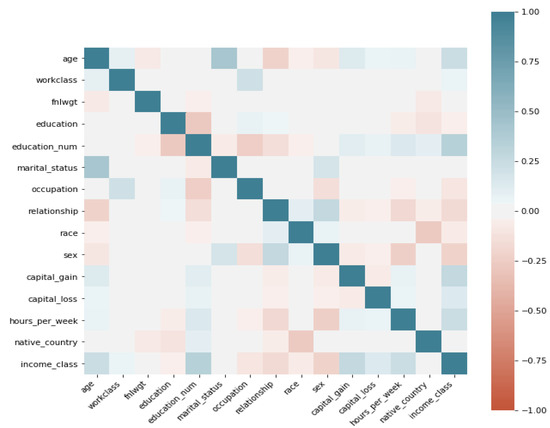 Figure 1. Correlation of adult data features.
Figure 1. Correlation of adult data features. - ID-ness: measures the fraction of unique values in each feature which provides a good basis for data cleaning.
- Stability: measures the fraction of constant non-missing values which informs us about the richness of our data and the extent of bias that can be produced in our classification models.
All these measures are essential in preparing, processing and analysing the dataset for three tasks it will be used for, which are: anonymisation with privacy-based clustering algorithms; dimensionality reduction with self-organising maps; and data prediction with classification models.
5. Methodology
This section presents a hybrid strategy for improving data quality and efficiency in PPDM using clustering-based algorithms such as the One-pass k-Means (OKA) and k-Member algorithm (KMA) in conjunction with SOM for dimensionality reduction. The algorithms applied substitute the values of a given attribute with more general values and suppress other values with a “*” as illustrated in Figure 2. The proposed strategy works in the following stages:
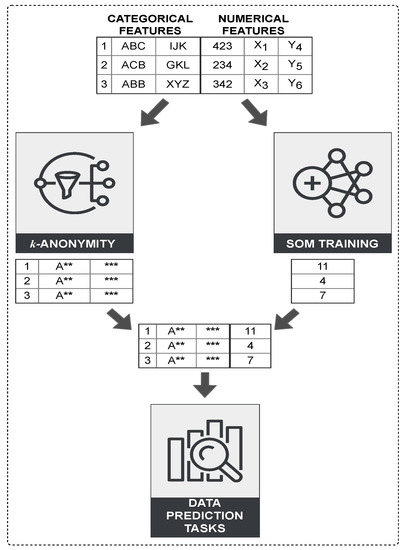
Figure 2.
Architecture of proposed strategy.
- Initially, the dataset is analysed and vertically partitioned based on the attribute set type: categorical or numerical.
- A traditional k-anonymity clustering algorithm is applied to a local dataset containing the categorical attribute set to produce a k-anonymised result.
- SOM is applied to compress the local dataset containing the numerical attribute set that are dropped by the clustering-based algorithms and generate a 1-dimensional representation of all input spaces.
- The partial results are unified in a combined dataset based on their index and reference vectors, ensuring that objects are in the same order as the original dataset.
- Classification techniques are applied on the combined results for generic data prediction tasks that apply to the Adult dataset.
In order to verify the precision of the proposed strategy, results from this approach are compared with those of conventional clustering-based strategies (OKA and KMA). The implementation of these algorithms available from [44] is specifically designed with the purpose of anonymising the Adult dataset, thus making it suitable for this experiment.
In the aforementioned implementation, a distance function is used to measure dissimilarities among data points for both categorical and numerical attributes. For numerical attributes, the difference between two values and of a finite numeric domain D is defined as:
where the domain size is the difference between the maximum and minimum values in D.
However, this is not applicable to categorical attributes as they cannot be enumerated in any specific order. For these attributes, every value in such domain is treated as a different entity to its neighbours when there are no semantic relationship amongst their values. For attributes with semantic relationships as is the case in Figure 3 and Figure 4, a taxonomy tree is applied to define the dissimilarity (i.e., distance). Therefore, the distance between two values and of a categorical domain D is defined as:
where is the subtree rooted at the lowest common ancestor of x and y, and represents the height of tree T.
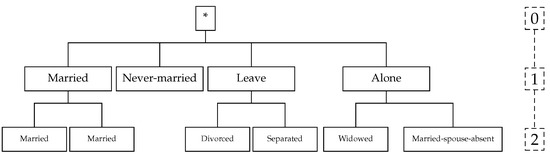
Figure 3.
Taxonomy tree of Marital-status.
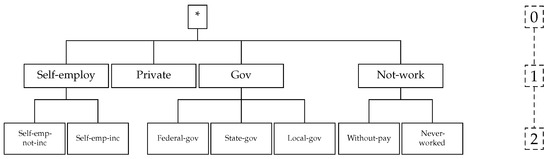
Figure 4.
Taxonomy tree of Workclass.
Example 1.

Consider attribute Workclass and its taxonomy tree in Figure 4. The distance between Federal-gov and Never-worked is 2/2 = 1, while the distance between Federal-gov and Private is 1/2 = 0.5. On the other hand, for attribute Race as defined in Figure 5, where the taxonomy tree has only one level, the distance between all values is always 1.

Figure 5.
Taxonomy tree of Race.
It is important to note that only the Marital-status and Workclass attributes have a predefined taxonomy tree in the clustering implementations published in [44]. The “*” symbol in Figure 3, Figure 4 and Figure 5 denote the maximum level of generalisation for all the attributes. It can be applied to reduce the amount of generalisation necessary to satisfy the k-anonymity constraint. Although, it provides better privacy protection of the microdata, it also causes great information loss.
In our SOM architecture, we use cosine similarity as a distance metric, which ensures the smallest distance between points from the same class and a large margin of separation of points from different classes. This is a particularly useful approach because the Adult dataset has a combination of categorical and numerical data and other more common measures do not translate the distance well between vectors with categorical data. The cosine similarity of two vectors of attributes, a and b, can be formally defined as:
Herein, we used a one-dimensional set of 150 neurons. For each sample i, we search for a neuron which is closest to it. The neuron with the smallest distance to the i-th sample is classified as the BMU, and the weight update is executed until all samples are mapped to an output neuron in the set.
We utilise a method known as hyper-parameter optimization for choosing an optimal set of neurons for our SOM based on their correlation with the Income attribute. The ultimate goal of the prediction task with the Adult dataset is to identify who earns a certain type of income, thus any set of neurons with the highest correlation with the label feature can enhance this task with the anonymised version of the dataset. With this method, we perform an exhaustive search of all possible neurons within a range of manually set bounds. Following this, the set of neurons with the highest correlation with the label feature (i.e., winning neurons or BMUs) is selected as the optimal neuron set.
Finally, we unify our anonymised features with the SOM feature in a central dataset based on their index and reference vectors. Then, we subject this output to 7 classification models for performing the prediction tasks the Adult dataset is intended for (i.e., income prediction). The seven classification models applied are: Naive Bayes, Generalised Linear Model, Logistic Regression, Deep Learning, Decision Tree, Random Forest and Gradient Boosted Trees.
To validate the experiment, several quality measures were used to evaluate and compare the results of our proposed strategy with the two traditional clustering approaches highlighted earlier (OKA and KMA). The quality measures are as follows:
- Normalised Certainty Penalty (): measures information loss of all formed equivalence classes.
- (a)
- For attributes that are numerical, the score of an equivalence class T is defined as:Where the numerator and denominator represent attribute ranges of for the class T and the whole table, respectively.
- (b)
- For attributes that are categorical, in which no distance function or complete order is present, is described w.r.t the attribute’s taxonomy tree:where u represents lowermost common predecessor of all values in that are included in T, is the number of leaves (i.e., values of attribute) in the subtree of u, and represents the total count of discrete values of .
- (c)
- The score of class T over all attributes classified as quasi-identifier is:where n represents number attributes in a quasi-identifier set. can either be a categorical or numerical attribute and has a weight , where .
- Accuracy: measures the percentage of correctly classified instances by the classification model used, which is calculated using the number of (true positives {TP}, true negatives {TN}, false positives {FP} and false negatives {FN}) [45]. Classification accuracy is defined mathematically as:
- Precision: is a class specific performance metric that quantifies the number of positive class predictions that actually belong to the positive class [45], which is defined as:
- Recall: is another important metric, which quantifies the number of positive class predictions made out of all positive examples in the dataset [45]. More formally:
- FMeasure: is another classification-based metric used to measure the accuracy of a classifier model. The metric score computes the harmonic mean between precision p and recall r. Therefore balancing both the concerns of recall and precision in one outcome.
- Time: indicates the length of time it takes to execute an algorithm based on an input data size and a k parameter.
6. Experiments
6.1. Experimental Environment
The anonymisation and classification experiments were performed on a Windows 10 Professional with an Intel(R) i5-7500T 2.7GHz 4-core processor and 16GB of memory. For the 3 anonymisation algorithms (OKA, KMA and Mondrian), we used the implementations publicly available in Github [44]. All implementations are using a common framework (e.g., using the same evaluation metrics and the same data structures for anonymisation), this allows for a fair performance comparison of all the algorithms as shown in Table 4. The Implementations are based on Python 2.7 and allow for different parameters to be used, thus why we apply 3 varying parameters for our k value (equivalence class). For our classification tasks, we used RapidMiner Studio 9.8, which is a data science tool for data preparation, machine learning and predictive model deployment. The reason for the choice of this tool is that it allows for the automation of creating predictive models easily with pre-built templates. This enables us to quickly create impactful machine learning models for immediate analysis as the goal of the classification task is only to see how the anonymised data affects the overall data utility. We use the hold-out validation method for our classification models, which provides similar quality of performance estimations as the cross-validation method but with lesser run time and computational power. For validating the classifcation models, different split ratios were used, e.g., 60/40 increasing to 70/30 and 80/20. They all performed well, however the 60/40 ratio split produced the best results for effective comparison of the multiple models. Therefore, we split the data to 60% for training the multiple models e.g., Naive Bayes, Generalised Linear Model, Logistic Regression, Deep Learning, Decision Tree, Random Forest and Gradient Boosted Trees. The remaining 40% were split into 20% for validation and selecting the best model and 20% for testing and evaluating the models based on the metrics highlighted in Section 5. Our implementation of SOM neural network is based on Python 3.7.3, which is publicly available [46].

Table 4.
score and running time of OKA and KMA with 3 different k thresholds.
6.2. Anonymisation Setup
First, we used the OKA, KMA and Mondrian algorithms for the purpose of anonymisation. We evaluated the score and execution of all the three algorithms, considering 3 different k thresholds for anonymity as illustrated in Table 4. It is observed that the score using OKA is always higher as compared to KMA, and by increasing k threshold for anonymity, the difference in loss also increases as shown in Figure 6. The reason behind this is that OKA only uses one iteration for clustering, which leads to higher information loss; however, its one-pass nature makes it more time efficient than KMA clustering, thus its execution time is significantly less than that of KMA. The Mondrian algorithm incurs the least execution time and suffers little information loss, however it has low usability due to its inconsistent anonymised data, and suffers from the data exploration problem as we will see in the next step.
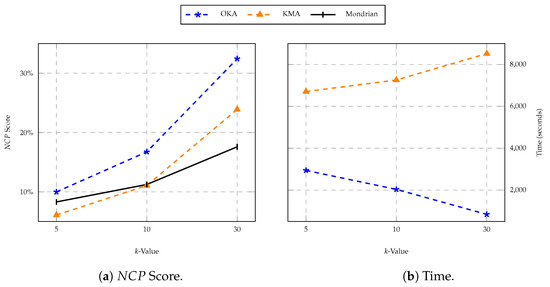
Figure 6.
Algorithm information loss and run time.
6.3. SOM Setup
Following this, we applied SOM clustering on some of the numerical features that are generally dropped on the Adult data set. These features include capital-gain, capital-loss, hours-per-week, and fnlwgt. Due to categorical features in the Adult dataset, we have used the cosine similarity metric because Euclidean distance-based results are biased. The bias arises because L1 and L2 distances are not applicable for vectors with text. We have used hyper-parameter tuning to identify the correct number of neurons for SOM, setting the stride size equal to 10 and iterating 100–300 times. After this, we determine the correlation between the results and the actual income group. We have selected the number of neurons with the highest linear correlation.
6.4. Classification Results
We modified the Adult dataset in five variations: one is OKA+SOM, in which we applied OKA and SOM on the original dataset and the other is KMA+SOM. The next two variations are obtained by just applying OKA and KMA techniques solely. The final variation is the Mondrian algorithm result. We have categorized the performance by 3 different thresholds of k-anonymity: 5, 10, and 30. Finally, we evaluated the performance of the 5 variations of the dataset with respect to accuracy, recall, precision and Fmeasure.
In Figure 7 we considered 5 members in a cluster. After applying the naive Bayes classification model, we observed that accuracy of the KMA+SOM version of the Adult dataset provides around 80% accuracy whereas on the original dataset it was around 83%. The OKA+SOM dataset accuracy is bit lower than that of KMA+SOM. Even on the original dataset, the lowest accuracy was given by the decision tree method, and the same applies to our versions. The highest accuracy achieved is around 82% using a deep learning classification model, whereas on the original dataset it is around 85%. The same trend is observed for fmeasure and precision as well.
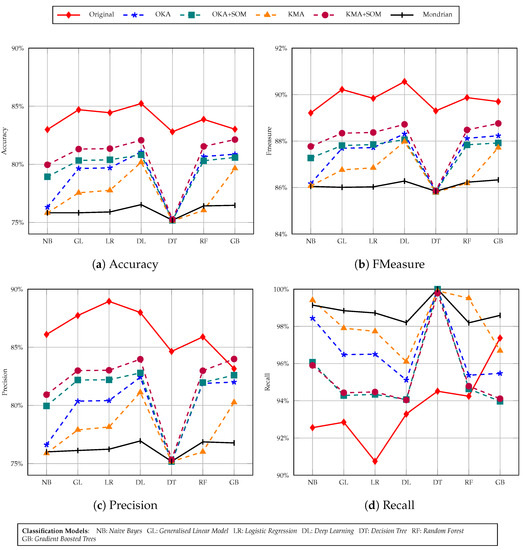
Figure 7.
Income prediction task with 5-anonymity Adult dataset using seven classification models.
In Figure 8 we considered the same variations of data with similar models as we used in previous experiment but with a k-anonymity threshold of 10. It is observed that the overall accuracy is lower for all variations of the dataset except for the original one. Still, the dataset generated with KMA+SOM gave higher accuracy than other variations on all of the models. In Figure 9 we evaluated our datasets with an anonymity threshold of 30, and we found that the accuracy of our datasets are slightly lower compared to 10-anonymity classification results, but the KMA+SOM dataset still has higher accuracy than other variations of original dataset. The OKA+SOM dataset accuracy has decreased more significantly than the others.
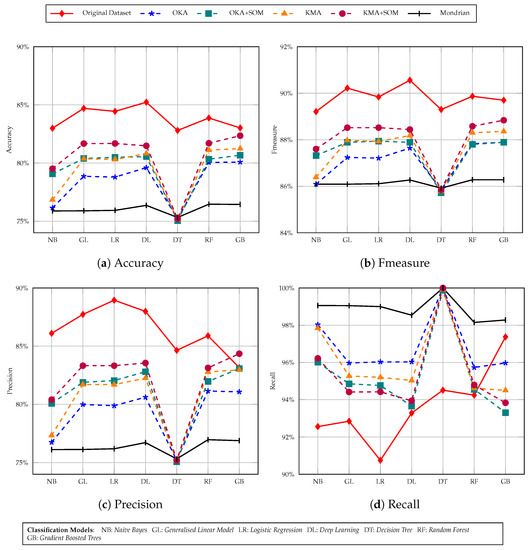
Figure 8.
Income prediction task with 10-anonymity Adult dataset using seven classification models.
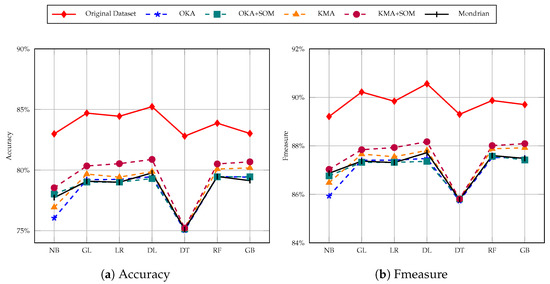
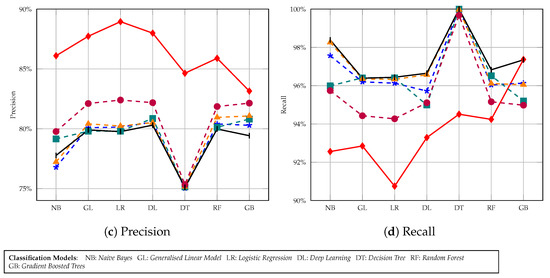
Figure 9.
Income prediction task with 30-anonymity Adult dataset using seven classification models.
In evaluations, we observed that, other than the original dataset, accuracy lowered on all other datasets when the cluster size increased from 5 to 10 to 30. KMA+SOM information loss is quite low, which is why its dataset accuracy improved, however, neither the KMA nor OKA based dataset performed better. Another aspect to consider is that OKA+SOM accuracy is lower than KMA+SOM because OKA uses only one iteration for clustering, which leads to greater time efficiency but also greater information loss compared to other methods. KMA+SOM has a trade-off of data loss with time efficiency. This experiment shows that dimensionality reduction is an effective method for preserving the topological and metric relationships of data features, while anonymising its sensitive content. In addition, results obtained from this process improves the utility of data in classification tasks, as shown in Figure 7, Figure 8 and Figure 9.
7. Open Issues
PPDM has evolved over the years as an effective method for accommodating privacy concepts during mining processes to ensure that the underlying data is not compromised. Despite this development the challenge of balancing data utility and data privacy continue to ensue as [47] suggests. Conventional PPDM techniques do not provide an adequate balance between data utility and privacy protection. They mostly optimise privacy and as a result cannot guarantee a sufficient level of data utility. For this reason, we proposed dimensionality reduction techniques like SOM to improve data utility in PPDM scenarios. The proposed model is appropriate for scenarios where the need for higher data utility supersedes the need for higher privacy with minimal privacy costs. The goal here is to preserve existing privacy while improving utility, which we have proven with our results. Therefore, our application of SOM should not be mistaken as a privacy protection mechanism but as a strategy to maximise data utility in PPDM techniques, with the overall aim of providing a more desirable balance between the two properties. However, the risk of unintended inferences remains in our model due to several reasons.
Firstly, the k-anonymity privacy model used in our model has its limitations, for example it is susceptible to background knowledge attack and homogeneity attack. Therefore, the chances of re-identification are higher with this model than l-diversity or t-closeness. Despite this, it is still a common privacy model with wide application and high uptake in various domains because it is less utility damaging. Alternative anonymisation models are too restrictive and will likely produce lower utility which is contrary to the goal of this work. In any case, the k-anonymity model can always be applied with a more-stringent parameter for higher privacy guarantees. In practice, most data practitioners tend to adopt the utility first approach, so reasonable data utility can be attainable.
Secondly, we selected SOM parameters based on the target variable of the adult dataset because our overall aim is to enhance utility. There is a potential risk that this can increase the likelihood of re-identification as we do not know how the compiled microdata will be used once published. However, this also applies to every data publishing scenario, and it is impractical to test all use cases of any microdata. In future work, we plan to investigate how best to select SOM parameters that aim to enhance data utility, while also taking re-identification risks into account. We also plan to explore selecting SOM parameters based on other variables of the adult dataset, with the ultimate goal of decreasing potential re-identification risks.
Finally, we employed a range of general-purpose privacy and utility metrics to capture different aspects of our implementation. Although this offers some informative assessment, there is a lack of re-identification risk measurement which can further validate our argument for utilising SOM to enhance data utility without the risk of potential disclosures. This can only be ascertained through the application of re-identification risk models like prosecutor, journal, and marketer models. We plan on addressing this issue in future works by developing a unifying framework that adequately evaluates disclosure risks for all applied PPDM techniques. Such framework will provide a more detailed quantification of associated privacy risks and allow for benchmark comparisons with other conventional techniques.
8. Conclusions
In this work, we proposed an effective hybrid strategy for improving data utility in PPDM approaches, which combines self organising maps with conventional privacy based clustering algorithms OKA & KMA. To illustrate this approach we apply it to the Adult data set and utilise rarely used attributes that are commonly dropped by conventional clustering approaches. By considering these additional attributes, we allow a revised balance between usefulness and protection. To validate our experiment, we employed several classification performance measures to evaluate our results and demonstrated an increase in precision on data prediction tasks with our anonymised output for 3 varying k thresholds. The results obtained from our work are useful in scenarios where the need for higher data utility supersedes the need for stringent data privacy, particularly if there are no privacy costs associated with more data utility.
Under the circumstances of emerging re-identification threats, it is necessary to revisit our work and apply additional metrics to provide more informative assessment and standardise the comparison among PPDM techniques. This will bring about novel standards for anonymisation that are robust and accountable for advanced re-identification threats. In addition, it will advance the development of provable PPDM algorithms that enable data practitioners to mine data effectively while ensuring adequate privacy protection. Future work will address all limitations discussed in Section 7. Furthermore, we will expand our experiments by utilising additional data sets to verify the generality of our approach. We will also attempt to optimise our SOM algorithm in order to increase data utility in dimensionality reduction problems, minimise instances of divergence in our results, and improve our interpretation of the performance measures. This will ensure more optimal neurons for data utility driven approaches.
Author Contributions
K.M. is the principal author of this article as part of his PhD thesis, A.A., E.B. were involved in planning and supervised the work. K.M. The specific contribution made by each author are as follows: Conceptualization, K.M., A.A. and E.B.; methodology, K.M.; software, K.M.; validation, K.M., A.A. and E.B.; formal analysis, K.M.; investigation, K.M.; resources, K.M.; data curation, K.M.; writing—original draft preparation, K.M.; writing—review and editing, K.M., A.A. and E.B.; visualization, K.M.; supervision, A.A., E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: UCI Machine Learning Repository [https://archive.ics.uci.edu/ml/datasets/Adult], accessed on 7 January 2021.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PPDM | Privacy Preserving Data Mining |
| ICT | Information & Communication Technology |
| PCA | Principal Component Analysis |
| SOM | Self Organising Maps |
| BMU | Best Matching Unit |
| NCP | Normalised Certainty Penalty |
| OKA | One-pass k-Means Algorithm |
| KMA | k-Member Algorithm |
| DR | Dimensionality Reduction |
References
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann Series in Data Management Systems; Morgan Kaufmann: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Narwaria, M.; Arya, S. Privacy preserving data mining—‘A state of the art’. In Proceedings of the 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; pp. 2108–2112. [Google Scholar]
- Sharma, S.; Shukla, D. Efficient multi-party privacy preserving data mining for vertically partitioned data. In Proceedings of the 2016 International Conference on Inventive Computation Technologies (ICICT), Tamilnadu, India, 26–27 August 2016; Volume 2, pp. 1–7. [Google Scholar] [CrossRef]
- Kaur, A. A hybrid approach of privacy preserving data mining using suppression and perturbation techniques. In Proceedings of the 2017 International Conference on Innovative Mechanisms for Industry Applications (ICIMIA), Bangalore, India, 21–23 February 2017; pp. 306–311. [Google Scholar] [CrossRef]
- Liu, W.; Luo, S.; Wang, Y.; Jiang, Z. A Protocol of Secure Multi-party Multi-data Ranking and Its Application in Privacy Preserving Sequential Pattern Mining. In Proceedings of the 2011 Fourth International Joint Conference on Computational Sciences and Optimization, Kunming, China, 15–19 April 2011; pp. 272–275. [Google Scholar] [CrossRef]
- Lin, J.L.; Wei, M.C. An efficient clustering method for k-anonymization. In Proceedings of the 2008 International Workshop on Privacy and Anonymity in Information Society—PAIS ’08, Nantes, France, 29 March 2008; ACM Press: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Lin, K.P.; Chen, M.S. On the Design and Analysis of the Privacy-Preserving SVM Classifier. IEEE Trans. Knowl. Data Eng. 2011, 23, 1704–1717. [Google Scholar] [CrossRef]
- Zainab, S.S.E.; Kechadi, T. Sensitive and Private Data Analysis: A Systematic Review. In Proceedings of the 3rd International Conference on Future Networks and Distributed Systems ICFNDS ’19, Paris, France, 1–2 July 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Yu, P.S. Aggarwal, C.C.; Yu, P.S. A Condensation Approach to Privacy Preserving Data Mining. In Advances in Database Technology—EDBT 2004; Bertino, E., Christodoulakis, S., Plexousakis, D., Christophides, V., Koubarakis, M., Böhm, K., Ferrari, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 183–199. [Google Scholar]
- Ciriani, V.; di Vimercati, S.D.C.; Foresti, S.; Samarati, P. k-Anonymous Data Mining: A Survey. In Privacy-Preserving Data Mining; Springer: Boston, MA, USA, 2008; pp. 105–136. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Yu, P.S. A General Survey of Privacy-Preserving Data Mining Models and Algorithms. In Privacy-Preserving Data Mining: Models and Algorithms; Springer: Boston, MA, USA, 2008; pp. 11–52. [Google Scholar] [CrossRef]
- Byun, J.W.; Kamra, A.; Bertino, E.; Li, N. Efficient k-Anonymization Using Clustering Techniques. In Advances in Databases: Concepts, Systems and Applications; Springer: Berlin/Heidelberg, Germany, 2007; pp. 188–200. [Google Scholar] [CrossRef]
- Oliveira, S.; Zaïane, O. Privacy Preserving Clustering By Data Transformation. J. Inf. Data Manag. 2010, 1, 37. [Google Scholar]
- Kabir, E.; Wang, H.; Bertino, E. Efficient systematic clustering method for k-anonymization. Acta Inform. 2011, 48, 51–66. [Google Scholar] [CrossRef]
- Xu, X.; Numao, M. An Efficient Generalized Clustering Method for Achieving K-Anonymization. In Proceedings of the 2015 Third International Symposium on Computing and Networking (CANDAR), Washington, DC, USA, 8–11 December 2015. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, Z.; Lv, T.; Ma, Y.; Jia, C. K-Anonymity Algorithm Based on Improved Clustering. Algorithms Archit. Parallel Process. 2018, 462–476. [Google Scholar] [CrossRef]
- Loukides, G.; Shao, J. Clustering-Based K-Anonymisation Algorithms. Database Expert Syst. Appl. 2007, 761–771. [Google Scholar] [CrossRef]
- Pin, L.; Wen-Bing, Y.; Nian-Sheng, C. A Unified Metric Method of Information Loss in Privacy Preserving Data Publishing. In Proceedings of the 2010 Second International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 24–25 April 2010; Volume 2, pp. 502–505. [Google Scholar] [CrossRef]
- Gkoulalas-Divanis, A.; Loukides, G. A Survey of Anonymization Algorithms for Electronic Health Records. In Medical Data Privacy Handbook; Springer International Publishing: Cham, Switzerland, 2015; pp. 17–34. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. Adult Data Set UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 7 January 2021).
- Mohammed, K.; Ayesh, A.; Boiten, E. Utility Promises of Self-Organising Maps in Privacy Preserving Data Mining. In Data Privacy Management, Cryptocurrencies and Blockchain Technology; Garcia-Alfaro, J., Navarro-Arribas, G., Herrera-Joancomarti, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 55–72. [Google Scholar]
- El Emam, K.; Dankar, F.; Issa, R.; Jonker, E.; Amyot, D.; Cogo, E.; Corriveau, J.P.; Walker, M.; Chowdhury, S.; Vaillancourt, R.; et al. A Globally Optimal k-Anonymity Method for the De-Identification of Health Data. J. Am. Med. Inform. Assoc. JAMIA 2009, 16, 670–682. [Google Scholar] [CrossRef]
- Samarati, P. Protecting respondents identities in microdata release. IEEE Trans. Knowl. Data Eng. 2001, 13, 1010–1027. [Google Scholar] [CrossRef]
- Ciriani, V.; Di Vimercati, S.D.C.; Foresti, S.; Samarati, P. k-anonymity. In Secure Data Management in Decentralized Systems; Springer: Boston, MA, USA, 2007; pp. 323–353. [Google Scholar] [CrossRef]
- Samarati, P.; Sweeney, L. Generalizing data to provide anonymity when disclosing information (abstract). In Proceedings of the Seventeenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems; Association for Computing Machinery: Seattle, WA, USA, 1998. [Google Scholar] [CrossRef]
- Bertino, E.; Lin, D.; Jiang, W. A Survey of Quantification of Privacy Preserving Data Mining Algorithms. In Privacy-Preserving Data Mining: Models and Algorithms; Aggarwal, C.C., Yu, P.S., Eds.; Springer: Boston, MA, USA, 2008; pp. 183–205. [Google Scholar] [CrossRef]
- Meyerson, A.; Williams, R. On the Complexity of Optimal K-Anonymity. In Proceedings of the Twenty-Third ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems PODS ’04, Paris, France, 14–16 June 2004; Association for Computing Machinery: New York, NY, USA, 2004; pp. 223–228. [Google Scholar] [CrossRef]
- Tripathy, B. Database Anonymization Techniques with Focus on Uncertainty and Multi-Sensitive Attributes. In Handbook of Research on Computational Intelligence for Engineering, Science, and Business; IGI Global: Hershey, PA, USA, 2013; pp. 364–383. [Google Scholar] [CrossRef]
- LeFevre, K.; DeWitt, D.J.; Ramakrishnan, R. Mondrian Multidimensional K-Anonymity. In Proceedings of the 22nd International Conference on Data Engineering (ICDE’06), Atlanta, GA, USA, 3–7 April 2006; p. 25. [Google Scholar] [CrossRef]
- Ayala-Rivera, V.; McDonagh, P.; Cerqueus, T.; Murphy, L. A Systematic Comparison and Evaluation of k-Anonymization Algorithms for Practitioners. Trans. Data Priv. 2014, 7, 337–370. [Google Scholar]
- Friedman, A.; Wolff, R.; Schuster, A. Providing k-anonymity in data mining. VLDB J. 2008, 17, 789–804. [Google Scholar] [CrossRef]
- Kawano, A.; Honda, K.; Kasugai, H.; Notsu, A. A Greedy Algorithm for k-Member Co-clustering and its Applicability to Collaborative Filtering. Procedia Comput. Sci. 2013, 22, 477–484. [Google Scholar] [CrossRef]
- Ye, J.; Ji, S.; Sun, L. Multi-Label Dimensionality Reduction, 1st ed.; Chapman & Hall: London, UK, 2011. [Google Scholar]
- Lee, J.A.; Verleysen, M. Nonlinear Dimensionality Reduction, 1st ed.; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer International: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Dogan, Y.; Birant, D.; Kut, A. SOM++: Integration of Self-Organizing Map and K-Means++ Algorithms. In Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2013; pp. 246–259. [Google Scholar] [CrossRef]
- Flavius, G.; Jose Alfredo, C. PartSOM: A Framework for Distributed Data Clustering Using SOM and K-Means. In Self-Organizing Maps; IntechOpen: London, UK, 2010. [Google Scholar] [CrossRef]
- Tsiafoulis, S.; Zorkadis, V.C.; Karras, D.A. A Neural-Network Clustering-Based Algorithm for Privacy Preserving Data Mining. In Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 269–276. [Google Scholar] [CrossRef]
- Domingo-Ferrer, J.; Torra, V. Disclosure risk assessment in statistical data protection. J. Comput. Appl. Math. 2004, 164–165, 285–293. [Google Scholar] [CrossRef]
- Byun, J.W.; Sohn, Y.; Bertino, E.; Li, N. Secure Anonymization for Incremental Datasets. In Secure Data Management; Jonker, W., Petković, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 48–63. [Google Scholar]
- Zare-Mirakabad, M.R.; Jantan, A.; Bressan, S. Privacy Risk Diagnosis: Mining l-Diversity. In Database Systems for Advanced Applications; Chen, L., Liu, C., Liu, Q., Deng, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 216–230. [Google Scholar]
- Wang, K.; Fung, B.C.M. Anonymizing Sequential Releases. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining KDD ’06, Beijing, China, 12–16 August 2006; ACM: New York, NY, USA, 2006; pp. 414–423. [Google Scholar] [CrossRef]
- Gong, Q. Clustering Based k-Anonymization. Available online: https://github.com/qiyuangong/Clustering_based_K_Anon (accessed on 8 February 2021).
- Mishra, A. Metrics to Evaluate your Machine Learning Algorithm. Available online: https://towardsdatascience.com/metrics-to-evaluate-your-machine-learning-algorithm-f10ba6e38234 (accessed on 11 February 2021).
- Mohammed, K. SOM Anonymisation. Available online: https://github.com/mkabir7/SOManonymisation (accessed on 24 March 2021).
- Rocher, L.; Hendrickx, J.M.; de Montjoye, Y.A. Estimating the success of re-identifications in incomplete datasets using generative models. Nat. Commun. 2019, 10, 3069. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).