Fair and Secure Multi-Party Computation with Cheater Detection

Abstract

Secure multi-party computation (SMC) is a cryptographic protocol that allows participants to compute the desired output without revealing their inputs. A variety of results related to increasing the efficiency of SMC protocol have been reported, and thus, SMC can be used in various applications. With the SMC protocol in smart grids, it becomes possible to obtain information for load balancing and various statistics, without revealing sensitive user information. To prevent malicious users from tampering with input values, SMC requires cheater detection. Several studies have been conducted on SMC with cheater detection, but none of these has been able to guarantee the fairness of the protocol. In such cases, only a malicious user can obtain a correct output prior to detection. This can be a critical problem if the result of the computation is real-time information of considerable economic value. In this paper, we propose a fair and secure multi-party computation protocol, which detects malicious parties participating in the protocol before computing the final output and prevents them from obtaining it. The security of our protocol is proven in the universal composability framework. Furthermore, we develop an enhanced version of the protocol that is more efficient when computing an average after detecting cheaters. We apply the proposed protocols to a smart grid as an application and analyze their efficiency in terms of computational cost.

1. Introduction

Secure multi-party computation (SMC) is a set of cryptographic techniques that allows a set of mutually distrusting parties to compute a predefined function on their private inputs and obtain an output without revealing the inputs. Due to this property, the SMC protocol has been used in many applications, such as electronic auctions, electronic voting, and privacy-preserving statistical analysis, as a building block [1,2,3,4,5,6]. Privacy-preserving data aggregation protocols that use SMC have been proposed in the literature to deal with user privacy in smart grids [7,8].

A smart grid is a convergence technology that combines a traditional grid and information communications technology (ICT). As the next generation of power grids, it allows two-way transmission between generation plants and customers. Using this bidirectional communication, power suppliers (e.g., utilities) and other service providers offer various convenient services to the customer and optimize energy consumption and cost. Smart meters collect customers’ data in real time. Meaningful information for beneficial services may be obtained by aggregating data collected by smart meters. For example, information such as power consumption patterns and time-of-use rates enable consumers to find a solution to sustain energy efficiency while reducing the cost of electricity. With time-of-use pricing for electricity, consumers can schedule energy-intensive activities for off-peak or mid-peak hours. Moreover, the power supplier utilizes the power consumption patterns of geographical areas to manage energy supply with the aim of load balancing. However, aggregating or collecting consumers’ energy usage data incurs privacy issues. Energy consumption patterns might contain very sensitive information because they reflect consumers’ daily life activities. For example, if such information is revealed, an attacker may be able to determine the number of residents in a house when the house is empty, the types of electronic devices in the house, and other details. Therefore, it is necessary to build a privacy-preserving data aggregation protocol in a smart gird that guarantees the privacy of the data related to each consumer. SMC is a proper solution to handle privacy issues, and several studies have explored the application of the SMC protocol to smart grids [7,8].

However, if malicious consumers tamper with their smart meters while performing computations, the utility as well as honest consumers will be unable to obtain accurate information (e.g., for load balancing or reducing energy cost). Thus, cheater detection is required in the SMC protocol. Cheater detection in SMC has been explored in [9,10,11], but the schemes proposed there have a few weaknesses. In these schemes [9,10,11], a malicious party can share its input with honest parties and create a final share by itself. (Each party performs the pre-defined computation using initial shares, the part of other parties¡¯ inputs, in order to create a final share. We can obtain a final output of the computation by reconstructing, e.g., summing up, final shares of all parties.) The malicious party can then broadcast a random value instead of the final share. In this case, only the malicious party obtains an accurate output by using the final shares of honest parties along with its own final share in the reconstruction phase. The honest parties in such a case obtain an inaccurate output because they reconstruct the values, including a random value by the malicious party. Although the values released by all parties may be used to detect the malicious parties, the final output in this case has already been revealed because the detection occurs following the computation. Therefore it is necessary to detect malicious parties before computing the final output. With this property, SMC guarantees fairness. (Roughly speaking, fairness means that either everyone participating in the SMC protocol can obtain an accurate result of computations or none can.)

In this paper, we propose an SMC protocol that guarantees fairness by detecting a cheater prior to computing the final output. The proposed protocol provides cheater detection and security even when $(n-1)$ of n parties in the protocol are corrupted. Our proposed protocol is based on the SPDZ protocol [12], which is an efficient SMC protocol that has been proven to be secure in the malicious model. (The SPDZ (Smart, N., Pastro, V., Damgard, I., Zakarias, S.) protocol is an SMC protocol for arithmetic circuits with a highly efficient online phase. The online phase of the SPDZ protocol is derived by preprocessing the task of the online phase in the offline phase of the protocol.) In this paper, we provide a definition of universally composable (UC) security for fair multi-party computation and prove the security of the proposed protocol according to this definition. Moreover, we propose an enhanced version of our protocol in case of computing the average, one of the most widely used computations in the smart grid that improves efficiency. We also analyze the efficiency of the enhanced version of our protocol.

Organization

The remainder of this paper is organized as follows: In Section 2 and Section 3, we review related works and briefly explain preliminaries in this area, respectively. In Section 4, we define the relevant notations and introduce the security model for fair SMC in the UC setting. We describe the proposed protocol in Section 5, followed by its security proof in Section 6. In Section 7, we apply the proposed protocol to a smart grid and describe the enhanced version of our protocol through an efficiency analysis. We offer our conclusions in Section 8.

2. Related Work

• Cheater Detection. Detecting cheaters on the Internet has been an important issue, such as astroturfing detection [13,14,15], and a diversity of techniques concerning this matter have been proposed so far. Several studies have been carried out on cheater detection in secret sharing schemes [16,17,18,19]. The results of these techniques are only applicable to secret sharing schemes and thus may not be used to verify the correctness of the new shares computed by secure multi-party computation (SMC) protocol. Several SMC protocols that can detect malicious parties have been proposed so far. Damgård and Orlandi proposed an SMC protocol where every party broadcasts the computed final shares and checks its commitments following the computation of its own final shares [10]. Baum et al. proposed an SMC protocol with an additional audit algorithm [20]. Since the SPDZ protocol was proposed, several SMC protocols have been built on top of the SPDZ protocl to achieve cheater detection and identification [21,22]. Furthermore, there have been efforts to improve the efficiency of SMC protocols with identifiable abort [23]. However, neither of these protocols can prevent malicious parties from learning the final result of computation, whereas honest parties may not. In other words, malicious parties can only be detected following the broadcast of the final shares or the reconstruction of the final output. In such a case, a malicious party can broadcast an incorrect value and obtain all correct final shares of the honest parties as well as its own. The malicious party would then be the only one that can reconstruct the correct output of the computation.
• Fair and Secure Multi-party Computation. It is known that any functionality can be fairly computed in the case of honest majority [24,25,26,27]. However, fairness is impossible to be guaranteed with corrupted majority [28]. Consequently, a number of definitions of security do not consider fairness, even in a Universal Composability (UC) framework, or only consider partial fairness [29,30,31,32]. To overcome this impossibility result, a few approaches to achieve fairness have been proposed. The gradual release approach makes parties take turns releasing their outputs in each round [33,34,35]. However, this approach is still somewhat unfair. Another approach involves employing semi-trusted third parties or physical assumptions [36,37,38]. As part of this approach, a technique using Bitcoin has been proposed [39,40]. It was recently shown that fair, secure, multi-party computation can be achieved by applying a multi-party fair exchange protocol to any SMC protocol [41]. Moreover, several results have been insisted on the possibility of utilizing reputation systems [42], public bulletin boards [43], and trusted hardware [44] to achieve fairness.
• Secure Multi-party Computation in Smart Grid. A number of studies on privacy-preserving aggregation of information for metering or billing have been conducted [45,46,47,48,49,50]. SMC techniques have recently been applied to smart grids to preserve user privacy [7,8]. The protocol proposed in [7] can be applied to smart grids but requires that all participating parties decrypt the final output together in an interactive manner. In [8], Clark and Hopkinson proposed an optimized SMC protocol called transferable multi-party computation (T-MPC) for smart grid networks. To improve efficiency and scalability, T-MPC allows small groups of users to compute the local results of sub-functions. However, it is unable to detect malicious parties and guarantee fairness at the same time.
• Implementations of Secure Multi-party Computation. Implementation and compiler design of SMC is an active area of research. In the early days of research, compilers were developed that convert code written in a high-level language called secure function definition language (SFDL) into a circuit representation (e.g., FairplayMP [3], VIFF [5], SEPIA [6]). Since then, research has been underway for implementations that are more suitable for real-world applications, that is, fast enough to evaluate complex functions and large data sets. For secure two-party computation, most protocols have been designed using circuit garbling [51], such as ABY [52], EzPC [53], and ABY2.0 [54]. For true multi-party computation, a variety of compilers that execute SMC in arbitrary functions have been developed, and representative examples include PICCO [55,56] and MP-SPDZ [57].

In this paper, we propose an SMC protocol that provides cheater detection and fairness. To prevent a malicious party from solely obtaining the final output, in our proposed protocol, detection occurs prior to the computation of the final output. Thus, the proposed protocol guarantees fairness. We also prove the security of our fair SMC protocol in the UC setting. Moreover, we apply our protocol to a smart grid for privacy-preserving aggregation of customers’ data. We also propose an enhanced version of our protocol, in the case of computing the average, and analyze its efficiency.

Contributions

Fairness is an important factor in SMC, and there have been numerous studies to detect malicious parties participating in the protocol. However, most of them focus on detecting and do not fully consider the benefits that malicious attacker can obtain from cheating. If malicious parties share invalid values while others share valid ones, they could be the only ones who can reconstruct a valid final output. Even detecting malicious parties, if they (and only they) can obtain the final output, it can in some cases cause considerable economic damage or invasion of privacy. The underlying cause of this problem is that cheater detection is performed by each party in the protocol individually checking whether the intermediate values (i.e., shares) received from other parties are fair or not. In other words, the detection of malicious parties in previous works occurs after or during reconstruction of the final shares, meaning that it could be after the malicious parties have already obtained the final output. Therefore, it is required that the detection should be executed before the reconstruction of the final output so that malicious parties could not obtain it.

In this paper, we assume that there exists a (semi-honest) server, which searches out malicious parties before the final output is computed. The server should not be able to obtain the secret input values of each party or the final output of the protocol. To this end, we adopt cryptographic techniques including broadcast encryption, commitment, and non-interactive zero-knowledge proof system. After all parties in the protocol have completed their computation individually, they encrypt their own final share using a broadcast encryption scheme and create a commitment to the final share. Then they generate a non-interactive zero-knowledge proof to prove that they committed the encrypted value through broadcast encryption. Finally, they encrypt these three values using the server’s public key and send them to the server. The server then detects the malicious parties by verifying the validity of the values sent from each party, and if all values are valid, the server sends the ciphertexts of each final share to all parties.

Our protocol prevents malicious parties from obtaining an accurate output because the server detects malicious parties prior to computing the final output. Following the execution of the proposed protocol, every honest party may obtain the correct output of the relevant computation whereas malicious parties may not. The proposed protocol guarantees fairness even when $(n-1)$ of n parties are corrupted. If all parties are corrupted, no one can obtain the correct output of the computation. We extend the definition of fair, secure, multi-party computation in the UC setting and give the security proof of our fair SMC protocol in the UC model.

Finally, we develop an enhanced version of our protocol in case of computing averages. The average may be re-computed by slightly modifying each honest party’s final share. Honest parties are not required to restart the protocol from the beginning. The final output is the accurate result of the computation using only fair shares of honest parties. In comparison with the version that involves restarting the protocol, our enhanced version reduces communication- and computation-based overhead in recomputing the final output following the detection of the malicious party. We apply this approach to a smart grid as an application.

3. Preliminaries

3.1. Secure Multi-Party Computation

Research on secure multi-party computation (SMC) can be divided into two groups, the garbled circuit group and the secret sharing group. In this paper, we focus on the secret sharing group because it is more commonly used for $n>2$. We provide a brief explanation of SMC based on the additive secret sharing scheme in particular on carrying out addition and multiplication using shares [10,58,59].

In this setting, each party splits its secret value $x_i$ into shares $x_{i,j}$ adding up to the secret value, i.e., $x_i={\sum }_j{x}_{i,j}$, and distributes them to other parties. All parties participating in the protocol jointly compute the secret values using shares sent from the other parties (and one share of its own secret) without revealing any intermediate or final results. More precisely, each party computes the final share using its own shares, and the final result of the computation is obtained by reconstructing the final shares of all parties.

Every computation is represented as a combination of addition and multiplication. Hence, it is sufficient to introduce the manner in which each party computes a new share for an addition and a multiplication of two secret values using its shares.

3.1.1. Addition

In terms of addition, each party can locally compute a new share. The new share is derived by adding the shares of each secret, e.g., the new share for $(x_1+x_2)$ of party $P_j$ can be computed by $(x_{1,j}+x_{2,j})$. Similarly, in case of a new share for $(a·x_1)$, where a is a constant, party $P_j$ can derive this by computing $(a·x_{1,j})$ for itself.

3.1.2. Multiplication

The multiplication of two secrets requires interactions among the parties. To reduce the numbers of required interactions, all parties pre-share a number of triples prior to the execution of the computation. Triples $(a_i,b_i,c_i)$ of party $P_i$ satisfy the equation ${\sum }_i{c}_i={\sum }_i{a}_i+{\sum }_i{b}_i$ and are independent of the computation to be performed.

Using these triples, parties can compute the multiplication of two secrets, $x_1$ and $x_2$, through a single round of interaction. To obtain a new share for $(x_1·x_2)$ of party $P_i$, $P_i$ first computes and reveals its shares of ${\epsilon }_i=x_{1,i}-a_i$ and ${\delta }_i=x_{2,i}-b_i$. The parties can then reconstruct $\epsilon ={\sum }_i{\epsilon }_i$ and $\delta ={\sum }_i{\delta }_i$. $P_i$ then locally computes its new share $t_i=c_i+\delta ·a_i+\epsilon ·b_i+\epsilon ·\delta$. This enables us to calculate any arithmetic circuit using the same number of interactions as the multiplicative depth of the circuit. For more details, please refer to [10,60].

3.2. Public-Key Broadcast Encryption

Public-key broadcast encryption (PKBE) allows a sender to securely distribute messages to a dynamically changing set of users over an insecure channel in the public key setting [61,62]. The PKBE system consists of three randomized algorithms:

Setup (n).

Takes as input the number of receivers n and outputs a public key $PK$ as well as n private keys $d_1,\dots ,d_n$.

Encrypt (S, PK).

Takes a subset $S\subseteq \{1,\dots ,n\}$ and a public key $PK$ as input, and outputs a pair $(Hdr,K)$, where $Hdr$ is the header and $K\in \mathcal{K}$ is a message encryption key. We often refer to $Hdr$ as the broadcast ciphertext.

Let M be a message to be broadcasted to set S and $C_M$ be the encryption of M under symmetric key K. A sender broadcasts $(S,Hdr,C_M)$ to users in S, where the pair $(S,Hdr)$ is often called the full header and $C_M$ is often called the broadcast body.

Decrypt (${\mathit{d}}_{\mathit{i}},\mathit{S},\mathit{Hdr},\mathit{PK}$).

Takes as input private key $d_i$ for user i, a subset $S\in \{1,\dots ,n\}$, a header $Hdr$, and the public key $PK$. If user i is in S, the algorithm outputs the message encryption key $K\in \mathcal{K}$, which is used to decrypt broadcast body $C_M$ and obtain message M.

3.3. Non-Interactive Zero Knowledge

Non-interactive zero knowledge (NIZK) is a kind of zero-knowledge proof system where no interaction is required between a prover and a verifier. The NIZK protocol usually assumes an initial setup that generates a common reference string (CRS) to eliminate any interaction. The CRS is a publicly shared random string between a prover and a verifier and is given to both a prover and a verifier in advance. Parameterized with relation R, the NIZK protocol proceeds as follows:

Prove. 

Takes as input $(x,w)$ if $(x,w)\notin R$ outputs ⊥. Otherwise, it outputs $(x,\pi )$, where $\pi$ is proof of the statement that $(x,w)\in R$.

Verify. 

Takes as input $(x,\pi )$ and outputs 1 to accept the proof. Otherwise, it outputs 0.

In this paper, we use the UC-secure NIZK protocol proposed in [63].

3.4. Universally Composable Security

In general, we prove the security of the protocol executed in isolation. However, in the real world, many executions occur simultaneously, and some protocols can be used as a sub-function of others. In a universal composability (UC) framework, one can guarantee the security of a protocol even when it is used as a sub-routine of any other protocol running concurrently in the system. The framework for UC was first proposed by Canetti [64].

In the UC framework, there is a “trusted party” that obtains the inputs of all parties and provides them with the desired outputs. A set of instructions for a trusted party describes the functionality of the protocol. Informally, a protocol securely carries out a given task if running the protocol amounts to “emulating” an ideal process, where the parties provide their inputs to a trusted party with the appropriate functionality and obtain their outputs from it without any other interaction. The algorithm operated by the trusted party is called an ideal functionality.

The UC framework is an enhanced version of the real–ideal security model, which includes parties and an adversary A. The notion of emulation in the UC framework is considerably stronger than that in the real–ideal security model because the adversarial entity, called the environment Z, is additionally adopted. The environment Z generates the inputs of all parties, reads all outputs, and interacts with the adversary A in an arbitrary manner throughout the computation. A protocol is said to securely realize a given ideal functionality $\mathcal{F}$ if, for any adversary A, there exists an “ideal-process adversary” S such that no environmentZ can tell whether it is interacting with A and parties executing the protocol, or with S and parties interacting with $\mathcal{F}$ in the ideal process. In a sense, Z here serves as an “interactive distinguisher” between a run of the protocol in the real world and the process with access to $\mathcal{F}$ in the ideal world. In summary, a protocol is UC secure if, for every real-world adversary A, there exists an ideal-world adversary (simulator) S such that the environment Z cannot distinguish between a real execution with A and an ideal execution with S.

4. Definitions

4.1. Notation

We define the notation used in this paper to clarify the representations of our protocol. The $⟦x⟧$ representation of x is defined as $⟦x⟧=(x_1,\dots ,x_n)$, where $x={\sum }_{i=1}^n{x}_i$. Each party $P_i$ will hold its own share $x_i$ of such a representation. For $x,y,e\in {\mathbb{Z}}_p$, we define the operations of this representation as follows:

$$\begin{gathered} ⟦x⟧+⟦y⟧:=(x_1+y_1,\dots ,x_n+y_n) \\ e·⟦x⟧:=(e·x_1,\dots ,e·x_n) \\ e+⟦x⟧:=(x_1+e,x_2,\dots ,x_n) \end{gathered}$$

Definition 1.

Let $x,r\in {\mathbb{Z}}_p$ and $g,h\in G$, where both g and h are generators of group G. We use the Pedersen commitment [65] $pc(x,r)=g^x{h}^r$ and define the commitment $Com(⟦x⟧)$ as follows:

$$Com(⟦x⟧)={\left[pc(x_i,r_i)\right]}_{i\in n}\text{, where} r_i{\in }_R{\mathbb{Z}}_p$$

Each party $P_i$ creates its own commitment $pc(x_i,r_i)$ of such a representation. For $x,y,x_{rand},y_{rand},a\in {\mathbb{Z}}_p$, we define the operations as follows:

$$\begin{gathered} Com\left(x\right)·Com\left(y\right)=pc(x,x_{rand})·pc(y,y_{rand}) \\ Com{\left(x\right)}^a={\left(pc(x,x_{rand})\right)}^a \end{gathered}$$

4.2. UC-Secure Fair Multi-Party Computation

In secure multi-party computation (SMC), a group of parties with their private inputs $x_i$ desire to compute a function $\varphi$. We can guarantee fairness in this case if either all of the parties learn the final output of the computation or none of them learns it. This is formalized by real–ideal world simulations [41]. We extend the real–ideal paradigm to the UC framework defined below, and prove the fairness and security of our protocol in the UC setting in Section 6.

In Figure 1, we present the ideal functionality of our fair SMC protocol in the UC setting. The ideal functionality is the protocol where a trusted party communicates with participants over a secure channel and computes the desired output. In the UC framework, running protocols in the real world is compared to an ideal functionality in the ideal world.   

Real World: Let P be a set of n parties, $P=P_C\bigcup P_H$. It consists of an adversary A that compromises the set $P_C$ of $m(m<n)$ corrupted parties, the set $P_H$ of remaining honest parties, and a server that detects malicious behavior during the execution of the protocol. The pair of outputs of the honest parties $\in P_H$ and A in the real execution of the protocol $\pi$, employing the server, is denoted by ${\mathrm{REAL}}_{\pi ,\mathbf{Server},\mathbf{A}\left(aux\right),\mathbf{Z}}(\lambda ,z,x_1,x_2,\dots ,x_n)$, where ${\left\{x_i\right\}}_{1\le i\le n}$ are the private inputs of each party, $aux$ is an auxiliary input of A, $\lambda$ is the security parameter, and z is the input of the environment.

Ideal World: It consists of an adversary S that controls the set $P_C$, the set $P_H$ of remaining honest parties, and the ideal functionality $\mathcal{F}$ (not the server). $\mathcal{F}$ receives inputs ${\left\{x_i\right\}}_{\{i\in P_C\}}$ or the message $\mathrm{ABORT}$ from S and ${\left\{x_j\right\}}_{\{j\in P_H\}}$ from the honest parties.

• If the inputs are invalid or S sends the message $\mathrm{ABORT}$, $\mathcal{F}$ sends ⊥ to all parties and halts.
• Otherwise, $\mathcal{F}$ computes $\varphi (x_1,\dots ,x_n)=\left({\varphi }_1(x_1,\dots ,x_n),\dots ,{\varphi }_n(x_1,\dots ,x_n)\right)$. Let ${\varphi }_i={\varphi }_i(x_1,\dots ,x_n)$ be the i-th output. Then, $\mathcal{F}$ sends ${\left\{{\varphi }_i\right\}}_{\{i\in P_C\}}$ to S and ${\left\{{\varphi }_j\right\}}_{\{j\in P_H\}}$ to the corresponding honest parties.

The outputs of the parties in an ideal execution involving the honest parties and S, where $\mathcal{F}$ computes $\varphi$, is denoted by ${\mathrm{IDEAL}}_{\mathcal{F},\mathbf{S}\left(aux\right),\mathbf{Z}}(\lambda ,z,x_1,x_2,\dots ,x_n)$, where $x_1,x_2,\dots ,x_n$, $aux,\lambda$, and z are as above.

Definition 2 (UC-secure Fair Multi-party Computation). 

Let π be a probabilistic polynomial time (PPT) protocol and $\mathcal{F}$ be a PPT multi-party functionality computing ϕ. We say that π computes ϕfairly and securelyif, for every non-uniform PPT real-world adversaryAattacking π, there exists a non-uniform PPT ideal world simulatorSsuch that for every $x_1,x_2,\dots ,x_n$, $\lambda \in {\{0,1\}}^{\ast }$, the environmentZwith input z cannot distinguish between a real execution withAand an ideal execution withS:

$$\begin{array}{cc}\hfill \{{\mathrm{REAL}}_{\pi ,}& {}_{\mathbf{Server},\mathbf{A}\left(aux\right),\mathbf{Z}}(\lambda ,z,x_1,x_2,\dots ,x_n)\}\hfill \\ & {\equiv }_c\left\{{\mathrm{IDEAL}}_{\mathcal{F},\mathbf{S}\left(aux\right),\mathbf{Z}}(\lambda ,z,x_1,x_2,\dots ,x_n)\right\}\hfill \end{array}$$

Note that since the server does not exist in the ideal world, the simulator should also simulate its behavior.

5. FSMC Protocol with Cheater Detection

We propose a fair and secure multi-party computation (FSMC) protocol that can detect malicious parties. In FSMC protocol, there are n parties that perform a predefined computation and a semi-honest server that detects malicious parties. The parties corrupted by an adversary are regarded as malicious. The malicious parties do not follow the protocol as described, thereby obtaining the inputs of honest parties or disrupting the computation so that the honest parties may not obtain a correct output.

Once the malicious parties are detected, they may not obtain any information regarding the final output. The protocol consists of three phases: the setup, the offline, and the online phases. In order to improve efficiency of the actual computation, the values used in the online phase were pre-computed in the offline phase.

We use ${\mathcal{F}}_{BE}$ and ${\mathcal{F}}_{NIZK}$ to satisfy the fairness of this protocol. Specifically, the functionality ${\mathcal{F}}_{BE}$ is used to conceal any information regarding the final output. The functionality ${\mathcal{F}}_{NIZK}$ is used to guarantee the connection between the commitment and the ciphertext generated by each party.

In this protocol, each party uses ${\mathcal{F}}_{NIZK}$ to generate the proof of the statement that the commitment and the ciphertext are generated based on the same value, namely the final share it creates. More formally, each party executes Prove with the following relation R:

$$R=\left\{\right(\left(\mathrm{Com}\text{,}\mathrm{CT}\right)\text{,}⟦y⟧\left)\right|\mathrm{Com}=Com⟦y⟧\text{,}\mathrm{CT}=BE⟦y⟧\}$$

5.1. Setup

Let $p\in \mathbb{P}$ be a prime number and G be a group of order p. The Discrete Logarithm Problem (DLP) is difficult to solve in group G. Let $g\in G$ be a generator of G. Choose $s\in {\mathbb{Z}}_p^{\ast }$ uniformly at random and set $h=g^s$. There is a server that verifies the correctness of each party’s values and detects malicious parties. This server must not be able to obtain any secret values of the parties or the final output of the protocol. We assume that a secure channel between the server and each party can be established and that a broadcast encryption functionality ${\mathcal{F}}_{BE}$ (Figure 2) and a non-interactive zero knowledge functionality ${\mathcal{F}}_{NIZK}$ (Figure 3) are available for every party. The notations in the functionalities ${\mathcal{F}}_{BE}$ and ${\mathcal{F}}_{NIZK}$ represent the same meanings as assigned to them in Section 3.2 and Section 3.3.

5.2. Offline Phase

In the offline phase, as a preprocessing stage, some values are pre-computed in order for parties to execute the online phase more efficiently. In Figure 4, we define functionality ${\mathcal{F}}_{Setup}$, which describes the offline phase. In Setup, the values to be used for commitments are generated. These values are used in Compute.Send in the online phase to generate commitments and Output in the online phase to verify them. In RandomValues, the values used to divide each party’s secret into shares are generated. These values are used in the Input of the online phase. In Triples, the multiplication triples and their commitments are generated. The multiplication triples are used in Compute.Multiply in the online phase to compute multiplications with minimal interaction. The commitments are used in Output in the online phase to detect malicious parties.

5.3. Online Phase

The online phase in our protocol is executed as shown in Figure 5. In Initialize, the parties obtain some pre-computed values through the functionalities, which are subsequently used to calculate a predefined circuit during the online phase of this protocol. Furthermore, the server obtains the commitments through the functionality which are used to detect malicious parties. In Input, each party creates the initial shares of its secret value and sends them to the other parties. Each party also obtains the shares of every other party. In Compute, all parties calculate the circuit and send the encrypted final shares, which are used to reconstruct the output of the computation, to the server. They also create some additional values to guarantee the fairness of this protocol. In Output, the server checks the validity of the final shares sent by all parties. If there is no malicious party, the server sends all encrypted final shares to each party. Otherwise, the server notifies the honest parties of the existence of the malicious party.

6. Security in the Online Phase

In this section, we prove the security of the online phase of our protocol. We assume at least one honest party participating in this protocol. We prove the computational security of our protocol, which means that every probabilistic polynomial-time (PPT) adversary succeeds in breaking the scheme with only negligible probability in a reasonable amount of time. We prove that for any polynomial-time adversary A, there exists a simulator ${\mathcal{S}}_{ONLINE}$ that makes protocol ${\prod }_{FSMC}$ indistinguishable from the functionality ${\mathcal{F}}_{SMC}$ to the polynomial–time environment Z.

Theorem 1.

In the ${\mathcal{F}}_{Setup},{\mathcal{F}}_{BE},{\mathcal{F}}_{NIZK}$-hybrid model with a random oracle, the protocol ${\prod }_{FSMC}$ fairly implements ${\mathcal{F}}_{SMC}$ with computational security against any static adversary corrupting up to $(n-1)$ parties, corresponding to Definition 2, if the $DLP$ is hard in the group G.

Proof. 

We prove the above theorem by constructing the simulator ${\mathcal{S}}_{ONLINE}$ in Figure 6. The simulator simulates a server and honest parties in the real world and corrupted parties in the ideal world. It runs an instance ∏ of ${\prod }_{FSMC}$ with simulated honest parties and those controlled by the environment Z. For Initialize, the simulator and the corrupted parties perform the same steps as in ${\prod }_{FSMC}$. During Input, the corrupted parties execute Input in ${\prod }_{FSMC}$ while a simulator simulates the honest parties with their inputs set to 0. The simulator extracts the input values of the corrupted parties from ∏ and sends them to ${\mathcal{F}}_{SMC}$. Moreover, the honest parties send their input values to ${\mathcal{F}}_{SMC}$. In view of environment Z, since the shares of each party’s input value are uniformly random and do not reveal any information regarding the input values, this stage, input, is indistinguishable from real execution.

During Compute, the simulator and the corrupted parties execute Compute.Add and Compute.Multiply in the same manner as in ${\prod }_{FSMC}$. For Compute.send, the simulator generates final shares of the simulated honest parties for ∏ as follows: first, the simulator computes the output of ∏, $y^{\prime }$, using all inputs from both corrupted and honest parties for ∏. Second, for any party $P_i$ of the simulated honest parties, it modifies the final share of $P_i$ by adding the value $(y-y^{\prime })$. For all honest parties except $P_i$, the simulator keeps their final values intact. The distribution of the shares of simulated honest parties is the same as in a real execution of the protocol. Finally, the simulator executes Step 1 of Compute.send in ${\prod }_{FSMC}$ with the modified final shares of the simulated honest parties. The corrupted parties execute the same steps as in Compute.send in ${\prod }_{FSMC}$. Furthermore, if Z decides to stop the execution, a simulator ${\mathcal{S}}_{ONLINE}$ forwards this to the ideal functionality ${\mathcal{F}}_{SMC}$. As in the real execution, Z will not obtain any additional information.

During Output, the simulator acts as a server in the real world. It executes Output in ${\prod }_{FSMC}$ with the corrupted parties. The simulator performs Steps 1 to 3 with values sent from the corrupted parties in Compute.Send. For Step 4, if any failures occur in Steps 2 or 3, the simulator outputs ⊥. Otherwise, it sends the ciphertexts of all final shares in ∏ to the corrupted parties.

Finally, we need to show that the probability that adversary A can cheat is negligible in real protocol execution. If A is able to generate a commitment with a random value, R, which can pass the verification, this random value is verified as a correct value in the Output stage. Following this, if A generates the ciphertext of R and the non-interactive zero-knowledge proof with respect to the ciphertext, the server has no choice but to verify R as a correct final share. However, since the DLP is hard in G, it is nearly impossible for A to generate faulty commitments that can pass verification. Therefore, the probability that A can cheat in real protocol execution is negligible.    □

7. Application

In this section, we provide a privacy-preserving data aggregation mechanism for advanced metering infrastructures in smart grids by applying our FSMC protocol. In Section 7.1, we propose a privacy-preserving data aggregation mechanism for general circuits. In other words, we may compute any function, not merely the sum or the standard deviation, by using this mechanism in smart grids. With our FSMC protocol, this privacy-preserving data aggregation mechanism prevents malicious parties from revealing the valid output of computation and disturbing load balancing. In Section 7.2, we propose an enhanced version of our FSMC protocol in the case of computing the average. We then analyze the efficiency of the enhanced protocol by comparison with the original FSMC protocol.

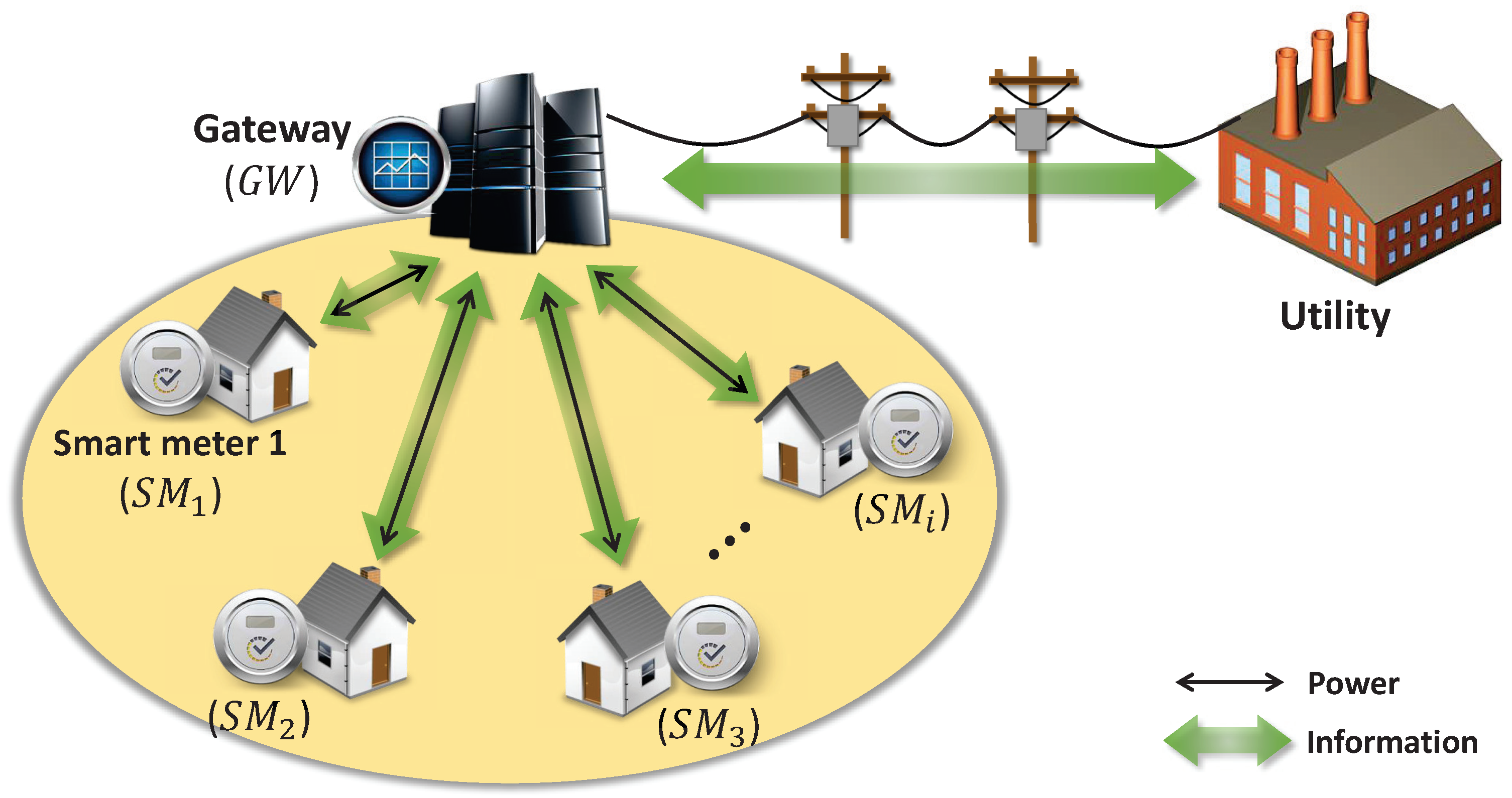
7.1. Applying FSMC Protocol to the Smart Grid

As shown in Figure 7, there are three types of entities in a smart grid: utility, gateway, and smart meters. The smart meters, $S{M}_i(1\le i\le n)$, collect the real-time usage data of each user. The data of users belonging to a specific area are relayed to a local gateway, $GW$. $GW$ aggregates the collected data into compacted data and forwards this information to users and the $utility$. In this process, the privacy of users’ data must be preserved because this information can reveal their living patterns (the number of people in a household, the hours at which they are typically at home and away, their sleeping patterns, etc.).

Our mechanism consists of four phases: (1) System Setup, (2) User Data Sharing, (3) Privacy-preserving Data Aggregation, and (4) Secure Data Retrieval. The details of each phase are as follows.

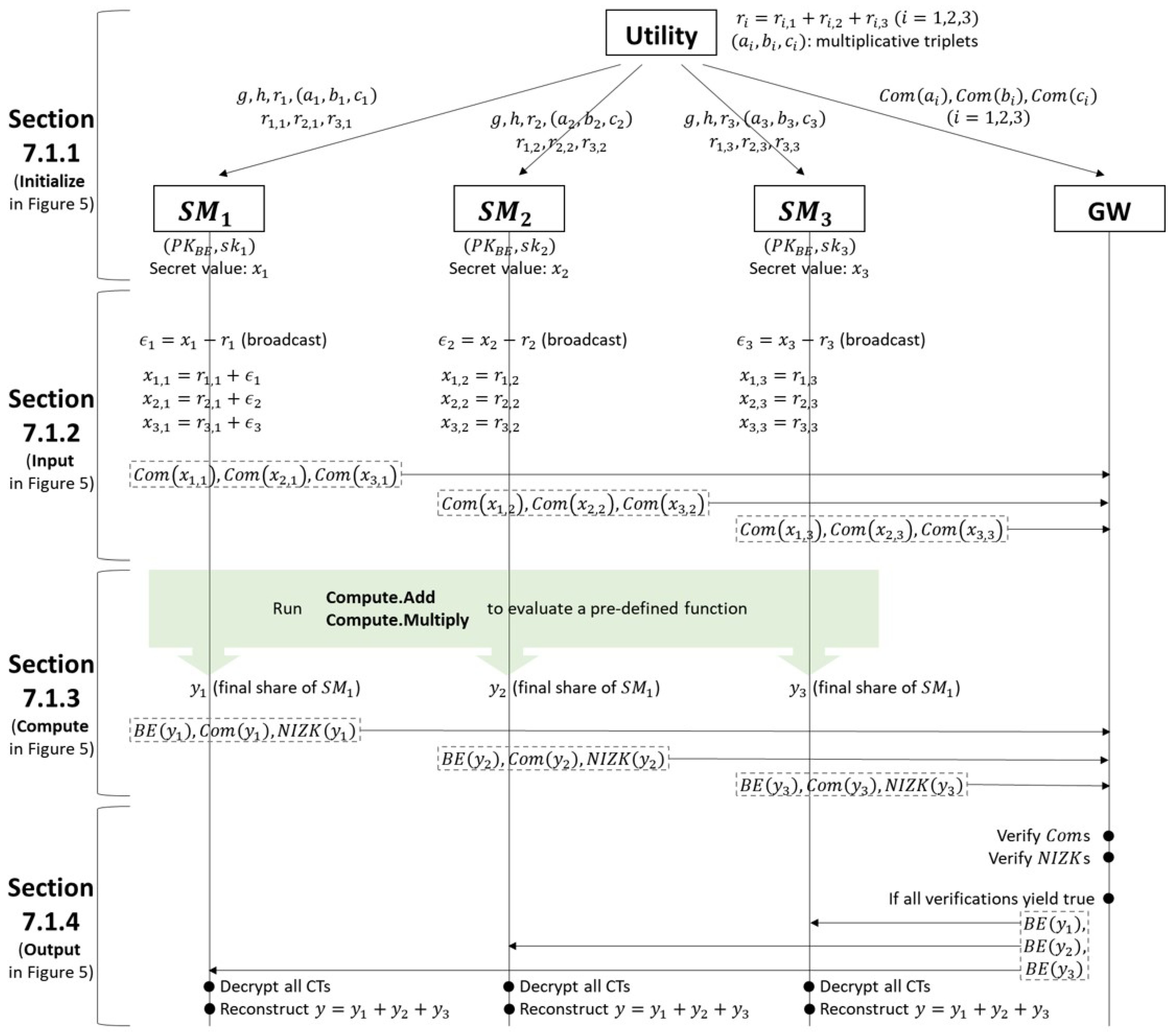
7.1.1. System Setup

We assume that there exists a trusted third party that generates key pairs for the public-key broadcast encryption (PKBE) scheme, and that the key pair used to execute the PKBE scheme in a local area should be embedded in each $S{M}_i$ in the manufacturing stage. In order to set up the system, the $utility$ executes the following steps:

• Step 1. Choose $g\in G$ and $s\in {\mathbb{Z}}_p^{\ast }$. Set $h=g^s$ and send $g,h$ to every $S{M}_i$. These values are used to compute commitment.
• Step 2. Choose uniformly random ${\mathbf{r}}_i\leftarrow {\mathbb{Z}}_p^n$ and send these values to each $S{M}_i$. These values are used to share the secret input of each $S{M}_i$.
• Step 3. Choose $a_i,b_i,c_i\in {\mathbb{Z}}_p^m$ such that $a=b·c$, where $a={\sum }_{j=1}^n{a}_i,b={\sum }_{j=1}^n{b}_i,$ and $c={\sum }_{j=1}^n{c}_i$. Send the triple $(a_i,b_i,c_i)$ to each $S{M}_i$. These values are used as multiplication triples.
• Step 4. Create the commitments of the multiplication triples, $[Com\left(a_i\right),Com\left(b_i\right),$$Com\left(c_i\right)]$ and send them to $GW$. These are used to detect malicious $S{M}_i$ in the Secure Data Retrieval phase. $(Com\left(x\right)=\left(g^x{h}^r\right)$ where r is a random value).

7.1.2. User Data Sharing

In order to perform computations with metering data collected by $S{M}_i$ while keeping them secret, each $S{M}_i$ splits its secret data into n shares using the following steps:

• Step 1.$⟦r⟧$ is privately opened as r to $S{M}_i$, where $⟦\mathbf{r}⟧\leftarrow$$({\mathbf{r}}_1,\dots ,{\mathbf{r}}_n)$.
• Step 2. Broadcast ${ϵ}_i=x_i-r$, where $x_i$ is the metering data for each $S{M}_i$.
• Step 3. Compute $⟦x_i⟧=⟦r⟧+{ϵ}_i$ locally, where $⟦x_i⟧$ is the share of $x_i$ for each $S{M}_i$.
• Step 4. Create the commitments of all shares, $Com\left(⟦x_i⟧\right)$, and send them to $GW$. These commitments are used to detect malicious $S{M}_i$ in the Secure Data Retrieval phase.

7.1.3. Privacy-Preserving Data Aggregation

Since each secret input data $x_i(i\in n)$ is divided into shares $⟦x_i⟧$, we can guarantee the privacy of each $S{M}_i$’s metering data. In order to perform aggregation by using the shares of each metering data $⟦x_i{⟧}_{i\in n}$, each $S{M}_i$ executes the following steps:

• Step 1. Run Compute.Add and Compute.Multiply in ${\prod }_{FSMC}$ to compute the final share of the output for computation.
• Step 2. Encrypt the final share using a PKBE scheme under the recipient set, including all $S{M}_i(i\in n)$, and the $utility$ in a local area.
• Step 3. Create the commitments and the non-interactive zero-knowledge proof as in Compute.Send of ${\prod }_{FSMC}$. Send them to $GW$.

In Step 1, each $S{M}_i$ computes the final share for the output of the pre-defined computation. The final share of any statistical function, not merely the sum or the standard deviation, can be computed. In Step 2, each $S{M}_i$ encrypts the final share. Since the ciphertexts of the final shares are encrypted under the recipient set, including all the $S{M}_i(i\in n)$ and the $utility$ only, $GW$ is unable to obtain any information regarding the final shares. In Step 3, each $S{M}_i$ creates the values used to detect the malicious $S{M}_j$ in the Secure Data Retrieval phase and guarantee the fairness of the protocol.

7.1.4. Secure Data Retrieval

In order to detect malicious $S{M}_i$, $GW$ executes the following steps:

• Step 1. Follow Step 1 of Output in ${\prod }_{FSMC}$ to verify the commitments sent from each $S{M}_i$.
• Step 2. Verify the non-interactive zero-knowledge proof sent from each $S{M}_i$.
• Step 3.

  –

  If all verifications yield true, send all ciphertexts sent from each $S{M}_i$ in the Privacy-preserving Data Aggregation phase to all $S{M}_i(i\in n)$ and the $utility$ in a local area.

  –

  Otherwise, notify each honest $S{M}_i$ of malicious $S{M}_j(j\ne i)$s identities.

Then, each honest $S{M}_i$ copes with the following situations as follows:

• Step 1.

  –

  If there is no malicious $S{M}_i$, decrypt the ciphertexts from $GW$ and reconstruct the output using the final shares.

  –

  Otherwise, restart the protocol from the beginning excluding malicious $S{M}_j$.

To detect malicious $S{M}_i$, $\left(GW\right)$ carries out the verification of each step of computation. Since a single $GW$ is in charge of a whole specific area, we may assume high computation power of $GW$ enough to perform this verification.

To facilitate a better understanding, we describe a simple example of the overall process with three smart meters participating in the protocol in Figure 8.

7.2. Analysis

7.2.1. Improving Efficiency (in terms of Average)

In Section 7.1, if a malicious $S{M}_j$ is detected, each honest $S{M}_i$ should restart the protocol from the beginning. In this case, additional interactions among the honest $S{M}_i$ are required. In this subsection, we provide an enhanced version of the original protocol described in Section 7.1 to compute the average. In the enhanced version, when each honest $S{M}_i$ performs a re-computation following cheater detection, no interactions are required among honest users and, thus, the computation overhead is drastically reduced.

This enhanced version of the protocol is executed in the same manner as before detecting malicious $S{M}_j$. Hence, the three phases of System Setup, User Data Sharing, and Privacy-preserving Data Aggregation are identical to those in the original protocol in Section 7.1. If a malicious $S{M}_j$ is detected by $GW$, each honest $S{M}_i$ reuses the previously computed final share to locally generate the new one. A detailed explanation is provided below.

• Secure Data Retrieval
  In order to detect the malicious $S{M}_j$, $GW$ executes the following steps:

  –

  Step 1. Follow Step 1 of Output in ${\prod }_{FSMC}$ to verify the commitments sent from each $S{M}_i$.

  –

  Step 2. Verify the non-interactive zero-knowledge proof sent by each $S{M}_i$.

  –

  Step 3.

  ∗

  If all verification outputs are true, send all ciphertexts sent by each $S{M}_i$ in the Privacy-preserving Data Aggregation phase to all $S{M}_i(i\in n)$ and the $utility$ in a local area.

  ∗

  Otherwise, notify each honest $S{M}_i$ of the identities of the malicious $S{M}_j(j\ne i)$s.

  If there is no malicious $S{M}_j$, each $S{M}_i$ decrypts the ciphertexts sent by $GW$ and reconstructs the average by adding all final shares. If there exists at least one malicious $S{M}_j$, each honest $S{M}_i$ executes the following steps:
  (Let $P_C$ be the set of identities of the malicious $S{M}_j$.)

  –

  Step 1. Compute $s_i^{\prime }=n·s_i-{\sum }_{j\in P_C}{x}_{j,i}+{\sum }_{j\in P_C}{x}_{i,j}$, where $s_i$ is a final share of $S{M}_i$ computed prior to detection and $x_{j,i}$ is an initial share that $S{M}_j$ assigned to $S{M}_i$.

  –

  Step 2. Set the new final share $s_i^{″}=\frac{1}{n-k}·s_i^{\prime }$, where $k=|P_C|$.

  –

  Step 3. Create the commitment of its new final share, $s_i^{″}$, and the non-interactive zero-knowledge proof as in Compute.Send of ${\prod }_{FSMC}$. Send these to $GW$.

  This phase should be repeated until no malicious party exists. Once $GW$ detects a malicious $S{M}_j$, each honest $S{M}_i$locally executes additional computations to generate the new final share. From the previously computed final share, each honest $S{M}_i$ removes shares $x_{j,i}$, which were provided by the malicious $S{M}_j$, and adds shares $x_{i,j}$, provided to the malicious $S{M}_j$. Since the parts related to the malicious $S{M}_j$ are removed through this process, the new final share $s_i^{″}$ is correct for all honest $S{M}_i$.

We can improve the efficiency of our FSMC protocol described in Section 5 in the same manner when computing the average. As mentioned above, in the enhanced version of the protocol, the Initialize, Input, and Compute phase are the same as in the original protocol ${\prod }_{FSMC}$. Figure 9 represents the Output phase in the enhanced version of the FSMC protocol for computing the average.

7.2.2. Efficiency Analysis

In this section, we compare the computation overhead incurred by each party in case of performing operations in the User Data Sharing phase and the Privacy-preserving Data Aggregation phase. (In terms of communication cost, our proposed protocol is less efficient than the SPDZ protocol [12]. We have combined the SPDZ protocol with a public-key broadcast encryption (PKBE) scheme, a commitment scheme, and a non-interactive zero-knowledge (NIZK) proof system to provide fairness and prevent malicious parties from obtaining the final output. This results in additional values to be shared by each party (i.e., public key of PKBE, commitment, and proof of NIZK), which incurs extra communication overhead).

We conduct an experiment using the PBC [66] and GMP [67] libraries on a laptop with an Intel Core i5-4200U CPU and 4 GB of RAM in order to calculate operation costs. In the original protocol, when each honest $S{M}_i$ executes the User Data Sharing phase during re-computation, it should generate the commitment of each share. The generation of a commitment, $g^x{h}^r$, requires two exponentiation operations in ${\mathbb{Z}}_p\left(\right|p|=1024$ bits) and a multiplication operation in $\mathbb{G}$ with 160 bits. On the contrary, in the enhanced version, there is no need to re-run the User Data Sharing phase.

We analyze the computation overhead of these protocols by dividing the cases into two types. In Section 1, we experiment with a case where detection occurs only once and the number of malicious $S{M}_j$ varies. In Section 1, we experiment with cases where only one malicious $S{M}_j$ is detected and the number of detections varies.

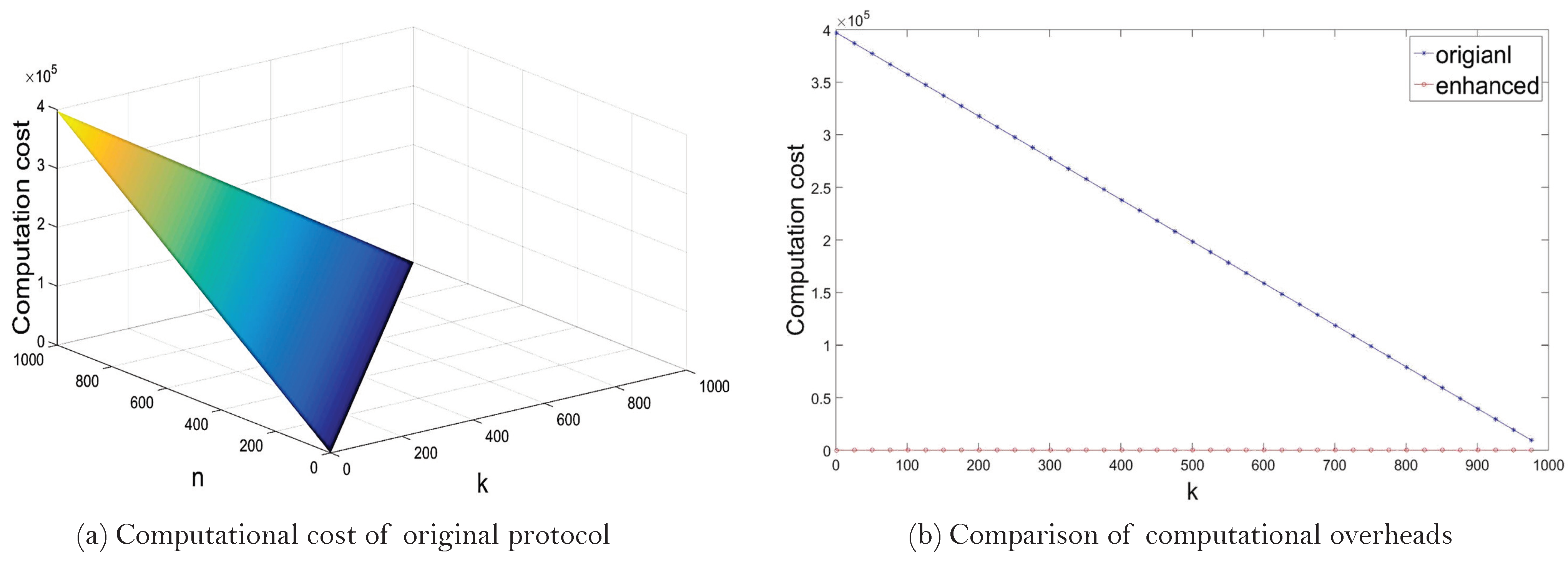
• One detection: k malicious users
  In this case, we compare the computational overhead of two protocols when detection occurs only once and k malicious $S{M}_j$ are detected. The number of generating commitments and computing addition operations are listed in

  Table 1. Comparison of Computational Complexity-One detection, k malicious users.

  	Original Protocol	Enhanced Version
  Input	$(n-k)\times {\mathcal{T}}_{com}$	-
  (commitment)
  Compute	$(n-k)\times {\mathcal{T}}_{add}$	$2k\times {\mathcal{T}}_{add}$
  (addition)

  , where n is the number of smart meters. According to the experimental results, a single addition operation in ${\mathbb{Z}}_p$ and a single commitment generation cost 0.0004 ms $\left({\mathcal{T}}_{add}\right)$ and 397.3102 ms $\left({\mathcal{T}}_{com}\right)$, respectively. Since the User Data Sharing phase is not required during re-computation in the enhanced version of the protocol, only the Privacy-preserving Data Aggregation phase influences the computational cost of the enhanced version.
  The computational cost of original protocol depends on both k and n. We show the variation in computational overhead in terms of both k and n in Figure 10a. Given that n is fixed, the greater the value of k, the smaller the computational cost of the protocol. On the contrary, computational cost of the enhanced version of the protocol depends only on k. We thus depict the difference in computational overhead between two protocols in terms of k in Figure 10b, given that n = 1000. From the figure, we see that the enhanced version is more efficient until k becomes approximately 999.99. This means that the enhanced version of the protocol is more efficient than the original one, excluding the case where all smart meters are detected as malicious.

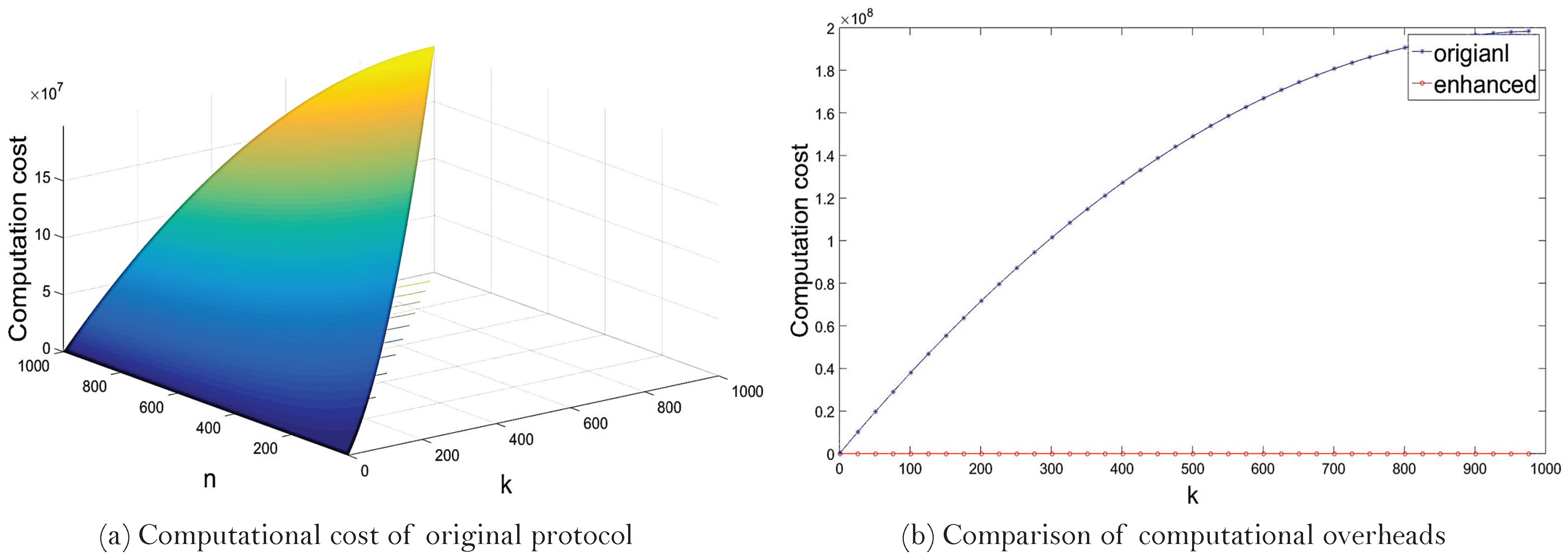
• One malicious user: k detection
  In this case, we compare the computation overhead of two protocols when detection occurs k times and one malicious $S{M}_j$ is detected at a time. The number of generating commitments and computing addition operations is listed in

  Table 2. Comparison of Computational Complexity-One malicious user, k detections.

  	Original Protocol	Enhanced Version
  Input	$\left\{nk-\frac{1}{2}k(k+1)\right\}\times {\mathcal{T}}_{com}$	-
  (commitment)
  Compute	$\left\{nk-\frac{1}{2}k(k+1)\right\}\times {\mathcal{T}}_{add}$	$2k\times {\mathcal{T}}_{add}$
  (addition)

  , where n is the number of smart meters. (As above, ${\mathcal{T}}_{add}$ = 0.0004 ms and ${\mathcal{T}}_{com}$ = 397.3102 ms.)
  We show the variation in computational costs of the original protocol in terms of both k and n in Figure 11a, where detection occurs k times and only one malicious $S{M}_j$ is detected at a time. Given that n is fixed, the greater the value of k, the greater the computational cost of the protocol. On the contrary, computational cost of the enhanced version of the protocol depends only on k. We thus depict the difference in computational overhead between two protocols in terms of k in Figure 11b, given that n = 1000. From the figure, we see that the enhanced version of the protocol is more efficient than the original one in all cases.

8. Conclusions and Future Research Directions

In this paper, we have proposed a secure multi-party computation (SMC) protocol that guarantees fairness and provides cheater detection. The proposed protocol has an efficient online phase because it is based on the SPDZ protocol and is secure if at least one party of n is honest. Our protocol guarantees both the correctness of the output of computation by detecting malicious parties as well as the fairness of the protocol by performing detection prior to deriving the final output. We provided a definition of UC-secure fair SMC and proved the security of fair SMC in the UC setting. Moreover, we proposed an enhanced version of our protocol, in terms of efficiency, for smart grids and analyzed the difference between the original protocol and an improved one.

In future work, we plan to construct an enhanced version of protocols for various kinds of operations, as well as reduce the overall communication overhead. The multi-party computation protocol requires a lot of communication by its nature, and it would be better to combine various kinds of techniques to reduce the amount of communication with our proposed protocol.