Abstract
Classical client remote state preparation (CC − RSP) is a primitive where a fully classical party (client) can instruct the preparation of a sequence of random quantum states on some distant party (server) in a way that the description is known to the client but remains hidden from the server. This primitive has many applications, most prominently, it makes blind quantum computing possible for classical clients. In this work, we give a protocol for classical client remote state preparation, that requires minimal resources. The protocol is proven secure against honest-but-curious servers and any malicious third party in a game-based security framework. We provide an instantiation of a trapdoor (approximately) 2-regular family of functions whose security is based on the hardness of the Learning-With-Errors problem, including a first analysis of the set of usable parameters. We also run an experimentation on IBM’s quantum cloud using a toy function. This is the first proof-of-principle experiment of classical client remote state preparation.
| Contents | ||
| 1 | Introduction and Related Works | 3 |
| 1.1 Related Work | 3 | |
| 1.2 Our Contributions | 4 | |
| 1.3 Applications | 5 | |
| 1.4 Overview of the Protocol and Proof | 6 | |
| 2 | Preliminaries | 9 |
| 2.1 Classical Definitions | 9 | |
| 2.2 Quantum Definitions | 11 | |
| 3 | CC − RSPθ Primitive | 11 |
| 4 | The Real Protocol | 12 |
| 5 | Security of HBC − QFactory | 15 |
| 5.1 Game-Based Security Definition | 15 | |
| 5.2 Game-Based Security of HBC − QFactory | 16 | |
| 5.3 Hardcore Function θ | 18 | |
| 6 | Function Constructions | 20 |
| 6.1 Obtaining Two-Regular, Collision Resistant/Second Preimage Resistant, Trapdoor One-Way Functions | 20 | |
| 6.2 Injective, Homomorphic Quantum-Safe Trapdoor One-Way Function from LWE | 24 | |
| 6.3 A Suitable δ-2 Regular Trapdoor Function | 25 | |
| 6.4 Parameter Choices | 27 | |
| 7 | Implementation of HBC−QFactory on IBM Quantum Cloud | 28 |
| 7.1 Function Construction for Simulation | 28 | |
| 7.2 Results of Implementation of HBC−QFactory | 29 | |
| 7.2.1 Randomness | 29 | |
| 7.2.2 Correctness | 29 | |
| 8 | Conclusions | 31 |
| 8.1 Summary of Results and Discussion | 31 | |
| 8.2 Future Directions | 32 | |
| A | CC−RSPθ within Several Applications | 33 |
| B | Full Proof of Theorem 7 | 34 |
| C | Proof of Theorem 9 | 41 |
| D | Proof of Theorem 11 | 42 |
| D.1 δ-2 Regularity | 43 | |
| D.2 Collision Resistance | 45 | |
| D.3 One-Wayness | 45 | |
| D.4 Trapdoor | 46 | |
| E | Proof of Lemma 7 | 46 |
| References | 48 | |
1. Introduction and Related Works
The recent interest in quantum technologies has brought forward a vision of quantum internet [1] that could implement a collection of known protocols for enhanced security or communication complexity [2]. On the other hand, the rapid development of quantum hardware has increased the computational capacity of quantum servers that could be linked in such a communicating network. This raised the necessity and importance of privacy-preserving functionalities such as the research developed around quantum computing on encrypted data (see a recent review in [3]).
However, there exist some challenges in adapting widely the above vision: A reliable long-distance quantum communication network connecting all the interested parties might be very costly and hard to realize. Moreover, currently, some of the most promising quantum computation devices (e.g., superconducting such as the devices developed by IBM, Google) do not yet offer the possibility of “networked” architecture, i.e., cannot receive and send quantum states.
Therefore, given the crucial role of quantum cloud services, the most important challenge imposing practicality limitations refers to the need of quantum communication. On the one hand, quantum communication is required for the most secure quantum computing primitives, but also for the development of extended quantum communication networks reaching all interested parties (even those with light devices) that need to ensure the compatibility between different quantum communication and computing platforms. For this reason, there has been extensive research focusing on the practicality aspect of quantum delegated computation protocols (and related functionalities). One direction is to reduce the required communications by exploiting classical fully-homomorphic-encryption schemes [4,5,6], or by defining their direct quantum analogues [7,8,9,10]. Different encodings, on the client-side, could also reduce the communication [11,12]. However, in all these approaches the client still requires some quantum capabilities. While no-go results indicate restrictions on which of the above properties are jointly achievable for classical clients [13,14,15,16], completing this picture remains an open problem.
Another very important direction is to consider fully-classical client protocols, compatible with the no-go results, that can therefore achieve more restricted levels of security. The first such procedure achieving statistical security (but not for universal computations) was proposed in [17].
In recent breakthrough results of Mahadev [18], a universal blind delegated protocol for a fully-classical client was proposed under post-quantum computational security. This work, as well as the result of Brakerski [19] which improves the security of [18], proposed quantum fully homomorphic encryption schemes for quantum computations.
The solution we propose in this work, takes a different modular approach. We replace the need for a quantum communication with a classical primitive mimicking a quantum channel. Specifically, what we define and achieve is a version of “classical client remote state preparation” (CC − RSP) formally defined in [20], where the security is post-quantum in the honest-but-curious model.
Note: We first introduced this primitive and the protocol presented here, in a preprint in 2018 that was also presented in QCrypt ’18, which appeared in between the above mentioned works, but was not published. Here we present an extended version of that work, where we have extended our initial work with a series of results which include: the formal proof of security in a game-based framework and realising the first proof-of-principle experiment on a quantum cloud service of such a primitive using a small-scale toy function.
1.1. Related Work
The first proposal for a fully-classical delegated quantum computation protocol appeared in [18], followed by another classical fully homomorphic encryption scheme for quantum computation with improved security parameters in [19]. However, unlike their solution, our approach is modular, as the primitive we propose can be used for a number of functionalities, including delegation of quantum computations (such as [21]), to replace the required quantum communication and make the functionalities directly accessible to classical parties.
Following the introduction of this family of primitives, known as classical client remote state preparation (CC − RSP), in our earlier work [22] (version 2), more works have arose that present constructions of CC − RSP achieving security against arbitrarily deviating, computationally bounded, adversaries. In [23], it is provided a CC − RSP protocol, whose security holds against any malicious server. Concurrently in [24], the authors provide a verifiable version of this CC − RSP primitive with composable security, but under some assumption known as “measurement buffer”. A thorough analysis for the security of this important class of resources was given in [20], where it is shown that the family of CC − RSP cannot be composably-secure unless they leak the description of the produced quantum state to the adversary. In the recent work of [25], the author proposes a delegated quantum computation protocol in which the quantum communication is independent of the size of the computation and depends only (polynomially) on the security parameter (and where the size of the quantum circuit the client has to perform, is also polynomial in the security parameter). This property referred here as “succinct” complexity for the client is achieved in a protocol whose security is proven in the quantum random oracle model. For more details on the general topic of quantum cryptography there are numerous reviews (see for example [26,27]).
1.2. Our Contributions
- We define the primitive classical client remote state preparation () in Section 3. In the earlier version of this work we called this primitive secret random qubit generator, but we switched to the term remote state preparation (RSP), which is the terminology established by the quantum cryptography community. The parameter refers to the set of quantum states produced by the primitive, which are the quantum states . can replace the need for quantum channel between parties in certain quantum communication protocols with the trade-off that the protocols become computationally secure (against quantum adversaries).
- We give a basic protocol () that achieves this functionality from a correctness point of view, given a trapdoor one-way function that is quantum-safe, two-regular and collision resistant in Section 4 and prove its correctness.
- We prove the security of the against honest-but-curious server (server follows the protocol specifications, but can try to infer any information about the secret from the classical transcripts) or against any malicious third party using a game-based security definition. To show the security, we prove that the classical description of the generated qubits is a hard-core function (following a reduction similar to that of the Goldreich–Levin Theorem) in Section 5.
- While the above-mentioned results do not depend on the specific function used, the existence of such specific functions (with all desired properties) makes the a practical primitive that can be employed as described in this paper. In Section 6, we first give methods for obtaining two-regular trapdoor one-way functions with extra properties (collision resistant or second preimage resistant) assuming the existence of simpler trapdoor one-way functions (permutation trapdoor or homomorphic, injective trapdoor functions). We use reductions to prove that the resulting functions maintain all the properties required. Furthermore, we give in Section 6.3 an explicit family of functions that respect all the required properties based on the security of the Learning-With-Errors problem as well as a possible instantiation of the parameters. This function is also quantum-safe, and thus directly applicable for our setting. Note, that other functions may also be used, such as the one in [28] or functions based on the Niederreither cryptosystem and the construction in [29].
- Finally, we implement on the quantum computer IBM Quantum Experience using a toy function (given the current limited number of available qubits we consider a 2-regular function acting on a small number of bits, consequently, it cannot be post-quantum secure). Hence, we provide in addition to the theoretical results, an experimental evidence of the correctness and output distribution of the protocol on a real quantum device. This is the first implementation of an protocol on a quantum cloud service.
1.3. Applications
The primitive, viewed as a resource, has a wide range of applications. Here we give a general overview of the applications, while for details on how to use the exact output of the obtained in this paper in specific protocols, we refer the reader to Appendix A. enables fully-classical parties to participate in many quantum protocols using only public classical channels and a single (potentially malicious) quantum server.
The first type of applications concerns a large class of delegated quantum computation protocols, including blind quantum computation and verifiable blind quantum computation. These protocols are of great importance, enabling information-theoretically secure (and verifiable) access to a quantum cloud. However, the requirement for quantum communication limits their domain of applicability. This limitation is removed by replacing the off-line preparation stage with our protocol. Concretely, we can use to implement the blind quantum computation protocol of [21], as well as the verifiable blind quantum computation protocols (e.g., those in [30,31,32]), in order to achieve classical client secure and verifiable access to a quantum cloud.
In all these cases, the cost of using is that the security becomes post-quantum computational (from information-theoretic). However, the possibility of information-theoretically secure classical client blind quantum computation seems highly unlikely due to strong complexity-theoretic arguments given in [15] and therefore this is the best we could hope for.
The second type of applications involves a more general family of protocols for which their quantum communication consists of random single qubits similar to those provided by the QFactory, such as: quantum-key-distribution [33], quantum money [34], quantum coin-flipping [35], quantum signatures [36], etc.
In the two previous families of applications, QFactory can be used in order to replace quantum clients with classical clients. There is a third type of applications of QFactory that is quite novel: QFactory could be used in order to improve the efficiency and security of some protocols. More specifically, it could be used in protocols where each party needs to make sure that all the other parties are honest. Three major examples of such applications would be the following: two-party quantum computation [37,38], multiparty quantum computation [39] and quantum one-time programs [40]. Indeed, most of these protocols suffer from the fact that one party could try to cheat by sending malicious states instead of the honest single qubit states. Using QFactory, all communications between the client(s) and the server become classical and this observation can be exploited to use classical techniques (e.g., zero-knowledge proofs) to achieve exponential security. Specifically, because of this issue, ref. [39] is proven secure only when there is no dishonest coalition between some clients and the server, while some other works like [38] try to resolve this issue by using a “cut-and-choose” technique where the client sends s qubits, as well as s commitments to their corresponding classical descriptions. All but one commitment are opened for testing and the remaining qubit is then used in the actual computation, leading to a security level of , i.e., security that can grow only linearly with the security parameter. QFactory can improve this in the following way. To make sure that the client(s) behave honestly, the client(s) are requested to send a (post-quantum, but classical) zero-knowledge proof, proving that all the data were generated honestly (i.e., that he knows the trapdoor corresponding to the public description k of the function, as well as the two preimages corresponding to the image y given by the server (see later). One could also add a distributed coin toss before the protocol (where the randomness provided by the client is not revealed, but used in the zero-knowledge proofs) to make sure that the randomness used by the client is not chosen in a malicious way). In this way, QFactory, can achieve an exponential security in the protocol of [38], and also improve the security proof of other protocols. This approach was recently used in the setting of two-party quantum computation [41].
1.4. Overview of the Protocol and Proof
The general idea is that a classical client gives instructions to a quantum server to perform certain actions (quantum computation). Those actions lead to the server having as output a single qubit, which is randomly chosen from within a set of possible states of the form , where . The randomness of the output qubit is due to the (fundamental) randomness of quantum measurements that are part of the instructions that the client gives. Moreover, the server cannot guess the value of r any better than if he had just received that state directly from the client (up to negligible probability). This is possible because the instructed quantum computation is generically a computation that is hard to (i) classically simulate and (ii) to reproduce quantumly because it is unlikely (exponentially in the number of measurements) that by running the same instructions the server obtains the exact same measurement outcomes twice. On the other hand, we wish the client to know the classical description and thus the value of r. To achieve this task, the instructions/quantum computation the client uses are based on a family of trapdoor one-way functions with certain extra properties (The functions should also be two-regular (each image has exactly two preimages), quantum safe (secure against quantum attackers) and collision resistant (hard to find two inputs with the same image)). Such functions are hard to invert (e.g., for the server) unless someone (the client in our case) has some extra “trapdoor” information . This extra information makes the quantum computation easy to classically reproduce for the client, which can recover the value r, while it is still hard to classically reproduce for the server. Sending random qubits of the above type, is exactly what is required from the client in most of the protocols and applications given earlier, while with simple modifications our protocol could achieve other similar sets of states.
Our protocol can heuristically be described in the next steps:
Preparation. The client randomly selects a function , from a family of trapdoor one-way, quantum-safe, two-regular and collision resistant functions. The choice of is public (server knows), but the trapdoor information needed to invert the function is known only to the client.
Stage 1: Preimages Superposition. The client instructs the server (i) to apply Hadamard(s) on the control register, (ii) to apply on the target register i.e., to obtain and (iii) to measure the target register in the computational basis, in order to obtain a value y. This collapses his state to the state , where are the unique two preimages of y.
Remarks. First we note that each image y appears with same probability (therefore, obtaining twice the same y happens with negligible probability). We now consider the first register , where the subscripts denote the different bits of the corresponding preimages x and . We rewrite this:
where is the set of bits positions where are identical, G is the set of bits positions where the preimages differ, while we have suitably changed the order of writing the qubits. It is now evident that the state at the end of Stage 1 is a tensor product of isolated and states, and a Greenberger–Horne–Zeilinger (GHZ) state with random X’s applied. The crucial observation is that the connectivity (which qubit belongs to the GHZ and which doesn’t) depends on the XOR of the two preimages and is computationally impossible to determine, with non-negligible advantage, without the trapdoor information .
Stage 2: Squeezing. The client instructs the server to measure each qubit i (except the output) in a random basis and return back the measurement outcome . The output qubit is of the form , where:
Intuitively, measuring qubits that are not connected has no effect to the output, while measuring qubits within the GHZ part, rotates the phase of the output qubit (by a angle). The above intuition shows that our protocol is correct, as fully proven in Theorem 5.
Security. The protocol is secure, if we can prove that the server (or other third parties) cannot guess (obtain noticeable advantage in guessing) the classical description of the state, i.e., the value of . We consider a quantum-honest-but-curious server which means that he essentially follows the protocol and the security reduces to proving that the server cannot use his classical information to obtain any advantage in guessing the classical description of the (honest) quantum output.
The server does not know the two preimages and needs to guess (which is a three-bit string) from the value of the image y. The key technical part of the security proof is showing a variant of the Goldreich–Levin theorem [42], that (informally) states that the predicate represented by the inner product of the preimage of a one-way function with a random vector, taken modulo 2, is indistinguishable from a random bit. In our case, has a similar expression (1) as it can be expressed as the inner product between the XOR of two preimages and a random vector taken modulo 8. We prove in Theorem 7 that if a computationally bounded server could obtain non-trivial advantage in guessing , then he could also break the property of “second preimage resistance” which we requested for our function . Note, that in our protocol, we actually request the strongest collision-resistance property that implies the second preimage resistance. To prove this theorem we first express each of the 3 bits of as an XOR between a Goldreich–Levin type of predicate and some extra functions. Each of these predicates, instead of having a preimage in the inner product, they have the (bitwise) XOR of the two preimages. We therefore show that guessing any of those predicates would break the (stronger) assumption of collision resistance, reaching a contradiction. Then, to connect the hardness of computing the bits of (each of the three predicates) with the hardness of computing , we use the result of [43] to address the issue of possible correlations. The technical hardest part of Theorem 7 is on the one hand, that we fix all but one variable in the expression of each predicate (bit of ), with an extra cost that is an inverse polynomial probability and on the other hand, that we then use a “disentangling” trick to express the bits as the XOR between a Goldreich–Levin predicate and an extra function (now independent of the other variables).
Using the property of mentioned above, we then prove the full security of the protocol by proving the game-based security holds by a reduction to the hardcore function property of in Theorem 6. More specifically, we show that if the server runs honestly the protocol, but keeps a record of the classical transcript of the protocol together with the measurement outcomes he performs, then it is hard for him to correlate this internal view of the protocol with the protocol output (, ).
The function. Our protocol relies on using functions that have a number of properties (one-way, trapdoor, two-regular, collision resistant (see Remark 1), quantum safe). Any function satisfying those conditions is suitable for our protocol. While in first thought some of these appear hard to satisfy jointly (e.g., two-regularity and collision resistance), we give two constructions that achieve those properties from simpler functions: one from injective, homomorphic trapdoor one-way function and one from bijective trapdoor one-way function. Both constructions define a new function that has domain extended by one bit, and the value of that bit “decides” whether one uses the initial basic function or not.
More specifically, for the first construction, let us denote the injective, homomorphic, trapdoor one-way function by , with k the public description of the function and the trapdoor—used for the inversion of the function . Then, we pick at random an element from the domain of . The public description of the new desired function f will be k along with and the corresponding trapdoor of f would be along with .
Then, the function f, which is evaluated by the server, is described as: , which due to the homomorphic property of g, can be rewritten as: . Now, we can see the 2-regularity property of f as, since is injective, f will always have exactly 2 preimages of the form: x and , which can always be efficiently computed from the image of f using . The one-wayness and quantum-safety of f are then proved by reduction to the one-wayness, respectively quantum-safety of g and finally, we prove the collision-resistance of f, by reducing it to the one-wayness of g.
For the second construction, we denote again by g, the bijective, trapdoor one-way function. Then, in order to construct f, we will basically use 2 such functions g: the public description of f will consist of and —the public descriptions of and and the trapdoor of will consist of the pair —the trapdoors of and .
Then, the function f, evaluated by the server, is described as: . Now, we can see the 2-regularity property of f as, since is bijective, every y from the image of f, will have 2 preimages, namely the unique preimage of and the unique preimage of , which can be both computed from y using . Then, in Appendix C we prove the one-wayness and quantum-safety of f by reduction to one-wayness and quantum-safety of g and finally, we prove the second preimage-resistance of f by reduction to the one-wayness of one of the 2 functions g.
We then give a real instantiation of the required function f based on the first type of construction, starting from the injective trapdoor one-way function defined in [44], which is derived from the Learning-With-Errors problem: , where and , so using the above notation, we have and . This function also seems to satisfy the homomorphic property with respect to addition modulo q: . Unfortunately, things are not so simple, because the domain of the error vector is such that each component of e is bounded by some value , in order for g to be injective and correctly inverted using the trapdoor. This implies that g is homomorphic as long as is also bounded (in infinite norm) by . In our case, this means that may not be small enough to lie within g’s domain, so it may be possible to have only one preimage for some image y. To overpass these problems, we do the following:
When we are constructing the trapdoor for the function f, in particular when we are sampling from the domain of g, we will in fact sample from a smaller set, such that when it will be added together with a random input e, the total noise vector will still be small enough to lie within the domain of g with some good probability.
What we prove is that as long as is sampled from a subset of the domain of g such that is now bounded by , we will get that with at least a constant probability, is inside the domain of g, or in other words that f is now 2-regular with at least a constant probability. What remains to be proven is that when is restricted to this smaller domain, still cannot be inverted by an adversary. Therefore, as a final step we prove that there exists an explicit choice of parameters such that both g and the restriction of g to the domain of are one-way functions and such that all the other properties of g are preserved.
As a result, under this choice of parameters, we obtain our desired function f, satisfying all required properties: one-wayness, trapdoor, collision-resistance and 2-regularity (with a least a constant probability), where the hardness of f is proven by reduction to worst-case hardness of approximating short vectors problems, with polynomial approximation factor, which is the current standard in lattice-based cryptosystems.
Remark 1.
It appears that the second preimage resistance property will be enough to prove the security of our scheme in the honest-but-curious setting. However, as soon as the server can be malicious, the collision resistance property will be very important, else the server might forge known valid states, which would break the security.
2. Preliminaries
2.1. Classical Definitions
We are considering protocols secure against quantum adversaries, so we assume that all the properties of our functions hold for a general Quantum Polynomial Time (QPT) adversary, rather than the usual Probabilistic Polynomial Time (PPT) one. We will denote D the domain of the functions, while is the subset of strings of length n.
Definition 1
(Quantum-Safe (informal)). A protocol/function is quantum-safe (also known as post-quantum secure), if all its properties remain valid when the adversaries are QPT (instead of PPT).
The following definitions are for PPT adversaries, however in this paper we will generally use quantum-safe versions of those definitions and thus security is guaranteed against QPT adversaries.
Definition 2
(One-way). A family of functions is one-way if:
- There exists a PPT algorithm that can compute for any index function k, outcome of the PPT parameter-generation algorithm Gen and any input ;
- any PPT algorithm can invert with at most negligible probability over the choice of k:where represents the randomness used by ;
Definition 3
(Second preimage resistant). A family of functions is second preimage resistant if:
- There exists a PPT algorithm that can compute for any index function k, outcome of the PPT parameter-generation algorithm Gen and any input ;
- for any PPT algorithm , given an input x, it can find a different input such that with at most negligible probability over the choice of k:where is the randomness of ;
Definition 4
(Collision resistant). A family of functions is collision resistant if:
- There exists a PPT algorithm that can compute for any index function k, outcome of the PPT parameter-generation algorithm Gen and any input ;
- any PPT algorithm can find two inputs such that with at most negligible probability over the choice of k:where is the randomness of ( will be omitted from now).
Theorem 1.
[45] Any function that is collision resistant is also second preimage resistant.
Definition 5
(k-regular). A deterministic function is k-regular if , we have .
Definition 6
(Trapdoor Function). A family of functions is a trapdoor function if:
- There exists a PPT algorithmGenwhich on input outputs , where k represents the index of the function;
- is a family of one-way functions;
- there exists a PPT algorithmInv, which on input (which is called the trapdoor information) output byGen() and can invert y (by returning all preimages of y) with non-negligible probability over the choice of and uniform choice of x. Note, that while in the standard definition of trapdoor functions it suffices for the inversion algorithmInvto return one of the preimages of any output of the function, in our case we require a two-regular trapdoor function where the inversion procedure returns both preimages for any function output.
Definition 7
(Hard-core Predicate). A function is a hard-core predicate for a function f if:
- There exists a PPT algorithm that for any input x can compute ;
- any PPT algorithm when given , can compute with negligible better than probability:, where represents the randomness used by ;
Definition 8
(Hard-core Function). A function is a hard-core function for a function f if:
- There exists a PPT algorithm that can compute for any input x;
- for any PPT algorithm when given , can distinguish between and a uniformly distributed element in E with at most negligible probability:
The intuition behind this definition is that as far as a QPT adversary is concerned, the hard-core function appears indistinguishable from a randomly chosen element of the same length.
Theorem 2
(Goldreich–Levin [42]). From any one-way function , we can construct another one-way function and a hard-core predicate for g. If f is a one-way function, then:
- is a one-way function, where .
- is a hard-core predicate for g.
Informally, the Goldreich–Levin theorem is proving that when f is a one-way function, then is hiding the xor of a random subset of bits of x from any PPT adversary. The Goldreich–Levin proof is using a reduction from breaking the hard-core predicate to breaking the one-wayness of g. In this paper, the functions we consider are one-way against quantum adversaries, and using the same reduction we conclude that is a hard-core predicate against QPT adversaries.
Theorem 3
(Vazirani–Vazirani XOR-Condition Theorem [43]). Function h is hard-core function for f if and only if the xor of any non-empty subset of h’s bits is a hard-core predicate for f.
The Learning-With-Errors problem (LWE) can be described in the following way:
Definition 9
(LWE problem (informal)). Given s, an n dimensional vector with elements in , the task is to distinguish between a set of polynomially many noisy random linear combinations of the elements of s and a set of polynomially many random numbers from .
Regev [46] and Peikert [47] have given quantum and classical reductions from the average case of LWE to problems such as approximating the length of the shortest vector or the shortest independent vectors problem in the worst case, problems which are conjectured to be hard even for quantum computers.
Theorem 4
(Reduction LWE, from ([46], Theorem 1.1)). Let n, q be integers and be such that . If there exists an efficient algorithm that solves , then there exists an efficient quantum algorithm that approximates the decision version of the shortest vector problem GapSVP and the shortest independent vectors problem SIVP to within in the worst case.
2.2. Quantum Definitions
We assume basic familiarity with quantum computing notions. For any function that can be described by a polynomially-sized classical circuit, we define the controlled-unitary , as acting in the following way:
where we name the first register control and the second register target. Given the classical description of this function f, we can always define a QPT algorithm that efficiently implements .
3. CC − RSPθ Primitive
In many distributed protocols the required communication consists of sending sequence of single qubits prepared in random states that are unknown to the receiver (and any other third parties). What we want to achieve through our primitive (Algorithm 1) is a way to generate remotely single qubits that are random and (appear to be) unknown to all parties but the “client” that gives the instructions.
Definition 10.
Let . We define the set of states
By including magic states (), this set of states can be viewed as a “universal” resource, as applying Clifford operations on those states is sufficient for universal quantum computation. Furthermore, it is sufficient to implement both blind quantum computation (e.g., [21]) and verifiable blind quantum computation (e.g., [32]).
We emphasize that the aim of defining an ideal functionality is to highlight the task we want to achieve (in terms of correctness) with our protocol , rather than using it in a simulation or composable security definition.
Remarks: (i) The outcome of this primitive is the client “sending” the qubit (that he knows) to the server, thus simulating a quantum channel. (ii) We note that there is an abort possibility and some auxiliary classical messages , both included to make the primitive general enough to allow for our construction. Furthermore, the classical description of the qubit, , and the classical messages are totally uncorrelated (as is chosen independently at random for each . (iii) While the server can learn something about the classical description (e.g., by measuring the qubit), this information is limited and is the exact same information that he could obtain if the client had prepared and sent him a random qubit.
| Algorithm 1 Primitive: Classical Channel Remote State Preparation () |
| Requirements: Client is a purely classical party with no access to quantum resources. Public Information: A distribution on pairs of lists M, intuitively containing the values of the classical variables used by the client and by the server. Trusted Party: – With some probability p returns to both parties , otherwise: – Samples – Samples – Prepares a qubit in state Outputs: – Either returns to both client and server – Or returns to the client, and to the server |
4. The Real Protocol
To construct our protocol (Algorithm 2) we assume the existence of a family of trapdoor one-way functions that are two-regular and collision resistant (or the weaker second preimage resistance property, see Remark 1) even against a quantum adversary. For any y, we will denote by and the two unique different preimages of y by (if the y is clear, we may remove it). Note that because of the two-regularity property . We use subscripts to denote the different bits of the strings. See Section 6 for our function. With that choice, we are guaranteed that the last bits of the two preimages are always different, and thus no need for an abort. We keep the protocol general so that different functions can be used.
| Algorithm 2: Real Protocol |
| Requirements: Public: A family of trapdoor one-way functions that are quantum-safe, two-regular and collision resistant (or second preimage resistant, see Remark 1) Input: – Client: uniformly samples a set of random three-bits strings where , and runs the algorithm . The and k are public inputs (known to both parties), while is the “private” input of the client. Stage 1: Preimages superposition – Client: instructs server to prepare one register at and second register initiated at – Client: sends k to server and the server applies using the first register as control and the second as target – Server: measures the second register in the computational basis, obtains the outcome y and returns this result y to the client. Here, an honest server would have a state with and . Stage 2: Squeezing – Client: instructs the server to measure all the qubits (except the last one) of the first register in the basis. Server obtains the outcomes and returns the result b to the client – Client: using the trapdoor computes . Then check if the n-th bit of x and (corresponding to the y received in Stage 1) are the same or different. If they are the same, returns , otherwise, obtains the classical description of the server’s state. Output: If the protocol is run honestly, when there is no abort, the state that server has is , where the client (only) knows the classical description (see Theorem 5): |
Remarks: The first thing to note is that the server should not only be unable to guess from his classical communications, but he should also be unable to distinguish it from a random string with probability greater than negligible. We will prove this later, but for now it is enough to point out that depends on the preimages x and of y (which the client can obtain using ).
The second thing to note is that while our expression of resembles the inner product in the Goldreich–Levin (GL) theorem, it differs in a number of places and our proof (that is a hard-core function), while it builds on the GL theorem proof, is considerably more complicated. Details can be found in the security proof, but here we simply mention the differences: (i) our case involves three-bits rather than a predicate, and the different bits, if we view them separately, may not be independent, (ii) we have a term rather than a single preimage, so rather than the one-way property of the function we will need the second preimage resistance and (iii) for the same reason, if we view our function as an inner product, it can take both negative and positive values ( could be negative).
A third thing to note is that we have singled-out the last qubit of the first register, as the qubit that will be the output qubit. One could have a more general protocol where the output qubit is chosen randomly, or, for example, in the set of the qubits that are known to have different bit values between x and , but this would not improve our analysis so we keep it like this for simplicity. Moreover, while the “inner product” normally involves the full string x that one tries to invert, in our case, it does not include one of the bits (the last) of the string we wish to invert. It is important to note that it does not change anything to our proofs, since if one can invert all of the string apart from one bit with inverse polynomial probability of success, then trivially one can invert the full string with inverse polynomial probability (by randomly guessing the remaining bit or by trying out both values of that bit). Therefore, all the proofs by contradiction are still valid and in the remaining; for notational simplicity, we will take the inner products to involve all n bits.
Correctness and Intuition
Theorem 5.
If both the client and the server follow Algorithm 2, the protocol aborts when , while otherwise the server ends up with the output (single) qubit being in the state , where θ is given by Equation (4).
Proof.
In the first stage, before the first measurement, but after the application of , the state is . What the measurement does, is that it collapses the first register in the equal superposition of the two unique preimages of the measured , in other words in the state . It is not possible, even for malicious adversary (not considered here), to force the output of the measurement to be a given y (see [48] for relation of PostBQP with BQP). This completes the first stage of the protocol. Before proceeding with the proof of correctness we make three observations.
By the second preimage resistance property of the trapdoor function, learning x is not sufficient to learn but with negligible probability, and intuitively, by the stronger collision resistance property, even a malicious server cannot forge a state (with ) fully known to him.
Then, we examine what happens if the last bit of x and are the same and see why the protocol aborts. In this case, in the first register, the last qubit is in product form with the remaining state, and therefore any further measurements in stage 2 do not affect it, leaving it in the state . As a result of this, the output state is not of the form of Equation (4), while including this states in the set of possible outputs would change considerably our analysis.
Finally, we should note that the resulting state is essentially a Greenberger–Horne–Zeilinger (GHZ) state [49]: let G be the set of bits positions where x and differ (which include n – output qubit), while is the set where they are identical. The state is then (where we no longer keep the qubits in order, but group them depending on their belonging to G or ):
This can be rewritten as (up to trivial re-normalization):
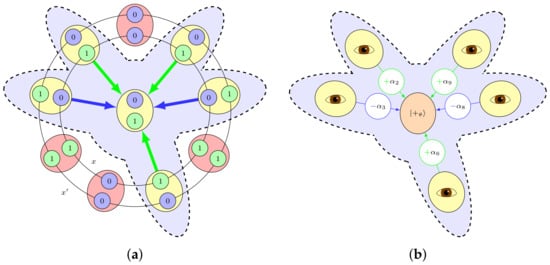
It is now evident that the state at the end of Stage 1 is a tensor product of isolated and states, and a GHZ state with random X’s applied. You can find in Figure 1 an illustration of this state, before and after the Stage 2. Note that GHZ-states when viewed as graph states correspond to stars due to the corresponding graph as we can see here too.

Figure 1.
A simplified representation of the protocol. The red and yellow ellipses represent the qubits, the inner circle contains the bits of x and the outer circle contains the bits of . The central qubit is the last one, which is not measured and which will be the output qubit. (a) End of Stage 1: The yellow qubits are in a big Greenberger–Horne–Zeilinger (GHZ)-like state. The server does not know which qubits are in the GHZ state, and which qubits are not (in red). (b) End of Stage 2: Measuring any qubit in the GHZ state will rotate the last (output) qubit depending on the angle (and result) of the measurement.
The important thing to note is that the set G, that determines which qubits are in the GHZ state and which qubits are not, is not known to the server (apart from the fact that the position of the output qubit belongs to G since otherwise the protocol aborts). Moreover, this set denotes the positions where x and differ, which is given by the XOR of the two preimages . As a result of second preimage resistance of the function, the server should not be able to invert and obtain apart with negligible probability (without access to the trapdoor ). This in itself does not guarantee that the server cannot learn any information about the XOR of the preimages, but we will see that the actual form of the state is such that being able to obtain information would lead to invert the full XOR and thus break the second preimage resistance.
Now, let us continue towards Stage 2. Measuring a qubit (other than the last one) in has no effect on the last qubit (since it is disentangled). When the qubit index is in G, then measuring it at angle gives a phase to the output qubit of the form as one can easily check. We remark that the -term arises because of the commutation of with the measurement angle, and the final gate gives an overall to the angle of deviation. Therefore, adding all the phases leads to the output state being:
As a result that is defined modulo and , we can express the output angle in a more symmetrical way:
Note that because the angles are defined modulo , one can represent this angle as a 3-bits string (interpretable as an integer) such that and eventually remove the if needed by choosing the suitable convention in defining x and . □
A final remark is that in an honest run of this protocol, the measurement outcomes and y are uniformly chosen from and respectively. This justifies why in the honest-but-curious model we can view the protocol as sampling randomly the different ’s.
5. Security of HBC − QFactory
Here we will prove the security of (Algorithm 2) against honest-but-curious adversaries in the game-based security model.
Before proceeding further, it is worth stressing that this security level has three-fold importance. Firstly, the honest-but-curious model concerns any application of that involves a protocol where the adversaries are third parties that have access to the classical communication and nothing else. In this case, we can safely assume that the quantum part of the protocol is followed honestly and we only require to prove that the third parties learn nothing about the classical description of the state from the classical public communication. Second case of interest is scenarios where the “server” does not intend to sabotage/corrupt the computation but may be interested to learn (for free) extra information. In such a case, the protocol should be followed honestly, since any non-reversible deviation other than copying classical information could corrupt the computation. Finally, the honest-but-curious case, as in the classical setting, is a first step towards proving the full security against malicious adversaries.
5.1. Game-Based Security Definition
Definition 11. 
In the following, is said to be secure if for all QPT adversaries the following game is won with probability at most :

Adversary wins the game if and only if .
Then what we want to show is that:
In other words:
Remark 2.
Note that a stronger game could have been defined, where the that is sent to the adversary is always , along with . This would be closer to the actual view of an honest-but-curious adversary, but it is not possible to prove the security of this game, no matter how secure the underlying protocol is. Indeed, given and , it is always possible to measure the in the basis and output only if the measurement outcome was 0.
The case corresponds to the adversary receiving a transcript of the protocol () along with the real output of the protocol () matching to this transcript. The case corresponds to adversary receiving a transcript of the protocol along with a random output of the protocol (). The game ensures that an adversary cannot distinguish these two views. The security of tries to capture the following idea: If an adversary (server) runs honestly the protocol and keeps a record of the measurements he performs together with the transcripts he receives during the protocol, it must be hard for him to correlate this internal view with the output of the protocol (). This is why in the game we ask the adversary to distinguish whether he has access to either a correlated or an uncorrelated .
5.2. Game-Based Security of
Theorem 6.
For any QPT adversary , the game can be won with probability at most .
To prove that is secure according to Definition 11, we will rely on the following result, proven in the next section:
Theorem 7.
The function θ expressed as:
as was defined in Algorithm 2, is a hard-core function with respect to .
NB: here the collision resistance is not needed and is replaced by the weaker second preimage resistance property.
Proof of Theorem 6. 
The main idea would be to use a reduction to the hardcore property of the state description . We will assume that there exists an adversary that can win with probability and we will construct an adversary that can break the hard-core function property of with probability . This implies that if the game can be won with inverse polynomial probability, the same applies to the hard-core function property, and hence we reach a contradiction.
More specifically, let us assume that the adversary can win with probability when and with probability when . Then, we have:
So we have: .
By denoting and , we obtain: .
Now we can define the following adversary that will attack the hardcore property of the state description using the adversary for the game . Namely, will receive the tuple —representing the messages that an adversary has during an honest run of and will try to determine the underlying state description .

Now we want to determine the probability that the output of the adversary is equal to the “true” that is obtained by .
We will consider separately two cases, namely: (i) and (ii) . Since is chosen randomly from the eight possible angles, it is clear that case (i) occurs with probability and case (ii) occurs with probability .
- (i)
- receives the “true” state (), so to win the game he needs to return . By definition, this happens with , and in this case also wins (since he outputs the correct state). The overall probability that all this happens, i.e., that succeeds in this case, is .
- (ii)
- receives one of the “false” states (), and thus to win he needs to return . By definition this happens with probability . Now, in this case, has essentially ruled-out one of the eight possible states. His random guess, after ruling-out one state, succeeds with probability . Combining all this together we see that succeeds with probability .
More explicitly, the probability that breaks the hardcore property of is (where we denoted the “true” by simply ):
We showed that Adversary succeeds with probability in guessing , where p is the advantage has in . However, we will prove in Theorem 7, that can’t win with probability better than . Contradiction. □
5.3. Hardcore Function θ
Proof Sketch of Theorem 7.
In Algorithm 2, the adversary (server) can only use the classical information that he possesses () in order to try and guess with some probability the value of in the case that there is no abort. Since the adversary follows the honest protocol, the choices of are truly random (and not determined by the adversary as he could in the malicious case). Outline of proof sketch: We first express the classical description of the state into expressions for each of the corresponding three bits. The aim is to prove that it is impossible to distinguish the sequence of these three bits from three random bits with non-negligible probability. To show this we follow five steps. In Step 1, we express each of the bits as a sum mod two, of an inner product (of the form present in GL theorem) and some other terms. In Step 2, we show that guessing the sum modulo two of the two preimages breaks the second preimage resistance of the function and thus is impossible. We assume that the adversary can achieve some inverse polynomial advantage in guessing certain predicates and in the remaining steps we show that in this case he can obtain a polynomial inversion algorithm for the one-way function , and thus reach the contradiction. In Step 3, we use the Vazirani–Vazirani Theorem 3 to reduce the proof of hard-core function to a number of single hard-core bits (predicates). In Step 4, we use a result that allows us to fix all but one variable in each expression, with an extra cost that is an inverse polynomial probability and therefore the (fixed variables) guessing algorithm still needs to have negligible success probability. Finally, in Step 5, we reduce all the predicates in a form of a known hard-core predicate XOR with a function that involves variables not included in that predicate. Using the previous step, it reduces to guessing the XOR of a hard-core predicate with a constant, which is bounded by the probability of guessing the (known to be hard-core) predicate.
Here we give the sketch described above, while the full proof can be found in the Appendix B. Let us start by defining:
where are single bits. Moreover, we treat as vectors in ; we define the vector that involves the bit of each of three-bit strings , and we define . We define z as a vector in defined as the element-wise differences of the bits of x and , i.e., . Finally, as in GL theorem, we use the notation for the inner product .
We will prove that any QPT adversary having all the classical information that server has , can guess with at most negligible probability:
where for simplicity we denote the function f instead of . This means that the adversary cannot distinguish from a random three-bit string with non-negligible probability.
Step 1: We decompose Equation (13) into three separate bits, and use the variable defined above.
where the derivation and exact expressions for the functions are given in Appendix B. We notice from Equation (15) that each bit includes a term of the form which on its own is a hard-core predicate following the GL theorem.
Step 2: By the second preimage resistance we have:
For each bit , separately we assume that the adversary can achieve an advantage in guessing which is . Then, similarly to GL theorem, we prove that if this is inverse polynomial, this leads to contradiction with Equation (16) since one can obtain an inverse-polynomial inversion algorithm for the one-way function f.
Step 3: While each bit includes terms that on its own it would make it hard-core predicate (as stated in Step 1), if we XOR the overall bit with other bits it could destroy this property. To proceed with the proof that is hard-core function, we use the Vazirani–Vazirani theorem which states that it suffices to show that individual bits as well as combinations of XOR’s of individual bits are all hard-core predicates. In this way, one evades the need to show explicitly that the guesses for different bits are not correlated. To proceed with the proof, we use a trick that “disentangles” the different variables.
Step 4: We would like to be able to fix one variable and vary only the remaining, while at the same time maintain some bound on the guessing probability.
The advantage that we assume the adversary has for guessing one bit (or a XOR) is calculated “on average” over all the random choices of . Using Lemma 1 we can fix one-by-one all but one variable (applying the lemma iteratively, see Appendix B). With suitable choices, the cardinality of the set of values that satisfies all these conditions is for each iteration. Unless is negligible, this size is an inverse polynomial fraction of all values. This suffices to reach the contradiction. The actual inversion probability that we will obtain is simply a product of the extra cost of fixing the variables with the standard GL inversion probability. This extra cost is exactly the ratio between the cardinality of the Good sets (defined below) and the set of all values.
Lemma 1.
Let , then for any variable , there exists a set of size at least , such that for all , we have:
where the latter probability is taken over all variables except .
Step 5: If the expression we wish to guess involves XOR of terms that depend on different variables, then by using Step 4 we can fix the variables of all but one term. Then we note that trying to guess a bit (that depends on some variable and has expectation value close to ) is at least as hard as trying to guess the XOR of that bit with a constant. For example, if the bit we want to guess is and we have a bound on the guessing probability where only is varied, then we have
We note that all bits of and their XOR’s can be brought in this form. Then using this, we can now prove security, as the r.h.s. is exactly in the form where the GL theorem provides an inversion algorithm for the one-way function f. For details, see Appendix B. □
6. Function Constructions
For our Algorithm 2, we need a trapdoor one-way function that is also quantum-safe, two-regular and second preimage resistant (or the stronger collision resistance property). These properties may appear to be too strong to achieve, however, we give here methods to construct functions that achieve these properties starting from trapdoor one-way functions that have fewer (more realistic) conditions, and we specifically give one example that achieves all the desired properties. In particular, we give:
- A general construction given either (i) an injective, homomorphic (with respect to any operation and in particular it is only required to be homomorphic once for this operation) trapdoor one-way function or (ii) a bijective trapdoor one-way function, to obtain a two-regular, second preimage resistant, trapdoor one-way function. In both cases the quantum-safe property is maintained (if the initial function has this property, so does the constructed function). We note that for (i) we prove the stronger collision resistant property.
- (Taken from [44]) A method of how to realise injective quantum-safe trapdoor functions derived from the LWE problem, that has certain homomorphic property.
- A way to use the first construction with the trapdoor from [44] that requires a number of modifications, including relaxation of the notion of two-regularity. The resulting function satisfies all the desired properties if a choice of parameters satisfying certain constraints can be found.
- A specific choice of these parameters satisfying all constraints, that leads to a concrete function with all the desired properties.
6.1. Obtaining Two-Regular, Collision Resistant/Second Preimage Resistant, Trapdoor One-Way Functions
Here we give two constructions. The first uses as a starting point an injective, homomorphic trapdoor function while the second a bijective trapdoor function. While we give both constructions, we focus on the first construction since (i) we can prove the stronger collision-resistance property and (ii) (to our knowledge) there is no known bijective trapdoor function that is believed to be quantum-safe.
Theorem 8.
If is a family of injective, homomorphic, trapdoor one-way functions, then there exists a family of two-regular, collision resistant, trapdoor one-way functions. Moreover, the family is quantum-safe if and only if the family is quantum-safe.
From now on, we consider that any function has domain D and range R and let be the closed operation on D and be the closed operation on R such that is the morphism between D and R with respect to these 2 operations:
We also denote the operation on D, the inverse operation of , specifically: and be the identity element for .
Then, the family is described by the following PPT algorithms:

The evaluation procedure receives as input an index of a function from and an element from the function’s domain ():
where every function from is defined as:
The last equality follows since each function from is homomorphic.

Proof.
To prove Theorem 8 we give below five lemmata showing that, the family of functions defined above, satisfies the following properties: (i) two-regular, (ii) trapdoor, (iii) one-way, (iv) collision resistant and (v) quantum-safe. □
Lemma 2
(two-regular). If is a family of injective, homomorphic functions, then is a family of two-regular functions.
Proof.
For every , where :
- Since and is injective, there exists a unique such that .
- Assume such that . By definition , but is injective and by assumption, therefore there exists a unique such that
Therefore, we conclude that:
□
Lemma 3
(trapdoor). If is a family of injective, homomorphic, trapdoor functions, then is a family of trapdoor functions.
Proof. 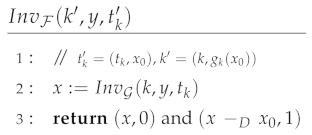
Let . We construct the following inversion algorithm:
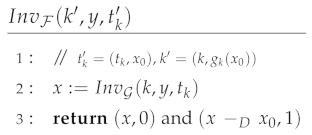
□
Lemma 4
(one-way). If is a family of injective, homomorphic, one-way functions, then is a family of one-way functions.
Proof. 
We prove it by contradiction. We assume that there exists a QPT adversary that can invert a function in with non-negligible probability P (i.e., given to return a correct preimage of the form with probability P). We then construct a QPT adversary that inverts a function in with the same non-negligible probability P reaching a contradiction, since is one-way by assumption.
From Equation (17) of Lemma 2, we know the two preimages of y are: (i) and (ii) . We see that information on is obtain in both cases, i.e., obtaining any of these two preimages, is sufficient to recover if is known. We now construct an adversary that for any function , inverts any output with the same probability P that succeeds.

□
Lemma 5
(collision-resistance). If is a family of injective, homomorphic, one-way functions, then any function is collision resistant.
Proof. 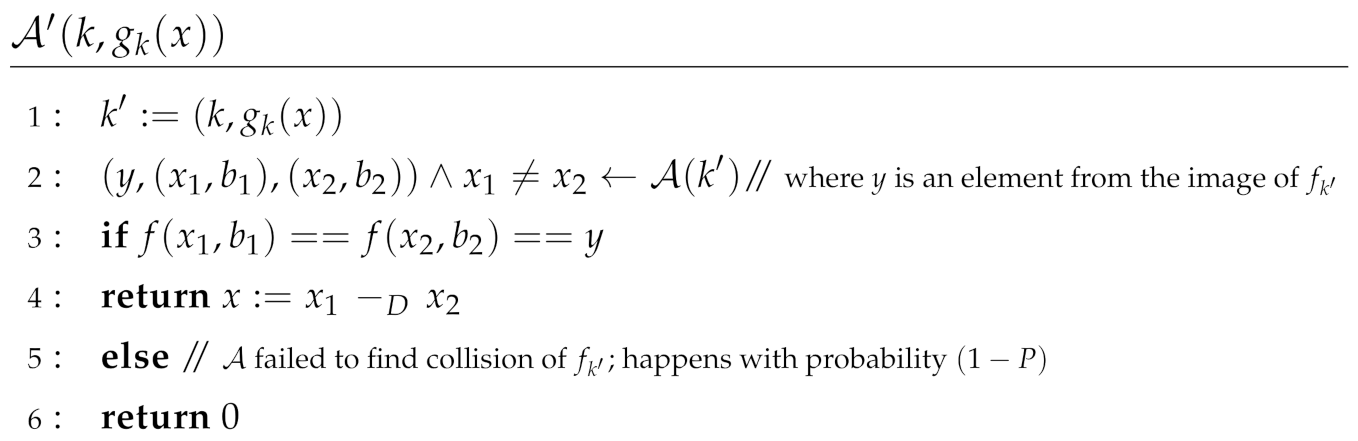
Assume there exists a QPT adversary that given can find a collision where with non-negligible probability P. From Equation (18), we know that the two preimages are of the form where . It follows that when is successful, by comparing the first arguments of the two preimages, can recover .
We now construct a QPT adversary that inverts the function with the same probability P, reaching a contradiction:
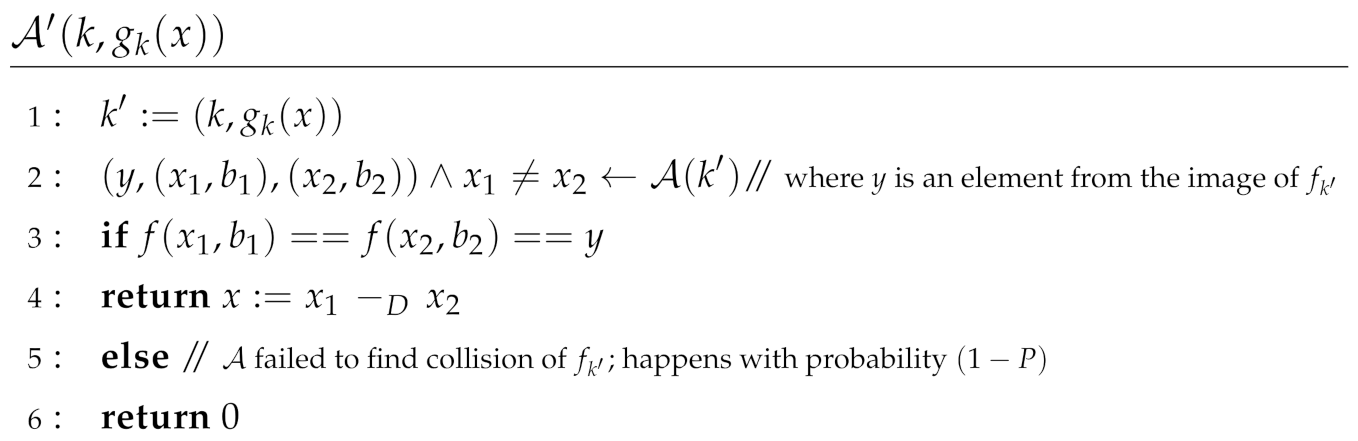
□
Lemma 6
(quantum-safe). If is a family of quantum-safe trapdoor functions, with properties as above, then is also a family of quantum-safe trapdoor functions.
Proof.
The properties that require to be quantum-safe is one-wayness and collision resistance. Both these properties of that we derived above were proved using reduction to the hardness (one-wayness) of . Therefore, if is quantum-safe, its one-wayness is also quantum-safe and thus both properties of are also quantum-safe. □
Theorem 9.
If is a family of bijective, trapdoor one-way functions, then there exists a family of two-regular, second preimage resistant, trapdoor one-way functions. Moreover, the family is quantum-safe if and only if the family is quantum-safe.
The family is described by the following PPT algorithms, where each function has domain D and range R:

where every function from is defined as:

The proof of Theorem 9, using the family of function defined above, follows same steps as of Theorem 8 and is given in the Appendix C.
6.2. Injective, Homomorphic Quantum-Safe Trapdoor One-Way Function from LWE
We outline the Micciancio and Peikert [44] construction of injective trapdoor one-way functions, naturally derived from the Learning-With-Errors problem. At the end we comment on the homomorphic property of the function, since this is crucial in order to use this function as the basis to obtain our desired two-regular, collision resistant trapdoor one-way functions.
The algorithm below generates the index of an injective function and its corresponding trapdoor. The matrix G used in this procedure, is a fixed matrix (whose exact form can be seen in [44]) for which the function from the family with index G can be efficiently inverted without any trapdoor.

where the parameters k, , q and are defined in Theorem 11.
The actual description of the injective trapdoor function is given in the evaluation algorithm below, where each function from is defined on: , and L is the domain of the errors in the LWE problem (the set of integers bounded in absolute value by the parameter ):
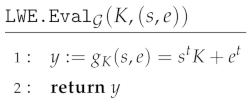
The inversion algorithm returns the unique preimage corresponding to . The algorithm uses as a subroutine the efficient algorithm for inverting the function , with G the fixed matrix mentioned before.
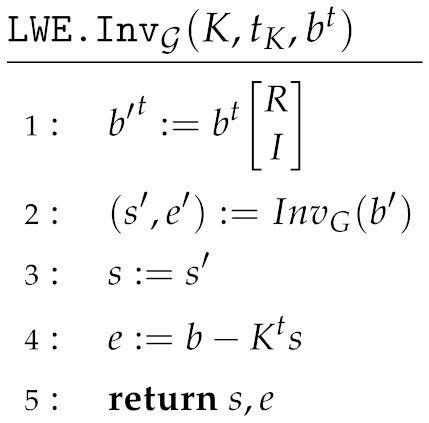
We examine now whether the functions are homomorphic with respect to some operation.
We first define the domain and the range as and . Then, given and , the operation is defined as:
Given and , the operation is defined as:
Then, we can easily verify that:
However, the sum of two error terms, each being bounded by , may not be bounded by . This means that the function is not (properly) homomorphic. Instead, what we conclude is that as long as the vector lies inside the domain of , then is homomorphic. To address this issue, we will need to define a weaker notion of 2-regularity, and a (slight) modification of the FromInj construction to provide a desired function starting from the trapdoor function of [44].
6.3. A Suitable δ-2 Regular Trapdoor Function
Using the injective trapdoor function of Micciancio and Peikert [44] and the construction defined in the proof of Theorem 8, we derive a family of collision resistant trapdoor one-way function, but with a weaker notion of 2-regularity, called -2 regularity:
Definition 12
(-2 regular). A family of functions is said to be δ-2 regular, with if:
Given this definition, we should note here that in Algorithm 2 we need to modify the abort case to include the possibility that the image y obtained from the measurement does not have two preimages (something that happens with at most probability ).
Theorem 10
(Existence of a -2 regular trapdoor function family). There exists a family of functions that are δ-2 regular (with δ at least as big as a fixed constant), trapdoor, one-way, collision resistant and quantum-safe, assuming that there is no quantum algorithm that can efficiently solve for .
Proof.
To prove this theorem, we define a function similar to the one in the FromInj construction, where the starting point is the function defined in [44]. Crucial for the security is a choice of parameters that satisfy a number of conditions given by Theorem 11 and proven in Appendix D. The proof is then completed by providing a choice of parameters given in Lemma 7 that satisfies all conditions as it is shown in Appendix E. □
Definition 13. 
For a given set of parameter chosen as in Theorem 11, we define the following functions, that are similar to the constructionFromInj, with the difference that the key generation requires the trapdoor error to be sampled from a smaller subdomain ():

Note, that the pairs and correspond to x and of the FromInj construction of Section 6.1. The idea behind this construction is that the noise of the trapdoor, , is sampled from a set which is small compared to the noise of the input function. That way, when we will add the trapdoor together with an input , the total noise will still be small enough to lie in the set of possible input noise with good probability, mimicking the homomorphic property needed in Theorem 8. Note that the parameters need to be carefully chosen, and a trade-off between probability of success and security exists.
We first introduce the following notation: for all , let us define:
- ,
- ,
- ,
- ,
- ,
- ,
- C the constant in Lemma 2.9 of [44] which is approximately ,
- if q is a power of 2, and otherwise.
Theorem 11
(Requirements on the parameters). If for all security parameters n (dimension of the lattice), there exist q (the modulus of LWE) and μ (the maximum amplitude of the components of the errors) such that:
- 1.
- m is such that (required for the injectivity of the function (see e.g., [50])),
- 2.
- ,
- 3.
- (required to have non-negligible probability to have two preimages),
- 4.
- (required for theLWEtoSIVPreduction),
- 5.
- is (representing, up to a constant factor, the approximation factor γ in the problem)—for the standard hardness of theSIVPproblem.
- 6.
- (required for the correctness of the inversion algorithm- represents the maximum length of an error vector that one can correct using the [44] function, and the last term is needed in the proof of collision resistance to ensure injectivity even when we add the trapdoor noise, as illustrated in Figure 2. We remark that we chose to use the computational definition of [44], but this theorem can be easily extended to other definitions of the same paper, or even to other construction of trapdoor short basis).
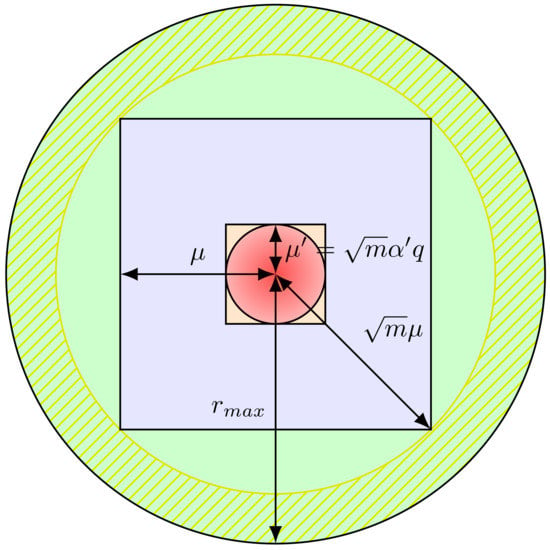 Figure 2. The red circle represents the domain of the error term from the trapdoor information, which is being sampled from a Gaussian distribution. The orange square is an approximation of this domain, which must satisfy that its length is much smaller (by a factor of at least m—the dimension of the error) than the length of the blue square, used for the actual sampling from the domain of the error terms, for which it is known that the trapdoor function is invertible, domain represented by the green circle (including the dashed part). The dashed part, representing the distance between the maximum domain for which the function is invertible (green circle) and the actual domain used for sampling (blue square) is needed to ensure that if there is a collision , then .
Figure 2. The red circle represents the domain of the error term from the trapdoor information, which is being sampled from a Gaussian distribution. The orange square is an approximation of this domain, which must satisfy that its length is much smaller (by a factor of at least m—the dimension of the error) than the length of the blue square, used for the actual sampling from the domain of the error terms, for which it is known that the trapdoor function is invertible, domain represented by the green circle (including the dashed part). The dashed part, representing the distance between the maximum domain for which the function is invertible (green circle) and the actual domain used for sampling (blue square) is needed to ensure that if there is a collision , then .
Then, the family of functions of Definition 13 is δ-2 regular (with δ at least as big as a fixed constant), trapdoor, one-way and collision resistant (all these properties hold even against a quantum attacker), assuming that there is no quantum algorithm that can efficiently solve for .
Proof.
The proof follows by showing that the function with these constraints on the parameters is: (i) -2 regular, (ii) collision resistant, (iii) one-way and (iv) trapdoor. In Appendix D, we give and prove one lemma for each of those properties. For an intuition of the choice of parameters see also Figure 2. □
6.4. Parameter Choices
Lemma 7
(Existence of parameters). The following set of parameters fulfils Theorem 11.
and are defined like in Theorem 11.
The proof is given in Appendix E. As a final remark, we stress that other choices of the parameters are possible (considering the trade-off between security and probability of success) and we have not attempted to find an optimal set.
7. Implementation of HBC − QFactory on IBM Quantum Cloud
Finally, we provide the first proof-of-principle demonstration of a classical remote state preparation protocol. Very importantly, this implementation is not secure against a quantum adversary. The reason is that, as our 2-regular trapdoor function needs to be hard to invert this requires the size of the function to be sufficiently large, but at the same time we need to implement on server’s quantum computer the unitary corresponding to this function. Therefore, given the current limited number of available qubits, we choose a 2-regular function that can be easily inverted by brute-force attacks. The scope of this implementation is to demonstrate the correctness and the randomness of the protocol.
For the implementation we use the IBM Quantum Experience service and will run all the experiments to prove the correctness and randomness of the protocol using both the simulator “ibmq_qasm_simulator” (32 available qubits) and the IBM real devices: “ibmq_athens” (5 available qubits) and “ibmq_melbourne” (16 available qubits).
7.1. Function Construction for Simulation
We will construct a specific 2-regular function (which given the limitations of the number of available qubits cannot be LWE-based or one-way). More specifically, we define the following 2-regular family of functions , where the public key is a pair of 2 matrices :
where by ∥ we denote the concatenation of the 2 bits.
To construct the Key Generation algorithm, we will proceed as follows. We first sample uniformly at random the trapdoor information, , and we will construct the public key as a function of the trapdoor in the following way:
For the Inversion algorithm, we proceed in the following way:
Given a function image , we compute its 2 preimages and as:
We emphasize that by constructing f in this particular way, we have the structure required for both and Malicious QFactory functions. Indeed, if we define the “hardcore predicate” (as in the Malicious QFactory protocol), then the two preimages x and of any are such that .
Moreover, the circuit to implement the unitary , it is simple to derive from A and B as we just need to implement a Toffoli gate (or CNOT if ) between i-th input qubit, j-th input qubit and the first output qubit whenever , and similarly with the second output qubit whenever .
7.2. Results of Implementation of HBC − QFactory
7.2.1. Randomness
We first want to indicate the randomness of the output of the protocol.
By this we mean that we want to show that the quantum output is a state, where is uniformly sampled from a set of 8 possible values: .
The following plot indicates the distribution of , can be seen in Figure 3.
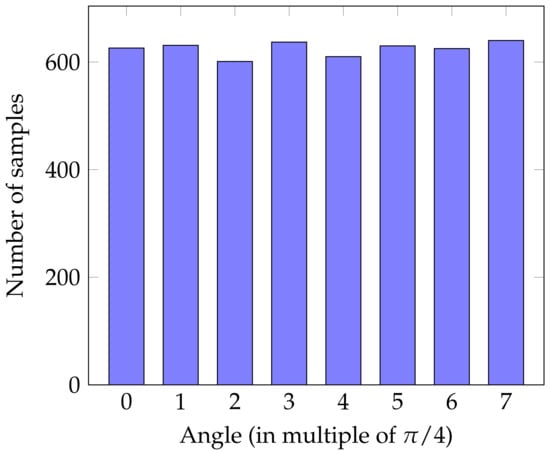
Figure 3.
5000 runs of using a fixed function described in Section 7.1. The plot depicts the resulting distribution, illustrating the randomness of the output distribution.
We run the protocol 5000 number of times, where the distribution is taken over the randomness of the 2 measurements: y (image register) and b (the final measurement—the preimage register) and over the uniform distribution of the measurement angles and the plot in Figure 3 indicated an almost uniform distribution of . We want to emphasize that the number of trial runs was chosen as the largest choice we could accommodate on the IBM Quantum Service, as a higher number of runs resulted in different failures of obtaining a result from the quantum service.
7.2.2. Correctness
For the correctness of the protocol, we want to show 2-fold:
- The server always obtains a type of state on his side;
- the client, by knowing the preimages of each image y, can always efficiently compute this .
Additionally, we will actually run 2 different types of experiments: using the simulator and a real quantum device. We proceed in the following two different manners.
Interestingly, we proceed in 2 different manners:
When running the simulator we check that the state description the client obtained and the quantum state resulted on the server’s side correspond to the same value of , in the following manner: For client we run the algorithm described in and we compute the value . To check that server obtained exactly the state , the simulator allows us to get the description of the corresponding final quantum output state (as a vector), and we are therefore able to check that it matches perfectly.
Therefore, the first correctness evidence is showed in Figure 4, which depicts the values of obtained by client and the values of , where is obtained by server. As observed for all the runs of our protocol.
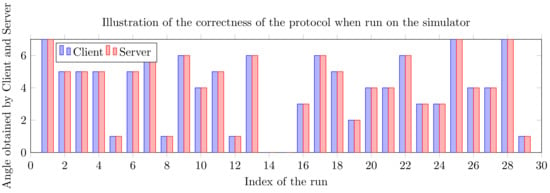
Figure 4.
Values of (written as multiples of ) obtained by client and the corresponding obtained by server for 29 different runs of on the simulator, illustrating the correctness of the protocol.
For the run on the actual quantum device, client obtains the in the same way. However, we are no longer able to get the vector description of the quantum state of server, because now it corresponds to an actual physical qubit. Now, the only way to see what state server has on his side is to perform a final measurement on the output qubit .
One way would be to measure the output state in the basis, where would be the angle obtained by client through her classical computations, and in this way for correctness we should have always outcome 1 for this measurement.
However, this is not possible, because the IBM does not allow for intermediate measurements. Therefore, the way we will proceed for this is the following:
At the beginning of the protocol, we pick a random , and then we measure the final state of server in the basis . Then, once we receive all the measurement outcomes (preimage, image registers and ) we first compute (using client’s algorithm) the actual and then we check:
- If , we should obtain measurement outcome 0 with probability 1;
- if we should obtain 1 with probability 1;
- if we should get 1 with probability ;
- if we should get 0 with probability ;
- and, in general, the probability of the outcome 0 is equal to: .
Therefore, in Figure 5a, we can see the expected probability of the measurement outcome to be 0-which corresponds to the “ideal” quantum computer case. Then, in Figure 5b we have the actual probability of outcome 0, as a result of running it on the “noisy” real quantum device—which corresponds to the real run.
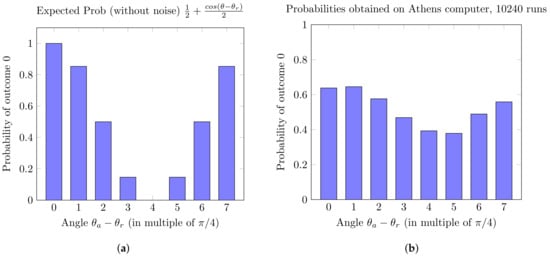
Figure 5.
(a) Ideal case: is the honest angle expected by client, and is the random angle used to measure the state obtained by server. (b) Real case: is the honest angle expected by client, and is the random angle used to measure the state obtained by server.
8. Conclusions
8.1. Summary of Results and Discussion
The current work studies the problem of secure delegation of quantum computations between a fully classical honest client and a quantum untrusted server. To achieve this, we introduce the classical client remote state preparation () primitive, whose purpose is to remove the need for quantum communication in quantum computation and communication protocols and replace it with classical communication and post-quantum security. Our protocol denoted as allows a fully classical party (client) to instruct the preparation of a sequence of random quantum states on some distant party (server) in a way that the description of the produced quantum states is known to the client but remains hidden from the server. This protocol relies on the existence of a cryptographic family of functions, specifically a trapdoor one-way function that is quantum-safe, two-regular and collision resistant. We prove the security of our construction against an honest-but-curious server, that follows the protocol specifications, but can try to learn about the secret from the classical transcripts. We show that the description of the output qubit is completely hidden from the server using an argument similar to the Goldreich–Levin theorem. Furthermore, to complete the picture, we show how to construct the required cryptographic functions, by giving an explicit family of functions and an instantiation of its parameters that satisfy all the required properties. These functions are based on the Learning-With-Errors problem. Finally, we provide an experiment of this protocol on IBM’s quantum computer using a toy function. This is the first proof-of-principle experiment of classical client remote state preparation.
The main motivation for the current work is that the primitive and particularly the construction, can be used by classical clients to replace a specific quantum channel and enable them to securely delegate quantum computations, for example, by combining with the protocol of [21]. However, we have noted that enabling classical parties to participate in quantum communication protocols opens numerous opportunities for the applications outlined in Section 1.3 and Appendix A. Indicatively, our protocol can be used in: quantum money, quantum coin-flipping, quantum signatures, etc. The classical client remote state preparation has also been recently employed to construct a quantum two-party computation between a quantum party and a fully classical party [41].
At this point we would like to discuss the practical setup advantages and limitations. The protocol we consider has two main aspects that are evaluated: security (maintaining the privacy of the classical description of the remote state prepared) and correctness (ensuring that an honest server produces the desired state in his lab). The fact that the client is fully classical and there is no quantum state prepared by the (honest) client means that any imperfections and noise could exist only on the server’s side. Since the server is the adversary, imperfections on his side only deteriorate his chances of cheating and thus the security of the protocol is not affected from such practical considerations. In other words, noise does not help the server to obtain further information on the classical description of the ideal state that is prepared. On the other hand, the correctness of the protocol is affected by noise as we have seen in our simulations in Section 7. This serves as a reminder, that our setting is more relevant when the server has the ability to perform universal (fault-tolerant) quantum computations. For example, attempts to use such protocol in Noisy Intermediate Scale Quantum (NISQ) devices, is likely to lead to very noisy output qubits and thus, is not really practically implementable in this setting.
8.2. Future Directions
Given the need for a practical solution for the classical secure delegation of quantum computations problem in order to exploit the full potential of quantum computers, an important priority is to reduce the cost and bring this primitive close to practice. There are a number of potential improvements to consider such as: finding trapdoor functions that lead to smaller overhead (either by using a different function construction, or a different implementation or a different “quantum-hard” problem) and making a more robust version that can tolerate noise on the server’s side, while maintaining the same security guarantees.
We have, somehow heuristically, mentioned that our primitive (classical client remote state preparation) can be combined with other protocols to achieve a number of applications. Another future direction is to make this intuition concrete and prove that those applications that could use our primitive as a subroutine, are secure (as it was done in the quantum multiparty computation setting [41]). The formal (and not always achievable) way to deal with composite protocols is to use a composable security framework. In the recent work of [20], the use of a classical client remote state preparation in bigger contexts has been studied using such a composable security framework, and an impossibility result for composable was proven. This implies that we cannot resort to such an “economic” solution, where one proves the security of the primitive and can then use it directly as subroutine. Instead, for each of the applications we outlined that would use as a sub-module, we have to prove the security of the resulting protocol afresh using a game-based security definition. This is an important future direction. Note, that in [20], this game-based approach was used for proving the security of a classical secure delegation of quantum computations protocol (combining a version of with the protocol of [21]).
Author Contributions
All authors contributed in the conception, proofs and writing of the paper. A.C. and L.C. performed the simulations, E.K. secured funding and E.K. and P.W. supervised the project. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EPSRC grants EP/N003829/1, EP/M013243/1, EP/T001062/1 and FA9550-17-1-0055.
Acknowledgments
A.C. and P.W. are very grateful to Thomas Zacharias, Aggelos Kiayias and especially Yiannis Tselekounis for many useful discussions about the security proofs. L.C. also thanks Atul Mantri and Dominique Unruh for useful preliminary conversations, with a special mention to Céline Chevalier whose discussions were a precious source of inspiration. A.C. would also like to show his appreciation to his grandmother, Petra Ilie for all the support and help she has given to him his entire life.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. CC−RSPθ within Several Applications
In Section 1.3 we listed several applications that can use the functionality to allow for fully classical parties to participate using, a potentially malicious, quantum server. Here we give details on how to use the exact output of our QFactory protocol in these applications. We emphasize that in all protocols in which the “server” used by the classical party is a malicious party, the cost of using our QFactory construction is that the security becomes computational and applies in the quantum-honest-but-curious setting.
- In the quantum homomorphic encryption scheme AUX in [4], where the target quantum computation must have constant T-gate depth, using our QFactory protocol would allow a classical client to participate (delegate such computation) provided, of course, that the input/output are classical. Specifically, as the input is classical, the client will instruct the server to prepare a quantum state of the classical one-time pad of this input (and then the client will also send to the server a classical homomorphic encryption of the classical one-time pad key of each of the input’s bits). Moreover, for every T-gate in the quantum computation, the auxiliary qubits in the evaluation key can be produced using QFactory: .We note that due to the use of a classical fully homomorphic encryption scheme, the AUX protocol [4] has computationally security, thus, the computational security offered by the QFactory is not downgrading the security of this protocol.
- In the blind delegated quantum computation protocol of [21], the client needs to prepare and send to the server qubits, randomly chosen, from the set of states . This is exactly the set of states of Equation (3) which are given by the QFactory. It follows that our construction eliminates the need for quantum communication and thus any classical client can use this protocol.
- The verifiable blind quantum computation protocol in [32], the only quantum ability that the verifier needs is to prepare and send to the prover single qubits, randomly chosen, from the set of states . Again, this is exactly the set of states given by the QFactory. Therefore, the quantum communication, and thus quantum abilities of the verifier, can be completely replaced by the primitive.
- For the quantum key-distribution construction in [33], we can use two conjugate bases to realise this protocol, namely: the diagonal basis and the left-right handed circular basis . All these four quantum states can be obtained by the QFactory protocol. We note that if one was interested in obtaining exactly and only this set of states, we can modify the QFactory to do so, in a way that actually simplifies the proofs too. For example, we could simply ask to measure the qubits in the second stage in the basis . As the quantum coin flipping protocol of [33], the quantum money protocol of [34] or the quantum digital signatures protocol of [36] only require, as in [33], any pair of conjugate bases, this implies that we can use QFactory in a straight forward way. On the other hand, for the quantum coin flip construction in [35], the single qubit quantum states needed are of the form , which might be achieved by a different construction of the .
- In the multiparty quantum computation protocol of [39], the n clients need to send multiple copies of quantum states in the set to the server, who entangles and measures them all but one. Using QFactory all these states will be prepared by the server, which would enable the n clients to be fully classical.
- The verifiable blind quantum computation protocols in [30,31] or the two-party quantum computation protocols in [37,38], require the honest party to prepare single qubit states from the set of states . While the QFactory primitive can output the states, in order to make the honest party fully classical, we need to change the construction of QFactory in order to also be able to output the and states, and maintain the same guarantees in privacy as in the QFactory.
Appendix B. Full Proof of Theorem 7
Proof.
From Equation (13), we have the definition of in terms of the three corresponding bits and we aim to prove that it is hard-core, i.e., that Equation (15) is satisfied. We will follow the five steps outlined in the main text. Before that let us define some simple identities that will be used. For any , we have:
We now return to Equation (13)
where , with We also define and be the vector defined as: .
Step 1: We will rewrite this expression in terms of single bits and obtain the expression of Equation (15). We have , or equivalently:
We define the following terms: , where are the 3 bits of and are the vectors consisting of the j-th bit of all values , ;
We also notice that under , we have that:
Then, we have:
Finally, we can derive :
Using (A7):
Using (A5):
Using (A6) we can rewrite the first term, and we get:
Combining the first and third term:
We notice that both and are even, so the first big term is 0:
which can be rewritten as:
Important observation:, , all depend on the same value of x and (or , or z). Therefore, to make our analysis easier, we can consider that z and are fixed. Then, if we define the function:
we can rewrite as in Equation (15) completing Step 1:
where:
Step 2: We see from Equation (A11) that each of the three bits involve a term similar to that of the GL Theorem 2 (the term), but with two the important differences. First, there is another term, and the bits of are XORs of the GL-looking term and that other one. The second type of terms (that involve ) depend on variables that appear in the expressions of other bits, potentially introducing correlations among the different bits. We will deal with the issue of correlations in Step 3, while with the effects of having extra terms in Steps 4 and 5. Here we deal with the second important difference, namely that the GL-looking terms (those of the form ) depend on rather than x in the inner product. For the remaining Step 2, we assume that the first issue is resolved and it all reduces to GL theorem subject to having rather than x.
Since we have in our expression, if we follow the same proof with that of the GL theorem we can follow the proof until the point that we end up with obtaining a polynomial number of guesses for of which one is the correct value with probability negligibly close to unity. Now to continue with the proof we are lacking two elements. First, in GL theorem they use the fact that computing given x is easy, and check one-by-one the polynomial guesses to see which one (if any) is correct. We cannot do this since we only obtain and there is no way with no extra information to check if actually corresponds to a given image . The second issue, is that even if we could check this, having obtained does not contradict the definition of one-way function (Definition 2).
We resolve both these issues with two observations. Observation 1: We notice that because of the 2-regularity property of f, is uniquely determined by x (, ). Observation 2: The assumption that our 2-regular trapdoor function f is second preimage resistant (i.e., a QPT adversary given x, cannot find the second preimage , where means that:
As
we have that:
As we have mentioned, following the GL theorem proof we would obtain polynomially many guesses for (where subscript g stands for guess). Now, by the second preimage resistance, if we are given x we should be unable to obtain in polynomial time. However, using our polynomially many guesses for and checking for each guess if , we can obtain with probability negligible close to unity the correct and therefore come to contradiction with Equation (A16).
Step 3: Since the different bits involve common variables, to prove that our function is hard-core we need to consider the issue of correlations. One way to deal with this would be to prove the independence of both the bits and of the optimal guessing algorithms. We, instead, use the Vazirani–Vazirani Theorem 3, which for our case means that it suffices to show that: , , , , , , are all hard-core predicates for f.
The most general expression that captures all these hard-core predicates (formed from the subsets of ) is:
where g can be any binary function. Using we can rewrite this as:
where . In other words, in order to prove that is a hard-core function for f, it suffices to prove that is a hard-core predicate for f.
Step 4: In this step, we will see how we can effectively fix all but one variables, and turn Equation (A18) to depend only on .
We want to prove that if there exists a QPT algorithm that can guess the predicate E as given in Equation (A18), with probability non-negligible better than , then the second preimage resistance assumption is violated by constructing a QPT algorithm that, when given x can obtain , , with non-negligible probability.
We now assume that the advantage has in computing is , without restricting to be non-negligible, aiming to reach a contradiction if this is inverse polynomial. We therefore assume:
Since the different variables () are chosen randomly and independently, we can effectively “fix” one variable. We can consider the set of values of that variable that satisfy some condition that we need and name these values “Good” values (e.g., the guessing algorithm to succeed with higher than negligible probability). Then we can work with the assumption that the fixed variable is within the “Good” set, with the only caveat that at the end, whatever probability of inversion we obtain, is conditional on the fixed variables being “Good” and thus we need to multiply that probability with the probability that the fixed variable is “Good”. For this reason, it is important that the probability of being “Good” (ratio between cardinality of Good values and total number of values) should be at least inverse polynomial.
We will, therefore, be using the following Lemma:
Lemma A1.
Let , then for any variable , there exists a set of size at least , such that for all , we have:
where the latter probability is taken over all variables except .
Proof.
□
Now we return to Equation (A19), we fix the set of , the set of inputs x such that:
and using Lemma A1 we have . Note that fixing x is equivalent with fixing or z, given the definition of the 2-regular function f. Starting with Equation (A22), we can now fix (conditional on ):
where using again Lemma A1 we have . Finally, we can fix (conditional on and ):
and again by Lemma A1 we have .
Step 5: In Equation (A24), the only variable is . Using Equation (A18) we can see that given that are all fixed, where is constant. As a result that c is a constant, we can define . Now, we can easily see that:
Therefore, using Equation (A24), we obtain
which is exactly the expression in GL theorem. There, one obtains guesses for inversion, i.e., to obtain with a polynomial in probability of success, given the fixed ’s. Multiplying this with the probability of actually being in and and we obtain another polynomial in . This rules out the possibility of being inverse polynomial, since that would break the second preimage resistance. As we have already stated, guessing with inverse polynomial success probability does not contradict the one-way property of the trapdoor function, but it does contradict the second preimage resistance, since given x and one can obtain deterministically .
Concretely, using GL proof to construct from , a QPT algorithm that obtains , for all inputs , when, , and , this algorithm succeeds with probability:
Then, we have:
We now see that:
By construction we have and and , which leads to
where we can view and as the internal randomness of the inversion algorithm . It is clear that if is non-negligible, it means that there exists polynomial such that , and then
which as explained in Step 2 breaks second preimage resistance, Equation (A16). Since all the terms given in Step 3 () are of the form as in Equation (A18), our analysis suffices to prove that is a hard-core function for f.
Appendix C. Proof of Theorem 9
Lemma A2
(two-regular). If is a family of bijective functions, then is a family of two-regular functions.
Proof.
For every , where :
- Since and is bijective, there exist unique such that .
- Since and is bijective, there exist unique such that .
Therefore, we conclude that:
□
Lemma A3
(trapdoor). If is a family of bijective trapdoor functions, then is a family of trapdoor functions.
Proof. 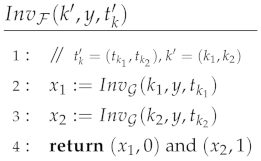
Let . We construct the following inversion algorithm:
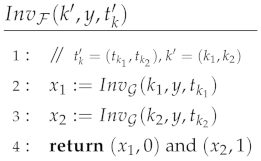
□
Lemma A4
(one-way). If is a family of bijective, one-way functions, then is a family of one-way functions.
Proof. 
We prove it by contradiction. We assume that a QPT adversary can invert a function in with non-negligible probability P (i.e., given to return a correct preimage of the form with probability P). We then construct a QPT adversary that inverts any function in with the same non-negligible probability P reaching the contradiction since is one-way by assumption.
From Equation (A28), we know the two preimages of y are: (i) and (ii) . We now construct an adversary that for , inverts any image with the probability .

The inversion algorithm succeeds with and thus reaches a contradiction. □
Lemma A5
(second preimage resistance). If is a family of bijective, one-way functions, then, any function is second preimage resistant.
Proof. 
Assume there exists a PPT adversary that given and such that can find such that with non-negligible probability P. From Equation (A27), we know that the two preimages have different bs. We now construct a PPT adversary that inverts the function with the same probability P, reaching a contradiction:

□
Lemma A6
(quantum-safe). If is a family of quantum-safe trapdoor functions, with properties as above, then is also a family of quantum-safe trapdoor functions.
Proof.
The properties that require to be quantum-safe is one-wayness and second preimage resistance. Both these properties of that we derived above were proved using reduction to the hardness (one-wayness) of . Therefore, if is quantum-safe, its one-wayness is also quantum-safe and thus both properties of are also quantum-safe. □
Appendix D. Proof of Theorem 11
In the following, we will denote by , the function REG2.Eval for k the index function obtained by REG2.Gen, and by the trapdoor information associated with this function f.
We now prove separately the -2 regularity, collision resistance, one-wayness and trapdoor property of the function in Definition 13.
Appendix D.1. δ-2 Regularity
Here, we describe how to achieve -2 regularity using the construction FromInj and specifically, the function in Definition 13.
This reduces to ensuring that the two function inputs and both lie within the domain of the function. The input is the result of the inversion algorithm, so it is by definition inside the domain. Additionally, as the first element of the domain is only required to be in and as is closed with subtraction , then for any s, . On the other hand, the second element of the domain is required to be in , such that each component is bounded in absolute value by some value . In this case, we are not guaranteed that adding or subtracting two such elements the result is still in the domain. What we want to ensure is that with (at least) constant probability over the choice of and , the result is in the domain of the function.
It is not difficult to show that if is chosen arbitrarily from the domain of the function, then lies within the domain of the function only with inverse exponential in m probability. This is why we consider restricting to be within a subset of the domain. By suitable choice of this subset we can make the success probability (of having two preimages)—seen as a function in m—to be at least a constant value. Firstly, we remark that the exact probability of success can be explicitly computed. Indeed, if the trapdoor noise is sampled from a Gaussian of dimension m, and standard deviation , and if the noise is sampled uniformly from an hypercube C of length (both distribution being centred on 0) then the probability that is still inside C is:
However, for simplicity, and because we do not aim to find optimal parameters, we will use a (simpler) lower bound of this probability (that will be less efficient by a factor of ). To do that, remark that using in [46], we have that if , such that each component of is sampled from a Gaussian distribution with parameter , then we have that every component of the vector is less than with overwhelming probability as m increases. Therefore, one can remark that, up to a negligible term, the Gaussian distribution with parameter is “closer to 0” than the uniform distribution on for sufficiently large m (i.e., for any x, the integral between and x of the Gaussian distribution is bigger, up to a negligible term, than the integral of the uniform distribution). Therefore, to obtain a lower bound on the probability of having two preimages, we can consider that is sampled according to the uniform distribution on a hypercube of length rather than according to the Gaussian distribution of parameter . This simplifies our analysis, and allows us to find the subset in which must reside, as seen in the following lemma. Note also that if one does not want to do any assumption on the input distribution, and only assume that the infinity norm is smaller than , then the same lemma applies with the constant 4 replaced by 2.
Lemma A7
(Domain Addition). Let be a vector space of dimension m, and let be the uniform distribution inside the hypercube of dimension m and length centred on 0. Then, for any , we have:
Moreover, if then the probability becomes lower bounded by a positive constant.
Proof.
As must be less than , which means that each component of the sum vector must be less than , and as each component of the 2 vectors and was independently sampled, then we can simplify our proof by considering that and are vectors in , essentially determining and then, we can compute .
Then, let us denote by the random variable sampled uniformly from , the random variable sampled uniformly from and E the random variable obtained as . Therefore, .
Now, we can compute the density function of E using convolution:
where and are the probability density functions of and (, when and 0 elsewhere and , when and 0 elsewhere).
Then, we are only interested in the cases when both the values of and are non-zero and for this we need to consider 3 cases for e, given by the intervals: . Thus, we can derive:
Finally, we have that .
Consequently, we have .
Now, given that is a function of m, , we want to determine the values of , such that this probability (seen as a function in m) is at least a positive constant number.
- If , then:Now, what we require is that = c , where c is a constant, as then, we have that the probability of success is at least a constant .
- If (and less than 1, as ), then:
Consequently, it is clear that in order to get a positive constant lower bound for the success probability, we must have:
□
Thus, in our case, if is sampled uniformly on a hypercube of length and from a Gaussian with parameter , by replacing the actual values of and , what we require is that:
Appendix D.2. Collision Resistance
We start by the observation that for the choices of Definition 13, no QPT adversary can infer the trapdoor information , as determining from would be equivalent to solving :
Corollary A1
(One-wayness of the trapdoor([46], Theorem 1.1)). Under the (with ) assumption, no QPT adversary can recover the trapdoor information .
Lemma A8
(Collision resistance). The function f defined in Definition 13 is collision resistant if the parameters are chosen accordingly to Theorem 11 assuming that is hard.
Proof.
By contradiction, let us suppose that this function is not collision resistant. Then, there exist two pairs , such that . Note that the last bits are necessary different since the two functions that fix the last bit, are injective when the error is smaller than (according to ([44], Theorem 5.4)). By the definition of f, and , i.e., both and has Euclidean norm smaller than . Then, by definition, . Now, we remark that with overwhelming probability (over the choice of the trapdoor), as stated in ([46], Lemma 2.5), so in this case, (last assumption of Theorem 11). Then, according to ([44], Theorem 5.4), there is exactly one element with e of length smaller than such that . As a result that is a solution, we then have that: and , i.e., and . Hence, it is possible to deduce the trapdoor information and from the collision pair, which is impossible by Corollary A1. □
Appendix D.3. One-Wayness
One could imagine that the one-wayness of the resulting function of Definition 13 is implied by the one-wayness of the function in [44] (as is the case in Lemma 4). However, we need more care here, since in our construction the error term e is not sampled from a Gaussian distribution with suitable parameters (unlike the error term ). We remark that while other ways to prove the one-wayness are possible, we give here one proof that uses the previous two lemmata.
Lemma A9
(Collision resistance to one-wayness). Let (with , where A is finite and can be efficiently sampled uniformly and let C be the set of all that admit 2 preimages. If the restriction of f to the set is a collision resistant function that admits with non-negligible probability two preimages for any y from its image and if is non-negligible, then f restricted to the set is a one-way function.
Proof.
By contradiction: suppose that f is not one-way on C, i.e., with a non-negligible probability we can find a preimage of y for y uniformly sampled in C, and from this we can show how to find a collision. The idea is to sample an input , and then compute . Then, as is non-negligible, we know that with non-negligible probability this y will have two preimages. Now, with non-negligible probability, this function will be easy to invert and one gets . As a result that we sample uniformly at the step before, we have the same probability to sample one image or the other, so with probability , , therefore, we found a collision. □
Corollary A2
(One-wayness from Lemmas A8 and A9). The function defined in Definition 13 is one-way for all y that admit two preimages, under the hardness assumption, when the parameters are chosen accordingly to Theorem 11.
Appendix D.4. Trapdoor
We want to prove that using the trapdoor information of the REG2 construction, which consists of and , the trapdoor information of the LWE function, we can efficiently derive the preimages of an output b of REG2.Eval. Firstly, we notice that to find all the preimages, we can simply run LWE.Inv on b as well as on and if we succeed we take only the preimages that lie in the input domain, i.e., whose error part e is bounded in infinity norm by : . As a result that the function is injective, these are all the possible preimages. However, because we are interested only in the case when there are exactly two preimages, the function REG2.Inv can also do the following: we first run LWE.Inv on b and obtain . Then, the inversion is completed by returning and , which are both valid preimages, if and only if the function has two preimages (see Lemma A8 for more details).
Appendix E. Proof of Lemma 7
Proof.
Using the following explicit values for the parameters of the Micciancio and Peikert injective trapdoor function [44], we want to prove that they fulfil all of the requirements of Theorem 11:
and are defined as in Theorem 11. Now, let us proof that these parameters satisfy all the requirements.
- The first three requirements are trivially satisfied.
- In the forth condition, the only difficulty is to show that . By definition,
- Now, let us show the fifth condition, i.e., . First we note that . Then, by defining , the condition is satisfied.
- For the fifth condition, i.e., is , we just need to remark that , and that both m and q are .
- Finally, to show that the last condition is satisfied, we note that:if and only ifNow, let us suppose that with and and we need to find such that . Note that we will include v in some constants and then find the good v at the end. First, remark that:So now,Finally, we observe that if and , we have , which concludes the proof.
□
References
- Elkouss, D.; Lipinska, V.; Goodenough, K.; Rozpedek, F.; Kalb, N.; van Dam, S.; Le Phuc, T.; Murta, G.; Humphreys, P.; Taminiau, T.; et al. Quantum internet: The certifiable road ahead. In Proceedings of the APS Meeting Abstracts, New Orleans, LA, USA, 13–17 March 2017. [Google Scholar]
- Broadbent, A.; Schaffner, C. Quantum cryptography beyond quantum key distribution. Des. Codes Cryptogr. 2016, 78, 351–382. [Google Scholar] [CrossRef]
- Fitzsimons, J.F. Private quantum computation: An introduction to blind quantum computing and related protocols. Npj Quantum Inf. 2017, 3, 23. [Google Scholar] [CrossRef]
- Broadbent, A.; Jeffery, S. Quantum homomorphic encryption for circuits of low T-gate complexity. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2015; pp. 609–629. [Google Scholar]
- Dulek, Y.; Schaffner, C.; Speelman, F. Quantum homomorphic encryption for polynomial-sized circuits. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–32. [Google Scholar]
- Alagic, G.; Dulek, Y.; Schaffner, C.; Speelman, F. Quantum fully homomorphic encryption with verification. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2017; pp. 438–467. [Google Scholar]
- Liang, M. Quantum fully homomorphic encryption scheme based on universal quantum circuit. Quantum Inf. Process. 2015, 14, 2749–2759. [Google Scholar] [CrossRef]
- Ouyang, Y.; Tan, S.H.; Fitzsimons, J. Quantum homomorphic encryption from quantum codes. arXiv 2015, arXiv:1508.00938. [Google Scholar] [CrossRef]
- Tan, S.H.; Kettlewell, J.A.; Ouyang, Y.; Chen, L.; Fitzsimons, J.F. A quantum approach to homomorphic encryption. Sci. Rep. 2016, 6, 33467. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.Y.; Chung, K.M. On statistically-secure quantum homomorphic encryption. arXiv 2017, arXiv:1705.00139. [Google Scholar]
- Mantri, A.; Pérez-Delgado, C.A.; Fitzsimons, J.F. Optimal blind quantum computation. Phys. Rev. Lett. 2013, 111, 230502. [Google Scholar] [CrossRef]
- Giovannetti, V.; Maccone, L.; Morimae, T.; Rudolph, T.G. Efficient universal blind quantum computation. Phys. Rev. Lett. 2013, 111, 230501. [Google Scholar] [CrossRef]
- Armknecht, F.; Gagliardoni, T.; Katzenbeisser, S.; Peter, A. General impossibility of group homomorphic encryption in the quantum world. In International Workshop on Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2014; pp. 556–573. [Google Scholar]
- Yu, L.; Pérez-Delgado, C.A.; Fitzsimons, J.F. Limitations on information-theoretically-secure quantum homomorphic encryption. Phys. Rev. A 2014, 90, 050303. [Google Scholar] [CrossRef]
- Aaronson, S.; Cojocaru, A.; Gheorghiu, A.; Kashefi, E. Complexity-Theoretic Limitations on Blind Delegated Quantum Computation. In Proceedings of the 46th International Colloquium on Automata, Languages, and Programming (ICALP 2019), Patras, Greece, 8–12 July 2019. [Google Scholar]
- Newman, M.; Shi, Y. Limitations on Transversal Computation through Quantum Homomorphic Encryption. arXiv 2017, arXiv:1704.07798. [Google Scholar]
- Mantri, A.; Demarie, T.F.; Menicucci, N.C.; Fitzsimons, J.F. Flow ambiguity: A path towards classically driven blind quantum computation. Phys. Rev. X 2017, 7, 031004. [Google Scholar] [CrossRef]
- Mahadev, U. Classical Homomorphic Encryption for Quantum Circuits. In Proceedings of the 59th IEEE Annual Symposium on Foundations of Computer Science (FOCS 2018), Paris, France, 7–9 October 2018; Thorup, M., Ed.; IEEE Computer Society: Washington, DC, USA, 2018; pp. 332–338. [Google Scholar]
- Brakerski, Z. Quantum FHE (Almost) As Secure As Classical. In Advances in Cryptology—CRYPTO 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 67–95. [Google Scholar]
- Badertscher, C.; Cojocaru, A.; Colisson, L.; Kashefi, E.; Leichtle, D.; Mantri, A.; Wallden, P. Security Limitations of Classical-Client Delegated Quantum Computing. In Advances in Cryptology—ASIACRYPT 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Broadbent, A.; Fitzsimons, J.; Kashefi, E. Universal blind quantum computation. In Proceedings of the 50th Annual Symposium on Foundations of Computer Science (FOCS ’09), Atlanta, GA, USA, 25–27 October 2009; IEEE Computer Society: Washington, DC, USA, 2009; pp. 517–526. [Google Scholar] [CrossRef]
- Cojocaru, A.; Colisson, L.; Kashefi, E.; Wallden, P. On the possibility of classical client blind quantum computing. arXiv 2018, arXiv:1802.08759. [Google Scholar]
- Cojocaru, A.; Colisson, L.; Kashefi, E.; Wallden, P. QFactory: Classically-Instructed Remote Secret Qubits Preparation. In Advances in Cryptology—ASIACRYPT 2019; Galbraith, S.D., Moriai, S., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 615–645. [Google Scholar]
- Gheorghiu, A.; Vidick, T. Computationally-Secure and Composable Remote State Preparation. In Proceedings of the 2019 IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS), Baltimore, MA, USA, 9–12 November 2019; pp. 1024–1033. [Google Scholar]
- Zhang, J. Succinct Blind Quantum Computation Using a Random Oracle. arXiv 2020, arXiv:2004.12621. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photon. 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Wallden, P.; Kashefi, E. Cyber Security in the Quantum Era. Commun. ACM 2019, 62, 120. [Google Scholar] [CrossRef]
- Brakerski, Z.; Christiano, P.; Mahadev, U.; Vazirani, U.; Vidick, T. Certifiable Randomness from a Single Quantum Device. arXiv 2018, arXiv:1804.00640. [Google Scholar]
- Freeman, D.M.; Goldreich, O.; Kiltz, E.; Rosen, A.; Segev, G. More constructions of lossy and correlation-secure trapdoor functions. In International Workshop on Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2010; pp. 279–295. [Google Scholar]
- Fitzsimons, J.F.; Kashefi, E. Unconditionally verifiable blind computation. arXiv 2012, arXiv:1203.5217. [Google Scholar]
- Broadbent, A. How to Verify a Quantum Computation. arXiv 2015, arXiv:1509.09180. [Google Scholar]
- Ferracin, S.; Kapourniotis, T.; Datta, A. Towards minimising resources for verification of quantum computations. arXiv 2017, arXiv:1709.10050. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Bozzio, M.; Orieux, A.; Vidarte, L.T.; Zaquine, I.; Kerenidis, I.; Diamanti, E. Experimental investigation of practical unforgeable quantum money. Npj Quantum Inf. 2018, 4, 5. [Google Scholar] [CrossRef]
- Pappa, A.; Chailloux, A.; Diamanti, E.; Kerenidis, I. Practical quantum coin flipping. Phys. Rev. A 2011, 84, 052305. [Google Scholar] [CrossRef]
- Wallden, P.; Dunjko, V.; Kent, A.; Andersson, E. Quantum digital signatures with quantum-key-distribution components. Phys. Rev. A 2015, 91, 042304. [Google Scholar] [CrossRef]
- Kashefi, E.; Wallden, P. Garbled Quantum Computation. Cryptography 2017, 1, 6. [Google Scholar] [CrossRef]
- Kashefi, E.; Music, L.; Wallden, P. The Quantum Cut-and-Choose Technique and Quantum Two-Party Computation. arXiv 2017, arXiv:1703.03754. [Google Scholar]
- Kashefi, E.; Pappa, A. Multiparty Delegated Quantum Computing. Cryptography 2017, 1, 12. [Google Scholar] [CrossRef]
- Broadbent, A.; Gutoski, G.; Stebila, D. Quantum One-Time Programs. In Advances in Cryptology—CRYPTO 2013; Canetti, R., Garay, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8043, pp. 344–360. [Google Scholar] [CrossRef]
- Ciampi, M.; Cojocaru, A.; Kashefi, E.; Mantri, A. Secure Quantum Two-Party Computation: Impossibility and Constructions. arXiv 2020, arXiv:2010.07925. [Google Scholar]
- Goldreich, O.; Levin, L.A. A Hard-core Predicate for All One-way Functions. In Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing (STOC ’89), Washington, DC, USA, 15–17 May 1989; ACM: New York, NY, USA, 1989; pp. 25–32. [Google Scholar] [CrossRef]
- Vazirani, U.V.; Vazirani, V.V. Efficient and Secure Pseudo-Random Number Generation (Extended Abstract). In Advances in Cryptology; Blakley, G.R., Chaum, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 193–202. [Google Scholar]
- Micciancio, D.; Peikert, C. Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller. In Advances in Cryptology—EUROCRYPT 2012; Pointcheval, D., Johansson, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 700–718. [Google Scholar]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. In Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing (STOC ’05), Baltimore, MD, USA, 22–24 May 2005; ACM: New York, NY, USA, 2005; pp. 84–93. [Google Scholar] [CrossRef]
- Peikert, C. Public-key Cryptosystems from the Worst-case Shortest Vector Problem: Extended Abstract. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing (STOC ’09), Bethesda, MD, USA, 31 May–2 June 2009; ACM: New York, NY, USA, 2009; pp. 333–342. [Google Scholar] [CrossRef]
- Aaronson, S. Quantum computing, postselection, and probabilistic polynomial-time. Proc. R. Soc. Lond. Ser. A 2005, 461, 3473–3482. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.A.; Zeilinger, A. Going beyond Bell’s theorem. In Bell’s Theorem, Quantum Theory and Conceptions of the Universe; Springer: Berlin/Heidelberg, Germany, 1989; pp. 69–72. [Google Scholar]
- Vaikuntanathan, V. Advanced Topics in Cryptography: Lattices. Available online: https://people.csail.mit.edu/vinodv/6876-Fall2015/L13.pdf (accessed on 7 December 2018).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).