E-ART: A New Encryption Algorithm Based on the Reflection of Binary Search Tree
Abstract
1. Introduction
1.1. Motivation and Research Goals
1.2. Contribution
- (1)
- A balanced tree data structure along with American Standard Code for Information Interchange (ASCII) values of text characters to encode data. This makes searching for a particular character value more efficient, as there is no need to visit every node when searching for a specific value. Thus, higher computational efficiency is achieved.
- (2)
- Dynamic keys based on a pseudo-random generator. Each character in the text document is encrypted with a different cryptographic key. The character’s position is used as a seed in the random number generation function to produce the pseudo-random number. This ensures a high level of security against classical and modern powerful attacks, which is traditionally ensured by increasing the key size, without scarifying performance.
2. Background and Related Work
3. Proposed Schema
3.1. A. Key Derivation
3.1.1. Initial Key
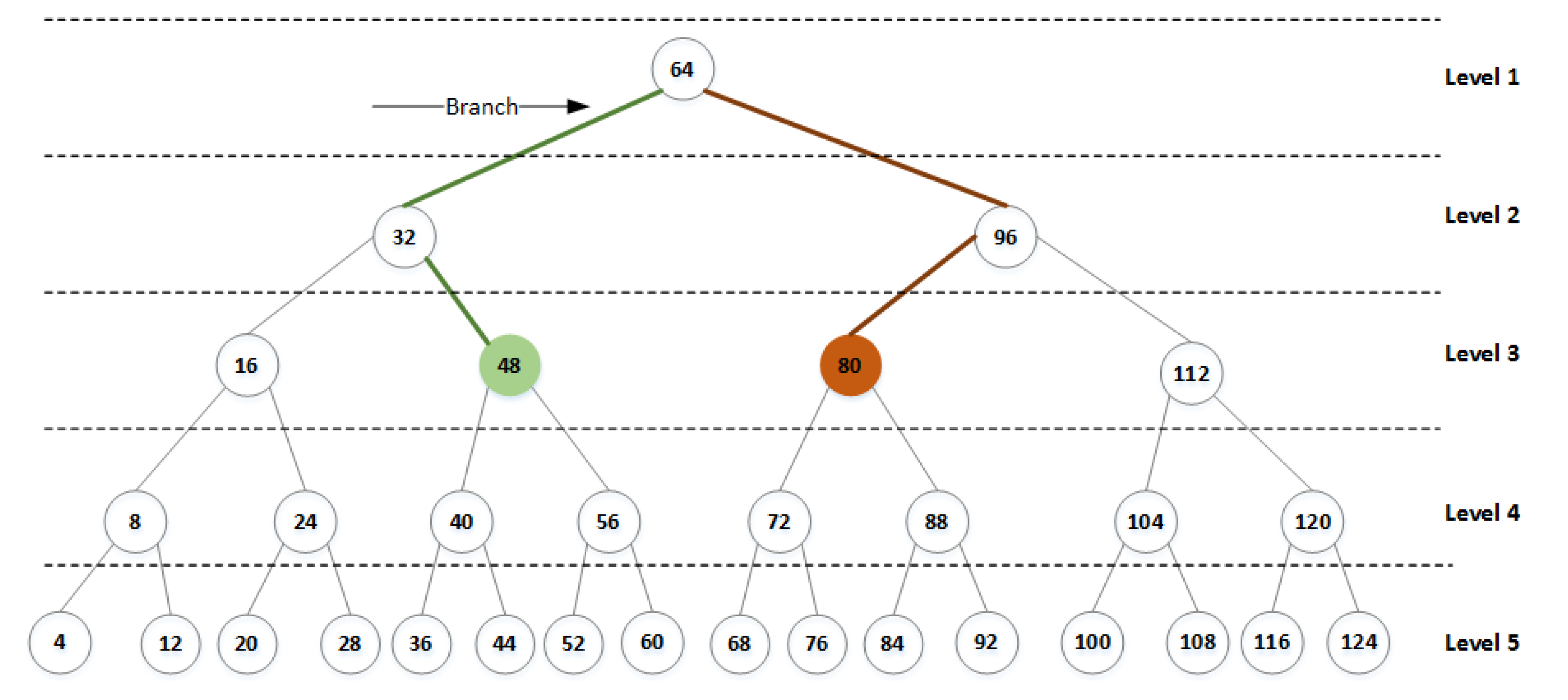
- Variable offset. It is calculated mathematically using the proposed tree properties. The left and right nodes are shown in Figure 1. It uses the N value derived from the initial key to calculate and its reflection node and then generate the value of . This value is added to the initial reflection value according to Equations (3) and (4) to add more complexity and prevent cryptanalysis attacks that take advantage of one-to-one mapping. It is computed as follows:
- Dynamic offset. It is produced automatically using a pseudo-random number and the second part of the initial key (Variance). The pseudo-random generator uses each character’s position in the text as a seed to generate a pseudo-random number of 64 or 128 bits. The pseudo-random number is then adjusted using the Variance value. This offset is added in the last step to produce the final encrypted characters and is changed for each character. This results in a high degree of robustness and resistance to known powerful attacks. The dynamic offset is calculated as follows:
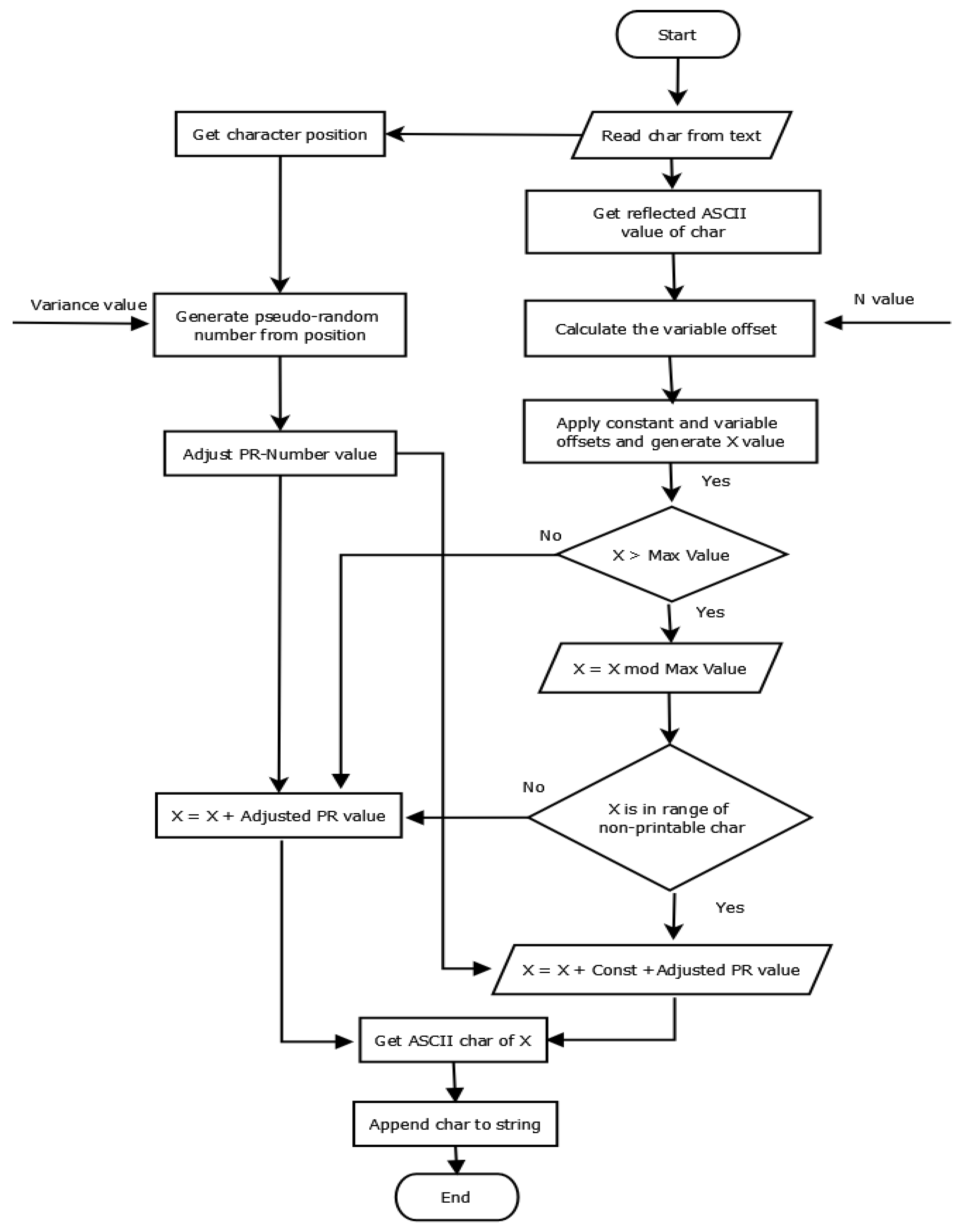
3.1.2. E-ART Structure
- (1)
- The presence of special characters, such as space, carriage return, and other text formatting characters, which range from 0 to 32 in the ASCII table, is not addressed.
- (2)
- Initially, the input textual data are stored in an array of characters (plaintext list).
- Each character in the list is converted into its corresponding ASCII values and stored in
- The variable offset is generated using N, the first value of the initial key, and the properties of the tree—R, , and —as shown in Equation (1).
- For each character in the list, the initial reflected value for each character is calculated using Equation (3).
- For each character in the list, the dynamic offset is generated by a pseudo-random generator using Variance on the second value of the initial key and characters’ positions, as shown in Equation (2).
- Then, value X is generated by adding the variable offset and constant offsets to the initial reflected value using Equation (4).
- Value X changes based on the maximum length () and non-printable character range. If the value of X is greater than , then apply the mod operation and then add , as shown in Equation (4).
- Then, the dynamic offset is added to the value of X using Equation (5) to generate the final reflection value
- is converted to the equivalent ASCII character to produce the encrypted character.
- Append the character to encrypted list.
- Once all characters in the plaintext are encrypted, the encrypted text file is generated.
| Algorithm 1: E-ART Algorithm |
| Input: R,, , input_text, N, Variance Output: Encrypted text 1: Initialization 2: input_list = Read all words from input file 3: Get the for each character 4: Get the from Equation (1) 5: while all words in input_list are not iterated, do 6: word = pop word from input_list 7: for each character in word do 8: Get character from Equation (3) 9: Get from Equation (2) with 10: Let X = + + 11: if X is greater than 12: [(X mod ) + + 13: else 14: [X + 15: end if 16: end for 17: append of to EncryptedWord 18: append word or EncryptedWord to EncryptedList 19: end while 20: Write all values from EncryptedList to output document |
- Initially, the input data are stored in an array of characters (ciphertext list).
- Each character in the list is converted into its corresponding ASCII value and stored in .
- The variable offset is generated using N, the first value of the initial key, and the properties of the tree—R, , and —as shown in Equation (1).
- For each character in the list, the dynamic offset is regenerated by a pseudo-random generator using the same parameters, Variance, with the second value of the initial key and the characters’ positions as shown in Equation (2).
- Value X is generated by subtracting the dynamic offset from .
- Then, we check: if subtraction of variable offset and constant offset from X is less than 0, then set Quotient to be equal to 1; otherwise, set Quotient value to be equal to 0.
- Generate the by multiplying and Quotient and then subtract X, variable offset and constant offset .
- Generate decrypted value by subtracting from plus 1.
- Decrypted value is converted to the equivalent ASCII character to produce the decrypted character.
- Append the character to the decrypted list.
- Once all characters in the ciphertext are decrypted, the decrypted text file is generated.
| Algorithm 2: Data Decryption Algorithm |
| Input: R,, , Encrypted Text, N, Variance Output: decrypted text 1: Initialization 2: input_list = Read all word from input file 3: Get the or each character 4: Get the from Equation (1) 5: while all words in input_list are not iterated, do 6: word = pop word from input_list 7: for each character in word do 8: Get rom Equation (2) 9: Let X = 10: if (X − < 0 11: Quotient = 1 12: else 13: Quotient = 0 14: [(xuotient + X) − 15: decrypted_value = () + 1 16: end if 17: end for 18: append of decrypted_value to decryptedWord 19: append word or decryptedWord to decryptedList 20: end while 21: Write all values from decryptedList to output document |
4. Experimental Evaluation
4.1. A. Performance Analysis
4.2. Security Analysis
4.2.1. Avalanche Effect
4.2.2. Bit Independence Criterion
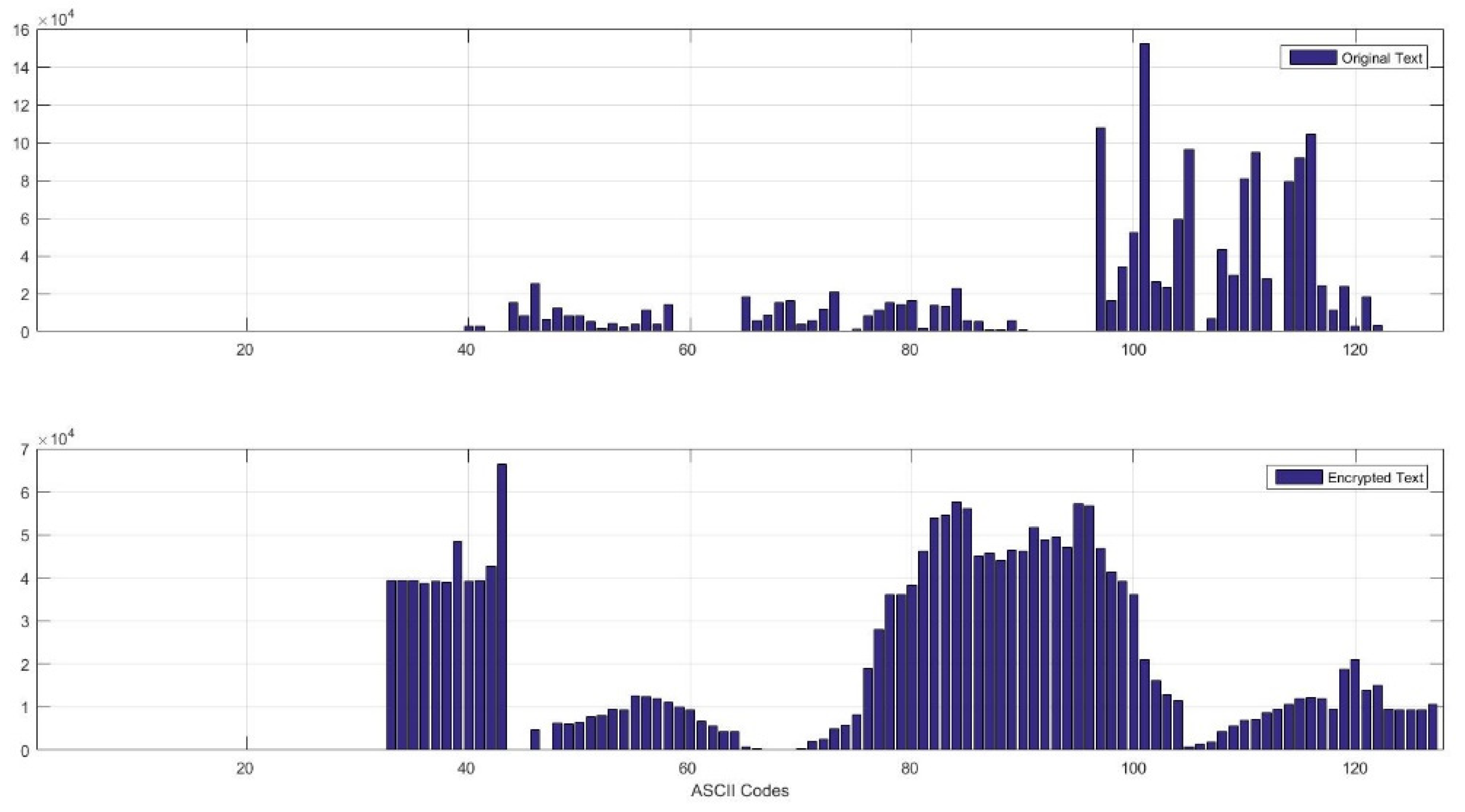
4.2.3. Frequency Analysis
4.2.4. Randomness Verification
- Frequency test
- Block frequency test
- Runs test
- Cumulative sums forward test
- Cumulative sums backward test
4.3. Security against Attacks
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tankard, C. Encryption as the cornerstone of big data security. Netw. Secur. 2017, 2017, 5–7. [Google Scholar] [CrossRef]
- Alabdullah, B. Rise of Big Data; Issues and Challenges. In Proceedings of the 2018 21st Saudi Computer Society National Computer Conference, Riyadh, Saudi Arabia, 25–26 April 2018; pp. 1–6. [Google Scholar]
- European Union. European Union Regulation 2016/679. Off. J. Eur. Communities 2014, 2014, 1–88. [Google Scholar]
- Editors, S.; Editors, A. Daemen. Springer—The Design of Rijndael.pdf; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 9783642076466. [Google Scholar]
- Abood, O.G.; Guirguis, S.K. A Survey on Cryptography Algorithms. Int. J. Sci. Res. Publ. 2018, 8, 8. [Google Scholar] [CrossRef]
- Ostrovsky, R.; Sahai, A.; Waters, B. Attribute-based encryption with non-monotonic access structures. In Proceedings of the 14th ACM Conference on Embedded Network Sensor Systems CD-ROM, Alexandria, VA, USA, 29 October–2 November 2007; pp. 195–203. [Google Scholar]
- Nie, T.; Zhang, T. A study of DES and blowfish encryption algorithm. In Proceedings of the TENCON 2009—2009 IEEE Region 10 Conference, Singapore, 23–26 January 2009; pp. 1–4. [Google Scholar]
- Çavuşoğlu, Ü.; Kaçar, S.; Zengin, A.; Pehlivan, I. A novel hybrid encryption algorithm based on chaos and S-AES algorithm. Nonlinear Dyn. 2018, 92, 1745–1759. [Google Scholar] [CrossRef]
- Gai, K.; Qiu, M.; Zhao, H.; Xiong, J. Privacy-Aware Adaptive Data Encryption Strategy of Big Data in Cloud Computing. In Proceedings of the 3rd IEEE International Conference on Cyber Security and Cloud Computing, Beijing, China, 25–27 June 2016; pp. 273–278. [Google Scholar]
- Forouzan, B.A. Cryptography and Network Security; McGraw-Hill, Inc.: New Delhi, India, 2007; Volume 1025, ISBN 9780131873162. [Google Scholar]
- Al-Kazaz, N.R.; Teahan, W.J. An automatic cryptanalysis of Arabic transposition ciphers using compression. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 738–745. [Google Scholar] [CrossRef]
- Agustini, S.; Rahmawati, W.M.; Kurniawan, M. Modified Vegenere Cipher to Enhance Data Security Using Monoalphabetic Cipher. Int. J. Artif. Intell. Robot. 2019, 1, 25. [Google Scholar] [CrossRef]
- Amalia; Budiman, M.A.; Sitepu, R. File text security using Hybrid Cryptosystem with Playfair Cipher Algorithm and Knapsack Naccache-Stern Algorithm. J. Phys. Conf. Ser. 2018, 978, 012114. [Google Scholar] [CrossRef]
- Marzan, R.M.; Sison, A.M.; Medina, R.P. An enhanced key security of Playfair cipher algorithm. Int. J. Adv. Trends Comput. Sci. Eng. 2019, 8, 1248–1253. [Google Scholar] [CrossRef]
- Aung, T.M.; Hla, N.N. A Complex Polyalphabetic Cipher Technique Myanmar Polyalphabetic Cipher. In Proceedings of the 2019 International Conference on Computer Communication and Informatics, Coimbatore, Tamil Nadu, India, 23–25 January 2019. [Google Scholar]
- Elmogy, A.; Bouteraa, Y.; Alshabanat, R.; Alghaslan, W. A New Cryptography Algorithm Based on ASCII Code. In Proceedings of the 2019 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 24–26 March 2019; pp. 626–631. [Google Scholar]
- Yadav, N.; Kapoor, R.K.; Rizvi, M.A. A Novel symmetric key cryptography using dynamic matrix approach. Adv. Intell. Syst. Comput. 2016, 439, 51–60. [Google Scholar]
- Biryukov, A. Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Ed.; Springer: Boston, MA, USA, 2005; ISBN 978-0-387-23483-0. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; ACM: New York, NY, USA, 1964; Volume 8, ISBN 9780252725487. [Google Scholar]
- Aleisa, N. A comparison of the 3DES and AES encryption standards. Int. J. Secur. Appl. 2015, 9, 241–246. [Google Scholar] [CrossRef]
- Manku, S.; Vasanth, K. Blowfish encryption algorithm for information security. ARPN J. Eng. Appl. Sci. 2015, 10, 4717–4719. [Google Scholar]
- Lamba, C.S. Design and Analysis of Stream Cipher for Network Security. In Proceedings of the 2010 Second International Conference on Communication Software and Networks, Singapore, 26–28 February 2010; Volume 76, pp. 526–567. [Google Scholar]
- Rajesh, S.; Paul, V.; Menon, V.G.; Khosravi, M.R. A secure and efficient lightweight symmetric encryption scheme for transfer of text files between embedded IoT devices. Symmetry 2019, 11, 293. [Google Scholar] [CrossRef]
- Hernández-Ramos, J.L.; Pérez, S.; Hennebert, C.; Bernabé, J.B.; Denis, B.; Macabies, A.; Skarmeta, A.F. Protecting personal data in IoT platform scenarios through encryption-based selective disclosure. Comput. Commun. 2018, 130, 20–37. [Google Scholar] [CrossRef]
- Aljawarneh, S.; Yassein, M.B.; Talafha, W.A. A multithreaded programming approach for multimedia big data: Encryption system. Multimed. Tools Appl. 2018, 77, 10997–11016. [Google Scholar] [CrossRef]
- Dawood, O.A.; Sagheer, A.M.; Al-Rawi, S.S. Design large symmetric algorithm for securing big data. In Proceedings of the 2018 11th International Conference on Developments in eSystems Engineering (DeSE), Cambridge, UK, 2–5 September 2018; pp. 123–128. [Google Scholar]
- Al-Omari, A.H. Lightweight Dynamic Crypto Algorithm for Next Internet Generation. Eng. Technol. Appl. Sci. Res. 2019, 9, 4203–4208. [Google Scholar] [CrossRef]
- Ngo, H.H.; Wu, X.; Le, P.D.; Wilson, C.; Srinivasan, B. Dynamic key cryptography and applications. Int. J. Netw. Secur. 2010, 10, 161–174. [Google Scholar]
- Chunka, C.; Goswami, R.S.; Banerjee, S. An efficient mechanism to generate dynamic keys based on genetic algorithm. Secur. Priv. 2018, e37. [Google Scholar] [CrossRef]
- Noura, H.N.; Reem, M.; Mohammad, M.; Ali, C. Lightweight and secure cipher scheme for multi-homed systems. Wirel. Netw. 2020, 1–18. [Google Scholar] [CrossRef]
- Noura, H.N.; Chehab, A.; Couturier, R. Efficient & secure cipher scheme with dynamic key-dependent mode of operation. Signal Process. Image Commun. 2019, 78, 448–464. [Google Scholar]
- Noura, H.; Chehab, A.; Couturier, R. Lightweight Dynamic Key-Dependent and Flexible Cipher Scheme for IoT Devices. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–8. [Google Scholar]
- Jallouli, O.; Assad, S.E.; Chetto, M.; Lozi, R. Design and analysis of two stream ciphers based on chaotic coupling and multiplexing techniques. Multimed. Tools Appl. 2018, 77, 13391–13417. [Google Scholar] [CrossRef]
- Wen, W.; Zhang, Y.; Su, M.; Zhang, R.; Chen, J.X.; Li, M. Differential attack on a hyper-chaos-based image cryptosystem with a classic bi-modular architecture. Nonlinear Dyn. 2017, 87, 383–390. [Google Scholar] [CrossRef]
- Teh, J.S.; Alawida, M.; Sii, Y.C. Implementation and practical problems of chaos-based cryptography revisited. J. Inf. Secur. Appl. 2020, 50, 102421. [Google Scholar] [CrossRef]
- Ding, L.; Liu, C.; Zhang, Y.; Ding, Q. A new lightweight stream cipher based on chaos. Symmetry 2019, 11, 853. [Google Scholar]
- Arab, A.; Rostami, M.J.; Ghavami, B. An image encryption method based on chaos system and AES algorithm. J. Supercomput. 2019, 75, 6663–6682. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process. 2019, 155, 44–62. [Google Scholar] [CrossRef]
- Dawood, O.A.; Khalaf, M.; Mohammed, F.M.; Almulla, H.K. Design a Compact Non-linear S-Box with Multiple-Affine Transformations; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1, ISBN 9783030387525. [Google Scholar]
- Zheng, Y.; Zhang, X.M. On relationships among avalanche, nonlinearity, and correlation immunity. Lect. Notes Comput. Sci. 2000, 1976, 470–482. [Google Scholar]
- Lee, J.; Sultana, N.; Yi, F.; Moon, I. Avalanche and bit independence properties of photon-counting double random phase encoding in gyrator domain. Curr. Opt. Photonics 2018, 2, 368–377. [Google Scholar]
- Webster, A.F.; Stafford, E.T. On the design of S-boxes. In Conference on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1985; pp. 523–534. [Google Scholar]
- Omran, S.S.; Al-Khalid, A.S.; Al-Saady, D.M. A cryptanalytic attack on Vigenère cipher using genetic algorithm. In Proceedings of the 2011 IEEE Conference on Open Systems, Langkawi, Malaysia, 25–28 September 2011; pp. 59–64. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Nist Spec. Publ. 2010, 22. [Google Scholar] [CrossRef]
- Roman’kov, V. Two general schemes of algebraic cryptography. Groups Complex. Cryptol. 2018, 10, 83–98. [Google Scholar] [CrossRef]
- Blondeau, C.; Leander, G.; Nyberg, K. Differential-Linear Cryptanalysis Revisited. J. Cryptol. 2017, 30, 859–888. [Google Scholar] [CrossRef]
| Symbol | Definition |
|---|---|
| Maximum ASCII character range (default is 127) | |
| Original ASCII character value | |
| Reflected value of the original ASCII character value | |
| Constant offset value used to avoid non-printable characters (32 by default) | |
| Reflected value of the original ASCII character value after adding the offset | |
| Variable offset computed based on the properties of the tree | |
| R | The root node of the tree |
| Adjusted value of N so that it is within the range of maximum value | |
| Reflection value of | |
| Pseudo | Pseudo-random number generated based on the character’s position in the text |
| Equivalent ASCII character for a given value |
| File Size (KB) | Encryption | Decryption | ||
|---|---|---|---|---|
| Processing Time (ms) | Memory (MB) | Processing Time (ms) | Memory (MB) | |
| 200 | 1433 | 17 | 1378 | 17 |
| 400 | 1956 | 21 | 1363 | 18 |
| 600 | 2118 | 27 | 1637 | 25 |
| 800 | 2335 | 30 | 1645 | 31 |
| 1000 | 2528 | 33 | 1995 | 35 |
| 2000 | 3616 | 55 | 1754 | 56 |
| File Size (KB) | Encryption | Decryption | ||
|---|---|---|---|---|
| Processing Time (ms) | Memory (MB) | Processing Time (ms) | Memory (MB) | |
| 200 | 1838 | 18 | 1992 | 19 |
| 400 | 2067 | 22 | 2444 | 25 |
| 600 | 2190 | 27 | 2750 | 29 |
| 800 | 2575 | 31 | 3183 | 37 |
| 1000 | 3034 | 34 | 3658 | 41 |
| 2000 | 4537 | 55 | 5500 | 49 |
| File Size (KB) | Encryption | Decryption | ||
|---|---|---|---|---|
| Processing Time (ms) | Memory (MB) | Processing Time (ms) | Memory (MB) | |
| 200 | 123 | 14 | 162 | 7 |
| 400 | 189 | 23 | 250 | 15 |
| 600 | 253 | 23 | 320 | 20 |
| 800 | 413 | 29 | 385 | 29 |
| 1000 | 479 | 32 | 460 | 36 |
| 2000 | 1854 | 65 | 775 | 68 |
| Technique | Hamming Distance | Avalanche Effect |
|---|---|---|
| E-ART | 57,852 | 50.1% |
| AES | 39,345 | 49.2% |
| DES | 39,425 | 49.3% |
| Test | p-Value | Remarks |
|---|---|---|
| Frequency test | 0.7399 | Random |
| Block frequency test | 0.7399 | Random |
| Runs test | 0.0668 | Random |
| Cumulative sums forward test | 0.1223 | Random |
| Cumulative sums backward test | 0.5341 | Random |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alabdullah, B.; Beloff, N.; White, M. E-ART: A New Encryption Algorithm Based on the Reflection of Binary Search Tree. Cryptography 2021, 5, 4. https://doi.org/10.3390/cryptography5010004
Alabdullah B, Beloff N, White M. E-ART: A New Encryption Algorithm Based on the Reflection of Binary Search Tree. Cryptography. 2021; 5(1):4. https://doi.org/10.3390/cryptography5010004
Chicago/Turabian StyleAlabdullah, Bayan, Natalia Beloff, and Martin White. 2021. "E-ART: A New Encryption Algorithm Based on the Reflection of Binary Search Tree" Cryptography 5, no. 1: 4. https://doi.org/10.3390/cryptography5010004
APA StyleAlabdullah, B., Beloff, N., & White, M. (2021). E-ART: A New Encryption Algorithm Based on the Reflection of Binary Search Tree. Cryptography, 5(1), 4. https://doi.org/10.3390/cryptography5010004





