ESPADE: An Efficient and Semantically Secure Shortest Path Discovery for Outsourced Location-Based Services
Abstract
:1. Introduction
- Privacy Objective 1 (PO1): User’s input information (i.e., source and destination locations) should not be revealed to the cloud service providers and any other users.
- Privacy Objective 2 (PO2): The contents of graph G should never be revealed to the cloud service providers and unauthorized users.
- Privacy Objective 3 (PO3): The shortest path information should be revealed only to the query issuer.
Main Contributions
- Semantic Security: ESPADE meets all three privacy objectives mentioned earlier. That is, the contents of the outsourced graph G and the user’s input query are never revealed to the cloud service providers and any unauthorized users. This is because our solution is designed to achieve semantic security under the semi-honest model of SMC. We refer the reader to Section 6.1 for more details.
- Efficiency: Our protocol is significantly efficient (in terms of both computation and communication-wise) compared to existing solutions. It is worth noting that the majority of expensive computations in ESPADE are performed by cloud providers, thus minimizing the costs on the end-user.
- Correctness: The steps involved in ESPADE are similar to the ones in the standard Dijkstra’s algorithm. The only difference is that the underlying operations are performed either over encrypted or randomized data. For any given G and shortest path query Q, the shortest path returned by our protocol is the same as the one that would be returned by executing Dijkstra’s algorithm on .
- Flexibility: Upon outsourcing the graph data to the cloud, the data owner does not have to participate in any other operations. Specifically, the end-users can issue SSSD queries directly to the cloud and the majority of the query processing task is done by the cloud providers, which suffices in the main purpose of outsourcing in the first place.
2. Problem Model
- Alice: We assume that Alice (data owner) holds sensitive geospatial data represented as a graph , where denotes the set of vertices, E denotes the edges connecting those vertices associated with weights W. In our model, we consider that G is an undirected weighted graph represented as an grid matrix (refer to Section 5 for more details). For example, consider a graph used by Google Maps where G represents a road network. Here each vertex in V will correspond to a given point on the road network, and each edge E will correspond to the road segment that connects any two points on the road network. In this case, weight can be the distance between junctions or traffic flow.
- Federated Cloud: Without loss of generality, let Alice outsource G (in encrypted format) to a Federated Cloud (FC) environment consisting of two cloud services providers and . We assume that and are semi-honest and do not collude. This is a realistic model as it is being used in several existing works (e.g., in [21,22,23,24]). This is because most of the cloud service providers are well-known IT organizations and it is highly unlikely that any two cloud service providers will collude as it may damage their reputation and can adversely affect their revenues.
- Bob: The end-user Bob issues SSSD shortest path queries to FC. and will collaboratively compute the shortest path from source s to t, and return the path to Bob.
3. Related Work
3.1. Privacy-Preserving Shortest Path over Plaintext Data
3.1.1. Obfuscation Methods
3.1.2. Private Information Retrieval (PIR) Methods
3.2. PPSP over Encrypted Graph Data
4. Preliminaries
4.1. The Dijkstra’s Algorithm
- ∘
- Vertices denoted by u or v;
- ∘
- Each edge that connects two vertices has weights associated with it, denoted by .
A. Initialization
- ∘
- The current vertex is marked as source s;
- ∘
- Each vertex in G is initially marked as unvisited;
- ∘
- All vertices are assigned with ∞ as the distance from s, while for s itself the distance is assigned as 0. That is, , ;
- ∘
- SP.
B. Iterative Process
- ∘
- Step 1: For the current vertex , consider all unvisited vertices that are directly connected to . Let us denote this set by L.
- ∘
- Step 2: For each vertex , calculate its new distance from the source as . If , then update vertex s distance as . Otherwise, it is unchanged.
- ∘
- Step 3: Mark as visited and update as . If , then terminate and return as the output. Otherwise, select the vertex , which has the smallest distance, set to m, and proceed to Step 1.
4.2. Homomorphic Encryption and Paillier Cryptosystem
- ∘
- Additive Homomorphism: The output of multiplying the ciphertexts of and is equivalent to the encryption of . That is,
- ∘
- Partial Multiplication: Given a constant , rising the ciphertext of to the power of b is equivalent to the encryption of . That is,
- ∘
- Semantic Security: Paillier’s encryption function is a probabilistic scheme meaning that encryptions of the same message will result in different ciphertexts. Therefore, given a set of ciphertexts, an adversary cannot deduce any information about the underlying plaintexts. That is, ciphertexts are indistinguishable from one another; thus, the scheme exhibits the semantic security property [18].
4.3. Secure Multiplication (SM)
| Algorithm 1 SM |
|
5. The Proposed ESPADE Protocol
- Alice’s geospatial data are represented as a weighted graph G with V vertices and W weights. The contents of G are sensitive and thus need to be kept confidential from cloud service providers and unauthorized parties. We assume that each vertex in G is associated with a unique identification number—for example, denoting the combination of latitude and longitude information.
- generates the public-private key pair based on the Paillier’s scheme and securely distributes to Alice, , and Bob. We assume that there exist secure communication channels (e.g., SSL) between each pair of parties participating in our protocol.
- Similar to existing work [14,15,16], we assume that all the participating parties in our protocol are semi-honest [19]. The semi-honest model is a practical security model, due to the following reasons. First, building protocols under the semi-honest model is an important first step for constructing protocols under stronger security models (e.g., against covert and malicious adversaries). Second, protocols under the semi-honest model are typically considered to be quite efficient, which may not be the case for other adversarial models. Third, protocols that are proven to be secure under the semi-honest model can prevent inadvertent leakage of information among participating parties. Finally, it is highly unlikely that the well-established cloud service providers (e.g., Amazon and Microsoft) would deviate from the prescribed protocol and collude, as this would damage their reputation and consumer trust. Therefore, we believe that the semi-honest model is a practical security model for our problem domain.
- ∘
- Stage 1—Secure Outsourcing of Graph G (SOG): In this stage, Alice transforms her graph data G into a proper grid matrix. During this process, Alice relies on our data aggregation technique to intelligently capture the information in each grid. After this transformation, Alice outsources the aggregated graph information to the federated cloud environment using the randomization approach. At the end of this stage, only knows the encrypted graph data.
- ∘
- Stage 2—Secure Retrieval of Shortest Path (SRSP): In this stage, Bob securely sends his shortest path query to FC. Then, and jointly involve secure computations to retrieve the shortest path in an iterative process, based on Dijkstra’s algorithm. At the end of this stage, only Bob knows the shortest path from s to t.
| Algorithm 2 ESPADE() → SP( |
|
5.1. Secure Outsourcing of Graph G (SOG)
5.2. Secure Retrieval of Shortest Path (SRSP)
- To start with, Bob creates a graph that initially contains no values except his starting point s. The goal of Bob is to expand by retrieving graph data from FC in an iterative manner until he has sufficient graph data to construct SP. First, he computes the grid location (e.g., using his GPS) in which his source location s resides, denoted by . He also sets the current vertex to s. Now, Bob wants to request ’s grid data from FC so that he can expand without revealing any information about to and . A trivial approach here is for Bob to encrypt and forward it to , but this would require exponentiation module operations, which are expensive. To avoid this, Bob splits into two random shares and , such that and , where . Bob sends and to and , respectively.
- Upon receiving , encrypts it under and forwards to .
- After receiving from Alice and from , computes by performing homomorphic operations, as . Then, it obliviously checks which grid’s information Bob is requesting. To achieve this, computes . The idea behind this operation is to subtract Bob’s requesting grid ID from all grid IDs under encryption. The observation here is that exactly one of the values of is an encryption of 0. randomizes by computing , where . Then, randomly permutes and sends Y to . Here is a random permutation function known only to .
- Upon receiving Y, decrypts it component-wise using the private key resulting in a new vector Z. It is worth noting that only one of the entries in Z is 0. Now, generates a new encrypted vector P based on whether the value of is 0 or not. Specifically, it generates P as follows and sends it to :
Algorithm 3 SRSP - Require:
- Bob holds SSSD query ; holds and holds the private key
- 1:
- Bob:
- (a).
- and
- (b).
- Compute the current grid ID of
- (c).
- Compute two random shares of as and , where
- (d).
- Send to and to
- 2:
- :
- (a).
- Receive from Bob
- (b).
- Compute and send to
- 3:
- :
- (a).
- Receive from Bob and from
- (b).
- (c).
- fordo:
- ∘
- ∘
- = mod ,where
- (d).
- ; Send Y to
- 4:
- :
- (a).
- Receive Y from
- (b).
- fordo:
- ∘
- ∘
- ifthen=else=
- (c).
- Send P to
- 5:
- (a).
- (b).
- fordo:
- ∘
- , for {SM requires participation of both and }
- (c).
- fordo
- ∘
- ∘
- Compute mod , where .
- ∘
- (d).
- Send to Bob and to
- 6:
- :
- (a).
- for
- (b).
- Send to Bob
- 7:
- Bob:
- (a).
- Receive from and from
- (b).
- , for
- (c).
- Update based on and execute Dijkstra’s algorithm
- (d).
- ift is marked as visited thenreturn SPelseIdentify the new neighboring vertex and proceed to step 1(b)
- performs inverse permutation on P to get . It is worth noting that equals if , and otherwise. After this, with private input and with private key are involved in a set of secure multiplication operations. Specifically, with input and jointly execute SM, for and . Suppose denotes the output of SM. Since Q consists of only for Bob’s current grid , secure multiplication will result in to store the aggregated grid information of . For , every other entry in is multiplied by ; thus, the result will be encryptions of 0’s for all other grids. Note that the output of SM—that is —is known only to , for and . Next, aggregates all the SM results column-wise locally. That is, computes . The important observation here is that contains the entire grid data in which resides. At this point, needs to somehow send the current grid data to Bob. In order to alleviate the overload on Bob, utilizes the randomization approach. That is, selects random numbers and adds it to using additive homomorphic properties by computing . Additionally, computes . Now, sends to Bob and to , for .
- After receiving the encrypted randomized vector , decrypts it component-wise using to get , for . Then, sends to Bob. Due to the randomization by , it is worth noting that the decrypted values in this step do not reveal any information to .
- Finally, upon receiving and from and , Bob adds them component-wise to get , for which consists of ’s grid data. Bob will then update based on this new grid information and executes the Dijkstra’s algorithm to determine the shortest path marking each vertex with minimum distance as visited. If Bob’s destination t is in this subgraph and marked as visited, Bob can calculate the shortest distance from s to t locally, and thus terminates the protocol by returning SP. Otherwise, Bob identifies the new vertex for which the grid information is missing and sets it as the new current vertex . Then, the algorithm is repeated (i.e., go to step 1(b) of Algorithm 3) with an updated as input to the next iteration.
- •
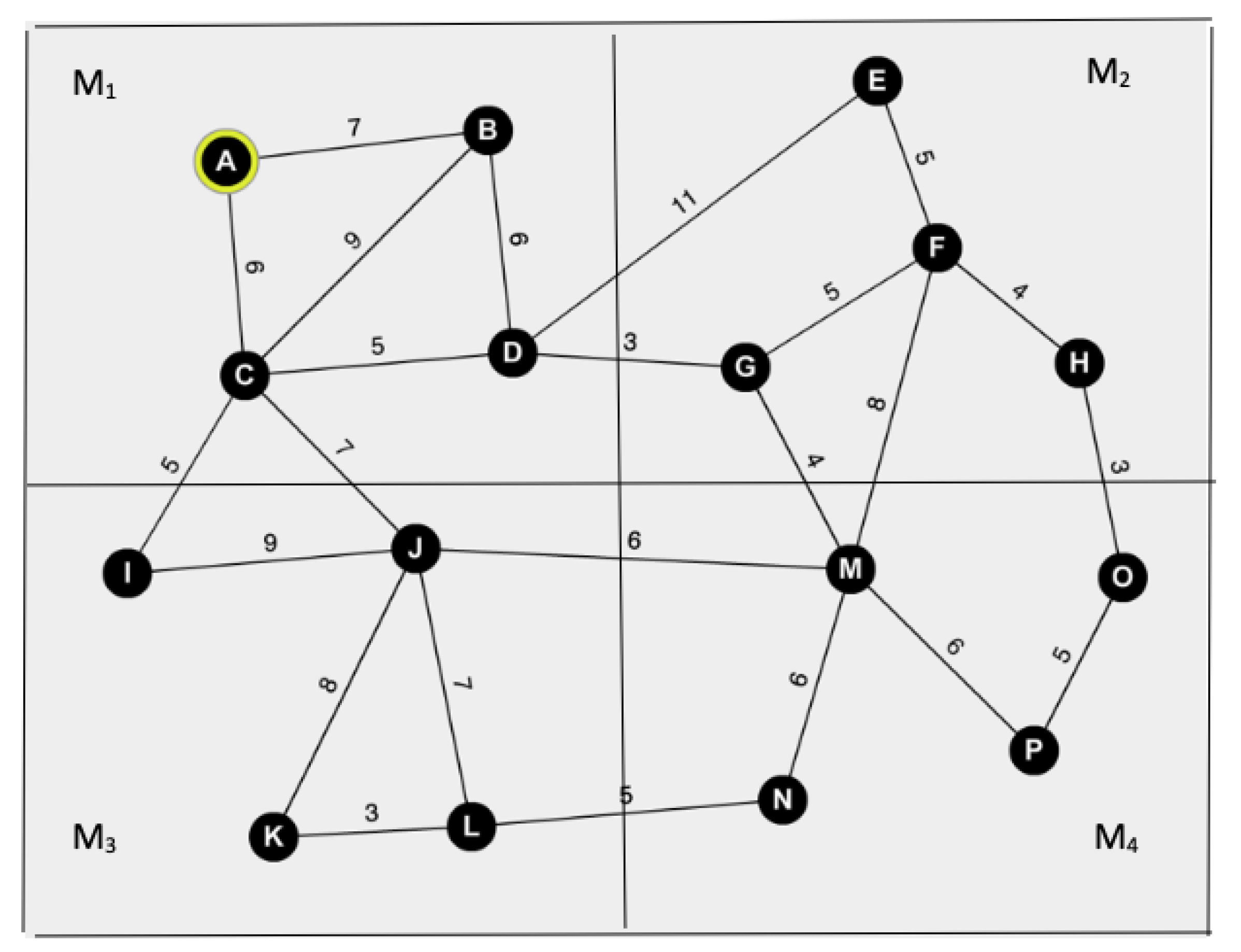
- Iteration 1: Initially, Bob sets his current vertex to A. In this case, the current grid ID of is 1 since resides in . That is, Bob sets . Bob randomly splits his information and sends them to and , separately. At the end of the first iteration, Bob receives all the vertex and associated edge weight information of . He updates his sub-graph (refer to Figure 3a) and executes Dijkstra’s algorithm. After marking C as visited, Bob makes I the current vertex.
- •
- Iteration 2: Bob updates the current grid ID value to 3, as vertex I resides in . is passed as input to the second iteration. At the end of the second iteration, Bob expands as shown in Figure 3b.
- ∘
- Similarly, Bob retrieves and information in iterations 3 and 4, respectively. Refer to Figure 3c,d. At the end, Bob finds out that SP.
6. Performance Analysis of ESPADE
6.1. Security Analysis under the Semi-Honest Model
6.1.1. Proof of Security for Stage 1
6.1.2. Proof of Security for Stage 2
6.2. Complexity Analysis
6.2.1. Computation Costs
6.2.2. Communication and Round Complexity
6.3. Performance Comparison with Existing Work
6.4. Experimental Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bennett, J.; Rokas, O.; Chen, L. Healthcare in the Smart Home: A Study of Past, Present and Future. Sustainability 2017, 9, 840. [Google Scholar] [CrossRef] [Green Version]
- Islam, S.M.; Kwak, D.; Kabir, M.H.; Hossain, M.; Kwak, K. The Internet of Things for Health Care: A Comprehensive Survey. IEEE Access 2015, 3, 678–708. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, W.J.; Cho, S. Internet of Things for Smart Manufacturing System: Trust Issues in Resource Allocation. IEEE Internet Things J. 2018, 5, 4418–4427. [Google Scholar] [CrossRef]
- Fraga-Lamas, P.; Fernández-Caramés, T.M.; Suárez-Albela, M.; Castedo, L.; González-López, M. A Review on Internet of Things for Defense and Public Safety. Sensors 2016, 16, 1644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, H.; Gartner, G.; Krisp, J.M.; Raubal, M.; Weghe, N.V. Location based services: Ongoing evolution and research agenda. J. Locat. Based Serv. 2018, 12, 63–93. [Google Scholar]
- Junglas, I.A.; Watson, R.T. Location-based services. Commun. ACM 2008, 51, 65–69. [Google Scholar] [CrossRef]
- Perusco, L.; Michael, K. Control, trust, privacy, and security: Evaluating location-based services. IEEE Technol. Soc. Mag. 2007, 26, 4–16. [Google Scholar] [CrossRef] [Green Version]
- Asuquo, P.; Cruickshank, H.; Morley, J.; Ogah, C.; Lei, A.; Hathal, W.; Bao, S.; Sun, Z. Security and Privacy in Location-Based Services for Vehicular and Mobile Communications: An Overview, Challenges, and Countermeasures. IEEE Internet Things J. 2018, 5, 4778–4802. [Google Scholar] [CrossRef]
- Rathod, A.; Jariwala, V. Investigation of Privacy Issues in Location-Based Services. In Recent Findings in Intelligent Computing Techniques; Sa, P., Bakshi, S., Hatzilygeroudis, I., Sahoo, M., Eds.; Springer: Singapore, 2019; Volume 707, pp. 55–65. [Google Scholar]
- Bokhari, M.U.; Makki, Q.; Tamandani, Y.K. A Survey on Cloud Computing. In Big Data Analytics; Aggarwal, V., Bhatnagar, V., Mishra, D., Eds.; Springer: Singapore, 2018; Volume 654, pp. 149–164. [Google Scholar]
- Stuedi, P.; Mohomed, I.; Terry, D. WhereStore: Location-based data storage for mobile devices interacting with the cloud. In Proceedings of the 1st ACM Workshop on Mobile Cloud Computing & Services: Social Networks and Beyond, San Francisco, CA, USA, 15–18 June 2010; ACM: New York, NY, USA, 2010; pp. 1–8. [Google Scholar]
- Ghinita, G.; Kalnis, P.; Khoshgozaran, A.; Shahabi, C.; Tan, K.-L. Private queries in location based services: Anonymizers are not necessary. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10–12 June 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 121–132. [Google Scholar]
- Yi, X.; Paulet, R.; Bertino, E.; Varadharajan, V. Practical k nearest neighbor queries with location privacy. In Proceedings of the IEEE 30th International Conference on Data Engineering, Chicago, IL, USA, 31 March– 4 April 2014; pp. 640–651. [Google Scholar]
- Samanthula, B.K.; Rao, F.; Bertino, E.; Yi, X. Privacy-Preserving Protocols for Shortest Path Discovery over Outsourced Encrypted Graph Data. In Proceedings of the IEEE International Conference on Information Reuse and Integration, San Francisco, CA, USA, 13–15 August 2015; pp. 427–434. [Google Scholar]
- Blanton, M.; Steele, A.; Alisagari, M. Data-oblivious graph algorithms for secure computation and outsourcing. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 7–10 May 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 207–218. [Google Scholar]
- Zhang, L.; Li, J.; Yang, S.; Wang, B. Privacy Preserving in Cloud Environment for Obstructed Shortest Path Query. Wirel. Pers. Commun. 2020, 96, 2305–2322. [Google Scholar] [CrossRef]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Advances in Cryptology—EUROCRYPT; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1592, pp. 223–238. [Google Scholar]
- Goldwasser, S.; Micali, S.; Rackoff, C. The knowledge complexity of interactive proof-systems. In Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing, Providence, RI, USA, 6–8 May 1985; Association for Computing Machinery: New York, NY, USA, 1985; pp. 291–304. [Google Scholar]
- Goldreich, O. General Cryptographic Protocols. In Foundations of Cryptography; Cambridge University Press: Cambridge, UK, 2004; Volume 2, pp. 599–746. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009; pp. 658–663. [Google Scholar]
- Bugiel, S.; Nürnberger, S.; Sadeghi, A.R.; Schneider, T. Twin Clouds: Secure Cloud Computing with Low Latency. In Communications and Multimedia Security; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7025, pp. 32–44. [Google Scholar]
- Wang, B.; Li, M.; Chow, S.M.; Li, H. Computing encrypted cloud data efficiently under multiple keys. In Proceedings of the 2013 IEEE Conference on Communications and Network Security, National Harbor, MD, USA, 21–23 October 2013; pp. 504–513. [Google Scholar]
- Samanthula, B.K.; Elmehdwi, Y.; Jiang, W. k-Nearest Neighbor Classification over Semantically Secure Encrypted Relational Data. IEEE Trans. Knowl. Data Eng. 2015, 27, 1261–1273. [Google Scholar] [CrossRef] [Green Version]
- Samanthula, B.K.; Albehairi, S.; Dong, B. A Privacy-Preserving Framework for Collaborative Association Rule Mining in Cloud. In Proceedings of the IEEE Cloud Summit, Washington, DC, USA, 8–10 August 2019; pp. 116–121. [Google Scholar]
- Barak, B.; Goldreich, O.; Impagliazzo, R.; Rudich, S.; Sahai, A.; Vadhan, S.P.; Yang, K. On the (im)possibility of obfuscating programs. J. ACM 2012, 59, 6. [Google Scholar] [CrossRef]
- Lee, K.C.K.; Lee, W.-C.; Leong, H.; Zheng, B. Navigational path privacy protection: Navigational path privacy protection. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 691–700. [Google Scholar]
- Ostrovsky, R.; Skeith, W.E. A Survey of Single-Database Private Information Retrieval: Techniques and Applications. In Public Key Cryptography; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4450, pp. 393–411. [Google Scholar]
- Kushilevitz, E.; Ostrovsky, R. Replication is not needed: Single database, computationally-private information retrieval. In Proceedings of the 38th Annual Symposium on Foundations of Computer Science, Miami Beach, FL, USA, 19–22 October 1997; pp. 364–373. [Google Scholar]
- Mouratidis, K.; Yiu, M.L. Shortest path computation with no information leakage. Proc. VLDB Endow. 2012, 5, 692–703. [Google Scholar] [CrossRef]
- Mehrotra, S.; Sharma, S.; Ullman, J.D.; Ghosh, D.; Gupta, P.; Mishra, A. Panda: Partitioned Data Security on Outsourced Sensitive and Non-sensitive Data. arXiv 2020, arXiv:2005.06154. [Google Scholar] [CrossRef]
- Li, L.; Lu, R.; Huang, C. EPLQ: Efficient Privacy-Preserving Location-Based Query over Outsourced Encrypted Data. IEEE Internet Things J. 2015, 3, 206–218. [Google Scholar] [CrossRef]
- Zhu, X.; Ayday, E.; Vitenberg, R. A privacy-preserving framework for outsourcing location-based services to the cloud. IEEE Trans. Dependable Secur. Comput. 2019. [Google Scholar] [CrossRef] [Green Version]
- Acar, A.; Aksu, H.; Uluagac, A.S.; Conti, M. A Survey on Homomorphic Encryption Schemes: Theory and Implementation. ACM Comput. Surv. 2018, 51, 35p. [Google Scholar] [CrossRef]
- Elmehdwi, Y.; Samanthula, B.K.; Jiang, W. Secure k-nearest neighbor query over encrypted data in outsourced environments. In Proceedings of the IEEE 30th International Conference on Data Engineering, Chicago, IL, USA, 31 March–4 April 2014; pp. 664–675. [Google Scholar]
- Goldreich, O. Encryption Schemes. In Foundations of Cryptography; Cambridge University Press: Cambridge, UK, 2004; Volume 2, pp. 373–470. [Google Scholar]
- Damgård, I.; Jurik, M. A Generalisation, a Simpli.cation and Some Applications of Paillier’s Probabilistic Public-Key System. In Public Key Cryptography Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1992, pp. 119–136. [Google Scholar]


| Notation | Description |
|---|---|
| SSSD-SP | Single-source single-destination shortest path |
| ESPADE | Efficient and semantically secure shortest path discovery over encrypted graph data |
| FC | A federated cloud environment consisting of two cloud service providers and |
| G | A weighted graph consisting of vertices with E edges and W weights |
| n | The total number of grids G is divided into |
| jth vertex in grid location i | |
| kth neighbor of vertex | |
| Weight between the two vertices: and | |
| Source and destination locations | |
| Shortest path from s to t based on G | |
| A pair of public-private key pair generated based on Paillier cryptosystem | |
| Epk | Paillier’s Encryption function with public key |
| Dsk | Paillier’s Decryption function with private key |
| A random number chosen uniformly in the group |
| Online Computation | Communication (in bits) | Round | |
|---|---|---|---|
| Alice (one-time) | additions | - | |
| Bob | additions | ||
| Federated Cloud | multiplications |
| PSPEG | PSPEG | ESPADE | |
|---|---|---|---|
| Cloud Model | Single-Cloud | Two-Cloud | Two-Cloud |
| Shortest-Path Accuracy | ✓ | ✓ | ✓ |
| Proof of Security | ✗ | ✗ | ✓ |
| Data Outsourcing Cost | mul. | mul. | add. |
| Bob’s Computation Cost | mul. | add. | add. |
| Total Computation Cost | mul. | mul. | mul. |
| Total Communication Cost | bits | bits | bits |
| Total Round Complexity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samanthula, B.K.; Karthikeyan, D.; Dong, B.; Kumari, K.A. ESPADE: An Efficient and Semantically Secure Shortest Path Discovery for Outsourced Location-Based Services. Cryptography 2020, 4, 29. https://doi.org/10.3390/cryptography4040029
Samanthula BK, Karthikeyan D, Dong B, Kumari KA. ESPADE: An Efficient and Semantically Secure Shortest Path Discovery for Outsourced Location-Based Services. Cryptography. 2020; 4(4):29. https://doi.org/10.3390/cryptography4040029
Chicago/Turabian StyleSamanthula, Bharath K., Divya Karthikeyan, Boxiang Dong, and K. Anitha Kumari. 2020. "ESPADE: An Efficient and Semantically Secure Shortest Path Discovery for Outsourced Location-Based Services" Cryptography 4, no. 4: 29. https://doi.org/10.3390/cryptography4040029
APA StyleSamanthula, B. K., Karthikeyan, D., Dong, B., & Kumari, K. A. (2020). ESPADE: An Efficient and Semantically Secure Shortest Path Discovery for Outsourced Location-Based Services. Cryptography, 4(4), 29. https://doi.org/10.3390/cryptography4040029




