1. Introduction
Communication is a vital aspect of society, and the ability to communicate securely is paramount. Classical communications today rely on the computational difficulty of certain mathematical problems. One of these problems involves the factorization of prime numbers, and there is no known algorithm that can solve the problem in less than exponential time. This does not mean that there is no algorithm that can solve it in less than exponential time, but that it just has not been found yet. Not only is it feasible to find an algorithm that performs the calculations in less than exponential time, it was shown by Shor, in his famous work [
1], that given the resources of a quantum computer the problem can be solved in polynomial time. This algorithm makes it feasible that encryption based on the computational difficulty of mathematical problems will in the future be no longer viable. As a result, this has turned the focus to using physical laws to encode messages instead. This idea is the foundation of a type of communication known as quantum key distribution (QKD) which was first developed by Bennett and Brassard in there BB84 protocol [
2]. In this, single photons polarized in orthogonal directions encode the 0 s and 1 s used to establish a key between a transmitter and receiver.
Although information can be sent using one polarization basis, the security of the protocol is only realized when two different bases are used to transmit the information (linear and diagonal polarization). By using two bases, it allows the quantum phenomena of superposition to be exploited in order to ensure security. QKD first builds a set of 1s and 0s randomly and then for each of these the transmitter chooses to send the information in either of the two polarization bases.
When the photon is received it is measured randomly in one of the two bases and the polarization state is recorded. To establish a key, the receiver then uses classical communication to tell the transmitter what polarization basis each photon was measured in, and the receiver checks for basis agreement based on their initially prepared state. The photons that were measured in the correct basis then make up the raw key used for encryption. Measurement and communication of the basis used allows the parties to not only establish a key but also to monitor the security of their communication channel. Monitoring is done by looking at the error between the shared keys and is caused by noise or active eavesdropping on the channel. An eavesdropper cannot gain information by copying the photons and measuring the copy due to the no-cloning theorem of quantum mechanics. Therefore, the only way is to actively measure the photons being sent through the channel. After measuring the eavesdropper must then send another photon to the receiver in order to not cease communication between the two. This process of measuring and sending a photon inevitably causes errors in the established raw key. This is caused by the eavesdropper measuring the photons in the wrong basis. Say the transmitter sends a 1 in the diagonal basis, but the eavesdropper measures in the linear basis. The outcome of the measurement is random since a polarization state can be written as an admixture of polarization states of another basis.
This means that the eavesdropper has an equal probability of measuring the photon in the |0⟩ or the |1⟩ state. Since measurement of a quantum state destroys the information encoded on it all knowledge of the initial state is lost, and the eavesdropper does not know they measured in the wrong basis. In order to not drastically reduce the photon reception rate between the transmitter and receiver, the eavesdropper must retransmit a photon in the bases it was measured in. If the measurement was done in the correct basis then there is no effect to the communication. If instead the measurement was wrong, then three outcomes are possible. First, the transmitter and receiver have a basis disagreement and the photon is not used as a key bit. Second, the transmitter and receiver have a basis agreement and the key bits agree. This would occur through the superposition of the photon’s states; since the eavesdropper sent it in the wrong basis when the receiver measured the photon, there is an equal probability of it collapsing into the state initially prepared or its orthogonal state. If the state collapses this way then the eavesdropper effect on the channel cannot be determined. Lastly, when the state collapses incorrectly then the communicating parties can tell the eavesdropper is affecting their communication since they both have a basis agreement, but their states disagree. Consequently, for 50% of the key the eavesdropper causes no error due to correct basis selection; in another 25% of the key it also causes no error due to states collapsing correctly. For the last 25% of the key the eavesdropper then causes an error, meaning if the error between the established keys is greater than 25% the parties know their communication is being listened to.
The ability to actively monitor communications is unique to quantum communications, but beyond this it is paramount that the security of a QKD scheme be proven, and many have been developed [
3,
4,
5]. Although theoretically the schemes are secure, in application security is lost due to physical aspects of the setup. The loss of security comes from the assumption that the photon source is truly a single photon source. In the realization of these types of schemes an attenuated laser is used as the single photon source, but instead of providing a single photon source it provides a probabilistic source with a nonzero probability of double-photon emissions [
6,
7]. As a note, not all security proofs rely on the single photon assumption, for instance, [
8]. Proofs such as these add extra requirements to the state preparation, namely, specific phases associated with the signal states, consequently adding to the complexity of the system. Therefore, to simplify the implementation using protocols that only involve polarization dependence is advantageous. Double photon emissions are detrimental to QKD by allowing the eavesdropper to measure the state of the photons, and by not being detected, since one of the photons can be measured and the other sent to the receiver. This means that as the probability of double-photon emission goes up, the effect of the eavesdroppers on the error in the raw key goes down. As a result of this, the reliability of detecting the eavesdropper goes down, leading to the possibility that an eavesdropper is present and not detected. This leakage of information causes the eavesdropper to gain a significant portion of the key. Firstly, half of the raw key is already known to them through the measurement of photons in the correct basis. Another quarter of the key is found by guessing the bit values of the photons measured in the wrong basis. Lastly, another 8th of the key found from the key reconciliation process between the communicating parties. This leads to the eavesdropper having only a 12.5% error in their constructed key. A third party with this information is then able to decode a significant portion of the message and gain knowledge of the secret information. However, in QKD it is not possible for the eavesdropper to gain full knowledge of the key due to the quantum nature of the states. For an overview of number spitting attacks see [
9,
10].
Attacks like these have hindered the application of schemes such as the BB84 protocol; consequently many different ways to combat number splitting attacks have been devised. One of the more prominent ways to avoid these attacks is using the decoy state method. This method, as described by [
11], utilizes photons in “decoy” states to monitor the channel for a number splitting attack. In this the transmitter sends two different states to the receiver. The first is the BB84 state used for key establishment, and the second is the decoy state. The difference between the two is the BB84 states are highly attenuated with mean photon number
while the decoy states have mean photon number
. As a consequence, the decoy states will have a high probability of multi-photon emission. During the number splitting attack the eavesdropper will filter out the single photon emissions while keeping the multi-photon emissions, and pick a photon out while letting the rest pass to the receiver. To combat this during the key establishment, the transmitter replaces some of the BB84 states with the decoy states. The two states to an eavesdropper look the same, so they perform all the same operations to the decoy states as the BB84 states. After all the photons have been collected and measured at the receiver, the transmitter then announces publicly which pulses were the decoy states. From this the yield of the BB84 states and at of the decoy states are measured
,
respectively. Then, provided a Poissonian source, the condition for security of the decoy state protocol is [
12].
This necessitates the characterization of the source and the quantum channel, since the yield for either state is related to the channel loss for each state. In determining the yield, the individual yields of each n photon state are determined at the detectors. These represent the relative frequencies that n-photons pulses, from the BB84 and decoy states, are registered at the receivers detectors. The requirement of accurate source characteristics as well as the ability for the receiver to distinguish multi-photon events causes the implementation to become more complicated. This along with the intrinsic error lead to the idea QKD should be used as a resource instead of a direct encryption technique. By doing this a scheme can be devised such that in order for an eavesdropper to decode the message they are required to gain more information about the key than they have access to.
This requires an encryption technique that would be sensitive to small perturbations in the key, causing decryption to become impossible. The most well-known systems that exhibit extreme sensitivity are chaotic systems, which can resemble random noise-like signals and have broadband characteristics. The sensitivity of chaotic systems can seem like a drawback to communications since it would be near impossible for a receiver to replicate the solutions without the exact initial conditions and parameters. In [
13] chaotic systems were used to mask the information, but what was sent through the quantum channel was the initial conditions and parameters. By doing this it is feasible that an eavesdropper could learn these variables using their immense knowledge of the key.
Typically, when considering chaotic systems, the only way to replicate them is through the exact knowledge of the initial conditions and parameters. In [
14] it was shown that identical solutions can be generated through the use of chaotic synchronization. This occurs when a solution is generated from a set of nonlinear coupled differential equations like the following Lorenz equations.
Then using one of these solutions like the
a corresponding subsystem can be driven to generate the solutions
and
. This subsystem is represented by the following equations.
The ability for this subsystem to synchronize with the original drive solutions is represented by the eigenvalues of the Jacobian of the system known as Lyapunov exponents. This value describes how the system converges, and only systems with strictly negative Lyapunov exponents exhibit convergence. If this is realized then as
,
and
. If QKD is used to transmit the solution
to the receiver they can then generate
and
;
and
are used to encrypt the message while
and
are used to decrypt it. Transmission of the
is done by converting each
in to a binary value, then using the generated key to encrypt the information. It will then be shown that the information gained by the eavesdropper is not be enough do generate a solution
and
such that as
,
and
.
The proposed protocol of this paper is designed to overcome the practical limitations of QKD, namely the ability of an eavesdropper to monitor the channel due to double-photon emissions. With this in mind, the rest of the paper is organized as follows.
Section 2 gives a description of the proposed protocol,
Section 3 shows the behavior of chaotic systems and synchronization,
Section 4 gives the application of the proposed protocol,
Section 5 draws the conclusions provided by the research.
2. Proposed Protocol
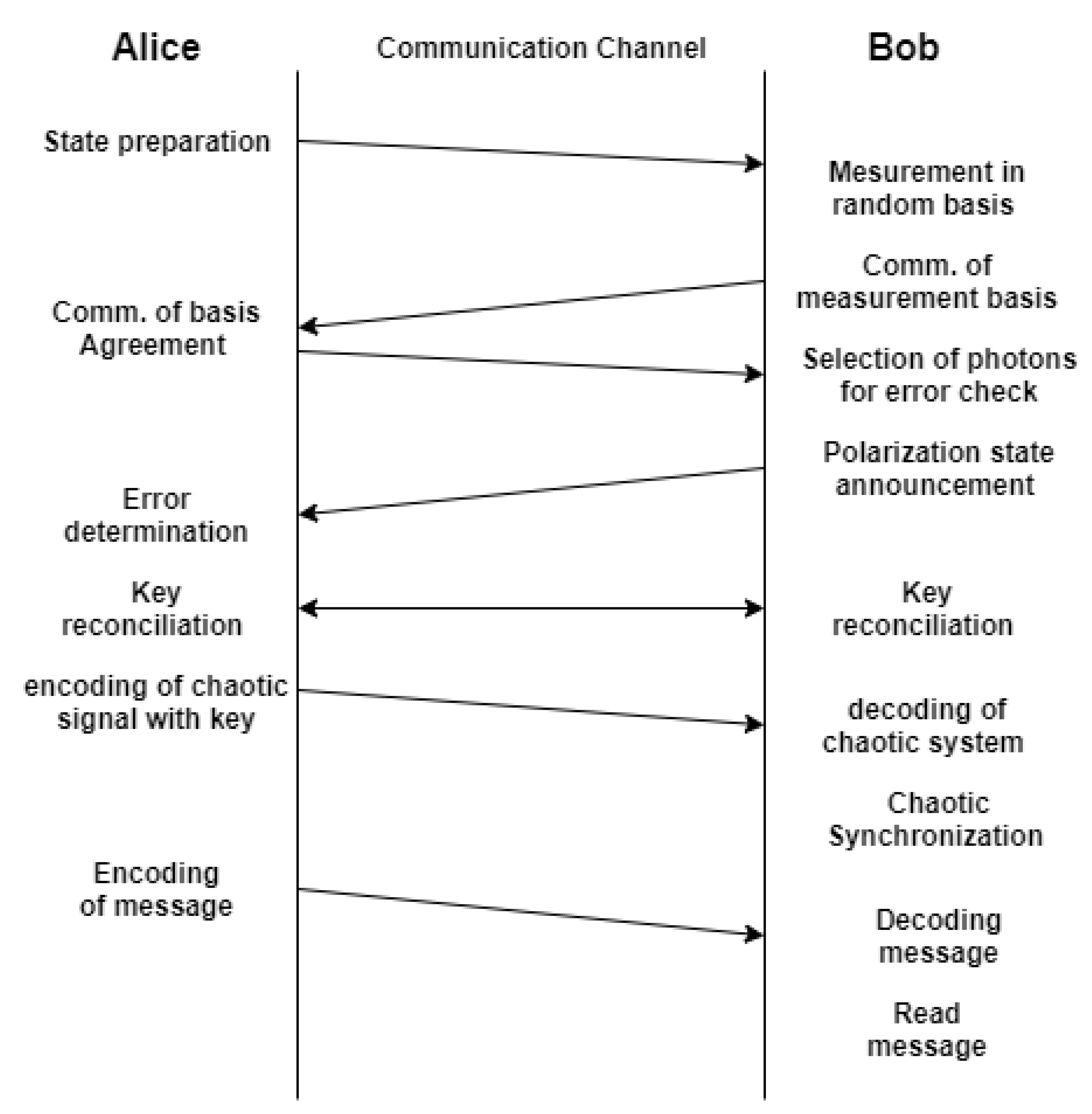
As mentioned previously, the proposed protocol utilizes a quantum channel to transmit a chaotic solution, which is then used to drive a corresponding system to reproduce the chaotic mask and decode the message. The following is the description of the proposed protocol, as shown in
Figure 1, where the transmitter is referred to as Alice, the receiver as Bob and the eavesdropper as Eve.
There exists a codebook of synchronization parameters represented by,
such that.
where
and represents the sets of possible parameters associated with Equation (
1). Using the pre-shared secret, Alice can then produce the set of solutions to Equation (
1)
.
Prior to key establishment, Alice and Bob must synchronize the transmitter and receiver stations in order to allow communication. During this process, key parameters of the detection systems are determined, such as the propagation length of the channel [
15,
16]. This device synchronization is independent of the chaotic synchronization, and utilized to allow the parties to compare photon states reliably.
Alice then performs a key establishment utilizing the BB84 protocol. She prepares a stream of photons where she knows the set
of her prepared polarization basis for each photon. Using time-bin establishment, for example [
17], Alice creates a random binary message,
, where
. Then, Alice, using the previously established polarization basis,
, encodes
M using the following pseudocode:
The time-bin assignment permits superposition of |0⟩ with polarization , and time shifted |1⟩ with , although any mutually orthogonal polarization or phases could be used. The output of the quantum encoding is the set .
Bob then randomly generates a set of measuring basis to measure each photon in. Once he measures each photon in his determined basis he records each state into the set . He then transmits classically back to Alice.
Using and Alice then determines which photons in each set were sent and measured in the same basis. Once Alice determines this she classically communicates the position of the elements of C where . Alice also finds her bits in and uses this to establish her raw key .
Bob then selects the elements of specified by the communication from Alice and produces his raw key . He then selects a small subset of and communicates back to Alice their states and positions.
Using this subset Alice then takes out her corresponding key bits and compares them to those sent by Bob. From this an estimate on the error rate is preformed; if this error is below the threshold established between Alice and Bob, then communication continues; otherwise, they try again.
If they confirm the error rate is below the threshold, they still need to correct these errors using a key reconciliation technique. Therefore, Alice and Bob utilize a CASCADE like protocol [
18] to reduce the error in the keys.
The CASCADE protocol assumes that there exists a source coding of Alice’s key,
, and a source coding of Bob’s estimate of Alice’s Key,
. Then Alice and Bob Share F, where
Further presume that the exchange of F between Alice and Bob results in errors that requires reconciliation. There exist
and
. CASCADE reconciles the errors between the two by iteratively comparing subdivided blocks of message. Assume a memoryless channel. There exists a joint probability
Given that
and
are equal length, no other additional coding bits are added to
F and the conditional information entropy between Alice and Bob on message
F is
, the efficiency of the reconciliation process is
Each iteration takes
F and subdivides into blocks of length
where the subscript denotes the iteration. At each step Alice and Bob compute the parity of their copy of the
of n message blocks. If the blocks differ, then at least one error exists in that block and the two parties iterativiely divide and compute until the error is resolved for all blocks. When this is complete, the two parties use key F to encrypt the chaotic solution [
19].
Once the key’s have been established, Alice takes one of her chaotic solutions () and converts the solution into a binary string and applies her key to the solution. This masked chaotic solution is then sent to Bob.
Upon reception of this encrypted chaotic solution, Bob applies his key to gain the corresponding binary string and then converts this back to a floating point number and receives the solution .
Bob then uses this solution to drive the response subsystem and reconstruct the other chaotic solutions and .
Alice uses her other two chaotic solutions to mask the intended message and transmits it to Bob.
Bob, using his reproduced chaotic solutions, decodes the message and can then read the intended message.
During the establishment of the raw key, Alice and Bob first must find a reasonable number of photons to share. To do this Alice must know how long the modulated message she intends to send is, and from this she can determine how long the chaotic signal must be. Once this is known Alice then converts one of the solutions to a binary value. During the simulations in this paper, 32 bits where used for each this means that the established key must be at least the . Since on average half of the photons are rejected due to incorrect basis selection the number of photons shared must be over twice the length of the binary message. Only in the case of no noise and no eavesdropper in the channel would this be enough photons to establish a key long enough to encode the message. When there is noise and an eavesdropper, key reconciliation must be performed. During this process, the keys are broken up into blocks of equal length. In order to do this, key bits have to be removed from the keys during the reconciliation. This means that an additional arbitrary number of photons can be added to ensure the key is long enough.
Once the key reconciliation process is done Alice can now send her information over the classical channel. The first bit of information sent during the process is the encoded chaotic signal
, where a simple digital frequency modulation is used to send the information. Upon reception Bob then can construct his synchronized chaotic solutions. With the chaotic solutions established at both the transmitter and receiver the intended information can then be sent over the classical channel. To encode the signal the chaotic solutions are not used to modulate the information, but instead is just used as mask as described by [
20]. In order to ensure the chaotic mask is much larger than the message, the solutions are multiplied by a fixed amount of 10,000. This multiplication of the solution must be done at both transmitter and receiver, meaning the two must establish this before or during the communication. To ensure security of the protocol, the best recourse for the two is to have this as a preshared resource. When having this as a preshared resource it means the eavesdropper is not able to determine the magnitude they must subtract away from the solution. Although this need not be a requirement, and in the simulations provided the multiplicative factor was known to all parties. From the simulation results it was seen that this information could be sent during the communication without loss of secrecy.
3. Chaotic Synchronization
Chaos is a very interesting subject, and its sensitivity to initial conditions hampers the predictability of many models. The system described by (1) does not always provide chaotic solutions, and instead can exhibit solutions that converge to an attractor. With the correct set of parameters, these attractors can be turned into what are known as strange attractors. These types of attractors are characteristic of chaotic systems and have strange characteristics such as fractal dimensions, also known as having non-integer dimensionality. Where a typical measure of the dimensionality is done using the Hausdorff–Besicovitch dimensionality [
21]. To compute this directly is not an easy task, consiquently a method known as the box counting method has been employed where a grid is generated and through a long time series simulation the points in each box is counted. The number of dimensions is then,
where
is the as size of the grid cells and
N is the number of cells covered by the fractal.
; then
[
22], which allows for an estimation on the dimensionality of a system, in the case of the Lorenz system
[
23].
Although these strange attractors and there propensity to have non-integer dimension are characteristic of chaotic systems, the most well known aspect of a chaotic system is its sensitivity to initial conditions. To examine this property, we can look at how the solutions diverge using a Jacobian analysis. The Jacobian of (1) is described by the following matrix.
where the parameters are
. If the eigenvalue problem is solved using these parameters we get the following cubic equation.
Using the assigned parameters the following are the resulting Lyapunov exponents:
. Systems like this only need one of the Lyapunov exponents to be positive in order to exhibit chaotic solutions. Consequently, since two of the values are
, a chaotic solution can be realized. To show this, two systems were run using the parameters described above and the following initial conditions
and
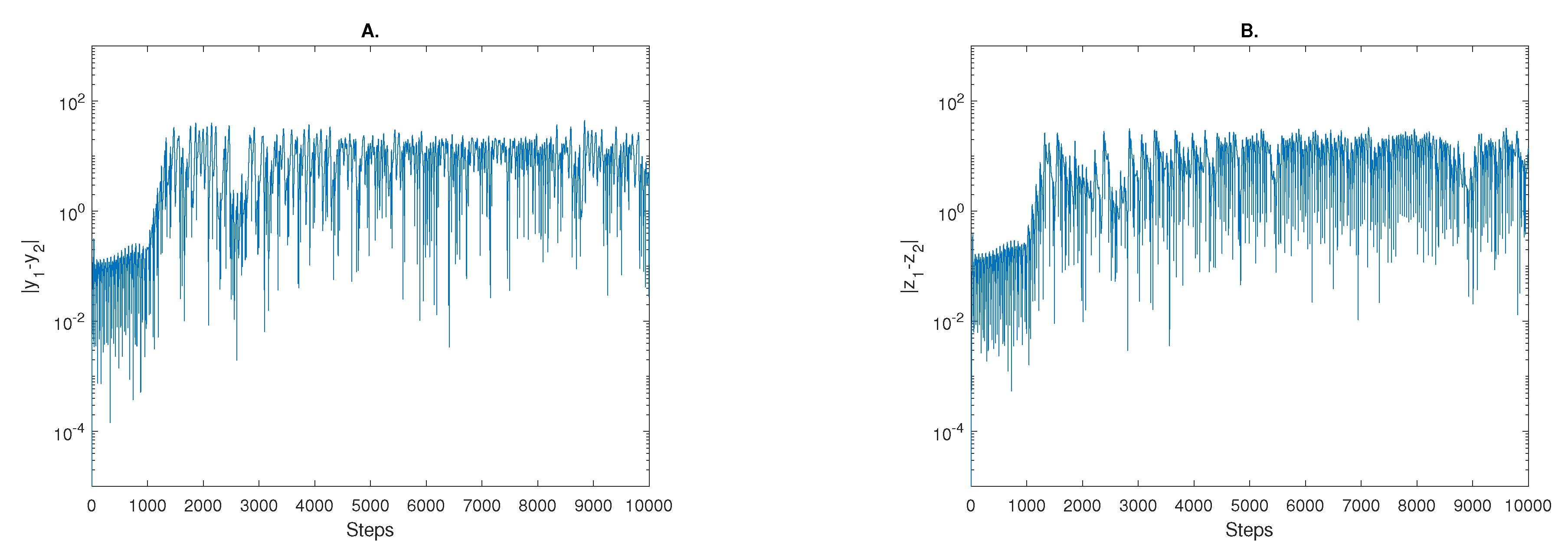
. To show how these two systems diverge the difference
and
are plotted in
Figure 2.
From
Figure 2, it is evident that the two systems start out close to each other, but as time progresses the difference grows until it seems to reach a saturation value. The saturation of the difference is due to the finite region spanned by the solutions, consequently this means that the solutions can only have a certain maximum distance and do not grow without bound. This property comes about from the dissipation that is built into the system. Considering this another way, if a general system is examined we have
. If a surface at
is described with volume
, where the points on S describe initial conditions for trajectories. Here they are allowed to transform over some time
then we get the surface
and volume
. The question is then what is this new volume, and since
is the velocity of the points then
denotes the outward normal component of the velocity. This means that in a time span
a infinitesimal area element
sweeps out a volume
. This means the new volume is described as follows.
If the expression is then rearranged a description of the time evolution of the volume can be realized.
Through the exploitation of the divergence theorem, the dynamics of the volume can be described as follows.
Using the Lorenz system as the components of
the divergence of the system is described as
. This also simplifies the differential equation for the volume to the simple form
. This equation is easily solved to obtain the time evolution of the volume as
. Which shows that the volume of the system does not exponentially grow, but instead contracts to the fixed points. In the chaotic region these equations converge to the strange attractors, which due to their fractal structure cause the solutions to not converge to a single point.
To realize the chaotic synchronization a solution is generated for the for the first system, then one of these solutions is used to drive a second subsystem containing the other two equations from the set [
14]. An example of this is if we take
and use it to drive the following system.
In order to predict if synchronization will occur for this subsystem, the eigenvalues of the Jacobian of the system is examined. With the parameters described above we find the Lyapunov exponents to be
and
. With these both being negative, it means the difference between the two solutions will exponentially converge as
. Therefore, if we supply the solution
we get the output
and
. If the difference between the drive system and the response is plotted versus time, then we get the results shown in
Figure 3.
From
Figure 3 it is seen that as time progresses the difference between the two systems exponentially decreases. The saturation in
Figure 3 is not due to the finite space spanned by the system, but instead comes about due to the decimal precision of Matlab, where differences can only be defined to be so small. Although synchronization has been shown, its applicability in the proposed scheme has not been fully proven. During the communication the elements of
are converted into binary numbers, but during this conversion only a specified amount of bits are used to store the information. Consequently, the fewer bits that are used to represent each element the greater the difference between the values of
and
recovered by Bob. In light of this, it is desirable to look at how synchronization is affected as the difference between the elements of the sets
and
grows.
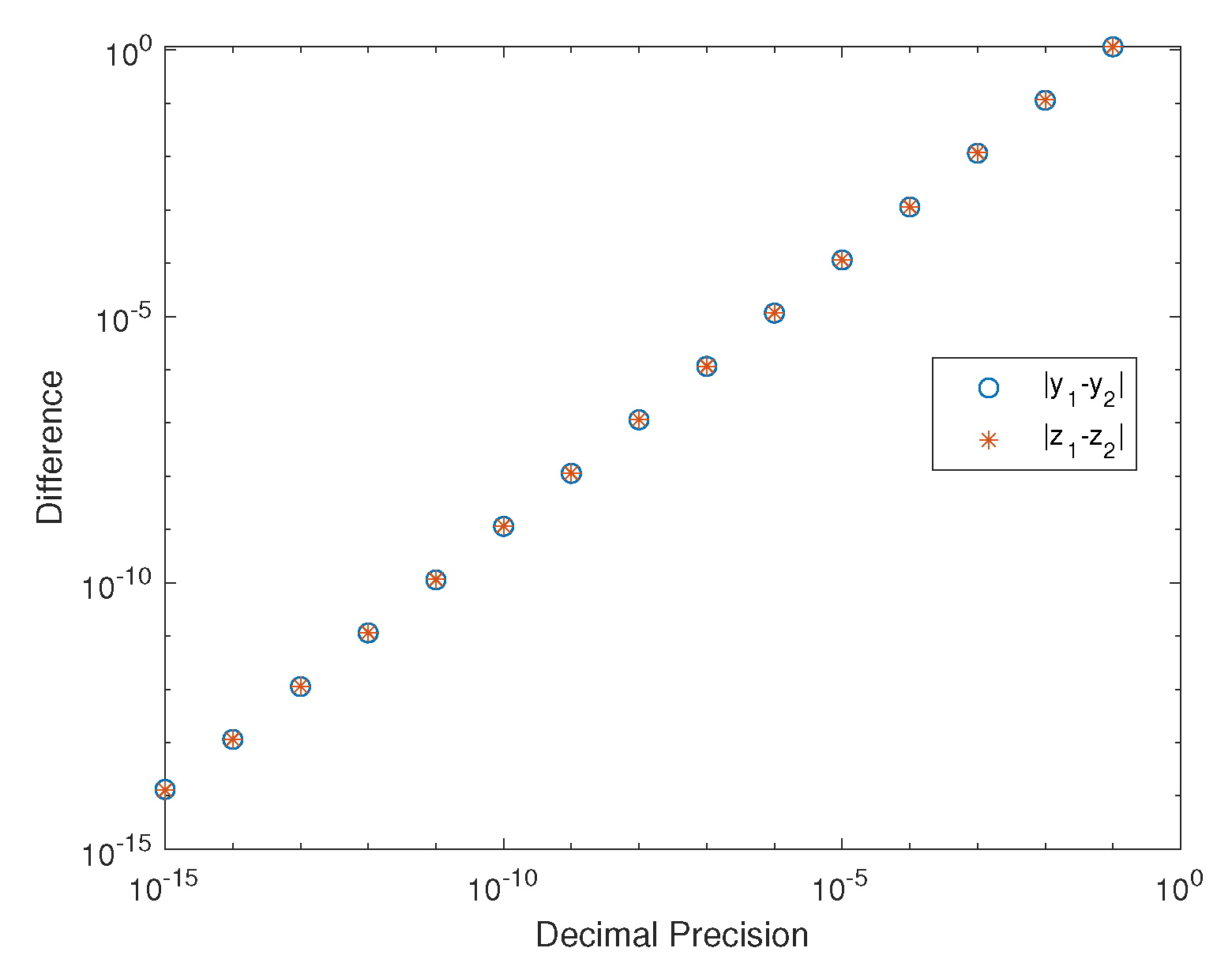
Figure 4 represents the average difference after convergence verses the accuracy of the number of decimal points.
During the conversion of floating point numbers, they are normally converted into 32 or 64 bits (single or double precision) and can be more based on the requirements. Using the formula
, where A is the number of bits used for the decimal precision, the decimal point precision of a number can be determined. For single precision we obtain 7.2 digits and 15.9 for double precision. From
Figure 4 it can be seen that if the decimal precision is 7 digits, it allows for a synchronization up to
. Where this form of synchronization is enough to ensure the message can be decoded by the receiver. Thus, by using single precision the number of bits needed is cut in half compared to double precision and still achieve a useful convergence of solutions.
4. Protocol Application
The proposed protocol gives an advantage over ordinary QKD by requiring Eve to have more information than she has access to. Therefore, when examining the validity of the protocol it is advantageous to look at the downside of encryption using just QKD. As mentioned previously the error percentage in Eve’s key is bounded below by an intrinsic 12.5% error, and if this is realized it is interesting what a communication would look like to the parties. Therefore, if we allow for a communication using ordinary QKD and key reconciliation we get the results shown in
Figure 5.
Examining
Figure 5 it can be easily seen that Eve has gained a significant amount of information during the transmission. As mentioned previously during the measurement process Eve has access to 50% of the key, then another 25% from guessing the bit value of the photons measured in the wrong basis. The last bit of information is gained by Eve during the key reconciliation using the CASCADE like protocol. In order to better understand how the CASCADE like protocol works
Figure 6 represents how error correction is performed. Firstly the key is split up into blocks of bits, where the block length is specified by the empirical formula
[
18,
19,
24], where
e is the error between the two keys. Once the key is split up like this the parity of each block is calculated. Bob then classically communicates to Alice the parity of each of his blocks. For the blocks where the parities disagree the two know there is at least one error in the block. For each block that does not agree the two split the corresponding blocks in half and communicate the parity of both halves. The two continue this until two bits are remaining, and a determination of the error source has been resolved. The protocol then moves on to the next block of bits and performs the same correction on this block. Once each block with disagreeing parities has been acted upon the block size is then doubled and the key is permuted and is run through again with each disagreeing block. The protocol is repeated until a desired error rate is achieved.
Since all communication of parity are done through the classical channel, Eve has full access to all the information being sent. During this process is when the last 12.5% of the key is revealed to Eve. During the error correction Alice and Bob share the bit value of all their errors meaning Eve can also correct these errors in her key. Why then, does Eve not have full access to the key? This is due to the process of measurement during QKD, specifically when Eve has measured a photon in the incorrect basis. As stated previously, when the measurement is performed in the incorrect basis the information is destroyed and the state collapses with equal probability into one of the two orthogonal states. Since the information was destroyed, the best Eve can do is to guess the bit value associated with the states she measured in the incorrect basis. She knows which photons she measured incorrectly through the classical communication of basis agreement between Alice and Bob. Since Eve has an equal probability of guessing the bit value correctly, she then has access to a full 75% of the key outright. After Eve measures a photon, she then transmits a photon in the same state and basis that she used in the measurement. As a result of this when a photon is measured in the wrong basis, it is also sent to Bob in the incorrect basis. This leads to three possibilities, the first being Bob and Alice’s basis disagree and the photon is rejected as a key bit. The other two possibilities are where things become interesting though. They correspond to when Bob measures in the same state as Alice. Since Eve has measured and transmitted to Bob in the other basis, when Bob goes to make his measurement his photon collapses with equal probability into either of the two orthogonal states. Thus, either the photon collapses into the state Alice initially prepared or it collapses into the orthogonal state. When it collapses incorrectly an error is produced in the key, which is then corrected in the reconciliation protocol. Since these bits are corrected Eve gains full knowledge of each one. On the other hand, when the state collapses correctly Bob and Alice do not have an error associated with this bit since the states sent and measured are the same. This means that during the key reconciliation no information about these bits are leaked to Eve. This means that during the whole communication Eve does not have access to these bits. To quantify this intrinsic error, we now look at the 25% of the key where Eve guesses the bit value incorrectly. These bits are associated with photons measured in the wrong basis, and which in this portion half collapse into the correct state and the other half into the incorrect state. Since key reconciliation only occurs on the half that collapsed incorrectly the other half is inaccessible, meaning Eve has an intrinsic 12.5% error that she ca not improve on.
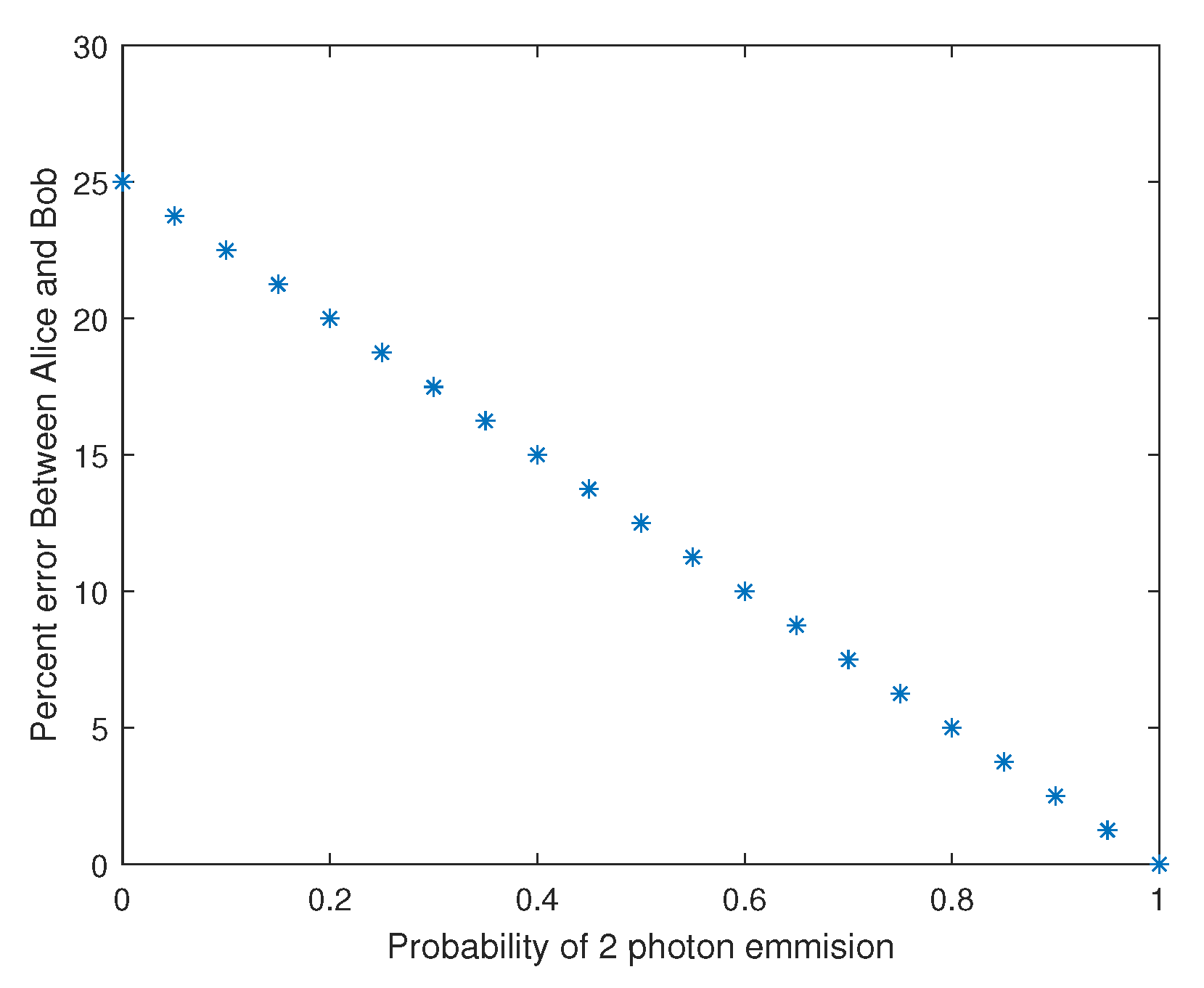
The other problem faced by the QKD is the double-photon emission. If the probability of a double-photon emission goes up the ability for Alice and Bob to tell if there is an eavesdropper goes down since Eve is not measuring the photon received by Bob.
Figure 7 represents how Alice and Bob’s error percentage goes down as the probability of double-photon emission goes up. This shows that only when there is no double-photon emissions that the error rate is above the cutoff rate. Although due to the presence of noise in the quantum channel, the error rate will go up meaning it would be possible to reject some communications where the probability of a double-photon emission is nonzero.
Although the double-photon emission allows for Eve to mask her presence in the channel, it does not allow her to gain the maximum amount of information. During the measurement process Eve does not produce as many errors in the key, meaning there is less information she has access to in the key reconciliation protocol. This is because when she measures the photon in the wrong basis no error is produced in Bob’s key when there was a double-photon emission. Since Eve only obtains information on photons that collapsed incorrectly she consequently will not gain any information on photons she measured in the wrong basis and that were members of a double emission pair. To illustrate this
Figure 8 shows how Eves error percentage changes through the reconciliation as the probability of a double-photon emission goes up. From this it can be seen that only when there are no double-photon emission is Eve able to obtain a maximum amount of information. Compounding this all, it means that ordinary QKD is not secure due the limitations brought on by the components used. This is where the masking from the chaotic synchronization can be utilized.
The ability for Eve to read a message with only a 12.5% error and the drawback of not being able to detect an eavesdropper when the probability of double-photon emissions is nonzero are the motivation for the proposed protocol. It will then be shown that with the maximum amount of information Eve will not be able to read the message. This is due to the sensitivity of the chaotic synchronization to the drive solution. Specifically, if we look at the generation of Eve’s chaotic system
Figure 9 shows that the graph resembles that of
Figure 2 instead of
Figure 3.
When examining the plots, it can be seen that the intrinsic error associated with Eve’s key does not allow for the chaotic systems to synchronize. This is also assuming that Eve has the parameters used in the communication. The plots also show that the parameters can be sent though a classical channel and still provide security since no information of the initial conditions of the system are relayed between Alice and Bob. The reason this is not done is that during chaotic synchronization the values of the initial conditions of the two systems can be arbitrarily far apart and still provide a synchronized system. This means that even with the knowledge of the parameters used Eve would not be able to select a set of initial conditions that allow for the replication of the system without the drive signal. To further prove the advantage of the chaotic QKD the communication is performed where Eve has the same information available to her as she did during the ordinary QKD communication.
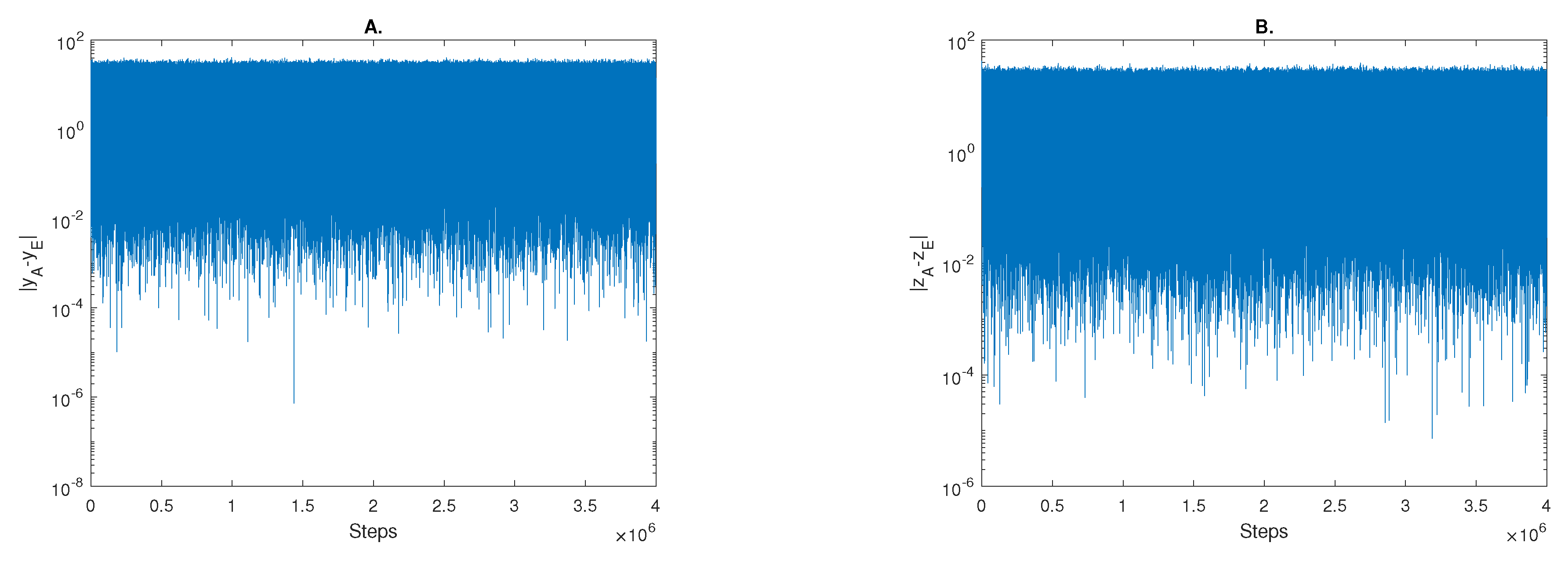
Figure 10 gives the results of the communication. From this it is evident that Eve does not have enough information of the chaotic system to decrypt the mask, while Bob is able to read the message faithfully. Meaning that chaotic communications can bridge the gaps of ordinary QKD by not requiring a true single photon source and allows for secure encryption even when a significant portion of the key is known by Eve.
Although chaotic QKD has been shown to be an improvement over the BB84 protocol, its advantage over other chaotic cryptography schemes has not been discussed. One of the major problems with chaotic cryptography is that it is vulnerable to dependencies in the dynamic system [
25]. This in-part comes from the parameter selection in the dynamic equations [
26]. Since not all parameters available lead to chaotic solutions an incorrect parameter selection can lead to a loss of security in the system. Only those parameters that lead to a positive Lyapunov exponent provides security. Consequently there are regions such that there are correlations that can be determined in the chaotic mask leaving the system vulnerable. The proposed chaotic QKD overcomes this by linking the chaotic solution to the quantum states of photons. This is done by linking the measurement of a photon to a bit associated with the chaotic solution. Therefore, requiring a correct measurement of the photon in order to receive the correct bit. As stated previously since the knowledge of the photon states is restricted by Eve’s measurements, a third party can not reproduce the chaotic solutions needed to decrypt the message.
5. Conclusions
As stated previously, the security of ordinary QKD protocols relies on the assumption that the photon sources produce strictly single photons. Due to the use of attenuated lasers the source becomes probabilistic in the number of photons emitted, which consequently means there is a nonzero probability for double-photon emissions. When these types of emissions are present, it reduces the ability for Alice and Bob to actively monitor the channel, meaning Eve can hide her presence and gain 75% of the key even before the key reconciliation. Although it was shown that during the reconciliation process double-photon emissions negatively affect the ability of Eve to gain her maximum available information, it was also shown that with this maximum amount of information during a classical QKD communication the information is not secure from being read. Compounding that, it has been shown that ordinary QKD does not provide a reliably secure form of communication. As a result, the proposed chaotic QKD protocol was developed in order to combat the drawbacks of ordinary QKD.
Chaotic QKD has an advantage over other QKD protocols by requiring the knowledge of the key to be beyond the limit accessible to Eve. It was shown that there was a maximum limit to the knowledge accessible to Eve; this came about due to quantum superposition and due the fact that a state vector can be written as a linear combination of states from different bases. Due to that, when an eavesdropper measures the channel, they unavoidably cause an intrinsic amount of error due to the measurement of states in the wrong basis. When this happens and the state collapses correctly after Bob’s measurement, it causes Eve to have to guess the bit value associated with the photon. Since there is an equal probability of it being either value, half of these bits will never be known to Eve when she guesses wrong. The exploitation of this information has made it possible to validate the proposed protocol, since it has been shown that giving Eve the maximum amount of information still does not allow her to decode the message.
The physical implementation of the communication protocol is an important steppingstone for the verification of a communications scheme. In future works the testing of this communication protocol will be performed, wherein an analysis of the physical drawbacks to the communication scheme will be examined. This will include the analysis of the uncertainty of state preparation, leading to further errors in the key. An analysis of the effects of noise in the quantum and classical channel will be examined, as will its ability to communicate over longer distances.