1. Introduction
The rise of communication technologies has formed multiple smart electronic devices (e.g., cell phones, sensors, wearables) with network connection, which produce a big amount of data every day. Remote, often untrusted, cloud servers are employed to store and process these data to be used by third parties, such as research institutions, hospitals, or electricity companies. Many applications (e.g., environmental monitoring, updating parameters in machine learning, statistics about electricity consumption) require joint computations on data coming from multiple clients. For example, using smart metering, data that are collected from sensors/clients can be used to compute statistics for the electricity consumption, while environmental sensors collect data that can be used to measure emissions and data collected from mobile phones can be aggregated and processed to appropriately update parameters in machine learning models for accurate user profiling.
Although decentralization has been a recent trend, we have witnessed a steady rise of massively distributed but not decentralized systems. When multiple clients outsource a joint computation using their joint inputs, multiple servers can be employed in order to avoid single points of failure and perform a reliable joint computations on the clients’ inputs. Although this distributed cloud-assisted environment is very appealing and offers exceptional advantages, it is also followed by serious security and privacy challenges. Thus, in this work, we present the formal and practical analysis of verifiable additive homomorphic secret sharing (VAHSS), a novel cryptographic primitive introduced [
1], which allows for multiple clients to outsource the joint addition of their inputs to multiple untrusted servers, providing guarantees that the clients’ inputs remain secret as well as that the computed result is correct (i.e., verifiability property). More precisely, this paper is an extended version of the preliminary article [
1].
We address the problem of cloud-assisted computing characterized by the following constraints: (i) multiple servers are recruited to perform joint additions on the inputs of
n clients; (ii) the inputs of the clients need to remain secret; (iii) the servers are untrusted; (iv) no communication between the clients is possible; and, (v) anyone should be able to confirm that the computed result is correct (i.e., public verifiability property). More precisely, let us consider
n clients (as illustrated in
Figure 1), which hold
n individual secret inputs
, and they want to deploy the joint computation of the function
on their joint inputs by releasing shares of their inputs to multiple untrusted servers (the latter denoted by
for
). We denote the share of a client
given to the server
by
. Tsaloli et al. [
2] addressed the problem of computing the joint multiplications of
n inputs corresponding to
n clients and introduced the concept of verifiable homomorphic secret sharing (VHSS). More precisely, VHSS allows to jointly perform the computation of a function
, including no communication between the clients, and allowing anyone to get a proof
that the computed result is correct, i.e., providing to anyone a pair (
y,
) which confirms the correctness of
y (i.e., public verification). However, the possibility to achieve verifiable homomorphic secret sharing for other functions (e.g., addition) has been left open.
In this paper, we revisit the concept of verifiable homomorphic secret sharing (VHSS) and we explore the possibility to achieve verifiable additive homomorphic secret sharing. Our research shows that the latter is possible and we propose three concrete constructions that employ
m servers to jointly compute the additions of
n clients’ inputs securely and privately, while, additionally, ensuring public verifiability. The proposed constructions can be utilized, for example, to compute statistics over electricity consumption when data are collected from multiple clients, in order to remotely monitor and determine a diagnosis for multiple patients according to their collected data, as well as to measure environmental conditions while using multiple sensors’ data that come from environmental sensors (e.g., temperature, humidity). We have substantially extended the preliminary article [
1] and added a detailed evaluation (both theoretical and experimental) of the three proposed VAHSS constructions. In the submitted paper, we present a detailed analysis for each of the constructions based on different conditions, providing both theoretical and experimental results.
Our Contribution. We address the problem of computing joint additions with privacy and security guarantees as the main requirements. More precisely, we treat the problem of verifiable multi-client aggregation that involves the following parties: (i) n clients, which hold secret inputs , respectively; (ii) m untrusted servers to whom the sum computation is outsourced; and, (iii) any verifier that would like to confirm that the computed sum is correct. We present, for the first time, three concrete constructions of verifiable additive homomorphic secret sharing (VAHSS).
We employ three different primitives (i.e., homomorphic hash functions, linearly homomorphic signatures, and threshold signatures) as the baseline for the generation of partial proofs (values that are used to confirm the correctness of the computed sum). The partial proofs are computed by either the servers or the clients. These characteristics lead to three different instantiations of VAHSS. Additionally, we have altered the original VHSS definition to capture the different scenarios on the proofs’ generation; therefore, allowing for the employment of VHSS in several application settings.
Our constructions rely on casting Shamir’s secret sharing scheme over a finite field
as an
n-client,
m-server, and
t-perfectly secure additive homomorphic secret sharing (HSS) for the function that sums
n field elements. Firstly, employing homomorphic collision-resistant hash functions [
3,
4] and incorporating them to the additive HSS, we design a construction, such that each server produces a partial proof. Next, a linearly homomorphic signature scheme [
5] is combined with the additive HSS, which results in an instantiation where each client generates a partial proof. Ultimately, the employment of a threshold RSA signature scheme [
6] in additive HSS allows a subset of servers to generate partial proofs that correspond to each client. In all three proposed constructions, we have provided detailed correctness, security, and verifiability analysis. Furthermore, we provide an evaluation of the three proposed constructions, in which we describe the cost of the required operations for each of the employed algorithms as well as present a detailed experimental evaluation. More precisely, we evaluate the performance of all three proposed VAHSS constructions and compare and illustrate how the employed algorithms perform, depending on the amount of the clients that participate during the computation and the required computation time for the verification process.
Organization.Section 2 gives an overview about the current state-of-the-art in homomorphic secret sharing and verifiable computation. Later,
Section 3 provides the background on verifiable homomorphic secret sharing and definitions that are necessary for the rest of the paper. We provide our VHSS constructions in
Section 4. Furthermore, in
Section 5 we give a theoretical analysis of the costs for the constructions and provide details of our implementation results. We present a discussion about the constructions and their costs in
Section 6. Finally, we provide our final considerations in
Section 7.
2. Related Work
Homomorphic Secret Sharing. The key idea of threshold secret sharing schemes [
7] is the ability to split a secret
x into multiple shares (denoted by, for example,
) while maintaining the following properties: (i) any subset greater than the threshold number of shares is enough to reconstruct the secret
x, and (ii) any smaller subset allows no inference of information related to the secret
x. Homomorphic secret sharing (HSS) [
8] can be seen as the secret-sharing analog of homomorphic encryption. In particular, HSS is employed in order to locally evaluate functions on shares of secret inputs (or just one input), by appropriately combining locally computed values with the shares of the secret(s) as input. At the same time, an HSS system ensures that the shares of the output are short. The first instance of additive HSS that is considered in the literature [
9] is computed in some finite Abelian group. Nevertheless, HSS gives no guarantee that the computed result is correct i.e., no verifiability is provided.
Verifiable Function Secret Sharing. To better realize function secret sharing (FSS) [
10], one can consider it as a natural extension of distributed point functions (DPF). More precisely, FSS is a method to create shares for a function
f, coming from a given function family
, that are additively combined to give
f. To visualize this, consider
m functions
, as described by the corresponding keys
. These functions are the shares of
f, such that
, for any input
x. The notion of verifiable FSS (VFSS) [
11] is introduced by Boyle et al. In particular, VFSS consists of interactive protocols that verify the consistency of some function
with keys
, which are generated by a potentially malicious user. However, VFSS [
11] is applicable in the setting of multiple servers and one client. On the contrary, VHSS can be applied when multiple clients (multi-input) outsource the joint computation to multiple servers. Moreover, in VFSS, verification refers to confirming that the shares
are consistent with some
f; while, in VHSS, the goal of the verification is to ensure that the final result is correct.
Publicly Auditable Secure Multi-party Computation. Secure multi-party computation (MPC) protocols are linked with outsourced computations. In MPC protocols [
12,
13,
14], non-interactive zero-knowledge (NIZK) proofs are generally used in order to achieve public verifiability. Baum et al. [
15] introduced the notion of
publicly auditable MPC protocols that are applicable when multiple clients and servers are involved. Given that publicly auditable MPC is based on the SPDZ protocol [
12,
13] and NIZK proofs, while it also employs Pedersen commitments (for enhancing each shared input
x), it can be viewed as a generalization of the classic formalization of secure function evaluation. In the work of Baum et al. [
15], anyone that has access to the published (in a bulletin board) transcript of the protocol can confirm that the computed result is correct (correctness property); while, the protocol provides privacy guarantees and requires at least one honest party. We should note that publicly auditable MPC protocols are very expressive regarding the class of functions being computed, but they often require heavy computations. To formalize auditable MPC, an extra non-corruptible party is introduced in the standard MPC model, namely the auditor. On the other hand, in VAHSS, we do not require any additional non-corruptible party as well as we do not employ expensive cryptographic primitives, such as NIZK proofs.
3. Preliminaries
Our concrete instantiations for the additive VHSS problem are based on the VHSS definition that was proposed in [
2]. However, we propose a slightly modified version of the VHSS definition to capture cases when partial proofs (used to verify the correctness of the final result) are computed either from the clients or the servers, which is reflected later in our instantiations. More precisely, depending on the construction, the execution of the
PartialProof algorithm is performed by either the clients or the servers. We added the
algorithm to allow for the generation of keys and we modified the
algorithm accordingly to allow the different scenarios.
Definition 1 (Verifiable Homomorphic Secret Sharing (VHSS)).
An n-client, m-server, t-secure verifiable homomorphic secret sharing scheme for a function, is a seven-tuple of PPT algorithms (Setup, ShareSecret, PartialEval, PartialProof, FinalEval, FinalProof, Verify), which are defined as follows:
Setup(): On input , where λ is the security parameter, a secret key , to be used by a client, and some public parameters .
ShareSecret(): The algorithm takes as input , which is the index for the client and which denotes a vector of one (i.e., ) or more secret values that belong to each client and should be split into shares. The algorithm outputs m shares (denoted also by when ) for each server , as well as, if necessary, a publicly available value (, when computed, can be included in the list of public parameters ) related to the secret .
PartialEval(): On input , which denotes the index of the server , and , which are the shares of the n secret inputs that the server has, the algorithm PartialEvaloutputs .
PartialProof(): on input, the secret key , public parameters , secret values (based on which the partial proofs are generated), denoted by ; and, the corresponding index k (where k is either i or j), a partial proof is computed. Note that k is a variable; thus, when PartialProof generates proofs per client or if it generates proofs per server.
FinalEval: On input , which are the shares of that the m servers compute, the algorithmFinalEvaloutputs y, the final result for .
FinalProof(): on input public parameters and the partial proofs , the algorithmFinalProofoutputs σ, which is the proof that y is the correct value. Note that , if the partial proofs are computed per client or , if they are computed per server.
Verify(): On input the final result y, the proof σ, and, when needed, public parameters , the algorithmVerifyoutputs either 0 or 1.
Correctness, Security, Verifiability. The algorithms (Setup, ShareSecret, PartialEval, PartialProof, FinalEval, FinalProof, and Verify) should satisfy the following correctness, verifiability, and security requirements:
Correctness: for any secret input
, for all
m-tuples in the set
coming from
, for all
computed by
,
computed from
, and for
y and
generated by
and
, respectively, the scheme should satisfy the following correctness requirement:
Verifiability: let T be the set of corrupted servers with (note that, for , the verifiabililty property holds; however, we do not have a secure system). Denote, by , any PPT adversary and consider n secret inputs . Any PPT adversary who controls the shares of the secret inputs for any j, such that can cause a wrong value to be accepted as with negligible probability.
We define the following experiment
- 1.
For all , generate ShareSecret() and publish .
- 2.
For all j, such that , give to the adversary.
- 3.
For the corrupted servers , the adversary outputs modified shares and . Subsequently, for j, such that , we set - and Note that we consider modified only when computed by the servers.
- 4.
Compute the modified final value and the modified final proof .
- 5.
If and , then output 1 else 0.
We require that for any
n secret inputs
, any set
T of corrupted servers and any PPT adversary
it holds:
Security: let T be the set of the corrupted servers with . Consider the following semantic security challenge experiment:
- 1.
The adversary gives to the challenger, where , and .
- 2.
The challenger picks a bit uniformly at random and computes where the secret input .
- 3.
Given the shares from the corrupted servers T and , the adversary distinguisher outputs a guess .
Let be the advantage of in guessing b in the above experiment, where the probability is taken over the randomness of the challenger and of . A VHSS scheme is t-secure if, for all with , and all PPT adversaries , it holds that for some negligible .
In our solution, we employ a simple variant of the (Strong) RSA based signature that was introduced by Catalano et al. [
16], which can be seen as a linearly homomorphic signature scheme on
.
Definition 2 (Linearly Homomorphic Signature [
5]).
A linearly homomorphic signature scheme is a tuple of PPT algorithms defined, as follows: takes as input the security parameter λ and an upper bound k for the number of messages that can be signed in each dataset. It outputs a secret signing key and a public key . The public key defines a message space , a signature space , and a set of admissible linear functions, such that any is linear.
algorithm takes as input the secret key , a dataset identifier , and the i-th message to be signed, and outputs a signature .
algorithm takes as input the verification key , a dataset identifier , a message m, a signature σ and a function f. It outputs either 1 if the signature corresponds to the message m or 0 otherwise.
algorithm takes as input the verification key , a dataset identifier , a function , and a tuple of signatures . It outputs a new signature σ.
We use homomorphic hash functions in order to achieve verifiability. Below, we provide the definition of such a function. More precisely, we employ a homomorphic hash function satisfying additive homomorphism [
4].
Definition 3 (Homomorphic Hash Function [
3]).
A homomorphic hash function , where is a finite field and is a multiplicative group of prime order q, is defined as a collision-resistant hash function that satisfies the homomorphism in addition to the properties of a universal hash function .- 1.
One-way: it is computationally hard to compute .
- 2.
Collision-free: it is computationally hard to find , such that .
- 3.
Homomorphism: for any , it holds , where is either or .
For completeness, we also provide the definition of a secure pseudorandom function PRF.
Definition 4 (Pseudorandom Function (PRF))
. Let S be a distribution over and be a family of functions indexed by strings s in the support of S. We say that is a pseudorandom function family if, for every PPT adversary D, there exists a negligible function ϵ, such that:where s is distributed according to S and R is a function sampled uniformly at random from the set of all functions from to . 4. Verifiable Additive Homomorphic Secret Sharing
In this section, we present three different instantiations to achieve verifiable additive homomorphic secret sharing (VAHSS). More precisely, we consider n clients with their secret values respectively, and m servers that perform computations on shares of these secret values. Firstly, the clients split their secret values into shares, which reveal nothing about the secret value itself and, then, they distribute the shares to each of the m servers. Each server performs some calculations in order to publish a value, which is related to the final result . Subsequently, partial proofs are generated in a different way, depending on the instantiation proposed. The partial proofs are values, such that their combination results in a final proof, which confirms the correctness of the final computed value . Note that, for all of the proposed constructions, the clients do not need to communicate with each other, which often is the case in settings where the clients are wireless devices spread in different regions and are not in the communication range of each other (e.g., sensors measuring electricity consumption or environmental conditions). However, the clients could potentially collude with some of the servers, without compromising the security of our constructions as long as at least two clients remain honest.
4.1. Construction of VAHSS Using Homomorphic Hash Functions
In this section, we aim to compute the function value
y, which corresponds to
as well as a proof
that
y is correct. We combine an additive HSS for the algorithms that are related to the value
y and hash functions for the generation of the proof
. Let
denote
n clients and
their corresponding secret inputs. Let, for any
,
be distinct non-zero field elements and
be field elements (“Lagrange coefficients"), such that, for any univariate polynomial
of degree
t over a finite field
, we have:
Each client
generates shares of the secret
, denoted by
, respectively, and gives the share
to each server
. The servers, in turn, compute a partial sum, denoted by
, and publish it. Anyone can then compute
, which corresponds to the function value
y =
. We suggest that every client
uses a homomorphic collision-resistant function
proposed by Krohn et al. [
4] to generate a public value
, which reveals nothing about
(under the discrete logarithm assumption). Afterwards, the servers compute values
, which will be appropriately combined so that they give the proof
that we are interested in. The value
y comes from the combination of partial values
, which are computed by the
m servers. More precisely, our solution is composed of the following algorithms:
- 1.
ShareSecret(
): for elements
selected uniformly at random, pick a
t-degree polynomial
of the form
. Notice that the free coefficient of
is the secret input
. Let
(with
g a generator of the multiplicative group of
) be a collision-resistant homomorphic hash function [
3]. Let
be the output of a pseudorandom function (PRF)
where
for a key
given to the clients and a timestamp
associated with client
i such that
. For
, we require
. Subsequently, compute
, define
(given thanks to the Equation (
1)) and output
).
- 2.
PartialEval (): given the j-th shares of the secret inputs, compute the sum of all for the given j and . Output with .
- 3.
PartialProof(): given the j-th shares of the secret inputs, compute and output the partial proof .
- 4.
FinalEval(): add the partial sums together and output y (where ).
- 5.
FinalProof(): given the partial proofs , compute the final proof . Output .
- 6.
Verify(): check whether holds. Output 1 if the check is satisfied or 0 otherwise.
Each client runs the
algorithm to compute and distribute the shares of
to each of the
m servers and a public value
, which is needed for the verification. Subsequently, each server
has the shares given from the
n clients and runs the
algorithm to output the public values
related to the final function value. Furthermore, each server runs the
algorithm and it produces the value
. Finally, any user or verifier is able to run the
algorithm to obtain
y and the
algorithm to get the proof
. Lastly,
algorithm ensures that
y and
match and, thus,
is correct.
Table 1 illustrates our construction.
Correctness: In order to prove the correctness of this construction, we need to prove that
By construction it holds that:
Additionally, by construction, we have:
Combining the last two results, we get that holds. Therefore, the algorithm Verify outputs 1 with probability 1.
Security: See [
17] for a proof that the selected hash function
H of our construction is a secure collision-resistant hash function under the discrete logarithm assumption.
We will now prove that for some negligible .
Proof. Game 0: consider corrupted servers. Subsequently, . Without a loss of generality, let the first servers be the corrupted ones. Therefore, the adversary has shares from the corrupted servers and no additional information.
For any fixed
i with
, it holds that
and, hence:
The adversary holds
. Furthermore, the adversary holds the public value
. Because
is the output of a PRF, then
is also a pseudorandom value.
Game 1: consider that the adversary holds the same shares and is now a truly random value.
Firstly, is just a value, which implies nothing to the adversary regarding whether it is related to or . Moreover, Game 0 and Game 1 are computationally indistinguishable due to the security of the PRF. Thus, any PPT adversary has the probability to decide whether is or and so, for some negligible . □
Verifiability: In this construction, for
, if
and
, then the verifiability follows:
which is a contradiction since
and
H is collision-resistant. Therefore,
4.2. Construction of VAHSS with Linear Homomorphic Signatures
Our goal is always to compute
as well as a proof
that
y is correct. We compute
y while using additive HSS and we employ a linearly homomorphic signature scheme, presented in [
5] as a simple variant of Catalano et al. [
16] signature scheme, for the generation of the proof. All of the clients hold the same signing and verification key. This could be the case if the clients are sensors of a company collecting information (e.g., temperature, humidity) that is useful for some calculations. Because the sensors/clients belong to the same company, sharing the same key might be necessary to facilitate configuration. In applications, scenarios where clients should be set up with different keys, a multi-key scheme [
18] could be used. However, in our construction, the clients can use the same signing key to sign their own secret value. In fact, they sign
, where
with
chosen from each client, as described in the
Section 4.1. The signatures, which are denoted by
, are public and, when combined, they form a final signature
, which verifies the correctness of
y. Our instantiation constitutes of the following algorithms:
- 1.
Setup(): let N be the product of two safe primes each one of length . This algorithm chooses two random (safe) primes each one of length , such that with . Subsequently, the algorithm chooses in at random. Subsequently, it chooses some (efficiently computable) injective function with . It outputs the public key to be used by any verifier; and, the secret key to be used for signing the secret values.
- 2.
ShareSecret(
): for elements
selected uniformly at random, pick a
t-degree polynomial
of the form
. Notice that the free coefficient of
is the secret input
. Subsequently, define
(given using the Equation (
1)) and output
.
- 3.
PartialEval(): given the j-th shares of the secret inputs, compute the sum of all for the given j and . Output with .
- 4.
PartialProof(): Parse the verification key to get , and . For the (efficiently computable) injective function H that is chosen from Setup, map to a prime: . We denote the i-th vector of the canonical basis on by . Choose random elements and solve, using the knowledge for and , the equation: , where denotes the j-th coordinate of the vector . Notice that, for our function , the equation becomes . Set . Output , where is the signature for w.r.t. the function .
- 5.
FinalEval(): add the partial sums together and output y (where ).
- 6.
FinalProof(): given the public verification key , the signatures , let . Define , where . Set , and . For , compute . Output where .
- 7.
Verify(): compute . Check that and holds. Output: 1 if all checks are satisfied or 0 otherwise.
All
n clients get the secret key
from
Setup and hold their secret value
, respectively. Each client runs
to split its secret value
into
m shares and
in order to produce the partial signature (for the secret
)
. The values
’s are not generated by the servers, since, in that case, malicious compromised servers would not be detected. Subsequently, each client distributes the shares to each of the
m servers and publishes
. Each server
computes and publishes the partial function value
by running
. Any verifier is able to get the function value
from the
and the proof
from the
. The
algorithm outputs 1 if and only if
.
Table 2 reports an illustration of our solution.
Correctness: To prove the correctness of our construction, we need to prove that
It holds that:
Thanks to the Equation (
2), it also holds that
. Subsequently,
and, thus,
with probability 1.
Security: The security of the signatures easily results from the original signature scheme that was proposed by Catalano et al. [
16]. Moreover,
for some negligible
as we have proven in the
Section 4.1. We should note that, since in this construction no
values are incorporated, the arguments related to the pseudorandomness of
are not necessary.
Verifiability: Verifiability is by construction straightforward since the final signature
is obtained using the correctly computed (by the clients)
and, thus,
in this case. Therefore, if
while
and
, then:
which is a contradiction!
Therefore,
4.3. Construction of VAHSS with Threshold Signature Sharing
We propose a scheme, where the clients generate and distribute shares of their secret values to the
m servers and the servers mutually produce shares of the final value
y similarly to the previous constructions. However, in order to generate the proof
that confirms the correctness of
y, our scheme employs the
-threshold RSA signature scheme proposed in [
6], so that a signature
is successfully generated, even if
servers are corrupted. Our proposed scheme (illustrated in the
Table 3) acts in accordance with the following algorithms:
- 1.
Setup (): Let be the RSA modulus, such that and , where are large primes. Choose the public RSA key , such that and then pick the private RSA key , so that . Output the public key and the private key .
- 2.
ShareSecret(
): for elements
selected uniformly at random, pick a
t-degree polynomial
of the form
. Notice that the free coefficient of
is the secret input
. Subsequently, define
(given thanks to the Equation (
1)). Let
be an
full-rank public matrix with elements from
for a prime
r. Let
be a secret vector from
, where
is the private RSA key and
are randomly chosen. Let
be the entry at the
i-th row and
j-th column of the matrix
. For all
, set
to be the share that is generated from the client
for the server
. It is now formed an
system
. Let
(with
g a generator of the multiplicative group of
) be a collision-resistant homomorphic hash function [
3]. Let
be randomly selected values, as described in the
Section 4.1. Output the public matrix
, the (
’s) shares
, the shares of the private key
, and
.
- 3.
PartialEval(): given the j-th shares of the secret inputs, compute the sum of all for the given j and . Output with .
- 4.
PartialProof(): For all , run the algorithm , where:
: Let
be the coalition of
servers (
) (w.l.o.g. take the first
), forming the system
. Let the
adjugate matrix of
be:
Denote the determinant of
by
. It holds that:
where
stands for the
identity matrix. Compute the partial signature of
:
. Output
.
PartialProof outputs .
- 5.
FinalEval(): add the partial sums together and output y (where ).
- 6.
FinalProof(): for all run the algorithm ) where:
FinalProof outputs .
- 7.
Verify(): check whether holds. Output 1 if the check is satisfied or 0 otherwise.
After the initialization with the , each client gets its public and private RSA keys, and , respectively. Subsequently, each runs to compute and distribute the shares of to each of the m servers, and form a public matrix , shares of the private key and the hash of the secret input and a randomly chosen value, , to be used for the signatures’ generation. is a publicly available value. Subsequently, each server runs to generate public values related to the final function value. A set of a coalition of the servers runs and obtains the partial signatures. For instance, is the vector that contains the partial signatures of , is the vector that contains the partial signatures of and so on. Anyone is able to run to get y and to get , which is the final signature that corresponds to the secret inputs . Finally, the algorithm succeeds if and only if the final value y is correct.
Correctness: to prove the correctness of our construction, we need to prove that
For convenience, here, denote
by
. By construction:
Therefore, with probability 1, as desired.
Security: the security of the signatures follows from the fact that the threshold signature scheme, which is employed in our construction, is secure, for
, under the static adversary model given that the standard RSA signature scheme is secure [
6]. Additionally, for
,
for some negligible
, as we have proven in
Section 4.1. Therefore, our construction is secure for
.
Verifiability: for
and
we have:
which is a contradiction! Thus,
5. Evaluation
In this section, we provide the evaluation of our proposed constructions. First, we perform a theoretical analysis and present the amount of operations required to implement each construction. Next, we provide a detailed experimental evaluation; we describe the experimental setup and provide the required computational time for each of the presented transactions for different conditions, from both the client and the server side.
5.1. Theoretical Analysis
We now present the basic operations that are required in our constructions. Recall that we denote the number of clients by n and the number of servers by m. The threshold for generating shares of the secret clients’ inputs is denoted by t, while the threshold used in the proposed third VAHSS construction i.e., based on threshold signature sharing, for generating shares of the private RSA key, is denoted by . All of the operations are reported per algorithm and, thus, considering the cost for each client or server, respectively. This means that if, for instance, additions correspond to the PartialEval algorithm in the table, this number represents the amount of operations that are required from each server that executes the PartialEval algorithm.
In our constructions, in the
Sharesecret algorithm, each client generates
m shares that are related to its secret inputs. Below, we present in detail how we calculate the cost for the client to compute these
m shares. Each client needs
m polynomial evaluations (denoted by
) as well as the computation of the Lagrange coefficients (denoted by
), as shown in Equation (
1). We consider Horner’s method [
19] to calculate
, which gives
t multiplications and
t additions for a polynomial of degree
t, as in our constructions. Furthermore,
requires 2 multiplications, 1 computation of inverse, and 1 addition (in
) for each factor out of
. One additional multiplication is needed in order to form the right hand side of Equation (
1). Therefore, the cost for generating
m secret shares can be demonstrated, as follows:
This amount of operations is added in the
Sharesecret algorithm costs. Let us now present the tables that summarize the cost of our constructions. In parentheses, we display by whom the algorithm is executed. Whenever not specified, the algorithm can be run from any verifier.
Table 4 illustrates the costs for the VAHSS construction while using homomorphic hash functions (also found as VAHSS-HSS). Observe that there is no
Setup algorithm in this construction.
Table 5 shows the number of operations required in the VAHSS construction while using linear homomorphic signatures (also found as VAHSS-LHS). Finally,
Table 6 gives the costs of the VAHSS construction while using threshold signature sharing (found also as VAHSS-TSS). Observe that the same variables are used to show the theoretical results. However, note that
appears in the VAHSS-TSS construction for the first time, denoting a different number than the threshold
t that is used for generating shares of the secret inputs. Moreover, the algorithms are executed from either a client or server, depending on the construction presented.
Looking at
Table 4,
Table 5 and
Table 6, we observe some differences regarding the costs that are expected in each algorithm. More precisely, we can see that the
ShareSecret algorithm is always run by the clients. In this respect, the VAHSS-HSS and VAHSS-LHS constructions slightly differ, since a client needs to produce some additional public values in the VAHSS-HSS case. The VAHSS-TSS is more expensive, since the client also generates shares of its private RSA key. Furthermore, as we have mentioned, VAHSS-HSS requires no
Setup, thus, it is computationally less expensive than the other two constructions from the client’s side. Subsequently, we can observe that the
PartialEval and
FinalEval algorithms are always run by the servers and are expected to have the same computational cost. The
PartialProof algorithm is run either by the servers or the clients. In the VAHSS-HSS construction, the computation is low and is made by the servers, while, in the VAHSS-LHS, the execution is made by the clients and it is also low-cost. In the VAHSS-TSS solution,
PartialProof is run by a coalition of servers and the cost depends on the amount of the servers that can be considered in the computation. Next,
FinalProof is quite practical in all cases, but it is not particularly comparable since there are several parameters that can affect this cost. Finally, the verification process (
Verify) has the same computational cost for the first and third construction, while it is slightly heavier for the VAHSS-LHS construction.
5.2. Prototype Analysis
In this section, we present our results from the experimental analysis regarding the performance of the three proposed VAHSS constructions. More precisely, we have implemented the following constructions: VAHSS based on homomorphic hash functions (VAHSS-HSS), VAHSS based on linear homomorphic signatures (VAHSS-LHS), and VAHSS based on threshold signature sharing (VAHSS-TSS) and compare them regarding their performance.
In our implementations, we used the programming language “C++” and the GMP Library (
https://gmplib.org/) for handling big numbers and their arithmetic operations. Furthermore, we ran the experiments on Arch Linux Kernel
over a Dell Latitude 5300 with processor Intel i
U CPU @
GHz (micro architecture codename Whisky Lake), with 16 GB RAM, 32KiB L1d cache, 32KiB L1i cache, 256KiB L2 cache, and 6MiB L3 cache. In order to perform a fair comparison, we have selected the following common parameters for all of the implementations: group generator, number of clients, number of servers, and the finite field for the Shamir’s secret sharing.
We have used a benchmarking dataset for the experimental evaluation. More precisely, we have used the individual household electric power consumption dataset by the UC Irvine machine learning repository (
https://archive.ics.uci.edu/ml/datasets/Individual+household+electric+power+consumption#). The values represent electricity consumption provided by smartmeters. We note that, since the values in the dataset are float numbers, we need to preprocess them in order to employ them in our constructions by multiplying all of the input values by 100. Below, we list the required computation cost (in time) for all different algorithms of the proposed constructions.
We test our constructions for 500 clients, 3 servers, and a
-bit prime number for forming the finite field
that is used for the secret inputs’ shares generation. Additionally, the primes that are used for the VAHSS-LHS and VAHSS-TSS constructions are randomly generated primes of 128 bits. The timing is measured and shown in microseconds. The
Sharesecret,
PartialEval, and
PartialProof costs are represented by their median values. For instance, for the
Sharesecret algorithm, each client generates a random polynomial to be used for the shares’ generation and, since we consider 500 clients, we need to take into account their different costs. Thus, we get all of the timings and sort them in order to obtain the 250th element of the list. Similarly, we also obtain the median values for
PartialEval and
PartialProof.
Table 7 illustrates the time in microseconds for 500 clients for the three different constructions.
Our tests were extended to different amounts of clients, ranging between 500 and 1000, while we fixed the number of servers to 3. Moreover, we should note that we ran our experiments for several prime numbers of various sizes and no significant change was noticed; therefore, these results are omitted. Below, we provide the results for the algorithms, which performed noticeably different for different parameters, as illustrated by figures.
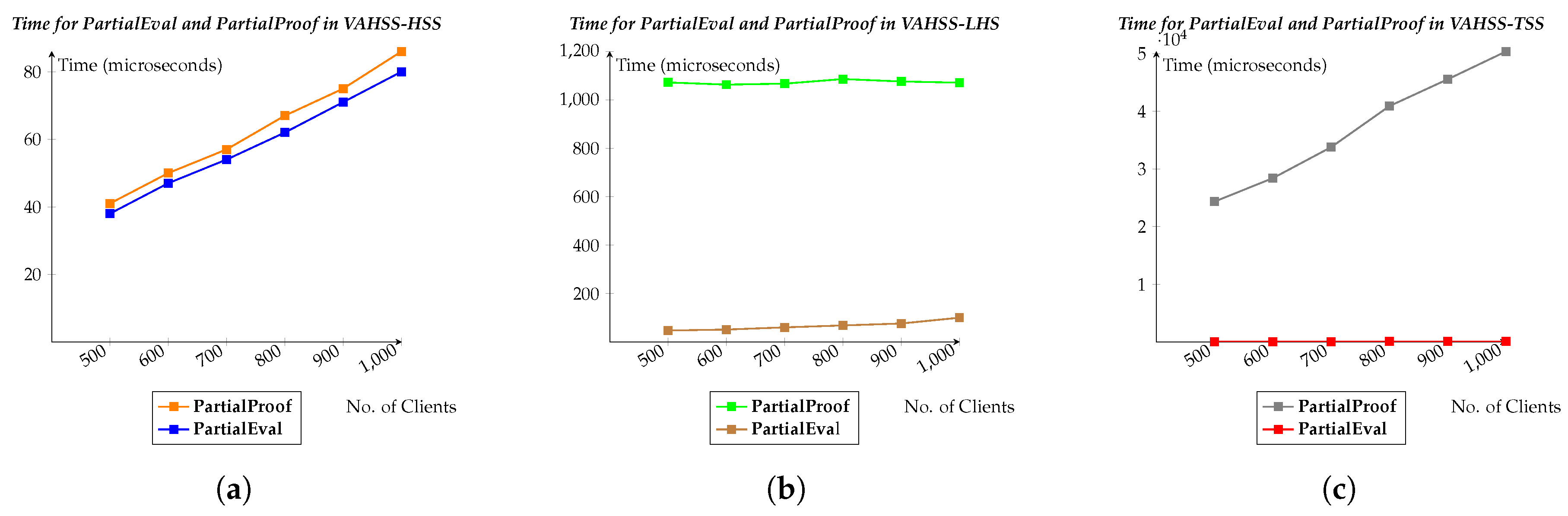
Figure 2 shows the timing for executing the
PartialEval and
PartialProof algorithms in each of our constructions. More precisely,
Figure 2a shows the VAHSS-HSS case,
Figure 2b demonstrates the VAHSS-LHS case, while the VAHSS-TSS case is depicted in
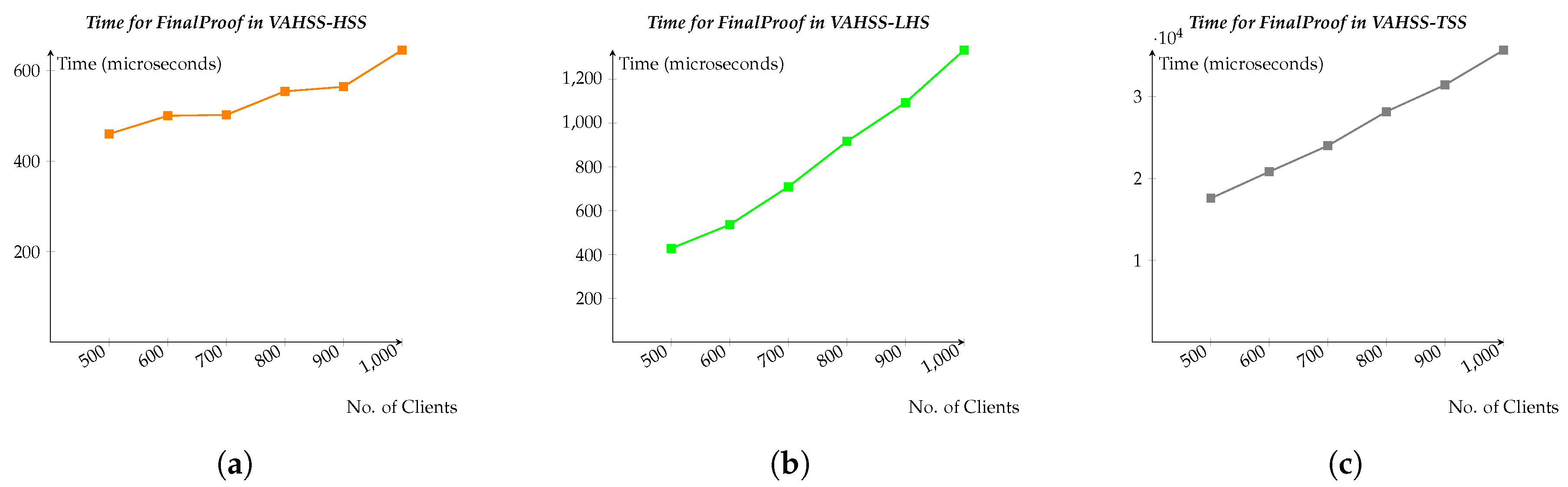
Figure 2c. The graphs show how the timing changes depending on the number of clients participating in the computation. Next,
Figure 3 shows the time that is required for computing the
Finalproof in each of the constructions, representing again how the performance varies according to a different amount of clients. Finally,
Figure 4 shows the timing for executing the
Verify algorithm given the outputs from each server and from the clients. We remind the reader that anyone may run the
Verify algorithm in order to check the correctness of the resulted
y value and obtain
y itself.
6. Discussion
We have presented three verifiable additive homomorphic secret sharing (VAHSS) constructions and, then, provided their theoretical evaluation. Furthermore, we developed a prototype and compared the performance (required computation time) of the proposed constructions for each used algorithm, given different parameters and conditions, as shown in
Section 5.2. To the best of our knowledge, no existing scheme achieves privacy-preserving distributed verifiable aggregation based on homomorphic operations.
As mentioned earlier, each construction relies on a different mathematical component and might be used in different application scenarios. More precisely, the constructions differ on how the partial evaluations (PartialEval) and the partial proofs (PartialProof) are generated and who performs each computation. For instance, in the VAHSS-HSS construction, clients are only needed to execute the Sharesecret algorithm for generating m shares, and the rest of the computations (required to produce the sum y and the proof ) are performed by the servers. Nevertheless, the VAHSS-LHS construction requires that each client deals with the Setup, ShareSecret, and PartialProof algorithms. In fact, in this case, the clients are the ones that generate the partial proofs instead of the servers, utilizing their private RSA key. Moreover, in the VAHSS-TSS construction, the client runs the Setup and ShareSecret, while the servers deal with the execution of the other algorithms. Additionally, the VAHSS-TSS solution is based on a threshold signature sharing scheme and, as a result, a coalition of servers is required to perform the PartialProof algorithm; not all of the m servers are needed.
The computation cost required by each construction is different, as demonstrated in
Section 5. However, this does not necessarily imply that one construction is better than another. Actually, it shows that there is a trade-off to choose from. For example, if the employed devices to function as clients have power/process constraints, then the best option could be the construction VAHSS-HSS, since it requires fewer computations and, as a consequence, it is less expensive regarding power consumption. However, if the employed clients are devices with significant power resources and the application requires that the clients produce the partial proofs, then the best option would be the VAHSS-LHS construction.
Furthermore, the metric of the number of operations could be used to establish which flavor of VAHSS is more appropriate, depending on the application setting and, in this case, the VAHSS-HSS construction requires fewer operations on the client-side. The prototype implementation and evaluation reinforces the fact that the VAHSS-HSS construction presents better timing for most of the required operations. As an additional metric for comparison, we employ the communication overhead (required bandwidth) for each of the proposed constructions. More precisely,
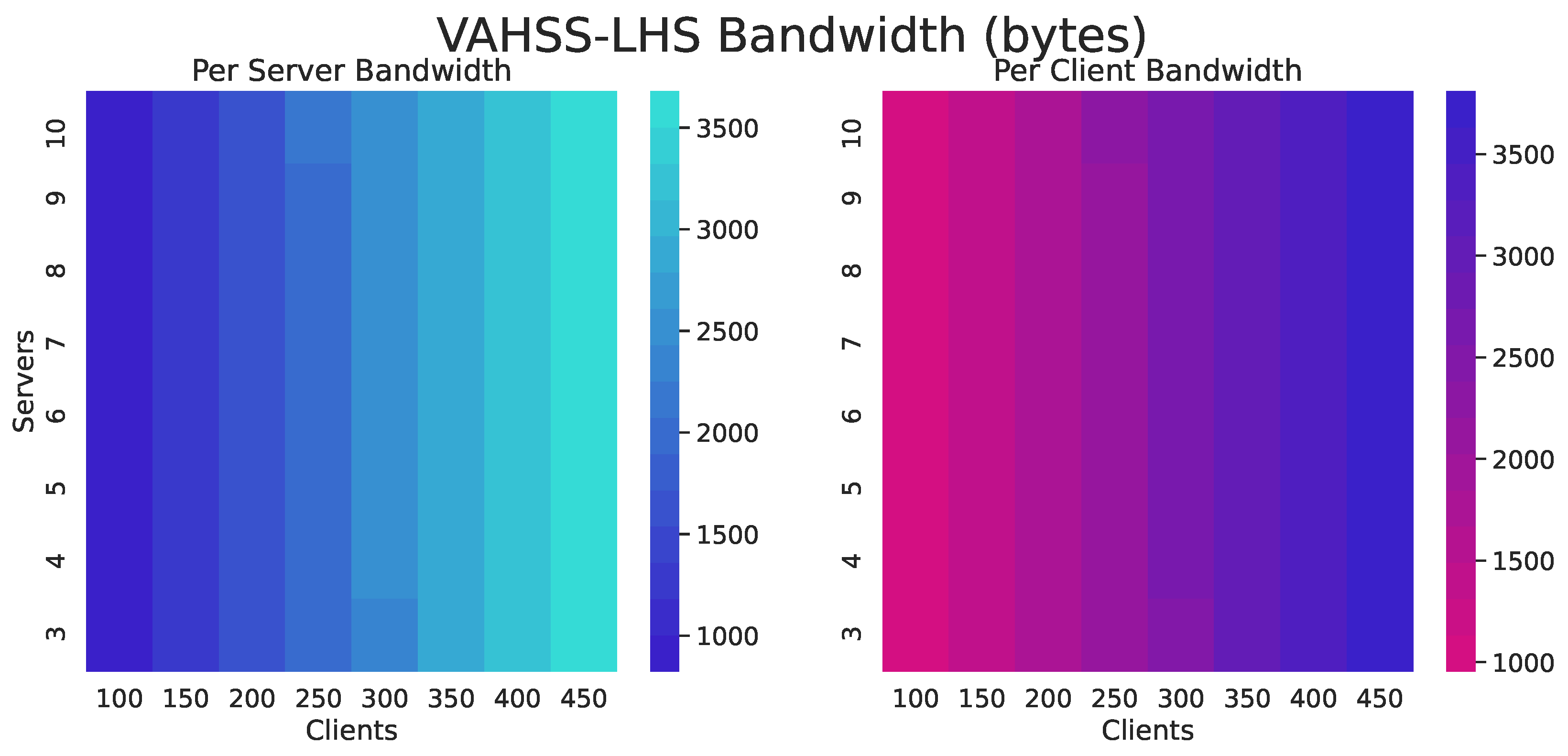
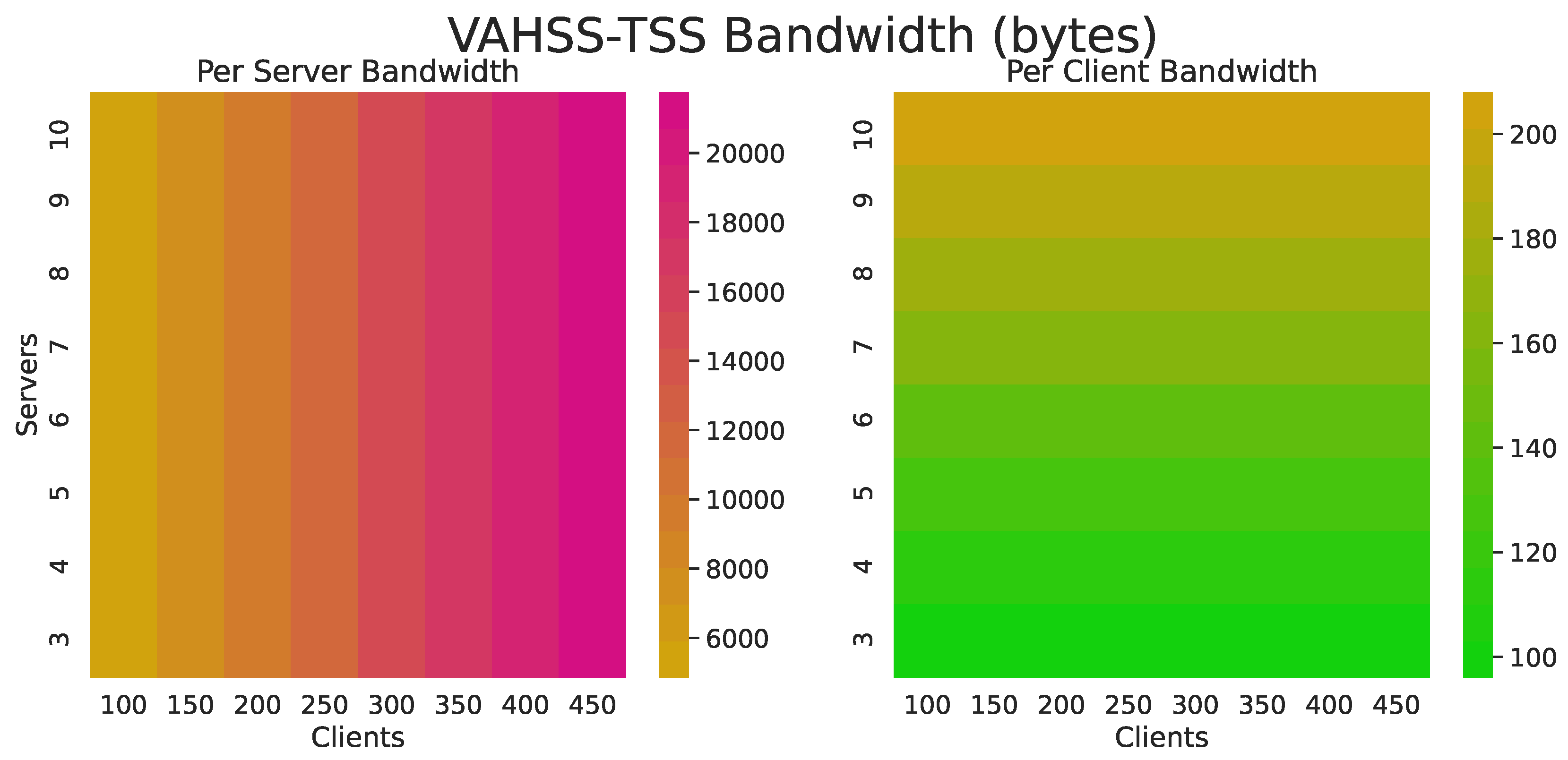
Figure 5,
Figure 6 and
Figure 7 show the required bandwidth usage for each construction. The figures give the number of bytes received and sent per client and per server.
Figure 5 shows that the VAHSS-HSS construction uses fewer bytes per client than the other constructions, since it only needs to send the shares. In the VAHSS-LHS construction, the client needs to receive the secret key and verification key, and the clients generate and share the proofs. In the VAHSS-TSS case, there is a significant reduction in the required transferred data. However, it is still higher than the required communication overhead in the VAHSS-HSS construction, since it needs to output a matrix and receive two big prime numbers.
Application scenarios: Mobile phones, wearables, and other Internet-of-Things (IoT) devices are all connected to distributed network systems. These devices generate a lot of data that often need to be aggregated to compute statistics, or even employed for user modeling and personalization of clients/users. For instance, a direct application of our constructions could be the measurement of electricity consumption (as well as water or gas consumption) in a specific region. More precisely, if we consider that each household in a specific region has an electricity consumption that is equal to , then, by employing our proposed constructions, the electricity production company could check what is the required energy consumption (by computing the sum , where n denotes the number of households) in that specific region and adjust the electricity production accordingly. Furthermore, by employing the verifiability property, the electricity consumption company can detect possible leaks of faults in how the electrical energy is handled. In our prototype, we use the data on the consumption of electricity and, more precisely, the UC Irvine machine learning repository. Because this is one of the most representative settings, all three constructions are suitable to be employed in this application, depending on the resources of the employed sensors/clients in different households. If we consider that multiple companies are collaborating in this aggregation process, then the collected data could be aggregated by multiple servers that collaborate or not.
Another scenario, where our constructions could be suitable are health monitoring settings, where a health provider may want to measure the average physical activity levels or patient conditions (e.g., temperature) in specific regions in order to draw conclusions about the health conditions of parts of the population and accordingly adjust services. For instance, health insurance companies could offer discounts to families or neighborhoods, depending on their physical activity, while the verifiability property provides transparency and fairness guarantees regarding the provided services from the health insurance company (
https://www.generaliglobalhealth.com/news/global-insights/insurtech/digital-technology-transforming-global-healthcare.html). Similarly, the proposed constructions would facilitate the aggregation process and collaboration between multiple hospitals that store confidential patient records and need to aggregate data in order to decide on the diagnosis and treatment of patients.
Besides, an important characteristic of our constructions is that the clients (from where the data are collected) do not need to communicate with each other. Thus, they could be easily employed in order to achieve reliable and verifiable environmental monitoring, when environmental sensors collecting appropriate measurements (e.g., temperature, humidity, CO, ozone, etc.) are spread in large regions and the sensors are not in the communication range of each other. More precisely, consider the setting where monitoring the air quality of specific neighborhoods in a city is needed. By employing sensors that are spread in large regions, data can be collected and then use the VAHSS-HSS construction to sum the measurement of CO. In this case, we do not rely only on one server, but on several servers to aggregate the measurements, while the verifiability property can be employed to guarantee the integrity of the aggregation process.
7. Conclusions
Major security and privacy challenges exist in the context of joint computations that are outsourced to untrusted cloud servers. Sensitive information of individuals might be leaked or malicious cloud servers might attempt to alter the aggregation results. In this work, we presented three concrete constructions for the verifiable additive homomorphic secret sharing (VAHSS) problem. We provided a solution based on homomorphic hash functions, a solution that uses linear homomorphic signatures and a construction based on a threshold signature sharing scheme. We proved all three constructions correct, secure, and verifiable. These constructions allow for any verifier to obtain the value y that is the sum of the clients’ secret inputs and confirm its correctness; without compromising the clients’ privacy or relying on trusted servers and without requiring any communication between the clients. We demonstrated the theoretical analysis of our work, showing the amount of computational cost that is required for each construction both from the clients’ and servers’ side. Subsequently, our experimental results illustrated how the different operations correspond to the required (computation) time with respect to the algorithms that are executed. Thus, the appropriate construction may be employed, depending on the available resources, requirements, and assumptions (e.g., communication between servers or no communication). We believe that our proposed VAHSS constructions can be employed in various applications that require the secure aggregation of data that were collected from multiple clients (e.g., smart metering, environmental monitoring, and health databases) and provide a practical and provably secure distributed solution, while avoiding single point of failures and any leakage of sensitive information.