Implementation of a New Strongly-Asymmetric Algorithm and Its Optimization
Abstract
1. Introduction
- The public parameter is removed.
- The constraints on Bob’s secret keys are reduced to the requirement that certain matrices should not be invertible.
2. Mathematical Setting and Key Agreement Protocol of SAA-5
- Step 1.
- Alice and Bob share following public information:
- Step 2.
- Bob creates his secret keys as matrices:and as a set of matrices:For all secret keys of Bob, the following conditions must be satisfied:- must be invertible- Each () must not be invertible.
- Step 3.
- Bob creates his public keys for all as:Here, the symbol denotes the matrix:which is called the Schur exponentiation of c by M.
- Step 4.
- Alice creates her secret key as a matrix set as:and creates her public key using one of Bob’s public key as: For each ,
- Step 5.
- Bob computes his secret shared key (SSK) using the public key of Alice and his own secret keys and as: For each ,
- Step 6.
- Alice computes her SSK by using and her own secret key as:
2.1. Breaking Complexity of SAA-5
- Common parameters d, p, I.
- Public keys of Bob , for all .
- Public key of Alice .
2.2. The Brute-Force Attack
3. Performance Estimation and Evaluation of SAA-5
3.1. Performance Estimation
3.2. Discussion: Efficient Parameters of SAA-5 and Comparison with D-H
- macOS Mojave ver10.14.6.
- 1.3 GHz Intel Core i5.
- 8 GB 1867 MHz LPDDR3.
- Language: JAVA.
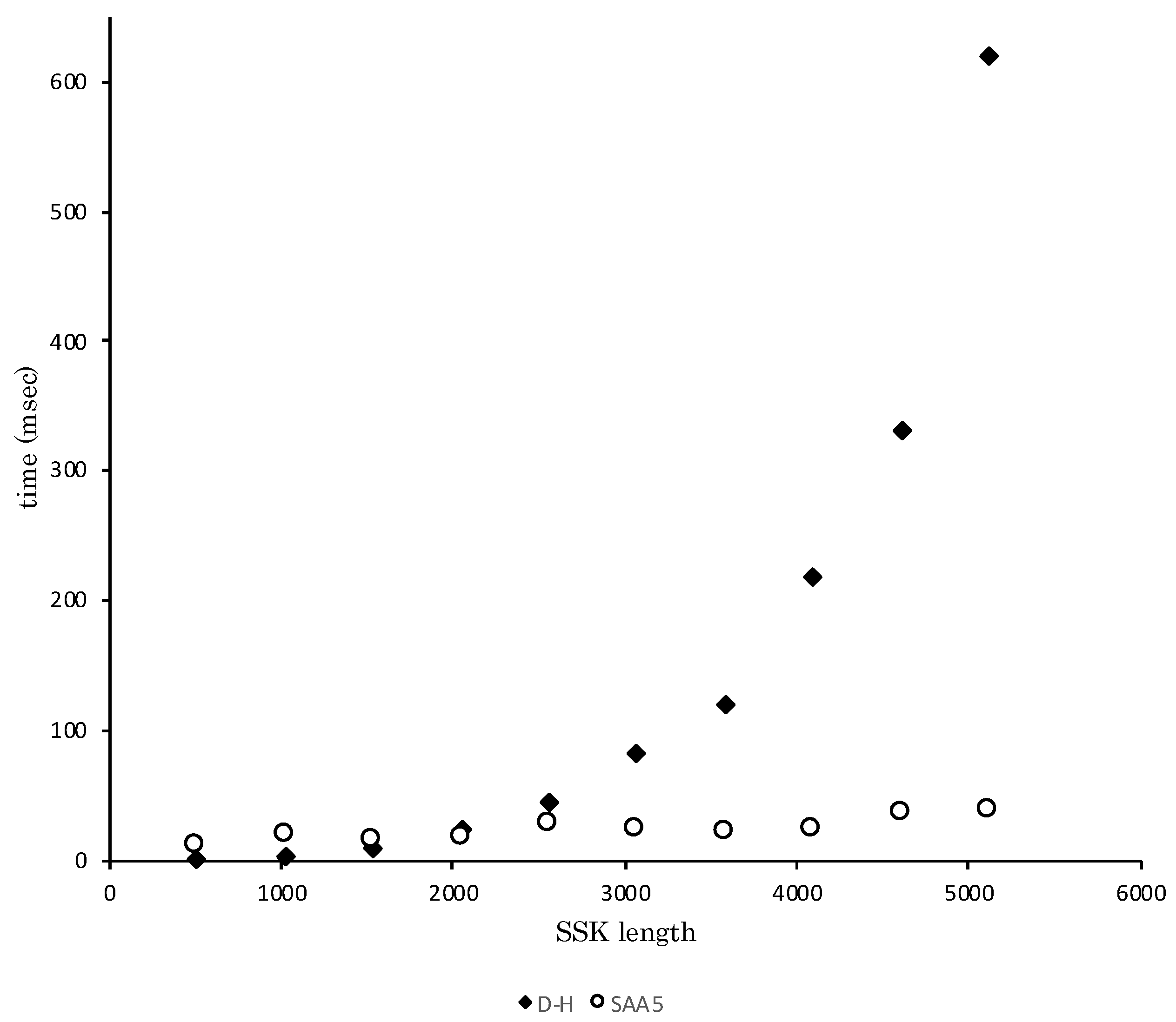
3.3. Experimental Result: Comparison with D-H
4. Performance Improvement
4.1. The SAPKA with Multiple Keys Class
- -
- a semigroup together with some operation •.
- -
- a set of easily invertible maps , called noise space.
- -
- a set of maps .
- -
- a finite set .
- Step 1.
- Bob chooses maps . By conjugating for each , Bob constructs quadruple:satisfies (9). and he uses as secret key of him as a function:and public keys as following functions:
- Step 2.
- Bob sends the public keys to Alice.
- Step 3.
- Alice chooses her secret key as a set then, she constructs her public key as an element:
- Step 4.
- Alice sends the public key to Bob.
- Step 5.
- Alice computes the secret shared key (SSK) as:
- Step 6.
- Bob computes as:
- 1.
- Each satisfies the equation:
- 2.
4.2. SAPKA-MK Version of SAA-5
4.3. SAA-5 without Schur-Exponentiations
- –
- –
- a set
- Step 1.
- Bob defines, for each , the following six maps:From the six-tuple , Bob constructs the quadruple as:for all . With this construction, (12) is satisfied, i.e.,Moreover, for any , satisfies:Thus, the multiple compatibility condition (9) is satisfied from Lemma 1.Hence, for any choice of (), following equation:is satisfied. Then, Bob prepares his secret key as a function:and produces the public keys as following functions:
- Step 2.
- In order to send the public keys to Alice, Bob sends the public matrices:
- Step 3.
- Alice chooses as her secret key a set of matrices:and constructs her public key:
- Step 4.
- Alice sends the public key to Bob.
- Step 5.
- The secret shared key (SSK) is:Alice knows the , so she can compute:
- Step 6.
- Bob computes as:
4.4. The Comparison of Breaking Complexity between SAA-5 And SAA-5-no-SE
4.5. Discussion: Performance of SAA-5-no-SE
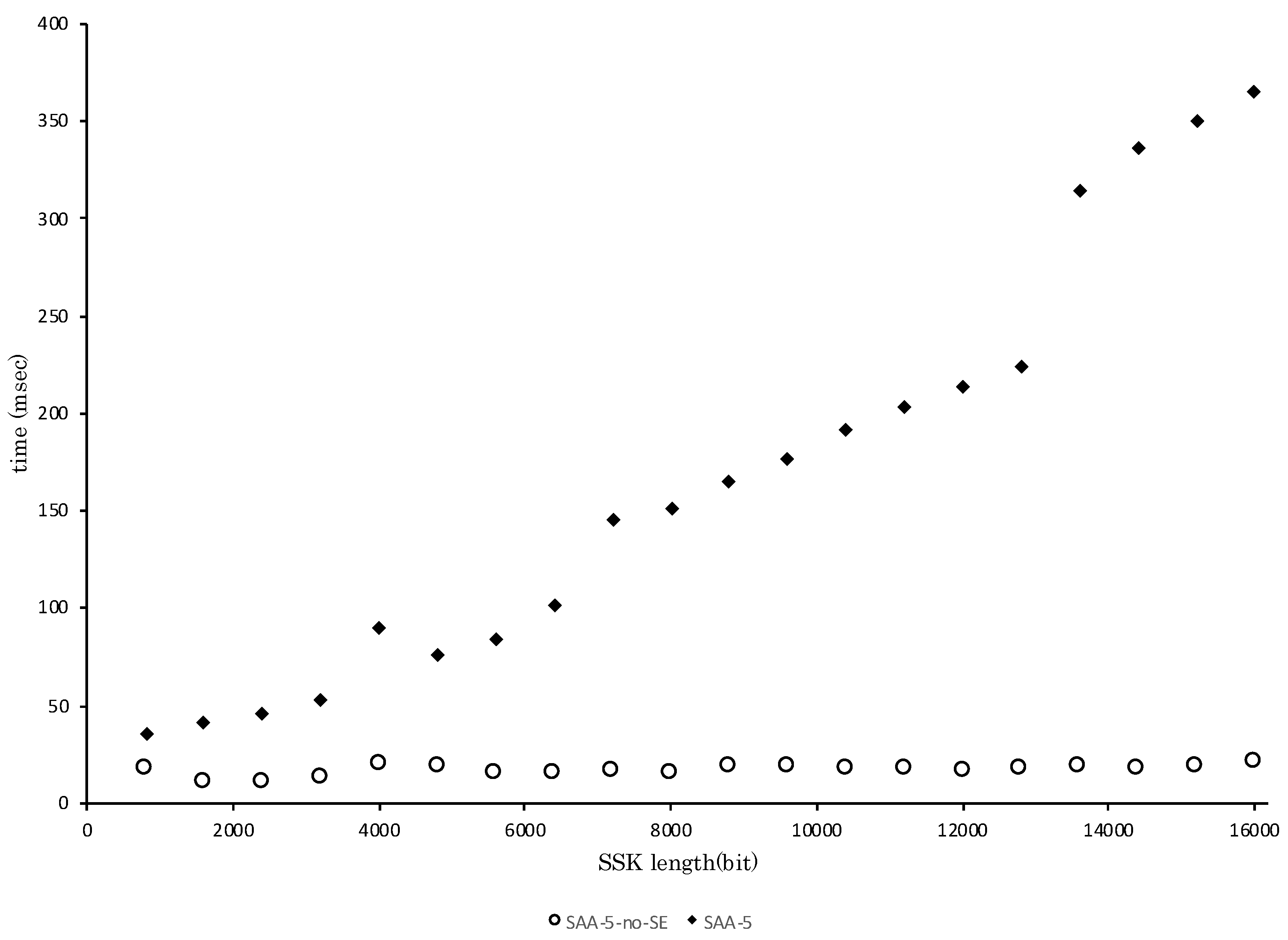
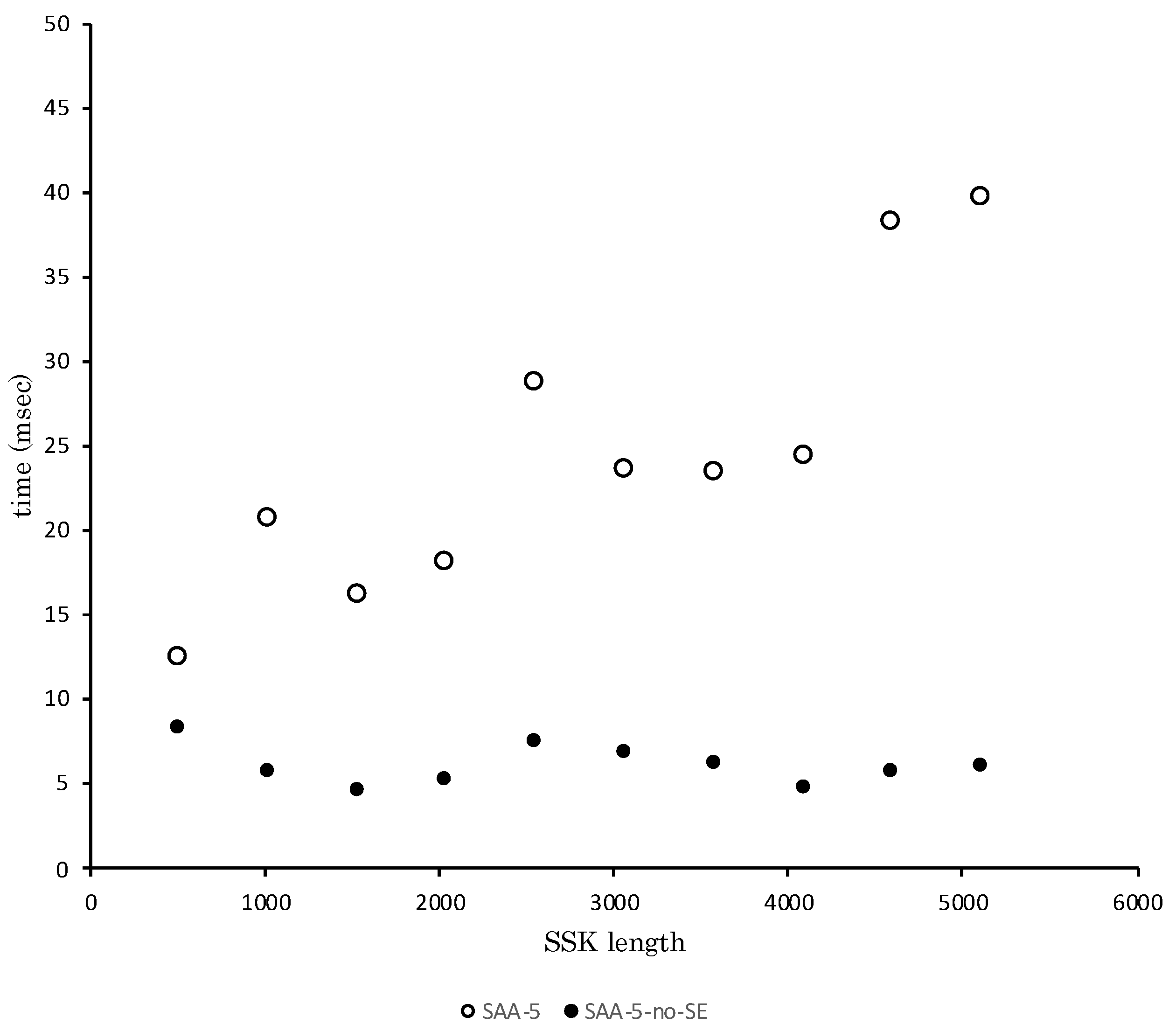
4.6. Experimental Result: Performance of SAA-5-no-SE
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PKA | public key agreement |
| D-H | Diffie-Hellman |
| SAPKA | strongly-asymmetric public key agreement |
| SAA | strongly-asymmetric algorithm |
| SSK | secret shared key |
References
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. Method for obtaining digital signatures and public key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- ElGamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Adrian, D.; Bhargavan, K.; Durumeric, Z.; Gaudry, P.; Green, M.; Halderman, J.A.; Heninger, N.; Springall, D.; Thome, E.; Valenta, L.; et al. Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 5–17. [Google Scholar]
- Shor, P. Polynomial-time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 25, 1484–1509. [Google Scholar] [CrossRef]
- Patarin, J. Hidden fields equations (HFE) and isomorphisms of polynomials (IP): Two new families of asymmetric algorithms. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Saragossa, Spain, 12–16 May 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 33–48. [Google Scholar]
- Porras, J.; Baena, J.; Ding, J. ZHFE, a new multivariate public key encryption scheme. In Proceedings of the International Workshop on Post-Quantum Cryptography, Waterloo, ON, Canada, 1–3 October 2014; pp. 229–245. [Google Scholar]
- Ajtai, M.; Dwork, C. A public-key cryptosystem with worst-case/average-case equivalence. In Proceedings of the 50th ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1997; pp. 284–293. [Google Scholar]
- Khot, S. Hardness of approximating the shortest vector problem in lattices. J. ACM (JACM) 2005, 52, 789–808. [Google Scholar] [CrossRef]
- Post-Quantum Cryptography Competition Round 2 Submittions. Available online: https://csrc.nist.gov/projects/post-quantum-cryptography/round-2-submissions (accessed on 24 July 2020).
- Alkim, E.; Ducas, L.; Poppelmann, T.; Schwabe, P. Post-quantum key exchange—A new hope. In Proceedings of the 25th USENIX Security Symposium (USENIX Security 16), Austin, TX, USA, 10–12 August 2016; pp. 327–343. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Proceedings of the International Algorithmic Number Theory Symposium, Portland, OR, USA, 21–25 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar]
- Casanova, A.; Faugere, J.C.; Macario-Rat, G.; Patarin, J.; Perret, L.; Ryckeghem, J. GeMSS: A Great Multivariate Short Signature. Available online: https://www-polsys.lip6.fr/Links/NIST/GeMSS_specification_round2_V2.pdf (accessed on 29 July 2020).
- Accardi, L.; Iriyama, S.; Regoli, M.; Ohya, M. Strongly Asymmetric Public Key Agreement Algorithms; Technical Report ISEC2011-20; IEICE: Tokyo, Japan, 2011; pp. 115–121. [Google Scholar]
- Accardi, L.; Regoli, M. On a class of strongly asymmetric PKA algorithms. J. Math. Crypt. 2015, 9, 151–159. [Google Scholar] [CrossRef]
- Accardi, L.; Iriyana, S.; Jimbo, K.; Regoli, M. A New Class of Strongly Asymmetric PKA Algorithms: SAA-5. Cryptography 2019, 3, 9. [Google Scholar] [CrossRef]
- Ottaviani, V.; Zanoni, A.; Regoli, M. Conjugation as public key agreement protocol in mobile cryptography. In Proceedings of the 2010 International Conference on Security and Cryptography (SECRYPT), Athens, Greece, 26–28 July 2010; pp. 1–6. [Google Scholar]
- Jimbo, K.; Iriyama, S.; Regoli, M. Project Name: Implementation of a New Strongly Asymmetric Algorithms and Its Optimization. GitHub Repository. 2020. Available online: https://github.com/jimbobmij/project_KSM (accessed on 29 July 2020).
- Großschädl, J.; Kizhvatov, I. Performance and security aspects of client-side SSL/TLS processing on mobile devices. In Proceedings of the International Conference on Cryptology and Network Security, Kuala Lumpur, Malaysia, 12–14 December 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 44–61. [Google Scholar]
- Okeyinka, A.E. Computational speeds analysis of RSA and ElGamal algorithms on text data. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 21–23 October 2015; Volume 1. [Google Scholar]

| Key | Bit Size | Steps |
|---|---|---|
| Total |
| SSK Length (bit) | SAA-5 (msec) | D-H (msec) |
|---|---|---|
| 512 | 12.45 | 1.45 |
| 1024 | 20.63 | 3.37 |
| 1536 | 16.19 | 10.87 |
| 2048 | 18.10 | 24.21 |
| 2560 | 28.77 | 45.68 |
| 3072 | 23.54 | 83.39 |
| 3584 | 23.35 | 120.29 |
| 4096 | 24.42 | 219.90 |
| 4608 | 38.12 | 332.46 |
| 5120 | 39.58 | 620.86 |
| SSK Length (bit) | (bit) | (bit) |
|---|---|---|
| 512 | 8 | 512 |
| 1024 | 16 | 1024 |
| 1536 | 24 | 1536 |
| 2048 | 32 | 2048 |
| 2560 | 40 | 2560 |
| 3072 | 48 | 3072 |
| 3584 | 56 | 3584 |
| 4096 | 64 | 4096 |
| 4608 | 72 | 4608 |
| 5120 | 80 | 5120 |
| Key | Bit Size | Steps |
|---|---|---|
| Total |
| SSK Length (bit) | p (bit) | SAA-5 | SAA-5-no-SE |
|---|---|---|---|
| 800 | 8 | 34.42 | 16.88 |
| 1600 | 16 | 40.26 | 9.58 |
| 2400 | 24 | 44.98 | 9.92 |
| 3200 | 32 | 52.36 | 12.86 |
| 4000 | 40 | 89.82 | 19.24 |
| 4800 | 48 | 75.18 | 18.78 |
| 5600 | 56 | 83.94 | 14.74 |
| 6400 | 64 | 101.16 | 14.76 |
| 7200 | 72 | 145.04 | 15.62 |
| 8000 | 80 | 150.58 | 14.68 |
| 8800 | 88 | 164.84 | 17.64 |
| 9600 | 96 | 176.44 | 17.68 |
| 10,400 | 104 | 191.20 | 17.46 |
| 11,200 | 112 | 202.76 | 17.22 |
| 12,000 | 120 | 213.36 | 15.96 |
| 12,800 | 128 | 223.30 | 16.54 |
| 13,600 | 136 | 314.08 | 18.24 |
| 14,400 | 144 | 336.24 | 17.58 |
| 15,200 | 152 | 349.96 | 18.02 |
| 16,000 | 160 | 364.66 | 20.30 |
| SSK Length (bit) | SAA-5-no-SE(msec) |
|---|---|
| 512 | 8.32 |
| 1024 | 5.63 |
| 1536 | 4.57 |
| 2048 | 5.26 |
| 2560 | 7.41 |
| 3072 | 6.84 |
| 3584 | 6.15 |
| 4096 | 4.80 |
| 4608 | 5.75 |
| 5120 | 6.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jimbo, K.; Iriyama, S.; Regoli, M. Implementation of a New Strongly-Asymmetric Algorithm and Its Optimization. Cryptography 2020, 4, 21. https://doi.org/10.3390/cryptography4030021
Jimbo K, Iriyama S, Regoli M. Implementation of a New Strongly-Asymmetric Algorithm and Its Optimization. Cryptography. 2020; 4(3):21. https://doi.org/10.3390/cryptography4030021
Chicago/Turabian StyleJimbo, Koki, Satoshi Iriyama, and Massimo Regoli. 2020. "Implementation of a New Strongly-Asymmetric Algorithm and Its Optimization" Cryptography 4, no. 3: 21. https://doi.org/10.3390/cryptography4030021
APA StyleJimbo, K., Iriyama, S., & Regoli, M. (2020). Implementation of a New Strongly-Asymmetric Algorithm and Its Optimization. Cryptography, 4(3), 21. https://doi.org/10.3390/cryptography4030021





