Security and Performance of Single Sign-on Based on One-Time Pad Algorithm
Abstract
1. Introduction
- Reduces Help Desk costs;
- Improves customer satisfaction;
- Boosts productivity;
- Improves compliance and security capabilities;
- Facilitates B2B collaboration.
2. Methodology
- Maintenance of security
- Without unauthorized disclosure of user’s personal information
- The affiliation of each information such as the user’s personal information, the key for encryption the user’s one, and the personal information of the service provider is clarified.
- The user’s personal information and the key used to encrypt the user’s one are not stored in the same storage.
- The user’s personal information and authentication information are not possessed at the same time.
- The key used to encrypt user’s personal information and authentication information are not possessed at the same time.
- Construction to mathematical SSO algorithm based on VE-based authentication algorithm;
- Prototype implementation and testing;
- Security discussion.
- Define parties;
- Define network configuration;
- Define parameters such as plaintext, etc.;
- Define the affiliation of each parameter;
- Construct mathematical algorithm;
- Implement.
3. Algorithm
3.1. Cryptosystem and Authentication Algorithm Based on VE
- S is a computation server and untrusted party;
- Alice is a prover;
- Bob is a verifier;
- The channel between Alice and Bob is secure;
- The channel between Bob and S is insecure;
- Alice does not have direct access to S.
- Step1
- Alice sends to Bob.
- Step2
- Bob generates k and calculates .
- Step3
- Bob sends to the server S.
- Step1
- Alice sends to Bob.
- Step2
- Bob generates and calculates .
- Step3
- Bob sends to S.
- Step4
- Server S calculates , and sends to Bob.
- Step5
- Bob calculates , and checks the result.
3.1.1. Mathematical Subclass of VE
- , and are the abelian groups that belong to a group G closed by the operator ∘
- Under the operation ∘, is composed as
- Under the operation ∘, is composed as
- Under the operation ∘, is composed as
- , and are the same arbitrary abelian groups, and , where G is a group closed by the operator ∘
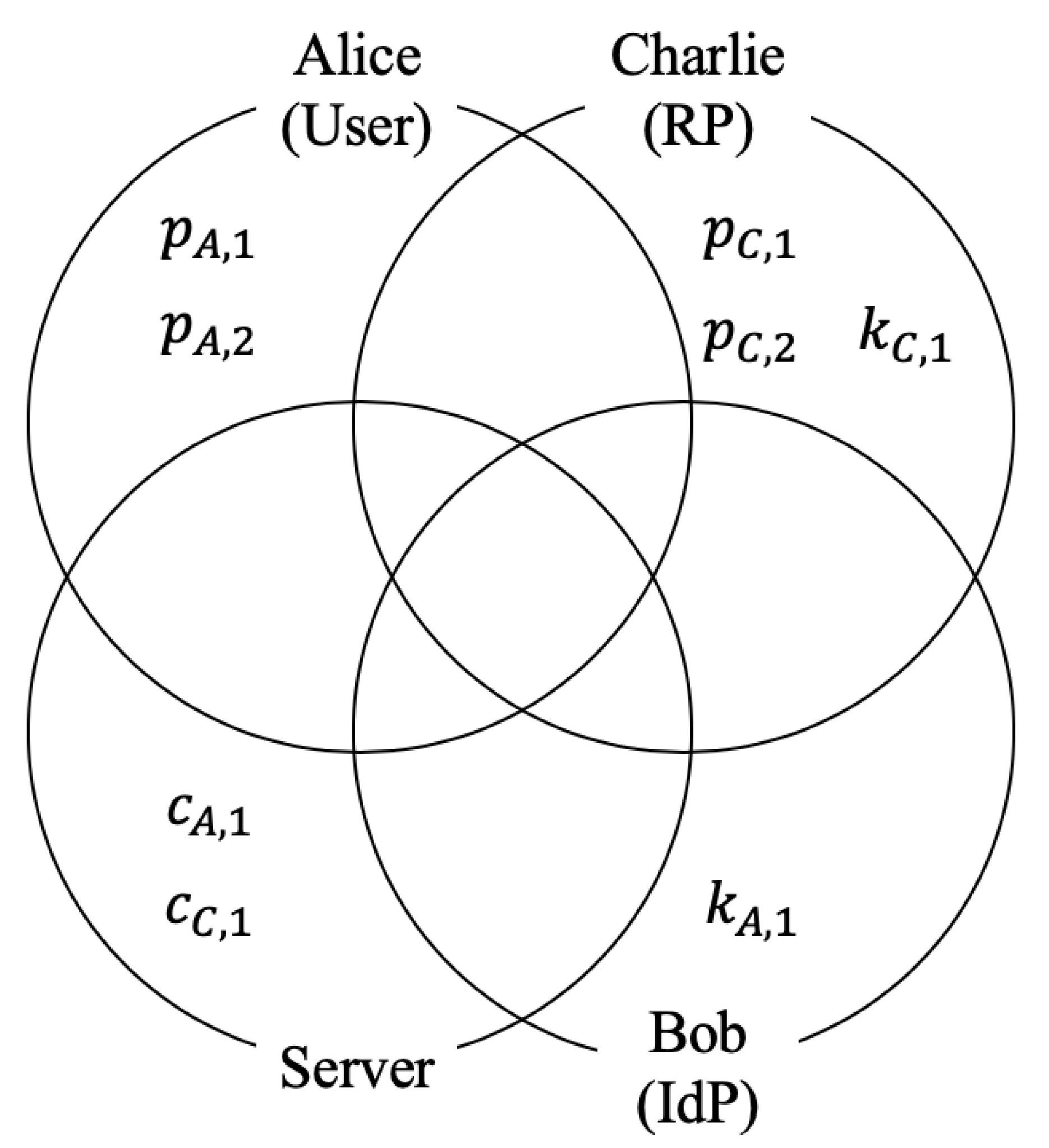
3.2. SSO Based on VE
- User
- A person whose identity is to be verified using one or more authentication protocols.
- Identity provider(IdP)
- A trusted entity that issues or registers a user’s identity. An IdP may be an independent third party.
- Verifier
- The entity that verifies the user’s identity using an authentication protocol.
- Relying party(RP)
- This entity relies upon the authentication information for user’s identity sent from a verifier typically to process a transaction or permit access to information or a system.
- IAL:
- IAL refers to the robustness of the identity proofing process to confidently determine the identity of an individual. An IAL is selected to mitigate the potential identity proofing errors. (18)
- AAL:
- AAL refers to the robustness of the authentication process as well as that of the binding between an authenticator and an individual’s identifier. An AAL is selected to mitigate the potential authentication errors (i.e., a false claimant using a credential that does not rightfully belong to them). (18)
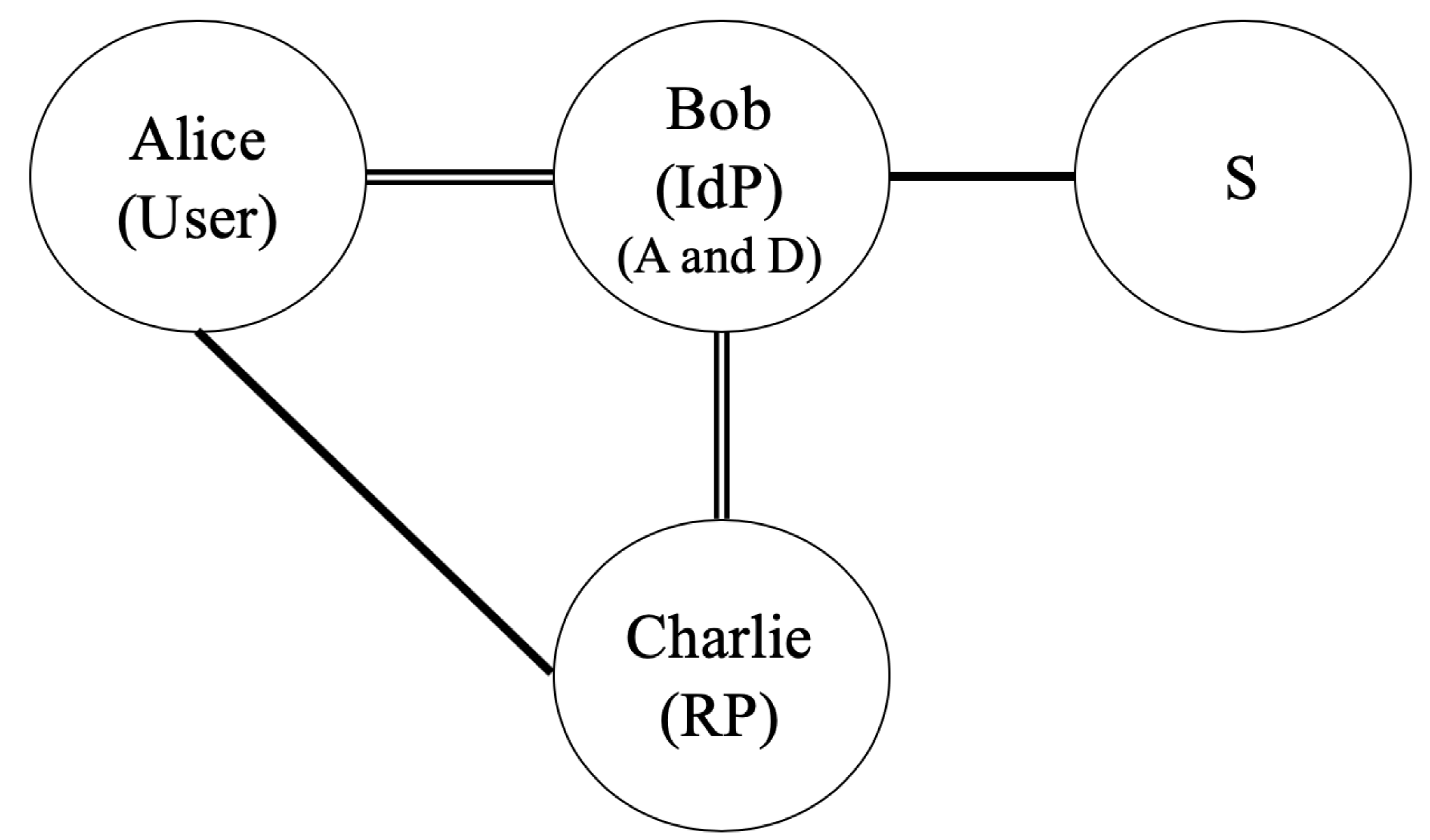
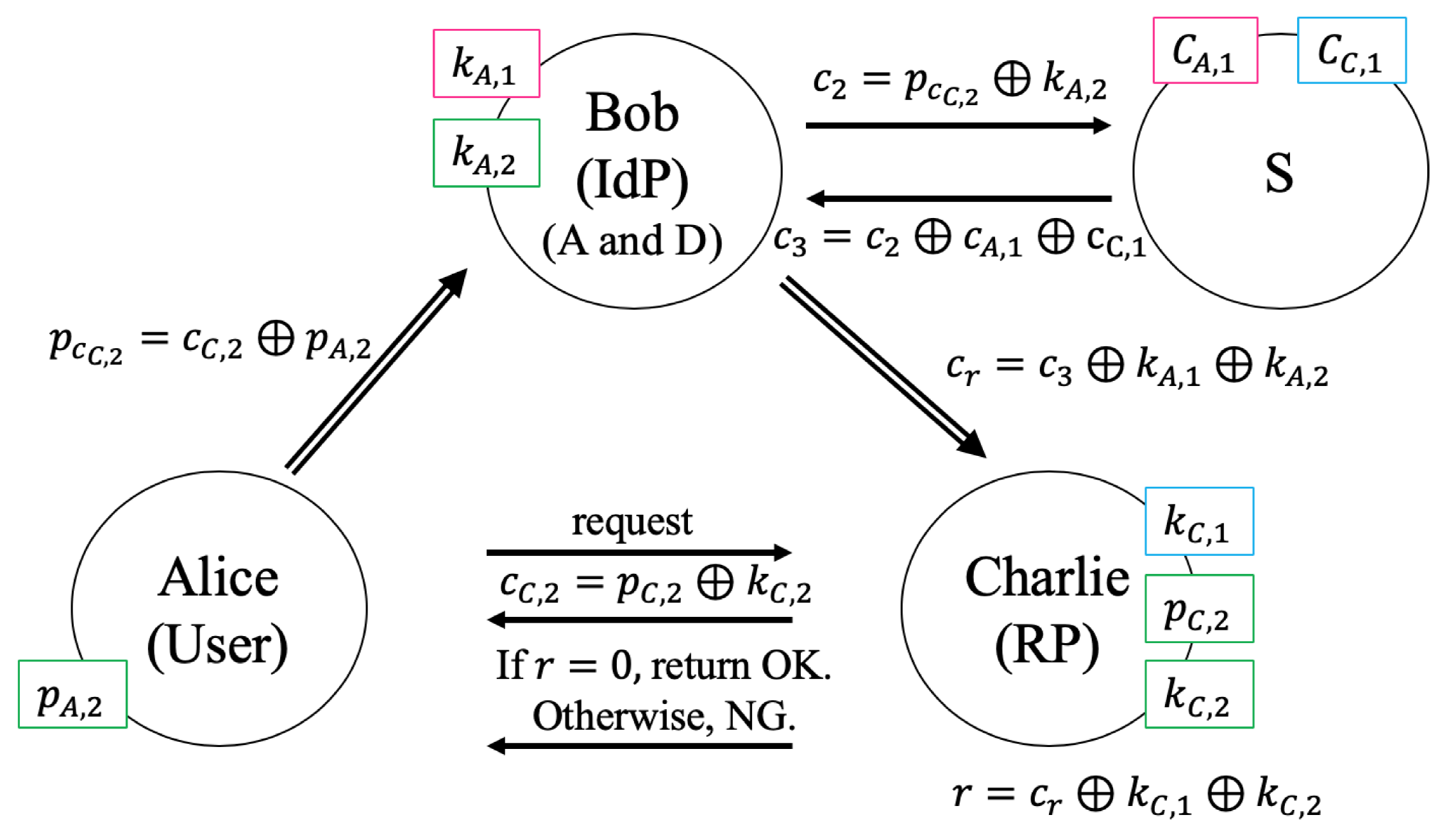
- Alice accesses Charlie’s service and does not reveal her identity to Charlie.
- Charlie provides service only to an authenticated user but does not handle the user’s identity.
- Alice and Charlie trust Bob.
- The channel between Alice and Bob is a secure channel.
- The channel between Bob and Charlie is a secure channel.
- The channel between Alice and Charlie is an insecure channel.
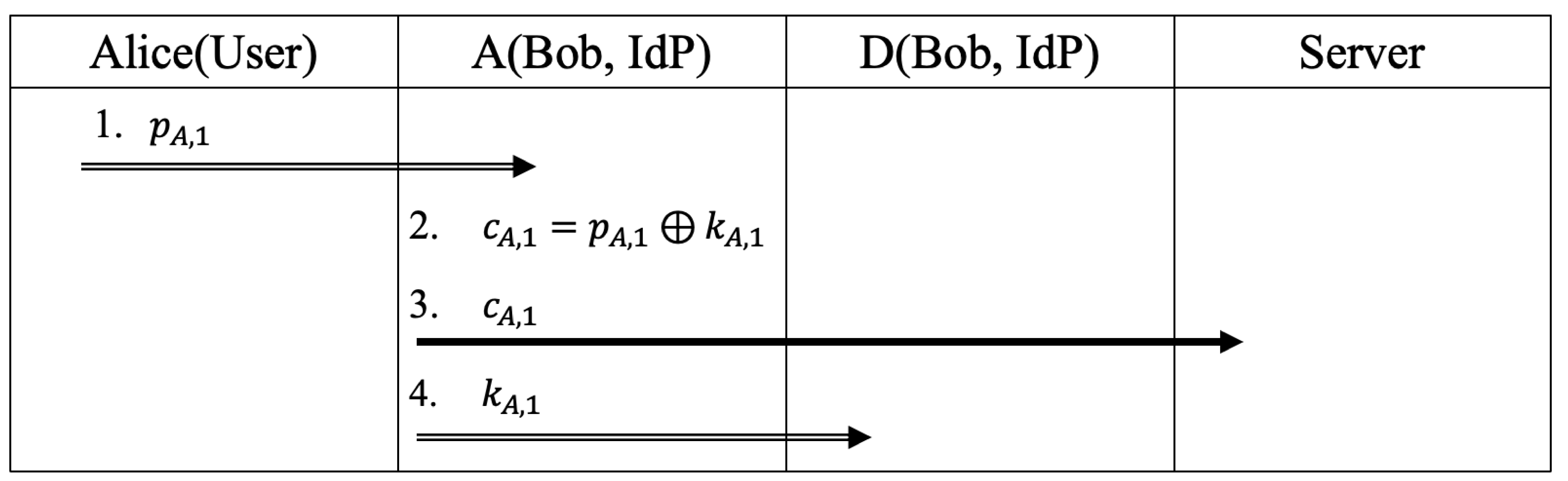
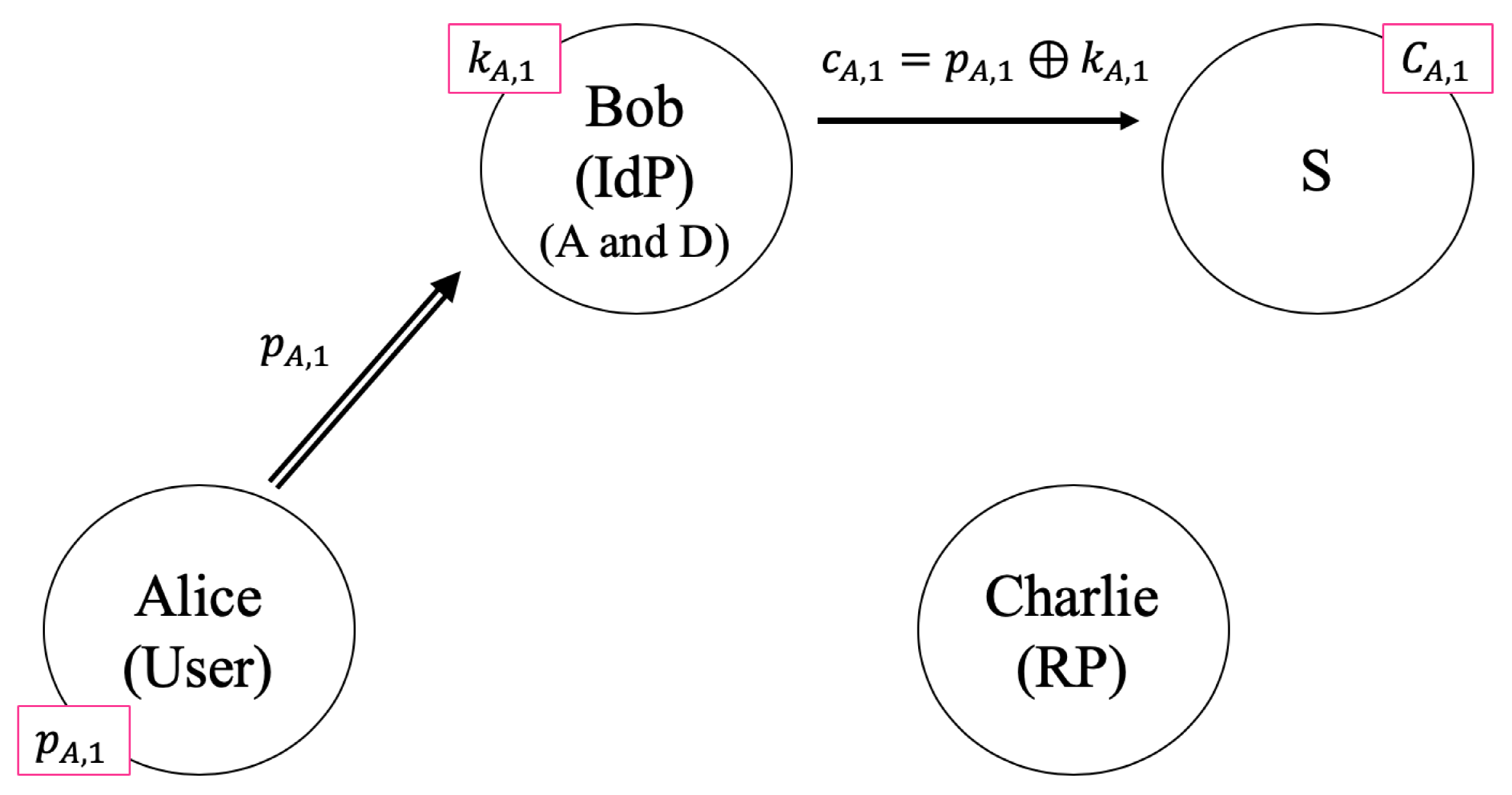
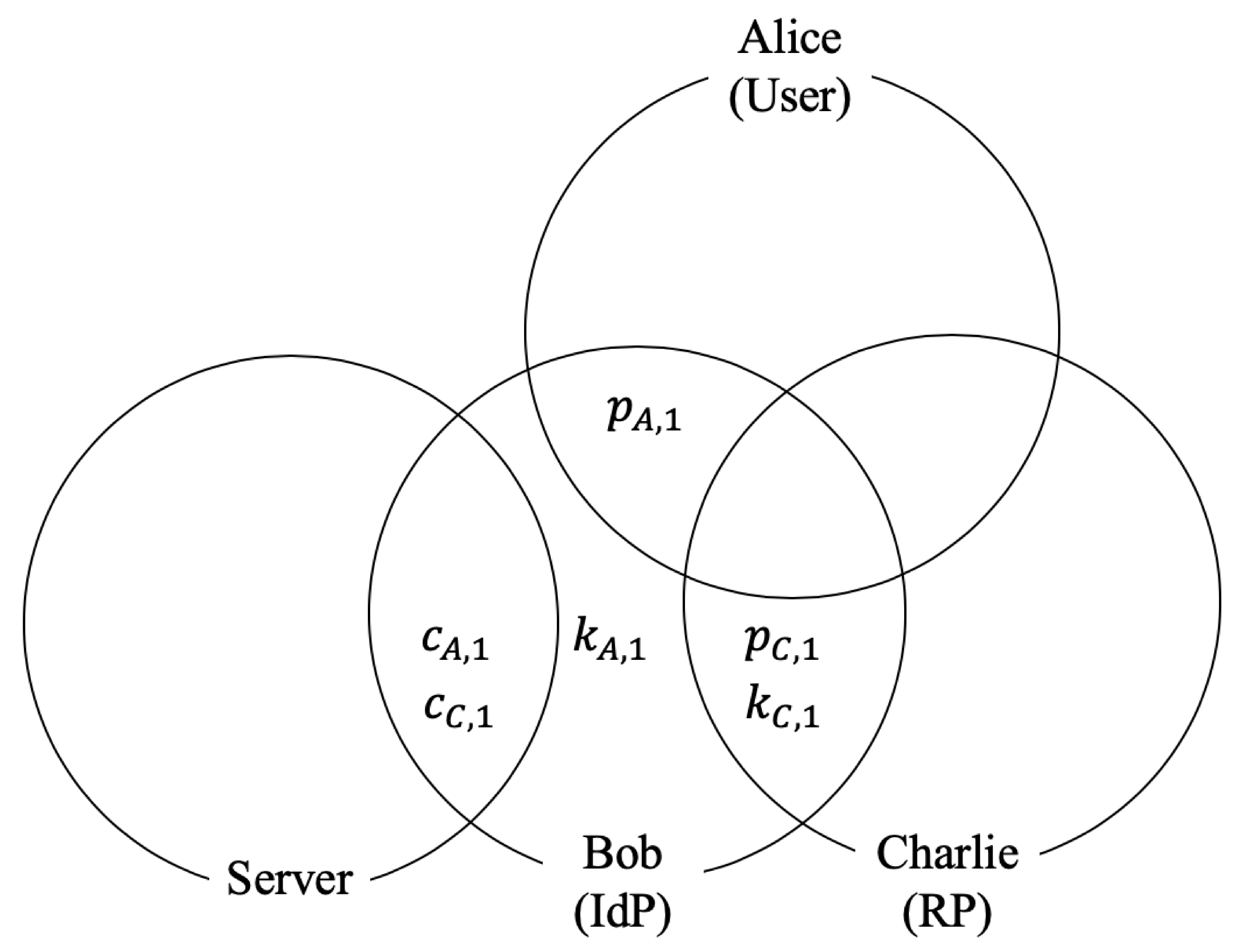
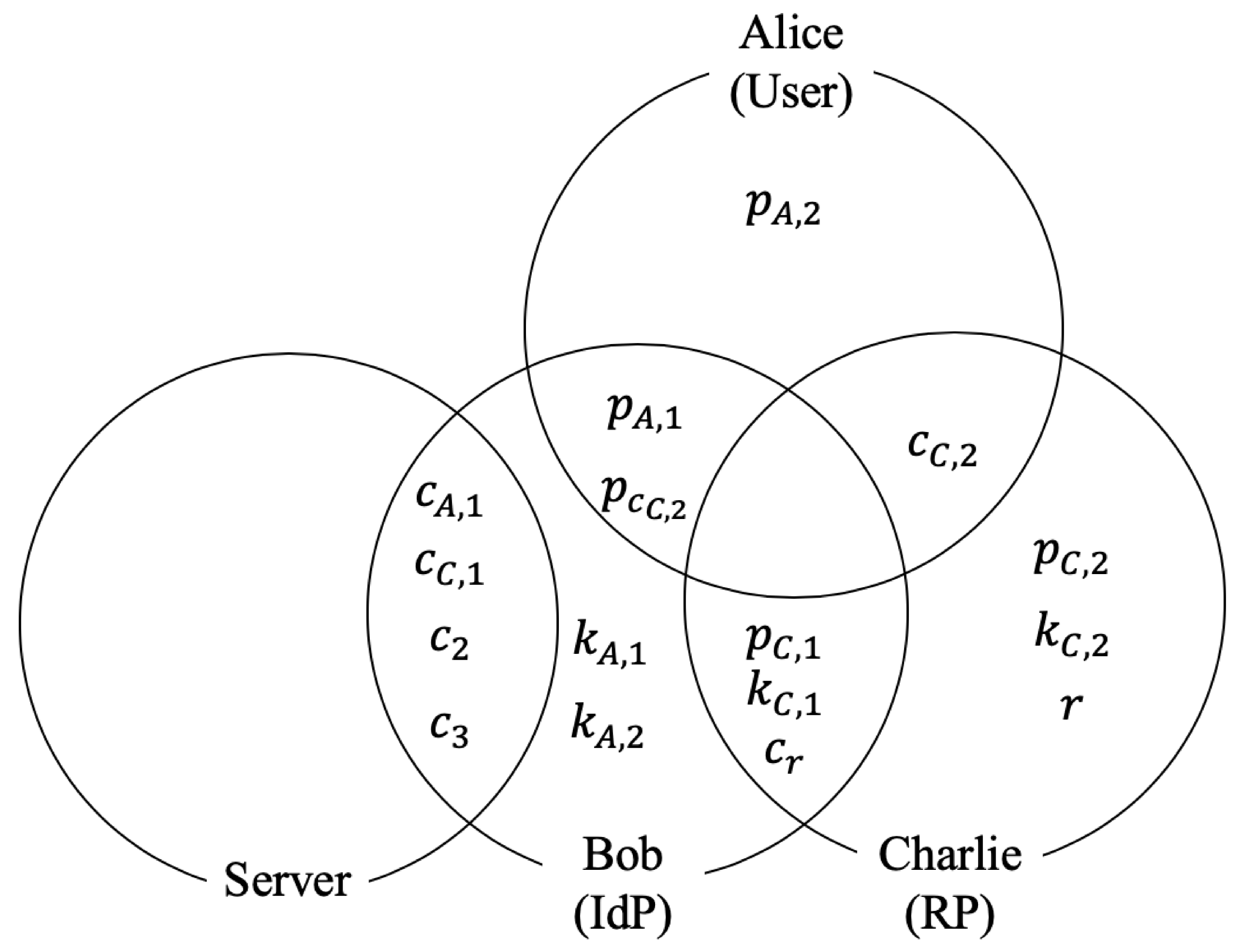
- Step1
- Alice sends to A
- Step2
- A generates and computes
- Step3
- A sends to S
- Step4
- A send to D
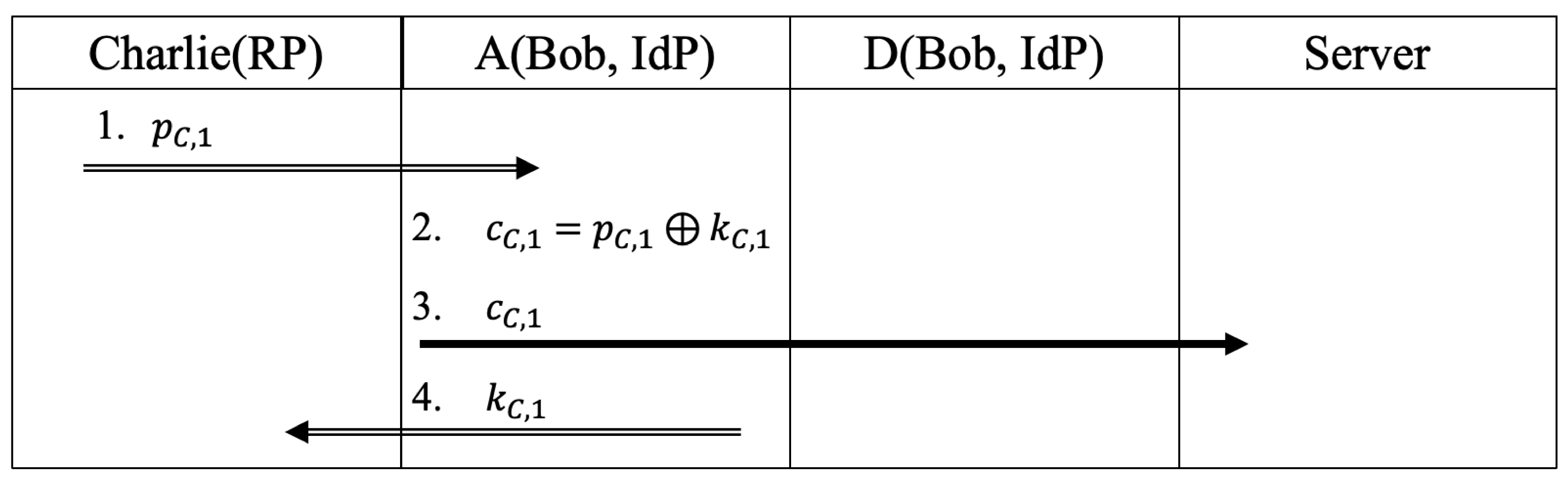
- Step1
- Charlie sends to A
- Step2
- A generates and computes
- Step3
- A sends to S
- Step4
- A sends to Charlie
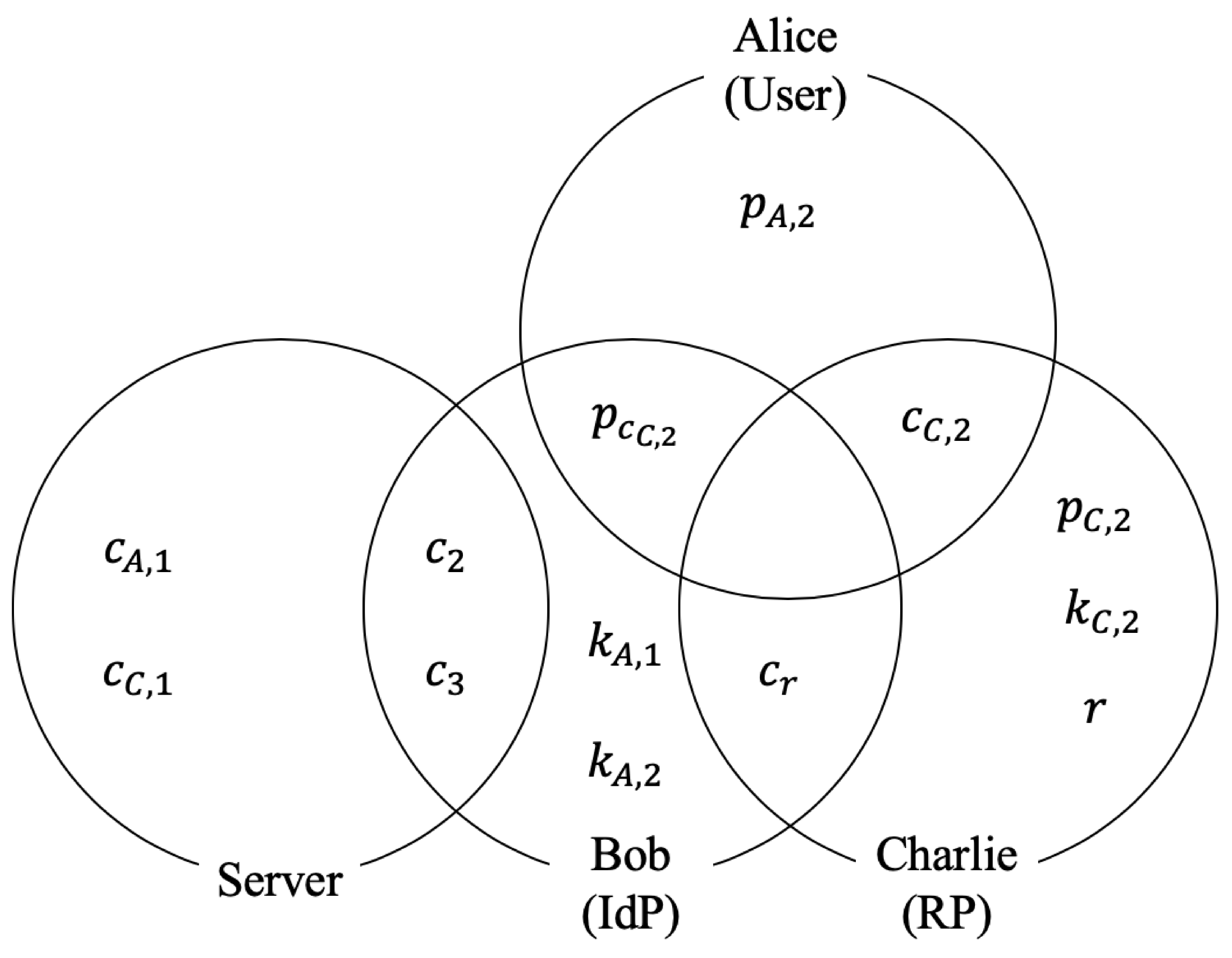
- Step1
- Alice sends request for Charlie’s service to Charlie
- Step2
- Charlie generates and computes
- Step3
- Charlie sends to Alice
- Step4
- Alice computes and sends to D
- Step5
- D generates and computes
- Step6
- D sends to S
- Step7
- S computes , where
- Step8
- S sends to D
- Step9
- D computes , where
- Step10
- D sends to Charlie
- Step11
- Charlie computes , where
- Step12
- If , Charlie returns OK to Alice. Otherwise, Charlie returns NG.
- , and are the same arbitrary abelian groups, and , where G is a group closed by the operator ∘
- Step 1
- Alice sends to A
- Step 2
- A generates and computes
- Step 3
- A sends to S
- Step 4
- A sends to D
- Step 1
- Charlie sends to A
- Step 2
- A generates and computes
- Step 3
- A sends to S
- Step 4
- A sends to Charlie
- Step 1
- Alice sends request for Charlie’s service to Charlie
- Step 2
- Charlie generates and computes
- Step3
- Charlie sends to Alice
- Step 4
- Alice computes and sends to D
- Step 5
- D generates and computes , where
- Step 6
- D sends to S
- Step 7
- S computes , where
- Step 8
- S sends to D
- Step 9
- D computes , where
- Step 10
- D sends to Charlie
- Step 11
- Charlie computes , where
- Step 12
- If , Charlie can obtain .
- Step 13
- Charlie confirms .
4. Demonstration
5. Discussion
5.1. Robustness against Attacks
5.1.1. Theoretical and Classical Attack
5.1.2. Man-in-the-Middle Attack
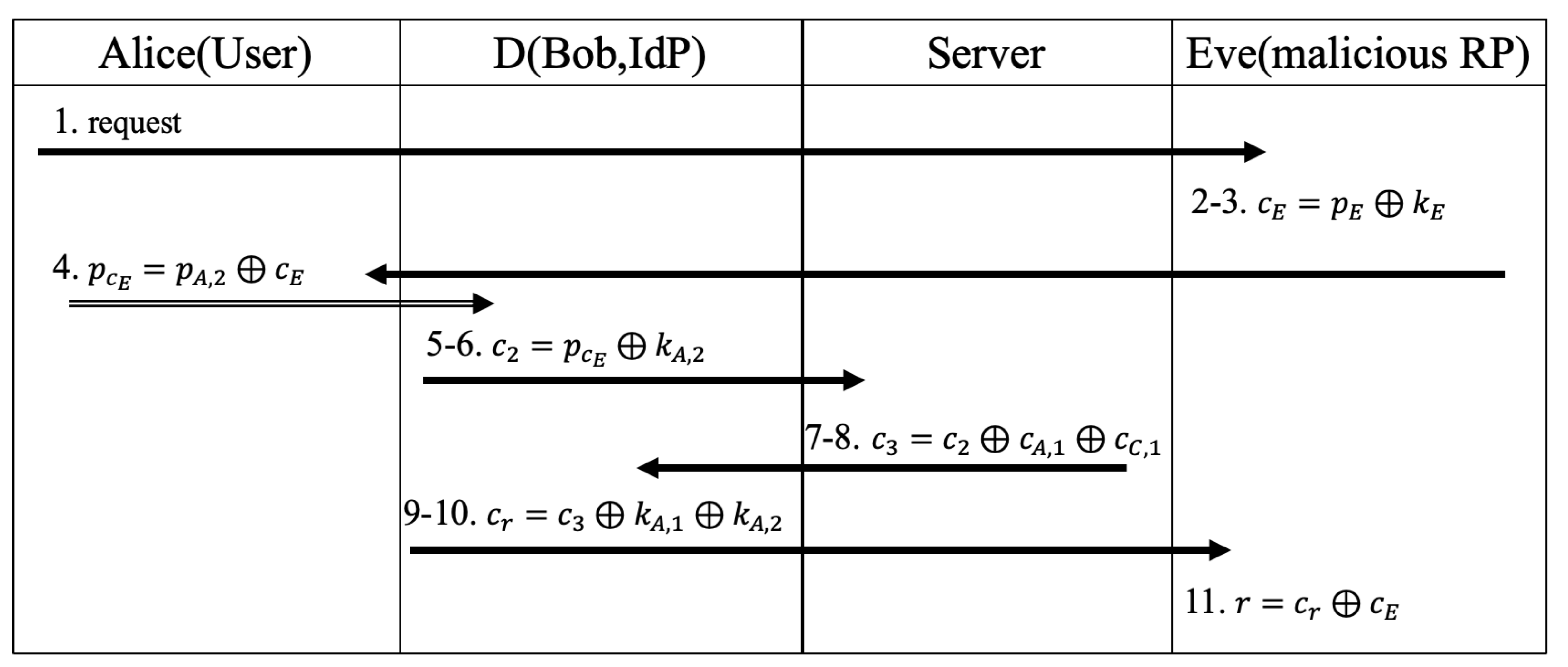
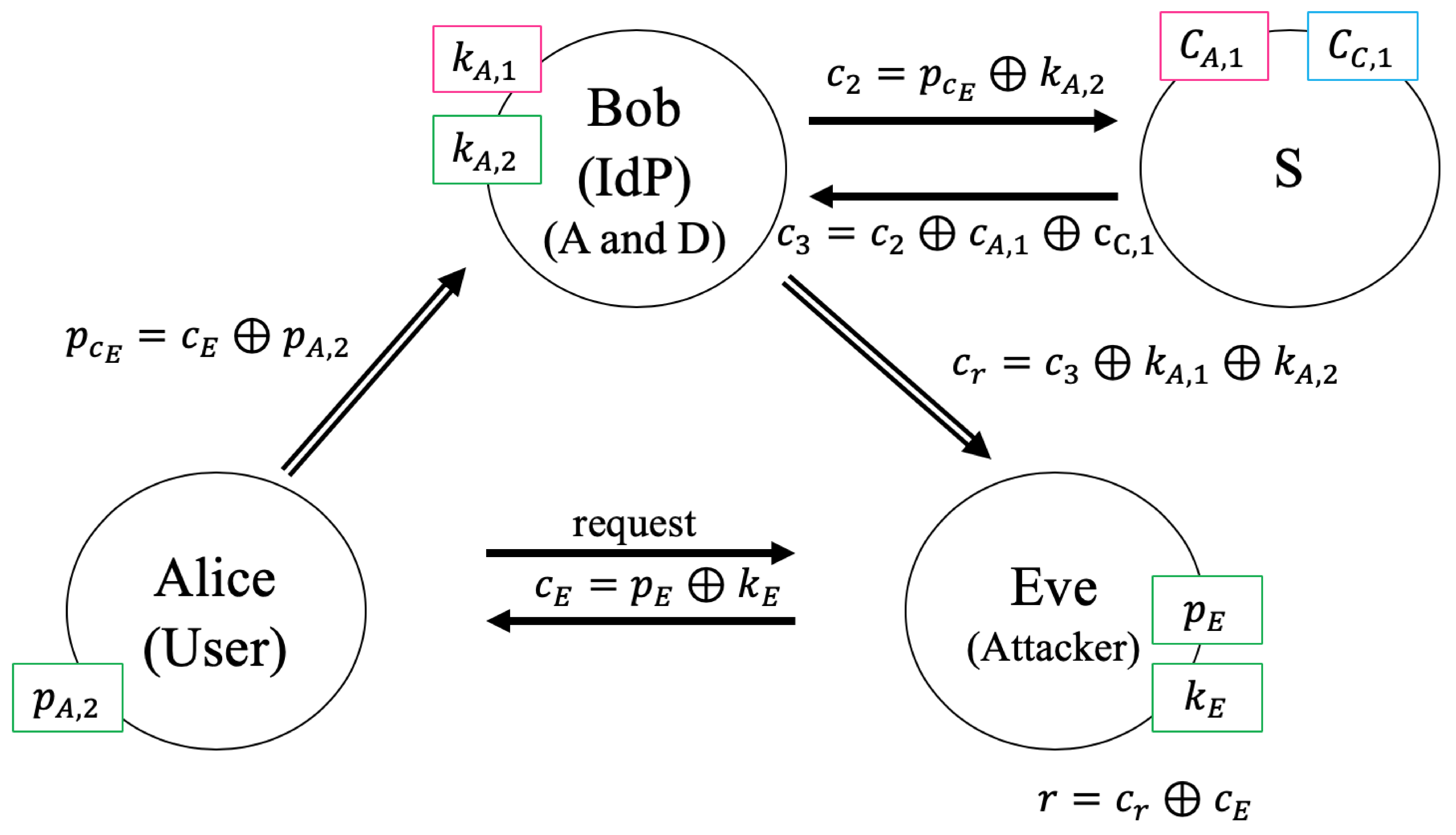
- Step 1
- Alice sends a request to Eve, impersonating Charlie’s service.
- Step 2
- Eve generates and computes
- Step 3
- Eve sends to Alice
- Step 4
- Alice computes and sends to D
- Step 5
- D generates and computes
- Step 6
- D sends to S
- Step 7
- S computes , where
- Step 8
- S sends to D
- Step 9
- D computes , where
- Step 10
- D sends to Eve who impersonates Charlie
- Step 11
- Eve computes , where
5.1.3. Security Analysis
5.2. Comparison
5.3. The Impact on Businesses
6. Conclusions
7. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Internet World Stats. Available online: https://www.internetworldstats.com/stats.htm (accessed on 31 March 2020).
- Hu, J.; Sun, Q.; Chen, H. Application of single sign-on (SSO) in digital campus. In Proceedings of the Third IEEE International Conference on Broadband Network and Multimedia Technology (IC-BNMT 2010), Beijing, China, 26–28 October 2010; IEEE: Piscataway, NJ, USA, 2011; pp. 725–727. [Google Scholar]
- Single Sign-on Market by Type (Enterprise, Federated & Web-Based, Windows Integrated), Organization Size (Small & Medium Enterprises, Large Enterprises), Deployment Mode (Cloud, On-Premises), Vertical, Region—Global Forecast to 2021. Markets and Markets. Available online: https://www.marketsandmarkets.com/Market-Reports/single-sign-on-market-83280444.html (accessed on 28 May 2020).
- Villanueva, J. 5 Big Business Benefits of Using SSO (Single Sign-On). Managed File Transfer and Network Solutions. Available online: https://www.jscape.com/blog/bid/104856/5-Big-Business-Benefits-of-Using-SSO-Single-Sign-On (accessed on 14 May 2020).
- Radha, V.; Reddy, D.H. A survey on single sign-on techniques. Proc. Technol. 2012, 4, 134–139. [Google Scholar] [CrossRef]
- Bazaz, T.; Khalique, A. A review on single sign on enabling technologies and protocols. Int. J. Comput. Appl. 2016, 151, 18–25. [Google Scholar] [CrossRef]
- De Clercq, J. Single sign-on architectures. In Proceedings of the International Conference on Infrastructure Security, Heidelberg, Germany, 1 October 2002; Springer: Berlin, Germany, 2002; pp. 40–58. [Google Scholar]
- Miller, S.P.; Neuman, B.C.; Schiller, J.I.; Saltzer, J.H. Project Athena Technical Plan. In Kerberos Authentication and Authorization System; Massachusetts Institute of Technology: Cambridge, MA, USA, 1988. [Google Scholar]
- Neuman, B.C.; Ts’o, T. Kerberos: An authentication service for computer networks. IEEE Commun. Mag. 1994, 32, 33–38. [Google Scholar] [CrossRef]
- Assertions and Protocols for the OASIS Security Assertion Markup Language (SAML) V2.0 OASIS Standard, OASIS. 2005. Available online: http://docs.oasis-open.org/security/saml/v2.0/saml-core-2.0-os.pdf (accessed on 6 April 2020).
- OpenID Foundation Website. Available online: http://openid.net/ (accessed on 6 April 2020).
- OAuth Website. Available online: https://oauth.net/2/ (accessed on 28 May 2020).
- Sun, S.T.; Pospisil, E.; Muslukhov, I.; Dindar, N.; Hawkey, K.; Beznosov, K. Beznosov KWhat makes users refuse web single sign-on? An empirical investigation of OpenID. In Proceedings of the Seventh Symposium on Usable Privacy and Security, Pittsburgh, PA, USA, 20–22 July 2011. [Google Scholar]
- Horie, S. Keeping Anonymity at the Consumer Behavior on the Internet: Proof of Sacrifice. Comput. Ethics-Philos. Enq. (CEPE) Proc. 2019, 2019, 5. [Google Scholar]
- Yang, F.; Manoharan, S. A security analysis of the OAuth protocol. In Proceedings of the 2013 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), Victoria, BC, Canada, 27–29 August 2013. [Google Scholar]
- Tsyrklevich, E.; Tsyrklevich, V. Single Sign-on for the Internet: A Security Story. 2007. Available online: https://bit.ly/2UCJZDo (accessed on 11 June 2020).
- Groß, T. Security analysis of the SAML single sign-on browser/artifact profile. In Proceedings of the 19th Annual Computer Security Applications Conference 2003, Las Vegas, NV, USA, 8–12 December 2003. [Google Scholar]
- Wu, T.D. A Real-World Analysis of Kerberos Password Security. Ndss, 3 February 1999. [Google Scholar]
- Kihara, M.; Iriyama, S. New authentication algorithm based on verifiable encryption with digital identity. Cryptography 2019, 3, 19. [Google Scholar] [CrossRef]
- Grassi, P.A.; Garcia, M.E.; Fenton, J.L. Digital Identity Guidelines; NIST Special Publication (NIST SP)-800-63-3; National Institute of Standards and Technology: Los Altos, CA, USA, 2017.
- Accardi, L.; Regoli, M.; Ohya, M. The QP-DYN algorithms. In QP–PQ Quantum Probability and White Noise Analysis; Accardi, L., Freudenberg, W., Ohya, M., Eds.; World Scientific: Singapore, 2010; pp. 1–16. [Google Scholar]
- Iriyama, S.; Tanaka, Y.; Hara, T.; Ohya, M. On a PRNG based on non-commutative algebra and its applications. SPT 2014, 13, 1–3. [Google Scholar]
- Proverif Webcite. Available online: https://prosecco.gforge.inria.fr/personal/bblanche/proverif/ (accessed on 2 June 2020).
- Security Assertion Markup Language (SAML) V2.0 Technical Overview. OASIS, 2008. Available online: http://docs.oasis-open.org/security/saml/Post2.0/sstc-saml-tech-overview-2.0.html (accessed on 14 May 2020).
- Iriyama, S.; Kihara, M. Encrypted Data Processing System and Program. Japan Patent PCT/JP2018/045505, 27 June 2019. [Google Scholar]
- Iriyama, S.; Kihara, M. Authentication System and Program. Japan Patent JP2020/25659, 18 February 2020. [Google Scholar]


| Types | Example |
|---|---|
| Token-based SSO | Kerberos |
| Public Key Infrastructure (PKI)-based SSO | BrowserID |
| Client-side credential caching | Windows Credential Manager |
| Server-side credential caching | CA ETrust SSO |
| Identity Assurance Level | |
|---|---|
| IAL1 | At IAL1, attributes, if any, are self-asserted or should be treated as self-asserted. |
| IAL2 | At IAL2, either remote or in-person identity proofing is required. IAL2 requires the identification attributes to be verified in person or remotely using, at least, the procedures described in SP 800-63A. |
| IAL3 | At IAL3, in-person identity proofing is required. Identification attributes must be verified by an authorized IdP representative by examining the physical documentation as described in SP 800-63A. |
| AAL | |
|---|---|
| AAL1 | AAL1 provides some assurance that a claimant controls an authenticator registered to the subscriber. AAL1 requires single-factor authentication using a wide range of available authentication technologies. Successful authentication requires a claimant to prove the possession and control of the authenticator(s) through a secure authentication protocol. |
| AAL2 | AAL2 provides high confidence that a claimant controls the authenticator(s) bound to the subscriber’s account. Proof of possession and control of two distinct authentication factors are required through secure authentication protocol(s). Approved cryptographic techniques are required at AAL2 and above. |
| AAL3 | AAL3 provides very high confidence that a claimant controls the authenticator(s) registered to the subscriber. Authentication at AAL3 is based on the proof of possession of a key through a cryptographic protocol. AAL3 is like AAL2, but also requires a “hard” cryptographic authenticator that provides verifier impersonation resistance. |
| Aspect | Specification |
|---|---|
| Operating System | macOS High Sierra 10.13.5 |
| CPU | Intel Core i7 1.7 GHz |
| Memory | 8 GB |
| Language | Python 2.7 |
| Type | Variable | Value |
|---|---|---|
| Plaintext | 11001101101010001011101111010001 00010011101111111001101110110100 01010100001011100100110001111101 10000000011111011100000001000010 | |
| Key | 11001011111110100100100110111010 10110110111001001110011110100001 11001001111000011011000110101110 11011111000111001010011100100100 | |
| Ciphertext | 00110101100110011100000000111111 10100101010110110111110000010101 10011101110011111111110111010011 01011111011000010110011101100110 |
| Type | Variable | Value |
|---|---|---|
| Plaintext | 11100111111100001010100100001110 01111000011111110101110010000110 10111011011010000110100100000000 11111000010101000101101010110000 | |
| Key | 10001000011100101001110011110010 01011100101000101011111100100111 01100110101000100111111010110101 01011101101111111011001101000000 | |
| Ciphertext | 01101111100000100011010111111100 00100100110111011110001110100001 11011101110010100001011110110101 10100101111010111110100111110000 |
| Type | Variable | Value |
|---|---|---|
| One-time key for Charlie | 11100101010100111100101001000100 10111111110010101110010110101100 10100100000011000000011111000111 00011111001101110110111001001100 | |
| Ciphertext | 00000010101000110110001101001010 11000111101101011011100100101010 00011111011001000110111011000111 11100111011000110011010011111100 | |
| Plaintext of Alice with cyphertext | 11111100110000001110101011001111 11010100000010100010001010011110 01001011010010100010001010111010 01100111000111101111010010111110 | |
| One-time key for Alice | 10100010100000000111100110001000 10001010101010000100000111010011 00111110001100110000001110011100 01101001011100010110101101000111 | |
| Ciphertext | 01011110010000001001001101000111 01011110101000100110001101001101 01110101011110010010000100100110 00001110011011111001111111111001 | |
| Encrypted result | 00000100010110110110011010000100 11011111001001001111110011111001 00110101011111001100101101000000 11110100111001010001000101101111 | |
| Result for Alice with encrypted result for Charlie | 01101101001000010101011010110110 11100011011010000101101010001011 11000010101011100111100101110010 01000010100010001101110100001100 | |
| Result | r | 0 |
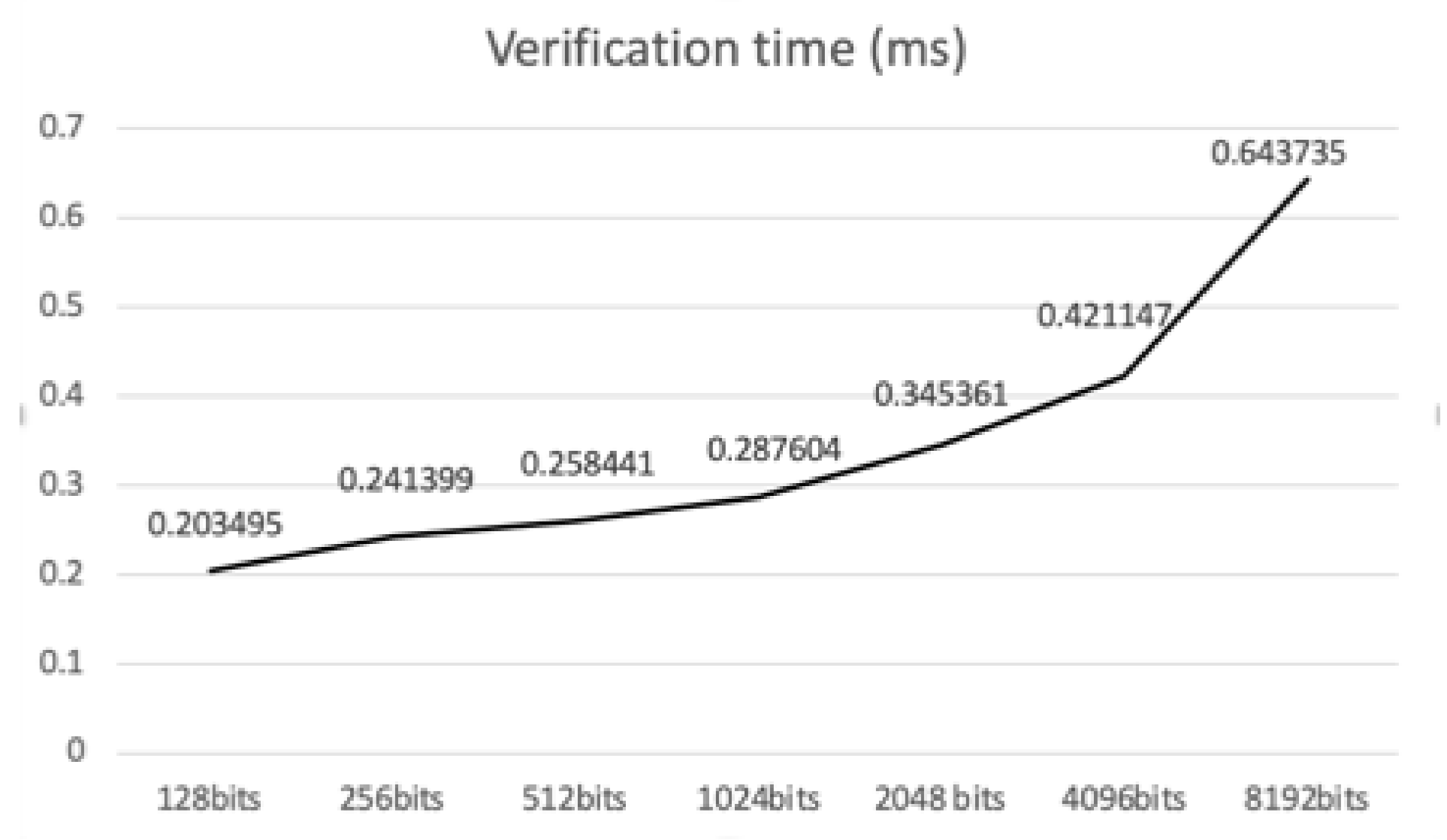
| Length of Plaintext | Verification Time |
|---|---|
| 128 bits | 0.203495 ms |
| 256 bits | 0.241399 ms |
| 512 bits | 0.258441 ms |
| 1024 bits | 0.287604 ms |
| 2048 bits | 0.345361 ms |
| 4096 bits | 0.421147 ms |
| 8192 bits | 0.643735 ms |
| Ciphertext | Contents |
|---|---|
| Combination | Calculation |
|---|---|
| Combination | Calculation |
|---|---|
| Combination | Calculation |
|---|---|
| 0 | |
| Combination | Calculation |
|---|---|
| Combination | Calculation |
|---|---|
| Combination | Calculation |
|---|---|
| Process 0 (that is, the initial process): {1}new ka1: key; ( {2}! {3}out(atob, pa1) ) | ( {4}! {5}in(atob, x: bitstring); {6}out(btos, senc(x,ka1)) ) – Query not attacker(pa1[]) in process 0. Completing… Starting query not attacker(pa1[]) RESULT not attacker(pa1[]) is true. |
| Verification summary: Query not attacker(pa1[]) is true. |
| Process 0 (that is, the initial process): {1}new kc1: key; ( {2}! {3}out(ctob, pc1) ) | ( {4}! {5}in(ctob, x: bitstring); {6}out(btos, senc(x,kc1)); {7}out(btoc, kc1) ) – Query not attacker(pc1[]) in process 0. Completing… Starting query not attacker(pc1[]) RESULT not attacker(pc1[]) is true. |
| Verification summary: Query not attacker(pc1[]) is true. |
| Process 0 (that is, the initial process): {1}new ka2: key; {2}new kc2: key; ( {3}! {4}out(atoc, request); {5}in(ctoa, cc2: bitstring); {6}out(atob, g(cc2,pa2)) ) | ( {7}! {8}in(atoc, req: bitstring); {9}out(ctoa, senc(pc2,kc2)); {10}in(btoc, cr: bitstring); {11}out(ctoa, result) ) | ( {12}! {13}in(atob, cp: bitstring); {14}out(btos, senc(cp,ka2)); {15}in(btos, c3: bitstring); {16}out(btoc, d(c3,ka1,ka2)) ) | ( {17}in(btos, c2: bitstring); {18}out(stob, f(c2,ca1,cc1)) ) – Query not attacker(pa2[]) in process 0. Completing… Starting query not attacker(pa2[]) RESULT not attacker(pa2[]) is true. – Query not attacker(pc2[]) in process 0. Completing… Starting query not attacker(pc2[]) RESULT not attacker(pc2[]) is true. |
| Verification summary: Query not attacker(pa2[]) is true. Query not attacker(pc2[]) is true. |
| Kerberos-Based [8,9] | OpenID [11] | SAML [10,24] | Proposed VE-Based SSO | |
|---|---|---|---|---|
| Independence of IdP and RP | Not independent | Independent | Not independent | Independent |
| Cryptosystem | AES | Diffie-Hellman | RSA | One-time pad |
| Usable identities | ID/Password | ID/Password | ID/Password | Any |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kihara, M.; Iriyama, S. Security and Performance of Single Sign-on Based on One-Time Pad Algorithm. Cryptography 2020, 4, 16. https://doi.org/10.3390/cryptography4020016
Kihara M, Iriyama S. Security and Performance of Single Sign-on Based on One-Time Pad Algorithm. Cryptography. 2020; 4(2):16. https://doi.org/10.3390/cryptography4020016
Chicago/Turabian StyleKihara, Maki, and Satoshi Iriyama. 2020. "Security and Performance of Single Sign-on Based on One-Time Pad Algorithm" Cryptography 4, no. 2: 16. https://doi.org/10.3390/cryptography4020016
APA StyleKihara, M., & Iriyama, S. (2020). Security and Performance of Single Sign-on Based on One-Time Pad Algorithm. Cryptography, 4(2), 16. https://doi.org/10.3390/cryptography4020016





