An Alternative Diffie-Hellman Protocol

Abstract

The Diffie–Hellman protocol, ingenious in its simplicity, is still the major solution in protocols for generating a shared secret in cryptography for e-trading and many other applications after an impressive number of decades. However, lately, the threat from a future quantum computer has prompted successors resilient to quantum computer-based attacks. Here, an algorithm similar to Diffie–Hellman is presented. In contrast to the classic Diffie–Hellman, it involves floating point numbers of arbitrary size in the generation of a shared secret. This can, in turn, be used for encrypted communication based on symmetric cyphers. The validity of the algorithm is verified by proving that a vital part of the algorithm satisfies a one-way property. The decimal part is deployed for the one-way function in a way that makes the protocol a post-quantum key generation procedure. This is concluded from the fact that there is, as of yet, no quantum computer algorithm reverse engineering the one-way function. An example illustrating the use of the protocol in combination with XOR encryption is given.

1. Introduction

More than 40 years ago, Whitfield Diffie and Martin Hellman introduced their paradigm-shifting protocol for encryption key generation [1]. By deployment of public parameters, their suggestion provides a means to secure privacy without the need for transmission of secret parameters. The security depends on the difficulty of solving the Diffie Hellman Problem, i.e., given integers q (the order of a group), g (a generator of that group), $g^a\text{mod}q$ (and possibly $g^b\text{mod}q$), guess the value of $g^{ab}\text{mod}q$. This problem has been proven to be equivalent to the Discrete logarithm Problem, i.e., given integers q, g and $g^a\text{mod}q$, guess the smallest positive integer value a. The Diffie–Hellman protocol was improved by adding authentication (to deal with threats such as the Man-in-the-middle-attack) and refined into descendants, e.g., the Needham–Shroeder and MQV protocols. The development of the Diffie–Hellman protocol by [2] provide a means for including three parties in the session key generation. The concept with a public key protocol for the generation of a shared secret was revolutionary and the achievement is well documented in the literature in the field (see e.g., [3]).

Nevertheless, since 1997, there has been the threat against the Diffie–Hellman protocol from a future more capable version of a quantum computer utilizing Shor’s algorithm for determining the discrete logarithm [4]. Therefore, the desire to develop encryption key algorithms which are resilient to this future threat has been pronounced.

Related Literature

The threat from the quantum computer threat has raised the demands for security assurance of algorithms in that they do not depend on the integer factoring problem or the discrete logarithm problem. One such new candidate for a different core mechanism is the shortest vector problem, in turn, related to the closest vector problem. These are the core guarantees for the security of the lattice-based alternatives among which the NTRU systems (see [5] for an introduction to NTRUEncrypt, [6] for the signature NTRU-SIGN and [7] about the key exchange algorithm NTRU-KE) have gained a leading position. Several properties of security and speed have been thoroughly investigated for this branch of the lattice procedures and the NTRU encryption algorithm is one of the foremost candidates in the NIST competition for the next-level post-quantum public-key encryption method. Still, according to [8], there is a need for improvements of NTRU-KE to make it resilient against man-in-the-middle attacks. Several NTRU descendants for key exchange based on the MaTRU cryptosystem, one of which was introduced by [9] and two other by [10] to mention a few. These protocols satisfy the perfect forward secrecy property and parameters are relatively smaller than the corresponding ones for the NTRU-KE. The other great branch of post-quantum technology is the code-based one. However, few key exchange algorithms have been developed from these systems. A third branch is supersingular isogeny techniques and here, [11] made a quantum computer-resilient Diffie–Hellman variant for ARM processors. Moreover, in [12], two variants of Diffie–Hellman are presented in which a quantum computer was used to synchronize clocks to initiate the process.

Here, a quantum computer-resilient encryption key agreement protocol is considered. It may be defined as indicated by Algorithm 1 in Section 2 below. To verify the validity of the protocol, the key generated by the sender and the key generated by the receiver must coincide. Other aspects such as computation complexity, quantum computer resilience, suggestions about what numbers, public and secret, that contribute to the security are dealt with in Section 3, and possible attacks and countermeasures to prevent them considered in Section 4. Finally an example is given as an illustration in Section 5 and conclusions are summarized in Section 6. Proof is presented in the Appendix A.

2. The Suggested Protocol

An initial transcendental parameter, $x\in \mathbb{R}\backslash \mathbb{Q}$, is common to both Alice and Bob. The security benefits from distributing x via a secure channel, but this is not necessary. This could be done in the spirit of [12], using a quantum particle state teleported from Alice to Bob or from a TTP to both. This number can, despite being transcendental, have a finite description (such as e or $\sqrt{2}$ or something). Thereafter, Alice calculates $a^{\prime }=ax\text{mod}1$ with some specified finite number of digits of accuracy. This she sends to Bob via an open insecure channel using her secret a. Bob uses his secret b to determine $b^{\prime }=bx\text{mod}1$, which he sends to Alice. Finally, Alice calculates $k=a{b}^{\prime }\text{mod}1,$ which coincides with Bob’s $k=a^{\prime }b\text{mod}1$ according to Theorem A1 in the Appendix A.

The suggested protocol for the generation of a common secret key is summarized in Algorithm 1. The function $F:\mathbb{Z}\to \mathbb{R}\backslash \mathbb{Q}$ is typically a pseudo random number generator (where s is the seed). $B_n$ is the set of the integers $\{2^{n-1},2^{n-1}+1,\dots ,2^n-1\}$. For a definition of the operation $(·\text{mod}1)$, see Definition A2 in the Appendix A. Thus, the shared secret, k, is established. The shared secret can subsequently be used for encrypted communication over an insecure channel via symmetric cyphers, such as XOR [13] or AES [14].

Algorithm 1: The suggested key agreement protocol.

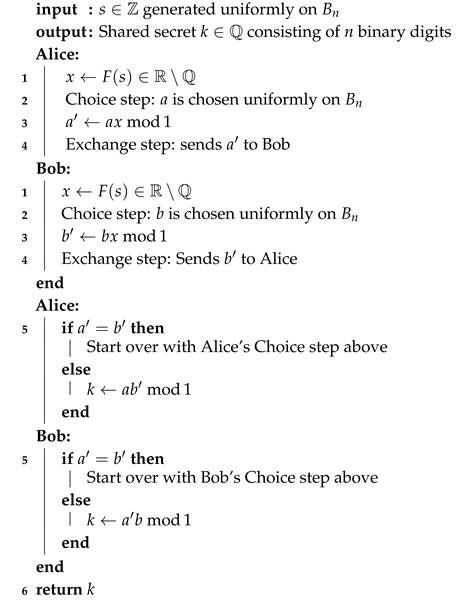Core Function

The protocol depends fundamentally on a core function, $C_x$, which should possess both a one-way property and a symmetry property. The parameter x belongs to a parameter space, S. Here, $S=\mathbb{R}\backslash \mathbb{Q}$.

The former property, the one-way property, means that given a, it should be simple to calculate $C_x\left(a\right)$ for any $x\in S$, while for any $x\in S$ and given c, it should be difficult to calculate a such that $C_x\left(a\right)=c$. This very problem, given x and c, both in $\mathbb{R}\backslash \mathbb{Q}$, the problem of guessing $a\in \mathbb{Z}$ such that $C_x\left(a\right)=ax\text{mod}1=c$ is henceforth referred to as the Modulo 1 Factoring Problem, M1FP as defined in Definition A3 in the Appendix A. Assuming that binary arithmetics is used, the maximum number of steps of $C_x$ are achieved in polynomial time (Theorem A2) while solving M1FP is $\mathcal{N}\mathcal{P}$-hard (Theorem A3).

The latter property is the symmetry property that

$$C_{C_x\left(b\right)}\left(a\right)=C_{C_x\left(a\right)}\left(b\right)$$

for all $x\in S$ in the parameter space and feasible values $a,b$. This has to be satisfied for establishment of a key agreement protocol. In this case, that function is the map $C_x:\mathbb{Z}\to (0,1)$ defined by $C_x\left(a\right)=ax\text{mod}1$. The symmetry property of $C_x$ is given by Theorem A1 stated and proven in the Appendix A.

3. Security Aspects

All aspects of robustness and security of a new means for encrypted communication need to be listed and scrutinized step by step. Regarding the proposed protocol, two points of scepticism that may come to mind are

• If the transcendental x is distributed via a secure channel, why not use this number directly as the encryption key?
• In computers, numbers are always finite—transcendental numbers with infinite extent are not possible, but rather floating point numbers with a finite extent are used as an approximation of the exact numbers. In what way does this use of finite floating point non-integers differ from the methods based on large integers?

As for point 1, using the transcendental x as the encryption key would, of course, be a possibility. A problem though is one of robustness; if the secrecy of this number was to be compromised, the encryption would be completely broken if this was the actual key. However, with this protocol, the rest of the procedure would then serve as an additional layer of security. Nevertheless, these treatments also add to the cryptanalytic computation complexity but two extra multiplications and an exchange of numbers are the prices to pay for this enhancement of security.

Regarding point 2, by specifying a transcendental number, there is no indication about how many decimals will be used for the finite key. Using software packages (like the Gnu Multiprecision Library, GMP, see [15]) arbitrarily makes many digits of the floating point approximations of the transcendental numbers possible. However, the length of the numbers $a^{\prime }$ and $b^{\prime }$ sent from Alice to Bob and vice versa via insecure channels, of course, reveal something about how many digits of accuracy are used in the floating point approximations. Moreover, for the final result (the secret shared between Alice and Bob) consisting of n digits, which are identical for both parties, the number of digits in both $a^{\prime }$ and $b^{\prime }$ needs to be at least $2n+1$. Then again, the security benefits by having the number of digits in $a^{\prime }$ and $b^{\prime }$ much larger than that.

3.1. One or Two Layers of Security

If both the initial number s and the parameters a and b are secret, this provides two layers of security. This version of the algorithm is referred to as Version 1. The use of such a protocol between parties unknown to each other would, of course, be awkward due to the necessity of having to secretly agree on the initial number. Nevertheless, for planned communication between parties prepared in advance, secret initial numbers can be distributed in advance and used later according to some scheme to gain an extra level of security when this is appropriate.

Alternatively, a one-layer security protocol may be implemented by letting the initial number be public. This version of the algorithm is referred to as Version 2. Then, all the security depends on M1FP and the secrecy of a and b. Still, if transcendental x is calculated with very many decimals, then there is an additional element of difficulty for the cryptanalyst provided by not knowing how many digits of accuracy in the transcendental are needed for the actual encryption key. The advantage of a public initial parameter is wanted in the case of initial contact for business communications by insecure channels [1]. In this situation, it is desired for the system for encrypted communication not to require parameters distributed by a secure channel. A protocol that allows the use of a public initial integer s is imperative to the establishment of successful communication and business deals between parties previously unknown to each other.

3.2. Comments about the Initial Transcendental Number

In the implementation of the suggested protocol, it is desired for the number $x=F\left(s\right)\in \mathbb{R}\backslash \mathbb{Q}$ to be entirely different for similar $s\in \mathbb{Z}$ to improve the unpredictability of the numbers involved. This means that if there is another $t\in \mathbb{Z}$ such that $s\ne t$ but $s\approx t$, this should not imply that $F\left(s\right)\text{mod}1\approx F\left(t\right)\text{mod}1$. More precisely, this property of discontinuity may be defined as

$$\exists ϵ>0\forall \delta >0:\left(\right|s-t|>\delta \wedge |F\left(s\right)-F\left(t\right)|<ϵ).$$

If a pseudo random number generator is used to this end, this discontinuity property should be satisfied to make the procedure less vulnerable.

3.3. Choices of the Secret Integers

As opposed to cryptography based on the integer factorization problem, discrete logarithm problem or elliptic curve versions of these problems, the integer parameters of the suggested protocol need not be prime numbers or satisfy any inter-relational conditions other than that secrets a and b must not be identical to each other.

4. Attacks and Countermeasures

Depending on whether the initial seed s is secret or not, a Naïve attack against the suggested protocol may be launched as indicated by Algorithm 2 below. It is done under the assumption that the function F, rendering the transcendental x from the seed s, is known to the attacker.

The case in which s is secret is referred to as Version 1 and the one when s is public is called Version 2. Having intercepted $a^{\prime }$ and $b^{\prime }$, Eve guesses at $s\in B_n=\{2^{n-1},2^{n-1}+1,\dots ,2^n-1\}$ whether this is a secret. Having made her guess $\sigma$ of s, she guesses $\theta$ at $a\in B_n$ and $b\in B_n$. Then, she calculates ${\theta }^{\prime }=\left[\alpha 2^{n}F\left(\sigma \right)\right]$ comparing ${\theta }^{\prime }$ to $a^{\prime }$ and ${\theta }^{\prime }=\left[\beta 2^{n}F\left(\sigma \right)\right]$ comparing this ${\theta }^{\prime }$ value to $b^{\prime }$. Once agreement (${\theta }^{\prime }=a^{\prime }$ or ${\theta }^{\prime }=b^{\prime }$) is established, the shared secret $\kappa =\theta {\theta }^{\prime }\text{mod}1$ is revealed. Based upon the number of digits in $a^{\prime }$ and $b^{\prime }$, she can infer how many digits N of accuracy the floating point x can be. The defense against this attack is the computation complexity, see Theorem A3 in the Appendix A.

Algorithm 2: Schematic description of the Naïve attack.

If the input $s\in B_n$ is public, Eve only needs to guess at $a\in B_n$ and $b\in B_n$ which obviously reduces the computation complexity. This corresponds to omitting the outer for-loop in the naïve attack Algorithm 2 above.

The most well known threat to the Diffie–Hellman protocol is the man-in-the-middle attack. This may, of course, also be carried out for the suggested protocol. Therefore, modifications corresponding to MQV and Needham–Schroeder protocols resilient to this attack through authentication procedures may be developed to block this opportunity for an eavesdropper.

4.1. Resilience against Quantum Computer

The core function of the suggested key agreement protocol involves arithmetic properties other than those of integer factorization and discrete logarithm. Thus, a capable future quantum computer so far does not impose a threat to the suggested algorithm.

4.2. Computation Complexity

According to Theorem A2 below, the computation complexity of the proposed algorithm is polynomial, while according to Theorem A3, the cryptanalysis by means of the naïve attack is $\mathcal{N}\mathcal{P}$-hard. These figures are on par with the computation efficiency of the Diffie–Hellman method [1].

5. An Example

Assume that Alice wants to send the message "I am Alice" to Bob. To facilitate the reading, the number base 10 is used in this example but for practical use, everything, of course, translates to binary numbers or any other base desired. She transforms the message “I am Alice” to a plaintext sequence of three-digit ASCII numbers $M=077032097109032065108105099101$. Then, for the key generation, Alice reads the number publically announced or secretly shared by them, uniformly picked on $D_n=\{{10}^n,{10}^n+1,\dots ,{10}^{n+1}-1\}$ (where n could be 1000 for a decent level of security with today’s capacity) where $D_n$ corresponds for decimal numbers to $B_n$ for binary numbers. This is a seed to be fed to a PRNG, which returns a real number, x, on $(0,1)$. Here, with, say, $s\mapsto log\left(s\right)\text{mod}1$ and the seed $s=2$ (for this simple example), Alice gets

$$x=0.693147180559945309417232121458\dots$$

She then chooses her secret a uniformly on $D_n$ (where n could be 1000 for decent security). Here, with $n=10$, she chooses, say, $a=9861328816$ and calculates

$$\begin{array}{cc}\hfill a^{\prime }& =ax\text{mod}1\hfill \\ \hfill & =6835352265.384943695140187286296328528834383488\dots \text{mod}1\hfill \end{array}$$

of which the first 61 decimals $0.3849436951401872862963285295789151385786568625756645191323560$ she sends to Bob for a 30-digit accuracy in the final k. Bob, on his end, chooses his secret $b=6913952452$ and calculates

$$\begin{array}{cc}\hfill b^{\prime }& =bx\text{mod}1\hfill \\ \hfill & =4792386648.629320605031170717208921697772544736\dots \text{mod}1\hfill \end{array}$$

of which the first 61 digits $0.6293206050311707172089216982945490750864162655735586555442321$ he sends to Alice. Then, after having checked that $a^{\prime }$ and $b^{\prime }$ differ, the final step of the key generation is realized. Alice generates the shared secret by

$$\begin{array}{cc}\hfill k& =a{b}^{\prime }\text{mod}1\hfill \\ \hfill & =6205937416.8964383718277266356796948498758244098716427375845541703221936\text{mod}1\hfill \\ \hfill & =0.8964383718277266356796948498758244098716427375845541703221936\dots \hfill \end{array}$$

as does Bob by

$$\begin{array}{cc}\hfill k& =a^{\prime }b\text{mod}1\hfill \\ \hfill & =2661482404.896438371827726635679694849875824409871642737584553678736912\dots \text{mod}1\hfill \\ \hfill & =0.896438371827726635679694849875824409871642737584553678736912\dots \hfill \end{array}$$

As for the encryption, Alice encrypts her plaintext

$$m=077032097109032065108105099101$$

e.g., by means of the XOR algorithm with the first 30 decimal digits of k, rendering the cryptotext

$$c=m\oplus k=697525738788675892280877652154$$

(using the decimal sequence of k as an integer and ⊕ as bitwise addition modulo 10), which she sends to Bob. Bob decrypts with the shared secret k consisting of his first 30 decimal digits simply by

$$c\ominus k=077032097109032065108105099101$$

(with ⊖ as bitwise subtraction modulo 10) which is readily transformed back to “I am Alice” by ASCII decoding.

6. Conclusions

Apart from being resilient to quantum computers, the great achievement of the suggested protocol as opposed to the Diffie–Hellman finite fields methodology is the use of the decimal part of a transcendental number rather than large finite integers. The use of transcendental numbers does not, by nature, restrict the number of digits in the calculation as do integers. In the case with finite fields, the secret numbers are limited by the order of the finite field q. For brute force guessing, one only has to systematically try all numbers less than q. With the proposed method, there is another bound indicated by the number of digits in the transmitted numbers $a^{\prime }$ and $b^{\prime }$. However, the cryptanalysis made possible by Shor’s and Grover’s algorithm does not seem to be a threat to this procedure.

Moreover, compared to the Diffie–Hellman method for the generation of a shared secret, the benefits of the suggested protocol are that it requires the transfer of fewer numbers initially and that the key size is unknown. This could, however, possibly be improved by the use of implementation of the algorithm in quantum computers because of their different treatments of transcendental numbers (see [16]). This remains an urgent path for pursuit in future research.