Key Management Systems at the Cloud Scale

Abstract

This paper describes a cloud-scale encryption system. It discusses the constraints that shaped the design of Amazon Web Services’ Key Management Service, and in particular, the challenges that arise from using a standard mode of operation such as AES-GCM while safely supporting huge amounts of encrypted data that is (simultaneously) generated and consumed by a huge number of users employing different keys. We describe a new derived-key mode that is designed for this multi-user-multi-key scenario typical at the cloud scale. Analyzing the resulting security bounds of this model illustrates its applicability for our setting. This mode is already deployed as the default mode of operation for the AWS key management service.

1. Introduction

Key management for a public cloud is based on the promise for availability, durability, and absolute security and privacy. This requires the following: (a) adherence to best known cryptographic practices and standards, in a highly available low-latency service; (b) the ability to provide (semantic) security while handling extremely large volumes of requests that are placed by an extremely large number of users that utilize different keys (i.e., a multi-user–multi-key scenario). The adversary is assumed to have a user’s capability (and credentials) and can eavesdrop and also make forgery attempts. We call such an encryption system that satisfies these requirements a “cloud-scale encryption system” ($\mathtt{CES}$). This paper examines the requirements for a $\mathtt{CES}$ against some engineering decisions that were made in deploying the real-world solution called Amazon Web Services (AWS) Key Management Service [1]. It describes an enhancement of an encryption mode that is used by the implementation, and demonstrates security bounds that surpass the initially designed properties of the underlying model, under the cloud’s multi-user–multi-key scenario.

An encryption service with high availability and durability requires redundancy, and therefore state management across redundant nodes. State replication introduces unwanted latency for many applications requiring consistency. To the extent feasible, state replication should be minimized across redundant nodes, especially for functions that are sensitive to latency. A $\mathtt{CES}$ should be able to handle simultaneous calls to encrypt and decrypt, without resource contention, noticing that encryption/decryption under a master key is a latency-sensitive functionality.

A fundamental decision of the $\mathtt{AWS}\mathtt{KMS}$ design is to allocate a user-specific master key ($\mathtt{CMK}$) as the root node for a user (customer). For operational and security reasons, the service provides only a limited set of data-plane operations using this master key, including encryption and decryption. Obviously, an adequate symmetric authenticated encryption with associated data (AEAD) mode of operation is a critical building block for the service, and AES-GCM [2] is a natural selection for such a primitive. It is a (NIST) standard model that enjoys overall acceptance, security proofs, and excellent performance with side-channel resistance when running on modern platforms (that have AES-NI and PCLMULQDQ instructions) which are the target platforms in our context. But is AES-GCM indeed suitable at the cloud-scale? Here are a few challenges.

The small block size of AES, 128-bits, is in contention with PRP-PRF bounds. Encryption rates within a cloud environment can easily reach the birthday bounds for 128-bit block ciphers. Furthermore, to reduce state management in the deployed system, AES-GCM needs to be used with random $IV$s. The restriction on $IV$ reuse with AES-GCM impinges further on the number of unsynchronized encryptions across distributed nodes. Conforming to standardized ciphers and modes induces requirements for avoiding $IV$ reuse. This imposes a need for frequent change of master keys before reaching $IV$ collision probability thresholds. This is too costly and cumbersome for real-world deployment.

These difficulties motivate the $\mathtt{AWS}\mathtt{KMS}$ solution to use a new mode of operation, which we call $\mathtt{CES-GCM}$. This mode uses a random nonce and $IV$ and applies a nonce-based key derivation before every encryption.

1.1. Related Work

The sensitivity of AES-GCM to a nonce reuse and the imposed limits on the use of a key when the $IV$s are chosen randomly are known issues. The idea of re-keying cipher schemes to extend the lifetime of a key was proposed by Abdalla and Bellare  [3] and standardization of its variants are being discussed by the IETF [4]. Multi-key scenarios for ciphers and MACs, with a one-of-many-keys key recovery goal, have also been studied (e.g., [5,6]). Analysis of AES-GCM in the multi-user scenario as used for TLS 1.3, is discussed by Bellare and Tackmann [7], and also in [8].

AES-GCM-SIV [9] builds on the synthetic $IV$ mechanism proposed by Rogaway and Shrimpton [10] and is in the process of standardization by the IETF [11]. This mode takes a nonce-misuse-resistant underlying scheme (GCM-SIV+) as the basis, and builds a per-nonce key derivation on top. This extends the lifetime of a key. AES-GCM-SIV is not yet standardized, but is already in use (by Google; for QUIC [12]).

Gueron and Lindell [13] described a general approach for taking any nonce based encryption scheme and prepending a nonce-based key derivation for each encryption in a way that the nonce is used for both the key derivation and the scheme itself. They showed that this extends the lifetime of a key and improves the security bounds. Such schemes lead to a multi-key situation due to the per-message key derivation. AES-GCM-SIV is a special case of this construction. A very recent study by Bose, Hoang, and Tessaro  [14] discusses the behavior of AES-GCM-SIV in a multi-user case, and establishes generalized and improved bounds. In fact, the composition of the results of [13,14] gives the analysis for AES-GCM-SIV in a multi-user-multi-key scenario.

This paper describes the $\mathtt{CES-GCM}$ mode currently used in $\mathtt{AWS}\mathtt{KMS}$. It does not claim that $\mathtt{CES-GCM}$ is necessarily superior to AES-GCM-SIV. Timeline wise, initial $\mathtt{AWS}\mathtt{KMS}$ deployment started in 2014, using AES-GCM, and was limited only to the “Elastic Block Storage” service. Subsequently, the difficulties described above, that emerged from scaling it to other services, required a different mode. Authenticated encryption solutions that could address the cloud-scale challenges were not known (at least not publicly) or standardized at the time. Thus, the reported work predates the excellent works of [9,13] (on AES-GCM-SIV) and of [14] (that enhanced its analysis), which were published in 2017/8. $\mathtt{CES-GCM}$ differs from AES-GCM-SIV in several respects, including the separation of the nonce that is used for key derivation and the $IV$ used for encryption. Such separation allows for the independent generation (at different steps of the encryption) of the random nonce and $IV$, thus insulating the implementation from a single system failure in the entropy injection. We call this property “nonce-misuse-independence”. Since $\mathtt{CES-GCM}$ builds directly over AES-GCM, its properties are achieved while straightforwardly adhering to FIPS certification requirements ($\mathtt{AWS}\mathtt{KMS}$ is FIPS certified).

1.2. Our Contribution

• We describe the challenges and considerations that need to be addressed by any design of a $\mathtt{CES}$. We explain why current modes (such as AES-GCM) are not a suitable solution to the problem and a tailored mode is required. Nevertheless, a $\mathtt{CES}$ for the public cloud should adhere to well established cryptographic standards in order to be trusted by cloud users. This restricts the flexibility of the choices that the tailored mode may have.
• We define and analyze a mode of operation ($\mathtt{CES-GCM}$) that is suitable for multi-user-multi-key large scale usages, and has nonce-misuse-independence. It builds on top of a nonce respecting mode (AES-GCM). To the best of our knowledge, this is the first multi-user-multi-key mode that is being deployed in a real cloud system.

The remainder of this paper includes Section 2 with some preliminaries and notation. Section 3 provides a detailed description of the constraints and desired properties of a $\mathtt{CES}$, design choices made while building the deployed $\mathtt{AWS}\mathtt{KMS}$, and the motivation for using the $\mathtt{CES-GCM}$ mode. Section 4 provides a security analysis of $\mathtt{CES-GCM}$, and Section 5 summarizes the paper.

2. Preliminaries and Notation

In this paper, we refer to the well known AES-GCM scheme as defined in [15]. For context and notation, we provide a brief parameterized description.

Let E be a block cipher with block size n bits, and key length $\kappa$. E-GCM is the straightforward formulation of AES-GCM using E for the block cipher. We fix a parameter $0<\delta <n$ and set the length of the initialization vector $IV$ to ${\ell }_{\mathtt{IV}}=n-\delta$. GHASH is the polynomial-evaluation universal hash function computed in $GF\left(2^n\right)$ using the hash key H, analogously to the definition of AES-GCM.

A block is an element of ${\{0,1\}}^n$. A valid message $\mathtt{M}$ consists of (up to) ${\ell }_M$ plaintext blocks, and (up to) ${\ell }_{AAD}$ Additional Authenticated Data (AAD) blocks $\mathtt{AAD}$, where ${\ell }_M\le 2^{\delta }-2$. For simplicity, we assume that plaintext and AAD lengths are integer multiples of n.

Consider the encryption of $\mathtt{M}$ under the key $\mathtt{K}$ and $IV$$\mathtt{IV}$. The outputs are the ciphertext $\mathtt{C}$ (of the same length as the plaintext) and the authentication tag $\mathtt{Tag}$ (of n bits) that are computed as follows. First the GHASH key is set to $H=E_{\mathtt{K}}\left(0\right)$. Then the ${\ell }_M+1$ blocks ${\mathtt{CTRBLOCK}}_{\mathtt{IV},j}=[\mathtt{IV}\parallel \#(j+1)]$, $j=0,\dots ,{\ell }_M$, are fixed, where $\#j$ denotes the encoding of the integer j as a string of $\delta$ bits and ∥ denotes concatenation. Note that for a given $\mathtt{IV}$, ${\mathtt{CTRBLOCK}}_{\mathtt{IV},j}$, $j=0,\dots ,{\ell }_M$, are distinct, and also different from the zero block, and that for every $0\le i,j\le {\ell }_M$ and ${\mathtt{IV}}^{\prime }\ne \mathtt{IV}$, we have ${\mathtt{CTRBLOCK}}_{\mathtt{IV},i}\ne {\mathtt{CTRBLOCK}}_{{\mathtt{IV}}^{\prime },j}$.

The ciphertext $\mathtt{C}$ consists of ${\ell }_M$ ciphertext blocks where the j-th ciphertext block is the XOR of the j-th plaintext block with $E_{\mathtt{K}}\left({\mathtt{CTRBLOCK}}_{\mathtt{IV},j}\right)$. The authentication tag is the XOR of the GHASH value (computed over the ciphertext blocks and the AAD) with $E_{\mathtt{K}}\left({\mathtt{CTRBLOCK}}_{\mathtt{IV},0}\right)$. The flows for decryption and tag verification are straightforward. Decryption takes $\mathtt{C}$, $\mathtt{Tag}$, $\mathtt{AAD}$, and $\mathtt{IV}$ as input, and returns $\mathtt{M}$ if the authentication passes, and ⊥ otherwise.

The list of ${\ell }_M+1$ counter blocks that are encrypted with E during the encryption of $\mathtt{M}$ using $\mathtt{IV}$ is denoted

$$\mathcal{L}(\mathtt{IV},{\ell }_M)$$

(1)

The additional encryption of the zero block to form the GHASH key $H=E_{\mathtt{K}}\left(0\right)$ is amortized over all encryptions under the same key $\mathtt{K}$. For encryption, the $IV$ can be chosen randomly, and in that case we call the scheme E-GCM with a random $IV$. However, it is critical to never encrypt two (or more) messages under the same key and with the same $IV$.

We use the following result of Suzuki et al. [16] for the probability of a multicollision.

Theorem 1

(Theorem 2 of [16]). Let $2\le r\le q\le A$ be integers. Suppose that q balls are thrown, one by one (independently) at random, into A bins. An r-multicollision is the event where there exists at least one bin that contains at least r balls. Denote this event by $MultiColl(A,q,r)$. Then

$$Pr\left[MultiColl(A,q,r)\right]\le \frac{q^r}{r!·A^{r-1}}$$

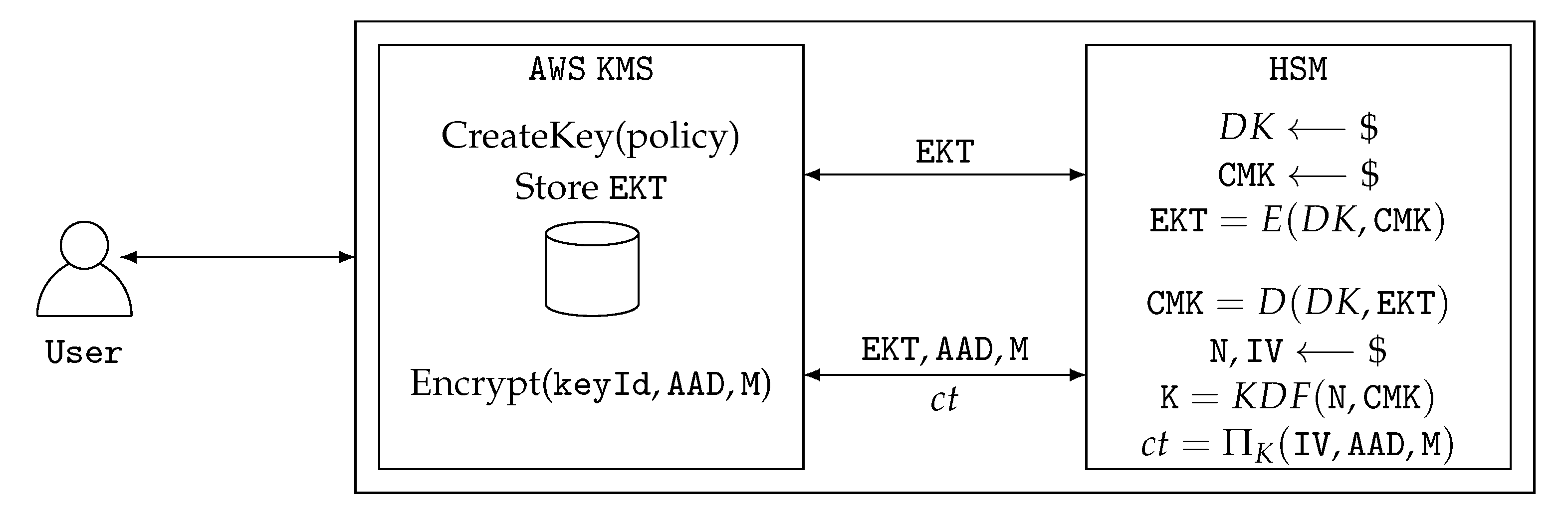
3. A Cloud-Based Key Management Service

The AWS Key Management Service allows customers to create and manage keys and control the use of these keys across a wide range of AWS services and applications. $\mathtt{AWS}\mathtt{KMS}$ protects these customer keys by ensuring they are never accessible outside of FIPS 140-2 validated hardware security modules. $\mathtt{AWS}\mathtt{KMS}$, while capable of being used as an encryption service, primary application is for generating, encrypting and decrypting data keys to be used in envelope encryption. Attempting to channel all data through a single service like $\mathtt{AWS}\mathtt{KMS}$ would be bandwidth and computationally infeasible at acceptable latency times. Additionally, it makes little sense to transmit the data over an encrypted channel only to receive it back encrypted under another key. To prevent these unwanted use-cases $\mathtt{AWS}\mathtt{KMS}$ limits the amount of data that can be encrypted to 4096 bytes.

We refer to the customer keys as Customer Master Keys ($\mathtt{CMK}$s). When a $\mathtt{CMK}$ is created, a key identifier ($\mathtt{keyId}$) and an access control policy is associated with the key. The policy restricts which users (principals) can call what APIs (actions) using this key. AWS provides a rich set of tools to specify access control policies [17].

$\mathtt{AWS}\mathtt{KMS}$ is a distributed tier-service where users call into a front-end service, which in turn communicate with the HSMs. Distributed services deliver greater availability and partition tolerance at the expense of latency to ensure consistency. $\mathtt{AWS}\mathtt{KMS}$ is designed to provide simultaneous data-plane calls (GenerateDataKey, Encrypt, and Decrypt) with minimal latency. This is accomplished by ensuring that data-plane calls do not require the distribution of state to ensure consistency. This introduces new requirements that impact how modern encryption modes, like AES-GCM, are used within a high-volume distributed service.

We depict the $\mathtt{AWS}\mathtt{KMS}$ in Figure 1 through two basic APIs. CreateKey is a control plane API, that results in a $\mathtt{CMK}$ being created on behalf of a customer. This causes a state change within $\mathtt{AWS}\mathtt{KMS}$ where a new $\mathtt{CMK}$ must be durably stored as an encrypted key token $\mathtt{EKT}$, and synchronized across the data storage layer. Encrypt is a data plane operation which utilizes a $\mathtt{CMK}$ but does not alter the state of $\mathtt{AWS}\mathtt{KMS}$.

The service is integrated with many other AWS services to help users protect the data stored in these services. $\mathtt{AWS}\mathtt{KMS}$ constitutes an instantiation of the $\mathtt{CES}$ model that is described in this paper.

3.1. Requirements

The design of a $\mathtt{CES}$ is naturally iterative, in which initial requirements are met with design decisions which impose new requirements. We start our description with constraints, and then identify new constraints imposed by design decisions.

Cloud computing provides on-demand compute power, database, storage, applications and other IT services. It provides these services through a web-based API, authenticated by using account credentials. Each API call is authenticated and authorized against policies associated with resources. Customers reason about their data differently, and a cloud-based key management system should be flexible in the ways it allows customers to use authorization policies to compartmentalize access to data. The ability to define a policy based on a customer master key ($\mathtt{CMK}$) object helps customers impose their logic onto the access control of data in cloud provider services.

A major benefit of cloud computing is the economies of scale using shared infrastructure. In cryptography, these benefits can only be realized if they are met with additional assurances that the cloud provider is providing comparable security measures. Thus, FIPS 140-2 certification of hardware components and clear SOC reports and audits that cover the system should be provided.

There are many ways to meet the challenges of key management in the cloud [18]. In addition to providing a secure interaction between the customer and the cloud services, and the integration of encryption into those services, the overall design must afford highly distributed encryption of data. In order to achieve this, a $\mathtt{CES}$ must support a distribution of roles of key generation and data encryption, a form of envelope encryption.

Additional requirements are derived from customer input and yielded the following:

• Copious: must support many $\mathtt{CMK}$s. Customers want to reason about use cases.
• FIPS: $\mathtt{CMK}$s can only be accessed within a FIPS 140-2 certified security module.
• Low-latency: generate, encrypt and decrypt of data keys under a $\mathtt{CMK}$ must have low-latency.
• Simultaneous use: A $\mathtt{CMK}$ can be used simultaneously within the system.
• Durability: $\mathtt{CMK}$s must be at least as durable as the data that they protect.
• High volume: each $\mathtt{CMK}$ must be able to encrypt a large number of objects.
• Scalability: a $\mathtt{CES}$ should be able to support a large volume of calls across many customers.
• Distributive: a $\mathtt{CES}$ should be able to distribute the role of key generation and bulk data encryption.

3.2. Desired Properties of a CES

A $\mathtt{CES}$ is not meant to be a general-purpose cryptographic service provider because transmitting all data over the network for encryption would cause unnecessary bottlenecks. Instead, a $\mathtt{CES}$ design facilitates envelope encryption, where a data key is generated on an HSM, and returned to the user in plaintext and encrypted under the user’s $\mathtt{CMK}$. The user can encrypt their data locally, delete the data key in memory, store the encrypted data, and $\mathtt{CMK}$-encrypted data key. Consequently, a $\mathtt{CES}$ design can limit the amount of data that can be encrypted in a single Encrypt call.

A CES should support IND-CPA and IND-CCA2 semantic security (i.e., be secure under non-adaptive and adaptive chosen plaintext and chosen ciphertext attacks). Ideally, it would use an encryption mode with 256-bit keys, in order to satisfy the strictest requirements that customers may require, and also accommodate multi-key and multi-user complications.

Message authenticity. A fully featured access control policy on a $\mathtt{CMK}$ allows authorization constraints that mimic aspects of public key cryptography. It is possible to write access control policies that separate a set of users who can call “Encrypt” or “GenerateDataKey” under a given $\mathtt{CMK}$, from a set of users that can call “Decrypt”. Further, a $\mathtt{CES}$ design should be able to enforce policies like “all users can encrypt before midnight”, and “only a specific user can decrypt after midnight”. This highlights a specific need for message authenticity for cases where the decrypting entity is different from the encrypting entity.

Message authenticity of a successfully decrypted message requires verification that the correct $\mathtt{CMK}$ was used to decrypt the message. This can be enforced by verifying the correct $\mathtt{CMK}$ is used during the decrypt call. Otherwise, consider the scenario where all the ciphertexts are replaced with a new set of ciphertexts, encrypted to an adversary’s $\mathtt{CMK}$. The adversary could set a permissive policy that lets all users decrypt under their $\mathtt{CMK}$. When the user calls Decrypt, the decryption will succeed, but the message will have been encrypted by the adversary. Default policies for a $\mathtt{CES}$ should prevent such a scenario, so by default users should not be allowed to call across accounts without modifications to default policies. In our design it is recommended that the input key identifier ($\mathtt{keyId}$) is verified against the expected key identifier. Furthermore, it is important that the service would provide configurable alert mechanisms on decryption failures to alert on potential forgery attempts.

Durability. Cloud providers deliver durability through redundant storage. A $\mathtt{CES}$ should support at least the amount of durability the cloud provider supports for the integrated services that are using it. This requires secure redundant storage of $\mathtt{CMK}$s. The requirement on redundancy and the number of independent $\mathtt{CMK}$s a $\mathtt{CES}$ needs to support preclude the ability to store $\mathtt{CMK}$s on cost-efficient commodity HSMs.

Auditability. Information systems require complete auditing. Especially since, unlike an on-premise system, customers cannot directly inspect cloud provider systems. Customers demand to have clear audit records of when attempts are made to access their data. Thus, a $\mathtt{CES}$ must also supply to its users all attempted access and use of their $\mathtt{CMK}$.

3.3. Requirement Driven Design

This section shows how the general requirements are translated to the set of design choices made for $\mathtt{AWS}\mathtt{KMS}$. The requirements for a $\mathtt{CES}$ include the ability to secure all $\mathtt{CMK}$s in a FIPS 140-2 certified HSM. The master keys themselves must be highly durable and accessible with low-latency. A service provider should strive to remove all limits on the customer’s use. Users should be able to protect quadrillions of objects under a single master key, and the service should be able to support trillions of master keys on behalf of its customers.

The FIPS requirement restricts the selection of cryptographic algorithms to the use of FIPS-approved methods. The obvious (and practically the only) choice for the authenticated encryption, that ensures the system provides the broadest use case, is AES-GCM [15]. This mode (more specifically, AES256-GCM with a 96-bit initialization vector) is indeed chosen for all encryptions done by $\mathtt{AWS}\mathtt{KMS}$. However, we show here why the straightforward application of AES-GCM involves some serious limitations in the $\mathtt{CES}$ setting, thus illustrating why some enhancement is required.

In AES-GCM, the reuse of an $IV$ results in major security issues. Repeating a derived counter value between two instantiations of AES-GCM under the same key leads to loss of confidentiality for these two messages. More critically, if an adversary observes two encryptions under the same $IV$ (and key), it is likely that the hash key (H) used in the scheme would be discovered. Learning the hash key would allow an adversary to modify the $AAD$ or ciphertext (or both), and use the exposed hash key to create a valid message authentication tag. The AES-GCM specification [15] addresses this concern and requires the following:

“The probability that the authenticated encryption function ever will be invoked with the same $IV$ and the same key on two (or more) distinct sets of input data shall be no greater than $2^{-32}$.”

This constraint is not limited to the single user scenario, but applies equally to the multi-user scenario of a $\mathtt{CES}$. In other words, this creates a requirement for a $\mathtt{CES}$ to ensure that this probability is not exceeded globally, across all keys and $IV$s, and is not simply limited to a single key.

High availability for continuously operating services requires redundancy. Delivering a consistent service across a redundant fleet of HSMs requires some state management. To the extent possible, state replication should be minimized. A $\mathtt{CES}$ needs to ensure that the most time-sensitive operations (in particular, encrypt and decrypt under a customer master key) do not involve a synchronized state change across the HSM fleet. This allows for delivering a highly available service with low latency. To reduce managed state, AES-GCM is used with random $IV$s. We note that alternative counter-based methods require, at a minimum, process or thread communication of state across encryption calls locally on an HSM. Unfortunately, the use of a 96-bit random $IV$ limits the amount of data that can be encrypted directly with a single $\mathtt{CMK}$ to $2^{32}$ ($\approx 4$ billion) messages (Note that using an $IV$ with bit-length different from 96, translates (by the definition of AES-GCM) to processing a “randomized” 96-bit portion in the resulting counter blocks. This leads to exactly the same limitation on the number of usages, as the case of using 96-bit $IV$). To illustrate, if a commercial $\mathtt{CES}$ is designed to support encryption rates of 1200 requests per second, then master key rotations would be required every 41 days. This would result in more state management, and increased storage within the service. This serious drawback is an indication that AES-GCM is not suitable for a $\mathtt{CES}$ in its native form, and some enhancements are needed.

The top of an individual user’s key hierarchy is a customer master key ($CMK$). It is important to understand that by the security design considerations, the owner of a $CMK$ can use it only implicitly, via (authenticated) web-based APIs.

In our CES, $\mathtt{AWS}\mathtt{KMS}$, a user’s $\mathtt{CMK}$ is generated on an HSM and is accessible only on the HSMs managed by the service. To meet our durability requirements, $\mathtt{CMK}$s are stored encrypted outside of the HSM fleet in an online distributive database and a highly durable offline data store. $\mathtt{CMK}$s are bound to a globally unique key identifier ($\mathtt{keyId}$) assigned by the distributive database system. It is bound by the HSM’s encryption of the $\mathtt{CMK}$. The $\mathtt{keyId}$ is returned to the user on a successful request to create a $\mathtt{CMK}$. $\mathtt{AWS}\mathtt{KMS}$ only allows access to encrypt and decrypt calls under a $\mathtt{CMK}$ using the secure defaults of the system. An access control policy is associated with $\mathtt{keyId}$, and enforced on every API call referencing $\mathtt{keyId}$. The policy controls which users can encrypt or decrypt using a specific $\mathtt{CMK}$.

For context, we provide some additional details on the AWS Key Management Service that utilizes FIPS-approved algorithms for the cryptographic operations. On an encryption call, a user who wishes to encrypt a message $\mathtt{M}$ under their $\mathtt{CMK}$, passes the $\mathtt{keyId}$, $\mathtt{M}$, and $\mathtt{AAD}$ to an “Encrypt” API. On an HSM, a freshly generated nonce $\mathtt{N}$ is used for deriving a fresh encryption key $\mathtt{K}$, using the NIST SP800-108 Key Derivation Function (KDF) in Counter Mode with PRF HMAC-SHA256 [19]. Subsequently, a fresh $\mathtt{IV}$ is used for encrypting $\mathtt{M}$ into ciphertext $\mathtt{C}$ and computing $\mathtt{Tag}$ for $\mathtt{C}$ and $\mathtt{AAD}$, under the derived key $\mathtt{K}$. In our concrete instantiation, the limit we analyze is 4096 bytes (256 blocks) for the plaintext message, and 8192 bytes (512 blocks) for $\mathtt{AAD}$. A single data structure $\mathtt{ciphertextBlob}$ containing an internal key identifier $\mathtt{u}$, $\mathtt{N}$, $\mathtt{IV}$, $\mathtt{C}$, and $\mathtt{Tag}$, is returned to the user. Figure 2 illustrates the process.

A good design of a $\mathtt{CES}$ should envision the possibility of separating the modules for generating per-message encryption keys from the modules handling the actual message encryption. This facilitates cryptographic isolation of the $\mathtt{CMK}$-handling modules and allows the components to scale independently. A primary function of $\mathtt{AWS}\mathtt{KMS}$ is to protect data keys for use in other applications through the “GenerateDataKey” API. This is the essential method for generating data keys to encrypt customer data within AWS. However, the design of $\mathtt{AWS}\mathtt{KMS}$ leaves the ability to encrypt larger amounts of data within $\mathtt{AWS}\mathtt{KMS}$ by moving the key $\mathtt{K}$ closer to the data to be encrypted, thus reducing bandwidth requirements. Within $\mathtt{AWS}\mathtt{KMS}$ the role to generate the $\mathtt{N}$ and derive $\mathtt{K}$ from the $\mathtt{CMK}$ can be separated from the the role to generate $\mathtt{IV}$ and encrypt the message $\mathtt{M}$. This reduces correlated errors in generation of the $\mathtt{N}$ and $\mathtt{IV}$, and allows for independent scaling of per-message key derivation and message encryption.

An authorized user can call a “Decrypt” API passing in $\mathtt{AAD}$ and $\mathtt{ciphertextBlob}$. An HSM will parse $\mathtt{ciphertextBlob}$, extract the key identifier $\mathtt{u}$, $\mathtt{N}$, $\mathtt{IV}$, $\mathtt{C}$, and $\mathtt{Tag}$, and obtain $\mathtt{K}$ using the referenced $\mathtt{CMK}$ and $\mathtt{N}$. The HSM will verify the message authenticity over $\mathtt{C}$ and $\mathtt{AAD}$, and (conditionally) decrypt the message. Upon successful tag verification, the plaintext and $\mathtt{CMK}$’s $\mathtt{keyId}$ are returned to the caller. A decryption error message is returned otherwise.

Part of the control privileges of a user in our design is that a user can configure key rotation for their $\mathtt{CMK}$ (see [20]). Key rotation would result in the generation of a new master key and an internal key identifier $\mathtt{u}$, under the existing $\mathtt{keyId}$. Obviously, the service must retain all key versions under $\mathtt{keyId}$ and enforce the associated key policy on subsequent calls using these keys. All new encryption calls will use the latest $\mathtt{CMK}$ version, and the version indicated by $\mathtt{u}$ in the $\mathtt{ciphertextBlob}$ will be used for all decryption calls. This way, key rotation at the $\mathtt{CMK}$ level is transparent to the user from the usability viewpoint. Since the designed $\mathtt{AWS}\mathtt{KMS}$ does not store $\mathtt{ciphertextBlob}$, only the user would be able to actively migrate already-encrypted data to a new $\mathtt{CMK}$ version. The design facilitates such migration through a “ReEncrypt” API.

4. Security Bounds for $\mathtt{AWS}\mathtt{KMS}$ Mode Of Operation

4.1. Abstraction of an Idealized AWS KMS Mode CES-GCM⁽ⁱ⁾

This section outlines an abstraction of the $\mathtt{AWS}\mathtt{KMS}$ mode of operation, $\mathtt{CES-GCM}$, modeled with ideal primitives for the key derivation (h) and the block cipher (E). In particular, it leaves the $\mathtt{AWS}\mathtt{KMS}$ authorization mechanism outside the scope of this discussion. We denote it ${\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}$.

The ${\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}$ mode is a variant of the derive key mode of [13], mounted on top of E-GCM. It operates in the context of a multi-users-multi-key system with the following parameters. The system supports U users, each one labeled by an identifier $\mathtt{u}$, $1\le \mathtt{u}\le U$, associated with a master key (${\mathtt{CMK}}_{\mathtt{u}}$), and has a budget of Q encryptions. The mode is nonce based, where the length of a nonce $\mathtt{N}$ is ${\ell }_{\mathtt{N}}$, satisfying ${\ell }_{\mathtt{N}}\le \kappa$. When a user $\mathtt{u}$ requests the encryption of a message $\mathtt{M}$ (plaintext and $\mathtt{AAD}$), the encryption flow executes the following: a) chooses a random $\mathtt{N}$ and a random $\mathtt{IV}$; b) applies a key derivation function $h(\mathtt{CMK},\mathtt{N})$ (that is modeled here as ideal), to derive a key $\mathtt{K}$; c) E-GCM encrypts $\mathtt{M}$ with $\mathtt{K}$ and $\mathtt{IV}$. The output is $\mathtt{C}$, $\mathtt{Tag}$$\mathtt{IV}$, and $\mathtt{N}$. A decryption request takes $\mathtt{C}$, $\mathtt{Tag}$, $\mathtt{IV}$, $\mathtt{N}$, $\mathtt{AAD}$, and a user identifier $\mathtt{u}$ as input. It triggers E-GCM decryption with a key $\mathtt{K}$ that is derived from ${\mathtt{CMK}}_{\mathtt{u}}$ and $\mathtt{N}$. The output is the plaintext of M if authentication passes, and ⊥ otherwise.

Remark 1.

In a concrete instantiation, AES256 is used for E, and PRF HMAC-SHA256 is used for h, $n=128$, $\kappa =256$, ${\ell }_{\mathtt{IV}}=96$, and ${\ell }_{\mathtt{N}}=128$. The maximum plaintext length is ${\ell }_M=256$ and $AAD$ length ${\ell }_{AAD}=512$. The targeted limits are for $U=2^{40}$ users and $Q=2^{50}$ encryptions for each.

Remark 2.

The CES-GCM⁽ⁱ⁾ mode can be viewed as a special case of the general derive key mode of [13], which can be applied over any $IV$ based AEAD scheme, Π, but with the following difference. The derive key mode uses a single nonce $\mathtt{N}$ for the derivation of a per-message key, and for the encryption with Π. In contrast, CES-GCM⁽ⁱ⁾ mode uses $\mathtt{N}$ only for the derivation, and a separate (independent) random $IV$ for Π. This decouples the per-request key derivation, from the actual message encryption.

Remark 3.

To illustrate the value of deriving a per-message key from CMK and N, consider a trivialized instantiation where, for a user u, the derivation is CMK_u$⟵$(CMK_u,N), i.e., a direct use of CMK_u. With this, for every u, the probability that Q encryptions would lead to a collision in the randomized $n-\delta$ bits $IV$ is at most $Q^2/2^{(n-\delta )}$. To ensure this probability remains below the target security margin of $2^{-\beta }$, the limit on Q is $2^{(n-\delta -\beta )/2}$. This imposes an undesired constraint on the users. For example, with $n=128$, $\delta =32$, $\beta =32$, Q is limited to $2^{32}$. The situation is even worse at the cloud scale, because if each one of U users encrypts Q messages, then the probability that (at least) one of them will repeat an $IV$ (with their key) is $\approx U{Q}^2/2^{(n-\delta )}$, and bounding this probability limits $U·Q^2$. The prepended nonce-based key derivation that is built into CES-GCM⁽ⁱ⁾, is intended to address these limitations.

4.2. Security Definitions for CES-GCM⁽ⁱ⁾

4.2.1. A ${\mathtt{CES-GCM}}^{\left(i\right)}$ Oracle

We define an oracle, $\mathcal{O}$, for ${\mathtt{CES-GCM}}^{\left(i\right)}$ encryption and decryption queries, which operates as follows.

Setup.

Select, uniformly at random,

(a)

a bit b.

(b)

U keys ${\mathtt{CMK}}_1,\dots ,{\mathtt{CMK}}_U$, each one of $\kappa$ bits.

(c)

a random function $h:{\{0,1\}}^{\kappa }\times {\{0,1\}}^{{\ell }_{\mathtt{N}}}\to {\{0,1\}}^{\kappa }$.

Response to an encryption query $\mathtt{u},\mathtt{M},\mathtt{AAD}$.

• Select, uniformly at random,

  (a)

  a string $\mathtt{N}$ of ${\ell }_{\mathtt{N}}$ bits,

  (b)

  a string $\mathtt{IV}$ of ${\ell }_{\mathtt{IV}}$ bits,

  (c)

  a string $\mathtt{S}$ of length ${\ell }_M+1$ blocks.

• Compute $\mathtt{K}=h({\mathtt{CMK}}_{\mathtt{u}},\mathtt{N})$.
• E-GCM encrypt M, $\mathtt{AAD}$ with $\mathtt{IV}$, under the key $\mathtt{K}$, obtaining the ciphertext $\mathtt{C}$ and the authentication tag $\mathtt{Tag}$.
• Output: $\mathtt{N}$, $\mathtt{IV}$, $\mathtt{C}\parallel \mathtt{Tag}$, if $b=0$, and $\mathtt{u}$, $\mathtt{N}$, $\mathtt{IV}$, $\mathtt{S}$, if $b=1$.

Response to a decryption query $\mathtt{u}$, $\mathtt{N}$, $\mathtt{IV}$, $\mathtt{C}\parallel \mathtt{Tag}$, $\mathtt{AAD}$.

• Compute $\mathtt{K}=h({\mathtt{CMK}}_{\mathtt{u}},\mathtt{N})$.
• E-GCM decrypt $\mathtt{C}$, $\mathtt{AAD}$, $\mathtt{Tag}$, using $\mathtt{IV}$, under the key $\mathtt{K}$, obtaining the plaintext of $\mathtt{M}$, and determining if the authentication passed or failed.
• Output: if $b=0$ then: $\mathtt{M}$ (plaintext) if authentication passed and ⊥ if it failed.
  If $b=1$ then: ⊥.

4.2.2. Adversary against ${\mathtt{CES-GCM}}^{\left(i\right)}$

An adversary $\mathcal{A}$ against ${\mathtt{CES-GCM}}^{\left(i\right)}$ is an algorithm that submits encryption and decryption queries to $\mathcal{O}$, and then outputs a bit $b^{\prime }$ (as its guess for b). For simplicity (and with no loss of generality), assume that $\mathcal{A}$ exhausts the allowed number (Q) of encryptions for each user. Suppose also that all messages have the maximum allowed plaintext and AAD lengths. With this, the total number of encrypted messages during $\mathcal{A}$’s queries is $U·Q$. Each query triggers ${\ell }_M+2$ evaluations of E (with some key), over the list of counter blocks $\mathcal{L}$, all of which, except the invocation of $E_{(·)}\left(0\right)$ (for the hash key) are revealed to $\mathcal{A}$ (whose encryption queries are with chosen plaintext). Since with nonzero probability, keys may repeat, the total number of different keys that are used with invocations of E, is at most $U·Q$.

To model an active adversary, $\mathcal{A}$ can also submit $Q_D$ decryption queries. We assume that $\mathcal{A}$ does not make superfluous decryption queries, i.e., it does not request to decrypt ($\mathtt{u}1$, $\mathtt{N}1$, $\mathtt{IV}1$, $\mathtt{C}1\parallel \mathtt{Tag}1$, $\mathtt{AAD}1$) if it has already submitted an encryption query with ($\mathtt{u}1$, $\mathtt{M}1$, $\mathtt{AAD}1$), and received the response ($\mathtt{N}1$, $\mathtt{IV}1$, $\mathtt{C}1\parallel \mathtt{Tag}1$). Note that a decryption query of the form ($\mathtt{u}2$, $\mathtt{N}1$, $\mathtt{IV}1$, $\mathtt{C}1\parallel \mathtt{Tag}1$), where $\mathtt{u}2\ne \mathtt{u}1$ is not superfluous. We call a non superfluous decryption query a forgery attempt.

We denote an event where $\mathcal{O}$ responds with a string (i.e., not ⊥) to a forgery attempt “$\mathtt{forge}$”. $\mathcal{A}$ can also make $T_E$ (offline) evaluations of E (or $E^{-1}$), using its chosen keys, as an attempt to guess a secret key that $\mathcal{O}$ uses. The event where $\mathcal{A}$ found such a key is called “$\mathtt{guess}$”. After the queries, $\mathcal{A}$ outputs a bit $b^{\prime }$ (as its guess for b).

Adversary advantage. The advantage of $\mathcal{A}$ against ${\mathtt{CES-GCM}}^{\left(i\right)}$ is $\left|Pr(b^{\prime }=1|b=1)-Pr(b^{\prime }=1|b=0)\right|$.

The PRF advantage of E in a multi-user-multi-key setting. Define a multi-user-multi-key oracle ${\mathcal{O}}^{\prime }$ for E as follows. Let U and Q be given parameters. At setup, ${\mathcal{O}}^{\prime }$ chooses a random bit c, $U·Q$ random keys of $\kappa$ bits, and $U·Q$ random functions $\mathtt{f}:{\{0,1\}}^n\to {\{0,1\}}^n$, such that if two selected keys are equal the corresponding functions are also equal. Assume the keys and functions are organized in a table of U rows and Q columns indexed by $\mathtt{u}$, and $\mathtt{ind}$. A query to ${\mathcal{O}}^{\prime }$ is a tripe $[\mathtt{u},\mathtt{ind},B]$ for some $\mathtt{u}$, $\mathtt{ind}$, and $B\in {\{0,1\}}^n$. The response is either $E_{K_{\mathtt{u},\mathtt{ind}}}\left(B\right)$ or ${\mathtt{f}}_{\mathtt{u},\mathtt{ind}}\left(B\right)$, depending on c. An adversary ${\mathcal{A}}^{\prime }$ against E (in this setting) is an algorithm that submits queries to ${\mathcal{O}}^{\prime }$ and outputs $c^{\prime }$ as its guess for c. The advantage of ${\mathcal{A}}^{\prime }$ after exhausting a budget of $q^{\prime }=U·Q·({\ell }_M+1)$ queries is $\left|Pr(c^{\prime }=1|c=1)-Pr(c^{\prime }=1|c=0)\right|$.

4.3. Security Bounds for ${\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}$

4.3.1. Events That May Occur during Encryption Queries

Consider the list of Q encryption queries with a given identifier $\mathtt{u}$, where the queried messages are $M_{\mathtt{u},1},\dots ,M_{\mathtt{u},Q}$, and the respective nonces, keys, and IV’s, used with these queries are ${\mathtt{N}}_{\mathtt{u},1},\dots ,{\mathtt{N}}_{\mathtt{u},Q}$, ${\mathtt{K}}_{\mathtt{u},1},\dots ,{\mathtt{K}}_{\mathtt{u},Q}$, ${\mathtt{IV}}_{\mathtt{u},1},\dots ,{\mathtt{IV}}_{\mathtt{u},Q}$. Denote also the lists of nonces, keys and IV’s, used during the queries, by $\mathcal{N}\left(\mathtt{u}\right)$, $\mathcal{K}\left(\mathtt{u}\right)$, $\mathcal{IV}\left(\mathtt{u}\right)$, respectively, and the list of the U$\mathtt{CMK}$’s by $\mathcal{CMK}$. Note that these lists may contains repeated values. Finally, denote the combined (concatenated) list of $(U·Q)$$IV$’s and of $U+U·Q$ keys, respectively, by

$$\begin{array}{c}\hfill \Sigma \mathcal{IV}=\mathcal{IV}\left(1\right)\parallel \mathcal{IV}\left(2\right)\parallel \dots \parallel \mathcal{IV}\left(U\right)\end{array}$$

(2)

$$\begin{array}{c}\hfill \Sigma \mathcal{K}=\mathcal{CMK}\parallel \mathcal{K}\left(1\right)\parallel \mathcal{K}\left(2\right)\parallel \dots \parallel \mathcal{K}\left(U\right)\end{array}$$

(3)

We now account for several types of events, as follows. Let ${\mu }_0$ be a parameter, (the value ${\mu }_0<<(U·Q)$ is to be determined later). Define the following events that may occur during the oracle’s setup and responses to queries.

• (${\mathrm{\Lambda }}_1$) There are two identifiers $1\le \mathtt{u}<\mathtt{v}\le U$, such that ${\mathtt{CMK}}_{\mathtt{u}}={\mathtt{CMK}}_{\mathtt{v}}$.
• (${\mathrm{\Lambda }}_2$) All the $\mathtt{CMK}$’s are distinct, and there are identifiers $1\le \mathtt{u}<\mathtt{v}\le U$, and indexes $1\le i,j\le Q$, such that ${\mathtt{K}}_{\mathtt{u},i}={\mathtt{K}}_{\mathtt{v},j}$.
• (${\mathrm{\Lambda }}_3$) There is an identifier $1\le \mathtt{u}\le U$, such that $\mathcal{K}\left(\mathtt{u}\right)$ contains a value that is repeated 3 or more times.
• (${\mathrm{\Lambda }}_4$) There is an identifier $1\le \mathtt{u}\le U$, and indexes i, j, $1\le i<j\le Q$, such that ${\mathtt{K}}_{\mathtt{u},i}={\mathtt{K}}_{\mathtt{u},j}$ and ${\mathtt{IV}}_{\mathtt{u},i}={\mathtt{IV}}_{\mathtt{u},j}$.
• (${\mathrm{\Lambda }}_5$) The combined list $\Sigma \mathcal{IV}$ includes a value that is repeated more than ${\mu }_0$ times.

Interpretation. Events ${\mathrm{\Lambda }}_1$, ${\mathrm{\Lambda }}_2$, ${\mathrm{\Lambda }}_4$ are “bad” events, that obviously compromise the security promise of ${\mathtt{CES-GCM}}^{\left(i\right)}$. Event ${\mathrm{\Lambda }}_1$ is a collision on master keys: users $\mathtt{u}$ and $\mathtt{v}$ are completely not isolated with respect to encrypting and decrypting messages. Event ${\mathrm{\Lambda }}_2$ is a cross-users key contamination. It allows user $\mathtt{v}$ to decrypt message ${\mathtt{M}}_{\mathtt{u},i}$ that was encrypted by user $\mathtt{u}$ with ${\mathtt{K}}_{\mathtt{u},i}$ (in the real $\mathtt{AWS}\mathtt{KMS}$ context, this bypasses a decryption privilege policy imposed by $\mathtt{u}$ on ${\mathtt{M}}_{\mathtt{u},i}$). Event ${\mathrm{\Lambda }}_4$ implies that user $\mathtt{u}$ looses the privacy (of ${\mathtt{M}}_{\mathtt{u},i}$ and ${\mathtt{M}}_{\mathtt{u},j}$) and the authenticity (with ${\mathtt{K}}_{\mathtt{u},i}$) due to an improper usage ($IV$ reuse) of E-GCM. Event ${\mathrm{\Lambda }}_5$ give a lower bound for the number of $IV$’s (and hence counter blocks) that were repeated during the encryption queries. The interpretation motivates why we focus on these events. We are actually interested in the case where none of these events occur. The following lemma analyzes the positive properties of no such event occurring.

Lemma 1.

Let Λ be the event where at least one of ${\mathrm{\Lambda }}_1$, ${\mathrm{\Lambda }}_2$, ${\mathrm{\Lambda }}_3$, ${\mathrm{\Lambda }}_4$, ${\mathrm{\Lambda }}_5$ happens during the encryption queries. Then, if the event Λ does not happen:

c1.

All the CMK’s are distinct.

c2.

For every $1\le \mathtt{u}\le U$, the usage of E-GCM by $\mathtt{u}$ was proper. Furthermore, $\mathcal{K}\left(\mathtt{u}\right)$ can be split to disjoint sub-lists: $\mathtt{s}\left(\mathtt{u}\right)$ keys that were used for encrypting a single message, and $\mathtt{d}\left(\mathtt{u}\right)$ keys that were used for encrypting two messages. These satisfy the relation $\mathtt{s}\left(\mathtt{u}\right)+2\mathtt{d}\left(\mathtt{u}\right)=Q$, and $\mathtt{s}\left(\mathtt{u}\right),\mathtt{d}\left(\mathtt{u}\right)\ge 0$.

c3.

Across all the $U·Q$ encryptions, every counter block is encrypted under at most ${\mu }_0$ distinct keys.

Proof. 

The proof follows directly from the definitions of the events ${\mathrm{\Lambda }}_1$, ${\mathrm{\Lambda }}_2$, ${\mathrm{\Lambda }}_3$, ${\mathrm{\Lambda }}_4$, ${\mathrm{\Lambda }}_5$, and the definition of $\mathrm{\Lambda }$. Specifically, note that the negation of $\mathrm{\Lambda }$ is the case where none of ${\mathrm{\Lambda }}_1$, ${\mathrm{\Lambda }}_2$, ${\mathrm{\Lambda }}_3$, ${\mathrm{\Lambda }}_4$, ${\mathrm{\Lambda }}_5$ occurs. ☐

Lemma 2.

$$\begin{array}{c}\hfill Pr\left({\mathrm{\Lambda }}_1\right)\le \frac{U^2}{2·2^{\kappa }},Pr\left({\mathrm{\Lambda }}_2\right)\le \frac{{(U·Q)}^2}{2·2^{\kappa }},Pr\left({\mathrm{\Lambda }}_3\right)\le U·\frac{Q^3}{2·2^{2{\ell }_{\mathtt{N}}}},\\ \hfill \\ \hfill Pr\left({\mathrm{\Lambda }}_4\right)\le U·\frac{Q^2}{2}·\left(\frac{1}{2^{\kappa }}+\frac{1}{2^{{\ell }_{\mathtt{IV}}}}\right)·\frac{1}{2^{{\ell }_{\mathtt{N}}}},Pr\left({\mathrm{\Lambda }}_5\right)\le \frac{{(U·Q)}^{{\mu }_0}}{{\mu }_0!·2^{{\ell }_{\mathtt{IV}}·({\mu }_0-1)}}\end{array}$$

(4)

Proof. 

The bound for $Pr\left({\mathrm{\Lambda }}_1\right)$ is the standard bound for the collision probability among U randomly chosen values from a pool of $2^{\kappa }$ possibilities.

If no $\mathtt{CMK}$ values collide, then $U·Q$ keys ${\mathtt{K}}_{u,i}=h({\mathtt{CMK}}_u,i)$, $1\le u\le U$, $1\le i\le Q$ are uniform random samples from a pool of $2^{\kappa }$ possibilities. Therefore,

$$Pr\left({\mathrm{\Lambda }}_2\right)\le \frac{{(U·Q)}^2}{2·2^{\kappa }}$$

(5)

To bound $Pr\left({\mathrm{\Lambda }}_3\right)$, fix some $\mathtt{u}$, and consider the event ${\mathrm{\Lambda }}_3^{\left(\mathtt{u}\right)}$, where the list $\mathcal{K}\left(\mathtt{u}\right)$ has a value that is repeated three times. For ${\mathrm{\Lambda }}_3^{\left(\mathtt{u}\right)}$ to happen, one of the conditions needs to be satisfied, for some distinct $1\le i,j,k\le Q$: (a) ${\mathtt{N}}_{\mathtt{u},i}={\mathtt{N}}_{\mathtt{u},j}={\mathtt{N}}_{\mathtt{u},k}$; (b) ${\mathtt{N}}_{\mathtt{u},i}={\mathtt{N}}_{\mathtt{u},j}\ne {\mathtt{N}}_{\mathtt{u},k}$ and $h({\mathtt{CMK}}_{\mathtt{u}},{\mathtt{N}}_{\mathtt{u},i})=h({\mathtt{CMK}}_{\mathtt{u}},{\mathtt{N}}_{\mathtt{u},k})$; (c) ${\mathtt{N}}_{\mathtt{u},i}\ne {\mathtt{N}}_{\mathtt{u},j}\ne {\mathtt{N}}_{\mathtt{u},k}$, and $h({\mathtt{CMK}}_{\mathtt{u}},{\mathtt{N}}_{\mathtt{u},i})=h({\mathtt{CMK}}_{\mathtt{u}},{\mathtt{N}}_{\mathtt{u},j})=h({\mathtt{CMK}}_{\mathtt{u}},{\mathtt{N}}_{\mathtt{u},k})$. Obviously (recall that ${\ell }_{\mathtt{N}}<\kappa$), the probabilities for #b and #c are smaller than the probability for #a. By Theorem 1, it follows that

$$Pr\left({\mathrm{\Lambda }}_3^{\left(\mathtt{u}\right)}\right)\le 3·\frac{Q^3}{6·2^{2{\ell }_{\mathtt{N}}}}=\frac{Q^3}{2·2^{2{\ell }_{\mathtt{N}}}}$$

(6)

Finally, $Pr\left({\mathrm{\Lambda }}_3\right)\le U·Pr\left({\mathrm{\Lambda }}_3^{\left(\mathtt{u}\right)}\right)$.

To bound $Pr\left({\mathrm{\Lambda }}_4\right)$, fix some $\mathtt{u}$, and consider the event ${\mathrm{\Lambda }}_4^{\left(\mathtt{u}\right)}$, where ${\mathtt{K}}_{\mathtt{u},i}={\mathtt{K}}_{\mathtt{u},j}$ and ${\mathtt{IV}}_{\mathtt{u},i}={\mathtt{IV}}_{\mathtt{u},j}$ for some $1\le i\ne j\le Q$. The collision ${\mathtt{K}}_{\mathtt{u},i}={\mathtt{K}}_{\mathtt{u},j}$ occurs if ${\mathtt{N}}_{\mathtt{u},i}={\mathtt{N}}_{\mathtt{u},j}$ or if $h(\mathtt{u},{\mathtt{N}}_{\mathtt{u},i})=h(\mathtt{u},{\mathtt{N}}_{\mathtt{u},j})$. The probability that this and ${\mathtt{IV}}_{\mathtt{u},i}={\mathtt{IV}}_{\mathtt{u},j}$ happen leads to

$$Pr\left({\mathrm{\Lambda }}_4^{\left(\mathtt{u}\right)}\right)\le \frac{Q^2}{2}·\left(\frac{1}{2^{\kappa }}+\frac{1}{2^{{\ell }_{\mathtt{N}}}}\right)·\frac{1}{2^{{\ell }_{\mathtt{IV}}}}$$

(7)

Finally, $Pr\left({\mathrm{\Lambda }}_4\right)\le U·Pr\left({\mathrm{\Lambda }}_4^{\left(\mathtt{u}\right)}\right)$.

The event ${\mathrm{\Lambda }}_5$ is a ${\mu }_0$-collision among $U·Q$ random samples from a pool of $2^{{\ell }_{\mathtt{IV}}}$ options, so the bound on $Pr\left({\mathrm{\Lambda }}_5\right)$ follows from Theorem 1. ☐

We now formulate the privacy bounds for the (idealized) ${\mathtt{CES-GCM}}^{\left(i\right)}$ mode, against a passive adversary that makes no forgery attempts.

Theorem 2 (${\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}$ privacy bound).

Let E be an ideal cipher. Let $\mathcal{A}$ make a total of $U·Q$ encryption queries, each one with ${\ell }_M$ plaintext blocks and ${\ell }_{AAD}$ AAD blocks, where for each identifier $\mathtt{u}=1,\dots ,U$, there are Q queries. Let $\mathcal{A}$ make also a total of $T_E$ (offline) evaluations of E or its inverse, using its chosen keys. Let ${\mu }_0$ be a (small) parameter. Then, the advantage of $\mathcal{A}$ against the (idealized) ${\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}$ has the following upper bound

$${\mathbf{Adv}}_{{\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}}^{}\left(\mathcal{A}\right)\le$$

$$\begin{array}{c}\hfill \frac{U^2}{2·2^{\kappa }}+\frac{{(U·Q)}^2}{2·2^{\kappa }}+U·\frac{Q^3}{2·2^{2{\ell }_{\mathtt{N}}}}+\frac{U·Q^2}{2}·\left(\frac{1}{2^{\kappa }}+\frac{1}{2^{{\ell }_{\mathtt{N}}}}\right)·\frac{1}{2^{{\ell }_{\mathtt{IV}}}}+\\ \hfill \frac{{(U·Q)}^{{\mu }_0}}{{\mu }_0!·2^{{\ell }_{\mathtt{IV}}·({\mu }_0-1)}}+2·U·Q·\frac{{({\ell }_M+1)}^2}{2^{n+1}}+{\mu }_0·\frac{T_E}{2^{\kappa }}\end{array}$$

(8)

Proof. 

Step 1. We define a random version of ${\mathtt{CES-GCM}}^{\left(i\right)}$, as follows. Choose a random function $\mathtt{F}:{\{0,1\}}^{\kappa }\times {\{0,1\}}^n\to {\{0,1\}}^n$. Then for every encryption query $[\mathtt{u}0,M0]$, for which the chosen nonce and $IV$ are $\mathtt{N}0$ and $\mathtt{IV}0$, respectively, and the derived key is ${\mathtt{K}}_{\mathtt{u}0,\mathtt{N}0}$, replace the invocations of $E_{{\mathtt{K}}_{\mathtt{u}0,\mathtt{N}0}}\left(B\right)$, for $B\in \mathcal{L}(\mathtt{IV}0,\mathtt{M}0)$ with $\mathtt{F}({\mathtt{K}}_{\mathtt{u}0,\mathtt{N}0},B)$. We call this scheme ${\mathtt{CES-GCM}}^{(\mathtt{i},\mathtt{rand})}$.

Step 2. We build an adversary ${\mathcal{A}}^{\prime }$ against the PRF security of E in the multi key setting, that has querying access to ${\mathcal{O}}^{\prime }$. ${\mathcal{A}}^{\prime }$ uses $\mathcal{A}$ as follows. ${\mathcal{A}}^{\prime }$ chooses U random keys ${\mathtt{CMK}}^{\prime }$, and runs algorithm $\mathcal{A}$. For each query $[\mathtt{u}0,\mathtt{M}0]$ that $\mathcal{A}$ prescribes, ${\mathcal{A}}^{\prime }$ generates a random nonce $\mathtt{N}{0}^{\prime }$ and a random $IV$, $\mathtt{IV}{0}^{\prime }$, and computes $X{0}^{\prime }=h({\mathtt{CMK}}_{\mathtt{u}0}^{\prime },\mathtt{N}{0}^{\prime })$. If $X{0}^{\prime }$ is not a value that has appeared in previous queries, ${\mathcal{A}}^{\prime }$ assigns the next index value $\mathtt{ind}{0}^{\prime }$ that has not been used (and uses the appropriate already-used index otherwise). Then, ${\mathcal{A}}^{\prime }$ queries ${\mathcal{O}}^{\prime }$ with queries of the form $[\mathtt{ind}{0}^{\prime },B]$ where $B\in \mathcal{L}(\mathtt{IV}{0}^{\prime },\mathtt{M}0)$ and uses these values to compute the response to $\mathcal{A}$. We note that during the $U·Q$ queries of $\mathcal{A}$, ${\mathcal{A}}^{\prime }$ queries ${\mathcal{O}}^{\prime }$$U·Q·({\ell }_M+1)$ times. We have

$${\mathbf{Adv}}_{{\mathtt{CES-GCM}}^{\left(\mathtt{i}\right)}}^{}\left(\mathcal{A}\right)\le {\mathbf{Adv}}_{\left(multi\right)E}^{\mathtt{PRF}}\left({\mathcal{A}}^{\prime }\right)+{\mathbf{Adv}}_{{\mathtt{CES-GCM}}^{(\mathtt{i},\mathtt{rand})}}^{}\left(\mathcal{A}\right)$$

(9)

Now, assume that $\mathrm{\Lambda }$ does not happen.

Under the negation of $\mathrm{\Lambda }$, and by Lemma 1, we can see that ${\mathbf{Adv}}_{{\mathtt{CES-GCM}}^{(\mathtt{i},\mathtt{rand})}}^{}\left(\mathcal{A}\right)=0$. This is because $\mathcal{A}$ gets to observe (at most) $U·Q·({\ell }_M+1)$ evaluations of the random functions over known blocks but distinct counter blocks.

To bound ${\mathbf{Adv}}_{\left(multi\right)E}^{\mathtt{PRF}}\left({\mathcal{A}}^{\prime }\right)$ (under the negation of $\mathrm{\Lambda }$), we use a standard hybrid argument (and the switching lemma). Fix some $\mathtt{u}$, and consider the PRP-PRF advantage against the Q queries labeled under $\mathtt{u}$. Using Lemma 1 (c2), we split the keys used for these messages to: $\mathtt{s}\left(\mathtt{u}\right)$ distinct keys, each one used for encrypting a single message, i.e., $({\ell }_M+1)$ blocks; $\mathtt{d}\left(\mathtt{u}\right)$ distinct keys, each one used for encrypting two messages, i.e., $2·({\ell }_M+1)$ blocks. We have $\mathtt{s}+2\mathtt{d}=Q$, so, the cumulative PRP-PRF advantage for identifier $\mathtt{u}$ is upper bounded by

$$\begin{array}{c}\hfill \mathtt{s}·\frac{{({\ell }_M+1)}^2}{2^{n+1}}+\mathtt{d}·\frac{{(2·({\ell }_M+1))}^2}{2^{n+1}}=\\ \hfill (Q+2\mathtt{d})·\frac{{({\ell }_M+1)}^2}{2^{n+1}}\le 2·Q·\frac{{({\ell }_M+1)}^2}{2^{n+1}}\end{array}$$

(10)

Note that we account for only ${\ell }_M+1$ encryptions per message, ignoring the encryption of the zero block, which we assume that ${\mathcal{A}}^{\prime }$ does not use for distinguishing (rather, only for computing GHASH in order to respond to $\mathcal{A}$). However, the time (in terms of calls to E) for ${\mathcal{A}}^{\prime }$ should take into account ${\ell }_M+1$ encryptions per message (just as the number of encryptions that the real usage of ${\mathtt{CES-GCM}}^{\left(i\right)}$ requires from the system). After summing over all U identifiers, we get

$$\begin{array}{c}\hfill {\mathbf{Adv}}_{\left(multi\right)E}^{\mathtt{PRF}}\left({\mathcal{A}}^{\prime }\right)\le 2·U·Q·\frac{{({\ell }_M+1)}^2}{2^{n+1}}\end{array}$$

(11)

To account for the key recovery, we use Lemma 1 (c3) to establish

$$Pr\left(\mathtt{guess}\right)\le T_E·\frac{{\mu }_0}{2^{\kappa }}$$

(12)

Using the bounds for the probabilities of ${\mathrm{\Lambda }}_1$ - ${\mathrm{\Lambda }}_5$, stated in Lemma 2, (12), and (11), gives the desired upper bound (8). ☐

Remark 4 (The parameter μ₀).

A selection of a value of ${\mu }_0$ balances between the key recovery probability term in (8), ${\mu }_0·\frac{T_E}{2^{\kappa }}$ (which is linear in ${\mu }_0$), and the upper bound on the probability for encountering an $IV$ value that is repeated ${\mu }_0$ times during the queries, namely ${(U·Q)}^{{\mu }_0}/\left({\mu }_0!·2^{{\ell }_{\mathtt{IV}}·({\mu }_0-1)}\right)$. For example, with ${\ell }_{\mathtt{IV}}=96$, selecting ${\mu }_0=20$ brings the probability term to

$$\frac{{(U·Q)}^{20}}{20!·2^{1824}}\approx \frac{{(U·Q)}^{20}}{2^{1924}}$$

which is smaller than $2^{-32}$ even when for $(U·Q)=2^{94}$. At the same time, the key recovery probability which is manifested through the term $20·\frac{T_E}{2^{\kappa }}$ remains negligible under any reasonable assumption, especially when $\kappa =256$.

Interpreting Theorem 2

Let us first label the seven terms that contribute to the advantage bound in (8) as follows.

$$\begin{array}{c}\hfill \underset{i}{\underbrace{\frac{U^2}{2·2^{\kappa }}}},\underset{ii}{\underbrace{\frac{{(U·Q)}^2}{2·2^{\kappa }}}},\\ \hfill \\ \hfill \underset{iii}{\underbrace{U·\frac{Q^3}{2·2^{2{\ell }_{\mathtt{N}}}}}},\underbrace{\frac{U·Q^2}{2}}·\left(\frac{1}{2^{\kappa }}+\frac{1}{2^{{\ell }_{\mathtt{N}}}}\right)·{\frac{1}{2^{{\ell }_{\mathtt{IV}}}}}_{iv},\underset{v}{\underbrace{\frac{{(U·Q)}^{{\mu }_0}}{{\mu }_0!·2^{{\ell }_{\mathtt{IV}}·({\mu }_0-1)}}}},\end{array}$$

$$\underset{vi}{\underbrace{2·U·Q·\frac{{({\ell }_M+1)}^2}{2^{n+1}}}},\underset{vii}{\underbrace{{\mu }_0·\frac{T_E}{2^{\kappa }}}}$$

(13)

Consider the viewpoint of an individual user, say $\mathtt{u}$. This can be deduced by taking $U=1$ in (8) (the term i actually vanishes, because the exact numerator is $U·(U-1)$; the theorem uses the more loose $U^2$ just for convenience). The single user $\mathtt{u}$ is in a multi-key situation, where we take ${\mu }_0$ to represent $IV$ collisions on queries made by $\mathtt{u}$. When $\kappa$ is sufficiently large, we can assume even a “moderate” value of ${\mu }_0$ (e.g., 20) and keep both v and $vii$ terms small (note that the term $vii$ which is linear in ${\mu }_0$ remains extremely small for any reasonable $T_E$). To illustrate consider the case where ${\ell }_{\mathtt{IV}}=96$, $\kappa =256$, and target a high number $Q=2^{50}$ for the maximum allowed number of encryptions. Then, it suffices to set (exaggerated) ${\mu }_0=20$, in order to dwarf both v and $vii$.

We now focus on terms $iv$ and $vi$. Term $vi$ represents the PRP-PRF distinguishing for Q queries, but when the messages (${\ell }_M$) are sufficiently short, the quadratic numerator is still well behaved. The term $iv$ represents the top concern of “repeated $\mathtt{K}$ and $\mathtt{IV}$” which breaks the usage of AES-GCM. The probability for this catastrophic collision is kept low if ${\ell }_{\mathtt{IV}}+{\ell }_{\mathtt{N}}$ is sufficiently large.

However, note that this does not cover all of $\mathtt{u}$’s concerns as a single user, in an environment that allows for $U>1$. In such cases, cross-users “contamination” may occur through collisions on $\mathtt{CMK}$’s or on derived keys (terms i and $ii$). This shows why the multi-user situation requires the use of a long encryption key, i.e., motivates the choice of $\kappa =256$ over $\kappa =128$ that could be acceptable with $U=1$.

Consider the remaining terms under the general case $U>1$. We deal with those that grow linearly or faster than linear with U. Term $ii$ which is quadratic in $(U·Q)$, is contained by the key length $\kappa$. In contrast, term $vi$, which is only linear in $(U·Q)$ becomes the dominant term when both U and Q are large. Unfortunately, it is the direct consequence of PRP-PRF distinguishing over a block cipher with n bits, regardless of $\kappa$. This term represents a tight bound on distinguishing at the cloud provider’s level of all of the messages of all U users, but not at the user’s perspective (where the distinguishing advantage of encryptions made with their $\mathtt{CMK}$ is linear in Q). However, it is reassuring to realize that with restricted-length messages, the cloud scale distinguishing advantage still remains below a reasonable bound. For example, even with $Q=2^{50}$ and $U=2^{40}$, an exaggerated extreme in real-world deployment, $vi$ is bounded by $2^{-22}$.

Accounting for Real Primitives

The bounds for ${\mathbf{Adv}}_{{\mathtt{CES-GCM}}^{\left(i\right)}}^{}\left(\mathcal{A}\right)$ use a model ${\mathtt{CES-GCM}}^{\left(i\right)}$, where E and h are ideal primitives. A real $\mathtt{CES-GCM}$ scheme that uses FIPS-approved methods might substitute AES256 for E and the NIST SP800-108 Key Derivation Function (in Counter Mode with PRF HMAC-SHA256 [19]) for h. To account for these substitutions, the bounds in (8) need to be updated: the PRP security of AES256 (with $U·Q·({\ell }_M+1)$ invocations, distributed as prescribed in Theorem 2), and the PRF security of HMAC-SHA256 (with $U·Q$ invocations) need to be added to the RHS of (8). Note that the AES256 invocations are distributed across multiple keys that are not controlled by the adversary. Thus, the situation is different from the case where $U·Q·({\ell }_M+1)$ samples of AES256 are harvested from the same key. We make the standard assumptions that the $PRP$ advantage of $AES256$ and the PRF advantage of HMAC-SHA256 are very small compared to the terms in (8) that are associated with ${\mathtt{CES-GCM}}^{\left(i\right)}$. With this, we conclude that Theorem 2 gives a good approximation for the bounds of a real instantiation of $\mathtt{CES-GCM}$ as well.

Accounting for an Active (Forging) Adversary

We explain the amendments needed in Theorem 2 and its proof in order to accommodate the case where $\mathcal{A}$ makes $Q_D$ forgery attempts in addition to the encryption queries specified above. In this case,

$${\mathbf{Adv}}_{{\mathtt{CES-GCM}}^{(\mathtt{i},\mathtt{rand})}}^{}\left(\mathcal{A}\right)\le Q_D·\frac{({\ell }_M+{\ell }_{AAD}+1)}{2^n}$$

(14)

instead of 0 when $Q_D=0$ with the passive adversary. This follows directly from the properties of GHASH as a polynomial evaluation and the bound on the combined message and AAD lengths ${\ell }_M+{\ell }_{AAD}+1$ (“$+1$” accounts for the length-encoding block in the GHASH computations).

We note that for a decryption query, $\mathcal{A}$ can choose to submit a query ($\mathtt{u}*$, $\mathtt{N}*$, $\mathtt{IV}*$, $\mathtt{C}*$||$\mathtt{Tag}*$) where the combination of $\mathtt{u}*$ and $\mathtt{N}*$ is not used for any of the encryption queries. This could (and most probably would) lead the key derivation procedure to generate a “new” key that was not generated (and used) in any of the encryption queries. In the proof of Theorem 2, this changes the distinguishing game of ${\mathcal{A}}^{\prime }$ against E and the setup and operation of ${\mathcal{O}}^{\prime }$ and ${\mathcal{A}}^{\prime }$, as follows. At setup, ${\mathcal{O}}^{\prime }$ will select $Q_D$ additional random keys and random functions that will be used in the analogous way for every decryption query that generates a new key. When $\mathcal{A}$ prescribes such a decryption query, ${\mathcal{A}}^{\prime }$ would point to an appropriate index (from the additional list) in order to get the encryption of the zero block from ${\mathcal{O}}^{\prime }$ and use it to check the authentication $Tag$. Then, ${\mathcal{A}}^{\prime }$ would pass the result of this check to $\mathcal{A}$. This means that ${\mathcal{A}}^{\prime }$ submits $Q_D$ more queries to ${\mathcal{O}}^{\prime }$, compared to the case where $Q_D=0$ (these are not used for the PRP-PRF distinguishing, but increase the time for ${\mathcal{A}}^{\prime }$). Inspection of (14) shows that accounting for $Q_D$ forgery attempts does not alter the security bounds of Theorem 2 in any meaningful way. In particular, since in addition to per-customer rate-limits, $Q_D$ should be small because our recommended $\mathtt{AWS}\mathtt{KMS}$ design includes mechanisms that alert on potential forgery attempts when multiple decryption failures are noticed. It should also be noted that a real adversary in the deployed system can only use valid values for $\mathtt{u}*$ that exist in the system, and to which the adversary is authorized to call the Decrypt API. Hence, the adversary needs to be an authorized user of the $\mathtt{CMK}$ for the Decrypt API.

5. Discussion

This paper discussed the challenges and considerations involved with building and deploying a $\mathtt{CES}$. These give rise to extremely heavy use of a block cipher in a multi-user-multi-key setting, over distributed systems that require randomized nonces and/or $IV$s. The challenges are aggravated at the cloud-scale where the system needs to support a huge number of users and allow each user to encrypt a virtually unlimited number of messages. After laying out some of the constraints, we showed one solution in the form of the $\mathtt{CES-GCM}$ mode, and provided analysis that illustrates its suitability for the problem. There are alternative $\mathtt{CES}$ designs that will lead to different trade-offs between cost, performance, complexity and security. This analysis is based on the design of the AWS Key Management Service and is intended to provide transparency into the design of the service. Without the same level of access to the design of alternative $\mathtt{CES}$ it is impossible to produce a comparative analysis.

We note that $\mathtt{CES-GCM}$ belongs to the family of derive key modes that have been recently proposed and analyzed in [13], in the multi-key context, where AES-GCM-SIV [9] is one instantiation. This work was very recently followed by [14] who provided improved bounds for the multi-user-multi-key scenario for AES-GCM-SIV. Since AES-GCM-SIV (the variant with random nonces) and $\mathtt{CES-GCM}$ addresses the same problems, it is interesting to see some of the differences between these modes.

As pointed out above, $\mathtt{CES-GCM}$ decouples the use of the nonce as a seed for the per-message key derivation, from the use of the $IV$ that seeds the underlying AEAD scheme (in this case, AES-GCM). This allows for using independent sources of entropy during the different steps of the encryption. Implementations can, therefore, enjoy an extra layer of protection against accidental misuse due to a failure in the entropy injection, which is detrimental for AES-GCM. This so-called nonce-misuse-independence feature of $\mathtt{CES-GCM}$ does not build on top of an underlying nonce-misuse resistant mode, but rather on top of the standardized AES-GCM. By comparison, AES-GCM-SIV starts from the nonce-misuse-resistant mode GCM-SIV+ and extends the lifetime of the key prepending a nonce-based key derivation step. $\mathtt{CES-GCM}$ can be viewed as an online mode, i.e., encryption does not need to have the full message prior to initialization. Furthermore, unlike any SIV construction (AES-GCM-SIV included) which serializes the universal hashing (of the plaintext and $AAD$) and the actual encryption, $\mathtt{CES-GCM}$ simply uses the standard AES-GCM but with a freshly derived key and a fresh $IV$. This allows for parallelizing the encryption and the GHASH computations, and achieves improved encryption performance on modern platforms. Of course, AES-GCM-SIV would be a viable $\mathtt{CES}$ mode alternative after it becomes a standard.

One conclusion of this paper is that cloud-scale encryption is pushing up against the natural birthday bounds of the standardized modes of a 128-bit block cipher. New standardized wide-block ciphers would alleviate the specialized engineering required to reach desired security bounds using existing schemes. Alternative simple solutions could be based on using 128-bit block ciphers (AES) with truncation or sum-permutation methods.

Finally, we note that the investment in analysis, FIPS-certified HSMs, and the availability and durability of $\mathtt{AWS}\mathtt{KMS}$ surpasses what most users of cloud computing can achieve on their own. It is not feasible for a cloud provider to integrate independent customer key management solutions into all their services. The $\mathtt{CES}$ system described in this paper is deployed and integrated into 34 AWS services.