S-Box on Subgroup of Galois Field

Abstract

In substitution–permutation network as a cryptosystem, substitution boxes play the role of the only nonlinear part. It would be easy for adversaries to compromise the security of the system without them. 8-bit S-boxes are the most used cryptographic components. So far, cryptographers were constructing 8-bit S-boxes used in cryptographic primitives by exhaustive search of permutations of order 256. However, now for cryptographic techniques with 8-bit S-boxes as confusion layers, researchers are trying to reduce the size of S-box by working with a small unit of data. The aim is to make the techniques compact, fast and elegant. The novelty of this research is the construction of S-box on the elements of the multiplicative subgroup of the Galois field instead of the entire Galois field. The sturdiness of the proposed S-box against algebraic attacks was hashed out by employing the renowned analyses, including balance, nonlinearity, strict avalanche criterion, and approximation probabilities. Furthermore, the statistical strength of the S-box was tested by the majority logic criterion. The fallouts show that the S-box is appropriate for applications for secure data communications. The S-box was also used for watermarking of grayscale images with good outcomes.

1. Introduction

Information security and privacy problems are growing day by day due to the presence of communication nets. There is a need for safe and authentic means of communication and cautiously weighing the issues connected with it. Therefore, network security and data encryption are becoming significant. Images can instantly be reckoned as one of the most functional forms of data. Image encryption has applications in several areas, including multimedia organizations, medical imaging, wireless communications, military communications, and telemedicine, etc. Owing to these wider applications of image encryption, a great deal of research work is devoted to this topic (see for instance [1,2,3,4,5]).

The S-box is used in various encryption techniques, and the complexity of encryption basically depends on the strength of S-box. Advanced encryption standard (AES) [6], affine–power–affine (APA) [7], Gray [8], Liu J [9], residue prime [10], $S_8$ AES [11], SKIPJACK [12], and Xyi [13] are some well-known 8 × 8 S-boxes that are usually used in encryption applications. These all are based on the elements of the Galois field $GF{\left(2\right)}^8$ with almost similar algebraic and statistical properties. In the past few years, researchers were trying to reduce the size of S-box by working with a small unit of data to make the techniques compact, fast and elegant [14,15,16]. In [14], an S-box of size $4\times 4$ was constructed on the maximal cyclic subgroup of the multiplicative group of units in a finite Galois ring, instead of on the Galois field. Despite the reduced size, this S-box can replace the data bytes. The suitability of the S-box for image encryption has been proved with the majority logic criterion. Additionally, it has also been used for watermarking of grayscale images with good outcomes.

In this paper, we construct an S-box of the same size on a subgroup of the Galois field $GF{\left(2\right)}^8$, with the following irreducible polynomial for multiplication: $f\left(x\right)=x^8+x^4+x^3+x^2+1$. We will discuss the algebraic strength of S-box by employing balance property, nonlinearity analysis, linear approximation probability analysis, differential approximation probability analysis, strict avalanche criterion and majority logic criterion, and observe its closeness with the S-box constructed in Reference [14]. The S-box has also been used for watermarking of grayscale images with good outcomes.

In Section 2, the construction methodology of S-box on a subgroup of the Galois field is presented. Section 3 is devoted to examining the security of the proposed S-box with balance property, nonlinearity analysis, linear approximation probability analysis, differential approximation probability analysis, strict avalanche criterion, and majority logic criterion. The results from the contrast analysis, correlation analysis, energy analysis, entropy analysis, homogeneity analysis, and mean of absolute deviation analysis are computed for the proposed S-box and compared with the S-box constructed in [14]. Section 4 gives an application of the proposed S-box in watermarking of grayscale images with some experimental results and discussion. The whole study is concluded in Section 5.

2. Construction of S-box on Subgroup of the Galois Field

S-box is the only non-linear transformation involved in almost all block ciphers that creates confusion in data. The size of the S-box can alter according to the scope of its application. In [14], Shah et al. constructed an S-box structure based on the elements of the maximal cyclic subgroup of the multiplicative group of units in a finite Galois ring. To the best of the author’s knowledge, this was the first time to construct a bijective S-box on a cyclic group instead of Galois field. They have constructed an $8\times 8$-bit S-box based on 16 elements, instead of 256 elements, and found that the new S-box satisfies the majority logic criterion with optimal values. They also justified the application of S-box in watermarking of a grayscale image with good outcomes. Therefore, further study in this area has opened new horizons using a subgroup of the Galois field. The S-box in this research is constructed on a fifteen-order subgroup of the Galois field of order 256. We name the subgroup as $K_{15}$. The procedure is explained below:

• S-1 Define an inversion function $p:K_{15}\cup \left\{0\right\}\to K_{15}\cup \left\{0\right\}$ by

  $$p\left(y\right)=\{\begin{array}{c}{y}^{-1}, if y\in K_{15}\\ 0, if y=0 \end{array}$$
• S-2 Define a linear scalar multiple function $q:K_{15}\cup \left\{0\right\}\to K_{15}\cup \left\{0\right\}$ by

  $$q\left(y\right)=uy, \forall y\in K_{15}\cup \left\{0\right\}, u\in K_{15 }\mathrm{is}\mathrm{fixed}.$$
• S-3 Take the composition of $p$ and $q$ and get an $8\times 8$-bit S-box.

Since fifteen linear scalar multiple functions $q$ can be defined on $K_{15}\cup \left\{0\right\}$, therefore fifteen different S-boxes can be obtained by the above procedure. For $u=10011000$, the construction of S-box on $K_{15}\cup \left\{0\right\}$ is given in

Table 1. Construction of S-box on $K_{15}\cup \left\{0\right\}$.

$\mathit{y}\in {\mathit{K}}_{15}\cup \left\{0\right\}$	$\mathit{q}\left(\mathit{y}\right)=\mathit{u}\mathit{y}$ $\left(\mathit{u}=10011000\right)$	$\mathit{p}\left(\mathit{q}\left(\mathit{y}\right)\right)={\left(\mathit{u}\mathit{y}\right)}^{-1}$
00000000	00000000	00000000
10011000	01001110	01000101
01001110	00001010	11011101
00001010	10011001	11011100
10011001	11010110	11010111
11010110	01000100	10010010
01000100	10010011	01001111
10010011	01001111	10010011
01001111	10010010	01000100
10010010	11010111	11010110
11010111	11011100	10011001
11011100	11011101	00001010
11011101	01000101	01001110
01000101	00001011	10011000
00001011	00000001	00000001
00000001	10011000	00001011

and is arranged in

Table 2. S-box on $K_{15}\cup \left\{0\right\}$ (in base 2).

LSB’s	00	01	10	11
00	00000000	00001011	11010110	10010011
01	01001111	10011000	10010010	10011001
10	01000101	11010111	11011100	00000001
11	00001010	01001110	11011101	01000100

, while

Table 3. S-box on $K_{15}\cup \left\{0\right\}$ (in base 10).

LSB’s	0	1	2	3
0	0	11	214	147
1	79	152	146	153
2	69	215	220	1
3	10	78	221	68

shows the elements of the S-box in base 10.

3. Analyses

In this section, the strength of the proposed S-box is analyzed and discussed by manipulating balance property, nonlinearity, differential approximation probability, linear approximation probability, strict avalanche criterion, and majority logic criterion.

3.1. Balance Property

A $n$ variables Boolean function $g\left(x\right)$ is said to be balanced if $\#\left\{x|g\left(x\right)=0\right\}=\#\left\{x|g\left(x\right)=1\right\}$. Balanced functions are considered cryptographically strong because the magnitude of the function’s imbalance represents a weakness in the function in terms of linear cryptanalysis [17]. $8\times 8$ S-boxes on $GF\left(2^8\right)$ comprise eight Boolean functions containing $256$ binary bits each and in this case, all the Boolean functions are balanced. However, in our case, as we are considering the subgroup of $GF{\left(2^8\right)}^{*}$, it is not evident for all the Boolean functions of the S-box to fulfill the balance property. Additionally, the higher the number of balanced functions, the stronger will be the S-box. In proposed S-box, there are eight Boolean functions with sixteen binary bits each, and among them, seven are balanced.

3.2. Nonlinearity Analysis

The nonlinearity of a Boolean function is defined as the number of bits which must change in its truth table to reach the closest affine function. Computationally, this is half the number of bits in the Boolean function, less the largest absolute value of the unexpected distance. The unexpected distance is computed with the fast Walsh transform (FWT) [18]. Nonlinearity is always positive, even if we have a balanced function. The optimal $4\times 4$ S-boxes exhibit nonlinear behavior with an average value of $4$. The seven balanced Boolean functions of the proposed S-box attain an optimal value of nonlinearity for sixteen input values. The results of nonlinearity of the Boolean functions $g_7,g_6,\dots ,g_0$ of the proposed S-box are listed in

Table 4. Results of nonlinearity analysis.

Boolean function	$g_7$	$g_6$	$g_5$	$g_4$	$g_3$	$g_2$	$g_1$	$g_0$	Average
Nonlinearity	4	4	0	4	4	4	4	4	3.5

.

3.3. Strict Avalanche Criterion

A Boolean function $g_n:Z_2^n\to Z_2$ is said to satisfy SAC if complementing a single bit results in changing the output bit with probability exactly one half, i.e.,

$${{\displaystyle \sum }}_{i=0}^{2^n-1}{g}_n\left(v_i\right)\oplus g_n\left(v_i\oplus e\right)=2^{n-1},$$

where $e$ denotes any element of $Z_2^n$ with hamming weight $1$ [19]. The results of the analysis of the strict avalanche criterion for our S-box are shown in

Table 5. Strict avalanche criterion of proposed S-box.

Boolean function	$g_7$	$g_6$	$g_5$	$g_4$	$g_3$	$g_2$	$g_1$	$g_0$	Average
SAC	0.5	0.5	0	0.5	0.5	0	0.5	0.75	0.4688

. The average value is 0.4688, which is closed to the ideal value 0.5.

3.4. Linear Approximation Probability Analysis

Linear approximation probability analyzes the value of the imbalance of an event. The parity of the input bits selected by the mask $\Gamma x$ is equal to the parity of the output bits selected by the mask $\Gamma y$. Linear approximation probability of a given S-box is defined as:

$$LP=\underset{\Gamma x,\Gamma y\ne 0}{\max }\left|\frac{\#\left\{x\in X|x.\Gamma x=S\left(x\right).\Gamma y\right\}}{\left|X\right|}-\frac{1}{2}\right|,$$

where $X$ is the set of all possible inputs [20]. The proposed S-box shows a reasonable resistance against linear attacks by a value $LP=0.125$.

3.5. Differential Approximation Probability Analysis

For strong S-boxes, it is desirable that the nonlinear transformation exhibits differential uniformity. Differential approximation probability measures the differential uniformity demonstrated by an S-box. The S-box is immune to the differential attack if differential at the input uniquely maps to an output differential [21]. The mathematical expression of the differential approximation probability for the S-box is:

$$D{P}^S\left(\Delta x\to \Delta y\right)=\underset{0\ne \Delta x\in X,\Delta y\in X}{\max }\left[\frac{\#\left\{xϵX|S\left(x\right)\oplus S\left(x\oplus \Delta x\right)=\Delta y\right\}}{\left|X\right|}\right].$$

(1)

The optimal differential bound (maximum of all differentials in an individual S-Box) for $4\times 4$ S-Boxes is $DP=0.25$. By using the above rule, the outcomes of the differential approximation probability of the most probable output XOR of the proposed S-box by applying the input and output differentials are given in

Table 6. Differential approximation probabilities of the proposed S-box.

0	1	2	3
---	0.25	0.25	0.25
0.25	0.25	0.25	0.25
0.25	0.25	0.25	0.25
0.25	0.25	0.25	0.25

. The maximum of the matrix is $0.25$, showing that the proposed S-box bears a solid immunity to hold out the differential approach.

3.6. Majority Logic Criterion

S-box is a basic constituent of many encryption schemes, which performs substitution. Generally, an S-box substitutes an input pixel of $m$ bits with an output pixel of $n$ bits, where $m$ and $n$ may or may not be equal. In our case, the pixels of an image are altered according to the above lookup Table 3. The pixels of the plain image are transformed in the following two simple steps to get the distorted image:

• Use LSB’s of the input pixel of the image to select an 8-bit S-box value.
• LSB’s of the S-box value become MSB’s of the output pixel and MSB’s of the input pixel become LSB’s of the output pixel.

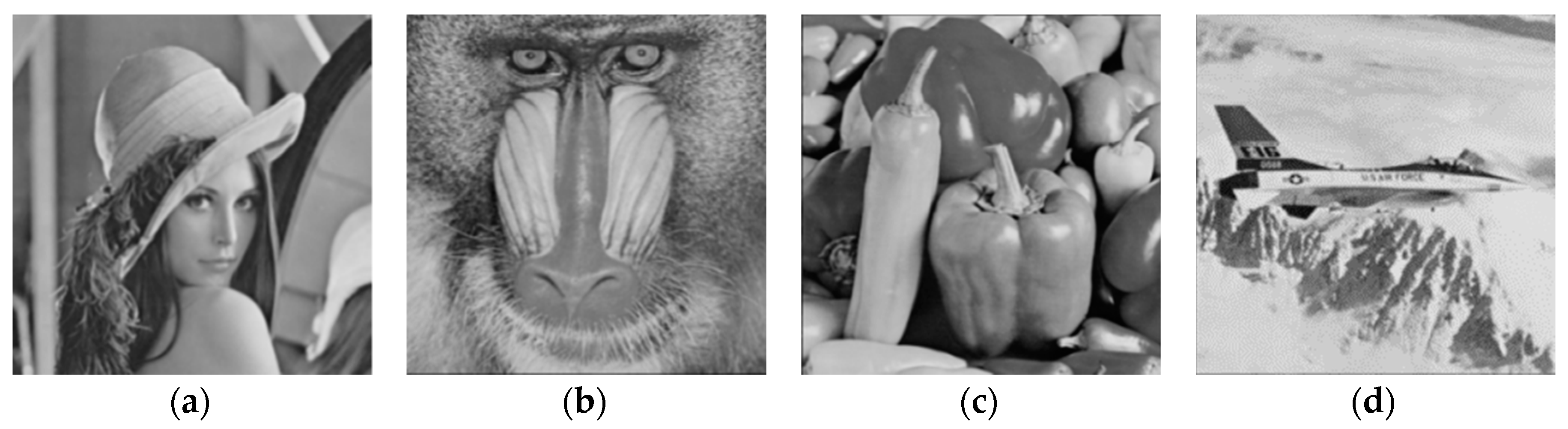
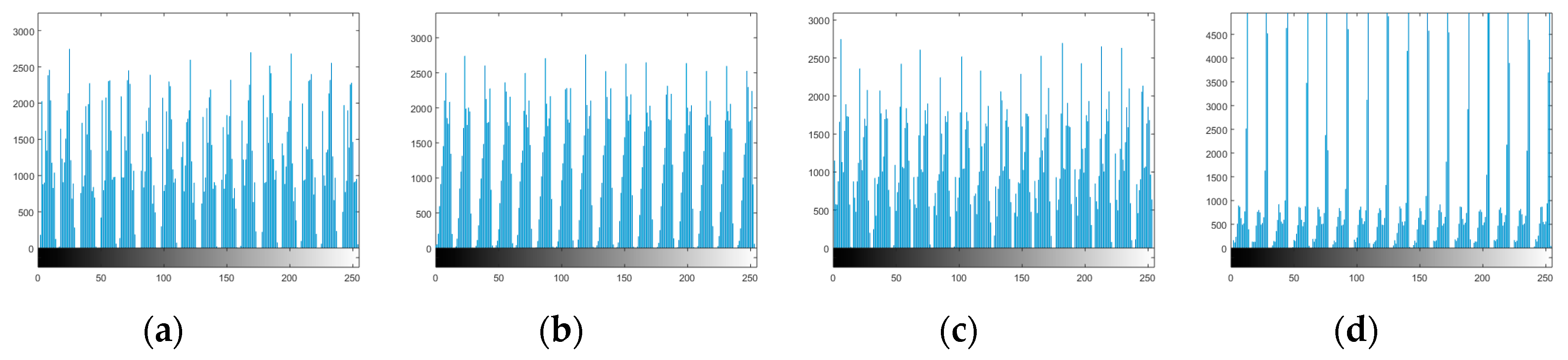
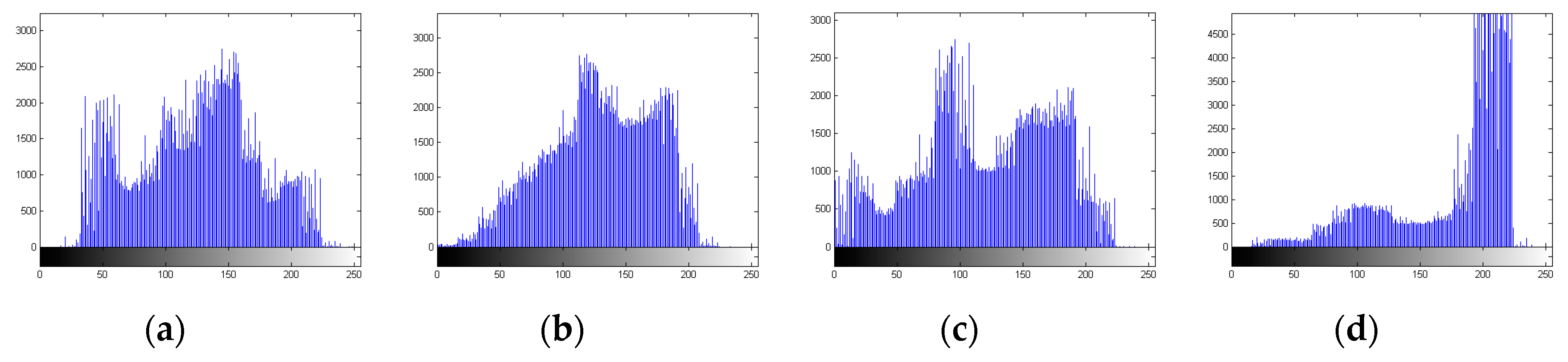
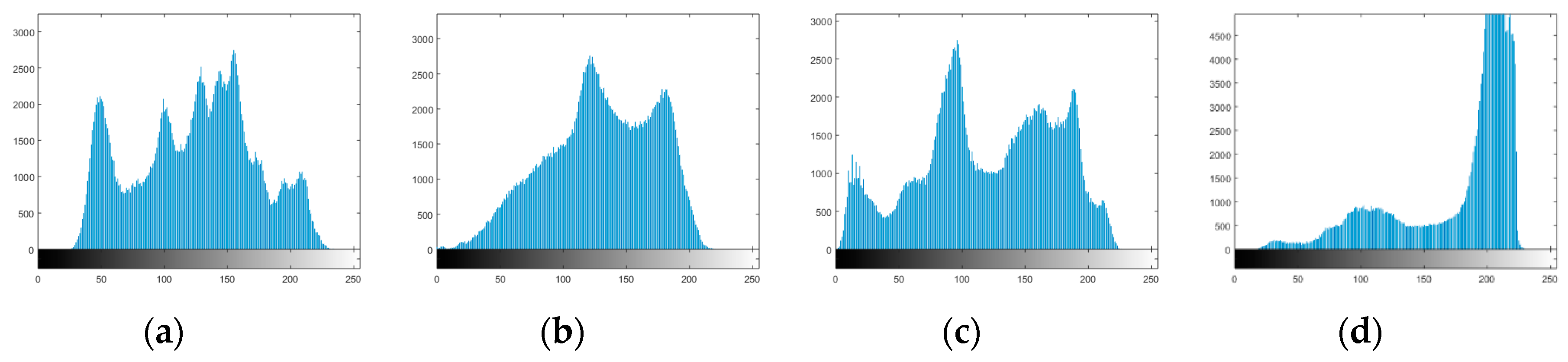
The standard grayscale images of size $512\times 512$ pixels each, consisting of ‘Lena’, ‘Baboon’, ‘Pepper’ and ‘Airplane’ were chosen as test images for experimental results, as depicted in Figure 1. The distortions produced in these images by using the proposed S-box are shown in Figure 2. The amount of distortion can be seen from histograms displayed in Figure 3, that show the distribution of the intensities of the picture elements after application of S-box. While the histograms of the original images are shown in Figure 4.

The suitability of the proposed S-box in image encryption applications is determined by majority logic criterion. This criterion uses the results from contrast analysis, correlation analysis, energy analysis, entropy analysis, homogeneity analysis, and mean of absolute deviation analysis [22]. These analyses are applied to the distorted images by using proposed S-box and then the majority logic criterion is used to determine the appropriateness of the S-box to image encryption applications. The results of these analyses for the proposed S-box and the S-box in Reference [14] are listed in

Table 7. Results of majority logic criterion.

Attribute	Ref. [14]	Proposed S-Box
		Lena	Baboon	Pepper	Airplane
Contrast	3.3220	10.4474	10.5164	10.6092	9.8911
Correlation	0.0879	0.0127	−0.0015	0.0004	0.0664
Energy	0.0244	0.0159	0.0156	0.0157	0.0172
Entropy	4.7301	7.4451	7.3583	7.5937	6.7025
Homogeneity	0.4835	0.4045	0.3900	0.3949	0.4376
MAD	36.3631	32.3756	31.8342	32.4054	32.2973

. According to MLC, small values of correlation, energy and homogeneity while the greater values of entropy, contrast and MAD are better.

4. Application of Proposed S-box in Image Watermarking

A pixel is a picture element that composes an image. Images can be classified into three primary types: Full color or 24-bit color images, grayscale images, and black and white images. In this segment, we present an application of proposed S-box for watermarking a grayscale image. Each picture element in a grayscale image consists of eight bits and it may have $2^8=256$ possible levels of gray running from zero (black) to 255 (white). Interestingly, the contribution of every bit of a picture element in the amount of information is not the same. The leftmost bit named as the most significant bit (MSB) contributes $1/2$ of the information, while the rightmost bit named as the least significant bit (LSB) contributes $1/{256}^{th}$ of the information. Therefore, changing that LSB only affects $1/{256}^{th}$ of the intensity and humans simply cannot detect the difference. In fact, it is difficult to perceive a difference in $1/{16}^{th}$ of an intensity change, so we can alter the 4 LSB’s with little or no perceptible difference.

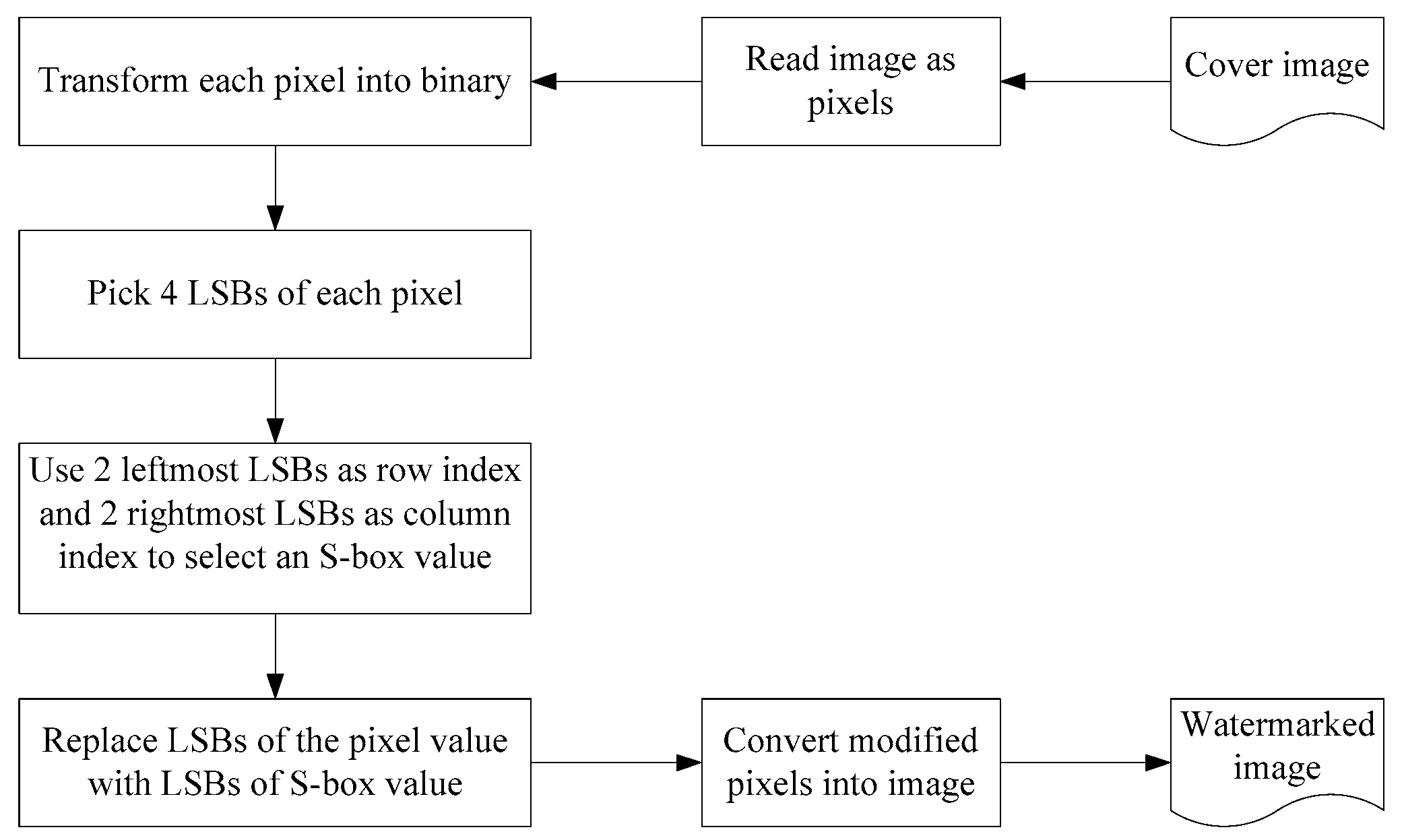
In the proposed watermarking algorithm, proposed S-box over subgroup of $GF{\left(2^8\right)}^{*}$ was used to transform the LSB’s of each pixel of the grayscale image. We will insert watermark in images based on modifications to the LSB’s of the pixel values which will not affect the quality of the image. Figure 5 gives a description of the watermark embedding algorithm, while the watermark extraction algorithm remains the same.

Experimental Results and Discussion

The standard grayscale images of size $512\times 512$ pixels each, consisting of ‘Lena’, ‘Baboon’, ‘Pepper’ and ‘Airplane’ were chosen as cover images for experimental results, as depicted in Figure 1. A watermark was embedded in these images by the transformation of the proposed S-box by the described algorithm and the watermarked images are listed in Figure 6. The experimental work was performed using MATLAB R2015a. One can note that there is no detectable difference between the corresponding images before and after embedding the watermark.

The histograms of watermarked images are revealed in Figure 7. There is only a little difference between the histograms of corresponding images (see Figure 4). The reason is that the S-box transformation is applied to the LSB’s of pixels of the cover image. Hence, the histogram analysis is justifying the accuracy of the algorithm.

The performance of the algorithm was evaluated based on mean square error (MSE), peak signal to noise ratio (PSNR) and structural similarity index measure (SSIM). $PSNR$ measures the quality of the reconstructed image. The numerical value of $PSNR$ of image $Y$ can be calculated by the expression: $PSNR=10\times lo{g}_{10}\left(\frac{MA{X}_Y{}^2}{MSE}\right)$, for grayscale images the value of $MA{X}_Y{}^2$ is taken as 255. $MSE$ of images $Y$ and $Z$ is defined as: $MSE=\frac{1}{M\times N}{\displaystyle \sum }_{m=0}^{M-1}{\displaystyle \sum }_{n=0}^{N-1}{\left[Y\left(m,n\right)-Z\left(m,n\right)\right]}^2$, where $Y$ is the original image and $Z$ is the watermarked image [23]. The similarity between two images can be estimated by the structural similarity index measure (SSIM) [24]. The closeness of the results in

Table 8. Analysis of the proposed algorithm.

Grayscale-Images/Analysis	Proposed S-Box				Ref. [14]
	Airplane	Baboon	Lena	Pepper
MSE	16.0383	15.9333	16.2827	15.8937	11.7755
PSNR	83.1537	83.2194	83.0025	83.2443	86.1651
SSIM	0.8280	0.9317	0.8198	0.8250	0.9145

for both S-boxes is indicating the appropriateness of the proposed S-box to watermarking applications.

5. Conclusions and Future Work

In this paper, an S-box construction method on a subgroup of the Galois field is presented. It is $4\times 4$ S-box of byte values. Some well-known analyses were applied to the proposed S-box and it is concluded that the S-box possesses desirable properties suitable for encryption applications for secure communications. The proposed S-box satisfies the MLC with optimal values and gives a good value as compared to the other ones. We used the proposed S-box in a watermarking scheme which makes the original image robust while the watermarked image is almost the same. MSE, PSNR, and SSIM analyses of watermarking are very reasonable.

The above study sets the grounds for the 16-byte S-boxes in information security applications. This can be extended by modifying and designing the existing cryptography, watermarking, and steganography applications that use $4\times 4$ and 8 $\times 8$ S-boxes by replacing them with these S-boxes. Some other algebraic structures can also be found for the construction of such S-boxes to enhance their strength. Further, there is space for discovering different cryptanalysis techniques for such S-boxes.