Abstract
Visual cryptography (VC) encrypts a secret image into n shares (transparency). As such, we cannot see any information from any one share, and the original image is decrypted by stacking all of the shares. The general (k, n)-threshold secret sharing scheme (SSS) can similarly encrypt and decrypt the original image by stacking at least k (≤ n) shares. If one stack is fewer than k shares, the secret image is unrecognizable. Another subject is progressive visual secret sharing, which means that when more shares are progressively stacked, the combined share becomes clearer. In this study, we constructed an advanced scheme for (k, n)-threshold SSS that can be encrypted in VC for any positive integers n ≥ k ≥ 2 through the method of combination, and the size of each share is the same as that of the original image. That is, no pixel expansion is required. Our scheme is novel, and the results from the theoretical analysis and simulation reveal that our scheme exhibits favorable contrast to that of other related schemes.
1. Introduction
Visual Cryptography (VC), a type of the visual secret sharing (VSS) scheme, involves the encoding of secret information into a message and can be decoded visually without computer assistance. In 1979, Blakley [1] and Shamir [2] introduced the (k, n)-threshold secret sharing scheme (SSS), in which a secret image was encoded into n (≥ 2) shares, and only when k (≥ n) shares were superimposed upon one another would the secret message be revealed. Furthermore, when fewer than k shares were collected, the secret information could not be decoded.
In 1995, Naor and Shamir proposed four types of (k, n)-threshold SSSs [3], but their schemes exhibited the expansion problem with each share. Some studies [3,4,5,6,7,8,9] related to VC have exhibited the common problem of pixel expansion. Pixel expansion occurs when each share is larger than the input secret image. Therefore, greater n values lead to greater expansion values. To remedy the restrictions of pixel expansion, a new scheme was proposed by Fang et al. in 2008 [10]. In their scheme, they adopted a Hibert curve [11] and two queues to enable all generated shares to remain the same size as the secret image. However, the size of the secret images was restricted to pixels, where r is a positive integer. Subsequently, studies have been conducted on the nonexpansion VSS scheme problem. In 2009, Shyu proposed a random grid (RG)-based (n, n)-threshold VSS scheme for binary, gray-level, and color images [12] in accordance with an idea proposed by [13]. Chen and Tsao developed an RG-based (2, n)-threshold VSS scheme [14] in the same year. Later, some researchers considered the use of XOR operations in their (k, n)-threshold VSS schemes [15,16]. In 2015, Ref. [17] designed a (2, 2)-threshold VSS scheme that encrypted a secret image four-pixel blocks at a time. The main idea was inspired by [3], but no pixel expansion occurred. However, they neither analyzed the security of their scheme nor calculated the contrast of the recovered image.
At the same time, some schemes related to the progressive VSS (PVSS) scheme have been proposed in recent years [18,19,20,21,22,23,24,25,26,27,28,29]. The term “progressive” indicates that the greater the number of shares stacked together, the clearer the restored image is. In 2011, Hou and Quan proposed a new (2, n)-threshold PVSS scheme [22] that seemed to be inspired by the (2, n)-threshold scheme of [3]. In the same year, Chen and Juan established a general (4, n)-threshold PVSS scheme [23]. Chen and Tsao [24] produced more general results for the (k, n)-threshold PVSS scheme with unexpanded shares in 2011. They designed their scheme using a random grid [13]. Several studies [25,26,27] have subsequently continued and extended the work on the scheme [24]. Moreover, Wan et al. proposed a VSS scheme based on a QR code (VSSQR) with a (k, n)-threshold in 2018 [28]. In the VSSQR scheme, the output shares were all valid QR codes that could be scanned and decoded through the utilization of a QR code reader. The secret image can be revealed through stacking and XOR decryptions. Because the (k, n)-threshold PVSS scheme they applied in the VSSQR scheme was [24], its performance was similar. Yan et al. designed their (k, n)-threshold PVSS scheme with unexpanded shares [29] based on [22]. However, the performance of these schemes can still be improved.
Some studies on the secret-image sharing problem have not been based on VC. Most of these schemes can recover high-quality images but require complicated cryptographic computations. Liu et al. used three Boolean operations, bit-level XOR, COV(1, 7, 3) from (7, 4), a Hamming code, and COV(2, 8, 4) from an (8, 4) shortened Hamming code, to propose three (k, n)-threshold progressive secret-image sharing schemes [30]. Their scheme operations are much more than typically efficient. However, the secret image cannot be recovered unless human vision is aided by additional computation.
All of the foregoing studies have confronted either the problem of pixel expansion or the topic of performance. As a result, this study proposed a novel (k, n)-threshold PVSS scheme with unexpanded shares and higher contrast. The remainder of the study is organized as follows. In Section 2, we present relevant research, and the details of the main proposed scheme are provided in Section 3. The experimental results are presented in Section 4. Analyses and comparisons are provided in the last section.
2. Related Works
Two properties are essential to a VSS scheme: visually recognizable and security [19]. For measuring the visual quality, which determines how well human eyes can recognize the recovered image, the recovered secret image S′ corresponding to the original secret image S is evaluated through contrast. Contrast is commonly defined in the following two respects [8,10,18,19]
Definition 1.
Light transmittance of the image S is denoted as T(S), and T(S) = w/t = 1 − (b/t), where b is the number of the black pixel, and w is the number of the white pixel, and t = w + b.
Definition 2.
The contrast of the recovered secret image S’ corresponding to the original secret image S is defined as
where) (resp.,)) denotes the average light transmittance of the area in S’ which correspond to the white (resp., black) area of the original secret image S; and t is referred to the pixel expansion.
Regardless of whether we use the definition of α1 or α2, larger values produce higher visual quality. In the following three definitions, we use α to represent α1 or α2.
Definition 3 (Visually recognizable).
Ina (k, n)-threshold VSS scheme, the recovered secret image S′ could berecognized as the corresponding original secret image S if α > 0 when staking more than or equal to k shares.
Definition 4 (Security).
Ina (k, n)-threshold VSS scheme, the scheme is secure if α = 0 when staking less than k shares, which means no information of S could be recognized through S′.
For “progressive,” we provide the following definition.
Definition 5 (Progressive).
Ina (k, n)-threshold PVSS scheme, when the number of shares collected is greater than or equal to k, the more the share is staked, the larger the contrast α will be.
In 1995, Naor and Shamir proposed a general (k, n)-threshold VSS scheme [8]. In their scheme, they used the stacking rules presented in Table 1, where 0 (or 1) represents white (or black) and the secret image can be restored by stacking the shares together. The size of the shares generated in [8] was tm × n pixels, whereas the size of the shares in our scheme was m × n pixels, where m (n) is the width (height) of the secret image, and t is a positive integer.

Table 1.
Stacking rules of two random pixels.
Some types (including (2, 2), (2, n), (k, k), and (k, n)) of general (k, n)-threshold VSS schemes have been introduced as follows.
The first type is a (2, 2)-threshold VSS scheme. A secret image is encoded in the two shares, and only when the two shares are stacked together can the secret image be seen. Based on Table 1, they construct the two matrices C0 and C1,
where C0 represents the matrix for the white pixel, and C1 represents the matrix for the black pixel. Entries in each matrix C0 or C1 are classified into two values, 0 and 1, where 1 is the black pixel and 0 is the white pixel. The first row in each matrix refers to the pixel of share 1, and the pixel of share 2 is indicated in the second row. In this type, t is equal to 2. As a result, the size of all shares is 2m × n pixels, where m is the width and n is the height of the secret image.
The second type is a (2, n)-threshold VSS scheme. A dealer provides a share of the secret to n users, but only when specific conditions are fulfilled are users able to restore the confidential information in the secret image from their shares. If the users collect at least two shares and stack them together, then they can obtain the secret. The two matrices C0 and C1 were designed as follows. Matrices C0 and C1 are n × n matrices.
In total, n shares are generated, and each row in either C0 or C1 is randomly selected by each share. We can see that each row contains one black pixel and n − 1 white pixels. When any k (≥ 2) shares are stacked together, C0 contains one black and n − 1 white pixels, and C1 contains k black and n − k white pixels. The difference between C0 and C1 reveals the secret image. The size of the shares is nm × n pixels.
The (k, k)-threshold VSS scheme is the third type; in this scheme, a secret is divided into k shares, and the secret information is not revealed when fewer than k shares are stacked. Furthermore, two k × matrices C0 and C1 are constructed. The sum of the 1’s in each column in C0 is even, and the sum of the 1’s in each column in C1 is odd. With similar characteristics to those described in the (2, n)-threshold, the contrast in this case is equal to 1/, and the size of the shares is m × n pixels.
Let C be a (k, k)-threshold VSS scheme and H be a collection of k-wise independent hash functions [31,32,33]. Noar and Shamir constructed the k-out-of-n VSS scheme C′ from C and H. In this (k, n)-threshold VSS scheme, the size of the shares is m) × n pixels, and the contrast reaches . As shown above, all schemes suffered from pixel expansion, regardless of the type.
For managing share expansion, Fang et al. proposed a scheme [10] that could generate nonexpanded shares and in which the combination of shares was the same size as the secret image. They used C0 and C1, constructed with a VSS scheme, and the two queues were created using a Hilbert curve [11]. A Hilbert curve is a specific path that passes through × pixels for any positive integer k, as illustrated in Figure 1.
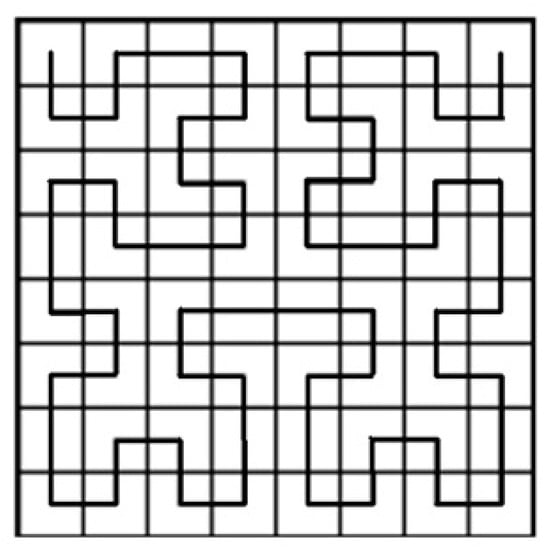
Figure 1.
Hilbert-curve for r = 3.
When employing a Hilbert curve for a square secret image, all pixels are scanned sequentially. In [10], these researchers prepared two queues, one for storing white pixels and one for storing black pixels. Accordingly, these researchers proposed two algorithms, one that was one dimension and another that was two dimensions, in which the one-dimensional algorithm concerns the line and the two-dimensional algorithm concerns the image. However, problems occur when an image is not ×, and some of the remaining pixels will be difficult to process.
In 2011, Chen and Tsao [24] proposed a (k, n)-threshold PVSS scheme with unexpanded shares based on a random grid. Wu and Sun [25], Guo et al. [26], and Yan et al. [27] have all continued and extended work on the scheme [24]. Of these studies, in 2018 Yan et al. reported the most favorable results. Their primary algorithm was as follows (Algorithm 1 (YLY scheme)), where the symbol ⊕ denotes the Boolean XOR operation.
| Algorithm 1. (YLY scheme [27]) |
| Input: A binary secret image S with size w × h pixels and the threshold parameters n and k Output: n shares SC1, SC2, …, SCn, each with size w × h pixels Step 1: For each position (i, j) ∈ {(i, j)|1 ≤ i ≤ w, 1 ≤ j ≤ h}, repeat Steps 2–6. Step 2: Select b1, b2, …, bk ∈ {0, 1} randomly. Step 3: If S(i, j) = b1 ⊕ b2 ⊕ … ⊕ bk, go to Step 5; else go to Step 4 Step 4: Randomly select p ∈ {1, 2, …, k} let bp = 1 − bp (that is, 0 → 1 or 1 → 0). Step 5: Set bk+1 = b1, bk+2 = b2, …, b2k = bk, b2k+1 = b1, … if (n mod k) = 0, bn = bk else bn = b(n mod k). Step 6: Randomly rearrangement b1, b2, …, bn to SC1(i, j), SC2(i, j), …, SCn(i, j). Step 7: Output the n shares SC1, SC2, …, SCn. |
In 2011, Chen et al. proposed another (4, n)-threshold VSS scheme [23] using a combinatorial idea. For the two matrices C0 and C1 constructed in [23], fewer than four shares stacked together produce a transmittance of C0 equal to that of C1; therefore, no secret is revealed. When superimposing more than three shares, the transmittance of C0 is greater than that of C1. As a result, the secret from the stacked shares is revealed. Their scheme exhibited favorable performance in comparison with the schemes proposed in [3,10,24]. We used a similar concept and devised an advanced (k, n)-threshold PVSS scheme in this study.
3. Our Scheme
Before detailing our proposed (k, n)-threshold progressive SSS, some definitions and lemmas must be provided. For convenience, let
Definition 6.
The Hamming weight of a column vector (respectively, a row vector) is the sum of each entry in this column (respectively, row).
Definition 7.
An n × m 0–1 matrix M(n, j) is totally symmetric where m = if each column has the same Hamming weight j and has different column vector among each column.
Definition 8.
An n × (mA + mB) combined matrix [A || B] is obtained by concatenating matrix A and B, where A is an n × mA matrix, and B is an n × mB matrix. A matrix [a × A || b × B] is generated by concatenating A for a times and B for b times.
Lemma 1.
Given an n × m totally symmetric matrix A = M(n, j), fi(A) is defined as the Hamming weight of the row vector that results from applying the OR operation for any i rows in A, where i = 1, 2, …, n. As a result, fi(A) = fi(M(n, j)) = .
Proof of Lemma 1.
The number of columns in M(n, j) =. When we selected any i rows in matrix A, the resultant entry from applying OR operation for these row vectors remains zero if one column vector has all zeros in these i rows. For any one column vector with all zeros in these i rows, the j ones must be present in the other n − i rows. As a result, the number of those column vectors is . □
Lemma 2.
fi(A || B) = fi(A) + fi(B) for any two totally symmetric matrices A and B with sizes n × m1 and n × m2, respectively.
Proof of Lemma 2.
A matrix [A || B] is obtained by concatenating matrices A and B, where A = M(n, jA) and B = M(n, jB). Then, fi(A || B) = fi([M(n, jA) || M(n, jB)]). Because using a Hamming weight for the row vector resulting from applying the OR operation for some i rows of [A || B] is equal to that [A || B] be divided into two parts A, B and doing the same thing to these two parts, then add those two results together. For this reason, fi([M(n, jA) || M(n, jB)]) = fi([M(n, jA)]) + fi([M(n, jB)]). That is, fi(A || B) = fi(A) + fi(B). □
Let [A1 || A2 || ...|| Ak] = [[ … [A1 || A2] || A3] || … || Ak] for any totally symmetric matrix A1, A2, …, Ak, where the size of Ai is n × mi for i = 1, 2, …, k. We have the following corollary.
Corollary 3.
For all k totally symmetric matrices A1, A2, …, Ak, where Ap = M(n, jp), for some 0 ≤ jp ≤ n for any 1 ≤ p ≤ k, let [A1 || A2 || ...|| Ak] = B. Then, fi(B) = fi(A1) + fi(A2) + …+ fi(Ak) for any 1 ≤ i ≤ n.
Definition 9.
For any 1 ≤ p ≤ k, given totally symmetric matrices Ap = M(n, jp), where 0 ≤ jp ≤ n, let [A1 || A2 || …|| Ak] = B, where B is an n × m matrix. Define T(B, i) = 1 − (fi(B)/m), where 1 ≤ i ≤ n.
When conducting a (k, n)-threshold SSS, two matrices, C0 and C1, should first be constructed according to the white and black pixels, respectively, in the secret image. In our scheme, the following two conditions must be met, in accordance with Definitions 2–4, because no pixel expansion to occur.
T(C0,t) = T(C1,t), for 1 ≤ t ≤ k − 1
T(C0,t) > T(C1,t), for t ≥ k
In the first condition, when adopting the OR operation for any t rows of C0, the Hamming weight is equal to that of C1 for 1 ≤ t ≤ k − 1. This indicates that when stacking fewer than k shares together, the light transmittance between C0 and C1 is the same. As a result, the secret image is not revealed under this condition. Regarding the second condition, C0 has a higher light transmittance than C1 when t is greater than or equal to k, enabling us to decode the confidential information in the secret image. According to these two rules, we provide the following main algorithm (Algorithm 2), referred to as the CHJ scheme. The case in [23] is a special case for our scheme, where k = 4. Proof of the scheme’s accuracy is presented in Section 3.1.
| Algorithm 2. (CHJ scheme) |
| Input: A binary secret image S with size w × h pixels and the threshold parameters n and k Output: n shares R1, R2, …, Rn, each with size w × h pixels if (k mod 2 == 1) C0 = [M(n, 2) || × M(n, 0) || ] C1 = [(n − k + 1) × M(n, 1) || × M(n, n) || ] m = ] else C0 = [M(n, 2) || × M(n, 0) || × M(n, n) || ] C1 = [(n − k + 1) × M(n, 1) || ] m = ] for (int j = 1; j ≤ h; j++) for (int i = 1; i ≤ w; i++) x = random(1, m) for (int t = 1; t ≤ n; t++) if (S(i, j) == 0) Rt(i, j) = C0(t, x) Else Rt(i, j) = C1(t, x) |
3.1. Proof of the CHJ Scheme
In this subsection, we aim to determine the accuracy of the CHJ scheme. That is, we want to demonstrate that the CHJ scheme is a (k, n)-threshold PVSS scheme.
Theorem 4.
In the CHJ scheme, stacking at least k shares reveals the secret; while stacking fewer than k shares does not reveal the secret. The CHJ scheme is therefore a (k, n)-threshold VSS scheme.
We used light transmittance to prove that the secret cannot be discerned if fewer than k shares are stacked, but the image can be viewed if at least k shares are stacked together. The proof is divided into two cases according to whether k is odd or even. In other words, we must prove that our scheme satisfies (1) and (2). We know that T(A, i) = 1 − (fi(A)/m) when A = C0 or C1; therefore, two formulas must be discussed in each case: the denominator m and the numerator fi(A). Because the entire proof of Theorem 4 is mathematical and encompasses more contexts, we only present an outline for proving the CHJ scheme in this study. First, regardless of how many shares are stacked, we prove that the denominator m of the light transmittance for the white and black pixels of the stacked image is always the same. That is,
and
Second, we prove that the numerators of the light transmittance fi(A) for the white and black pixels of the stacked image are different when we stack at least k shares (i ≥ k). However, the light transmittance fi(A) for the white and black pixels of the stacked image is the same when stacking fewer than k shares (i < k). After providing such proof, we certified the CHJ scheme is a (k, n)-threshold VSS sharing scheme. Notably, the principle of mathematical induction and the Pascal theorem, for any positive integer 1 ≤ r ≤ n, are used in the proof.
Theorem 5.
In the CHJ scheme, when we stack at least k shares, progressively stacking more shares results in greater clarity in the recovered image. That is, the CHJ scheme is demonstrably a PVSS scheme.
Proof of Theorem 5.
According to Definition 5, we were required to demonstrate that α is larger when stacking more shares (more than k). Here, we only use the α1 in Definition 2 to represent α, and the proof for α2 is similar to this proof. We therefore prove that the difference between the light transmittance of the white and black pixels is greater when we stack more shares. That is, [T(C0, i + 1) − T(C1, i + 1)] is greater than [T(C0, i) − T(C1, i)] for i ≥ k. Because [T(C0, i + 1) − T(C1, i + 1)] − [T(C0, i) − T(C1, i)] = [fi+1(C1)/m − fi+1(C0)/m] − [fi(C1)/m − fi(C0)/m], we can prove [fi+1(C1) − fi+1(C0)] − [fi(C1) − fi(C0)] > 0. We divide the proof into two cases for when k is odd and even. The proof for the second case, when k is even, is similar to that of the first case; we therefore prove only the first case, for when k is odd. □
We know, by definition, that fi(M(n, j)) = − . Recall that when k is odd,
We first compute the difference between fx(C1) and fx(C0). By Corollary 3,
Replace x by i + 1 and i, we have
We can simplify the equation to . Because i ≥ k (≥ 3), so n − i − 1 ≤ n − k − 1 < n − k + 2 ≤ n − 2t − 1 < n − 2t, for any t = 1, 2, …, (k − 3)/2. And . Therefore, this equation becomes i − k + 2 > 0, and [T(C0, i + 1) − T(C1, i + 1)] > [T(C0, i) − T(C1, i)] can be concluded for when k is odd.
4. Experimental Results
This study proposes an advanced PVSS scheme, the CHJ scheme, that can encode a secret image into n (≥ 2) shares without pixel expansion, and in which the hidden secret can be restored only when k (≤ n) shares are stacked together. To demonstrate the feasibility of the proposed CHJ scheme, we conducted five experiments in the following order: (4, 5)-, (4, 6)-, (4, 7)-, (5, 6)-, and (5, 7)-threshold PVSS schemes.
4.1. Simulation 1: (4, 5)-Threshold PVSS Scheme
In the first experiment, the parameter k was set at 4, and n was set at 5; C0 and C1 could be generated by the CHJ scheme described in Section 3 as follows.
C1 = [(n − 3) × M(n, 1) || M(n, n − 1)] = [2 × M(5, 1) || M(5, 4)]
Figure 2a is the input secret image with size 449 × 341 pixels, and the five shares (G1, G2, G3, G4, and G5) generated by the CHJ scheme are displayed in Figure 2b–f. The result of stacking the two shares is presented in Figure 2g, where the symbol ⊗ denotes the Boolean OR operation. The result of stacking any other two shares was nearly the same; therefore, we only present one combined image of stacking G1 and G2. Any two shares stacked together revealed no information regarding the secret image. The simulation of superimposing three shares is presented in Figure 2h, and we only display the combination of G1, G2, and G3. Furthermore, the confidential message could not be seen in such a case. Figure 2i presents the result of stacking G1, G2, G3, and G4. From watching this simulation, we were able to distinguish the secret image. By superimposing all of the shares, we achieved greater clarity when viewing the secret image, as displayed in Figure 2j. A greater number of stacked shares (must greater than or equal to the threshold value k) produced a clearer restored image.

Figure 2.
The experimental results of the proposed (4, 5)-threshold PVSS scheme.
4.2. Simulation 2: (4, 6)-Threshold PVSS Scheme
In the second experiment, we encrypted a secret image with the size of 449 × 341 pixels into six shares (G1, G2, G3, G4, G5, and G6), as displayed in Figure 3b–g, respectively. Regarding the threshold value k = 4, we expected that the secret image could be seen when stacking more than three shares. The result of stacking G1 and G2 is depicted in Figure 3h, and Figure 3i is the result of stacking G1, G2, and G3 together. The result of stacking G1, G2, G3, and G4 is displayed in Figure 3j; stacking of G1, G2, G3, G4, and G5 is displayed in Figure 3k; and stacking of G1, G2, G3, G4, G5, and G6 is presented in Figure 3l. The secret image can be seen in Figure 3j–l with varying clarity.

Figure 3.
The experimental results of the proposed (4, 6)-threshold VSS scheme.
4.3. Simulation 3: (4, 7)-Threshold PVSS Scheme
Regarding the (4, 7)-threshold PVSS scheme, the image with the size 449 × 341 pixels presented in Figure 4a was encoded into seven individual shares, referred to as G1, G2, G3, G4, G5, G6, and G7. Figure 4b–h present the cipher shares generated with the CHJ scheme. The result of stacking G1 and G2 is displayed in Figure 4i, and Figure 4j is the result of stacking G1, G2, and G3 together. Figure 4k is the result of stacking G1, G2, G3, and G4, and the result of stacking G1, G2, G3, G4, and G5 together is presented in Figure 4l. Figure 4m and Figure 4n are the results of stacking G1, G2, G3, G4, G5, and G6 and stacking all of the shares together, respectively. Only Figure 4k–n reveals information regarding the secret image.

Figure 4.
The experimental results of the proposed (4, 7)-threshold VSS scheme.
4.4. Simulation 4: (5, 6)-Threshold PVSS Scheme
In the fourth experiment, we encrypted the image with the size of 449 × 341 pixels displayed in Figure 5a; Figure 5b–g are the cipher shares (G1, G2, G3, G4, G5, and G6, respectively). When stacking G1 and G2, we achieved the result depicted in Figure 5h. Staking the three shares G1, G2, and G3 produced the result displayed in Figure 5i. The result of stacking G1, G2, G3, and G4 is shown in Figure 5j. The result of stacking five shares together, G1, G2, G3, G4, and G5, is displayed in Figure 5k. Figure 5l reveals the result of stacking all of the shares together. For the (5, 6)-threshold PVSS scheme, the secret image could only be seen when more than four shares were stacked.

Figure 5.
The experimental results of the proposed (5, 6)-threshold VSS scheme.
4.5. Simulation 5: (5, 7)-Threshold PVSS Scheme
In the last experiment, which involved the (5, 7)-threshold PVSS scheme, an image with a size of 449 × 341 pixels, as presented in Figure 6a, was encrypted into seven shares (G1, G2, G3, G4, G5, G6, and G7) as displayed in Figure 6b–h, respectively. The results of stacking fewer than five shares are indicated in Figure 6i–k. Figure 6l and Figure 6m present the results of stacking G1, G2, G3, G4, and G5 and G1, G2, G3, G4, G5, and G6, respectively. When stacking all of the shares, the result presented in Figure 6n. Similarly, when more than four shares were stacked together, we could see the secret image.

Figure 6.
The experimental results of the proposed (5, 7)-threshold VSS scheme.
5. Analysis and Comparison
In this paper, we provide an advanced (k, n)-threshold PVSS scheme for any integer 2 ≤ k ≤ n. We constructed the CHJ scheme through a technique of combination. The visual and security analyses of our scheme are detailed in Section 5.1 and Section 5.2, respectively.
5.1. Visual Analysis
In Section 2, we define two contrasts α1 and α2 using the definition of light transmittance when stacking k shares. Because the CHJ scheme has no pixel expansion and in accordance with the design of the algorithm, we use T(C0, k) and T(C1, k) to rewrite the definition of contrast.
Property 6.
The contrastα1 = T(C0, k) − T(C1, k), and α2 = (T(C0, k) − T(C1, k))/(1 + T(C1, k)), when staking k shares, where C0 and C1 are the designed matrices for white and black pixels, respectively, in the proposed CHJ scheme.
Because [3,10] use the definition of α1 for contrast, we offer a comparison of α1 in their scheme and our scheme according to the k and n values in Table 2. Notably, the contrast of the shares generated by [10] was the same as that in the basic scheme that they applied. Because they applied the scheme developed in [3], their scheme exhibits the same contrast performance as [3]. For cases in which k = 2 or 3, the contrast of our scheme was the same as that in [3]; therefore, we only discuss the condition of n ≥ k ≥ 4. The value of α1 in the (4, 5)-threshold SSS of [3] approached 1/4261, whereas the contrast α1 in our scheme was 3/15 − 2/15 = 1/15. For any (k, n) such that n ≥ k ≥ 4, our proposed scheme exhibited superior contrast performance in comparison with (Table 2) [3]. For the scheme in [10], the contrast was dependent on which basic scheme was applied. For example, if [10] is based on [3], then the contrast is the value presented in the second column in Table 2. Furthermore, the contrast is the same as in our scheme if [10] is based on our proposed CHJ scheme.

Table 2.
The comparison of contrast α1 between Ref. [3] and our scheme.
For compare to our scheme, those in [24,25,26,27,29] have all used the second definition of α2 for contrast; thus, we conducted another comparison, as presented in Table 3. In Table 3, those values for [29] were calculated by averaging the two values used in their paper. Because no results were reported for the (4, 6)- or (5, 6)-threshold in [29], we wrote “N/A” in the relevant place in Table 3. In [24], the researchers provided a formula for estimating the contrast when stacking t shares together: , where k ≤ t ≤ n. Therefore, we obtained those values for [24] in Table 3 by directly calculating the formula for different k, t, and n values. In [27], the researchers calculated the value of α2 from their experimental result for all schemes ([24,25,26,27]). Therefore, we obtained those values for [25,26,27], as presented in Table 3. Unfortunately, the value for a large n (≥ 6) was not provided, but we reached the following conclusions based on the algorithms. (1) When n = k = t, the contrast α2 is equal to 1/2k – 1 for all of these schemes. (2) When N = ⌊n/k⌋ = 1, the schemes in [24,26] are the same. (3) When q = n mod k = 1, the values of α2 of the schemes in [25,27] are the same. (4) The contrast of the scheme in [27] is always greater than or equal to that of the others. The experimental results in [27] support the results of our theoretical analysis. We then compared the contrast α2 of the scheme in [27] with that of our scheme. Although in [27] the exact value α2 for general (k, n, t) was difficult to obtain (The Principle of Inclusion and Exclusion was required), obtaining the value for k = t was relatively simple. The value was 2p/(2t + 1 − p), where p = (N + 1)qNk – q/. Therefore, some information in Table 3 could be provided.

Table 3.
The comparison of contrast when stacking t shares together.
From the data listed in Table 3, we determined that when n > 4, the contrast of the scheme in [24] is small, indicating inadequate performance. In [25,26,27,29], when k < 4, the contrast of the scheme in [29] is similar to that of our scheme. However, when n and k are both ≥ 4 and the value of k is close to that of n, the contrast decreases, as indicated in the bold rows of Table 3. Because our scheme demonstrated higher contrast, it demonstrates superior performance for larger k values. Therefore, our scheme offers superior contrast of stacked images under the general (k, n)-threshold for larger k and n values.
The Hibert curve [11] was not used in our scheme; therefore, unlike in [10], the size of the secret image has no restrictions. The method used in [3] has the problem of pixel expansion; because the shares generated by our scheme are all the same size as the input image, no expansion occurs. The scheme in [23] can only satisfy the conditions of the (4, n)-threshold; however, we can meet the general conditions of the (k, n)-threshold. Notably, [23] is a special case of our proposed scheme. For greater k and n values, the contrast is relatively small for the schemes in [24,25,26,27,29]; therefore, our proposed scheme is preferable. Moreover, the output shares of the VSSQR scheme [28] proposed in 2018 all possessed valid QR codes. In comparing their scheme with others, for equality, we only discuss the scheme which the secret image can be revealed visually through stacking. In this kind of view, the performance of their scheme is similar to that of [24]. All comparisons between ours and related schemes are presented in Table 4.

Table 4.
The comparison of our scheme with some related schemes.
5.2. Security Analysis
A correlation test was performed to evaluate the security of a secret-image sharing scheme. This test has been widely used in secret-image sharing, such as in [15,34,35]. Through this test, we were able to determine whether high correlations existed among pixels in each share of our proposed scheme. Four types of correlations were observed, those between two horizontally adjacent pixels, two vertically adjacent pixels, two diagonally adjacent pixels, and two vice-diagonally adjacent pixels in the input secret images, with shares computed as usual. The correlation coefficient of two adjacent pixels R(x, y) can be obtained by using the following formula, where x and y are the values of two adjacent pixels in one image, and w × h is the number of pairs of adjacent pixels:
The correlation test involved 448 × 341 (or 449 × 340, or 448 × 340) pairs of two neighboring pixels (horizontally adjacent pixels, vertically adjacent pixels, diagonally adjacent pixels, and vice-diagonally adjacent pixels) for the first experiment, described in Section 4. Four types of correlation coefficients of one secret image and five shares are presented in Table 5.

Table 5.
The correlation coefficients of two adjacent pixels in Simulation 1.
As indicated in Table 5, the correlation coefficients of the five shares were nearly 0 (irrespective of whether the value was negative or positive), and the restored image exhibited similar results when fewer than k (4, in this example) shares were stacked, indicating a weak correlation among all of the pixels in each share and unauthorized restored shares. Therefore, the shares can be viewed as random shares. Correlation test results from Experiments 2–5 are presented in Table 6. Here we only list the correlation coefficients of share one, because the results for the other shares are all similar to share one. Note that, the secret images were all identical to that in Experiment 1 (already shown in Table 5). As indicated by the results, no share revealed sufficient information regarding the input image. From the results of these correlation tests, we conclude that all of the shares generated by our scheme were merely noise-like, demonstrating that the secret message could not be discerned in any share.

Table 6.
The correlation coefficients of neighboring pixels for the first share in Simulation 1~5.
As a result, the secret image is revealed when at least k shares are stacked in our proposed scheme and increases in clarity in accordance with the number of shares stacked together. That is, our scheme is a (k, n)-threshold PVSS scheme. The data in Table 2, Table 3, Table 4, Table 5 and Table 6 indicate the following four advantages of our proposed CHJ scheme: no pixel expansion, greater contrast α, and the abilities to process an image of any size and for any values of k or n. In practical use, it is a more flexible method for encoding a secret image.
Author Contributions
All authors discussed the main idea and scientific contribution. Y.-Y.C. provided the presented idea, the main algorithm and performed the experiments. B.-Y.H. contributed in analyzed some of the results, and drafted the manuscript. J.S.-T.J. analyzed the results, modified the manuscript, and supervised the whole project.
Funding
This research was funded by the Ministry of Science and Technology of the Republic of China, grant number: MOST 106-2221-E-260-009.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the AFIPS, New York, NY, USA, 4–7 June 1979; pp. 313–317. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Naor, M.; Shamir, A. Visual cryptography. Eurocrypt94, Lecture Notes in Computer Science; Springer: Berlin, Germany, 1995; Volume 950, pp. 1–12. [Google Scholar]
- Blundo, C.; Santis, A.D.; Stinson, D.R. On the contrast in visual cryptography schemes. J. Cryptol. 1999, 12, 261–289. [Google Scholar] [CrossRef]
- Eisen, P.A.; Stinson, D. Threshold visual cryptography schemes with specified whiteness levels of reconstructed pixels. Des. Codes Cryptogr. 2002, 25, 15–61. [Google Scholar] [CrossRef]
- Hofmeister, T.; Krause, M.; Simon, H.U. Contrast-optimal k out of n secret sharing schemes in visual cryptography. Theory Comput. Sci. 2000, 240, 471–485. [Google Scholar] [CrossRef]
- Lin, C.C.; Tsai, W.H. Secret multimedia information sharing with data hiding capability by simple logic operations. Pattern Recognit. Image Anal. 2004, 14, 594–600. [Google Scholar]
- Linial, N.; Nisan, N. Aprroximate inclusion-exlusion. Combinatorica 1990, 10, 349–365. [Google Scholar] [CrossRef]
- Yang, C.N. New visual secret sharing schemes using probabilistic method. Pattern Recognit. Lett. 2004, 25, 481–495. [Google Scholar] [CrossRef]
- Fang, W.-P.; Lin, S.-J.; Li, J.-C. Visual cryptography (VC) with nonexpanded shadow images: A hilbert-curve approach. In Proceedings of the IEEE International Conference on Intelligence and Security Informatics, Taipei, Taiwan, 17–20 June 2008; pp. 271–272. [Google Scholar]
- Hilbert, D. Üeber die stetige abbildung einer linie aufein flächenstück. Math. Ann. 1891, 38, 459–460. [Google Scholar] [CrossRef]
- Shyu, S.-J. Image encryption by multiple random grids. Pattern Recognit. 2009, 42, 1582–1596. [Google Scholar] [CrossRef]
- Kafri, O.; Keren, E. Encryption of pictures and shapes by random grids. Opt. Lett. 1987, 12, 377–379. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.H.; Tsao, K.H. Visual secret sharing by random grids revisited. Pattern Recognit. 2009, 42, 2203–2217. [Google Scholar] [CrossRef]
- Wu, X.; Sun, W. Random grid-based visual secret sharing with abilities of OR and XOR decryptions. J. Vis. Commun. Image Represent. 2013, 24, 48–62. [Google Scholar] [CrossRef]
- Nag, A.; Biswas, S.; Sarkar, D.; Sarka, P.P. Secret image sharing scheme based on a boolean operation. Cybern. Inf. Technol. 2014, 14, 98–113. [Google Scholar] [CrossRef]
- Al-Tamimi, A.G.T.; Gaafar, A. A New Simple Non-Expansion Algorithm for (2, 2)-Visual Secret Sharing Scheme. Int. J. Comput. Appl. 2015, 113, 3. [Google Scholar]
- Chen, S.K.; Lin, J.C. Fault-tolerant and progressive transmission of images. Pattern Recognit. 2005, 38, 2466–2471. [Google Scholar] [CrossRef]
- Fang, W.P. Multi-layer progressive secret image sharing. In Proceedings of the 7th WSEAS, Athens, Greece, 24–26 August 2007; pp. 112–116. [Google Scholar]
- Fang, W.P.; Lin, J.C. Progressive viewing and sharing of sensitive images. Pattern Recognit. Image Anal. 2006, 16, 638–642. [Google Scholar] [CrossRef]
- Chen, Z.-H.; Lee, Y.-S. Yet another friendly progressive visual secret sharing scheme. In Proceedings of the 2009 Fifth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kyoto, Japan, 12–14 September 2009; pp. 353–356. [Google Scholar]
- Hou, Y.-C.; Quan, Z.-Y. Progressive visual cryptography with unexpanded shares. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 1760–1764. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Juan, J.S.T. A 4 out of n Secret Sharing Scheme in Visual Cryptography without Expansion. In Proceedings of the International Conference on Foundations of Computer Science (FCS), Stanford, CA, USA, 18–21 July 2011. [Google Scholar]
- Chen, T.H.; Tsao, K.H. Threshold visual secret sharing by random grids. J. Syst. Softw. 2011, 84, 1197–1208. [Google Scholar] [CrossRef]
- Wu, X.; Sun, W. Improving the visual quality of random grid based visual secret sharing. Signal Process. 2013, 93, 977–995. [Google Scholar] [CrossRef]
- Guo, T.; Liu, F.; Wu, C. Threshold visual secret sharing by random grids with improved contrast. J. Syst. Softw. 2013, 86, 2094–2109. [Google Scholar] [CrossRef]
- Yan, X.; Liu, X.; Yang, C.N. An enhanced threshold visual secret sharing based on random grids. J. Real-Time Image Process. 2018, 14, 61–73. [Google Scholar] [CrossRef]
- Wan, S.; Lu, Y.; Yan, X.; Wang, Y.; Chang, C. Visual secret sharing scheme for (k, n) threshold based on QR code with multiple decryptions. J. Real-Time Image Process. 2018, 14, 25–40. [Google Scholar] [CrossRef]
- Yan, X.; Wang, S.; Niu, X. Threshold progressive visual cryptography construction with unexpanded shares. Multimed. Tools Appl. 2016, 75, 8657–8674. [Google Scholar] [CrossRef]
- Liu, Y.X.; Yang, C.N.; Wu, S.Y.; Chou, Y.S. Progressive (k, n) secret image sharing schemes based on Boolean operations and covering codes. Signal Process. Image Commun. 2018, 66, 77–86. [Google Scholar] [CrossRef]
- Alon, N.; Spencer, J. The Probabilistic Method; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Carter, J.L.; Wegman, M.N. Universal classes of hash functions. J. Comput. Syst. Sci. 1979, 18, 143–154. [Google Scholar] [CrossRef]
- Wegman, M.N.; Carter, J.L. New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 1981, 22, 265–279. [Google Scholar] [CrossRef]
- Chang, C.; Lin, C.; Lin, C.; Chen, Y. A novel secret image sharing scheme in color images using small shadow images. Inf. Sci. 2008, 178, 2433–2447. [Google Scholar] [CrossRef]
- Shankar, K.; Eswaran, P. A new k out of n secret image sharing scheme in visual cryptography. In Proceedings of the 10th International Conference on IEEE Intelligent Systems and Control (ISCO2016), Coimbatore, India, 7–8 January 2016; pp. 1–6. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).