Abstract
Secure booting within a field-programmable gate array (FPGA) environment is traditionally implemented using hardwired embedded cryptographic primitives and non-volatile memory (NVM)-based keys, whereby an encrypted bitstream is decrypted as it is loaded from an external storage medium, e.g., Flash memory. A novel technique is proposed in this paper that self-authenticates an unencrypted FPGA configuration bitstream loaded into the FPGA during the start-up. The internal configuration access port (ICAP) interface is accessed to read out configuration information of the unencrypted bitstream, which is then used as input to a secure hash function SHA-3 to generate a digest. In contrast to conventional authentication, where the digest is computed and compared with a second pre-computed value, we use the digest as a challenge to a hardware-embedded delay physical unclonable function (PUF) called HELP. The delays of the paths sensitized by the challenges are used to generate a decryption key using the HELP algorithm. The decryption key is used in the second stage of the boot process to decrypt the operating system (OS) and applications. It follows that any type of malicious tampering with the unencrypted bitstream changes the challenges and the corresponding decryption key, resulting in key regeneration failure. A ring oscillator is used as a clock to make the process autonomous (and unstoppable), and a novel on-chip time-to-digital-converter is used to measure path delays, making the proposed boot process completely self-contained, i.e., implemented entirely within the re-configurable fabric and without utilizing any vendor-specific FPGA features.
1. Introduction
SRAM-based field-programmable gate arrays (FPGAs) need to protect the programming bitstream against reverse engineering and bitstream manipulation (tamper) attacks. Fielded systems are often the targets of attack by adversaries seeking to steal intellectual property (IP) through reverse engineering, or attempting to disrupt operational systems through the insertion of kill switches known as hardware Trojans. Internet-of-things (IoT) systems are particularly vulnerable, given the resource-constrained and unsupervised nature of the environments in which they operate.
FPGAs implementing a secure boot usually store an encrypted version of the programming bitstream in an off-chip non-volatile memory (NVM) as a countermeasure to these types of attacks. Modern FPGAs provide on-chip battery-backed random-access memory (RAM) or E-Fuses for the storage of a decryption key, which is used by vendor-embedded encryption hardware functions, e.g., the Advanced Encryption Standard (AES), within the FPGA in order to decrypt the bitstream as it is read from the external NVM during the boot process [1]. Recent attack mechanisms have been shown to read out embedded keys, and therefore on-chip key storage threatens the security of the boot process [2].
In this paper, we propose a physical unclonable function (PUF)-based key generation strategy that addresses the vulnerability of on-chip key storage. Moreover, the proposed secure boot technique is self-contained, in that none of the FPGA-embedded security primitives or FPGA clocking resources are utilized. We refer to the system as Bullet-Proof Boot for FPGAs (BulletProoF). BulletProoF uses a PUF implemented in the programmable logic (PL) side of an FPGA to generate the decryption key at boot time, and then uses the key for decrypting an off-chip NVM-stored second stage boot image. The second stage boot image contains PL components as well as software components, such as an operating system and applications. BulletProoF decrypts and programs the PL components directly into those portions of the PL side that are not occupied by BulletProoF using dynamic partial reconfiguration, while the software components are loaded into DRAM for access by the processor system (PS). The decryption key is destroyed once this process completes, minimizing the time the decryption key is available.
Similar to PUF-based authentication protocols, enrollment for BulletProoF is carried out in a secure environment. The enrollment key generated by BulletProoF is used to encrypt the second stage boot image. Both the encrypted image and the unencrypted BulletProoF bitstreams are stored in the NVM. During the in-field boot process, the first stage boot loader (FSBL) loads the unencrypted BulletProoF bitstream into the FPGA. BulletProoF reads the entire set of configuration data that has just been programmed into the FPGA using the internal configuration access port (ICAP) interface [3], and uses this data as challenges to the PUF to regenerate the decryption key. Therefore, BulletProoF self-authenticates. The BulletProoF bitstream instantiates the SHA-3 algorithm, and uses this cryptographic function both to compute hashes and as the entropy source for the PUF. As we will show, BulletProoF is designed so that the generated decryption key is irreversibly tied to the data integrity of the entire unencrypted bitstream.
BulletProoF is stored unencrypted in an off-chip NVM, and is therefore vulnerable to manipulation by adversaries. However, the tamper-evident nature of BulletProoF prevents the system from booting the components present in the second stage boot image if tampering occurs, because an incorrect decryption key is generated. In such cases, the encrypted bitstring is not decrypted and remains secure.
The hardware-embedded delay PUF (HELP) is leveraged in this paper as a component of the proposed tamper-evident, self-authenticating system implemented within BulletProoF. HELP measures path delays through a CAD-tool-synthesized functional unit—in particular, the combinational component of SHA-3 in the proposed system. Within-die variations that occur in path delays from one chip to another allow HELP to produce a device-specific key. Challenges for HELP are two-vector sequences that are applied to the inputs of the combinational logic that implements the SHA-3 algorithm. The timing engine within HELP measures the propagation delays of paths sensitized by the challenges at the outputs of the SHA-3 combinational block. The digitized timing values are used in the HELP bitstring processing algorithm, in order to generate the AES key.
The timing engine times paths using either the fine-phase shift capabilities of the digital clock manager on the FPGA, or by using an on-chip time-to-digital-converter (TDC) implemented using the carry-chain logic within the FPGA. The experimental results presented in this paper are based on the TDC strategy.
The BulletProoF boot process is summarized as follows:
- The first-stage boot loader (FSBL) programs the PL side with the unencrypted (and untrusted) BulletProoF bitstream.
- BulletProoF reads the configuration information of the PL side (including configuration data that describes itself) through the ICAP, and computes a set of digests using SHA-3.
- For each digest, the mode of the SHA-3 functional unit is switched to PUF mode, and the HELP engine is started.
- Each digest is applied to the SHA-3 combinational logic as a challenge. Signals propagate through SHA-3 to its outputs, and are timed by the HELP timing engine. The timing values are stored in an on-chip block RAM (BRAM).
- Once all timing values are collected, the HELP engine uses them (and helper data stored in the external NVM) to generate a device-specific decryption key.
- The key is used to decrypt the second stage boot image components also stored in the external NVM and the system boots.
Self-authentication is ensured because any change to the configuration bitstream will change the digest. When the incorrect digest is applied as a challenge in PUF mode, the set of paths that are sensitized to the outputs of the SHA-3 combinational block will change (when compared to those sensitized during enrollment using the trusted BulletProoF bitstream). Therefore, any change made by an adversary to the BulletProoF configuration bitstring will result in missing or extra timing values in the set used to generate the decryption key.
The key generated by HELP is tied directly to the exact order and cardinality of the timing values. It follows that any change to the sequence of paths that are timed will change the decryption key. As we discuss below, multiple bits within the decryption key will change if any bit within the configuration bitstream is modified by an adversary, because of the avalanche effect of SHA-3 and because of a permutation process used within HELP to process the timing values into a key. Note that other components of the boot process, including the first-stage boot loader (FSBL), can also be included in the secure hash process, as well as FPGA-embedded security keys, as needed.
The rest of this paper is organized as follows. Related work is discussed in Section 2. An overview of the existing Xilinx boot process is provided in Section 3. Section 4 describes the proposed BulletProoF system, while Section 5 describes BulletProoF countermeasures, including an on-chip time-to-digital-converter (TDC), which leverages the carry-chain component within an FPGA for measuring path delays. Section 6 presents a statistical analysis of bitstrings generated by the TDC as proof-of-concept. Conclusions are provided in Section 7.
2. Background
Although FPGA companies embed cryptographic primitives to encrypt and authenticate bitstreams as a means of inhibiting reverse engineering and fault injection attacks, such attacks continue to evolve. For example, a technique that manipulates cryptographic components embedded in the bitstream as a strategy to extract secret keys is described in [4]. A fault injection attack on an FPGA bitstream is described in [5] to accomplish the same goal, where faulty cipher texts are generated by fault injection and then used to recover the keys. A hardware Trojan insertion strategy is described in [6] that is designed to weaken FPGA-embedded cryptographic engines.
There are multiple ways to store the secret cryptographic keys in an embedded system. While one of the conventional methods is to store them in non-volatile memory (NVM), Konopinski and Kenyon [7] and others [8] discuss several ways to extract cryptographic keys stored in NVMs, which makes these schemes insecure. Battery-backed RAM (BBRAM) and E-Fuses are also used for storing keys in FPGAs. BBRAMs complicate and add cost to a system design because of the inclusion and limited lifetime of the battery. E-Fuses are one-time-programmable (OTP) memory, and are vulnerable to semi-invasive attacks designed to read out the key via scanning technologies [8]. These types of issues and attacks on NVMs are mitigated by physical unclonable functions (PUFs), which do not require a battery and do not store secret keys in digital form on the chip [9].
3. Overview of a Secure Boot under Xilinx
A hardwired 256-bit AES decryption engine is used by Xilinx to protect the confidentiality of externally stored bitstreams [1]. Xilinx provides software tools to allow a bitstream to be encrypted using either a randomly generated or user-specified key. Once generated, the decryption key can be loaded through JTAG into a dedicated E-Fuse NVM or battery-backed BRAM (BBRAM). The power-up configuration process associated with fielded systems first determines whether the external bitstream includes an encrypted-bitstream indicator, and if so, decrypts the bitstream using cipher block chaining (CBC) mode of AES. To prevent fault injection attacks [5], Xilinx authenticates configuration data as it is loaded. In particular, a 256-bit keyed hashed message authentication code (HMAC) of the bitstream is computed, using SHA-256 to detect tamper and to authenticate the sender of the bitstream.
During provisioning, Xilinx software is used to compute an HMAC of the unencrypted bitstream, which is then embedded in the bitstream itself and encrypted by AES. A second HMAC is computed in the field as the bitstream is decrypted, and compared with the HMAC embedded in the decrypted bitstream. If the comparison fails, the FPGA is deactivated. The security properties associated with the Xilinx boot process enable the detection of transmission failures, and attempt to program the FPGA with a non-authentic bitstream and tamper attacks on the authentic bitstream.
The secure boot model in modern Xilinx system-on-chip (SoC) architectures differs from that described above, because Xilinx SoCs integrate both programmable logic (PL) and processor components (PS). Moreover, the SoC is designed to be processor-centric, i.e., the boot process and overall operation of the SoC is controlled by the processor. Xilinx SoCs use public key cryptography to carry out authentication during the secure boot process. The public key is stored in an NVM and is used to authenticate configuration files, including the first-stage boot loader (FSBL), and therefore, the key provides secondary authentication and primary attestation.
The Xilinx Zynq 7020 SoC used in this paper incorporates both a processor (PS) side and programmable logic (PL) side. The processor side runs an operating system (OS), e.g., Linux, and applications on a dual core ARM cortex A-9 processor, which is tightly coupled with the PL side through an AMBA AXI interconnect.
The flow diagram shown on the left side of Figure 1 identifies the basic elements of the Xilinx Zynq SoC secure boot process. The Xilinx BootROM loads the FSBL from an external NVM to DRAM. The FSBL programs the PL side and then reads the second-stage boot loader (U-Boot), which is copied to DRAM, and passes control to U-Boot. U-Boot loads the software images, which can include a bare-metal application, or the Linux OS, as well as other embedded software applications and data files. A secure boot first establishes a root of trust, and then performs authentication on top of the trusted base at each of the subsequent stages of the boot process. As mentioned, Rivest–Shamir–Adleman (RSA) is used for authentication and attestation of the FSBL and other configuration files. The hardwired 256-bit AES engine and SHA-256 are then used to securely decrypt and authenticate boot images using a BBRAM or E-Fuse embedded key. Therefore, the root of trust and the entire secure boot process depends on the confidentiality of the embedded keys.

Figure 1.
Xilinx Zynq SoC boot process.
4. Overview of BulletProoF
BulletProoF is designed to be self-contained, utilizing only components typically available in the FPGA PL fabric. Specialized, vendor-supplied embedded security components, including E-Fuse, BBRAM, and cryptographic primitives like AES are not used. The BulletProoF boot-up process is illustrated in Figure 2 as a flow diagram. Similar to the Xilinx boot process, the BootROM loads the FSBL, which then programs the PL side, in this case with the unencrypted BulletProoF bitstream. The FSBL then hands control over to BulletProoF, which carries out some of the functions normally delegated to U-Boot. BulletProoF’s first task is to regenerate the decryption key. It accomplishes this by reading all of the configuration information programmed into the PL side using the ICAP interface [3]. As configuration data is read, it is used as a challenge to time paths between the ICAP and the SHA-3 functional unit (see Figure 3), and as inputs to the SHA-3 cryptographic hash function to compute a chained set of digests.

Figure 2.
Proposed Zynq SoC boot process.

Figure 3.
BulletProoF enrollment and regeneration process.
As configuration data is read and hashed, BulletProoF periodically changes the mode of SHA-3 from hash mode to a specialized PUF mode of operation. PUF mode configures SHA-3 such that the combinational logic of SHA-3 is used as a source of entropy for key generation. The HELP PUF uses each digest as a challenge to the SHA-3 combinational logic block. HELP measures and digitizes the delays of paths sensitized by these challenges at high resolution and stores them in an on-chip BRAM for later processing. The same timing operation is carried out for paths between the ICAP and SHA-3 outputs, as discussed above, and Field-programmable gate arrays the timing data combined and stored with the SHA-3 timing data in the BRAM. This process continues with additional configuration data added to the existing hash (chained), until all of the configuration data is read and processed.
BulletProoF then reads the externally stored Helper Data and delivers it to the HELP algorithm as needed during the key generation process that follows. The decryption key is transferred to an embedded PL-side AES engine. BulletProoF reads the encrypted second stage boot image components (labeled 3 through 9 in Figure 2) from the external NVM and transfers them to the AES engine.
An integrity check is performed at the beginning of the decryption process as a mechanism to determine if the proper key was regenerated. The first component decrypted is the key integrity check component (labeled 3 in Figure 2). This component can be an arbitrary string or a secure hash of, for instance, U-Boot.elf, which is encrypted during enrollment and stored in the external NVM. An unencrypted version of the key integrity check component is also stored as a constant in the BulletProoF bitstream. The integrity of the decryption key is checked by comparing the decrypted version with the BulletProoF version. If they match, then the integrity check passes and the boot process continues. Otherwise, the FPGA is deactivated and the secure boot fails.
If the integrity check passes, BulletProoF then decrypts and authenticates components 4 through 9 in Figure 2 using 256-bit AES in CBC mode and HMAC, resp., starting with the application (App) bitstream. An application bitstream is programmed into the unused components of the PL side by BulletProoF, using dynamic partial reconfiguration. BulletProoF then decrypts the software components, e.g., Linux, etc. and transfers them to U-Boot. The final step is to bootstrap the processor to start executing the Linux OS (or bare-metal application).
4.1. BulletProoF Enrollment Process
BulletProoF uses a physical unclonable function (PUF) to generate the decryption key, as a mechanism for eliminating the vulnerabilities associated with on-chip key storage. Key generation using PUFs requires an enrollment phase, which is carried out in a secure environment, i.e., before the system is deployed to the field. During enrollment, when the key is generated for the first time, HELP generates the key internally and transfers helper data off of the FPGA. As shown in Figure 2, the helper data is stored in the external NVM unencrypted. The internally generated key is then used to encrypt the other components of the external NVM (second-stage boot image, or SSBI) by configuring AES in encryption mode.
BulletProoF uses a configuration I/O pin (or an E-Fuse bit) to determine whether it is operating in Enroll mode or Boot mode. The pin is labeled “Enroll/Boot config. pin” in Figure 3. The trusted party configures this pin to Enroll mode, in order to process the “UnEncrypted SSBI” to an “Encrypted SSBI”, and to create the helper data. The Encrypted SSBI and helper data are stored in an External NVM and later used by the fielded version to boot (see “Enroll” annotations along the bottom of Figure 3). Therefore, the Enroll and Boot versions of BulletProoF are identical. Note that the “Enroll/Boot config. pin” allows the adversary through board-level modifications, in order to create new versions of the Encrypted SSBI, but the primary goal of BulletProoF, i.e., to protect the confidentiality and integrity of the trusted authority’s second-stage boot image, is preserved.
4.2. BulletProoF Fielded Boot Process
A graphical illustration of the secure boot process carried out by the fielded device is illustrated in Figure 3. As indicated above, the FSBL loads the unencrypted version of BulletProoF from the external NVM into the PL of the FPGA, and hands over control to BulletProoF. As discussed further below, BulletProoF utilizes a ring oscillator as a clock source that cannot be disabled during the boot process once it is started. This prevents attacks that attempt to stop the boot process at an arbitrary point in order to reprogram portions of the PL using external interfaces, e.g., PCAP, SelectMap, or JTAG. The steps and annotations in Figure 3 are defined as follows:
- BulletProoF reads configuration data using the ICAP interface, using a customized controller.
- Every n-th configuration word is used as a challenge to time paths between the ICAP and the SHA-3 outputs with SHA-3 configured in PUF mode (this is done to prevent a specific type of reverse-engineering attack, discussed later.). The digitized timing values are stored in an on-chip BRAM.
- The remaining configuration words are applied to the inputs of SHA-3 in functional mode to compute a chained sequence of digests.
- Periodically, the existing state of the hash is used as a challenge with SHA-3 configured in PUF mode, to generate additional timing data. The digitized timing values are stored in an on-chip BRAM.
- Once all configuration data is processed, the HELP algorithm processes the digitized timing values into a decryption key using helper data, which are stored in an external NVM.
- BulletProoF runs an integrity check on the key.
- BulletProoF reads the encrypted second-stage boot image (SSBI) from the external NVM. AES decrypts the image and transfers the software components to U-Boot, and the hardware components into the unused portion of the PL, using dynamic partial reconfiguration. Once completed, the system boots.
4.3. Security Properties
The primary goal of BulletProoF is to protect the second-stage boot images, i.e., prevent them from being decrypted, changed, encrypted, and installed back into the fielded system. The proposed system has the following security properties in support of this objective:
- The enrollment and regeneration process proposed for BulletProoF never reveals the key outside the FPGA. Therefore, physical, side-channel-based attacks are necessary in order to steal the key. We do not address side-channel attacks in this paper, but it is possible to design the AES engine with side-channel attack resistance using circuit countermeasures, as proposed in [10].
- Any type of tampering with the unencrypted BulletProoF bitstream or helper data by an adversary will only prevent the key from being regenerated, and a subsequent failure of the boot process. Note that it is always possible to attack a system in this fashion, i.e., by tampering with the contents stored in the external NVM, independent of whether it is encrypted or not.
- Any attempt to reverse-engineer the unencrypted bitstream, in an attempt to insert logic between the ICAP and SHA-3 input, will change the timing characteristics of these paths, resulting in key regeneration failure. For example, the adversary may attempt to rewire the input to SHA-3, in order to allow external configuration data (constructed to exactly model the data that exists in the trusted version) to be used instead of the ICAP data.
- The adversary may attempt to reverse-engineer the helper data to derive the secret key. As discussed in [11], the PUF used by BulletProoF uses a helper data scheme that does not leak information about the key.
- The proposed secure boot scheme stores an unencrypted version of the BulletProoF bitstream, and therefore, adversaries are free to change components of BulletProoF or add additional functionality to the unused regions in the PL. As indicated, changes to configuration data read from ICAP are detected, because the paths that are timed by the modified configuration data are different, which causes key regeneration failure.
- BulletProoF uses a ring oscillator as a clock source. Therefore, once BulletProoF is started, it cannot be stopped by the adversary as a mechanism for stealing the key (this attack is elaborated on below).
- BulletProoF disables the external programming interfaces (PCAP, SelectMap, and JTAG) prior to starting to prevent adversaries from attempting to perform dynamic partial reconfiguration during the boot process. BulletProoF actively monitors the state of these external interfaces during the boot, and destroys the timing data and keys if any changes are detected.
- BulletProoF erases the timing data from the BRAM once the key is generated, and destroys the key once the second-stage boot image is decrypted. The key is also destroyed if the key integrity check fails.
5. Additional BulletProoF Countermeasures
The primary threat to BulletProoF is key theft. This section discusses two important attack scenarios, as well as countermeasures designed to deal with them.
5.1. Internal Configuration Access Port Data Spoofing Countermeasure
The first important attack scenario is shown by the red dotted lines in Figure 3. The top left dotted line labeled “Attack scenario” represents an adversarial modification, which is designed to re-route the origin of the configuration data from the ICAP to I/O pins. With this change, the adversary can stream in the expected configuration data, and then freely modify any portion of the BulletProoF configuration. The simplest change one can make is to add a key leakage channel, as shown by the red dotted line along the bottom of the figure.
The countermeasure to this attack is to ensure that the adversary is not able to make changes to the paths between the ICAP and the SHA-3, without changing the timing data and decryption key. A block diagram of the BulletProoF architecture that addresses this threat is shown in Figure 4. In particular, timing data is collected by timing the paths identified as “A” and “B”. For “A”, the two-vector sequence (challenge) V1–V2 is derived directly from the ICAP data. In other words, the launch of transitions along the “A” paths is accomplished within the ICAP interface itself. Signal transitions emerging on the ICAP output register propagate through the SHA-3 combinational logic to the time-to-digital converter (TDC) shown on the right (discussed below). The timing operation is carried out by de-asserting hash_mode, and then launching V2 by asserting ICAP control signals using the ICAP input register (not shown). The path selected by the 200-to-1 MUX is timed by the TDC. This operation is repeated to enable all of the 72 individual paths along the “A” route to be timed. Note that the ICAP output register is only 32 bits, which is fanned out to 72 bits, as required by the keccak-f[200] version of SHA-3 [12].

Figure 4.
Implementation details of the internal configuration access port (ICAP) and SHA-3 interface, with annotations showing paths that are timed (“A” and “B”) and hash mode (“C”).
The timing operation involving the “chained” sequence of hashes’ time paths along the routes is labeled “B” in Figure 4. The current state of the hash is maintained in kstate when hash_mode is deasserted, by virtue of disabling updates to the flip-flops (FFs), using the en input. Vector V1 of the two-vector sequence is all 0s, and the launch of V2 is accomplished by deasserting LaunchMUXCtrl.
The hash mode of operation, labeled “C” in Figure 4, is enabled by asserting hash_mode. Configuration data is hashed into the current state by asserting load_msg on the first cycle of the SHA-3 hash operation. LaunchMUXCtrl remains de-asserted in hash mode.
5.2. Clock Manipulation Countermeasure
The adversary may attempt to stop BulletProoF, either during key generation or after the key is generated; reprogram portions of the PL; or create a leakage channel that provides direct access to the key. The clock source and other inputs to the Xilinx digital clock manager (DCM), including the fine phase-shift functions used by HELP to time paths, therefore represent an additional vulnerability [13].
A countermeasure that addresses clock manipulation attacks is to use a ring oscillator (RO) to generate the clock and a time-to-digital-converter (TDC), as an alternative path timing method that replaces the Xilinx DCM. The RO and TDC are implemented in the programmable logic, and therefore the configuration information associated with them is also processed and validated by the hash-based self-authentication mechanism described earlier.
As discussed previously, HELP measures path delays in the combinational logic of the SHA-3 hardware instance. The left side of the block-level diagram in Figure 5 shows an instance of SHA-3 configured with components that were described in the previous section (Figure 4). The right side shows an embedded time-to-digital converter (TDC) engine, with components labeled “Test Paths”, “Carry Chain”, and “Major Phase Shift”, which are used to obtain high-resolution measurements of the SHA-3 path delays.
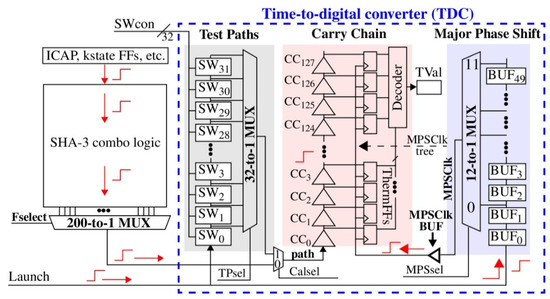
Figure 5.
Functional unit and time-to-digital converter (TDC) engine architecture.
The white- and orange-colored routes and elements in the Xilinx “implementation view” diagram of Figure 6 highlight carry-chain (CARRY4) components within the FPGA that are leveraged within the TDC. A CARRY4 element is a sequence of four high-speed hardwired buffers, with outputs connected to a set of four FFs, labeled “ThermFFs” in Figure 5 and Figure 6. The carry-chain component in Figure 5 is implemented by connecting a sequence of 32 CARRY4 primitives in a series, with individual elements labeled as CC0 to CC127 in Figure 5. Therefore, the carry-chain component implements a delay chain with 128 stages. The path to be timed (labeled “path” in Figure 5 and Figure 6) drives the bottom-most CC0 element of the carry chain. Transitions on this path propagate upwards at high speed along the chain, where each carry-chain element adds approximately 15 ps of buffer delay. As the signal propagates, the D inputs of the ThermFFs change from 0 to 1, one by one, over the length of the chain. The ThermFFs are configured as positive-edge-triggered FFs, and therefore, they sample the D input when their Clk input is 0. The Clk input to the ThermFFs is driven by a special major phase shift Clk (MPSClk) that is described further below.

Figure 6.
Xilinx slice with a CARRY4 primitive.
The delay of a path through the SHA-3 combinational logic block is measured as follows. First, the MPSClk signal at the beginning of the path delay test is set to 0, in order to make the ThermFFs sensitive to the delay chain buffer values. The path to be timed is selected using Fselect, and is forced to 0 under the first vector (V1) of the two-vector sequence. Therefore, the path signal and the delay chain buffers are initialized to 0, as illustrated on the left side of the timing diagram in Figure 7. The launch event is initiated by applying V2 to the inputs of SHA-3, while simultaneously asserting the Launch signal, which creates rising transitions that propagate, as shown by the red arrows on the left side of Figure 5. The Launch signal propagates into the MPS BUFx delay chain, shown on the right side of Figure 5, simultaneous with the path signal’s propagation through SHA-3 and the carry chain. The Launch signal eventually emerges from the major phase shift unit on the right, as MPSClk (to minimize Clk skew, the MPSClk signal drives a Xilinx BUFG primitive and a corresponding clock tree on the FPGA.). When MPSClk goes high, the ThermFFs store a snapshot of the current state of the carry chain buffer values. Assuming this event occurs, as the rising transition on path is still propagating along the carry chain, the lower set of ThermFFs will store 1s while the upper set store 0s (see timing diagram in Figure 7 for an illustration). The sequence of 1s followed by 0s is referred to as a thermometer code, or TC. The decoder component in Figure 5 counts the number of 0s in the 128 ThermFFs, and stores this count in the TVal (timing value) register. The TVal is added to an MPSOffset (discussed below) to produce a PUF Number (PN), which is stored in BRAM for use in the key generation process.

Figure 7.
Timing diagram for the timing engine.
5.2.1. Underflow and Overflow
The differences in the relative delays of the path and MPSClk signals may cause an underflow or overflow error condition, which is signified when the TVal is either 0 or 128. Although the carry chain can be extended in length as a means of avoiding these error conditions, it is not practical to do so. This is because of a very short propagation delay associated with each carry-chain element (approximately 15 ps), as well as the wide range of delays that need to be measured through the SHA-3 combinational logic (approximately 10 ns), which would require the carry chain to be more than 650 elements in length.
In modern FPGAs, a carry chain of 128 elements is trivially mapped into a small region of the programmable logic. The shorter length also minimizes adverse effects created by across-chip process variations, localized temperature variations, and power supply noise. However, the shorter chain does not accommodate the wide range of delays that need to be measured, and instances of underflow and overflow become common events.
The major phase shift (MPS) component is included as a means of dealing with underflow and overflow conditions. Its primary function is to extend the range of the paths that can be timed. With 128 carry-chain elements, the range of path delays that can be measured is approximatelly 128 × 15 ps, which is less than 2 ns. The control inputs to the MPS, labeled “MPSsel” in Figure 5, allow the phase of MPSClk to be adjusted in order to accommodate the 10 ns range associated with the SHA-3 path delays. However, a calibration process needs to be carried out at start-up, to allow continuity to be maintained across the range of delays that will be measured.
5.2.2. Calibration
The MPS component and calibration are designed to expand the measurement range of the TDC, while minimizing inaccuracies introduced as the configuration of the MPS is tuned to accommodate the length of the path being timed. From Figure 5, the MPSClk drives the ThermFF Clk inputs, and therefore controls how long the ThermFFs continue to sample the CCx elements. The 12-to-1 MUX associated with the MPS can be controlled using the MPSsel signals, to delay the Clk with respect to the path signal. The MPS MUX connects to the BUFx chain at 12 different tap points, with 0 selecting the tap point closest to the origin of the BUF path along the bottom, and 11 selecting the longest path through the BUFx chain. The delay associated with MPSsel when set to 0 is designed to be less than the delay of the shortest path through the SHA-3 combinational logic.
An underflow condition occurs when the path transition arrives at the input of the carry chain (at CC0), after the MPSClk is asserted on the ThermFFs. The MPS controller configures the MPSsel to 0 initially, and increments this control signal until underflow no longer occurs. This requires the path to be retested at most 12 times, once of each MPSsel setting. Note that paths timed when MPSsel > 0 require an additional delay along the MPS BUFx chain, called an MPSOffset, to be added to the TVal. Calibration is a process that determines the MPSOffset values associated with each MPSsel > 0.
The goal of calibration is to measure the delay through the MPS BUFx chain between each of the tap points associated with the 12-to-1 MUX. In order to accomplish this, during calibration, the role of the path and MPSClk signals are reversed. In other words, the path signal is now the ‘control’ signal and the MPSClk signal is timed. The delay of the path signal needs to be controlled in a systematic fashion to create the data required to compute an accurate set of MPSOffset values associated with each MPSsel setting.
The calibration process utilizes the Test Path component from Figure 5, to allow systematic control over the path delays. During calibration, the Calsel is set to 1, which redirects the input of the carry chain from SHA-3 to the Test Path output. The TPsel control signals of the Test Path component allow paths of incrementally longer lengths to be selected during calibration, from 1 LUT to 32 LUTs. Although paths within the SHA-3 combo logic unit can be used for this purpose, the Test Path component allows a higher degree of control over the length of the path. The components labeled SW0 through SW31 refer to a “switch”, which is implemented as two parallel 2-to-1 MUXs (similar to the arbiter PUF, but with no constraints with regard to matching delays along the two paths [14]). The rising transition entering the chain of switches at the bottom is fanned out, and propagates along two paths. Each SW can be configured with a SWcon signal to either route, the two paths straight through both MUXs (SWcon = 0), or the paths can be swapped (SWcon = 1). The configurability of the Test Path component provides a larger variety of path lengths that the calibration can use, which improves the accuracy of the computed MPSOffsets.
The tap points in the MPS component are selected such that any path within the Test Path component can be timed without underflow or overflow by at least two consecutive MPSsel control settings. If this condition is met, then calibration can be performed by selecting successively longer paths in the Test Path component and timing each of them under two (or more) MPSsel settings. By holding the selected test path constant and varying the MPSsel setting, the computed TVals represent the delay along the BUFx chain within the MPS between two consecutive tap points.
Table 1 shows a subset of the results of applying calibration to a Xilinx Zynq 7020 FPGA. The left-most column identifies the MPSsel setting (labeled MPS). The rows labeled with a number in the MPS column give the TVals obtained for each of the test paths (TP) 0-31 under a set of SWcon configurations from 0–7. The SWcon configurations are randomly selected 32-bit values that control the state of Test Path switches from Figure 5. In our experiments, we carried out calibration with eight different SWcon vectors, as a means of obtaining sufficient data to compute the set of seven MPSOffsets accurately.

Table 1.
Calibration data from Chip C1.
TVals of 0 and 128 indicate underflow and overflow, respectively. The rows labeled “Diffs” are differences computed using the pair of TVals shown directly above the Diffs values in each column. Note that if either TVal of a pair is 0 or 128, the difference is not computed, and is signified using “NA” in the table. Only the data and differences for MPS 0 and 1 (rows 3–5) and MPS 1 and 2 (rows 6–8) are shown from the larger set generated by the calibration. As an example, the TVals in rows 3 and 4 of column 2 are 91 and 17, respectively, which represents the shortest test path 0 delay under MPSsel settings 0 and 1, respectively. Row 5 gives the difference as 74. The Diffs in a given row are expected to be same because the same two MPSsel values are used. Variations in the Diffs occur because of measurement noise and within-die variations along the carry chain, but are generally very small, e.g., 2 or smaller, as shown by the data in the table.
The “Ave.” column on the right gives the average values of the Diffs across each row, using data collected from eight SWcon configurations. The “MPSOffset” column on the far right is simply computed as a running sum of the “Ave.” column values from top to bottom. Once calibration data was available and the MPSOffset values computed, delays of paths within the SHA-3 were measured by setting MPSsel to 0, and then carrying out a timing test. If the TVal was 128 (all 0s in the carry chain) then the MPSClk arrived at the ThermFFs before the transition on the functional unit path arrived at the carry chain input. In this case, the MPSsel value was incremented, and the test was repeated until the TVal was non-zero. The MPSOffset associated with the first test of a path that produced a valid TVal was added to the TVal, to produce the final PN value (see Figure 7).
6. Statistical Analysis
The HELP PUF within BulletProoF must be able to regenerate the decryption key without bit-flip errors and without any type of interaction with a server. We propose a bit-flip error avoidance scheme in [15] that creates three copies of the key, and uses majority voting to eliminate inconsistencies that occur in one of the copies at each bit position. The scheme is identical to traditional triple-modular-redundancy (TMR) methods used in fault tolerance designs. We extend this technique here to allow additional copies, e.g., 5 MR, 7 MR, 9 MR, etc., and combine it with a second reliability-enhancing method, called margining [9,11]. We call the combined method secure-key-encoding (SKE), because the helper data does not leak any information about the secret key. The helper data generated during enrollment is stored in an NVM, and is read during the key regeneration process as discussed earlier, in reference to Figure 3.
The margining method creates weak bit regions to identify PUF Numbers (PN, from Figure 7) that have a high probability of generating bit-flip errors. We refer to these PN as unstable, and their corresponding bits as weak. A helper data bitstring is generated during enrollment, which records the positions of the unstable PN in the sequence that is processed. Helper data bits that are 0 inform the enrollment and regeneration key generation process to skip over these PN. On the other hand, the PN classified as stable are processed into key bits, called strong bits. The SKE enrollment process constructs an odd number of strong bit sequences, where each sequence is generated from independent PN but are otherwise identical (redundant) copies of each other. During regeneration, the same sequences are again constructed possibly with bit-flip errors. Majority voting is used to avoid bit-flip errors in the final decryption key, by ignoring errors in 1 of the 3 copies (or 2 of the 5 copies, etc.) that are inconsistent with the bit value associated with the majority. The number of copies is referred to as the redundancy setting, and is given as 3, 5, 7, etc.
Reference [11] describes several other features of the HELP algorithm. For example, HELP processes sets of 4096 PN into a multi-bit key, in contrast to other PUFs, which generate key bits one at a time. HELP also includes several other parameters beyond the margin, and the number of redundant copies used in the majority voting scheme just discussed. For example, HELP allows the user to specify a pair of linear feedback shift registers (LFSR) seeds that are then used to pseudo-randomly pair the 4096 PN to create 2048 PN differences. HELP also defines a third reliability-enhancing technique that is based on applying linear transformations to the 2048 PN differences, and includes a modulus operation designed to remove path-length bias effects. The decryption key produced by HELP is dependent on the values assigned to these parameters. It follows, then, that a comprehensive evaluation of bitstring statistical quality requires the analysis to be performed under different parameter combinations.
The statistical results reported here investigate one set of challenges, two margins of 3 and 4, and nine moduli between 14 and 30. The statistics are averaged across 400 groups of 2048 PN differences, created using different LFSR seed pairs. Although this represents only a small portion of the total challenge–response space of HELP, it is sufficiently diverse to provide a good model of the expected behavior under different challenge sets and parameter combinations.
Unlike previously reported statistics on the HELP PUF, the results shown here were generated using the TDC described in Section 5.2. The three standard statistical quality metrics evaluated included uniqueness (using the inter-chip hamming distance), reliability (using the intra-chip hamming distance), and randomness (using the National Institute of Standards and Technology (NIST) statistical test suite). The analysis was carried out using data collected from a set of 30 Xilinx Zynq 7020 chips (on Zedboards [16]). The data was collected under enrollment conditions at 25 °C and 1.00 V, and over a set of 15 temperature-voltage (TV) corners represented by all combinations of temperatures (−40 °C, 0 °C, 25 °C, 85 °C, and 100 °C) and voltages (0.95 V, 1.00 V, and 1.05 V).
The bar graphs shown in Figure 8 present the statistical results for the inter-chip hamming distance (HD), in (a) and (b); the probability of failure, in (c) and (d); and the smallest bitstring size in (e) and (f) for SKE, using redundancy settings of 5 (top row) and 7 (bottom row). Here, the final bitstring was constructed by using majority voting across 5 and 7 copies of strong bit sequences, respectively. The results for the nine Moduli and two Margins are shown along the x- and y-axes, respectively. As indicated earlier, HELP processes 2048 PN differences at a time, which produces a bitstring of length 2048 bits.

Figure 8.
Inter-chip Hamming Distance (left), probability of failure (middle), and smallest bitstring size (right) statistics obtained from physical unclonable function numbers (PN) generated from a set of 30 Xilinx Zynq 7020 chips across extended industrial temperature–voltage specifications (−40 °C to 100 °C, +/−5% supply voltage). Statistical results are reported for multiple values of the HELP algorithm parameter margins and moduli, averaged across 400 LFSR seed-pairing combinations (mean values are used the reference mean and range parameters, see [11] for details).
The inter-chip hamming distance (HD) was computed by pairing enrollment bitstrings (of length 2048 bits) under all combinations, and is given by Equation (1). The symbol NC indicates the number of chips, which is 30 in our experiments, and NCC indicates the number of chip combinations, which is 30 × 29/2 = 435. The symbol NBa is the number of bits classified as strong in both bitstrings of the (i, j) pair. The subscript (i, 1, k) is interpreted as chip i, TV corner 1 (enrollment), and bit k. The hamming distance is computed by summing the XOR of the individual bits from the bitstring pair, under the condition that both bits are strong (bit positions that have a weak bit in either bitstring of the pair are skipped). The HDinter values are computed individually using 400 different LFSR seed pairs, which are averaged and reported in Figure 8a,b. The bar graph shows near-ideal results with inter-chip HDs between 48% and 51% (ideal is 50%).
The probability of failure results shown in Figure 8c,d are computed using the HDintra expression given by Equation (2). Here, bitstrings from the same chip under enrollment conditions are paired with the bitstrings generated under the remaining 15 TV corners. The symbol NC is the number of chips (30), NT is the number of TV corners (16), and NBe is the number of bits classified as strong during enrollment. Note that margining creates a helper data bitstring only during enrollment, which is used to select bits in the enrollment and regeneration bitstrings for the XOR operation. An average HDintra is computed using the values computed for each of the 400 LFSR seeds. The bar graphs plot the average HDintra as an exponent to 10x, where 10−6 indicates 1 bit-flip error in 1 million bits inspected. The best results are obtained from SKE 7, with a margin of 4 (Figure 8d), where the probability of failure is <10−6 for moduli ≥22.
The smallest bitstring size results are plotted in Figure 8e,f. These results portray the worst-case NBe values, which is associated with one of the chips from the HDintra analysis carried out using Equation (2). The smallest bitstring sizes (and the average bitstring sizes, which are not shown) remain relatively constant across moduli, and are in the range of 7–12 bits per set of 2048 PN differences for margin 4, and 20–25 bits for margin 3. Therefore, to generate a 128-bit decryption key, approximately 20 LFSR seed pairs need to be processed, in the worst case.
The NIST statistical test results are not shown in a graph, but are summarized as follows. Unlike the previous analyses, the bitstrings used as input to the NIST software tools are the concatenated bitstrings produced across all 400 seeds for each chip. With 30 chips, NIST requires that at least 28 chips pass the test, for the test to be considered passed overall. The following NIST tests are applicable given the limited size of the bitstrings: Frequency, BlockFrequency, two CumulativeSums tests, Runs, LongestRun, FFT, ApproximateEntropy, and two Serial tests. Most of ApproximateEntropy tests failed by up to 7 chips for SKE 5, margin 3 (all of the remaining tests are passed). For SKE 5, margin 4, all but four of the tests passed, and the fails were only by one chip, i.e., 27 chips passed instead of 28 chips. For SKE 7, all but one test was passed for margins 3 and 4, and the test that failed (LongestRun) failed by one chip.
In summary, assuming that the reliability requirements for BulletProoF are 10−6, the HELP PUF parameters need to be set to SKE 7 and margin 4, and the modulus should be set to be >20. When these constraints are honored, the inter-chip HD is >48%, and nearly all NIST tests are passed. Decryption key sizes of 128 or larger can be obtained by running the HELP algorithm with 20 or more LFSR seed pairs, or by generating additional sets of 4096 PNs as configuration data is read and processed, as described in Section 4.
7. Conclusions
A PUF-based secure boot technique called BulletProoF is proposed that is designed to self-authenticate, as a mechanism to detect tampering. An unencrypted version of BulletProoF, which is stored in an external NVM, is loaded by the first-stage boot loader. The PUF within BulletProoF regenerates a decryption key, using bitstream configuration information as challenges, and this key is used to decrypt the second-stage boot images and to boot the system. The configuration information is read using the ICAP interface, and represents the FPGA implementation of BulletProoF itself. This self-authenticating process detects tampering attacks that modify the LUTs, or routing within BulletProoF done in an attempt to create a leakage channel for the key. The conceptual design of BulletProoF is described, and experimental results are presented that demonstrate a novel embedded time-to-digital-converter, which is used by the HELP PUF to measure path delays and generate the encryption/decryption key.
Author Contributions
Conceptualization and methodology were completed by J.P.; Critical reviews and security analysis were completed by D.O.J., M.A., D.H., C.C., W.C., and F.S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Trimberger, S.M.; Moore, J.J. FPGA Security: Motivations, Features, and Applications. Proc. IEEE 2014, 102, 1248–1265. [Google Scholar] [CrossRef]
- Skorobogatov, S. Flash Memory ‘Bumping’ Attacks. In Cryptographic Hardware and Embedded Systems, CHES 2010: Proceedings of the 12th International Workshop, Santa Barbara, CA, USA, 17–20 August 2010; Springer: Cham, Switzerland, 2010. [Google Scholar]
- 7 Series FPGAs Configuration; User Guide. Available online: https://www.xilinx.com/support/documentation/user_guides/ug470_7Series_Config.pdf (accessed on 15 June 2018).
- Swierczynski, P.; Fyrbiak, M.; Koppe, P.; Paar, C. FPGA Trojans through Detecting and Weakening of Cryptographic Primitives. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1236–1249. [Google Scholar] [CrossRef]
- Swierczynski, P.; Becker, G.T.; Moradia, A.; Paar, C. Bitstream Fault Injections (BiFI)—Automated Fault Attacks against SRAM-based FPGAs. IEEE Trans. Comput. 2018, 67, 348–360. [Google Scholar] [CrossRef]
- Swierczynski, P.; Fyrbiak, M.; Koppe, P.; Moradi, A.; Paar, C. Interdiction in practice—Hardware Trojan against a high-security USB flash drive. J. Cryptogr. Eng. 2017, 7, 199. [Google Scholar] [CrossRef]
- Konopinski, D.; Kenyon, A. Data recovery from damaged electronic memory devices. In Proceedings of the London Communications Symposium 2009, University College London, London, UK, 3–4 September 2009. [Google Scholar]
- Why Anti-Fuse is the Only Secure Choice for Encryption Key Storage. Available online: http://chipdesignmag.com/display.php?articleId=5045 (accessed on 15 June 2018).
- Aarestad, J.; Ortiz, P.; Acharyya, D.; Plusquellic, J. HELP: A Hardware-Embedded Delay-Based PUF. IEEE Des. Test 2013, 30, 17–25. [Google Scholar] [CrossRef]
- Tiri, K.; Verbauwhede, I. Charge Recycling Sense Amplifier Based Logic: Securing Low Power Security ICs Against DPA. In Proceedings of the 30th European Conference on Solid-State Circuits 2004, Leuven, Belgium, 23 September 2004. [Google Scholar] [CrossRef]
- Che, W.; Martin, M.; Pocklassery, G.; Kajuluri, V.K.; Saqib, F.; Plusquellic, J. A Privacy-Preserving, Mutual PUF-Based Authentication Protocol. Cryptography 2017, 1, 13. [Google Scholar] [CrossRef]
- Keccak. Available online: https://keccak.team/keccak.html (accessed on 15 June 2018).
- 7 Series FPGAs Clocking Resources; User Guide. Available online: https://www.xilinx.com/support/documentation/user_guides/ug472_7Series_Clocking.pdf (accessed on 15 June 2018).
- Gassend, B.; Clarke, D.; van Dijk, M.; Devadas, S. Silicon Physical Random Functions. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, 18–22 November 2002; pp. 148–160. [Google Scholar]
- Chakraborty, R.; Lamech, C.; Acharyya, D.; Plusquellic, J. A transmission gate physical unclonable function and on-chip voltage-to-digital conversion technique. In Proceedings of the 50th Annual Design Automation Conference, Austin, TX, USA, 7 June 2013; pp. 1–10. [Google Scholar]
- Which Zynq SOM is Right for You? Available online: http://zedboard.org/ (accessed on 15 June 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).