An Efficient Tate Pairing Algorithm for a Decentralized Key-Policy Attribute Based Encryption Scheme in Cloud Environments

Abstract

Attribute-based encryption (ABE) is used for achieving data confidentiality and access control in cloud environments. Most often ABE schemes are constructed using bilinear pairing which has a higher computational complexity, making algorithms inefficient to some extent. The motivation of this paper is on achieving user privacy during the interaction with attribute authorities by improving the efficiency of ABE schemes in terms of computational complexity. As a result the aim of this paper is two-fold; firstly, to propose an efficient Tate pairing algorithm based on multi-base number representation system using point halving (TP-MBNR-PH) with bases 1/2, 3, and 5 to reduce the cost of bilinear pairing operations and, secondly, the TP-MBNR-PH algorithm is applied in decentralized KP-ABE to compare its computational costs for encryption and decryption with existing schemes.

1. Introduction

Cloud computing, as an emerging computing paradigm, empowers client to remotely store information on a cloud in order to access services on request. Over the past few years, it has been observed that cloud computing has become a full-fledged promising business idea for the IT sector. As data related to people and organizations resides in the cloud, to a large extent, a concern for security is addressed. This issue reduces the potentiality of cloud computing technologies in terms of giving protection and assurance to the end user information and, at the same time, it plaguies the market. In order to secure information from being disclosed, clients need to encipher their information before it is shared. Access control is elementary, as it is the primary line of defense that avoids unauthorized access to the shared information. In considering the above facts, attribute-based encryption (ABE) is given much more attention in providing information security and in comprehending fine-grained, one-to-numerous, and non-interactive access control. Thus it is evident that ABE supports both confidentiality and access control with a single encryption for data sharing in a cloud environment.

In 2005, Sahai and Waters [1] proposed another sort of IBE scheme called fuzzy IBE (FIBE) which compliments identities as a collection of descriptive attributes. FIBE is viewed as the primary idea of ABE in which the information owner encrypts a message to all users having a specific collection of attributes. In the same period, Nali et al. [2] also proposed a threshold-based ABE technique to convey the fact that this technique forestalls the collusion attacks and opens a new weakness in which threshold semantics are restricted in planning broader frameworks that require expressive access control. Data user, data owner, attribute authority (AA), and cloud storage server are the four kinds of parties involved in ABE. In the ABE scheme, attributes are assumed to be the critical part. Attributes use public keys for encrypting data and are also utilized as an access policy for controlling users’ access. It is realized in healthcare and smart grid applications that ABE provides fine-grained access control and broadcasting of a single encrypted message to a specific group of users, respectively. In view of the access policy, ensuing studies are generally ordered [3] either as a key-policy ABE (KP-ABE) or cipher text-policy ABE (CP-ABE).

In 2006, Goyal et al. [3] introduced the concept of KP-ABE in which each secret key is associated with an access structure that specifies the type of cipher text which can be decrypted by this secret key. The cipher texts are labelled with a collection of descriptive attributes. In case the attribute set fulfils the access structure indicated in the secret key, the user can decrypt the cipher text. It is one of the prominent encryption techniques with fine-grained access control for applications, say, sharing audit log information. The major drawback in this technique is that no sooner is the access policy built into the secret key, the data owner in this scheme cannot choose the person who is decrypting the cipher text, but can only decide a collection of attributes controlling the access of cipher texts. Later, Ostrovsky et al. [4] proposed a scheme with a non-monotonic access structure where the secret keys are stamped with a collection of attributes comprising positive and negative attributes. Analogously, the ABE scheme with a non-monotonic access structure elicits a more convoluted access policy. Unfortunately, the main flaw in this mechanism is that it doubles the size of the cipher text, and secret key and adds encryption/decryption overheads at the same time. Attrapadung et al. [5] suggested the first KP-ABE scheme with non-monotonic access structures and constant cipher text size. The drawback is that the secret key has a quadratic size in the number of attributes.

Goyal et al. [3] proposed the feasibility of a CP-ABE scheme, but not yet endeavored any constructions. In a CP-ABE scheme, a user’s secret key is associated with a subjective number of attributes representing strings, and cipher text with an access structure. A user may have the capacity to decrypt a cipher text if user’s attributes fulfil the access structure of the cipher text. In 2007, utilizing a monotonic access structure, Bethencourt et al. [6] proposed the main CP-ABE development. This technique sustains adaptable access control strategies like the KP-ABE [3] technique.

Considering the security aspects under the standard model, Cheung and Newport [7] contributed a provably secure CPABE scheme which, in turn, boosted the security proof in Bethencourt et al. [6]. This scheme supported AND gate on positive and negative attributes as its access policy and is proved to be the chosen plain text attack (CPA), secure under the decisional bilinear Diffie-Hellman (DBDH) assumption. Even though it has some advantages, there are some disadvantages, too. Mostly, this scheme is not adequately expressive because it supports only policies with logical conjunction. The next one is that the size of the cipher text and the secret key increments in a linear fashion with the aggregate number of attributes in this scheme. These two weaknesses made this scheme less proficient than Bethencourt et al.’s [6].

In view of Cheung and Newport’s scheme [7], Nishide et al. [8] enhanced the effectiveness and accomplished hidden policies by proposing a scheme with multi-value attributes as its access policy. Emura et al. [9] utilized a similar access policy and proposed an enhanced scheme accomplishing a steady length of cipher text and a consistent number of bilinear pairing operations. Liang et al. [10] enhanced the bounded CP-ABE (BCP-ABE) by improving the proficiency of the encryption/decryption algorithm and reducing the length of the public key, secret key, and cipher text.

The initial ABE scheme was created utilizing single AA [1]. Later multiple-authority-based ABE (MA-ABE) was proposed in [11], since the single-authority ABE technique permitted a large volume of data at a single entity. In the MA-ABE technique, there are numerous AAs in charge of disjoint collections of attributes. In the customary MA-ABE technique, users co-operate with various AAs to obtain decryption credentials for their attributes. On the other hand, there is no security assurance for users; instead all AAs can share (collude) the specific user’s data (attributes) to uncover the user’s identity. Hence, the motivation of this paper is on achieving user privacy during the interaction with AAs by improving the efficiency of ABE schemes in terms of computational complexity. To the best of our knowledge, almost all the ABE schemes available are constructed from bilinear pairings. However, bilinear pairing has a higher computational complexity, which makes algorithms inefficient to some extent. Therefore, the main focus of this paper is in reducing the cost of bilinear pairing operations to improve the efficiency of the ABE scheme.

1.1. Our Contributions

The main contributions of this paper are highlighted as follows:

• An efficient Tate pairing algorithm based on multi-base number representation system using point halving (TP-MBNR-PH) with bases 1/2, 3, and 5 has been proposed. This scheme mitigates the cost of bilinear pairing when compared to existing Tate pairing schemes. The efficiency is calculated using the computational costs and pre-computed costs of addition, subtraction, halving, tripling, and quintupling operations.
• The TP-MBNR-PH algorithm is applied in decentralized KP-ABE to show the reduction in computational costs for encryption and decryption when compared with existing schemes [12,13].

1.2. Paper Organization

The rest of this paper is organized as follows: Section 2 covers the related work. Section 3 deals with the proposed work of this paper. It consists of two subsections: firstly, Section 3.1 describes the proposed work of an efficient Tate pairing algorithm based on a multi-base number representation system using point halving (TP-MBNR-PH) with bases 1/2, 3, and 5; secondly, Section 3.2 describes the applicability of the TP-MBNR-PH algorithm in decentralized KP-ABE. Section 4 concludes the paper.

2. Related Work

There are two fundamental sorts of ABE, particularly cipher text-policy ABE (CP-ABE) and key-policy ABE (KP-ABE). The ABE scheme is categorized into two: single-authority ABE (SA-ABE) and multi-authority ABE (MA-ABE). In the MA-ABE scheme, there are two sub-categories; with a central authority (CA) and without a central authority. Chase introduced an MA-ABE scheme [14] utilizing a trusted CA for disbursing all the keys. The main drawback of utilizing a CA is that it increases the computation and communication cost. Lin et al. [15] resolved the secure threshold multi-authority fuzzy identity based encryption (threshold MA-FIBE) scheme in the absence of a central authority.

In the same lines, Chase and Chow in [11] introduced an MA-ABE scheme removing the CA using distributed pseudorandom functions. In this scheme, every pair of AAs firmly exchange a shared secret among them in the setup process. Users must submit their global identities (GIDs) to every AA to get the decryption credentials in [14]. This cleaves the user protection since a collection of perverted AAs can pool together each of the attributes that belong to the specific GID.

In [11], Chase and Chow introduced an anonymous key-issuing protocol to mitigate the privacy vulnerability in which a user can acquire the decryption keys from AAs without exposing his/her GID. Despite the fact that the scheme introduced by Chase and Chow avoids the central AA, all the AAs must be online and collude with each other to set up the ABE system. Thus, it is not fully decentralized. Furthermore, different protocols are proposed to decentralize the ABE scheme [11,14,16,17]; nonetheless, each scheme has its own benefits and bad marks.

The first known completely decentralized MA-ABE scheme is suggested in [16] where any party can turn into an AA and there is no prerequisite for any global co-ordination other than the production of a pioneer collection of common reference parameters. This overcomes the collusion vulnerability without providing co-ordination between AAs with novel strategies to tie key parts together and anticipate collusion attacks between users with various global identifiers. This scheme does not protect the user privacy as attributes of users are gathered by AAs following users’ GIDs. The scheme in [11] considers privacy, however, it is not completely decentralized. Han et al. suggested a PP decentralized scheme for KP-ABE in [18] for preserving the user privacy based on the decisional bilinear Diffie-Hellman (DBDH) standard complexity assumption.

In [18], the GID of the user is utilized to tie all the decryption keys together, where blind key generation protocol has been used to issue the decryption keys. Subsequently, perverted AAs cannot pool the users’ attributes by following the GIDs’ of the users from the decryption keys. Unluckily, the scheme cannot counteract user collusion, thus, two users can pool their decryption keys to produce decryption keys for an unauthorized user [19]. This is because of weak binding between users’ GID and the decryption keys.

Rahulamathavan et al. [12] constructed the privacy-preserving decentralized KP-ABE scheme in a cloud environment. It protects the users’ privacy when they communicate with multiple authorities to obtain decryption credentials. It reduces the user collusion vulnerability found in [19] and used an anonymous key-issuing protocol based on anonymous credentials. Thus, it cannot generate decryption credentials for malicious users even if two or more users collude their keys. It is both leak-free and selective-failure blind. This scheme is verified using decisional bilinear Diffie-Hellman standard complexity assumption. Yang et al. [13] proposed a scheme to improve privacy and security in decentralizing multi-authority attribute-based encryption in cloud computing. Most often existing ABE schemes are constructed from bilinear pairings. This makes an algorithm inefficient due to its high computational complexity of bilinear pairing. In this paper, first, an efficient Tate pairing based on multi-base number representation system using point halving (TP-MBNR-PH) with point halving, tripling, and quintupling is proposed and then applied in decentralized KP-ABE [12] to determine its computational costs of encryption and decryption.

3. Proposed Work

The proposed work consists of two parts. Firstly, we propose an efficient Tate pairing algorithm based on multi-base number representation system using point halving (TP-MBNR-PH) with bases 1/2, 3, and 5 with the aim to reduce the cost of bilinear pairing operations. Secondly, the TP-MBNR-PH algorithm is applied in decentralized KP-ABE to determine its computational costs for encryption and decryption.

3.1. Proposed Tate Pairing Algorithm Construction

3.1.1. Bilinear Maps

Let $G_1$, $G_2$, and $G_T$ be three cyclic groups of prime order q. $G_1$ and $G_2$ are a source group and $G_T$ is a target group. Let $g_1$ and $g_2$ be generators of $G_1$ and $G_2$, respectively. A bilinear map $e$ is defined as $e: G_1\times G_2\to G_T$ which has the following properties:

• Bilinearity: $e\left(g_1^a,g_2^b\right)$ = $e{\left(g_1,g_2\right)}^{ab}$, where $a, b \in Z$.
• Computability: The bilinear map e is efficiently computable by $G_1\times G_2$ for any pairs.
• Non-degeneracy: $e\left(g_1,g_2\right)\ne 1$. This means all pairs of the source group do not map to the identity of the target group.

Note: If $G_1=G_2$, then it is a symmetric map, otherwise it is an asymmetric map.

3.1.2. Point Halving (PH)

Fundamentally all the scalar multiplication is ascertained by utilizing the double and add method. However, Knuden (1999) and Schroeppel (2000), in parallel, proposed a strategy to speed up scalar multiplication on elliptic curves characterized over binary augmentation fields. Their technique depends on a novel elliptic curve primitive called point halving, which can be characterized as follows: Given a point Q of odd order, compute P such that $Q=2P$. The point $P$ is denoted as $1/2 Q$. That means, in this technique the previous double and add method is replaced by the half and add method, which is the exact inverse operation of point doubling. The strategies replaced all point doublings in the double-and-add algorithm with another operation called point halving. This technique is executed for conducting scalar multiplication on non-super singular elliptic curves in characteristic 2. Point halving is applied to the curves with minimal two-torsion. Since, hypothetically, point halving is up toward three times as quick as point doubling, it is conceivable to enhance the execution of scalar multiplication calculation $Q=nP$ by supplanting the double-and-add algorithm.

Let $P=\left(x,y\right)$ be a point on the elliptic curve defined over binary field using affine coordinates. A point doubling requires calculating the coordinates of the point $Q=2P=\left(u,v\right)$ using the following equations:

$$\lambda =x+\frac{y}{x}$$

(1)

$$u={\lambda }^2+\lambda +a$$

(2)

$$v=x^2+u \left(\lambda +1\right)$$

(3)

Point halving is just the opposite, i.e., given $Q=\left(u,v\right),$ find $P=\left(x,y\right)$ such that $Q=2P$. This is computed by solving Equation (2) for $\lambda$, Equation (3) for $x$, and finally, Equation (1) for $y$. This means that we have to solve ${\lambda }^2+ \lambda = u + a$, for $\lambda$, $v=x^2 + u \left(\lambda +1\right)$ for $x$, and finally obtain $y=\lambda x + x^2$. A detailed analysis of the computational complexity of point halving was made in [20]. It was reported that the point halving method is 15% to 24% faster than point doubling.

3.1.3. The Double-Base Number System (DBNS)

In [21], a ternary/binary methodology was proposed for fast Elliptic Curve Cryptography. An equivalent tactic was suggested in [22] where an integer k is represented in the double-base number system. The following definitions are needed [23]:

Definition 1 (S-integer).

Given a set of primes S, an S-integer is a positive integer whose prime factors all belong to S.

Definition 2 (double-base number system).

Given$p, q$, two relatively prime positive integers, the double-base number system (DBNS) is a representation scheme into which every positive integer n is represented as the sum or difference of$\left\{p, q\right\}$-integers, i.e., numbers of the form$p^a{q}^b$:$n={\displaystyle {{\displaystyle \sum }}_{i=1}^m}{s}_{i }{p}^{b_i}{q}^{t_i}$, with$s_{i }\in \left\{-1,1\right\},$and$b_i$,$t_i\ge 0.$

If the sequences of binary and ternary exponents decrease monotonically, i.e., $b_1\ge b_2\ge \dots \ge b_m\ge 0$ and $t_1\ge t_2\ge \cdots \ge t_m\ge 0$, a double-base chain is formed.

Take the example of 314,159 as used in [24]. Its double-base chain representation is:

$$314,159=2^{12}{3}^4-2^{11}{3}^2+2^8{3}^1+2^4{3}^1-2^0{3}^0$$

3.1.4. Multi-Base Number Representation (MBNR)

Let k be an integer and let B = {b₁, …, b_l} be a set of “small” integers. A representation of k as a sum of powers of elements of B is called a multi-base representation [25] of n using the base B. The base set size of the double-base representation, i.e., $\left|B\right|=2,$ and that of multi-base representation is greater than two, i.e., $\left|B\right|>2$.

Definition: A multiple representation l = ${\displaystyle {{\displaystyle \sum }}_{i=1}^m}{s}_{i }{2}^{b_i}{3}^{t_{i }}{5}^{r_{i }}$ using the bases {2, 3, 5} is called a step multi-base number representation, where each exponent {b_i}, {t_i}, and {r_i} refes to separate monotonic decreasing sequences.

The MBNR is compared to DBNS, which is shorter in length and more redundant. For example, in

Table 1. The number of MBNR of small numbers using various bases.

N	B = {2, 3}	B = {2, 3, 5}	B = {2, 3, 5, 7}
10	5	8	10
20	12	32	48
50	72	489	1266
100	402	8425	43,777
150	1296	63,446	586,862
200	3027	316,557	4,827,147
300	11,820	4,016,749	142,196,718

, 200 has 3027 DBNS representation (base 2 and 3), 316,557 representations using the bases 2, 3 and 5 and has 4,827,147 representations using the bases 2, 3, 5, and 7.

A multiple representation l = ${\displaystyle {{\displaystyle \sum }}_{i=1}^m}{s}_{i }{\left(\frac{1}{2}\right)}^{b_i}{3}^{t_{i }}{5}^{r_{i }}$ using the bases {$\left(\frac{1}{2}\right)$, 3, 5} is called a modified multi-base number representation [26], where each exponent {b_i}, {t_i} and {r_i} refers to separate monotonic decreasing sequences.

Take the example of 314,159 as used in [26]. Its MBNR is represented as:

$$314,159={\left(\frac{1}{2}\right)}^{17}{3}^3{5}^1-{\left(\frac{1}{2}\right)}^{14}{3}^3{5}^1+{\left(\frac{1}{2}\right)}^{10}{3}^1{5}^1+{\left(\frac{1}{2}\right)}^3{3}^1{5}^0$$

The advantages of MBNR over DBNS are it is very shorter and more redundant. In the number of base elements, the number of representations of n grows aggressively. For example, 300 has 11,820 DBNS representations (base 2 and 3), 4,016,749 representations using the base 2, 3, and 5, and has 142,196,718 representations using the base 2, 3, 5, and 7.

In [26], mixed powers of 2, 3, and 5 have been proposed for representing the scalar. Instead, in [25], the authors proposed mixed powers of 1/2, 3, and 5 to obtain the faster elliptic curve cryptography (ECC) scalar multiplication. In this method, the point halving is used instead of point doubling and quadrupling while maintaining tripling and quintupling operations.

3.1.5. Proposed Tate Pairing Algorithm Based on Multi-Base Number Representation System Using Point Halving (TP-MBNR-PH)

We propose a Tate pairing algorithm based on multi-base number representation system using point halving.

The proposed Tate Pairing algorithm is based on Point Halving Technique. It takes input as an integer of MBNR representation with bases 1/2, 3, and 5 along with points P and Q which should be within the finite field FQ. Let $\mathrm{L}$ and $\mathrm{V}$ represented as line and vertical line passes through the points. ${\mathsf{Ɲ}}_1$ be represented as function with the divisor. If the sign value ${\mathrm{s}}_1$ is 1, then set ${\mathsf{Ɲ}}_1$ to 1 as is shown in step 3, else ${\mathsf{Ɲ}}_1$ is set to ${\mathsf{Ɲ}}_{-1}$ as is shown in step 6. The computation of ${\mathsf{Ɲ}}_{-1}$ is shown in step 2. The variables ${\mathrm{b}}_i,{\mathrm{t}}_i$, and ${\mathrm{r}}_i$ represents the exponents of base 1/2, 3, and 5, respectively, while inside the main for loop, TP-MBNR-PH initially calculates $\mathsf{\alpha }$, $\mathsf{\beta }$, and $\mathsf{\gamma }$ which are the exponents of 1/2, 3, and 5 bases, as shown in steps 8–10. If the computed base 2 exponent $\mathsf{\alpha }$ is equal to zero, then calculate the function ${\mathsf{Ɲ}}_1$ as shown in step 13. If the computed base 3 exponent $\mathsf{\beta }$ is equal to zero, then compute the function ${\mathsf{Ɲ}}_1$ as shown in step 17. If both of the computed bases $\mathsf{\alpha }$ and $\mathsf{\beta }$ are equal to zero, then calculate ${\mathsf{Ɲ}}_1$ as shown in step 21. If none of the above conditions are satisfied, then the algorithm computes ${\mathsf{Ɲ}}_1$ as shown in steps 24, 26 and 28. In step 29, if the signed value ${\mathrm{s}}_{\mathrm{i}+1}$ is equal to 1, then ${\mathsf{Ɲ}}_1$ and $\mathrm{C}$ is computed as shown in step 30, else ${\mathsf{Ɲ}}_1$ and $\mathrm{C}$ is computed as shown in step 32. TP-MBNR-PH finally returns ${\mathsf{Ɲ}}_1^{\left({\mathrm{q}}^{\mathrm{k}}-1\right)/\mathrm{l}}$.

Algorithm 1. TP-MBNR-PH
Input: An integer $l={\displaystyle {{\displaystyle \sum }}_{i=1}^m}{s}_{i }{\left(\frac{1}{2}\right)}^{b_i}{3}^{t_{i }}{5}^{r_{i }}$, $s_i\in \left\{-1,1\right\}$, $b_1\ge b_2 \ge \dots \ge b_m \ge 0, t_1\ge t_2 \ge \dots \ge t_m\ge 0$ and $r_1\ge r_2\ge \dots \ge r_m\ge 0$, $P=\left(x_P,y_P\right)\in E\left(F_q\right)\left[l\right]$, $Q=\left(x_Q,y_Q\right)\in E\left(F_{q^k}\right)\left[l\right]$   Output: ${\mathrm{e}}_{\mathrm{l}}\left(\mathrm{P},\mathrm{Q}\right)$
1.	$C\leftarrow P$
2.	${\mathsf{Ɲ}}_{-1}\leftarrow \frac{1}{x_Q-x_P}$
3.	$If s_1=1,\mathrm{then}$
4.	${\mathsf{Ɲ}}_1\leftarrow 1$
5.	$else$
6.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_{-1}$
7.	$\mathrm{for}\mathrm{i}=1,2,\dots ,\mathrm{n}-1\mathrm{do}$
8.	$\alpha \leftarrow b_i-b_{i+1}$
9.	$\beta \leftarrow t_i-t_{i+1}$
10.	$\gamma \leftarrow r_i-r_{i+1}$
11.	$If \alpha =0 then$
12.	$\mathrm{for}\mathrm{j}=1,2,\dots \dots ,\beta \mathrm{do}$
13.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1^3\frac{L_{C/4,C/4}\left(Q\right)L_{C/2,5C/2}\left(Q\right)}{V_{C/2}\left(Q\right)V_{3C}\left(Q\right)},$ $C\leftarrow 3\mathrm{C}$
14.	$Else If \beta =0 then$
15.	$\mathrm{for}\mathrm{j}=1,2,\dots \dots ,\alpha \mathrm{do}$
16.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1^2\frac{L_{C/4,C/4}\left(Q\right)}{V_{C/2}\left(Q\right)}, C\leftarrow \frac{1}{2}\mathrm{C}$
17.	$Else If \alpha =0 and \beta =0 then$
18.	$\mathrm{for}\mathrm{j}=1,2,\dots \dots ,\gamma \mathrm{do}$
19.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1^5\frac{L_{C/4,C/4}^2\left(Q\right)L_{C/2,5C/2}\left(Q\right)L_{5C/2, 5C/2}\left(Q\right)}{V_{C/2}^2\left(Q\right)V_{3C}\left(Q\right)V_{5C}\left(Q\right)},$
	$C\leftarrow 5\mathrm{C}$
20.	$Else$
21.	$\mathrm{for}\mathrm{j}=1,2,\dots ,\alpha \mathrm{do}$
22.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1^2\frac{L_{C/4,C/4}\left(Q\right)}{V_{C/2}\left(Q\right)}, C\leftarrow \frac{1}{2}\mathrm{C}$
23.	$\mathrm{for}\mathrm{j}=1,2,\dots ,\beta \mathrm{do}$
24.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1^3\frac{L_{C/4,C/4}\left(Q\right)L_{C/2,5C/2}\left(Q\right)}{V_{C/2}\left(Q\right)V_{3C}\left(Q\right)},$ $C\leftarrow 3\mathrm{C}$
25.	$\mathrm{for}\mathrm{j}=1,2,\dots ,\gamma \mathrm{do}$
26.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1^5\frac{L_{C/4,C/4}^2\left(Q\right)L_{C/2,5C/2}\left(Q\right)L_{5C/2, 5C/2}\left(Q\right)}{V_{C/2}^2\left(Q\right)V_{3C}\left(Q\right)V_{5C}\left(Q\right)},$ $C\leftarrow 5\mathrm{C}$
27.	$If s_{i+1}=1 then$
28.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1\frac{L_{C,P}\left(Q\right)}{V_{C+P}\left(Q\right)}, C\leftarrow \mathrm{C}+\mathrm{P}$
29.	$Else$
30.	${\mathsf{Ɲ}}_1\leftarrow {\mathsf{Ɲ}}_1. {\mathsf{Ɲ}}_{-1}\frac{L_{C,P}\left(Q\right)}{V_{C-P}\left(Q\right)}, C\leftarrow \mathrm{C}-\mathrm{P}$
31.	$return {\mathsf{Ɲ}}_1^{\left(q^k-1\right)/l}$

3.1.6. Experimental Results

To obtain the results of the proposed TP-MBNR-PH, initially we have to apply the formula for computing the Tate pairing of elliptic curves over finite fields. Integers with at least 160 bit size which are represented with bases 1/2, 3, and 5 are used in Miller’s algorithm.

Table 2. Operational costs in the proposed Tate pairing algorithm.

Operation	Cost						Pre-Computed Cost
	${\mathit{M}}_{\mathit{k}}$	${\mathit{S}}_{\mathit{k}}$	${\mathit{M}}_{\mathit{b}}$	$\mathit{I}$	$\mathit{S}$	$\mathit{M}$	${\mathit{M}}_{\mathit{k}}$	${\mathit{S}}_{\mathit{k}}$	${\mathit{I}}_{\mathit{k}}$	${\mathit{M}}_{\mathit{k}/2}$	${\mathit{I}}_{\mathit{k}/2}$
TADD	1	-	2.5	1	1	3	2	-	-	7	1
TSUB	1	-	-	1	1	2$\mathrm{k}$+3	2	-	1	-	-
THAL	1	1	3.5	-	-	4	2	-	-	-	-
TTRL	3	1	2	1	4	9	-	1	-	-	-
TQNT	4	1	5	1	4	12	-	2	-	-	-

shows the cost and pre-computed cost for the operations TADD, TSUB, THAL, TTRL, and TQNT in the proposed TP-MBNR-PH. Let TADD, TSUB, THAL, TTRL, and TQNT denote the addition, subtraction, halving, tripling, and quintupling operations, respectively, as shown in Table 2. Figure 1 and

Table 3. Number of multiplication operations of proposed Tate pairing algorithm and existing algorithms.

Method	Embedding Degree
	$\mathit{k}=4$	$\mathit{k}=6$	$\mathit{k}=8$
Izu et al. [28]	12,328M	20,353M	28,379M
Kobayashi et al. [29]	9196M	13,685M	18,121M
Chang’an et al. [27]	8350M	12,554M	17,085M
Proposed Algorithm	6978.8M	10,805.8M	1,4642.8M

shows the number of multiplication operation to compute Tate pairing using different methods. Let $I, S$ and $M$ denote the cost of inversion, squaring and multiplication in $F_q^{*}$ respectively as shown in Table 1. Let $I_k,S_k$ and $M_k\left(\approx k^{1.6}M\right)$ denote the cost of inversion, squaring, and multiplication in $F_{q^k}^{*}$, respectively, as shown in Table 1. Let $M_b\left(\approx kM\right)$ denote the cost of multiplication between $F_q^{*}$ and $F_{q^k}^{*}$. An embedding degree denoted as $k$, which takes the values of 4, 6, and 8 [27]. In

Table 4. Efficiency of proposed Tate pairing algorithm with the existing algorithms.

Method	Embedding Degree
	$\mathit{k}=4$	$\mathit{k}=6$	$\mathit{k}=8$
Izu et al. [28]	43.4%	46.9%	48.4%
Kobayashi et al. [29]	24.1%	21%	19.1%
Chang’an et al. [27]	16.4%	13.9%	14.3%

, we significantly improves the proposed TP-MBNR-PH and show the comparison of the proposed TP-MBNR-PH with an existing algorithm.

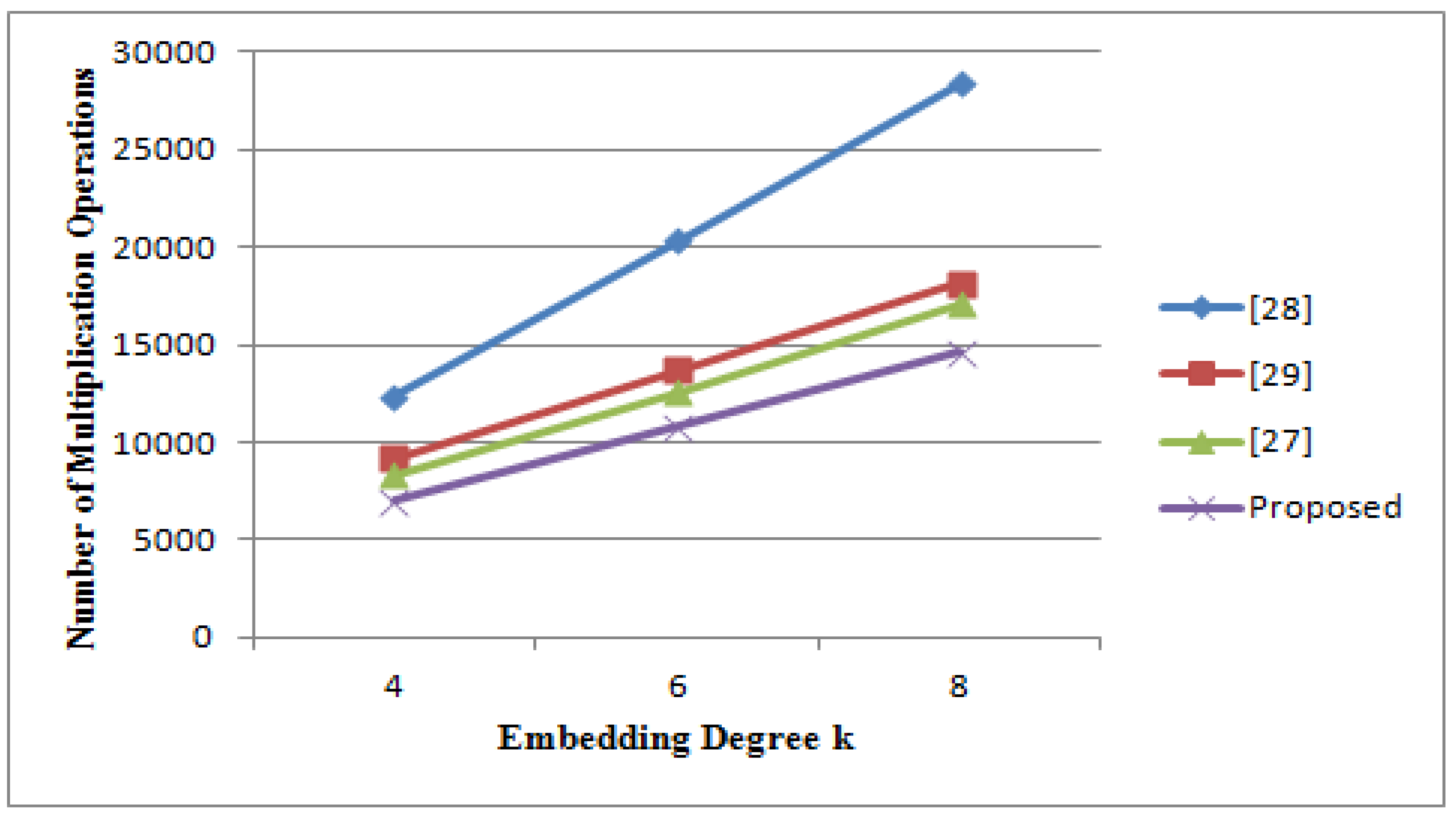
3.1.7. Efficiency of the Proposed Algorithm

The total pre-computed cost of the proposed TP-MBNR-PH is:

$$T_{pre}=6M_k+3S_k+I_k+7M_{k/2}+I_{k/2}$$

By taking $M_4=9M$, $M_6=18M$, $M_8=27M$, $M_k=kM$, $I=10M$, $S=0.8M$, $I_k=I+k^{2}M$.

The total cost of the proposed algorithm is:

$$\begin{gathered} T_{total}=b_{max}THAL+t_{max}TTRL+r_{max}TQTP+\frac{n}{2}\left(TADD+TSUB\right)+T_{pre} \\ {T}_{total}=(b_{max}+3t_{max}+4r_{max}+n+6) M_k+(b_{max}+t_{max}+r_{max}+3) S_k+ \\ (\frac{7}{2}{b}_{max}+2t_{max}+5r_{max}+\frac{5}{4}n) M_b+(4b_{max}+9t_{max}+12r_{max}+\left(k+3\right)n) M \\ +\left(t_{max}+r_{max}+n\right) I+\left(4t_{max}+4r_{max}+n\right)S+I_k+7M_{k/2}+I_{k/2} \end{gathered}$$

3.2. Applying the Proposed TP-MBNR-PH in a Decentralized KP-ABE Scheme

The TP-MBNR-PH algorithm is applied in a decentralized KP-ABE [12]. The detailed steps are as follows:

• $Global setup \left(GS\right):$ Take input as a security parameter $\lambda$ and it generates the bilinear group $G_{1 }and G_2\left(GS\left(1^{\lambda }\right)\to \left\{G_{1 },G_2\right\}\right)$ with prime order $P.$ Let $\mathrm{e}:G_{1 }\times G_{1 } \to G_2$ be the bilinear map and $g_{1 }, g_2, g_3$ are generators of the group $G_1$. The $N$ number of authorities are denoted as $\left\{A_1,A_2,\dots ,A_N\right\}$: $A_k$ monitor $n_k$ attributes i.e., ${\tilde{A}}_k=\left\{a_{k,1},\dots ,a_{k, n_k}\right\},\forall k$.
• $Attribute Authorities setup \left(AAs\right):$ It is executed by each AA to randomly generate the Security parameter $(S{K}_k)$ of authority $A_k$ and public parameter $\left(P{K}_k\right)$ of authority $A_k$:

  $${\mathbb{Z}}_p\stackrel{randomly}{\to }S{K}_k=\left\{{\mathsf{\varkappa }}_{\mathrm{k}},{\mathsf{\varrho }}_{\mathrm{k}},\left[{\mathsf{Ҷ}}_{k,1},\dots ,{\mathsf{Ҷ}}_{k, n_k}\right]\right\},\forall k$$

  $$P{K}_k=\left\{{\mathrm{Y}}_{\mathrm{k}}={\mathrm{e}}_{\mathrm{TP}-\mathrm{MBNR}-\mathrm{PH}}{\left(g_1,g_1\right)}^{{\mathsf{\varkappa }}_{\mathrm{k}}},{\mathrm{Z}}_{\mathrm{k}}=g_1^{{\mathsf{\varrho }}_{\mathrm{k}}},\left[{\mathsf{Ҷ}}_{k,1}=g_1^{{\mathsf{Ҷ}}_{k,1}},\dots ,{\mathsf{Ҷ}}_{k, n_k}=g_1^{{\mathsf{Ҷ}}_{k, n_k}}\right]\right\},\forall k$$

  Each ${\mathrm{A}}_{\mathrm{k}}$ specifies ${\mathrm{m}}_{\mathrm{k}}$ as the minimum number of attributes required to satisfy the access structure $({\mathrm{m}}_{\mathrm{k}}<{\mathrm{n}}_{\mathrm{k}}).$
• $Key Generation \left(KG\right):$ The attribute set of the user is ${\tilde{A}}_u:{\tilde{A}}_u\cap {\tilde{A}}_k={\tilde{A}}_u^k, \forall k$. $A_k$ generates $r_{k,u}{\in }_{randomly}{\mathbb{Z}}_p$ and polynomial $q_x$ for each node $x$ (including the leaves) $\mathbb{T}$. For each node $x,$ the degree $d_x$ of the polynomial $q_x$ is $d_x=k_x-1$ where $k_x$ is the threshold value of that node. For the root node $root$, set $q_{root}\left(0\right)=r_{k,u}$. For any other node $x$, $q_x\left(0\right)=q_{parent\left(x\right)}\left(index\left(x\right)\right)$. Now decryption key for the user $u$ is generates as follows:

  $$DK=D{K}_{k,u}=g_1^{-{\mathsf{\varkappa }}_{\mathrm{k}}}{g}_2^{\frac{{\mathsf{\varrho }}_{\mathrm{k}}}{r_{k,u}+u}}{g}_3^{\frac{r_{k,u}}{{\mathsf{\varrho }}_{\mathrm{k}}+u}},D{K}_{k,u}^1=g_2^{\frac{1}{r_{k,u}+u}},D{K}_{k,u}^j=g_3^{\frac{q_{a_{k,j}}\left(0\right)}{\left({\mathsf{\varrho }}_{\mathrm{k}}+u\right){\mathsf{Ҷ}}_{k,j}}}, \forall a_{k,j}\in {\tilde{A}}_u^k$$
• $Encryption \left(E\right):$ Attribute set for the message $\mathrm{m}$ is ${\tilde{A}}_m:{\tilde{A}}_m\cap {\tilde{A}}_k={\tilde{A}}_m^k,\forall k, i.e. {\tilde{A}}_m=\left\{{\tilde{A}}_m^1,\dots ,{\tilde{A}}_m^k,\dots ,{\tilde{A}}_m^N\right\}.$ Data owner of message $\mathrm{m}$ randomly chooses $\mathrm{s}{\in }_{\mathrm{randomly}}{\mathbb{Z}}_{\mathrm{p}},$ and output the ciphertext as follows:

  $$\mathrm{C}=\left\{\begin{array}{c}{\mathrm{C}}_1=\mathrm{m}.{\displaystyle {\displaystyle \prod }_{\mathrm{k}\in {\mathrm{I}}_{\mathrm{C}}}}{\mathrm{e}}_{\mathrm{TP}-\mathrm{MBNR}-\mathrm{PH}}{\left({\mathrm{g}}_1,{\mathrm{g}}_1\right)}^{{\mathsf{\varkappa }}_{\mathrm{k}}\mathrm{s}},{\mathrm{C}}_2={\mathrm{g}}_1^{\mathrm{s}},{\mathrm{C}}_3={\displaystyle {\displaystyle \prod }_{\mathrm{k}\in {\mathrm{I}}_{\mathrm{C}}}}{\mathrm{g}}_1^{{\mathsf{\varrho }}_{\mathrm{k}}\mathrm{s}},\\ {\left\{{\mathrm{C}}_{\mathrm{k},\mathrm{j}}={\mathsf{Ҷ}}_{\mathrm{k},\mathrm{j}}^{\mathrm{s}}\right\}}_{\forall \mathrm{k}\in {\mathrm{I}}_{\mathrm{C}},{\mathrm{a}}_{\mathrm{k},\mathrm{j}}\in {\tilde{\mathrm{A}}}_{\mathrm{m}}^{\mathrm{j}}}\end{array}\right\}$$

  where $I_C$ denotes the index set of the authorities.
• $Decryption \left(D\right):$ In order to decrypt $C$, the user $u$, computes $X,Y, \mathrm{and} S_k$ as follows:

  $$\begin{gathered} S_k={\displaystyle {\displaystyle \prod }_{a_{k,j}\in {\tilde{A}}_m^k}}{e}_{\mathrm{TP}-\mathrm{MBNR}-\mathrm{PH}}{\left(C_{k,j},D{K}_{k,u}^j\right)}^{{\Delta }_{a_{k,j},{\tilde{A}}_m^j}\left(0\right)} \\ Y={\displaystyle {\displaystyle \prod }_{k\in I_C}}{e}_{\mathrm{TP}-\mathrm{MBNR}-\mathrm{PH}}\left(C_3,D{K}_{k,u}^1\right) \\ {S}_k={\displaystyle {\displaystyle \prod }_{a_{k,j}\in {\tilde{A}}_m^k}}{e}_{\mathrm{TP}-\mathrm{MBNR}-\mathrm{PH}}{\left(C_{k,j},D{K}_{k,u}^j\right)}^{{\Delta }_{a_{k,j},{\tilde{A}}_m^j}\left(0\right)} \end{gathered}$$

The user then decrypts the message $m$ as follows:

$$m=\frac{C_{1}X}{Y{{\displaystyle \prod }}_{k\in I_C} S_k}$$

The $N$ number of AAs are denoted as $\left\{A_1,A_2,\dots ,A_N\right\}$. Let ${\tilde{A}}_k=\left\{a_{k,1},\dots ,a_{k, n_k}\right\}$ be the attribute set managed by Attribute Authority (AA), which is denoted as $A_k$. The global setup algorithm takes the security parameter as input for generating bilinear group order $G_{1 }\mathrm{and} G_2$. Each AA execute the $AAs$ algorithm to randomly generate the public keys and the corresponding secret keys. The public-secret key pair for $A_k$ is given as $\{S{K}_k=\left\{{\mathsf{\varkappa }}_{\mathrm{k}},{\mathsf{\varrho }}_{\mathrm{k}},\left[{\mathsf{Ҷ}}_{k,1},\dots ,{\mathsf{Ҷ}}_{k, n_k}\right]\right\},\forall k,P{K}_k=\left\{{\mathrm{Y}}_{\mathrm{k}},{\mathrm{Z}}_{\mathrm{k}},\left[{\mathsf{Ҷ}}_{k,1},\dots ,{\mathsf{Ҷ}}_{k, n_k}\right]\right\},\forall k\}$.

The key-generation algorithm issues the decryption keys to user $u$ with a set of attributes, ${\tilde{A}}_u$. The output of the algorithm is a decryption key which permits the user to decrypt a message which is encrypted under a set of attributes ${\tilde{A}}_u^k$ which is based on the threshold policy, which relays on the tree-based access structure.

In the encryption algorithm, let ${\tilde{A}}_m$ denotes the attribute set which is used to encrypt message $m$, ${\tilde{A}}_m^k$ denotes the set of common attributes between message $m$ and the $AA$, i.e., ${\tilde{A}}_m=\left\{{\tilde{A}}_m^1,\dots ,{\tilde{A}}_m^k,\dots ,{\tilde{A}}_m^N\right\}.$ Additionally, let $I_C$ denote the set of index of attribute authorities $AAs$ involved in the ciphertext of message $m$. To encrypt the message $m$, the message owner has to generate $s$ randomly and also he hast to calculate the cipher text $C$; $C=\left\{C_1,C_2,C_3,C_{k,j},\forall a_{k,j}\in {\tilde{A}}_m^k\right\}$. To decrypt the message $m$, the user should have access to the decryption keys for the attributes. By executing the decryption algorithm, by following the four steps he can obtain the message $m$ from the ciphertext as follows: (1) Initially the user has to compute $X$ using $C_2$ and $D{K}_{k,u}$. (2) Next, the user uses decryption key $D{K}_{k,u}^1$ and $C_3$ to calculate $Y$. (3) Then the user has to use $D{K}_{k,u}^j$ and $C_{k,j},a_{k,j}\in {\tilde{A}}_m^j$ and polynomial interpolation to obtain $r_{k,u}$. (4) Finally, the user can obtain the message $m$ using $C_1$ and pre-computed values $X,Y$ and $S_k$, $\forall k.$

3.2.1. Anonymous Key-Issuing Protocol

In order to avoid user collusions, we have used anonymous key-issuing protocol which is based on anonymous credential system which, in turn, allows users to access decryption keys from the AAs without enlightening their GIDs. The user $U$ and the attribute authority $A_k$ jointly construct the key-issuing protocol, which consists of the following steps:

• The two-party protocol (2PC) is used for the interaction between the user $u$ and the attribute authority $A_k$. The 2PC protocol takes $u, {ℌ}_1 \mathrm{and} {ℌ}_2$ from user $\{r_{k,u},{\mathsf{\varrho }}_{\mathrm{k}}\}$ from $A_k$ and return $x=\left(u+{\mathsf{\varrho }}_{\mathrm{k}}\right){ℌ}_1 \mathrm{mod} p$ and $y=\left(u+r_{k,u}\right){ℌ}_2 \mathrm{mod} p$ to $A_k$.
• Once the 2PC protocol gets executed, the user $u$ now computes $P=g_1^{\frac{1}{{ℌ}_1{ℌ}_2}}, Q=g_2^{\frac{1}{{ℌ}_2}} \mathrm{and} R=g_3^{\frac{1}{{ℌ}_1}}$ and then sends to $A_k$.
• Attribute Authority $A_k$ computes $\widetilde{D_{k,u}}$, $\widetilde{D_{k,u}^1}$, $\widetilde{D_{k,u}^j}$, $\forall a_{k,j}\in {\tilde{A}}_u^k$ and proof of knowledge with the help of $P, Q, R, x, \mathrm{and} y$ and send them to the user:

  $$\widetilde{D_{k,u}}=P^{-{\mathsf{\varkappa }}_{\mathrm{k}}}{Q}^{\frac{{\mathsf{\varrho }}_{\mathrm{k}}}{x}}{R}^{\frac{r_{k,u}}{y}}$$

  $$\widetilde{D_{k,u}^1}=Q^{\frac{1}{x}}$$

  $$\widetilde{D_{k,u}^j}=R^{\frac{r_{k,u}\left(a_{k,j}\right)}{y{\mathsf{Ҷ}}_{k,j}}},\forall a_{k,j}\in {\tilde{A}}_u^k$$
• User $u$ exponentiates the received values by ${ℌ}_1{ℌ}_2$ to get the decryption keys.

The key advantage of the proposed key issuing protocol is both $leak free$ and $selective-failure blind$. Suppose for the message $m$, the attribute set is ${\tilde{A}}_m=\left\{a_1,a_2\right\}.$ If the users $U_1$ and $U_2$ with identifiers $u_1$ and $u_2$ respectively have access to decryption credential for attribute $\left\{a_1\right\}$, while another user $U_3$ with identifier $u_3$ has access to attribute $\left\{a_2\right\}$ alone; none of the users can decrypt the ciphertext alone. However, there is a possibility that users can collude together so that they can generate the decryption credentials to decrypt the cipher text. This algorithm overcomes the user collusion vulnerability since $u_1$ and $u_2$ cannot be substituted with $u_3$ without the knowledge of ${\mathsf{\varrho }}_1,r_{1,u_1}$, and $r_{1,u_2}.$

3.2.2. Proposed Scheme: Proof of Security

Decisional Bilinear Diffie-Hellman (DBDH) assumption: Let $a, b, c, z \in {\mathbb{Z}}_p$ be chosen at random, $G$ be the group of prime order $q$ and $g$ is the generator of the group $G$. The DBDH problem [30] is a problem that no polynomial time adversary is able to distinguish the tuple $\left(g^a, g^b, g^c, e{\left(g,g\right)}^{abc}\right)$ from the tuple $\left(g^a, g^b, g^c, e{\left(g,g\right)}^z\right)$ with a non-negligible advantage. This can be formalized as follows:

$$\left(\left|\mathrm{Pr}\left[\mathcal{𝒜}\left(g,g^a, g^b, g^c, e{\left(g,g\right)}^{abc}\right)=0\right]-\mathrm{Pr}\left[\mathcal{𝒜}\left(\mathrm{g},{\mathrm{g}}^{\mathrm{a}},{\mathrm{g}}^{\mathrm{b}},{\mathrm{g}}^{\mathrm{c}},\mathrm{e}{\left(\mathrm{g},\mathrm{g}\right)}^{\mathrm{z}}\right)=0\right]\right|\ge \epsilon \right)$$

Theorem 1.

Under Decisional Bilinear Diffie-Hellman (DBDH) assumptions, no polynomial time attacker can selectively break the proposed system.

Proof. 

The security game is based on the hardness of the DBDH assumption. Suppose attacker $atk$ can win the FH-CP-ABE game with advantage $\epsilon$. We construct a simulator $sim$ that can distinguish a DBDH tuple from a random tuple with advantage $\frac{\epsilon }{2}$. Let $G_1$ be the source group and $G_2$ be the target group. Let $g$ be the generator of the group $G_1$. The challenger chooses the fair binary coin $\mathsf{ɦ}\in \left\{0,1\right\}$, $g\in G_1$, $R\in G_2$ and $a, b, c\in {\mathbb{Z}}_p$. If $\mathsf{ɦ}=0$, then the challenger defines $T$ to be $e{\left(g,g\right)}^{abc}$. Otherwise, he sets $T=e{\left(g,g\right)}^z or R$. The challenger then gives the simulator the DBDH details and then simulator $sim$ now plays the role of challenger in the security game.

$Init$: During the init phase, $sim$ receives the challenge access structure ${\mathcal{𝒜}}^{*}$ from attacker $atk$.

$Setup$: To provide a public key $PK$ to $atk$, $sim$ randomly chooses ${\mathsf{\varkappa }}_{\mathrm{k}}{}^{\prime }\in {\mathbb{Z}}_p$ and note ${\mathsf{\varkappa }}_{\mathrm{k}}={\mathsf{\varkappa }}_{\mathrm{k}}{}^{\prime }+ab$. It calculates $e{\left(g,g\right)}^{{\mathsf{\varkappa }}_{\mathrm{k}}}$ as: $e{\left(g,g\right)}^{{\mathsf{\varkappa }}_{\mathrm{k}}}=e{\left(g,g\right)}^{{\mathsf{\varkappa }}_{\mathrm{k}}{}^{\prime }}.e{\left(g,g\right)}^{ab}$. Finally, $sim$ sends public key $PK$ to $atk$.

$Phase 1$: During this phase, $atk$ submits an attribute set ${\mathcal{W}}_j\in \mathcal{𝒜}$ such that ${\mathcal{W}}_j\notin {\mathcal{𝒜}}^{*}$, to $sim$. Simulator $sim$ chooses $r_{k,u}{}^{\prime }{\in }_{randomly}{\mathbb{Z}}_p$. It can be obtained as follows: $D{K}_{k,u}=g^{-{\mathsf{\varkappa }}_{\mathrm{k}}}{g}^{\frac{\left(\mathsf{\gamma }+\mathsf{\delta }\right){\mathsf{\varrho }}_{\mathrm{k}}}{r_{k,u}{}^{\prime }+u}}{g}^{\frac{\mathsf{\gamma }\mathsf{\eta }{r}_{k,u}{}^{\prime }}{{\mathsf{\varrho }}_{\mathrm{k}}+u}}$. For each attribute in ${\mathcal{W}}_j$, $sim$ has to choose ${\mathsf{Ҷ}}_{k,j}{\in }_{randomly}{\mathbb{Z}}_p$. It computes the rest of the secret key as follows: $D{K}_{k,u}^1=g^{\frac{\left(\mathsf{\gamma }+\mathsf{\delta }\right)}{r_{k,u}{}^{\prime }+u}}$, $D{K}_{k,u}^j=g^{\frac{\mathsf{\gamma }\mathsf{\eta }{q}_{parent\left(a_{k,j}\right)}\left(index\left(a_{k,j}\right)\right)}{\left({\mathsf{\varrho }}_{\mathrm{k}}+u\right){\mathsf{Ҷ}}_{k,j}}}.$ Finally, $sim$ sends the $SK$ to $atk$.

$Challenge$: The attacker $atk$ submits two equal length messages ${\mathrm{m}}_1$ and ${\mathrm{m}}_2$ along with a challenge access structure ${\mathcal{𝒜}}^{*}$. $sim$ randomly generates a bit $\widehat{\mathsf{ɦ}}\in \left\{0,1\right\}$ and computes $C{T}^{*}$ as ${\mathrm{C}}_1=\frac{m_{\widehat{\mathsf{ɦ}}}Y{{\displaystyle \prod }}_{k\in I_C} S_k}{X}$. Finally, $sim$ sends the $C{T}^{*}$ to $atk$.

$Phase 2$: Same as $\mathrm{Phase}1$.

$Guess$: The attacker $atk$ outputs a guess ${\widehat{\mathsf{ɦ}}}^{\prime }$ of $\widehat{\mathsf{ɦ}}$. If $\widehat{\mathsf{ɦ}}={\widehat{\mathsf{ɦ}}}^{\prime }$, simulator $sim$ guesses that $T=e{\left(g,g\right)}^{abc}$. Otherwise, $T$ is a random target group element in $G_2$.

The advantage of the attacker is $\epsilon$, when $T=e{\left(g,g\right)}^{abc}$. The advantage of the attacker is $\frac{1}{2}$, when $T$ is a random target group element in $G_2$. Finally, the advantage of the simulator in this security game is $\frac{\epsilon }{2}$. ☐

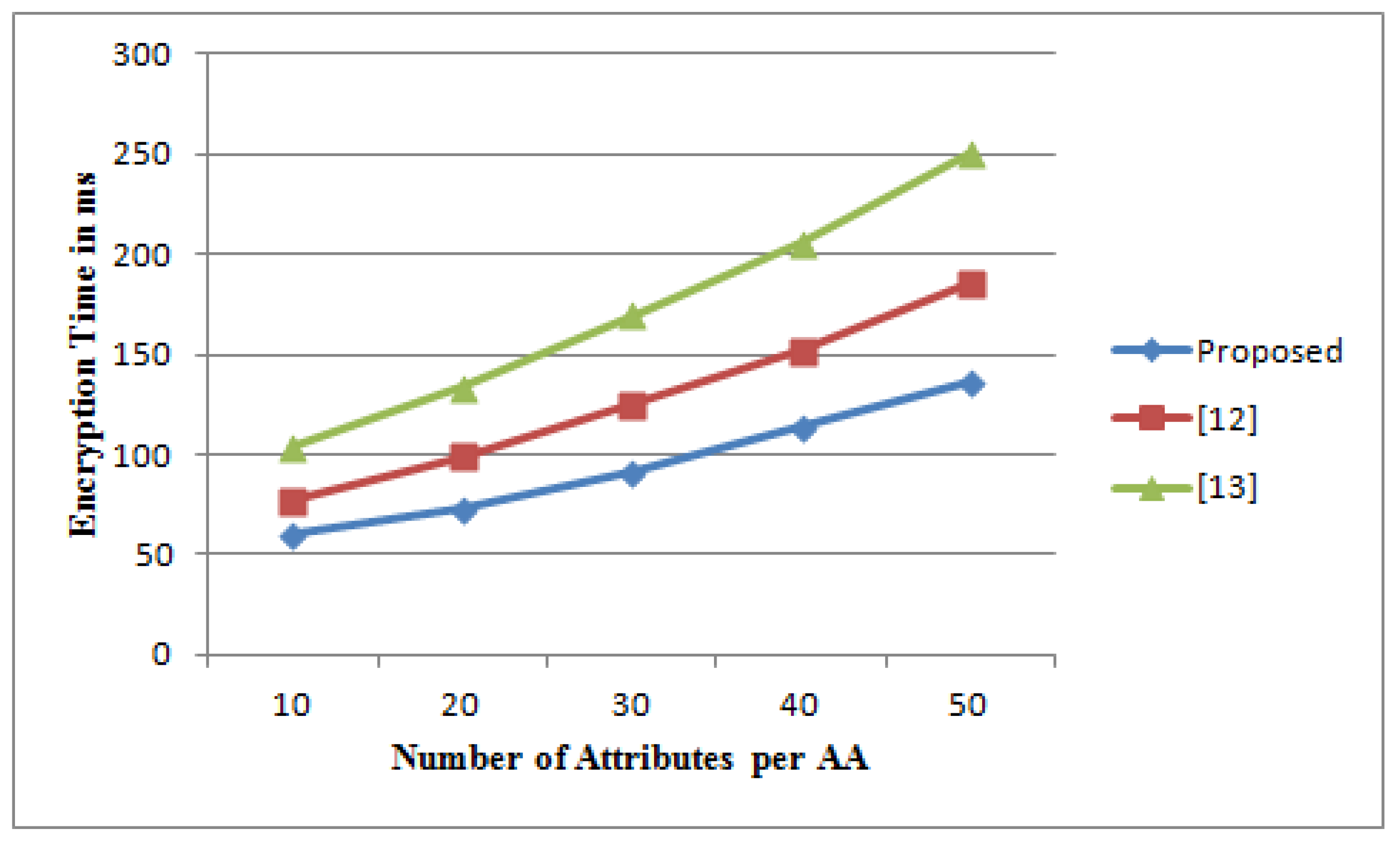
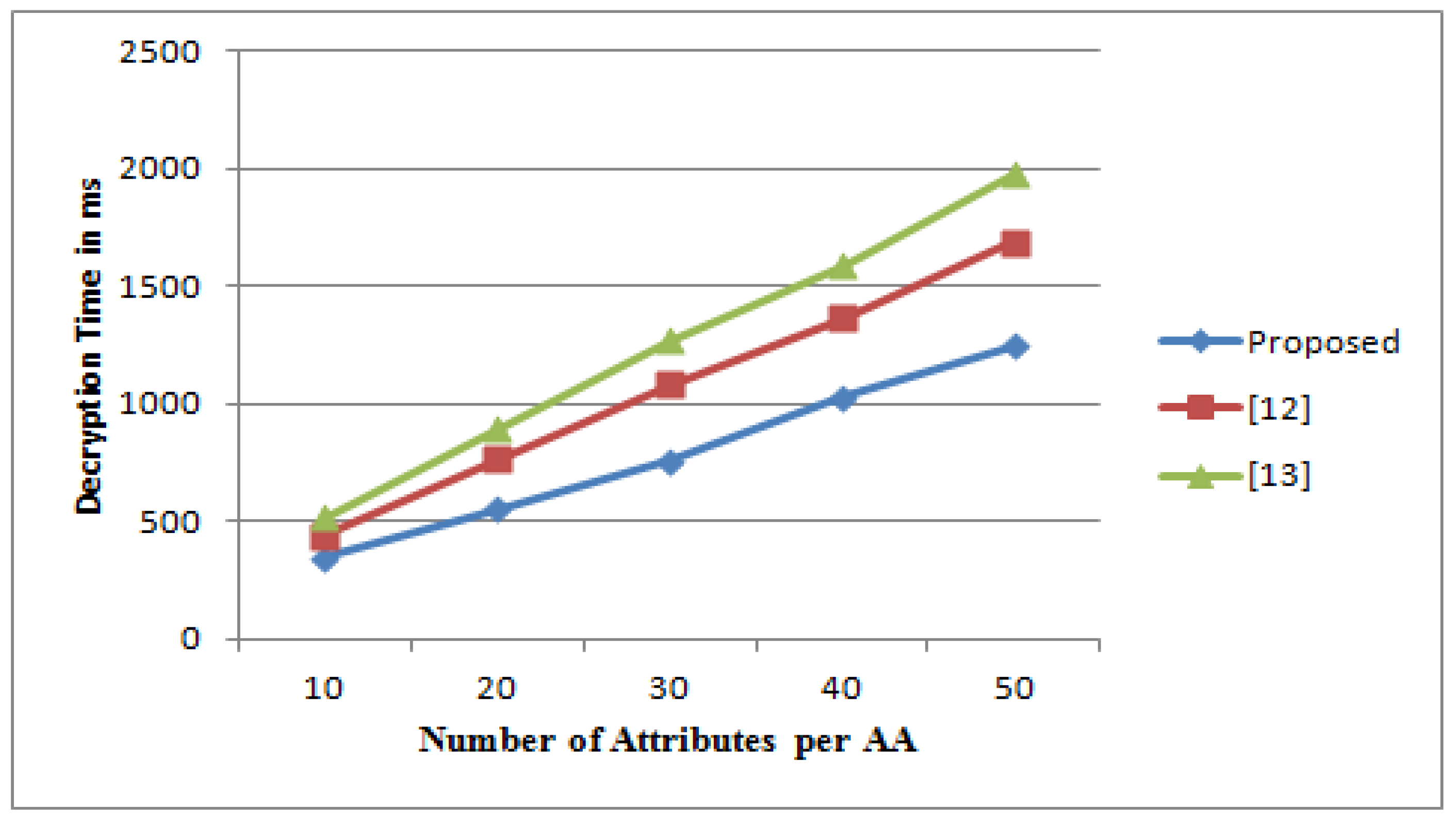
3.2.3. Experimental Results

In this section, we show the total computation cost of encryption and decryption for the MA-ABE. The proposed Tate pairing algorithm is discussed in detail in Section 3. The proposed decentralized KP-ABE is constructed with the help of the proposed TP-MBNR-PH and compared with MA-ABE using an existing Tate pairing algorithm. In this experiment, we used an Intel Core i3-3217U CPU processor (Intel, China) with 1.80 GHz and 8 GB RAM. Let us assume the number of attribute authorities, $N=2$, and say, attribute n varies from 10 to 50.

Figure 2 depicts the comparison of total encryption cost of MA-ABE for the proposed scheme and [12,13]. The time complexity of proposed encryption algorithm increases linearly with respect to the attributes. Figure 2 clearly shows the significant improvement of the proposed encryption algorithm when compared with the existing schemes [12,13]. Figure 3 depicts the comparison of the total decryption cost of MA-ABE for the proposed scheme and [12,13]. The time complexity of the proposed decryption algorithm increases linearly with respect to the attributes. Figure 3 clearly shows the significant improvement of the proposed decryption algorithm when compared with the existing schemes [12,13].

4. Conclusions

In this paper, we presented an efficient Tate pairing algorithm based on multi-base number representation system using point halving (TP-MBNR-PH) with bases 1/2, 3, and 5 to reduce the cost of bilinear pairing operations. The efficiency of the proposed algorithm has been significantly improved when compared with the existing Tate pairing algorithms. In [12,13], the schemes have proved that an anonymous key issuing protocol is free from leaks, selective-failures, and avoids user collusion. The TP-MBNR-PH algorithm is then applied in decentralized KP-ABE [12] in cloud environment to compute the cost for encryption and decryption. It is inferred that the TP-MBNR-PH algorithm, when applied in a KP-ABE scheme, has shown a significant improvement than the existing schemes [12,13] in terms of computational cost for encryption and decryption.