Fault Attacks on the Authenticated Encryption Stream Cipher MORUS

Abstract

This paper investigates the application of fault attacks to the authenticated encryption stream cipher algorithm MORUS. We propose fault attacks on MORUS with two different goals: one to breach the confidentiality component, and the other to breach the integrity component. For the fault attack on the confidentiality component of MORUS, we propose two different types of key recovery. The first type is a partial key recovery using a permanent fault model, except for one of the variants of MORUS where the full key is recovered with this model. The second type is a full key recovery using a transient fault model, at the cost of a higher number of faults compared to the permanent fault model. Finally, we describe a fault attack on the integrity component of MORUS, which performs a forgery using the bit-flipping fault model.

1. Introduction

MORUS [1,2] is a family of stream cipher based authenticated encryption (AE) algorithms and is a third-round candidate in the CAESAR Authenticated Encryption (AE) competition [3]. There are three variants: MORUS-640-128, MORUS-1280-128 and MORUS-1280-256; where the first and second integers represent the state size and the key size, respectively. The cipher is intended to provide both confidentiality and integrity assurance for the input data. Despite being in the final round of the competition, there is little public analysis of the security of this algorithm. This motivates our research.

This paper investigates the application of fault attacks on MORUS [1]. A fault attack is a type of side channel attack applied to the physical implementation of a cryptographic algorithm which introduces some errors in the implementation of the underlying algorithm. The adversary can compare multiple faulty outputs, or a faulty output with a fault-free output; which may reveal some information that can compromise the security of the algorithm. Fault attacks with two different goals on MORUS are proposed in this paper. The goal of our first fault attack is to perform a secret key recovery by injecting faults into the confidentiality component, using either the permanent or the transient fault model. The permanent fault model partially recovers the secret key, while the transient fault model recovers the entire secret key. The goal of our second fault attack is to perform a forgery (without key recovery) by injecting faults into the integrity component.

This paper is organized as follows. Section 1.1 describes the notations and operations used in this paper. Section 2 provides a description on the working principle of MORUS. Section 3 discusses the existing analysis of MORUS. Section 4 provides an overview of fault attacks in general. Section 5 discusses the application of fault-based key recovery attacks on different variants of MORUS. Section 6 discusses the fault-based forgery attack on MORUS. Finally, Section 7 concludes this paper.

1.1. Notations and Operations

Notations and operations used in this paper are as follows:

• ⊕: Bit-wise XOR operation.
• ⊗: Bit-wise AND operation.
• Word: A sequence of 32 bits or 64 bits, for MORUS-640 and MORUS-1280, respectively.
• Block: A sequence of 128 bits or 256 bits, for MORUS-640 and MORUS-1280, respectively.
• $l_s$: Length of a block set to 128 bits or 256 bits for MORUS-640 and MORUS-1280, respectively.
• $Rotl\_xxx\_yy(x,b)$: Divide a $xxx$-bit block x into 4 $yy$-bit words and rotate each word to the left by b bits.
• K: The secret key of size $l_k$ bits.
• V: The initialization vector of size 128 bits.
• $cons{t}_0$: A 128-bit constant in hexadecimal format $\mathtt{0}\mathtt{x}\mathtt{000101020305080}\mathtt{d}\mathtt{1522375990}\mathtt{e}\mathtt{97962}$.
• $cons{t}_1$: A 128-bit constant in hexadecimal format $\mathtt{0}\mathtt{xdb}\mathtt{3}\mathtt{d}\mathtt{18556}\mathtt{dc}\mathtt{22}\mathtt{ff}\mathtt{12011314273}\mathtt{b}\mathtt{528}\mathtt{dd}$.
• $M^t$: The external input to the state at step t.
• $P^t$: The input plaintext block at step t.
• $D^t$: The input associated data block at step t.
• $C^t$: The output ciphertext block at step t.
• $msglen$: Length of the plaintext/ ciphertext in bits where $0\le msglen<2^{64}$.
• $adlen$: Length of the associated data in bits where $0\le adlen<2^{64}$.
• $l_p$: Number of input plaintext blocks.
• $l_d$: Number of input associated data blocks.
• $\tau$: Authentication tag.
• $S^t$: The internal state at step t.
• $S_j^t$: The internal state at the jth round of step t.
• $S_{j,k}^t$: kth element of state $S_j^t$.
• X: A sequence of length $l_X$.
• ${\overleftarrow{X}}^r$: Left rotation of X by r bits.

2. Description of MORUS

The internal state of MORUS consists of five state elements $S_{0,0},\dots ,S_{0,4}$. These state elements are of length 128 bits or 256 bits, for MORUS-640 and MORUS-1280, respectively. This gives the cipher a total internal state size of 640 and 1280 bits, for MORUS-640 and MORUS-1280, respectively.

The MORUS family of stream ciphers supports a key K of either 128 bits or 256 bits. The initialization vector V is 128 bits for all the variants of MORUS. The cipher takes an input plaintext P of arbitrary length. Confidentiality is achieved by encrypting the plaintext P by XOR-ing with the output keystream generated by the cipher to obtain the ciphertext C. The cipher also takes associated data D of arbitrary length as input. The associated data is not encrypted. MORUS provides integrity assurance for both the plaintext P and associated data D.

MORUS uses different component functions in the different operation phases of the cipher. Section 2.1 and Section 2.2 discuss the component functions and operation phases of MORUS, respectively.

2.1. MORUS Component Functions

The operations performed in different phases of MORUS are based on several component functions. These are: 1. State Update Function 2. Keystream Generation Function and 3. Combining Function. Figure 1 shows the different component functions of MORUS in generic form.

2.1.1. State Update Function

MORUS uses the state update function $Update(S^t,M^t)$ to update the contents of the state elements. Figure 1 shows the operations involved in the state update function. At each step t, there are 5 rounds with similar operations. Two of the state elements $S_{j,k}^t$ are updated at each round. The operations in the state update function include AND, XOR and rotation operation. MORUS uses the bitwise left rotation ${\overleftarrow{X}}^{w_i}$ which is a simple rotation of the input X to the left by $w_i$ bits, where $0\le i\le 4$. It also uses the $Rotl\_xxx\_yy(x,b_i)$ operation which divides a $xxx$-bit block input x into 4 $yy$-bit words and rotates each word to the left by $b_i$ bits, where $0\le i\le 4$. The rotation constants $b_i$ and $w_i$ are listed in

Table 1. Rotation Constants Used in MORUS.

	MORUS-640	MORUS-1280
$b_0$	5	13
$b_1$	31	46
$b_2$	7	38
$b_3$	22	7
$b_4$	13	4
$w_0$	32	64
$w_1$	64	128
$w_2$	96	192
$w_3$	64	128
$w_4$	32	64

.

The state update function takes inputs from the internal state and also an external input M. Depending on the phase the cipher is in, the external input M can be: all zero, the associated data, the plaintext, or a representation of the length of the associated data and the plaintext.

2.1.2. Keystream Generation Function

The keystream generation function is used during the encryption phase of MORUS. It outputs a keystream block at each step of the encryption phase. This is computed as a function of the first four state elements $S_{0,0},\dots ,S_{0,3}$ of MORUS. The keystream generation function is defined as:

$$\begin{array}{c}\hfill Z^t=S_{0,0}^t\oplus {\overleftarrow{S_{0,1}^t}}^{w_2}\oplus (S_{0,2}^t\otimes S_{0,3}^t)\end{array}$$

(1)

where $w_2$ is a left rotation constant, set to 96 bits or 192 bits for MORUS-640 and MORUS-1280, respectively.

2.1.3. Combining Function

The combining function used during the encryption phase of MORUS is a simple XOR operation. That is, the ciphertext block is computed by XOR-ing the input plaintext and keystream block.

2.2. MORUS Operation Phases

Operations performed in MORUS can be divided into five phases: Initialization, Processing associated data, Encryption, Finalization, and Decryption and tag verification. Note that there are two versions of the MORUS family of authenticated encryption cipher: MORUSv1 [1] and MORUSv2 [2]. The two versions differ only in the finalization phase, and this difference does not affect the analysis provided in this paper. The general description of the MORUS operation phases provided in this section are based on MORUSv2 [2].

2.2.1. Initialization

At the beginning of the initialization phase, the state elements of MORUS are loaded with the key, initialization vector and two constants. Particularly, for MORUS-640, the state elements $S_{0,0}^{t=0}$, $S_{0,1}^{t=0}$, $S_{0,2}^{t=0}$, $S_{0,3}^{t=0}$, $S_{0,4}^{t=0}$ are loaded with the 128-bit initialization vector V, 128-bit key K, sequence of 128 bits of value 1, $cons{t}_0$ and $cons{t}_1$, respectively.

Similar to MORUS-640, in the initialization phase the state elements of MORUS-1280 are loaded with the key, initialization vector and some constant values. There are two key sizes that can be used with MORUS-1280. When a 128-bit key is used, the state elements $S_{0,0}^{t=0}$, $S_{0,1}^{t=0}$, $S_{0,2}^{t=0}$, $S_{0,3}^{t=0}$, $S_{0,4}^{t=0}$ are loaded with $V\left|\right|0^{128}$, $K\left|\right|K$, $1^{256}$, $0^{256}$ and $cons{t}_0\left|\right|cons{t}_1$, respectively (where K is 128 bits in length). When a 256-bit key is used, the state elements $S_{0,0}^{t=0}$, $S_{0,1}^{t=0}$, $S_{0,2}^{t=0}$, $S_{0,3}^{t=0}$, $S_{0,4}^{t=0}$ are loaded with $V\left|\right|0^{128}$, K, $1^{256}$, $0^{256}$ and $cons{t}_0\left|\right|cons{t}_1$, respectively (where K is 256 bits in length).

After this, the state update function $Update(S^t,M^t)$ of MORUS is applied 16 times. During these updates the external input $M^t$ is set to zero and the cipher does not produce any output. After these 16 updates the content of state element $S_{0,1}^{t=16}$ is XOR-ed with the key. The state value formed after this process is the initial internal state of MORUS.

2.2.2. Processing Associated Data

At the beginning of the associated data processing phase, the internal state of MORUS is the initial internal state. For MORUS-640, the input associated data is divided and processed in blocks of size 128 bits. For MORUS-1280 the processing of associated data handling is similar to MORUS-640, except that the input associated data is divided and processed in blocks of size 256 bits for this instance. If the last associated data block is not a full block, then it is padded with zeroes to create a 128-bit or 256-bit block, for MORUS-640 and MORUS-1280, respectively.

At each step the cipher takes an input associated data block $D^t$ and uses this as the external input $M^t$ to update the state of MORUS. This process is continued $l_d$ times where $l_d$ is the number of associated data blocks. Note that during this process the cipher does not produce any output. This phase is not performed if the length of the associated data is zero.

2.2.3. Encryption

After completing the associated data processing phase, MORUS processes the input plaintext. Similar to the associated data processing, the plaintext $P^t$ is also divided and processed in blocks of size 128 bits (for MORUS-640) or 256 bits (for MORUS-1280). If the last plaintext block is not a full block, then it is padded with zeroes to create a 128-bit or 256-bit block, for MORUS-640 and MORUS-1280, respectively. At each step t of the encryption phase, MORUS computes a 128-bit output keystream block using Equation (1). This output keystream block $Z^t$ is XOR-ed with the plaintext block $P^t$ to compute the respective ciphertext block. The ciphertext computation is shown in Equation (2).

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill C^t& =P^t\oplus Z^t\hfill \\ \hfill & =P^t\oplus S_{0,0}^t\oplus {\overleftarrow{S_{0,1}^t}}^{w_2}\oplus (S_{0,2}^t\otimes S_{0,3}^t)\hfill \end{array}\end{array}$$

(2)

After computing the ciphertext block, the input plaintext block $P^t$ is used as the external input $M^t$ to update the state of MORUS. This process is continued until all of the plaintext blocks are processed, i.e., $l_p$ times where $l_p$ is the number of plaintext blocks.

2.2.4. Finalization

After processing all of the input plaintext, the cipher goes through the finalization phase to generate the authentication tag. The first step of the finalization phase is updating state element $S_{4,0}^t$ by XOR-ing its content with the content of state element $S_{0,0}^t$, i.e., $S_{4,0}^t=S_{4,0}^t\oplus S_{0,0}^t$. The internal state is then updated 10 times using the state update function $Update(S^t,M^t)$ of MORUS. The external input $M^t$ is set as $adlen\left|\right|msglen$ for these 10 iterations. During these 10 updates the cipher does not produce any output. Finally, the tag $\tau$ is computed by using Equation (3), and sent to the receiver with the message.

$$\begin{array}{c}\hfill \tau =S_{0,0}^t\oplus {\overleftarrow{S_{0,1}^t}}^{w_2}\oplus (S_{0,2}^t\otimes S_{0,3}^t)\end{array}$$

(3)

2.2.5. Decryption and Tag Verification

To carry out the decryption, first the initialization process is performed to obtain the initial internal state. The associated data processing phase is also performed as described in Section 2.2.2, if the length of associated data $adlen>0$. At each step t of the decryption process the output keystream block is computed using Equation (1). This output keystream block $Z^t$ is XOR-ed with the ciphertext block $C^t$ to compute the corresponding decrypted plaintext block. The recovered plaintext block computation is shown in Equation (4).

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P^t& =C^t\oplus Z^t\hfill \\ \hfill & =C^t\oplus S_{0,0}^t\oplus {\overleftarrow{S_{0,1}^t}}^{w_2}\oplus (S_{0,2}^t\otimes S_{0,3}^t)\hfill \end{array}\end{array}$$

(4)

At each step, the recovered plaintext block $P^t$ is used as the external input $M^t$ to update the state. This process is continued $l_c$ times to process all the ciphertext blocks, where $l_c$ is the number of ciphertext blocks. After processing all the ciphertext blocks, the tag is generated following the procedure discussed in Section 2.2.4.

Finally, for the tag verification, the received tag is compared with the tag generated after the decryption process. If the received tag is not the same as the tag computed after the decryption process then the tag verification fails, and the ciphertext and computed tag should not be released. Otherwise the tag verification process is considered successful.

3. Existing Analysis of MORUS

There is little public analysis of MORUS. In this section we briefly discuss the existing cryptanalysis of MORUS.

3.1. Distinguishing Attack on MORUS

Mileva et al. [4] described the existence of a distinguisher for MORUS-640 which can analogously be used for MORUS-1280. Their analysis shows that, for a given ciphertext $C_1$ computed on a message $(D_1,P)$, an adversary can predict 125 bits of a different ciphertext $C_2$ computed over message $(D_2,P)$, where $D_1$ and $D_2$ differ in one bit. However, these distinguishers are obtained when message $(D_1,P)$ and message $(D_2,P)$ are processed using the same key and initialization vector. This falls under the nonce-reuse scenario for which the designer of MORUS does not claim any security.

3.2. State Collisions and Forgery Attack on MORUS

Mileva et al. [4] also analysed the state update function of MORUS, reporting collisions in the internal state. To obtain the collision, an adversary needs to be capable of injecting specific differences in both the internal state and the external input. The designer of MORUS claims that this type of collision can not be achieved in practice because the adversary can only manipulate and inject differences in the external input.

Mileva et al. [4] also described a tag forgery attack by producing the state collision discussed above. The analysis is performed by generating and solving a system of equations which satisfies the state collision criterion. However, they reported no solutions were found apart from the trivial one where the difference between the input messages is zero.

3.3. Rotational and Differential Cryptanalysis of MORUS

Dwivedi et al. [5] applied differential and rotational cryptanalysis on a reduced version of MORUS, where the initialization phase is reduced from 16 to 3.6 steps. Their application of differential cryptanalysis on MORUS-1280-256 with 18 initialization rounds (3.6 steps) can recover the 256-bit key with a complexity of $2^{253}$. They have also described a rotational attack on MORUS-1280-256 with 8 initialization rounds (1.6 steps) which can recover the key with a complexity of $2^{251}$. Both of these attack complexities are almost the same as exhaustive key search attack.

3.4. SAT Based State Recovery

Dwivedi et al. [6] analysed the complexity of SAT based state recovery for MORUS-640. Their approach based on SAT solver requires a complexity of $2^{370}$. The SAT based approach does not work for MORUS because it requires more time complexity than the exhaustive key search.

3.5. Cube Attack on MORUS

In our previous work [7], we have applied a cube attack on a reduced version of MORUS, where the initialization phase is reduced from 16 steps to 4 steps. This cube attack can recover the secret key for this reduced version of the cipher with a complexity of $2^{10}$ and $2^9$ for MORUS-640 and MORUS-1280-128, respectively. This work also demonstrated a distinguishing attack for 5 steps of the initialization phase of MORUS-1280, with a complexity of $2^8$. To date this is the best result published for a reduced version of MORUS.

4. Fault Attack

A fault attack [8] is an active attack which introduces errors/faults in the underlying cryptographic algorithm. An adversary can compare the faulty output with the original output or compare multiple faulty outputs, which may reveal information related to the secret key or internal states. The goal of the attack can be key recovery, state recovery, or to create a forgery.

The fault injection techniques can be categorised as non-invasive, invasive, and semi-invasive. The non-invasive techniques do not cause any physical damage to the device, while the invasive techniques tamper the device and may even destroy the device. The semi-invasive technique falls in between non-invasive and invasive technique. These techniques can use different means of physical tampering, such as changing the power supply voltage, tampering with the clock signal, optical fault injections, electromagnetic pulses, temperature or light radiation.

4.1. Fault Attack Model

The fault model determines the characteristics of the underlying fault. This can be catagorised based on the required number of faulty bits, fault type, control on the fault location and time and duration of the fault [9]. These are discussed below.

Fault type: The fault type defines the type of the error introduced in the underlying cryptographic implementation. This can be mainly divided into three types: Stuck-at fault, bit flipping fault and random fault.

• Stuck-at faults set the faulty bits to a specific value, of either zero or one. This type of fault can also be referred as set-to-zero or set-to-one fault.
• Bit flipping fault flips/complements bit(s) to introduce error(s) in the cryptographic algorithm.
• Random fault introduces a random error in the cryptographic algorithm. With this type of fault the faulty bits can be set to either zero or one with equal probability.

Number of faults: Based on the fault model, the number of bits required to be affected may be a single bit, multiple bits or may be even multiple words.

Control on the Fault Location and Time: The adversarial model based on the precision of the fault location and time can be categorised in three types: precise, loose and random.

• In the precise control model, the adversary is assumed to have access to fault injection techniques that can inject faults at a precise location of the internal components. The adversary can introduce these faults at a specific time of the operation of the algorithm. This is the strongest model based on the fault location.
• In the loose control model, the adversary has some control on the fault injection location and time.
• In the random model, the adversary does not have any control on the fault injection location and time. In this model, the adversary can just introduce fault(s) at a random time in a random location of the internal components of the cryptographic algorithm.

Duration of the Fault: The duration of the fault determines the time period that the fault remains active. The fault model can be categorised into transient and permanent.

• For a transient fault, the faulty bits are changed for a certain period of time. This is also known as a temporary fault, since the fault remains active temporarily.
• For a permanent fault, the faulty bits are changed for the entire duration in the underlying hardware platform. This is also known as a hard fault.

4.2. Feasibility of Fault Attacks

A permanent fault may be easier to apply than a transient fault, as it can be obtained by destroying the memory cells. An adversary with access to the physical implementation could do this. The cost associated with different fault models varies depending on the fault injection technique [9]. The permanent fault injection can be achieved by simply cutting a wire [10] or by using sophisticated technology such as using laser beam as adopted in [11]. Injecting the faults with laser beam will require a higher cost but possibly provides more accuracy [9].

For the transient faults, adversary needs access to the physical implementation of the algorithm as well as additional equipment to apply the attack. This model can work with low budget equipment such as simple flashgun or laser pointer to set or reset bit(s) of SRAM in a microcontroller [12].

In terms of the type of faults, the random fault model seems to be the most practical one. This model has been applied in several research papers and shown to work in the actual hardware [9,12]. The stuck at fault models has been reported to require a comparatively higher cost for a precise application of the fault injection [9]. The bit-flipping fault model has been applied on a 8-bit micro-controller [13], however; this model is still considered largely theoretical for a precise application of the fault location.

5. Fault Based Key Recovery Attacks on MORUS

This section describes our fault-based key recovery attacks on MORUS. We propose two different fault-based key recovery attack on MORUS. The first is a permanent fault attack, whereas the second is a transient fault attack.

For MORUS the initialization phase is updated 16 times to mix the key and initialization vector into the 640 bits internal state. However after these 16 operations the key is directly XOR-ed to update the contents of state element $S_{0,1}^{t=16}$. The state element $S_{0,1}^{t=16}$ may then be used in the computation of the first block of output keystream generated at time $t=16$ (see Equation (1)). We discuss a scenario in which these key bits can be revealed. This is the goal of our fault attacks.

MORUS processes the input plaintext after completing the initialization and associated data processing phase. During the associated data processing phase no output keystream is generated. Output keystream bits are generated only during the encryption phase. If the associated data processing phase is skipped (when there is no associated data) then the key bits will be directly XOR-ed in the output keystream function while processing the first plaintext block and faults can be applied to reveal the secret key bits. On the other hand, if the associated data processing phase is performed, then the key bits will get mixed with the contents of other state elements before appearing in the output keystream. In that case, the fault attack will not directly reveal the key bits.

When there is no associated data processing phase, Equation (2) for the first plaintext block of MORUS can be represented as:

$$\begin{array}{c}\hfill C^{16}=P^{16}\oplus S_{0,0}^{16}\oplus {\overleftarrow{(S_{0,1}^{16}\oplus K)}}^{w_2}\oplus (S_{0,2}^{16}\otimes S_{0,3}^{16})\end{array}$$

(5)

In Equation (5), if we can remove the effect of $S_{0,0}^{t=16}$, $S_{0,1}^{t=16}$, $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ then the first ciphertext block $C^{t=16}$ will just be the XOR of the first plaintext block $P^{t=16}$ and the key K. In such a scenario an adversary can apply set-to-zero faults in specific state elements to recover the key bits under a known plaintext model. In the following we discuss the effect of removing these state elements by introducing faults in some of the internal states of the cipher.

5.1. Permanent Fault Attack on MORUS-640

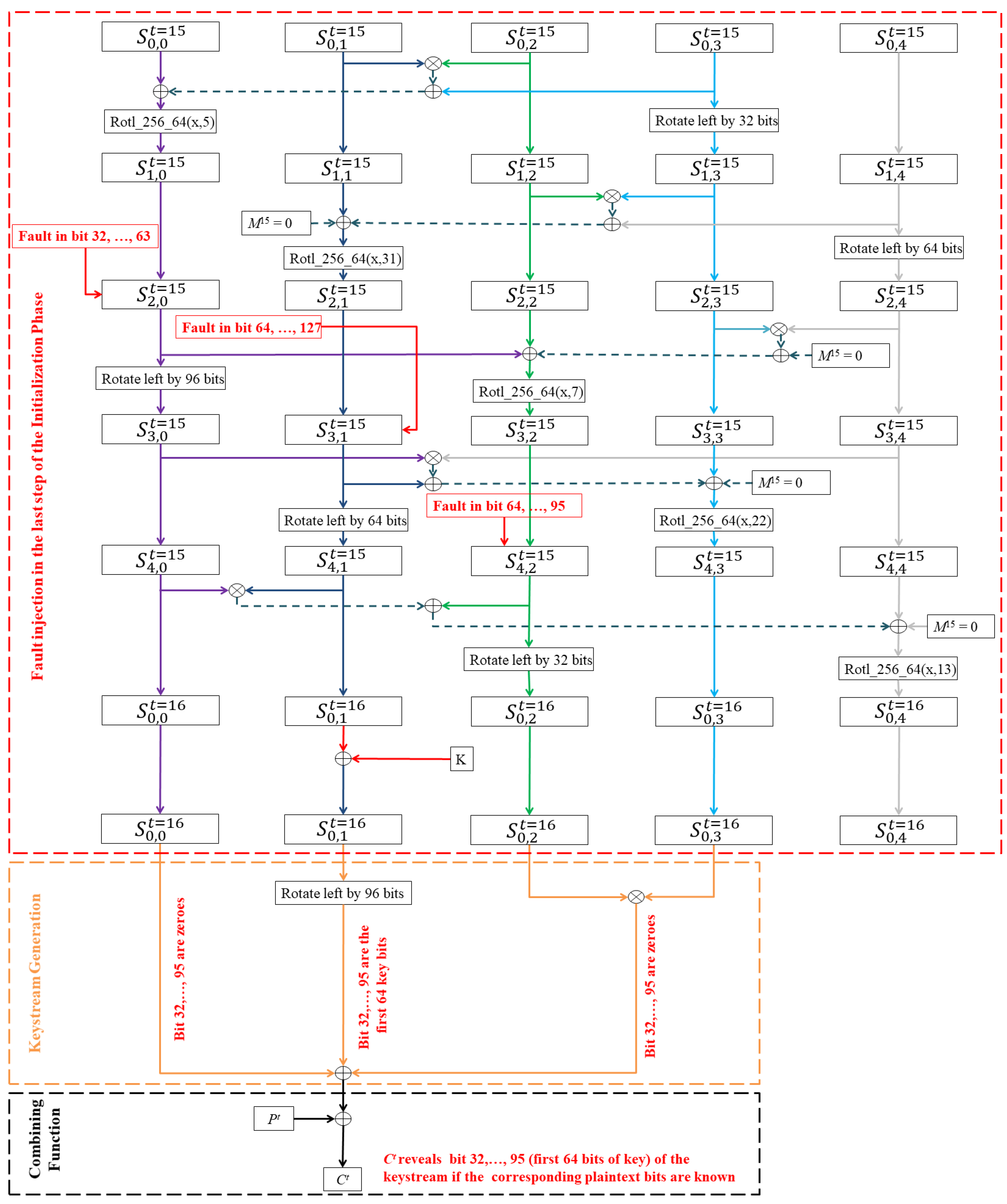
To remove the effect of $S_{0,0}^{t=16}$, $S_{0,1}^{t=16}$, $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$, an adversary can introduce permanent faults to set the contents of some specific registers of MORUS-640 to zero, thereby deleting the register contents. The locations that we target for our fault attack are shown in Figure 2 and discussed in detail below.

We observe that during the 16th step (last update step) of the initialization phase, destroying the last 64 registers (i.e., register 64 to 127) of state element $S_{3,1}^{t=15}$ will result in all zero bits in the state element $S_{4,1}^{t=15}$. This is due to the fact that at the fourth round of each step, the contents of $S_{3,1}$ are rotated left by 64 bits. The left rotation will bring the zero valued contents of the last 64 bits (faulty bits valued zero) into the first 64 register bits of state element $S_{4,1}^{t=15}$. Since the last 64 registers are permanently set to zero, the rotation will not have any effect on these bits. After the left rotation there are no changes in the state element $S_{4,1}^{t=15}$ for that step, i.e., $S_{4,1}^{t=15}=S_{0,1}^{t=16}$.

The key bits are XOR-ed with the contents of the state element $S_{0,1}^{t=16}$ after 16 updates in the initialization phase. As a result, at the end of the initialization phase the first 64 bits of state element $S_{0,1}^{t=16}$ will contain the first 64 bits of the key bits. Due to the permanent fault, XOR-ing of the last 64 bits of the key will have no effect on the corresponding bits of this state element. Note that in the encryption phase, the combining function rotates the contents of this state element by 96 bits. Thus the first 64 key bits will actually be XOR-ed at the bit position $32,\dots ,95$ during the ciphertext computation. To recover the first 64 bits of the corresponding key we must eliminate the effect of bits $32,\dots ,95$ of state elements $S_{0,0}^{t=16}$, $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ from the first ciphertext block, using a similar technique to that used for state element $S_{0,1}^{t=16}$.

To eliminate the effect of bits $32,\dots ,95$ of state element $S_{0,0}^{t=16}$ in the keystream computation, one can permanently set bits $32,\dots ,63$ of state element $S_{2,0}^{t=15}$ to zero (i.e., destroy the register bit 32 to 63). At the third round of each step, contents of state element $S_{2,0}$ goes through a left rotation of 96 bits. The left rotation will bring the zero valued contents of the bit $32,\dots ,63$ (faulty bits) into the register bits $64,\dots ,95$ of state element $S_{3,0}$. The left rotation will not have any effect on the register bits $32,\dots ,63$ due to the permanent fault. As a result bits $32,\dots ,95$ of state element $S_{0,0}^{t=16}$ will be set to zero, since there are no changes in state element $S_{3,0}$ after the third round of each step.

In addition, in Equation (5) observe that $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ are multiplied bitwise and used in the ciphertext computation. Therefore setting bits $32,\dots ,95$ of either of these two state elements to zero will eliminate the effect of both in the keystream computation. To introduce zero valued contents in bits $32,\dots ,95$ of state element $S_{0,2}^{t=16}$, one can permanently set bits $64,\dots ,95$ of state element $S_{4,2}^{t=15}$ to zero, i.e., destroy the corresponding registers. At the fifth round of each step, contents of state element $S_{4,2}$ goes through a left rotation of 32 bits. The left rotation will bring the zero valued contents of state bits $64,\dots ,95$ (faulty bits) into the register bits $32,\dots ,63$ of state element $S_{0,2}$. The left rotation will not have any effect on the register bits $64,\dots ,95$ due to the permanent fault. As a result bits $32,\dots ,95$ of state element $S_{0,2}^{t=16}$ will be set to zero, which will eliminate the effect of state $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ in the keystream computation.

In summary, an adversary using this technique must introduce a total of 128 bits of permanent faults in the 640-bit internal state of MORUS-640 to recover the first 64 bits of the key. One can recover the remaining 64 key bits by exhaustive search, which will require a complexity of about $2^{64}$. Note that it is not possible to recover the full key of MORUS-640 using only permanent faults, as the faults applied to $S_{3,1}^{t=15}$ will result in permanent zero values in 64 bits of $S_{0,1}^{t=16}$, even after the key K has been XOR-ed with this state word. In particular, the attack described above is unable to recover bits 64 to 127 of the key, as these bits of $S_{0,1}^{t=16}$ have been permanently set to zero.

However, it is possible to obtain the full key of MORUS-640 by using a combination of permanent and transient faults. With an additional 128 faults (combination of permanent and transient faults) in carefully chosen parts of the state, the entire keystream output for that step will be the key. That is, for $S_{2,0}^{t=15}$ registers $32,\dots ,63$ and now additionally $96,\dots ,127$ are permanently zero, and for $S_{4,2}^{t=15}$ registers $64,\dots ,95$ and now additionally $0,\dots ,31$ are permanently zero. For $S_{3,1}^{t=15}$ registers $0,\dots ,127$ are temporarily set to zero. These 64 permanent faults in each of $S_{2,0}^{t=15}$ and $S_{4,2}^{t=15}$, together with 128 transient faults in $S_{3,1}^{t=15}$ would remove the contribution of the internal state values to the output and allow the full key to be obtained.

5.1.1. Attack Algorithm

The steps involved in recovering 64 bits of the secret key of MORUS-640 using 128 permanent faults are outlined in Algorithm 1. The steps involved in recovering the full 128-bit secret key using 256 faults (combination of permanent and transient faults) are outlined in Algorithm 2.

Algorithm 1 Algorithm for Partial Key Recovery Attack on MORUS-640 using a Permanent Fault Model.

1: Load key and initialization vector and continue the initialization phase. 2: Insert permanent set to zero faults in registers 32 to 63 of state element $S_{2,0}^{t=15}$. 3: Insert permanent set to zero faults in registers 64 to 127 of state element $S_{3,1}^{t=15}$. 4: Insert permanent set to zero faults in registers 64 to 95 of state element $S_{4,2}^{t=15}$. 5: Complete the initialization phase and construct the first block of the keystream. 6: Output bit 32 to 95 of the keystream as the first 64 bits of the secret key.

Algorithm 2 Algorithm for Full Key Recovery Attack on MORUS-640 using a Combination of Permanent and Transient Fault Model.

1: Load key and initialization vector and continue the initialization phase. 2: Insert permanent set to zero faults in registers 32 to 63 and 96 to 127 of state element $S_{2,0}^{t=15}$. 3: Insert transient set to zero faults in registers 0 to 127 of state element $S_{3,1}^{t=15}$. 4: Insert permanent set to zero faults in registers 64 to 95 and 0 to 31 of state element $S_{4,2}^{t=15}$. 5: Complete the initialization phase and construct the first block of the keystream. 6: Rotate the keystream to the left by 32 bits and output this as the 128-bit secret key.

5.2. Permanent Fault Attack on MORUS-1280

Similar to the technique used for MORUS-640, if the associated data processing phase is skipped, i.e., there is no input associated data, then the key bits will be directly XOR-ed in the output keystream function while processing the first plaintext block. In Equation (5), an adversary can apply permanent set to zero faults to eliminate the effect of $S_{0,0}^{t=16}$, $S_{0,1}^{t=16}$, $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ and recover the secret key of MORUS-1280, under a known plaintext model. The locations that we target for our fault attack are shown in Figure 3 and discussed in detail below.

During the last step of the initialization phase, destroying the last 128 registers (i.e., register 128 to 255) of state element $S_{3,1}^{t=15}$ will result in all zero bits in the state element $S_{4,1}^{t=15}$. There are no changes in the state element $S_{4,1}^{t=15}$ for that step, that is $S_{4,1}^{t=15}=S_{0,1}^{t=16}$. Since the secret key is XOR-ed with the contents of this state element after these 16 steps, the first 128 bits of state element $S_{0,1}^{t=16}$ will contain the first 128 bits of the secret key. Due to the permanent fault, XOR-ing of the last 128 bits of the secret key will have no effect on these bits.

Note that in the encryption phase, the combining function rotates the contents of this state element by 192 bits. Following a similar technique to that used for MORUS-640, an adversary can select the relevant bits of state element $S_{0,0}^{t=16}$, $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ based on the rotation distance of MORUS-1280, and apply permanent set to zero faults in the corresponding bits. By introducing such faults, an adversary can easily recover the first 128 bits of the secret key under a known-plaintext scenario. Recall that this is the entire key when the key size is 128-bit, while it represents the first 128 bits of the key when the key size is 256-bit.

An adversary using this technique must introduce a total 256 bits of permanent fault in the 1280 bits internal state of MORUS-1280. An adversary recovers the whole key when the key size is 128-bit, whereas an adversary recovers the first 128 bits of the key when the key size is 256-bit. An adversary can recover the remaining bits of the key for MORUS-1280-256 by exhaustive search, which will require a complexity of about $2^{128}$.

Note that similar to MORUS-640 it is not possible to recover the full key of MORUS-1280-256 using only permanent faults, as the faults applied to $S_{3,1}^{t=15}$ will result in permanent zero values in 128 bits of $S_{0,1}^{t=16}$, even after the key K has been XOR-ed with this state word. In particular, the attack described above is unable to recover bits 128 to 255 of the key, as these bits of $S_{0,1}^{t=16}$ have been permanently set to zero.

However, it is possible to obtain the full key of MORUS-1280-256 by using a combination of permanent and transient faults. With an additional 256 faults (combination of permanent and transient faults) in carefully chosen parts of the state, the entire keystream output for that step will be the key. That is, for $S_{2,0}^{t=15}$ registers $64,\dots ,127$ and now additionally $192,\dots ,255$ are permanently zero, and for $S_{4,2}^{t=15}$ registers $128,\dots ,191$ and now additionally $0,\dots ,63$ are permanently zero. For $S_{3,1}^{t=15}$ registers $0,\dots ,255$ are temporarily set to zero. These 128 permanent faults in each of $S_{2,0}^{t=15}$ and $S_{4,2}^{t=15}$, together with 256 transient faults in $S_{3,1}^{t=15}$ would remove the contribution of the internal state values to the output and allow the full key of MORUS-1280-256 to be obtained.

5.2.1. Attack Algorithm

The steps involved in recovering 128 bits of the secret key of MORUS-1280 using 256 permanent faults are outlined in Algorithm 3. The steps involved in recovering the full 256-bit secret key of MORUS-1280 using 512 faults (combination of permanent and transient faults) are outlined in Algorithm 4.

Algorithm 3 Algorithm for Key Full Recovery Attack on MORUS-1280-128/Partial Key Recovery Attack on MORUS-1280-256 using a Permanent Fault Model.

1: Load key and initialization vector and continue the initialization phase. 2: Insert permanent set to zero faults in registers 64 to 127 of state element $S_{2,0}^{t=15}$. 3: Insert permanent set to zero faults in registers 128 to 255 of state element $S_{3,1}^{t=15}$. 4: Insert permanent set to zero faults in registers 128 to 191 of state element $S_{4,2}^{t=15}$. 5: Complete the initialization phase and construct the first block of the keystream. 6: Output bit 64 to 191 of the keystream as the first 128 bits of the secret key.

Algorithm 4 Algorithm for Full Key Recovery Attack on MORUS-1280-256 using a Combination of Permanent and Transient Fault Model.

1: Load key and initialization vector and continue the initialization phase. 2: Insert permanent set to zero faults in registers 64 to 127 and 192 to 255 of state element $S_{2,0}^{t=15}$. 3: Insert transient set to zero faults in registers 0 to 255 of state element $S_{3,1}^{t=15}$. 4: Insert permanent set to zero faults in registers 128 to 191 and 0 to 63 of state element $S_{4,2}^{t=15}$. 5: Complete the initialization phase and construct the first block of the keystream. 6: Rotate the keystream to the left by 64 bits and output this as the 256-bit secret key.

5.3. Reducing the Required Number of Permanent Faults

The attacks presented in Section 5.1 and Section 5.2 demonstrate that it is possible to fully recover the key using a combination of permanent and transient faults, but if the number of faults is reduced, then partial key recovery is possible using only a permanent fault model. For example, in MORUS-640 256 faults were required for full key recovery using a combination of permanent and transient faults, whereas 128 permanent faults permitted recovery of 64 bits of the 128-bit key.

Alternatively, we could take a probabilistic approach to key recovery, based on the bias of the AND operation in the combining function. The combining function for the first plaintext block of MORUS described in Equation (5) has three XOR operations and an AND operation. During the processing of the first input plaintext block, the AND operation in Equation (5) takes input from the state elements $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$. The output of the AND operation is heavily biased towards zero, so we can remove the output of the AND operation from Equation (5) with a high probability. Equation (5) can be rewritten as

$$\begin{array}{c}\hfill C^{16}=P^{16}\oplus S_{0,0}^{16}\oplus {\overleftarrow{(S_{0,1}^{16}\oplus K)}}^{w_2}\end{array}$$

(6)

For MORUS-640, the output of the first 64 bits of the AND operation is zero with a probability of ${(3/4)}^{64}\approx 2^{-26.56}$. In this case, applying a modified version of Algorithm 1 (with step 4 omitted) an adversary needs to introduce 96 permanent faults at the last step of the initialization phase in order to recover the first 64 bits of the key with a probability of $2^{-26.56}$. Similarly, applying a modified version of Algorithm 2 (with step 4 omitted) an adversary needs to introduce 192 faults at the last step of the initialization phase in order to recover the entire 128-bit key with a probability of $2^{-53.12}$.

Alternatively, for MORUS-1280 the output of the corresponding 128 bits of the AND operation is zero with a probability of ${(3/4)}^{128}\approx 2^{-53.1}$. Therefore applying a modified version of Algorithm 3 (with step 4 omitted) an adversary needs to introduce 192 permanent faults at the last step of the initialization phase in order to recover the first 128 bits of the key with a probability of $2^{-53.1}$. Similarly, applying a modified version of Algorithm 4 (with step 4 omitted) an adversary needs to introduce 384 faults at the last step of the initialization phase in order to recover the entire 256-bit key with a probability of $2^{-106.25}$.

5.4. Transient Fault Attacks on MORUS

The observation from the above sections can be extended in an approach that induces transient faults in the MORUS states to recover the secret key. An adversary can introduce transient set to zero faults at specific times and locations to eliminate the effect of the contents from state elements $S_{0,0}^{t=16}$, $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$. Following this adversary can observe the corresponding bit in the first keystream block to recover one bit of the secret key.

The contents of state elements $S_{0,2}^{t=16}$ and $S_{0,3}^{t=16}$ are multiplied bitwise and used in the keystream generation function. Setting any of the bits of these two state elements to zero (inducing transient set to zero fault) will set the output of the bitwise multiplication for the corresponding bits to zero.

In particular, the adversary needs to introduce three bits of faults to recover a single bit of the secret key. To recover the jth bit of the secret key an adversary can introduce a one bit transient fault on the jth register of state element $S_{4,1}^{t=15}$ and $((l_s-w_2+j)mod{l}_s)$th register of state elements $S_{4,0}^{t=15}$ and $S_{4,3}^{t=15}$, where $l_s$ is the block size of 128-bit or 256-bit for MORUS-640 and MORUS-1280, respectively. The transient fault introduced here is a set to zero fault which temporarily resets the corresponding bits to zero. With the introduction of these three bit faults in state elements $S_{4,0}^{t=15},S_{4,1}^{t=15},S_{4,3}^{t=15}$, an adversary can recover the jth bit of the secret key. At each time step, an adversary needs only three faults in specific locations, but depending on the key size this process must be repeated 128 or 256 times in order to reveal the whole key.

Consider the scenario where an adversary can induce such faults to different locations of the initial internal states, which are computed from the same key but with different initialization vectors. For MORUS-640, an adversary can select 128 different initial states computed from the same key but different initialization vectors, and for each initial state induce the faults in 3 specific location of state elements $S_{4,0}^{t=15},S_{4,1}^{t=15},S_{4,3}^{t=15}$. With this the adversary can recover the whole secret key of MORUS-640-128. This will require $128\times 3=384$ bits of transient faults.

For MORUS-1280-128, an adversary can select 128 different initial states computed from the same key but different initialization vectors, and for each initial states induce the transient set to zero faults in 3 specific location of state elements $S_{4,0}^{t=15},S_{4,1}^{t=15},S_{4,3}^{t=15}$. With this the adversary can recover all the secret key of MORUS-1280-128. This will also require $128\times 3=384$ bits of transient faults.

Similarly for MORUS-1280-256, an adversary needs to introduce transient set to zero faults in 3 specific location of state elements $S_{4,0}^{t=15},S_{4,1}^{t=15},S_{4,3}^{t=15}$, and continue this process 256 times with 256 different initial states computed from the same key but with different initialization vectors. This will require $256\times 3=768$ bits of transient faults to recover the 256-bit secret key of MORUS-1280-256.

5.4.1. Attack Algorithm

The steps for the transient fault-based key recovery attack are outlined in Algorithm 5.

Algorithm 5 Algorithm for Transient Fault Based Key Recovery Attack.

1: Repeat steps 2 to 5 for $j=0,\dots ,l_k-1$. 2: Load the key and a fresh initialization vector and continue the initialization phase. 3: Insert transient set to zero fault in register j of state element $S_{4,1}^{t=15}$. 4: Insert transient set to zero faults in register $((l_s-w_2+j)mod{l}_s)$ of state elements $S_{4,0}^{t=15}$ and $S_{4,3}^{t=15}$. 5: Complete the initialization phase and construct the first block of the keystream. 6: Output keystream bit $((l_s-w_2+j)mod{l}_s)$ as the jth bit of the secret key.

5.5. Comparison of Fault Based Key Recovery Attacks

We described two fault-based key recovery attacks on different variants of MORUS. The first attack uses permanent set to zero fault injection into the internal state of MORUS. The second attack uses transient set to zero fault injection into the internal state of MORUS. The results from these fault attacks are presented in

Table 2. Summary of Fault Attacks on MORUS.

	Key Size	Type of Fault	Number of Faults	Recovered Key Bits
MORUS-640	128	Permanent	128	64
MORUS-640	128	Permanent & Transient	256	128
MORUS-640	128	Transient	384	128
MORUS-1280-128	128	Permanent	256	128
MORUS-1280-128	128	Transient	384	128
MORUS-1280-256	256	Permanent	256	128
MORUS-1280-256	256	Permanent & Transient	512	256
MORUS-1280-256	256	Transient	768	256

.

The fault model for these stuck-at fault-based key recovery attacks requires fault injections at a specific time and location. This can be achieved using optical fault injection. The difference between the permanent fault and the transient fault is in the number of faults and the number of key bits recovered.

With permanent faults, the adversary is able to recover at least half the secret key. If the entire key is not recovered, then the remaining key bits may be obtained through exhaustive search. Alternatively, a larger number of faults (combination of permanent and transient faults) may reveal the entire key. The key recovery using permanent fault model or a combination of permanent and transient fault model requires fewer faults than that for transient fault model. For the transient fault, an adversary can recover the entire key; however, this requires up to three times as many faults compared to the permanent fault attacks.

The adversary needs to have access to the physical implementation of the algorithm to apply these fault attacks. Also note that both of these transient and permanent fault attacks described in this paper are based on the assumption that there is no associated data. These attacks are not feasible otherwise.

The fault model described here requires an adversary to use faults which set specific bits of the registers to zero, i.e., set to zero fault. These results are theoretical, and we did not perform any experiments since the results are straightforward given that the faults can be applied in the implementation of the algorithm. However, we note that the fault models for our proposed key recovery attacks have been shown to work in hardware [12], and also adopted in several other research papers [11,14].

6. Fault Based Forgery Attack on MORUS

This section discusses a fault-based forgery attack on MORUS. The goal of the attack is to modify the input message by flipping specific message bit(s) and have this modified message accepted as legitimate at the receiver side. The modification can be either in the associated data or in the plaintext. In order to achieve this, we require the production of the appropriate tag value for the modified message.

Fault based forgery attacks on the authenticated encryption ciphers CLOC and SILC were introduced by Roy et al. [15]. Later, in the CAESAR Google discussion forum it was pointed out by Iwata et al. [16] that any authenticated encryption scheme can be forged using faulty encryption queries. This requires an adversary to inject faults in the inputs submitted to the encryption oracle and then use the output of the encryption oracle with the faulty inputs to continue with the forgery. We describe here a similar fault injected forgery, however; we propose the injection of faults into the internal state instead of the inputs, and apply this fault injection based forgery to MORUS.

In the associated data processing and encryption phases of MORUS, the input associated data and the plaintext are loaded into the internal state of the cipher. Therefore, any changes in the input associated data or the plaintext will affect the internal state. An adversary can apply a forgery attack by injecting faults into the internal state of MORUS to reflect the changes made in either the associated data or in the plaintext. For the following discussion we use the term M to represent either the associated data or the plaintext.

Suppose the adversary wants to modify the ith bit of the message block $M^t$ as received by the receiver. Let $M^{\prime t}$ denote the modified message block, where the modification is a bit flip in the ith bit of the original message block $M^t$. We observe that the input message block $M^t$ is XOR-ed with the contents of state element $S_{1,1}^t$, $S_{2,2}^t$, $S_{3,3}^t$ and $S_{4,4}^t$. Thus XOR-ing $M^{\prime t}$ with the contents of the state element $S_{1,1}^t$, $S_{2,2}^t$, $S_{3,3}^t$ and $S_{4,4}^t$ will flip the ith bit of the respective state element.

To perform a forgery attack on the message $M^t$, the adversary can apply bit flipping faults to the ith bit of the state elements $S_{1,1}^t$, $S_{2,2}^t$, $S_{3,3}^t$ and $S_{4,4}^t$. This is equivalent to modifying the input message block from $M^t$ to $M^{\prime t}$ at the sender’s device, where the modification is a complementation of the ith bit of the original input message block $M^t$. Figure 4 illustrates the locations of the fault injections to achieve the fault-based forgery attack on MORUS.

Let ${\tau }^{\prime }$ denote the tag generated for the fault induced version of the state. The adversary can use this faulty tag ${\tau }^{\prime }$ to perform the forgery attack. Note that the fault was introduced in the internal state bits after the computation of the ciphertext block $C^t$, and so the fault does not affect the transmitted ciphertext. Therefore, an adversary needs to also modify the ith bit of the corresponding ciphertext block $C^t$ (by flipping the ith bit) in the case where $M^t$ is a plaintext block. Similarly an adversary needs to modify the ith bit of the corresponding associated data block $D^t$ in the case where $M^t$ is an associated data block. The adversary can simply intercept and change the transmitted message block $M^t$ to $M^{\prime t}$, and send it with the faulty tag ${\tau }^{\prime }$ as the output. The adversary does not need to apply any faults at the receiver’s side.

In the decryption and tag verification phase, the receiver will XOR the recovered message block with the state element $S_{1,1}^t$, $S_{2,2}^t$, $S_{3,3}^t$ and $S_{4,4}^t$ of MORUS. The modified ciphertext block $C^{\prime t}$, or the modified associated data block $D^{\prime t}$ ensures that the recovered message will be the same as $M^{\prime t}$. The recovered message $M^{\prime t}$ is then XOR-ed with the state elements $S_{1,1}^t$, $S_{2,2}^t$, $S_{3,3}^t$ and $S_{4,4}^t$, which complements the ith bit of the respective state elements. So the internal state contents in the receiver’s device are now the same as those after applying the bit-flipping faults at the sender’s device.

Once the message is processed, the finalization process at the receiver side generates the tag ${\tau }^{\prime \prime }$. Clearly, both of the tags are generated from the same state contents; thus, the tag ${\tau }^{\prime \prime }$ generated at the receiver is the same as the tag ${\tau }^{\prime }$ sent by the sender. Therefore using the faulty tag ${\tau }^{\prime }$ the modified message will be accepted as legitimate at the receiver.

Let $n_f$ denote the number of bits flipped in an input message block $M^t$. Then the total number of faults required for the forgery attack is equal to $4\times n_f$. This is because a single bit flip in the input affects four bits in the state of MORUS.

6.1. Attack Algorithm for Fault Based Forgery

The steps involved in the fault-based forgery attack on MORUS are outlined in Algorithm 6.

Algorithm 6 Algorithm for Fault Based Forgery Attack on MORUS.

1: Insert bit flipping faults at the ith bit of state element $S_{1,1}^t$, $S_{2,2}^t$, $S_{3,3}^t$ and $S_{4,4}^t$ of the sender device. 2: Continue the finalization process at the sender and observe the faulty tag ${\tau }^{\prime t}$. 3: Modify the $i\mathrm{th}$ bit of the associated data block $D^t$ to $D^{\prime t}$, if the goal is associated data modification. Alternatively, modify the ith bit of the ciphertext block $C^t$ to $C^{\prime t}$. 4: Send the modified associated data $D^{\prime t}$ or the modified ciphertext $C^{\prime t}$, with the faulty tag ${\tau }^{\prime }$.

6.2. Feasibility of Fault Based Forgery Attack on MORUS

The fault-based forgery attack applied in this paper requires precise application of bit-flipping faults. This model imposes a restrictive criteria on the adversary’s capability since it requires the injection of the bit-flipping faults in a precise location. Note that bit-flipping faults have been applied in practice [13]; however, the fault may affect more than a single bit. Therefore, our fault model does not prohibit the adversary from applying the bit-flipping faults, but application of these faults in precise location may not be achieved yet in practice. This paper demonstrates a vulnerability in the integrity component of MORUS if such a fault model can be applied in practice.

7. Conclusions

This paper examines the applicability of fault attacks on the authenticated encryption cipher MORUS. In particular, we described fault attacks with two different goals: one to breach the confidentiality component of MORUS and the other to breach the integrity component. This is a first attempt at analysing the security of MORUS with respect to fault attacks, and although these attacks are relatively direct applications of the fault models, it may be possible to augment this for more effective attacks. This is planned as future work.

We introduced a fault-based key recovery attack on MORUS-640-128 which can recover 64 bits of the secret key by introducing 128 bit permanent faults in the 640-bit internal state. Similarly, we introduced a fault attack for MORUS-1280, which can recover 128 bits of the secret key with 256 bits of permanent faults. This is the entire key for MORUS-1280, if the key size is 128-bit. We demonstrated that permanent faults can be also combined with transient faults to recover the entire secret key for all the variants of MORUS.

We analysed the injection of transient faults into the internal state of MORUS. Our analysis shows that the secret keys of MORUS-640-128 and MORUS-1280-256 can be recovered, with 384 and 768 bits of transient faults, respectively. Note that all of these fault-based key recovery attacks apply only when there is no associated data. These attacks are not feasible when there is associated data input.

We also introduced a fault-based forgery attack on MORUS. This is a simple and trivial attack which works by flipping specific bits of the message during transmission and introducing bit flipping faults in the corresponding bit(s) of state elements at the sender’s device. The adversary can use the faulty tag to have the modified message accepted as legitimate. This attack works because the message is directly XOR-ed into the state. This attack requires the introduction of four bits of faults in the MORUS state elements, for a single bit flip in the input message.

We demonstrated that physical attacks such as fault injections can be powerful against all variants of MORUS. The fault-based key recovery attack on MORUS works because the secret key of MORUS is XOR-ed with a particular component of the internal state after performing the last round of the initialization phase. This operation is performed to prevent a key recovery attack when the initial internal state is recovered. To provide security against the fault-based key recovery of MORUS, an additional state update step can be introduced after this operation and before generating keystream.

The fault attacks proposed in this paper do not require nonce-reuse. Thus, the designer restrictions on nonce-reuse do not prohibit these attacks. However, these are attacks on the implementation rather than the algorithm itself. Therefore, it is important to have appropriate physical protection for cryptographic devices to prevent these type of fault attacks.