Multiparty Delegated Quantum Computing
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement-Based Quantum Computing
2.2. Multiparty Delegated Quantum Computing
- Each client’s strategy consists of a set of local quantum operators such that for .
- The server’s strategy consists of a set of local quantum operators such that for .
- The oracle is a set of global quantum operators such that for .
2.2.1. Properties
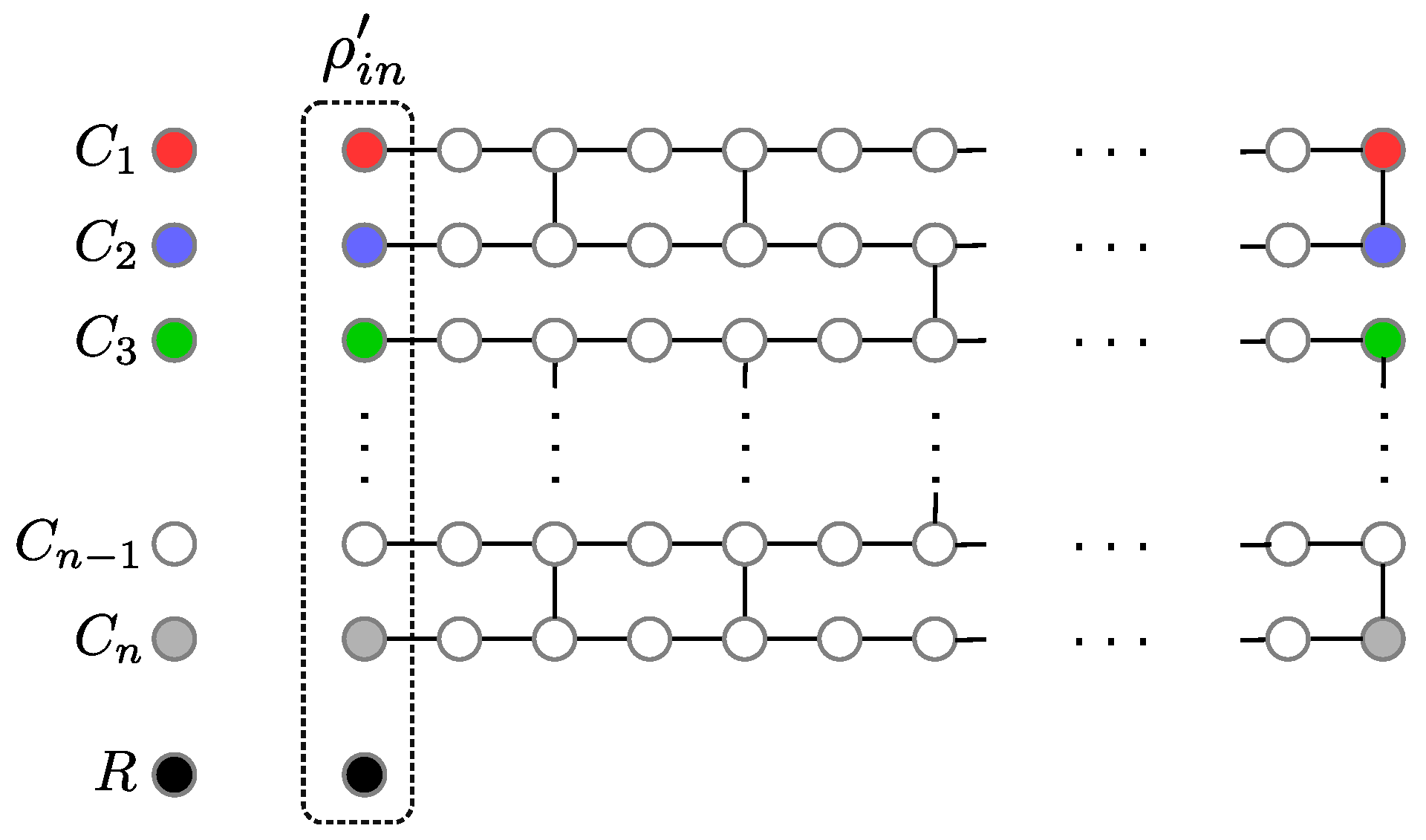
3. The Protocol
| Algorithm 1 State preparation for . |
| server stores states received from clients to distinct registers (); for if then break; if and then break; if , then CNOT on ; else CNOT on ; end; measure state in and get outcome ; end; if then CNOT on ; measure state in and get outcome ; else CNOT on ; measure state in and get outcome ; end; |
| Algorithm 2 (State preparation for ). |
| server stores states received from clients to distinct registers (); for CNOT on ; measure state in and get outcome ; end; |
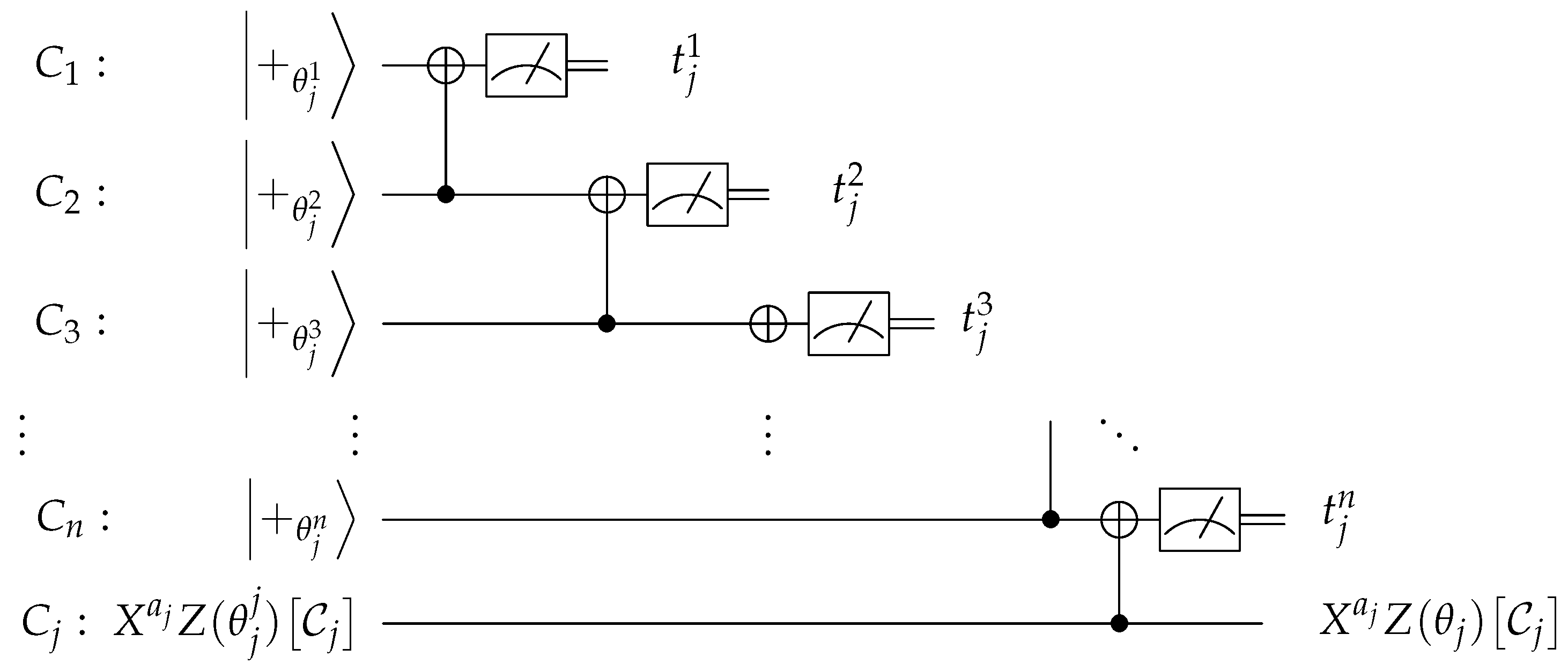
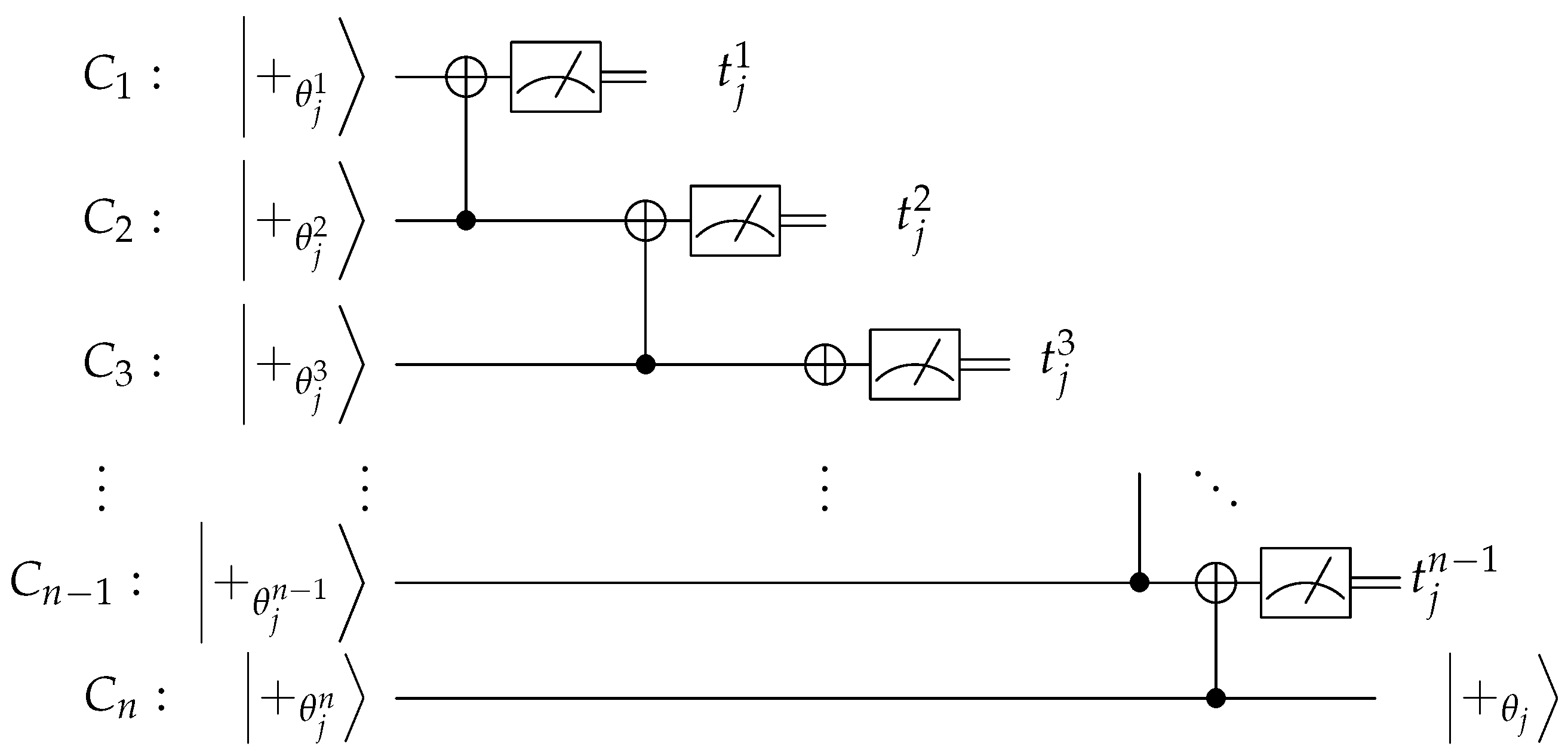
| Algorithm 3 (Enforcing honest behaviour for client ). |
|
4. Analysis of the Protocol
4.1. Correctness
| Algorithm 4 Multiparty quantum computing protocol. |
Preparation phase quantum input: For
non-output/non-input qubits: For
graph state: The server entangles the qubits to a brickwork state by applying ctrl-Z gates. Computation phase non-output qubits: For
output qubits: For , the server sends the “encrypted” quantum state to client . All participants jointly compute and and send it to client , who applies operation to retrieve the actual quantum output. |
4.2. Malicious Server
| Algorithm 5 Simulator for the server. |
non-output qubits: For
output qubits: For
|
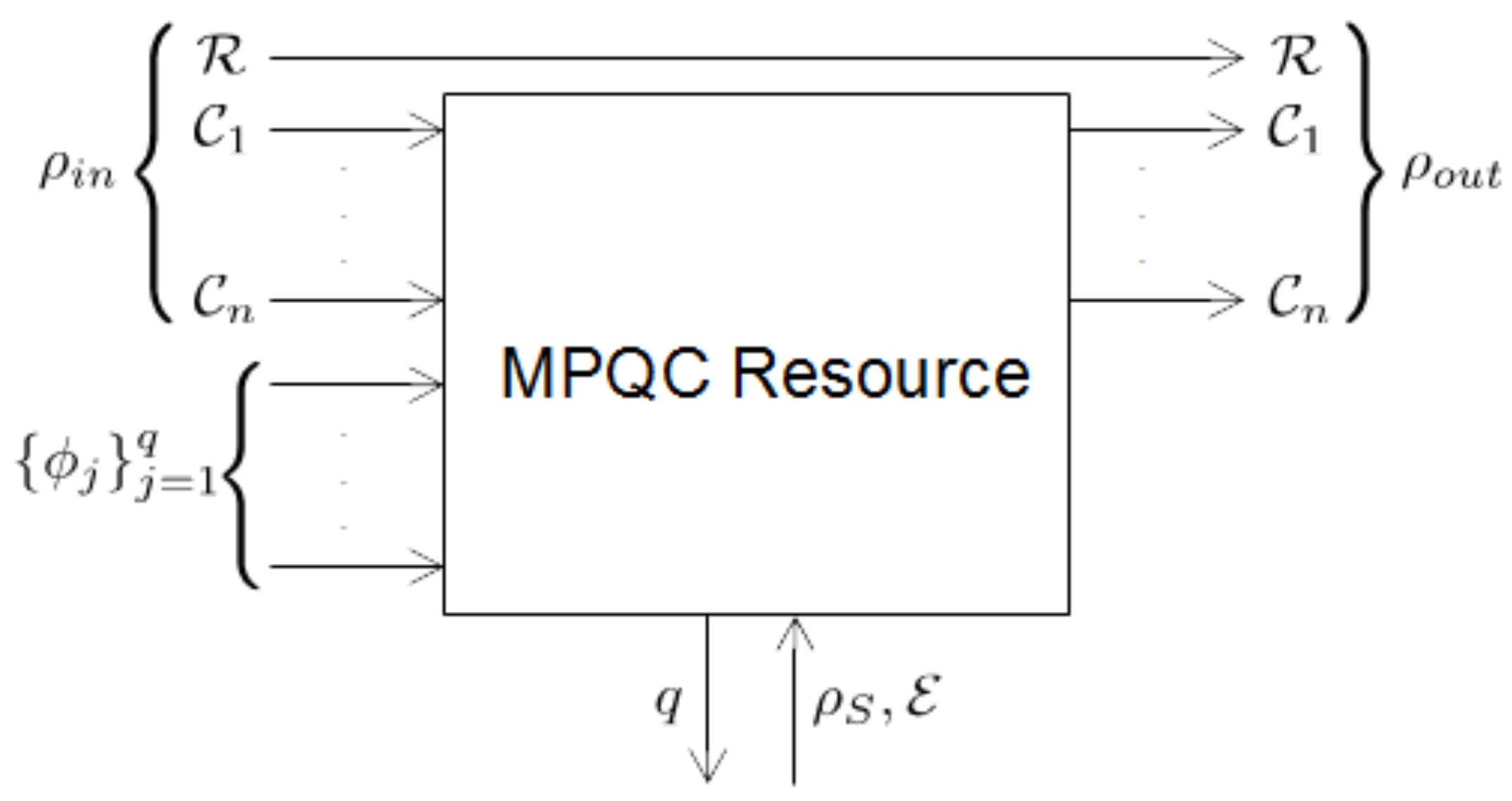
| Algorithm 6 MPQC resource. |
|
4.3. Malicious Clients
| Algorithm 7 Simulator for clients. |
|
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- For : .
- For : .
- For :
- For :
| Algorithm A1 Multiparty quantum computing. |
quantum input: For
non-output/non-input qubits: For
graph state: The server entangles the qubits to a brickwork state by applying ctrl-Z gates. Computation phase non-output qubits: For
All participants jointly compute and and send it to client , who applies operation to retrieve the actual quantum output. |
| Algorithm A2 Multiparty quantum computing (using EPR pairs). |
quantum input: For
non-output/non-input qubits: For
output qubits: For , the server prepares states. graph state: The server entangles the qubits to a brickwork state by applying ctrl-Z gates. Computation phase non-output qubits: For
All participants jointly compute and and send it to client , who applies operation to retrieve the actual quantum output. |
| Algorithm A3 Multiparty quantum computing (using EPR pairs and delaying teleportation). |
Preparation phase quantum input: For
non-output/non-input qubits: For
graph state: The server entangles the qubits to a brickwork state by applying ctrl-Z gates. Computation phase non-output qubits: For
All participants jointly compute and and send it to client , who applies operation to retrieve the actual quantum output. |
| Algorithm A4 Simulator for server. |
non-output qubits: For
output qubits: For
|
| Algorithm A5 MPQC resource. |
|
References
- Lo, H.-K.; Chau, H.F. Is quantum bit commitment really possible? Phys. Rev. Lett. 1997, 78, 3410–3413. [Google Scholar] [CrossRef]
- Mayers, D. Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 1997, 78, 3414–3417. [Google Scholar] [CrossRef]
- Lo, H.-K. Insecurity of quantum secure computations. Phys. Rev. A 1997, 56, 1154–1162. [Google Scholar] [CrossRef]
- Salvail, L.; Schaffner, C.; Sotakova, M. On the Power of Two-Party Quantum Cryptography. In Proceedings of the ASIACRYPT 2009, Tokyo, Japan, 6–10 December 2009; Volume 5912, pp. 70–87. [Google Scholar]
- Dupuis, F.; Nielsen, J.B.; Salvail, L. Secure two-party quantum evaluation of unitaries against specious adversaries. In Proceedings of the CRYPTO 2010, Santa Barbara, CA, USA, 15–19 August 2010; Volume 6223, pp. 685–706. [Google Scholar]
- Dupuis, F.; Nielsen, J.B.; Salvail, L. Actively Secure Two-Party Evaluation of any Quantum Operation. In Proceedings of the CRYPTO 2012, Santa Barbara, CA, USA, 19–23 August 2012; pp. 794–811. [Google Scholar]
- Ben-Or, M.; Crépeau, C.; Gottesman, D.; Hassidim, A.; Smith, A. Secure Multiparty Quantum Computation with (Only) a Strict Honest Majority. In Proceedings of the IEEE FOCS 2006, Berkeley, CA, USA, 21–24 October 2006; pp. 249–260. [Google Scholar]
- Raussendorf, R.; Briegel, H.J. A One-Way Quantum Computer. Phys. Rev. Lett. 2001, 86, 5188. [Google Scholar] [CrossRef] [PubMed]
- Leung, D.W. Quantum computation by measurements. Int. J. Quantum Inf. 2004, 2, 33–43. [Google Scholar] [CrossRef]
- Broadbent, A.; Fitzsimons, J.F.; Kashefi, E. Universal blind quantum computation. In Proceedings of the FOCS 2009, Atlanta, GA, USA, 25–27 October 2009; pp. 517–526. [Google Scholar]
- Fitzsimons, J.F.; Kashefi, E. Unconditionally Verifiable Blind Computation. arXiv 2012, arXiv:1203.5217. [Google Scholar]
- Kashefi, E.; Wallden, P. Garbled Quantum Computation. arXiv 2016, arXiv:1606.06931. [Google Scholar] [CrossRef]
- Danos, V.; Kashefi, E. Determinism in the one-way model. Phys. Rev. A 2006, 74, 052310. [Google Scholar] [CrossRef]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the FOCS 2001, Las Vegas, NV, USA, 14–17 October 2001; pp. 136–147. [Google Scholar]
- Ishai, Y.; Prabhakaran, M.; Sahai, A. Founding cryptography on oblivious transfer–efficiently. In Proceedings of the CRYPTO 2008, Santa Barbara, CA, USA, 17–21 August 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 572–591. [Google Scholar]
- Goldwasser, S.; Lindell, Y. Secure Computation without Agreement. In Distributed Computing (DISC 2002); Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2508. [Google Scholar]
- Unruh, D. Universally Composable Quantum Multiparty Computation. In Proceedings of the EUROCRYPT 2010, French Riviera, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6110, pp. 486–505. [Google Scholar]
- Maurer, U.; Renner, R. Abstract cryptography. In Innovations in Computer Science; Tsinghua University Press: Beijing, China, 2011. [Google Scholar]
- Kumaresan, R.; Patra, A.; Rangan, C.P. The round complexity of verifiable secret sharing: The statistical case. In Proceedings of the ASIACRYPT 2010, Singapore, 5–9 December 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6477, pp. 431–447. [Google Scholar]
- Laud, P.; Pankova, A. Verifiable Computation in Multiparty Protocols with Honest Majority. In Proceedings of the Provable Security (ProvSec 2014), Hong Kong, China, 9–10 October 2014; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2014; Volume 8782. [Google Scholar]
- Dunjko, V.; Kashefi, E.; Leverrier, A. Universal Blind Quantum Computing with Weak Coherent Pulses. Phys. Rev. Lett. 2012, 108, 200502. [Google Scholar] [CrossRef] [PubMed]
- Dunjko, V.; Fitzsimons, J.F.; Portmann, C.; Renner, R. Composable security of delegated quantum computation. In Proceedings of the ASIACRYPT 2014, Kaoshiung, Taiwan, 7–11 December 2014; pp. 406–425. [Google Scholar]
- Hirt, M.; Nielsen, J.B. Upper Bounds on the Communication Complexity of Optimally Resilient Cryptographic Multiparty Computation. In Proceedings of the ASIACRYPT 2005, Chennai, India, 4–8 December 2005; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2005; Volume 3788. [Google Scholar]
- Morimae, T.; Fujii, K. Blind quantum computation protocol in which Alice only makes measurements. Phys. Rev. A 2013, 87, 050301. [Google Scholar] [CrossRef]
- Broadbent, A.; Jeffery, S. Quantum homomorphic encryption for circuits of low T-gate complexity. In Proceedings of the CRYPTO 2015, Santa Barbara, CA, USA, 16–20 August 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 609–629. [Google Scholar]
- Dulek, Y.; Schaffner, C.; Speelman, F. Quantum homomorphic encryption for polynomial-sized circuits. arXiv 2016, arXiv:1603.09717v1. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashefi, E.; Pappa, A. Multiparty Delegated Quantum Computing. Cryptography 2017, 1, 12. https://doi.org/10.3390/cryptography1020012
Kashefi E, Pappa A. Multiparty Delegated Quantum Computing. Cryptography. 2017; 1(2):12. https://doi.org/10.3390/cryptography1020012
Chicago/Turabian StyleKashefi, Elham, and Anna Pappa. 2017. "Multiparty Delegated Quantum Computing" Cryptography 1, no. 2: 12. https://doi.org/10.3390/cryptography1020012
APA StyleKashefi, E., & Pappa, A. (2017). Multiparty Delegated Quantum Computing. Cryptography, 1(2), 12. https://doi.org/10.3390/cryptography1020012



