Abstract
Many e-voting techniques have been proposed but not widely used in reality. One of the problems associated with most existing e-voting techniques is the lack of transparency, leading to a failure to deliver voter assurance. In this work, we propose a transparent, auditable, stepwise verifiable, viewable, and mutual restraining e-voting protocol that exploits the existing multi-party political dynamics such as in the US. The new e-voting protocol consists of three original technical contributions—universal verifiable voting vector, forward and backward mutual lock voting, and in-process check and enforcement—that, along with a public real time bulletin board, resolves the apparent conflicts in voting such as anonymity vs. accountability and privacy vs. verifiability. Especially, the trust is split equally among tallying authorities who have conflicting interests and will technically restrain each other. The voting and tallying processes are transparent/viewable to anyone, which allow any voter to visually verify that his vote is indeed counted and also allow any third party to audit the tally, thus, enabling open and fair election. Depending on the voting environment, our interactive protocol is suitable for small groups where interaction is encouraged, while the non-interactive protocol allows large groups to vote without interaction.
1. Introduction
Voting is the pillar of modern democracies. Traditional voting, however, suffers from both low efficiency and unintentional errors. The event surrounding the 2000 US presidential election witnessed the shortcomings of punch-cards and other antiquated voting systems. The Help America Vote Act [1] and the creation of the Election Assistance Commission (EAC) [2] highlighted the determination of the US to deploy more modern voting systems. A survey sponsored by EAC shows that 17.5% of votes in the 2008 US presidential election were cast as absentee ballots [3]. This demonstrates a demand for less centralized voting procedures. One potential solution is to allow voters to cast ballots on Internet-enabled mobile devices [4].
Online voting (electronic voting) has been an active research topic with many advantages over traditional voting, but presents some unique challenges. For example, if a discrepancy is found in the tally, votes need to be recounted and the source of the discrepancy needs to be identified. The recounting and investigating should nevertheless preserve votes’ anonymity and voters’ privacy. Other voting requirements, such as verifiability and receipt-freeness, make the problem even more challenging due to their inherently contradicting nature [5,6].
Several online voting solutions [7,8,9,10,11] have been proposed. Some suggest keeping non-electronic parallels of electronic votes, or saving copies of votes in portable storage devices. They either fail to identify sources of discrepancy or are susceptible to vote selling and voter coercion. Most solutions [6,7,12,13,14,15,16] are based on cryptographic techniques, such as secret sharing, mix-nets, and blind signature. These solutions are often opaque: Except casting their votes, voters do not directly participate in collecting and tallying votes, and the voting results are typically acquired through decryption by third parties only, such as talliers. This raises concerns over the trustworthiness and transparency of the entire voting process. In addition, these solutions sometimes entrust the fairness of the voting process onto the impartiality of authorities. Voting under multiple conflicts-of-interest parties is not addressed by these solutions.
Furthermore, examination of current voting systems including online voting techniques shows a gap between casting secret ballots and tallying/verifying individual votes. This gap is caused either by the disconnection between the vote-casting process and the vote-tallying process (e.g., dropping the ballot into a ballot box), or by the opaque transition (e.g., due to encryption) from the vote-casting to the vote-tallying, thus damaging voter assurance associated with an open question: “Will my vote count?” [17].
In terms of opaqueness, the term was raised as early as in a 2004 paper [18]: “Voting machines are black boxes whose workings are opaque to the public.” Later in 2008, the authors in [12] states “some people believe that any use of cryptography in a voting system makes the system too opaque for the general public to accept.” Furthermore, authors in [19] states “once the vote is cast the voter loses sight of it.” Finally, the authors in [20] states that the mixing part in Helios (and Zeus) is a black box to voters. Thus, in this paper, by opaqueness we mean that the use of complex cryptographic techniques involving encryption, mix-net, zero-knowledge, etc. causes some part of vote-casting, tallying and/or verification not viewable to the general public even though the background cryptographic techniques are mathematically sound and can fundamentally guarantee the integrity of the voting process and the tallying result. On the other hand, by transparency, we mean that the voting process from vote-casting, tallying, and verification is viewable to the general public and the integrity of the voting process and tally are visually verifiable by any one, besides technical guarantee of the integrity of the tallying result.
In this work, we propose a transparent, auditable, and step-wise verifiable voting protocol that exploits conflicts of interest in multiple tallying authorities, such as the two-party political system in the US. It consists of a few novel techniques—universal verifiable voting vector, forward and backward mutual lock voting, and proven in-process check and enforcement—that, in combination, resolves the apparent conflicts such as anonymity vs. accountability and privacy vs. verifiability.
Our main contributions are as follows:
1. Light-weight ballot generation and tallying. The new e-voting protocol needs only (modular) addition and subtraction in ballot generation and vote tallying, rather than encryption/decryption or modular exponentiations. Thus, the newly proposed protocol is efficient.
2. Seamless transition from ballots to plain votes. In our protocol, individual ballots can be aggregated one by one and the final aggregation reveals all individual votes (in their plain/clear format). The aggregation is simply modular addition and can be performed by any one (with modular addition knowledge and skills) without involvement of a third-party entity. The aggregation has the all-or-nothing effect in the sense that all partial sums reveal no information about individual votes but the final (total) sum exposes all individual votes. Thus, the newly proposed protocol delivers fairness in the voting process.
3. Viewable/visual tallying and verification. The cast ballots, sum(s) of ballots, votes, and sum(s) of votes (for each candidate) are all displayed on a public bulletin board. A voter or any one can view them, verify them visually, and even conduct summations of ballots (and as well as votes) himself. Thus, the newly proposed protocol delivers both individual verification and universal verification.
4. Transparency of the entire voting process. Voters can view and verify their ballots, plain votes, and transition from ballots to votes and even perform self-tallying [21,22]. There is no gap or black-box [20] which is related to homomorphic encryption or mix-net in vote-casting, tallying and verification processes. Thus, in the newly proposed protocol, the voting process is straightforward and it delivers visible transparency.
5. Voter assurance. The most groundbreaking feature of our voting protocol, different from all existing ones, is the separation and guarantee of two distinct voter assurances: (1) vote-casting assurance on secret ballots—any voter is assured that the vote-casting is indeed completed (i.e., the secret ballot is confirmatively cast and viewably aggregated), thanks to the openness of secret ballots and incremental aggregation, and (2) vote-tallying assurance—any voter is assured that his vote is visibly counted in the final tally, thanks to the seamless transition from secret ballots having no information to public votes having complete (but anonymous) information offered by the simplified ()-secret sharing scheme. In addition, step-wise individual verification and universal verification allow the public to verify the accuracy of the count, and political parties to catch fraudulent votes. Thus, the newly proposed protocol delivers broader voter assurance.
Real time check and verification of any cast secret ballots and their incremental aggregation, along with visibility and transparency, provide strong integrity and auditability of the voting process and final tally. In particular, we relaxed the trust assumption a bit in our protocol. Instead of assuming that tallying authorities who conduct tally are trustworthy, (Some protocols realize trustworthiness (tally integrity) by using commitments and zero-knowledge proof to prevent a tallying authority from mis-tallying and some use threshold cryptography to guarantee the trustworthiness of tallying results (and vote secrecy) as long as t out of n tallying authorities behave honestly) the new protocol, like the split trust in the split paper ballot voting [23], splits the trust equally among tallying authorities. As long as one tallying authority behaves honestly, misbehaviors from one or all other tallying authorities will be detected. In addition, as we will analyze later, any attacks, regardless of from inside such as collusion among voters or between voters and one tallying authority or from outside such as external intrusion, which lead to any invalid votes, can be detected via the tallied voting vector. All these properties are achieved while still retaining what is perhaps the core value of democratic elections—the secrecy of any voter’s vote. Thus, in order not to impress readers that we need trusted central authorities, we chose to use a relatively neutral term called collectors in the rest of the paper. We assume collectors will not collude since they represent parties with conflicting interests.
We understand the scalability concern with very large number of voters, but this concern can be addressed by incorporating a hierarchical voting structure. In reality, most voting systems [24] present a hierarchical structure such as a tree where voting is first carried out in each precinct (for example, towns or counties) with relatively small number of voters and then vote totals from each precinct are transmitted to an upper level central location for consolidation. We will have a more detailed discussion about this later.
The rest of the paper is organized as follows. Section 2 gives an overview of the protocol including assumptions and attack models. Building blocks are also introduced here. The technical details of the voting protocol are presented in Section 3, followed by security and property analysis in Section 4. Complexity analysis and simulation result are given in Section 5. Section 6 is the related work and protocol comparison. Section 7 discusses scalability of our protocol. Section 8 concludes our paper and lays out the future work.
This paper is an extension of our INFOCOM’14 work [25]. Mainly, we add the interactive protocol design in Section 3.1, modify Sub-protocol 1 which suffered a possible brute-force attack originally in [25] in Section 3.2.1, along with the rigorous proof of the revised Sub-protocol 1 in Section 4.1, and provide an example of bulletin board dynamics in Section 3.4. The attack model covers more diverse scenarios as mentioned in Section 2.1, with corresponding security analysis later in Section 4. Additional experiments were conducted and the results are presented in Section 5. The related work in Section 6 is more comprehensive. Section 7 is new for further discussion.
Notations used are summarized in Table 1.

Table 1.
Notations.
2. Mutual Restraining Voting Overview
2.1. Assumptions and Attack Models
Suppose there are N () voters, (), and two tallying parties, or collectors, and (The protocol can be extended to more than two with no essential difficulties). The number of candidates in the election is M and each voter votes one out of M candidates. and have conflicting interests: Neither will share information (i.e., the respective shares they have about a voter’s vote) with the other. The assumption of multiple conflict-of-interest collectors was previously proposed by Moran and Naor [23], and applies to real world scenarios like the two-party political system in the US.
For the interactive voting protocol presented in Section 3.1, secure uncast channel is needed between voters and between a voter and each collector. However, for the non-interactive protocol in Section 3.3, secure uncast channel between a voter and each collector is needed only. Such a secure channel can be easily provided with a public key cryptosystem. Our protocols utilize two cryptographic primitives (1) simplified ()-secret sharing and (2) tailored secure two-party multiplication (STPM) as building blocks. We also use DLP under its hardness assumption. Simplified ()-secret sharing is used in vote-casting and STPM and DLP are used by two collectors to check the validity of the vote cast by the voter.
In terms of attack model, we assume that majority of voters are benign since the colluding majority can easily control the election result otherwise. The malicious voters can send inconsistent information to different parties or deliberately deviate from the protocol, e.g., trying to vote for more than one candidate. We will show that the protocol can detect such misbehaviors and identify them without compromising honest voters’ privacy.
One fundamental assumption of the protocol is that the collectors are of conflict-of-interest and will not collude. Here “collusion” specifically means that the collectors exchange the shares of the voter’s vote directly, thus, discovering the voter’s vote (each of the two collectors has roughly half amount of shares respectively). However, they DO collaborate to check and enforce the voter to follow the protocol using STPM without compromising voter secrecy. Moreover, the collectors mutually check and restrain each other, and thus, are assumed to follow the protocol. However, unlike many protocols in which tallying authorities perform vote-tallying and certain trust is assumed on tallying authorities for the integrity of the tallying result (In some protocols, trustworthiness of tallying authorities may be achieved via cryptographic techniques such as commitment/zero knowledge proof), we do not assume trustworthiness on the collectors for such integrity in the new protocol. The primary role of the collectors in the protocol is to check the validity of the voter’s vote, i.e., the vote is for one and only one candidate. It is not needed for the collectors to provide/guarantee vote secrecy or the integrity of tallying result. Tallying and verification can be conducted by voters themselves. In fact, if we assume voters are honest, they can execute the protocol themselves (that is why our interactive voting protocol works) without the need/involvement of collectors. If one collector is honest, the misbehaviors of other collectors will be detected. Furthermore, even though all collectors misbehave (independently), such misbehaviors will be easily detected with overwhelming probability because such behaviors will mostly result in an invalid voting vector.
We consider two types of adversaries: passive and active adversaries. The attacks can be either misbehavior from voters, collusion among voters or voters and one collector, or external attack. In this paper, we consider the attacks targeting at the voting protocol only, rather than those targeting at general computers or network systems such a denial-of-service (DoS), DDoS, jamming, and Sybil attacks. The purposes of the attacks are either to infer a voter’s vote (i.e., passive adversaries) or to change the votes which favor a particular candidate or simply invalidate the votes (i.e., active adversaries). As shown in Section 4, all these attacks can either be prevented or detected.
2.2. Cryptographic Primitives
2.2.1. Simplified ()-Secret Sharing ((-SS)
A secret s is split into n shares (), , over group where . For a group of n members, each receives one share. All n members need to pool their shares together to recover s [26]. The scheme is additively homomorphic [27]: The sum of two shares (corresponding to s and , respectively) is a share of the secret .
Theorem 1.
The simplified ()-SS scheme is unconditionally indistinguishable. That is, collusion of even up to participants cannot gain any bit of information on the shares of the rest.The proof is given in [27].
2.2.2. Tailored Secure Two-Party Multiplication (STPM)
Tailored STPM (Secure two-party multiplication (STPM) in the original paper [28] does not reveal the final product to both parties, which is different from the typical STPM where both parties know the final product. In order not to confuse readers, we rename it to tailored STPM) is proposed in [28]. Initially, each party, (), holds a private input . At the end of the protocol, will have a private output , such that . The protocol works as follows:
- (1)
- chooses a private key d and a public key e for an additively homomorphic public-key encryption scheme, with encryption and decryption functions being E and D, respectively.
- (2)
- sends to .
- (3)
- selects a random number , computes , and sends the result back to .
- (4)
- decrypts the received value into , resulting in .
2.3. Web Based Bulletin Board
A web based bulletin board allows anyone to monitor the dynamic vote casting and tallying in real time. Consequently, the casting and tallying processes are totally visible (i.e., transparent) to all voters. The bulletin board will dynamically display (1) on-going vote-casting; (2) incremental aggregation of the secret ballots; and (3) incremental vote counting/tallying. Note that all the incremental aggregations of secret ballots, except the final one, reveal no information of any individual vote or any candidate’s count. Only at the time when the final aggregation is completed are all individual votes suddenly visible in their entirety, but in an anonymous manner. It is this sudden transition that precludes any preannouncement of partial voting results. Moreover, this transition creates a seamless connection from vote-casting and ballot confirmation to vote-tallying and verification so that both voter privacy and voter assurance can be achieved simultaneously. This is a unique feature of our voting protocol, comparing to all existing ones.
2.4. Technical Components (TPs)
The protocol includes three important technical components.
TP1: Universal verifiable voting vector. For N voters and M candidates, a voting vector for is a binary vector of bits. The vector can be visualized as a table with N rows and M columns. Each candidate corresponds to one column. Via a robust location anonymization scheme described in Section 3.5, each voter secretly picks a unique row. A voter will put 1 in the entry at the row and column corresponding to a candidate votes for (let the position be ), and put 0 in all other entries. During the tally, all voting vectors will be aggregated. From the tallied voting vector (denoted as ), the votes for candidates can be incrementally tallied. Any voter can check his vote and also visually verify that his vote is indeed counted into the final tally. Furthermore, anyone can verify the vote total for each candidate.
TP2: Forward and backward mutual lock voting. From ’s voting vector (with a single entry of 1 and the rest of 0), a forward value (where ) and a backward value (where ) can be derived. Importantly, , regardless which candidate votes for. During the vote-casting, uses simplified ()-SS to cast his vote using both and respectively. and jointly ensure the correctness of the vote-casting process, and enforce to cast one and only one vote; any deviation, such as multiple voting, will be detected.
TP3: In-process check and enforcement. During the vote-casting process, collectors will jointly perform two cryptographic checks on the voting values from each voter. The first check uses tailored STPM to prevent a voter from wrongly generating his share in the vote-casting stage. The second check prevents a voter from publishing an incorrect secret ballot when collectors collect it from him. The secret ballot is the modular addition of a voter’s own share and the share summations that the voter receives from other voters in the interactive protocol or from collectors in the non-interactive protocol.
We argue that there is no incentive for a voter to give up his own voting right and disrupt others. However, if a voter indeed puts the single 1 in another voter’s location, the misbehaving voter’s voting location in and will be 0, leading to invalid and . If this happens, and can jointly find this location and then, along with the information collected during location anonymization, identify the misbehaving person.
To prevent any collector from having all shares of , the protocol requires that have only half of s shares and have the other half. Depending on whether the voting protocol is interactive or non-interactive, the arrangement of which collector getting exactly which shares is slight different as shown in Section 3.1 and Section 3.3.
2.5. High-Level Description of the E-Voting Protocol
Let be a voting vector. Each is a bit vector, 1 bit per candidate. To cast a ballot, a voter obtains a secret and unique index , which only knows. To vote for the candidate , sets bit of , and clears the other bits.
- Voter registration. This is independent of the voting protocol. Each registered voter obtains a secret index using a Location Anonymity Scheme (LAS) described in Section 3.5.
- Voting. The voter votes for the candidate as follows:
- (a)
- Set and all other bits in and the other , , to 0. Call this set bit ; it is simply the number of the bit when is seen as a bit vector. See TP1 in Section 2.4.
- (b)
- Compute and . This converts the bit vector to integers. Note , which is a constant. See TP2 in Section 2.4.
- (c)
- Think of shares of all voters’ ballots forming an matrix (as shown in Table 2). Row i represents the vote and Column i represents the ballot . computes and casts his ballot as follows:
 Table 2. The collectors generate all shares for each voter, with each collector generating half of shares. is s vote. () is generated by , and () is by . is the sum of all shares () in Row i generated by (for ), and is the sum of all shares () in Row i by (for ). . is the sum of all shares () in Column i generated by , and is the sum of all shares () in Column i by .
Table 2. The collectors generate all shares for each voter, with each collector generating half of shares. is s vote. () is generated by , and () is by . is the sum of all shares () in Row i generated by (for ), and is the sum of all shares () in Row i by (for ). . is the sum of all shares () in Column i generated by , and is the sum of all shares () in Column i by .- i.
- In the non-interactive protocol, and generate (about) shares each for . They send the sum of the shares, and respectively, to . In the interactive protocol, himself generates these shares. then computes his own share as , which corresponds to all elements on the main diagonal of the matrix.
- ii.
- In the non-interactive protocol, sends voter the sum of the shares generated for the first half of the voters (the “lower half”). Similarly, sends voter the sum of the shares generated for the second half of the voters (the “upper half”). In the interactive protocol, receives them from other voters. Then computes and publishes his ballot .
- (d)
- The previous step (c) is repeated, but with instead of . The share retains from this is and the ballot from this is called and is also public.
- (e)
- Simultaneously with the previous step, the voter also publishes his commitments , where g is the base for the discrete logarithm problem. Two authorities jointly verify the validity of each cast ballot. See TP3 in Section 2.4.
- Tally and verification. The authorities (in fact any one can) sum all the ballots to get (and the corresponding ). P and are public too. and are in a binary form of P and , respectively. and are bit-wise identical in reverse directions. Any voter (authority, or a third party) can verify individual ballots, tallied voting vectors and , individual plain votes exposed in and , sum of each candidate’s votes, and final tally.
3. Mutual Restraining Voting Protocol
In this section, we first elaborate on the protocol in two scenarios: interactive protocol and non-interactive protocol, together with two sub-protocols for in-process voting check and enforcement. An example of a bulletin board is given next. In the end, we discuss the design of our location anonymization scheme.
3.1. Interactive Voting Protocol
Stage 1: Registration (and initialization). The following computations are carried out on a cyclic group , on which the Discrete Logarithmic Problem (DLP) is intractable. , in which is a prime larger than and is a prime larger than .
All voters have to register and be authenticated first before entering the voting system. Typical authentication schemes, such as public key authentication, can be used. Once authenticated, voter executes LAS (in Section 3.5) collaboratively with other voters to obtain a unique and secret location . Then generates his voting vector of the length bits and arranges the vector into N rows (corresponding to N voters) and M columns (corresponding to M candidates); fills a 1 in his row (i.e., the th row) and the column for the candidate he votes, and 0 in all other entries. Consequently, the aggregation of all individual voting vectors will create a tallied vector allowing universal verifiability (TP1). This arrangement of vector can support voting scenarios including “yes-no” voting for one candidate and 1-out-of-M voting for M candidates with abstaining or without.
Stage 2: Vote-casting. From the voting vector (with a singleton 1 and all other entries 0), derives two decimal numbers and . is the decimal number corresponding to the binary string represented by , while is the decimal number corresponding to in reverse.
In other words, if sets the th bit of to 1, we have and , thus . and are said to be mutually restrained (TP2). This feature will lead to an effective enforcement mechanism that enforces the single-voting rule with privacy guarantee: The vote given by a voter will not be disclosed as long as the voter casts one and only one vote.
Next, shares and with other voters using ()-SS. Note that the sharing process of and is independent. Assume that a secure communication channel exists between any two voters and between any voter and any collector. The following illustrates of the sharing of :
- randomly selects shares (, ) and distributes them to the other voters with getting . When i is odd, sends to if l is odd and otherwise to ; when i is even, sends to if l is even and otherwise to . The objective is to prevent a single collector from obtaining enough information to infer a voter’s vote. then computes his own share , and publishes the commitment .Let the sum of shares that receives from be . ’s own share can also be denoted as: .
- Upon receiving shares from other voters, computes the secret ballot, , which is the sum of the received shares and his own share , and then broadcasts .Two collectors also have these shares, with each having a subset. Let the sum of the subset of shares held by the collector be . The secret ballot can also be denoted as: .
The sharing of is the same as above, and is also published during this process. In addition, publishes . These commitments, , and , are used by the collectors to enforce that a voter generates and casts his vote by distributing authentic shares and publishing an authentic secret ballot (i.e., the two sub-protocols described in Section 3.2).
Stage 3: Collection/Tally. Collectors (and voters if they want to) collect secret ballots () from all voters and obtain . P is decoded into a tallied binary voting vector of length L. The same is done for () to obtain , and consequently . If voters have followed the protocol, these two vectors will be reverse to each other by their initialization in Stage 1.
It might be possible that some voters do not cast their votes, purposely or not, which can prevent or from being computed. If ’s vote does not appear on the bulletin board after the close of voting, all shares sent to and received from other voters have to be canceled out from P. Since and , we have:
Without casting his secret ballot, we simply deduct () from P. Similar deduction also applies to .
Stage 4: Verification. Anyone can verify whether is a reverse of and whether each voter has cast one and only one vote. can verify the entry (corresponding to the candidate that votes for) has been correctly set to 1 and the entries for other candidates are 0. Furthermore, the tallied votes for all candidates can be computed and verified via and . In summary, both individual and universal verification are naturally supported by this protocol.
3.2. Two Sub-Protocols
A voter may misbehave in different ways. Examples include: (1) multiple voting; (2) disturbing others’ voting; and (3) disturbing the total tally. All examples of misbehavior are equivalent to an offender inserting multiple 1s in the voting vector. The following two sub-protocols, which are collectively known as in-process check and enforcement (TP3), ensure that each voter should put a single 1 in his voting vector, i.e., vote once and only once.
3.2.1. Revised Sub-Protocol 1
Sub-protocol 1 in [25] suffers from a possible brute-force attack, so Step 3 here has been redesigned accordingly to avoid such an attack.
(1) Recall that in Stage 2, sends shares of his secret vote to the other voters as well as the two collectors; each of the two collectors, and , has a subset of the shares denoted as and respectively. Similarly for , gets .
(2) Since has published and , can compute and . In addition, computes . Similarly, computes , , and .
(3) and cooperatively compute . A straightforward application of Diffie-Hellman key agreement [29] to obtain and will not work. (If exchanges his and with ’s and , since and are published by , and each can obtain and which correspond to and . Because there are only L possibilities of each voter’s vote, and each can simply try L values to find out the vote . This violates both vote anonymity (the vote is known) and voter privacy (the location is known)) Hence, tailored STPM is used to compute without disclosing and as follows:
- Execute tailored STPM, and obtain and respectively such that .
- Execute tailored STPM, and obtain and respectively such that . (Exchanging and or and between and will not work. (If and exchange and for an example, can obtain since he has and . With being public, and , can get by trying out L values and consequently find out the vote . Likewise, can also find out .)
- computes , computes . Obviously . ( and cannot exchange and directly. Doing so will result in a brute-force attack which is able to obtain the voter’s vote, as described in Section 4.1.)
(4) computes a combined product and similarly, computes a combined product and then they exchange and .
(5) Using ′s commitment and , each collector obtain . The collectors can verify that the product equals . If not, must have shared and/or incorrectly.
3.2.2. Sub-Protocol 2
While the revised Sub-protocol 1 ensures that should generate and all shares properly, Sub-protocol 2 enforces that should faithfully publish the secret ballots, and .
(1) Recall that in the sharing of , receives shares from other voters, and these shares are also received by collectors. Each of the collectors, and , receives a subset of these shares, so trust is split between two collectors. The sum of the subset of shares held by the collector is . will publish . Similarly for , will publish .
(2) From the published and , the collectors compute and . Since and are published and verified in Sub-protocol 1, collectors will verify that and . If either of these fails, must have published the wrong secret ballots and/or .
3.3. Non-Interactive Voting Protocol
The protocol presented in Section 3.1 is suitable for voting scenarios such as small group election where voters are encouraged to interact with each other. However, it is often the case that an election involves a large group of people where the interaction is impossible to be realistic. In this scenario, we allow collectors to carry the duties of creating voters’ shares. While this eliminates the interaction between voters, the properties of our voting protocol remain held as we will discuss in the next section.
In the interactive voting, a voter depends on other voters’ shares in order to cast his ballot. However, it is not practical to require all voters to interact with each other during vote-casting for a large group of voters. Fortunately, our ()-SS based voting protocol can be designed to allow voters to vote non-interactively. Table 2 illustrates how the two collectors generate respective shares for voters. In this non-interactive vote-casting, two collectors generate shares for every voter, and interact with a voter for vote-casting whenever the voter logs into the system to vote. Compared to the interactive protocol, only Stage 2 is different, while the rest of the stages are the same. Steps in this new Stage 2 are given below.
- The two collectors work together to generate all shares for each voter in advance as shown in Table 2, with () by and () by . is derived by himself. Specifically, for the voters to , generates their first shares (up-left of the matrix) and generates their last shares (up-right of the matrix). For the voters to , generates their last shares (lower-right of the matrix) and generates their first shares (lower-left of the matrix). Figure 1 (left) illustrates a case of four voters.
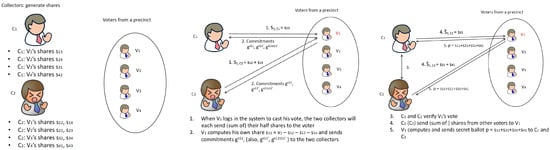 Figure 1. Collectors interact with voters to avoid voters’ interaction among themselves: left—generate shares for voters; middle—interact with a casting voter; right—interact with the casting voter.
Figure 1. Collectors interact with voters to avoid voters’ interaction among themselves: left—generate shares for voters; middle—interact with a casting voter; right—interact with the casting voter. - Whenever a voter logs into the system to cast his vote, the two collectors will each send their half of shares (in fact, the sum of these shares, denoted as in Table 2, where or 2) to this voter. Specifically, sends (sum of shares in one half of the ith row) to the voter, and sends (sum of shares in the other half of the ith row) to the voter. The voter will compute his own share as , and send the two collectors his commitments (i.e., , , ). Figure 1 (middle) shows the communication between collectors and voters. Under the assumption that the two collectors have conflicting interests, neither of them can derive the voter’s vote from ’s commitment.
- The two collectors verify a voter’s vote using Sub-protocol 1 and if passed, send the shares from the other voters (one from each voter) to this voter. Specifically, sends (sum of shares in one half of the ith column as shown in Table 2) to the voter, and similarly sends (sum of shares in the other half of the ith column). The voter sums the shares from the two collectors and his own share, and then sends the secret ballot of to the two collectors, as shown in Figure 1 (right) as an example. (Optionally, the voter can send to only one of the collectors to prevent the collector initiated voter coercion.) The two collectors can verify the voter’s ballot using Sub-protocol 2.
It is clear that although the two collectors generate shares for a voter, neither of them can obtain the voter’s own share or the voter’s vote , unless two collectors collude and exchange the shares they generated. As proven by Theorem 1, any k voters, as long as , can not obtain the share (thus, the vote) of any other voters in an unconditionally secure manner. Again, as in the interactive protocol, it may be possible that some voters do not cast their votes, preventing from being computed. The solution discussed in Stage 3 of Section 3.1 still applies.
3.4. One Example of Web Based Bulletin Board
As discussed earlier, our web based bulletin board displays the on-going vote casting and tallying processes. The incremental aggregation of secret ballots does not reveal information about any individual vote. Only when the final aggregation is completed, all individual votes in the voting vector are suddenly visible in their entirety to the public, but in an anonymous manner. It is this sudden transition that precludes preannouncement of any partial voting results.
Table 3 gives an example of 4 voters with their corresponding shares and secret ballot in a case of 2 candidates. Figure 2 illustrates the aggregation and tallying on the bulletin board. It is obvious that the incremental aggregation does not disclose any information until the last secret ballot, ’s 30, is counted in.

Table 3.
A voting example involving 4 voters and 2 candidates (R and B).
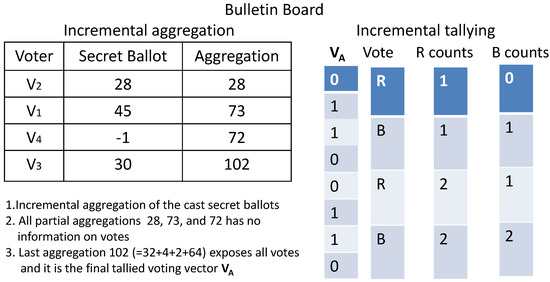
Figure 2.
Real Time Bulletin Board.
3.5. Design of a Robust and Efficient LAS
Inspired by the work in [27], we propose a new location anonymization scheme (LAS) that is robust and efficient. Our new scheme solves the following problem with the previous scheme: If a member misbehaves in next rounds by selecting multiple locations or a location that is already occupied by another member, the location selection in [27] may never finish. Our new LAS is based on the mutual lock voting mechanism and works as follows:
- Each voter initializes a location vector (of length ) with 0s. randomly selects a location () and sets the th element/bit of to 1.
- From , obtains two values and by: (1) encoding into a decimal number (A decimal encoding, instead of a binary one, is used to encode . The motivation is illustrated below. Assume that the binary encoding is adopted. Let the location vectors of voters , and be , , and , respectively. Therefore, : Voters cannot tell if they have obtained unique locations. This will not be the case if uses a larger base. However, encoding in a larger base consumes more resources. Decimal is a trade-off we adopted to strike a balance between fault tolerance and performance. The probability of having more than 10 voters collide at the same location is considerably lower than that of 2); and (2) reversing to be and encoding it into a decimal number . For example, if , we obtain and . Evidently, .
- shares and using ()-SS as in Stage 2. All voters can obtain the aggregated location vector and . If has followed the protocol, and are the reverse of the other.
- checks if the th element/bit of is 1. If so, has successfully selected a location without colliding with others. also checks if everyone has picked a non-colliding location by examining whether . If there is at least one collision, steps 1 through 3 will restart. In a new round, voters who have successfully picked a location without collision in the previous round keep the same location, while others randomly select from locations not been chosen.
- The in-process check and enforcement mechanism (in Section 3.2) is concurrently executed by collectors to enforce that a voter will select one and only one location in each round. Furthermore, the mechanism, to be proved in Section 4.5, ensures that any attempt of inducing collision by deliberately selecting an occupied position will be detected. Hence, such misbehavior will be precluded.
- Once all location collisions are resolved in a round, each voter removes non-occupied locations ahead of his own and obtains his real location . After the adjustment, the occupied locations become contiguous. The length of the adjusted equals to the number of voters, N.
We will complement the above discussion with analysis (in Section 4.5) and simulation result (in Section 5.2).
Notes: (1) Location anonymization, a special component in our protocol, seems to be an additional effort for voters. However, it is beneficial since voters not only select their secret locations, but also learn/practice vote-casting ahead of the real election. The experiments show that 2 to 3 rounds are generally enough; (2) Location anonymization can be executed non-interactively; (3) A malicious participant deliberately inducing a collision by choosing an already occupied location will be identified.
Under the assumption that and have conflicting interests and thus will check each other but not collude, more deterministic and efficient LAS can be designed. One algorithm can be: two collectors perform double encryption (of 1 to N) and double shuffle before sending results to voters in a way such that neither can determine which voter gets which number, even though a collector may collude with some voter(s).
4. Security and Property Analysis
In this section, we demonstrate a few important properties and also analyze the robustness of our protocol.
4.1. Analysis of Main Properties
Here we give main properties of our voting protocol.
Attack-resistance. A random attack against the tallied voting vector with this vector being valid will succeed with the probability of .
Since and N is large, the probability of any attack without being detected is negligibly small. As an example, with and , the probability is !
Furthermore, even if a valid tallied vector is generated, there must be a certain location containing a vote which does not match what the voter in this location has voted for. Thus, it can be detected and reported by the voter who owns this location.
Completeness (Correctness). All votes are counted correctly in this voting protocol. That is, the aggregated voting vector of the length N in binary is the sum of all individual voting vector from each voter (). Likewise, .
Verifiability. Due to its transparency, the protocol provides a full range of verifiability with four levels:
- A voter can verify that his secret ballot is submitted correctly.
- A voter (and any third party) can verify that the aggregated voting vector is computed correctly.
- A voter can verify that his vote is cast correctly.
- A voter (and any third party) can verify that the final tally is performed correctly.
About individual verification, different techniques may have different meanings and adopt different mechanisms to implement. For example, majority of typical e-voting techniques encrypt the votes and a voter verifies his cast ballot in an encrypted format [30,31], rather than in plain text format/clear vote. In this case, tallying is normally done via homomorphic cryptosystem. Here due to the fundamental principle of homomorphic encryption, voters should be convinced that the final tally is accurate and their votes are accurately included in the final tally. Some e-voting techniques utilize pairs of (pseudo-voter ID, vote) and a voter verifies his cast vote (in plain format) according to his pseudo-voter ID. The relation between a voter’s real identity and his pair is hidden/anonymized via an anonymous channel or Mix-nets [13,32]. One representative case of this kind is the technique in the paper [33]. A voter casts his encrypted vote via an anonymous channel, and then sends his encryption key via the same channel for the counter to decrypt/open his vote. The voter can verify his vote in plain format (as well as in encrypted format). In this case, the voter’s real identity is hidden by blind signature and anonymous channel. Here the assumption is that the anonymous channel, Mix-nets and blind signature are trustworthy or they can prove their faithful conformation to the protocol via commitment/zero-knowledge proof. Furthermore, for all these verification scenarios, the mechanisms used for anonymization and individual verification act as one kind of black-box and introduce a gap between a voter’s ballot and real vote.
Like the technique in [33], our technique allows a voter to verify his vote in plain text format. However, different from [33], the verification in our technique is visibly realized due to transparency and seamless transition from ballots (no information about any vote) to all individual votes (each clear vote is anonymous to any one except the vote’s owner). No gap exists and no trustworthy assumptions are required.
Anonymity. The protocol preserves anonymity if no more than voters collude. This claim follows the proof of Theorem 1. Also, the protocol splits trust, traditionally vested in a central authority, now between two non-colluding collectors with conflicting interests. One collector does not have enough information to reveal a vote.
Especially in the revised Sub-protocol 1, we eliminate the possibility for an attacker to perform brute-force search against the intermediate result as in the original Sub-protocol 1 in [25]. Basically, in the original Sub-protocol 1, two collectors exchange and , so both obtain such that
Without loss of generality, let us assume wants to find out . Since has and , and are published, and , guesses (with being ) for , and constructs and based on Equations (2) and (3) respectively.
then verifies if (corresponding to the right hand side RHS of Equation (1)) equals to (the left hand side LHS of Equation (1)). If they are equivalent, ’s vote is found to be . Otherwise, guesses next until he finds out the correct .
However, in the revised Sub-protocol 1 presented here, contains a random value of , and similarly, has . can compute either as shown in LHS of Equation (4), or as shown in LHS of Equation (5) to get rid of the randomness. then guesses as before and plugs it into RHS of Equation (4) or (5) to verify if the equations hold true. But they will always hold true no matter what value is guessed. Thus, will not be able to find out with brute-force search. Vote anonymity is preserved.
Ballot validity and prevention of multiple voting. The forward and backward mutual lock voting allows a voter to set one and only one of his voting positions to 1 (enforced by Sub-protocol 1).
The ballot of and is ensured to be generated correctly in the forms of and (enforced by Sub-protocol 2).
Fairness. Fairness is ensured due to the unique property of ()-SS: no one can obtain any information before the final tally, and only when all N secret ballots are aggregated, all votes are obtained anonymously. It is this sudden transition that precludes any preannouncement of partial voting results, thus achieving fairness.
Eligibility. Voters have to be authenticated for their identities before obtaining voting locations. Traditional authentication mechanisms can be integrated into the voting protocol.
Auditability. Collectors collaboratively audit the entire voting process. Optionally we can even let collectors publish their commitment to all shares they generate (using hash functions, for example). With the whole voting data together with collectors’ commitments, two collectors or a third authority can review the voting process if necessary.
Transparency and voter assurance. Many previous e-voting solutions are not transparent in the sense that although the procedures used in voting are described, voters have to entrust central authorities to perform some of the procedures. Voters cannot verify every step in a procedure [34]. Instead, our voting protocol allows voters to visually check and verify their votes on the bulletin board. The protocol is transparent where voters participate in the whole voting process.
4.2. Robustness Against Voting Misbehavior
The protocol is robust in the sense that a misbehaving voter will be identified. In the interactive voting protocol, a misbehaving voter may:
- submit an invalid voting vector () with more than one (or no) 1s;
- generate wrong (), thus wrong commitment ();
- publish an incorrect secret ballot () such that ().
First, we show that a voter submitting an invalid voting vector () with more than one 1s will be detected. Without loss of generality, we assume two positions, and , are set to 1. (A voter can also misbehave by putting 1s at inappropriate positions, i.e., positions assigned to other voters; we will analyze this later.) Thus the voter obtains (), such that
All the computations are moduli operations. By using , which has at least elements/bits, we have , thus . Assuming generates an invalid voting vector without being detected, this will lead to the following contradiction by Sub-protocol 1:
Similar proof applies to an invalid voting vector without 1s.
Next, we show that cannot generate wrong or such that or . If Sub-protocol 1 fails to detect this discrepancy, there is: Since the computation is on , we have: Given that:
there must exist one and only one position which is set to 1 and . This indicates that gives up his own voting positions, but votes at a position assigned to another voter (). In this case, ’s voting positions in and will be 0 (Unless, of course, another voter puts a 1 in ’s position. We can either trace this back to a voter that has all 0s in his positions, or there is a loop in this misbehaving chain, which causes no harm to non-misbehaving voters). This leads to an invalid tallied vector where ’s voting positions have all 0s and possibly ’s have multiple 1 s. If this happens, and can collaboratively find ’s row that has all 0 s in the voting vector (arranged in an array).
Third, we show that a voter cannot publish an incorrect () to disturb the tally. Given that a misbehaving publishes ( such that (), we obtain ( which will fail in Sub-protocol 2. Note that and have passed the verification of Sub-protocol 1, and and (also, and ) are computed by two collectors with conflicts of interest. Thus, there is no way for the voter to publish an incorrect () without being detected.
The discussion shows all these misbehaviors should be caught by the collectors using Sub-protocol 1 or Sub-protocol 2. However, assume two cases as below:
- One misbehavior mentioned above mistakenly passes both Sub-protocol 1 and Sub-protocol 2;
- does give up his own voting locations and cast vote at ’s locations ().
For Case 1, the possibility leading to a valid voting vector is negligibly small as we have discussed earlier in this section. Even if the voting vector is valid, any voter can still verify whether the vote in his own location is correct. This is the individual verifiability our protocol provides.
For Case 2, if casts the same as at ’s locations, there will be a carry, ending up one 1, but not the vote has cast. If casts a vote different from , there will be two 1s at ’s locations. Because all ’s locations now have 0 s, the tallied voting vector will be invalid for both scenarios. Furthermore, can detect it since his vote has been changed. Again, as we assumed earlier, there is no reason/incentive for a voter to give up his own voting right and disturb other unknown voters.
The analysis above also applies to the non-interactive voting protocol.
4.3. Robustness against Collusion
Here we analyze the robustness against different collusions and attacks. With the assumption that collectors have conflicting interests, they will not collude, so we exclude such a scenario.
4.3.1. Robustness against Collusion among Voters
By Theorem 1, the protocol is robust against collusions among voters to infer vote information (passive adversaries) as long as no more than voters collude.
The protocol is robust against cheating by colluding voters such as double or multiple voting (active adversaries). Colluding voters want to disrupt the voting process. However, even they collude, the commitments and the secret ballots of each colluding voter have to pass the verification of both Sub-protocol 1 and Sub-protocol 2 by two collectors. Thus the disruption will not succeed as discussed in Section 4.2.
The analysis above applies to both the interactive protocol and the non-interactive protocol.
4.3.2. Robustness against Collusion among Voters and a Collector
In the interactive protocol, one collector has only a subset of any voter’s shares, so the discussion about passive adversaries in Section 4.3.1 still holds here. That is, if no more than voters collude with a collector, no information of votes can be disclosed before the final tally is done.
In the non-interactive protocol, the situation is slightly different. Since collectors generate shares for each voter, they seem to be more powerful than in the interactive protocol. However, all shares of an individual voter are jointly generated by two collectors as shown in Table 2, with each creating only half of shares. The property of ()-SS still applies here. As long as no more than voters collude with a collector, the robustness against collusion among voters and a collector to infer vote information still holds.
For both interactive and non-interactive protocols, when voters collude with a collector to disrupt the voting by cheating, each individual voter still has to pass Sub-protocol 1 and Sub-protocol 2 by two collectors. However, since one collector is colluding, the voter may succeed in passing the verification.
Assume colludes with . generates and (deviating from authentic and ) and publishes commitments , , and . For Sub-protocol 1, can derive and (deviating from authentic and ) based on ’s and , such that:
Similarly, ’s and (deviating from authentic and ) can also pass Sub-protocol 2 by colluding with .
However, since there are non-colluding voters, the probability of leading to a valid tallied voting vector is negligibly slim as discussed earlier in this section. Even by any chance a valid tallied voting vector is created, any voter can still tell if the vote in the final vector is what he intended by the property of individual verifiability.
As a result, such collusion with the purpose of cheating will be detected too.
4.4. Robustness against Outside Attack
The protocol is robust against an outsider inferring any vote information. The outsider does not have any information. If he colludes with insiders (voters), he will not gain any information as long as no more than voters collude with him.
The protocol is also robust against an outsider disrupting the voting. First, if the outsider intercepts data for a voter from secure channel during the voting, he will not learn any information about vote because the data itself is encrypted. Second, if the outsider wants to change a voter’s vote or even the tallied voting vector by colluding with voters or a collector, he will not succeed as discussed in Section 4.3.
4.5. Robustness of Location Anonymization
The analysis in Section 4.2 shows that no voter can choose more than one positions during the location anonymization process. However, this does not address the problem that a malicious participant deliberately induces collisions by choosing a location that is already occupied by another voter. We will demonstrate that our proposed LAS is robust against this.
Let the collision happen at , i.e., is chosen by in the previous round, and both and claim in the current round. In this case, is the voter who deliberately introduces collision. To identify a voter who chooses in a given round, and do the following collaboratively. For each voter, using the tailored STPM, and compute () and check if (). By doing this, the collectors identify the voter who selects without divulging others’ locations. Although the honest voter who chooses is exposed along with the malicious , can restore location anonymity by selecting another location in the next round and should be punished.
Of course, voters may collude to infer location information. If k voters collude, they will know that the rest non-colluding voters occupy the remaining voting locations. Since we assumed in Section 2.1 that majority of voters is benign, we consider the leaking of location information in this case is acceptable and will not endanger the voting process.
5. Complexity Analysis and Simulation
We provide complexity analysis and then simulation results.
5.1. Performance and Complexity Analysis
Here we analyze the computational complexity and communication cost for both voters and collectors in the protocol. Suppose that each message takes T bits. Since the protocol works on a cyclic group (, in which is a prime greater than and is a prime greater than ), we see that .
The voting protocol involves two independent sharing processes of and . The communication cost is calculated as follows. In the interactive protocol, each voter sends shares of to the other voters and the two collectors, which costs . In the non-interactive protocol however, each voter receives shares from the collectors only, so the cost is . In both protocols, each voter also publishes and the commitments , , and , which costs . Therefore, the total communication cost of sharing of for a voter is in the interactive protocol and in the non-interactive protocol. The cost of sharing is the same.
Each voter’s computation cost includes computing , generating N shares (in the interactive protocol only), computing the secret ballot , and computing the commitments , , and , each of which costs , (in the interactive protocol only), in the interactive protocol and in the non-interactive protocol, and respectively. The same cost applies to the sharing of . Notes: The commitments can typically be computed by a calculator efficiently, thus, the complexity of will not become a performance issue.
The collector ’s communication cost involves: (1) receiving shares from voters in the interactive protocol with the cost of , or sending sums of shares in the non-interactive protocol with the cost of ; (2) exchanging data with the other collector in Sub-protocol 1 with the cost of (assuming that the STPM messages are encoded into -bits); and (3) publishing or for each voter in Sub-protocol 2 with the cost of . With N voters, the total cost for each collector is for the interactive protocol and for the non-interactive protocol.
The computation cost of each collector includes generating shares for all voters (in the non-interactive protocol only) which costs , summing up the during voting collection/tally, which costs , and the computation costs of Sub-protocol 1 and Sub-protocol 2.
In Sub-protocol 1, for the collector , (1) computing and costs ; (2) computing involves tailed STPM; and (3) computing costs . Computing consists of obtaining () with tailored STPM, computing and multiplying this with other terms. Let the complexity for tailored STPM be . The total computation cost of Sub-protocol 1 for each collector is per voter.
In Sub-protocol 2, the collectors: (1) compute and ; (2) compute and ; (3) multiply , and , and also , and ; and (4) compute and . These computations cost , , and , respectively. Thus, the total computation cost of Sub-protocol 2 is for each voter.
LAS uses similar mechanisms of the voting protocol during each round. Thus for each round, we obtain similar complexity. Roughly, the message length T in LAS is .
5.2. Simulation Result
The results presented here are from our protocol simulation implemented in Java. The experiments were carried out on a computer with a 1.87 GHz CPU and 32 GB of memory. For each experiment, we took the average of 10 rounds of simulation. 1-out-of-2 voting is simulated. Thus, the length of the voting vector is where N is the number of voters.
Figure 3 shows the number of rounds needed for completing location anonymization. The length of the location vector varied from 1.5, 2, to 3 times of number of voters N. The number of voters N varied from 64 to 1000 by an increment of 16. As shown in Figure 3, the number of rounds needed for completing location anonymization is relatively stable for different N under a given ratio .
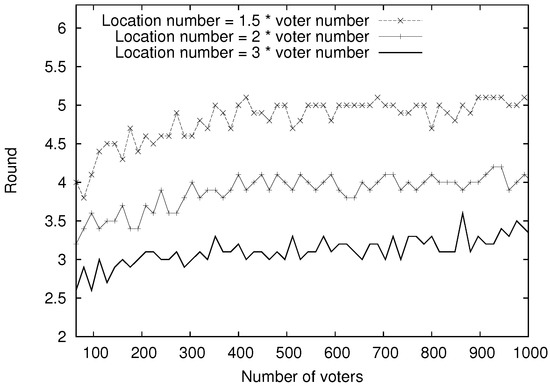
Figure 3.
Location Anonymity Scheme (LAS): number of rounds needed for location anonymization.
Figure 4 shows the time spent on location anonymization by each voter. The length of the location vector and the number of voters N varied the same as in Figure 3. The length of the location vector is ; the aggregation of location vectors is dominated by the ()-SS. The execution time is . Thus, the time spent on location anonymization is . When the ratio , 2 to 3 rounds were sufficient for completing location anonymization. For example, with 1000 voters, it took no more than 0.05 s to anonymize voters’ locations. This demonstrates the efficiency of the proposed LAS.
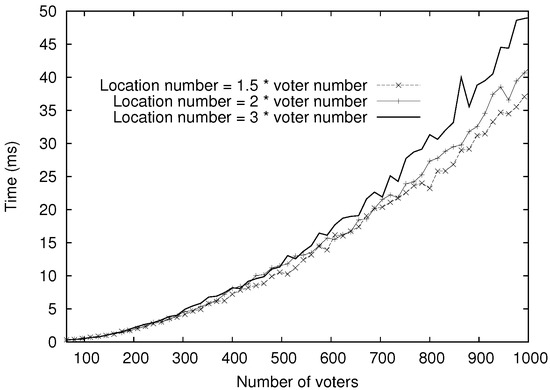
Figure 4.
LAS: time needed for location anonymization per voter.
In the non-interactive protocol, the computation time for a voter is negligible since only two subtractions are needed for and two additions for , and the commitments can be obtained by using a calculator sufficiently. Collectors however require heavy load of calculation, so our simulation focuses on collectors’ operations.
Figure 5 and Figure 6 show the computation time of Sub-protocol 1 and Sub-protocol 2, respectively. Sub-protocol 1 was dominated by tailored STPM, due to the computationally intensive Paillier Cryptosystem used in our implementation. However, this should not be an issue in real life since the collectors usually possess much greater computing power.
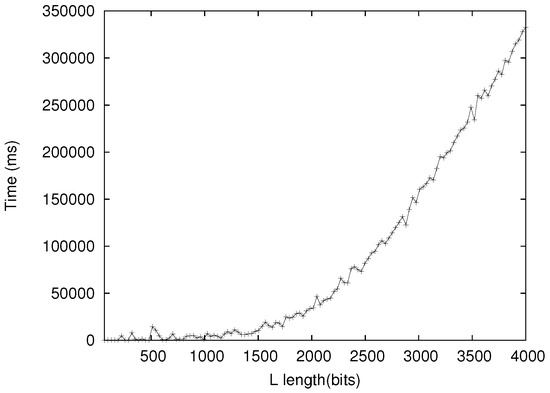
Figure 5.
Collectors run Sub-protocol 1 in TP3 against one voter.
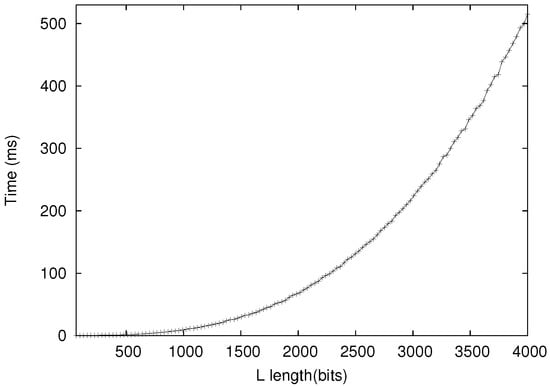
Figure 6.
Collectors run Sub-protocol 2 in TP3 against one voter.
Figure 7 shows the time for one collector to collect and tally votes. The execution time depends on the number of voters N and the length L. As L increases, the voting collection/tally time increases by .
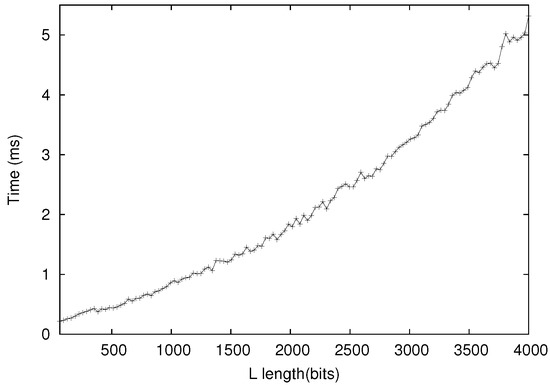
Figure 7.
One collector collects/tallies votes.
The simulation results confirm the performance analysis in Section 5.1. Most operations are quite efficient. For example, when (and ), collecting and tallying votes took only 0.005 s. For the in-process enforcement protocol however, it took the collectors 332 s to complete Sub-protocol 1 and 0.515 s to complete Sub-protocol 2. To amortize the relatively high cost, the collectors may randomly sample voters for misbehavior checking and only resort to full checking when a discrepancy in the tally is detected or reported.
6. Related Work and Comparison
Extensive research on voting, particularly online voting recently, has been conducted. A number of voting schemes and systems have been proposed [7,8,9,10,11,12,17,30,35,36,37,38,39,40,41,42,43].
Cryptographic technique has been an indispensable component of most online voting systems. A variety of cryptographic techniques, such as mix-nets, blind signature, homomorphic encryption, zero-knowledge proof, and secret sharing, are deployed in electronic voting protocols to secure voter’s vote. The first e-voting scheme proposed by Chaum [44] in 1981 utilizes anonymous channels (i.e., mix-nets). Additional schemes [7,13,45,46,47,48,49,50] based on mix-nets are proposed afterwards with various optimization. For example, Aditya et al. [49] improve the efficiency of Lee et al.’s scheme [46] through modified optimistic mix-nets. The scheme in [7] uses two kinds of mix-nets to prevent vote updating from being detected by coercers. However, due to the usage of mix-nets, transparency cannot be guaranteed.
A blind signature allows an authority to sign an encrypted message without knowing the message’s context [14,33,50,51,52,53,54,55]. However, it is difficult to defend against misbehavior by authorities. Moreover, some participants (e.g., authorities) know intermediate results before the counting stage. This violates fairness of the voting protocol. Ring signature is proposed to replace the single signing authority. The challenge of using the ring signature is in preventing voters from double voting. Chow et al. [56] propose using a linkable ring signature, in which messages signed by the same member can be correlated, but not traced back to the member. A scheme combining blind signature and mix-nets is proposed in [52]. Similarly, blind signature is used in a debate voting [55] with messages of varying length where anonymous channel is assumed.
Voting schemes based on homomorphic encryption can trace back to the seminal works by Benaloh [16,57] and later development in efficiency [31,58], and receipt-freeness [15,59,60,61]. Rjaskova’s scheme [15] achieves receipt-freeness by using deniable encryption, which allows a voter to produce a fake receipt to confuse the coercer. But eligibility and multi-voting prevention are not addressed. DEMOS-2 proposed by Kiayias et al. [62] utilizes additively homomorphic public keys on bilinear groups with assumption that symmetric external Diffie-Hellman on these groups is hard. Its voting support machine (VSD) works as a “voting booth” and the voting protocol is rather complex.
Several voting schemes exploit homomorphism based on secret sharing [15,16,57,59,60,61]. Some schemes [31,58] utilize Shamir’s threshold secret sharing [63], while some [64] are based on Chinese remainder theorem. In contrast, ours is based on a simplified ()-SS scheme. In existing voting schemes, the secret sharing is utilized among authorities in two ways generally: (a) to pool their shares together to get the vote decryption key which decrypts the tallied votes [15,16,57,58,59,60,65]; and (b) to pool their shares together to recover the encrypted or masked tally result [31,64]. Instead, in our scheme, the secret sharing is used among voters to share their secret votes and then recover their open yet anonymous votes.
Particularly, some existing protocols require physical settings such as voting booths [23], a tamper resistant randomizer [46,60,66,67], or specialized smart cards [68]. Our protocol does not require specialized devices and is distributed by design.
We also examined experimental voting systems. Most existing systems have voter verifiability and usually provide vote anonymity and voter privacy by using cryptographic techniques. Typically, the clerks/officers at the voting places will check eligibility by verifying voters’ identity.
Using the voting booth settings, system scalability in terms of voter numbers is hard to evaluate. Prêt à Voter [45,69] encodes a voter’s vote using a randomized candidate list. The randomization ensures the secrecy of a voter’s vote. After casting his vote in a voting booth, a voter is given a receipt such that the voter can verify if his receipt appears on the bulletin board. Unlike our proposed protocol however, a voter will not see directly that his vote is counted. A number of talliers will recover the candidate list through the shared secret key and obtain the voter’s vote.
ThreeBallot [70,71] solves the verification and anonymity problem by giving each voter three ballots. The voter is asked to choose one of the three ballots to be verifiable. The ThreeBallot system requires a trusted authority to ensure that no candidate is selected on all three ballots to avoid multiple-vote fraud.
Punchscan/Scantegrity [72,73,74,75] allows the voter to obtain a confirmation code from the paper ballot. Through the confirmation code, the voter can verify the code is correct for his ballot. Similarly to Prêt à Voter, a voter will not directly see that his vote is counted. A number of trustees will generate the tally which is publicly auditable.
SplitBallot [23] is a (physical) split ballot voting mechanism by splitting the trust between two conflict-of-interest parties or tallying authorities. It requires the untappable channels to guarantee everlasting privacy.
Prêt à Voter, Punchscan/Scantegrity, ThreeBallot, and SplitBallot utilize paper ballots and/or are based on voting booths, but ours does not. ThreeBallot and SplitBallot seem similar to ours in terms of split trust, however both of them depend on splitting paper ballots, unlike our protocol which utilizes electronic ballots that are split equally between two tallying collectors.
Bingo Voting [76] requires a random number list for each candidate which contains as many large random numbers as there are voters. In the voting booth, the system requires a random number generator.
VoteBox [77,78] utilizes a distributed broadcast network and replicated log, providing robustness and auditability in case of failure, misconfiguration, or tampering. The system utilizes an immediate ballot challenge to assure a voter that his ballot is cast as intended. Additionally, the vote decryption key can be distributed to several mutually-untrusted parties. VoteBox provides strong auditing functionality but does not address how a voter can verify if his vote is really counted.
Prime III [79,80] is a multimodal voting system especially devoted to the disabled and it allows voters to vote, review, and cast their ballots privately and independently through speech and/or touch. It offers a robust multimodal platform for the disabled but has not considered how individual or universal verification is done.
Scytl [81,82,83,84] requires dedicated hardware - a verification module (a physical device) on top of the DRE. Also, the trust, previously on the DRE, is transferred to the verification module. In contrast, ours is cost-efficient and does not require additional hardware devices.
In the ADDER [85] system, a public key is set up for the voting system, and the private key is shared by a set of authorities. Each voter encrypts his vote using the public key. The encrypted vote and its zero-knowledge proof are published on the bulletin board. Due to the homomorphic property, the encrypted tally is obtained by multiplying all encrypted votes on the bulletin board. The authorities then work together to obtain the decrypted tally. ADDER [85] is similar to ours in terms of Internet based voting and split trust, yet ADDER does not provide a direct view for a voter to see if his vote is indeed counted in the tally.
Unfortunately, due to the strict and conflicting e-voting requirements [5], there is not any scheme/system currently satisfying all voting properties at the same time [42]. Security weakness is found even in highly referenced voting schemes [86]. The papers [87,88] particularly analyze two fundamental but important properties, privacy and verifiability. They reviewed the formal definitions of these two properties in the literature, and found that the scope and formulation of each property vary from one protocol to another. As a result, they propose a new game-based definition of privacy called BPRIV in [87] and a general definition of verifiability in [88].
Comparison with Helios. Helios [89] implements Benaloh’s vote-casting approach [90] on the Sako-Kilian mix-nets [91]. It is a well-known and highly-accepted Internet voting protocol with good usability and operability. Our voting protocol shares certain features with Helios including open auditing, integrity, and open source.
However, there exist some important differences. First, about individual verification, Helios allows voters to verify their encrypted votes but our new protocol allows voters to verify their plain votes, in a visual manner. Thus, individual verification in the new protocol is more straightforward. Second, about transparency, as acknowledged by the author of Zeus, the mixing part in Helios (and Zeus) is a black box to voters [20]. Instead, in our new protocol, the voting process including ballot-casting, ballot aggregation, plain vote verification, and tallying are all viewable (on public bulletin board) to voters. Thus, our new protocol is visibly transparent. Third, in terms of voter assurance, the transition from ballots to plain votes in Helios involves mix-net (shuffling and re-encryption) and decryption. In contrast, such transition in our new protocol is seamless and viewable. In addition, the voter can conduct self-tallying. Thus, voter assurance in our new protocol is direct and personal. Fourth, about the trust issue (in terms of integrity of the tallying result), Helios depends on cryptographic techniques including zero knowledge proof to guarantee the trustworthiness of the mix-net which finally transforms to the integrity of the tallying result. In contrast, our new protocol is straightly based on simple addition and viewable verification. Thus, accuracy of the tallying result in our new protocol is self-evident and is easier to justify. Fifth, about the trust issue (in terms of vote secrecy), Helios can use two or more mix-servers to split trust. However, it assumes that at least a certain number of mix-servers do not collude. In this case, it is similar to our assumption that two or more collectors have conflicting interests and will not collude. Sixth, about computational complexity, Helios’ ballot preparation requires modular exponentiations for each voter and the tallying process involves exponentiations (decryption). However, our ballot generation and tallying need only modular subtractions and additions. Thus, our new protocol is more efficient.
Besides Zeus [20] and Helios 2.0 [92], there are some variants of Helios such as BeleniosRF [93]. BeleniosRF is built upon Belenios. It introduces signatures on randomizable ciphertexts to achieve receipt-freeness. A voting authority is assumed to be trustworthy.
Comparison with existing interactive voting protocols. In aforementioned voting protocols, most are centralized. Our non-interactive protocol is similar in this regard. However, some e-voting protocols are decentralized or distributed: each voter bears the same load, executes the same protocol, and reaches the same result autonomously [94]. One interesting application domain of distributed e-voting is boardroom voting [21]. In such scenario, the number of voters is not large and all the voters in the voting process will interact with each other. Two typical boardroom voting protocols are the ones in [22,95] and our interactive voting protocol is similar to them too. In all these protocols including ours, tallying is called self-tallying: each voter can incrementally aggregate ballots/votes themselves by either summing the votes [95]) (as well as ours) or multiplying the ballots [22]) (and then verify the correctness of the final tally). One main advantage of our interactive voting protocol over other distributed e-voting protocols is its low computation cost for vote casting and tallying. As analyzed in [21], in terms of vote casting, the protocol in [22] needs exponentiations per voter and the protocol in [95] needs . However, our interactive voting protocol needs only 6. In terms of tallying [21], the protocol in [22] needs and the protocol in [95] needs (here t is the threshold in distributed key generation scheme). However, our interactive voting protocol does not need any exponentiations beyond simple modular additions. Another property of our interactive voting protocol in terms of transparency is the viewability of the voter’s plain vote: each voter knows and can see which plain vote is his vote. However, in [22], plain votes are not viewable, and in [95], even though plain votes are viewable but the voter does not know which one is his because the shuffling process changes the correspondence between the initial ballots and (decrypted) individual plain votes.
7. Discussion of Scalability and Hierarchical Design
In this section, we discuss about scalability and design of our protocol, mainly for the non-interactive protocol.
Given the number of candidates M, the size of the voting vector determines the number of voters in one voting group and furthermore determines how large the integral vote values can be. Currently, most languages support arithmetical operations on big integers of arbitrary sizes. We conducted preliminary experiments with a voting group of 2000 voters and 2 candidates (i.e., voting vectors of 4000 bits) in Section 5.2. The results showed an encouraging and impressive running time. Based on a 2004 survey by the US EAC on voting booth based elections, the average precinct size is approximately 1100 registered voters in the US 2004 presidential election [96]. Thus, our proposed voting system is realistic and practical. Furthermore, by following the US government structure and the precinct based election practice, we propose the following hierarchical tallying architecture which can apply to various elections of different scales.
- Level 1: Precinct based vote-casting. Voters belonging to a precinct form a voting group and execute the proposed vote-casting. Precincts may be based on the physical geography previously using voting booths or logically formed online to include geographically remote voters (e.g., overseas personnel in different countries).
- Level 2: Statewide vote tally. Perform anonymous tally among all precincts of a state.
- Level 3: Conversion of tallied votes. There can be a direct conversion. The numbers of votes for candidates from Level 2 remain unchanged and are passed to Level 4 (the popular vote). Otherwise, they may be converted from Level 2 by some rules before being passed to Level 4, to support hierarchies like the Electoral Colleges in the US.
- Level 4: National vote tally.
8. Conclusions and Future Work
We proposed a fully transparent, auditable, and end-to-end verifiable voting protocol to enable open and fair elections. It exploits the conflicts of interest in multiple tallying authorities, such as the two-party political system in the US. Our protocol is built upon three novel technical contributions—verifiable voting vector, forward and backward mutual lock voting, and proven in-process check and enforcement. These three technical contributions, along with transparent vote casting and tallying processes, incremental aggregation of secret ballots, and incremental vote tallying for candidates, deliver fairness and voter assurance. Each voter can be assured that his vote is counted both technically and visually. In particular, the interactive protocol is suitable for election within a small group where interaction is encouraged, while the non-interactive protocol is designed for election within a large group where interaction is not needed and not realistic. Through the analysis and simulation, we demonstrated the robustness, effectiveness, and feasibility of our voting protocol.
As the future work, we plan to further improve our protocol, focusing particularly on receipt freeness and voter coercion. They are the most challenging problems in e-voting, compared to other requirements. As pointed out in [20], e-voting is inherently coercible. Specifically in our protocol, since the tallied voting vector contains all individual votes, a voter’s location can potentially become a self-claimed receipt and the voter can exploit it for vote selling.
To prevent vote selling, we plan to have collectors jointly shuffle/shift the locations together with votes in randomly and then publish the skewed . In this case, individual verification cannot be done visually but a voter can perform 1 out of N oblivious transfer with collectors for verification. To prevent voter coercion, we plan to let each voter have multiple locations, for example, one real location and one fake location. The coerced voter can cast the vote as what a coercer asked for using the fake location during the presence of the coercer and then cast his real vote in the real location afterward. To prevent both, some combination of these can be deployed, or solutions based on secure two-party computation can be developed.
Recent research by Grewal et al. [6] acknowledges the toughness of the voter coercion issue, and they propose to redefine its meaning and scope. Even for the century-old Australian ballot which used to be coercion free, voter coercion is becoming an issue because of new emerging video technology [97].
Author Contributions
X.Z. initiated the design of the protocol and led the writing and proof-reading of the paper. H. L., F. L., W.P., and Y. S. joined the discussion, security proof, enhancement, and experiment of the protocol. H.L. contributed significantly to the writing and editing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wikipedia. Help America Vote Act, The Free Encyclopedia. 2013. Available online: https://en.wikipedia.org/wiki/Help_America_Vote_Act (accessed on 1 July 2013).
- Wikipedia. The U.S. Election Assistance Commission. 2013. Available online: https://www.eac.gov/about/help-america-vote-act/ (accessed on 1 July 2013).
- Commission, T.U.E.A. 2008 Election Administration and Voting Survey. Available online: http://www.eac.gov/ (accessed on 1 September 2009).
- Campbell, B. The Usability Implications of Long Ballot Content for Paper, Electronic, and Mobile Voting Systems. Ph.D. Thesis, RICE University, Houston, TX, USA, 2014. [Google Scholar]
- Chevallier-Mames, B.; Fouque, P.A.; Pointcheval, D.; Stern, J.; Traoré, J. On some incompatible properties of voting schemes. (book chapter). In Towards Trustworthy Elections; Chaum, D., Jakobsson, M., Rivest, R.L., Ryan, P.A., Benaloh, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 191–199. [Google Scholar]
- Grewal, G.S.; Ryan, M.D.; Bursuc, S.; Ryan, P.Y. Caveat Coercitor: Coercion-evidence in electronic voting. In Proceedings of the IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 19–22 May 2013; pp. 367–381. [Google Scholar]
- Araújo, R.; Barki, A.; Brunet, S.; Traoré, J. Remote Electronic Voting Can Be Efficient, Verifiable and Coercion-Resistant. In Financial Cryptography and Data Security: FC 2016 International Workshops, BITCOIN, VOTING, and WAHC, Christ Church, Barbados, 26 February 2016, Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2016; pp. 224–232. [Google Scholar]
- Li, C.; Hwang, M.; Lai, Y. A Verifiable Electronic Voting Scheme over the Internet. In Proceedings of the Sixth International Conference on Information Technology: New Generations (ITNG ’09), Las Vegas, NV, USA, 27–29 April 2009; pp. 449–454. [Google Scholar]
- Howlader, J.; Nair, V.; Basu, S.; Mal, A. Uncoercibility In E-Voting and E-Auctioning Mechanisms Using Deniable Encryptiony. Int. J. Netw. Secur. Appl. 2011, 3, 97–109. [Google Scholar]
- Lee, C.; Chen, T.; Lin, S.; Hwang, M. A New Proxy Electronic Voting Scheme Based on Proxy Signatures. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 164, pp. 3–12. [Google Scholar]
- Spycher, O.; Koenig, R.; Haenni, R.; Schläpfer, M. A New Approach towards Coercion-Resistant Remote E-Voting in Linear Time. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kralendijk, Bonaire, 27 February–2 March 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7035, pp. 182–189. [Google Scholar]
- Clarkson, M.; Chong, S.; Myers, A. Civitas: Toward a secure voting system. In Proceedings of the IEEE Symposium on Security and Privacy, Oakland, CA, USA, 18–22 May 2008; pp. 354–368. [Google Scholar]
- Juels, A.; Catalano, D.; Jakobsson, M. Coercion-resistant electronic elections. In Proceedings of the 2005 ACM Workshop on Privacy in the Electronic Society, Alexandria, VA, USA, 7 November 2005; ACM: New York, NY, USA, 2005; pp. 61–70. [Google Scholar]
- Chaum, D. Elections with unconditionally-secret ballots and disruption equivalent to breaking RSA. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques (EUROCRYPT ’88), Davos, Switzerland, 25–27 May 1988; pp. 177–182. [Google Scholar]
- Rjaskova, Z. Electronic Voting Schemes. Ph.D. Thesis, Comenius University, Bratislava, Slovakia, 2002. [Google Scholar]
- Benaloh, J. Verifiable Secret Ballot Elections. Ph.D. Thesis, Yale University, New Haven, CT, USA, 1987. [Google Scholar]
- Jones, D.; Simons, B. Broken Ballots: Will Your Vote Count? The University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Shamos, M.I. Electronic Voting Records—An Assessment. In Developing an Analysis of Threats to Voting Systems: Preliminary Workshop Summary; NIST: Gaithersburg, MD, USA, 2004; pp. 227–251. [Google Scholar]
- McGaley, M.; McCarthy, J. Transparency and e-voting: Democratic vs. commercial interests. Proc. GI 2012, 47, 153–163. [Google Scholar]
- Tsoukalas, G.; Papadimitriou, K.; Louridas, P.; Tsanakas, P. From Helios to Zeus. In Proceedings of the 2013 Electronic Voting Technology Workshop/Workshop on Trustworthy Elections (EVT/WOTE ’13), Washington, DC, USA, 12–13 August 2013; pp. 1–17. [Google Scholar]
- Kulyk, O.; Neumann, S.; Budurushi, J.; Volkamer, M.; Haenni, R.; Koenig, R.; Bergen, P. Efficiency Evaluation of Cryptographic Protocols for Boardroom Voting. In Proceedings of the 2015 10th International Conference on Availability, Reliability and Security (ARES), Toulouse, France, 24–27 August 2015; pp. 224–229. [Google Scholar]
- Khader, D.; Smyth, B.; Ryan, P.Y.; Hao, F. A fair and robust voting system by broadcast. In Proceedings of the EVOTE’12: 5th International Conference on Electronic Voting, Bregenz, Austria, 11–14 July 2012; pp. 1–13. [Google Scholar]
- Moran, T.; Naor, M. Split-ballot voting: Everlasting privacy with distributed trust. ACM Trans. Inf. Syst. Secur. 2010, 13, 16. [Google Scholar] [CrossRef]
- Wikipedia. Vote Counting System 2012. Available online: https://en.wikipedia.org/wiki/Vote_counting (accessed on 21 June 2012).
- Zou, X.; Li, H.; Sui, Y.; Peng, W.; Li, F. Assurable, Transparent, and Mutual Restraining E-Voting Involving Multiple Conflicting Parties. In Proceedings of the IEEE INFOCOM, Toronto, ON, Canada, 27 April–2 May 2014; pp. 136–144. [Google Scholar]
- Stinson, D.R. Cryptography: Theory and Practice; CRC Press: Boca Raton, FL, USA, 1995; Chapter 11; pp. 330–331. [Google Scholar]
- Zhao, X.; Li, L.; Xue, G.; Silva, G. Efficient anonymous message submission. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 2228–2236. [Google Scholar]
- Samet, S.; Miri, A. Privacy preserving ID3 using Gini Index over horizontally partitioned data. In Proceedings of the IEEE/ACS International Conference on Computer Systems and Applications (AICCSA ’08), Doha, Qatar, 31 March–4 April 2008; pp. 645–651. [Google Scholar]
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Benaloh, J.; Tuinstra, D. Receipt-free secret-ballot elections. In Proceedings of the 26th Annual ACM Symposium on Theory of Computing, Montréal, QC, Canada, 23–25 May 1994; ACM: New York, NY, USA, 1994; pp. 544–553. [Google Scholar]
- Schoenmakers, B. A Simple Publicly Verifiable Secret Sharing Scheme and Its Application to Electronic Voting. In Proceedings of the 19th Annual International Cryptology Conference on Advances in Cryptology (CRYPTO ’99), Santa Barbara, CA, USA, 15–19 August 1999; pp. 148–164. [Google Scholar]
- Clark, J.; Hengartner, U. Selections: Internet Voting with Over-the-Shoulder Coercion-Resistance. In Financial Cryptography and Data Security; Lecture Notes in Computer Science; Danezis, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7035, pp. 47–61. [Google Scholar]
- Fujioka, A.; Okamoto, T.; Ohta, K. A practical secret voting scheme for large scale elections. In Advances in Cryptology—AUSCRYPT ’92; Springer: Berlin/Heidelberg, Germany, 1993; pp. 244–251. [Google Scholar]
- Spafford, E.H. Voter Assurance. In Voting Technologies; National Academy of Engineering: Washington, DC, USA, 2007; pp. 28–34. [Google Scholar]
- Clarkson, M.; Chong, S.; Myers, A. Civitas: Toward a Secure Voting System; Technical Report; Cornell University: Ithaca, NY, USA, 2008. [Google Scholar]
- Shirazi, F.; Neumann, S.; Ciolacu, I.; Volkamer, M. Robust electronic voting: Introducing robustness in Civitas. In Proceedings of the International Workshop on REVOTE, Trento, Italy, 29 August 2011; pp. 47–55. [Google Scholar]
- Volkamer, M.; Grimm, R. Determine the Resilience of Evaluated Internet Voting Systems. In Proceedings of the International Workshop on REVOTE, Atlanta, GA, USA, 31 August 2009; pp. 47–54. [Google Scholar]
- Li, C.; Hwang, M. Security Enhancement of Chang-Lee Anonymous E-Voting Scheme. Int. J. Smart Home 2012, 6, 45–52. [Google Scholar]
- Staff, C. Seven principles for secure e-voting. Commun. ACM 2009, 52, 8–9. [Google Scholar] [CrossRef]
- Epstein, J. Electronic voting. IEEE Comput. 2007, 40, 92–95. [Google Scholar] [CrossRef]
- Kusters, R.; Truderung, T.; Vogt, A. Clash Attacks on the Verifiability of E-Voting Systems. In Proceedings of the 2012 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–23 May 2012; pp. 395–409. [Google Scholar]
- Fouard, L.; Duclos, M.; Lafourcade, P. Survey on Electronic Voting Schemes. Available online: http://www-verimag.imag.fr/~duclos/paper/e-vote.pdf (accessed on 1 July 2013).
- Benaloh, J.; Byrne, M.; Kortum, P.; McBurnett, N.; Pereira, O.; Stark, P.; Wallach, D. STAR-Vote: A Secure, Transparent, Auditable, and Reliable Voting System. arXiv 2012, arXiv:1211.1904. [Google Scholar]
- Chaum, D. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM 1981, 24, 84–90. [Google Scholar] [CrossRef]
- Chaum, D.; Ryan, P.; Schneider, S. A practical voter-verifiable election scheme. In Proceedings of the 10th European Conference on Research in Computer Security (ESORICS ’05), Milan, Italy, 12–14 September 2005; pp. 118–139. [Google Scholar]
- Lee, B.; Boyd, C.; Dawson, E.; Kim, K.; Yang, J.; Yoo, S. Providing Receipt-Freeness in Mixnet-Based Voting Protocols. In Proceedings of the International Conference on Information Security and Cryptology, Seoul, Korea, 27–28 November 2003; Volume 2971, pp. 245–258. [Google Scholar]
- Weber, S. A Coercion-Resistant Cryptographic Voting Protocol—Evaluation and Prototype Implementation. Master’s Thesis, Darmstadt University of Technology, Darmstadt, Germany, 2006. [Google Scholar]
- Chaum, D. Secret-ballot receipts: True voter-verifiable elections. IEEE Secur. Priv. 2004, 2, 38–47. [Google Scholar] [CrossRef]
- Aditya., R.; Lee, B.; Boyd, C.; Dawson, E. An Efficient Mixnet-Based Voting Scheme Providing Receipt-Freeness. In Proceedings of the International Conference on Trust and Privacy in Digital Business, Zaragoza, Spain, 30 August–1 September 2004; Volume 3184, pp. 152–161. [Google Scholar]
- Okamoto, T. Receipt-free electronic voting schemes for large scale elections. In Proceedings of the International Workshop on Security Protocols, Paris, France, 7–9 April 1997; Springer: Berlin/Heidelberg, Germany, 1998; pp. 25–35. [Google Scholar]
- Radwin, M. An Untraceable, Universally Verifiable Voting Scheme. Available online: https://www.researchgate.net/publication/2867316_An_Untraceable_Universally_Verifiable_Voting_Scheme (accessed on 16 August 2017).
- Ohkubo, M.; Miura, F.; Abe, M.; Fujioka, A.; Okamoto, T. An Improvement on a Practical Secret Voting Scheme. In Proceedings of the 2nd International Workshop on Information Security (ISW ’99), Kuala Lumpur, Malaysia, 6–7 November 1999; pp. 225–234. [Google Scholar]
- Kim, K.; Kim, J.; Lee, B.; Ahn, G. Experimental Design of Worldwide Internet Voting System Using PKI. In Proceedings of the SSGRR, LÁquila, Italy, 6–12 August 2001; pp. 1–7. [Google Scholar]
- Boyd, C. A new multiple key cipher and an improved voting scheme. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT ’89), Houthalen, Belgium, 10–13 April 1989; pp. 617–625. [Google Scholar]
- García, D.L. A flexible e-voting scheme for debate tools. Comput. Secur. 2016, 56, 50–62. [Google Scholar] [CrossRef]
- Chow, S.; Liu, J.; Wong, D. Robust Receipt-Free Election System with Ballot Secrecy and Verifiability. In Proceedings of the 16th Annual Network & Distributed System Security Symposium (NDSS), San Diego, CA, USA, 8–11 February 2008; pp. 81–94. [Google Scholar]
- Benaloh, J.; Yung, M. Distributing the power of a government to enhance the privacy of voters. In Proceedings of the Fifth Annual ACM Symposium on Principles of Distributed Computing (PODC ’86), Calgary, AB, Canada, 11–13 August 1986; pp. 52–62. [Google Scholar]
- Cramer, R.; Gennaro, R.; Schoenmakers, B. A secure and optimally efficient multi-authority election scheme. In Proceedings of the 16th Annual International Conference on Theory and Application of Cryptographic Techniques (EUROCRYPT ’97), Konstanz, Germany, 11–15 May 1997; pp. 103–118. [Google Scholar]
- Hirt, M.; Sako, K. Efficient receipt-free voting based on homomorphic encryption. In Proceedings of the 19th International Conference on Theory and Application of Cryptographic Techniques, Bruges, Belgium, 14–18 May 2000; pp. 539–556. [Google Scholar]
- Lee, B.; Kim, K. Receipt-free Electronic Voting through Collaboration of Voter and Honest Verifier. In Proceedings of the JW-ISC, Naha, Japan, 25–26 January 2000; pp. 101–108. [Google Scholar]
- Adewole, A.P.; Sodiya, A.S.; Arowolo, O.A. A Receipt-Free Multi-Authority E-Voting System. Int. J. Comput. Appl. 2011, 30, 15–23. [Google Scholar]
- Kiayias, A.; Zacharias, T.; Zhang, B. DEMOS-2: Scalable E2E Verifiable Elections without Random Oracles. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; ACM: New York, NY, USA, 2015; pp. 352–363. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Iftene, S. General Secret Sharing Based on the Chinese Remainder Theorem with Applications in E-Voting. Electron. Notes Theor. Comput. Sci. 2007, 186, 67–84. [Google Scholar] [CrossRef]
- Cramer, R.; Franklin, M.; Schoenmakers, B.; Yung, M. Multi-Authority Secret-Ballot Elections with Linear Work. In Advances in Cryptology— EUROCRYPT ’96; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1070, pp. 72–83. [Google Scholar]
- Baudron, O.; Fouque, P.A.; Pointcheval, D.; Stern, J.; Poupard, G. Practical multi-candidate election system. In Proceedings of the 20th ACM Symposium on Principles of Distributed Computing (PODC ’01), Newport, RI, USA, 26–28 August 2001; pp. 274–283. [Google Scholar]
- Hirt, M. Receipt-free K-out-of-L voting based on elgamal encryption. In Towards Trustworthy Elections; Chaum, D., Jakobsson, M., Rivest, R.L., Ryan, P.A., Benaloh, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 64–82. [Google Scholar]
- Han, W.; Chen, K.; Zheng, D. Receipt-Freeness for Groth’s E-Voting Schemes. J. Inf. Sci. Eng. 2009, 25, 517–530. [Google Scholar]
- Ryan, P.; Peacock, T. Prêt à Voter: A Systems Perspective; Technical Report CS-TR-929; University of Newcastle: Newcastle, Australia, 2005. [Google Scholar]
- Rivest, R. The ThreeBallot Voting System. Available online: http://theory.lcs.mit.edu/rivest/Rivest-TheThreeBallotVotingSystem. pdf (accessed on 1 July 2013).
- Rivest, R.; Smith, W. Three voting protocols: ThreeBallot, VAV, and Twin. In Proceedings of the USENIX Workshop on Accurate Electronic Voting Technology (EVT ’07), Boston, MA, USA, 6–10 August 2007; Volume 16, pp. 1–14. [Google Scholar]
- Fisher, K.; Carback, R.; Sherman, A. Punchscan: Introduction and system definition of a high-integrity election system. Proceedings of Workshop on Trustworthy Elections, Cambridge, UK, 29–30 June 2006; pp. 19–29. [Google Scholar]
- Popoveniuc, S.; Hosp, B. An introduction to Punchscan. In Proceedings of the IAVoSS Workshop on Trustworthy Elections (WOTE 2006), Cambridge, UK, 29–30 June 2006; pp. 28–30. [Google Scholar]
- Chaum, D.; Essex, A.; Carback, R.; Clark, J.; Popoveniuc, S.; Sherman, A.; Vora, P. Scantegrity: End-to-end voter-verifiable optical-scan voting. IEEE Secur. Priv. 2008, 6, 40–46. [Google Scholar] [CrossRef]
- Chaum, D.; Carback, R.; Clark, J.; Essex, A.; Popoveniuc, S.; Rivest, R.; Ryan, P.; Shen, E.; Sherman, A. Scantegrity II: End-to-end verifiability for optical scan election systems using invisible ink confirmation codes. EVT 2008, 8, 1–13. [Google Scholar]
- Bohli, J.; Müller-Quade, J.; Röhrich, S. Bingo voting: Secure and coercion-free voting using a trusted random number generator. In Proceedings of the International Conference on E-Voting and Identity, Bochum, Germany, 4–5 October 2007; pp. 111–124. [Google Scholar]
- Sandler, D.; Wallach, D. Casting votes in the auditorium. In Proceedings of the USENIX Workshop on Accurate Electronic Voting Technology (EVT ’07), Boston, MA, USA, 6–10 August 2007; pp. 1–15. [Google Scholar]
- Sandler, D.; Derr, K.; Wallach, D. VoteBox: A tamper-evident, verifiable electronic voting system. In Proceedings of the USENIX Security Symposium, San Jose, CA, USA, 28 July–1 August 2008; Volume 4, pp. 349–364. [Google Scholar]
- Cross, E.V., II; McMillian, Y.; Gupta, P.; Williams, P.; Nobles, K.; Gilbert, J.E. Prime III: A user centered voting system. In Proceedings of the Extended Abstracts on Human Factors in Computing Systems (CHI ’07), San Jose, CA, USA, 28 April–3 May 2007; pp. 2351–2356. [Google Scholar]
- Dawkins, S.; Sullivan, T.; Rogers, G.; Cross, E.V., II; Hamilton, L.; Gilbert, J.E. Prime III: An innovative electronic voting interface. In Proceedings of the 14th International Conference on Intelligent User Interfaces (IUI ’09), Sanibel Island, FL, USA, 8–11 February 2009; pp. 485–486. [Google Scholar]
- Scytl. White paper: Auditability and Voter-Verifiability for Electronic Voting Terminals. Available online: http://www.scytl.com/images/upload/home/PNYX.VM_White_Paper.pdf (accessed on 1 July 2013).
- SCYTL. Pnyx.VM: Auditability and Voter-Verifiability for Electronic Voting Terminals; SCYTL: Barcelona, Spain, 2004. [Google Scholar]
- SCYTL. Pnyx.core: The Key to Enabling Reliable Electronic Elections; SCYTL: Barcelona, Spain, 2005. [Google Scholar]
- Clarkson, M.; Hay, B.; Inge, M.; Wagner, D.; Yasinsac, A. Software Review and Security Analysis of Scytl Remote Voting Software. Available online: http://www.cs.cornell.edu/~clarkson/papers/scytl-odbp.pdf (accessed on 16 August 2017).
- Kiayias, A.; Korman, M.; Walluck, D. An Internet voting system supporting user privacy. In Proceedings of the 22nd Annual Computer Security Applications Conference (ACSAC’06), Miami Beach, FL, USA, 11–15 December 2006; IEEE Computer Society: Washington, DC, USA, 2006; pp. 165–174. [Google Scholar]
- Karlof, C.; Sastry, N.; Wagner, D. Cryptographic Voting Protocols: A Systems Perspective. In Proceedings of the 14th conference on USENIX Security Symposium, Baltimore, MD, USA, 31 July–5 August 2005; Volume 5, pp. 33–50. [Google Scholar]
- Bernhard, D.; Cortier, V.; Galindo, D.; Pereira, O.; Warinschi, B. SoK: A comprehensive analysis of game-based ballot privacy definitions. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 18–20 May 2015; IEEE Computer Society: Los Alamitos, CA, USA, 2015; pp. 499–516. [Google Scholar]
- Cortier, V.; Galindo, D.; Küsters, R.; Müller, J.; Truderung, T. SoK: Verifiability Notions for E-Voting Protocols. In Proceedings of the 37th IEEE Symposium on Security and Privacy (S&P ’16), San Jose, CA, USA, 23–25 May 2016; pp. 779–798. [Google Scholar]
- Adida, B. Helios: Web-based open-audit voting. In Proceedings of the USENIX Security Symposium, San Jose, CA, USA, 28 July–1 August 2008; USENIX Association: Berkeley, CA, USA, 2008; Volume 17, pp. 335–348. [Google Scholar]
- Benaloh, J. Simple verifiable elections. In Proceedings of the USENIX/Accurate Electronic Voting Technology Workshop 2006 on Electronic Voting Technology Workshop (EVT/WOTE. USENIX), Vancouver, BC, Canada, 1 August 2006; pp. 1–10. [Google Scholar]
- Sako, K.; Kilian, J. Receipt-free mix-type voting scheme. In Advances in Cryptology—UROCRYPT ’95; Springer: Berlin/Heidelberg, Germany, 1995; pp. 393–403. [Google Scholar]
- Adida, B.; De Marneffe, O.; Pereira, O.; Quisquater, J. Electing a University President Using Open-Audit Voting: Analysis of Real-World Use of Helios. In Proceedings of the Conference on Electronic Voting Technology/Workshop on Trustworthy Elections (EVT/WOTE), Montreal, QC, Canada, 10–11 August 2009. [Google Scholar]
- Cortier, V.; Fuchsbauer, G.; Galindo, D. BeleniosRF: A Strongly Receipt-Free Electronic Voting Scheme.Cryptology ePrint Archive, Report 2015/629, 2015. Available online: http://eprint.iacr.org/2015/629 (accessed on 16 August 2017).
- Nakajima, A. Decentralized voting protocols. In Proceedings of the International Symposium on Autonomous Decentralized Systems, Kawasaki, Japan, 30 March–1 April 1993; IEEE Computer Society Press: Los Alamitos, CA, USA, 1993; pp. 247–254. [Google Scholar]
- Kulyk, O.; Neumann, S.; Feier, C.; Volkamer, M.; Koster, T. Electronic voting with fully distributed trust and maximized flexibility regarding ballot design. In Proceedings of the 6th International Conference on Electronic Voting (EVOTE), Lochau, Austria, 29–31 October 2014; IEEE: Piscataway, NJ, USA; pp. 1–10. [Google Scholar]
- Commission, T.U.E.A. Polling Places 2004 General Election: EAC Election Day Survey. Available online: https:/ electioncenter.org/documents/EAC-2004%20election%20surveyFull_Report_wTables.pdf (accessed on 16 August 2017).
- Benaloh, J. Rethinking Voter Coercion: The Realities Imposed by Technology. In Proceedings of the 2013 Electronic Voting Technology Workshop/Workshop on Trustworthy Elections (EVT/WOTE ’13), Washington, DC, USA, 12–13 August 2013; USENIX: Berkeley, CA, USA, 2013; pp. 82–105. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).