Multiparty Delegated Quantum Computing

Abstract

Quantum computing has seen tremendous progress in the past few years. However, due to limitations in the scalability of quantum technologies, it seems that we are far from constructing universal quantum computers for everyday users. A more feasible solution is the delegation of computation to powerful quantum servers on the network. This solution was proposed in previous studies of blind quantum computation, with guarantees for both the secrecy of the input and of the computation being performed. In this work, we further develop this idea of computing over encrypted data, to propose a multiparty delegated quantum computing protocol in the measurement-based quantum computing framework. We prove the security of the protocol against a dishonest server and against dishonest clients, under the assumption of common classical cryptographic constructions.

1. Introduction

Since the early days of quantum computing and cryptography, research has been focused on finding secure communication protocols for different cryptographic tasks. However, the no-go results for bit commitment [1,2] and oblivious transfer [3] soon provided evidence that it is not possible to guarantee perfect security against any type of quantum adversary. In fact, the authors of [4] showed that any non-trivial protocol that implements a cryptographic primitive necessarily leaks information to a dishonest player. It directly follows that two-party unitaries, and by consequence multi-party ones, cannot be used without further assumptions, to securely implement cryptographic protocols. An important question that arises then is what are the cryptographic assumptions that are needed in order to achieve secure multiparty computation.

Dupuis et al. [5,6] examined the case of two-party computation and showed that in order to guarantee security, access to an AND gate for every gate that is not in the Clifford group plus a final SWAP gate between the two parties’ registers are required. In the multiparty setting, Ben-Or et al. [7] rely on an honest majority assumption in order to build a verifiable quantum secret sharing scheme that is the basis of the multiparty quantum computation. From a different perspective, much research in quantum computing has been focused on delegation of computation [8,9,10,11]. This is because the current state-of-the-art is still far from constructing scalable quantum devices, and it seems that the first quantum networks will rely on the use of a limited number of powerful quantum servers. Common requirements from delegated computation schemes are that they are provably secure (the input of the computation remains private), blind (the computation performed is hidden from the server) and verifiable (honest participants can verify the correctness of the computation).

In this work, we extend previous research on quantum computing, by examining the problem of secure delegation of a multiparty quantum computation to a powerful server. More specifically, we suppose that a number of clients holding some quantum input state want to perform a unitary operation on it, but are lacking the computational abilities to do so. They would therefore like to delegate the computation to a server, while keeping their quantum inputs, quantum outputs and the performed computation secret. In the proposed protocol, the quantum operations required from the clients are limited to creating $\left|+\right.⟩$ states and applying X gates and rotations around the z-axis.

As already mentioned, in order to provide any type of security in the multiparty setting, we need to make some assumptions about the dishonest parties. In this work, we will need two assumptions. First, we will assume that the clients have secure access to classical multiparty functionalities, which we will treat as oracles. This is a common construction in classical secure multiparty computation and uses assumptions on the participating parties, like honest majority or difficulty inverting specific one-way functions. The second assumption is that a set of malicious clients cannot corrupt the server, and the other way around. We therefore prove security against two adversarial models, against a dishonest server and against a coalition of dishonest clients. To achieve this type of security, all clients contribute to some form of quantum encryption process, while at the same time, they commit to the values that they use for the encryption. Security in the more general scenario, where a server and some clients collaborate to cheat, remains an open question (however, see [12] for a relevant model with only one client, where the server is also allowed to provide an input).

A big advantage over previous protocols [7] is that quantum communication between all clients is no longer required in order to provide security against dishonest participants. By using a remote state preparation procedure, we manage to remove any quantum communication between clients, making our protocol adaptable to a client/server setting. More interestingly, the quantum communication from the clients to the server can be done in single-qubit rounds, not necessitating any quantum memory from the clients. Furthermore, all quantum communication takes place in the preparation (offline) phase, which makes the computation phase much more efficient, since it only requires classical communication.

Finally, we should note that in this work, we are focusing on proving security against malicious quantum adversaries in order to provide a simple protocol for quantum multiparty computation. As such, no guarantee is given on the correctness of the computation outcome. However, it is normal to assume that in future quantum networks, the quantum servers would want to maintain a good reputation and provide the correct outcome to the clients in case the results get cross-checked with other competing servers. In principle though, it seems possible to add verification processes in our protocol, by enforcing honest behaviour, following the work of [6,11].

2. Materials and Methods

2.1. Measurement-Based Quantum Computing

Delegated computation is commonly studied in the Measurement Base Quantum Computing (MBQC) model [8], where a computation is described by a set of measurement angles on an entangled state. A formal way to describe an MBQC computation was proposed in [13] and is usually referred to as an MBQC pattern. In the general case of quantum input and quantum output, such a pattern is defined by a set of qubits (V), a subset of input qubits (I), a subset of output qubits (O) and a sequence of measurements $\{{\varphi }_j\}$ acting on qubits in $O^c:=V\backslash O$. Due to the probabilistic nature of the measurements, these angles need to be updated according to a specific structure. This structure is described by the flow f of the underlying graph G of the entangled state. The flow is a function from measured qubits to non-input qubits along with a partial order over the nodes of the graph such that each qubit j is X-dependent on qubit $f^{-1}(j)$ and Z-dependent on qubits i for which $j\in N_G(f(i))$, where $N_G(j)$ is the set of neighbours of node j in graph G. We will denote the former set of qubits by $S_j^X$ and the latter set of qubits by $S_j^Z$. If we define the outcome of a measurement on qubit i as $s_i$, then the new measurement angle for qubit j is:

$${\varphi }_j^{\prime }={(-1)}^{s_j^X}{\varphi }_j+s_j^z\pi$$

(1)

where $s_j^X={⨁}_{i\in S_j^X}{s}_i$ and $s_j^Z={⨁}_{i\in S_j^Z}{s}_i$ (we will use this notation throughout the paper).

2.2. Multiparty Delegated Quantum Computing

In this section, we will give some necessary definitions for multiparty delegated quantum computing protocols. We will consider multiple clients $C_1,...,C_n$ that have registers ${\mathcal{C}}_1,...,{\mathcal{C}}_n$. To allow the computation to be done in a delegated way, we also introduce the notion of a server S, who is responsible for performing the computation of a unitary U on input ${\rho }_{in}$. The server has register $\mathcal{S}$, but no legal input to the computation. We also denote with $\mathcal{D}(\mathcal{A})$ the set of all possible quantum states (i.e., positive semi-definite operators with Trace 1) in register $\mathcal{A}$. We denote the input state (possibly entangled with the environment R) as:

$${\rho }_{in}\in \mathcal{D}({\mathcal{C}}_1\otimes \cdots \otimes {\mathcal{C}}_n\otimes \mathcal{R})$$

(2)

In what follows, we consider that the input registers of the participants also contain the classical information necessary for the computation. We denote with $\mathcal{L}(\mathcal{A})$ the set of linear mappings from $\mathcal{A}$ to itself, and we call a superoperator $\mathsf{\Phi }:\mathcal{L}(\mathcal{A})\to \mathcal{L}(\mathcal{B})$ that is completely positive and trace preserving a quantum operation. Finally, we will denote with ${\mathbb{I}}_{\mathcal{A}}$ and ${\mathbf{1}}_{\mathcal{A}}$ the totally mixed state and the identity operator, respectively, in register $\mathcal{A}$.

In order to analyse the properties of the protocol to follow, we will first consider an abstract system that takes as input ${\rho }_{in}$ and the computation instructions for implementing U in MBQC (i.e., the measurement angles $\{{\varphi }_j\}$) and outputs a state ${\rho }_{out}$. We will call such a resource an ideal functionality because this is what we want to implement. In order to allow the server to act dishonestly, we also allow the ideal functionality to accept input from the server, which dictates the desired deviation in the form of quantum input and classical information (Figure 1). In the case where the server is acting honestly, the ideal functionality is outputting the correct output ${\rho }_{out}=(U\otimes {\mathbf{1}}_{\mathcal{R}})·{\rho }_{in}$, where for the ease of use, we will write $U·\rho$ instead of $U\rho U^{†}$ each time we talk about applying a unitary operation U to a quantum state $\rho$.

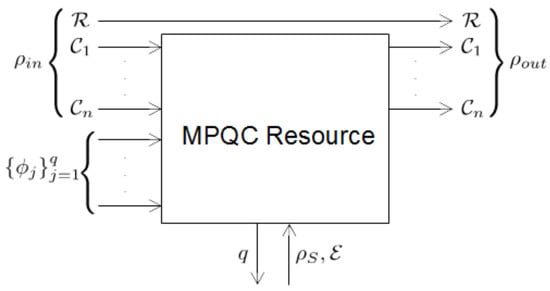
Figure 1. The ideal functionality that implements a multiparty quantum computation (MPQC), given by measurement angles ${\{{\varphi }_j\}}_{j=1}^q$ on input ${\rho }_{in}$.

Definition 1 (MPQC Delegated Resource).

A multiparty quantum computation (MPQC) delegated resource gets input ${\rho }_{in}$ and computation instructions from n clients and leaks the size of the computation q to the server. The server can then decide to input a quantum map and a quantum input. The output of the computation is ${\rho }_{out}=(U\otimes {\mathbf{1}}_{\mathcal{R}})·{\rho }_{in}$ if the server does not deviate; otherwise, the output is defined by the quantum deviation on the inputs of the server and the clients.

A protocol can in general be modelled by a sequence of local quantum operations on the participants’ registers together with some oracle calls, which are joint quantum operations on the registers. Here, we will consider the delegated version of communication protocols [5,6,7], where n clients are delegating the computation to a server.

Definition 2.

We denote a t-step delegated protocol with oracle calls between clients $C_k$ $(k\in [n])$ and a server S, with $\pi \mathcal{O}=({\{{\pi }_k\}}_{k=1}^n,{\pi }_S,\mathcal{O})$. If we denote by ${\mathcal{C}}_k$ and $\mathcal{S}$ the registers of the clients and the server, respectively, then:

• Each client’s strategy ${\pi }_k,k\in [n]$ consists of a set of local quantum operators $(L_1^k,\cdots ,L_t^k)$ such that $L_i^k:\mathcal{L}({\mathcal{C}}_k)\to \mathcal{L}({\mathcal{C}}_k)$ for $1\le i\le t$.
• The server’s strategy ${\pi }_S$ consists of a set of local quantum operators $(L_1^S,\cdots ,L_t^S)$ such that $L_i^S:\mathcal{L}(\mathcal{S})\to \mathcal{L}(\mathcal{S})$ for $1\le i\le t$.
• The oracle $\mathcal{O}$ is a set of global quantum operators $\mathcal{O}=({\mathcal{O}}_1,\cdots ,{\mathcal{O}}_t)$ such that ${\mathcal{O}}_i:\mathcal{L}({\mathcal{C}}_1\otimes \cdots \otimes {\mathcal{C}}_n\otimes \mathcal{S})\to \mathcal{L}({\mathcal{C}}_1\otimes \cdots \otimes {\mathcal{C}}_n\otimes \mathcal{S})$ for $1\le i\le t$.

Therefore, at each step i of the protocol $\pi \mathcal{O}$, all participants apply their local operations, and they also jointly apply a global ${\mathcal{O}}_i$. If we define the joint quantum operation $L_i=L_i^1\otimes \cdots \otimes L_i^n\otimes L_i^S$, then the quantum state at step i when the input state ${\rho }_{in}$ is defined by Equation (2) is:

$${\rho }_i({\rho }_{in}):=({\mathcal{O}}_i{L}_i\cdots {\mathcal{O}}_1{L}_1)·{\rho }_{in}$$

(3)

At the end of the protocol, the output will be:

$$\pi \mathcal{O}({\rho }_{in})=({\mathcal{O}}_t{L}_t\cdots {\mathcal{O}}_1{L}_1)·{\rho }_{in}$$

(4)

A commonly-used oracle is the communication oracle that transmits information from one participant to the other, by just moving the state between registers. Due to no-cloning, however, when the information transmitted is a quantum state, we require that the oracle also erases the transmitted information from the original party’s register.

Another oracle that we will use in our protocol is what we call the computation oracle, which can be thought of as a classical ideal functionality (i.e., a box that takes inputs from all parties and outputs the correct outputs of the functionality on the specific inputs). All classical multiparty computation in this work will be done with the help of such a computation oracle. Under standard cryptographic assumptions, there exist classical protocols for building such oracles that emulate in a composable way any classical multiparty functionality. In [14], this is shown for an honest majority of participants, given that they share pairwise secure classical channels and a physical broadcast channel. Since the last physical requirement is quite strong and constructions of broadcast channels in a non-physical way are usually based on authenticated Byzantine agreement, which is non-composable, we are led to relax the requirement of the honest majority to either having more than $2/3$ of honest participants or to allow them access to other cryptographic constructions like oblivious transfer [15,16]. The quantum lifting theorem of Unruh [17] states that if there exists such a construction that is secure against classical adversaries, then the same also holds against quantum adversaries, therefore allowing us to replace any classical multiparty computation in a quantum protocol, by using the computation oracle. This result was proven in the universal composability framework, but it also holds in the Abstract Cryptography (AC) framework that we will use in this paper, since the two are equivalent when there is only one malicious participant (i.e., we need to build one global simulator).

2.2.1. Properties

In the following section, we will present a delegated protocol $\pi \mathcal{O}$ and claim that it emulates the MPQC resource of Figure 1. We can evaluate how well this is done by measuring how well a global distinguisher can understand whether it is interacting with one system or the other. This is quantified by using a pseudo-metric on the space of the resources that is often referred to as the distinguishing advantage of the distinguisher. The reason why a global distinguisher is used to quantify security instead of an adversary is composability. In what follows, we will use the AC composable framework [18] to model the properties of our protocol and prove its indistinguishability from the ideal functionality of Figure 1.

We will deal with three distinct cases of malicious behaviour: (a) when all clients and the server are honest, (b) when the server is dishonest and (c) when a subset $\mathcal{D}$ of clients is dishonest. For Case (a) where everyone acts honestly, we consider that the MPQC resource $\mathcal{M}$ has a filter ⊥ blocking all dishonest behaviour, and therefore, we want to prove that:

$$d(\pi \mathcal{O},{\mathcal{M}}_{\perp })\le ϵ$$

(5)

In Case (b) when the server is acting dishonestly, we want that:

$$d({\pi }_1\cdots {\pi }_n\mathcal{O},{\sigma }_S\mathcal{M})\le ϵ$$

(6)

where ${\sigma }_S$ is a simulator for the dishonest server. Finally, for Case (c), when a subset $\mathcal{D}$ of clients is dishonest, we want to prove that:

$$d({\pi }_{\mathcal{H}}\mathcal{O}{\pi }_S,{\sigma }_{\mathcal{D}}{\mathcal{M}}_{\perp })\le ϵ$$

(7)

where $\mathcal{H}$ is the set of honest clients and ${\sigma }_{\mathcal{D}}$ is a simulator for the dishonest clients.

In the above equations, the filter ⊥ blocks input from the server’s side, since the MPQC resource of Definition 1 accepts deviated behaviour only from the server. The clients, on the other hand, have the liberty to choose the quantum state that they will give as input to the MPQC resource. However, this does not mean that the clients behave honestly during the protocol. We will see that the protocol “enforces” honest behaviour on clients by asking them to secretly share their classical values in a verifiable way, in order to commit to using the same values during the protocol. This is done using Verifiable Secret Sharing (VSS) schemes, where a dealer wants to share their secret information with all parties, in such a way that a group of honest parties can reconstruct the sharing without the help of the dealer. There are two stages in a VSS protocol: the sharing stage, where the dealer and the parties exchange messages depending on the dealer’s secret and the parties’ chosen randomness, and the reconstruction stage, where the parties apply a function on their received messages in order to reconstruct the dealer’s secret. VSS schemes can be viewed as a multiparty computation, and we can therefore use a computation oracle under the same cryptographic assumptions as previously discussed (see [19,20] for examples of VSS based on different constructions).

The distinguishing advantage of Equations (5)–(7) can reduce to simple measures of distance between the states that a distinguisher sees, when interacting with the real and ideal system. For example if the outputs of the resources are classical strings, then a distinguisher will be given strings sampled from either the probability distribution produced by the ideal or the real resource. He/she then needs to decide from which one the strings were sampled; therefore, the distinguishing advantage is equal to the total variation distance between the two probability distributions. If the outputs of the resources are quantum states, then the distinguishing advantage is given by the Helstrom measurement, which depends on the trace distance of the states of the two systems.

3. The Protocol

In this section, we propose a cryptographic protocol that constructs an MPQC resource using quantum and classical communication between the n clients and the server. We suppose that the clients want to perform a unitary U on their quantum inputs, translated in an MBQC pattern on a brickwork state using measurement angles ${\{{\varphi }_j\}}_{j=1}^q$, where $q=|O^c|$. For simplicity, we consider that each client $C_k$ ($k\in [n]$) has one qubit as input and one qubit as output, but it is easy to generalize to any other case. We will use the following labelling: client $C_k$ has as input qubit “k” and as output qubit “$q+k$”, while the first qubit of the second column in Figure 2 has label “$n+1$”, the last one in the second column “$2n$”, etc.

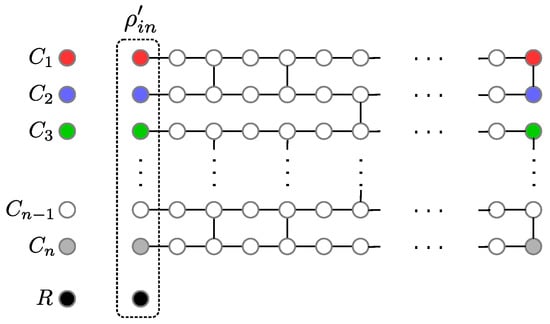
Figure 2. The brickwork state with the encrypted quantum input in the first layer of computation. The colours of the qubits denote their origin, while the encrypted input state can also be entangled with the environment R. During the computation, all qubits will be measured except the last layer.

We want to guarantee that the private data of the clients remain secret during the protocol. Here, each client’s data consist of the quantum input and output, while we consider that the measurement angles are not known to the server (they can be known to all clients or to a specific client that delegates the computation). The protocol first starts with a process named “remote state preparation” [21]. The clients send quantum states to the server, who then entangles them and measures all but one. In the case where one of the clients has a quantum input, he/she sends that quantum state one-time padded to the server, while the rest of the clients send Z-rotated $\left|+\right.⟩$ states to the server (Algorithm 1, Figure 3). In the case of the extra “operational” qubits in $O^c\backslash I$, all clients send rotated $\left|+\right.⟩$ states to the server (Algorithm 2, Figure 4). In this way, the clients remotely prepare quantum states at the server’s register that are “encrypted” using secret data from all of them, without having to communicate quantum states to each other.

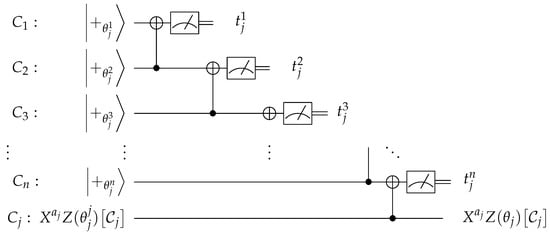
Figure 3. Remote state preparation with quantum input (Algorithm 1). Client $C_j$ performs a one-time pad on his/her register ${\mathcal{C}}_j$, and the result of the circuit remains one-time padded, where ${\theta }_j={\theta }_j^j+{\sum }_{k=1,k\ne j}^n{(-1)}^{{⨁}_{i=k}^n{t}_j^i+a_j}{\theta }_j^k$.

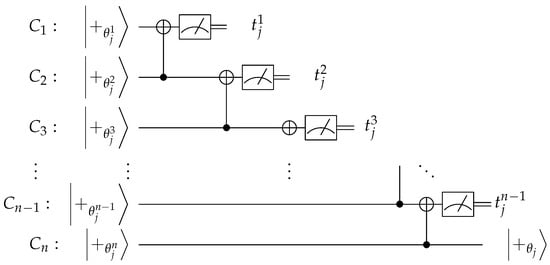
Figure 4. Remote state preparation without quantum input (Algorithm 2), where ${\theta }_j={\theta }_j^n+{\sum }_{k=1}^{n-1}{(-1)}^{{⨁}_{i=k}^{n-1}{t}_j^i}{\theta }_j^k$.

However, since each client is supposed to only choose their own quantum input, and not affect the input of the other clients, the protocol should ask the clients to commit to using the same classical values for the duration of the protocol. This is done by using a VSS scheme each time a classical value is chosen by a client. In the case of the “remote state preparation” process, each time a client sends a Z-rotated $\left|+\right.⟩$ state, that rotation needs to be corrected at a later point in the protocol. In order to ensure that the “reverse” rotation is used later, the clients send many copies of randomly Z-rotated $\left|+\right.⟩$ states (Algorithm 3) and commit (via VSS) to the rotations used. They then get tested by the server and the rest of the clients on the correctness of the committed values. A similar commitment takes place for the quantum one-time pad that each client performs on their quantum input, since the classical values used affect the measurement angles of consecutive layers of computation.

At the end of the “remote state preparation” phase, the server entangles the non-measured states in a universal graph state (for example, in the brickwork state of Figure 2 [11]). Since the proposed protocol uses MBQC to compute the desired functionality, there is an unavoidable dependency between measurement angles of the qubits in different layers of computation. This means that the clients need to securely communicate between them and with the server, in order to jointly compute the updated measurement angles, taking into account the necessary corrections from the previous measurements and the dependency sets of each qubit. This procedure is purely classical and uses VSS schemes and a computation oracle to calculate the necessary values at each step of the protocol and to ensure that the clients behave honestly.

Algorithm 1 State preparation for $j\in I$.

server stores states received from clients $C_k$ to distinct registers ${\mathcal{S}}_k\subset \mathcal{S}$ ($k=1,\cdots ,n$); for $k=1,\cdots ,n-1$        if $k=j$ then               break;        if $k=n-1$ and $j=n$ then               break;        if $k=j-1$, then               CNOT on ${\mathcal{S}}_k\otimes {\mathcal{S}}_{k+2}$;        else               CNOT on ${\mathcal{S}}_k\otimes {\mathcal{S}}_{k+1}$;        end;        measure state in ${\mathcal{S}}_k$ and get outcome $t_j^k$; end; if $j=n$ then        CNOT on ${\mathcal{S}}_{n-1}\otimes {\mathcal{S}}_n$;        measure state in ${\mathcal{S}}_{n-1}$ and get outcome $t_n^{n-1}$; else        CNOT on $({\mathcal{S}}_n\otimes {\mathcal{S}}_j)$;        measure state in ${\mathcal{S}}_n$ and get outcome $t_j^n$; end;

Algorithm 2 (State preparation for $j\in O^c\backslash I$).

server stores states received from clients $C_k$ to distinct registers ${\mathcal{S}}_k\subset \mathcal{S}$ ($k=1,\cdots ,n$); for $k=1,\cdots ,n-1$        CNOT on ${\mathcal{S}}_k\otimes {\mathcal{S}}_{k+1}$;        measure state in ${\mathcal{S}}_k$ and get outcome $t_j^k$; end;

Finally, in the output phase, each output qubit $j\in O$ is naturally encrypted due to the corrections propagated during the computation. Qubit j is sent to the legitimate recipient $C_{j-q}$, while the operation that is needed to decrypt it is the $X^{s_j^X}{Z}^{s_j^Z}$. The classical values necessary to compute $s_j^X$ and $s_j^Z$ are then computed from the secret shares of all clients and sent to client $C_{j-q}$, who applies the necessary quantum operation.

Algorithm 3 (Enforcing honest behaviour for client $C_k$).

Client $C_k$ sends m qubits $\left|{+}_{{\theta }_i^k}\right.⟩=\frac{1}{\sqrt{2}}(\left|0\right.⟩+e^{i{\theta }_i^k}\left|1\right.⟩)$ to the server and secretly shares the values ${\{{\theta }_i^k\}}_{i=1}^m$ with all clients, using a VSS scheme. The server requests the shared values from the clients for all, but one qubit, and measures in the reconstructed bases. If the bases agree with the results of the measurements, then with high probability, the remaining state is correctly formed in relation to the shared angle.

4. Analysis of the Protocol

4.1. Correctness

Theorem 1.

Algorithm 4 emulates the filtered ideal resource ${\mathcal{M}}_{\perp }$ of Figure 1.

The validity of Theorem 1 comes directly from the correctness of the individual circuits implementing Algorithms 1 and 2, as well as the propagation of Z and X corrections through the flow of the computation. A detailed proof is given in the Appendix that shows that:

$$d(\pi \mathcal{O},{\mathcal{M}}_{\perp })=0$$

therefore, a distinguisher cannot tell the difference between the real communication protocol and an interaction with the ideal MPQC resource when all participants are honest.

Algorithm 4 Multiparty quantum computing protocol.

A quantum input ${\rho }_{in}$ and measurement angles ${\{{\varphi }_j\}}_{j=1}^q$ for qubits $j\in O^c$. Preparation phase quantum input: For $j\in I$ Client $C_j$ applies a one-time pad $X^{a_j}Z({\theta }_j^j)$ to his/her qubit, where $a_j{\in }_R\{0,1\}$ and ${\theta }_j^j{\in }_R{\{l\pi /4\}}_{l=0}^7$ and sends it to the server. He/she secretly shares the values $a_j$ and ${\theta }_j^j$ with the other clients. Each client $C_k(k\ne j)$, runs Algorithm 3 with the server. If all clients pass the test, the server at the end has $n-1$ states $\left|{+}_{{\theta }_j^k}\right.⟩=\frac{1}{\sqrt{2}}(\left|0\right.⟩+e^{i{\theta }_j^k}\left|1\right.⟩)$ for $k\ne j$. The server runs Algorithm 1 and announces outcome vector ${\mathbf{t}}_j$.  At this point the server has the state ${\rho }_{in}^{\prime }=\left(X^{a_1}Z({\theta }_1)\otimes \cdots \otimes X^{a_n}Z({\theta }_n)\otimes {\mathbf{1}}_{\mathcal{R}}\right)·{\rho }_{in}$, where $${\theta }_j={\theta }_j^j+\sum _{k=1,k\ne j}^n{(-1)}^{{⨁}_{i=k}^n{t}_j^i+a_j}{\theta }_j^k$$ (8) non-output/non-input qubits: For $j\in O^c\backslash I$ 4. All clients $C_k$, $k\in [n]$ run Algorithm 3 with the server. If all clients pass the test, the server at the end has n states $\left|{+}_{{\theta }_j^k}\right.⟩=\frac{1}{\sqrt{2}}(\left|0\right.⟩+e^{i{\theta }_j^k}\left|1\right.⟩)$ for $k=1,\cdots ,n$. 5. The server runs Algorithm 2 getting outcome vector ${\mathbf{t}}_j$. He/she ends up with the state $\left|{+}_{{\theta }_j}\right.⟩$, where: $${\theta }_j={\theta }_j^n+\sum _{k=1}^{n-1}{(-1)}^{{⨁}_{i=k}^{n-1}{t}_j^i}{\theta }_j^k$$ (9) output qubits: For $j\in O$, the server prepares $\left|+\right.⟩$ states. graph state: The server entangles the $n+q$ qubits to a brickwork state by applying ctrl-Z gates. Computation phase non-output qubits: For $j\in O^c$ All clients $C_k$, $k=1,\cdots ,n$ choose random $r_j^k\in \{0,1\}$, which they secretly share with the other clients. Then, using a computation oracle, they compute the measurement angle of qubit j: $${\delta }_j:={\varphi }_j^{\prime }+\pi r_j+{\theta }_j$$ (10) where undefined values are equal to zero, or otherwise: ${\varphi }_j^{\prime }={(-1)}^{a_j+s_j^X}{\varphi }_j+s_j^Z\pi +a_{f^{-1}(j)}\pi$. $r_j={⨁}_{k=1}^n{r}_j^k$. $s_i=b_i\oplus r_i$, for $i\le j$. The server receives ${\delta }_j$ and measures qubit j in basis $\{\left|{+}_{{\delta }_j}\right.⟩,\left|{-}_{{\delta }_j}\right.⟩\}$, getting result $b_j$. He/she announces $b_j$ to the clients. output qubits: For $j\in O$, the server sends the “encrypted” quantum state to client $C_{j-q}$.    All participants jointly compute $s_j^X$ and $s_j^Z$ and send it to client $C_{j-q}$, who applies operation    $Z^{s_j^Z}{X}^{s_j^X}$ to retrieve the actual quantum output.

4.2. Malicious Server

The proof of security against a malicious server that is allowed to deviate from the protocol, by applying operations on the data he/she receives, is based on quantum teleportation. As observed in [22], for all of the quantum states sent to the server in Algorithm 4, there exists an equivalent circuit that sends half an EPR pair $\frac{1}{\sqrt{2}}(\left|00\right.⟩+\left|11\right.⟩)$ to the server and then ’teleports’ to them via measurement of the quantum input. It is then easy to build a simulator for the server ${\sigma }_S$, which creates EPR pairs and sends half to the server and half to an MPQC resource that performs the delayed measurement for the teleportation.

Theorem 2.

Algorithm 4 is secure against a malicious server.

Proof. 

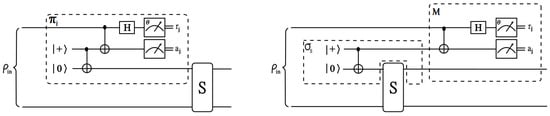
In order to show that Algorithm 4 is secure against a malicious server, we will argue that Equation (6) holds for a simulator and an MPQC resource running Algorithms 5 and 6, respectively. We want to be sure that the two resources ${\pi }_1\cdots {\pi }_n\mathcal{O}$ and ${\sigma }_S\mathcal{M}$ implement the same map, in other words that the outputs are indistinguishable. The equivalence comes from the fact that every time there is a quantum message sent to the server, there is an equivalent circuit based on teleportation that uses an EPR pair to transmit the same quantum state to the server.

More specifically, in Step 1 of Algorithm 4, client $C_j$ can equivalently create an EPR pair, entangle it to their quantum input and then measure the input wire using angle ${\theta }_j^j$ and the EPR-half in the computational basis. The unmeasured EPR-half now contains the information of the input wire (up to corrections depending on the measurement outcomes of the other two wires). Due to no-signalling, the two measurements can also be delayed till a later stage (for example till after the server has sent some reply). This is very convenient when deciding on what angles ${\delta }_j$ to send to the server in Step 1 of the computation phase; since the angle ${\theta }_j$ can be decided later, angle ${\delta }_j$ can be chosen at random and then corrected by the measurement done on the entangled state (i.e., instead of choosing ${\theta }_j$ at random and fixing ${\delta }_j$, it is equivalent to doing it the other way around).

From this, it is easy to break the procedure into two processes (see Figure 5). The first one creates the EPR pair, sends half to the server, chooses random measurement angles ${\delta }_j$ to send to the server and receives messages from them. The second entangles the other EPR half with the quantum input and chooses their measurement angles based on ${\delta }_j$, the measurement pattern $\{{\varphi }_j\}$ and the information received from the server. If we now name the first process the simulator ${\sigma }_S$ and the second process the MPQC resource $\mathcal{M}$, we can see that ${\sigma }_S$ has at no point access to any information on either the quantum input of the clients or the measurement pattern that is being implemented.

Figure 5. The equivalence between the circuit of client $C_j$ sending his/her encrypted quantum input in Algorithm 4 and the delayed measurement circuits of the simulator and the MPQC resource of Algorithms 5 and 6 for the same action (see also [22]).

The same holds for any quantum message sent from any client to the server: there is an equivalent circuit based on teleportation that allows the client to delay the choice of measurement angle ${\theta }_j$ till after receiving information from the server. For a detailed proof based on a series of equivalent protocols that show the full transition from Algorithm 4 to Algorithms 5 and 6, see Appendix A. ☐

Algorithm 5 Simulator for the server.

non-output qubits: For $j\in O^c$ ${\sigma }_S$ creates an EPR pair and sends one half of it to the server. ${\sigma }_S$ runs Algorithm 3 on behalf of the clients $C_k,k\ne j$ when $j\in I$ and of the clients $C_k,k\in [n-1]$ for $j\in O^c\backslash I$ sending to the server half EPR pairs and always accepting. ${\sigma }_S$ receives vector ${\mathbf{t}}_j$. ${\sigma }_S$ sends ${\delta }_j{\in }_R{\{l\pi /4\}}_{l=1}^7$ to the server and receives a reply $b_j\in \{0,1\}$. output qubits: For $j\in O$ ${\sigma }_S$ receives n qubits from the server. ${\sigma }_S$ sends the other halves of the EPR pairs, the received quantum states, as well as ${\delta }_j$, $b_j$ and ${\mathbf{t}}_j$ for $j=1,\cdots ,q$, to the MPQC resource.

Algorithm 6 MPQC resource.

The resource receives the n qubits of ${\rho }_{in}$ from the clients and all the information from ${\sigma }_S$. For $j\in I$: the resource performs a CNOT on the corresponding EPR half with the input qubit as control and measures the EPR half in the computational basis, getting result $a_j$. It chooses random measurement angles ${\widehat{\theta }}_j^k$ for the qubits coming from clients $C_k,k\ne j$, sets: $${\widehat{\theta }}_j^j:={\delta }_j-{\varphi }_j^{\prime }-\sum _{k=1,k\ne j}^n{(-1)}^{{⨁}_{i=k}^n{t}_j^i+a_j}{\widehat{\theta }}_j^k$$ and measures the corresponding qubits. For $j\in O^c\backslash I$, it chooses random measurement angles ${\widehat{\theta }}_j^k$ for clients $C_k,k\in [n-1]$, sets: $${\widehat{\theta }}_j^n:={\delta }_j-{\varphi }_j^{\prime }-\sum _{k=1}^{n-1}{(-1)}^{{⨁}_{i=k}^{n-1}{t}_j^i}{\widehat{\theta }}_j^k$$ and measures the corresponding qubits. In the computation of the angles, undefined values are equal to zero, and: ${\varphi }_j^{\prime }={(-1)}^{a_j+s_j^X}{\varphi }_j+s_j^Z\pi +a_{f^{-1}(j)}\pi$. $r_j={⨁}_{k=1}^n{r}_j^k$. $s_i=b_i\oplus r_i$, for $i\le j$. For $j\in O$: the resource performs corrections $Z^{s_j^Z}{X}^{s_j^X}$ on the remaining qubits.

We have proven that a server does not learn anything about the inputs of the clients, since the protocol emulates an ideal MPQC resource and a simulator that reproduces the view of the malicious server without having access to the clients’ input. From this result, we prove at the same time that the computation is done in a blind way, meaning that the server does not know what computation he/she is performing or equivalently that the measurement pattern (i.e., the angles ${\varphi }_j$) remains hidden from him/her.

Corollary 1.

The protocol is blind against a malicious server.

The proof of blindness follows directly from Theorem 2, since in the simulated model, the server interacts only with the simulator ${\sigma }_S$, which just gives input to the MPQC resource and therefore has no access to the measurement angles during the computation.

4.3. Malicious Clients

Theorem 3.

The protocol is secure against a coalition of malicious clients.

Proof. 

Algorithm 7 presents a simulator ${\sigma }_C$ that receives communication from a malicious coalition of clients on its external interface. For the ease of use, we will consider one malicious client $C_c$ with one input qubit, but this can easily be extended by thinking of all malicious clients as one client that has multiple input qubits. It is straightforward to see that Equation (7) holds, since the malicious clients never receive quantum information from the other clients, and the only information they share is the one used in the computation oracles that are implemented using secure classical multiparty computation protocols. The quantum outcome they receive is the correct outcome of an honest server, encoded by some information ($r_j$) that is chosen by the malicious clients in a previous step. ☐

Algorithm 7 Simulator for clients.

${\sigma }_C$ receives a quantum state from client $C_c$ as well as the secret shares of $a_j$ and ${\theta }_j^j$. For all other nodes of the brickwork state, ${\sigma }_C$ runs Algorithm 3 with client $C_c$ and aborts if the secret shares of the classical values do not all match the measurement outcomes of the quantum states. For $j\in O^c$, ${\sigma }_C$ receives the secret shares of the randomness $r_j^c$, chosen by the client $C_c$ and interacts according to the communication protocol simulating the oracle of computing ${\delta }_j$, choosing uniformly at random the value of ${\delta }_j$. ${\sigma }_C$ also replies with random $b_j$. ${\sigma }_C$ undoes rotation $X^{a_c}Z({\theta }_c^c)$ on the input qubit of $C_c$, inputs it to the Ideal MPQC resource and gets back the output corresponding to $C_c$. Finally, ${\sigma }_C$ rotates the output qubit $j\in O$ corresponding to client $C_c$, applying the operation $Z^{s_j^Z}{X}^{s_j^X}$, and participates in the computation protocol to compute $s_j^X$ and $s_j^Z$ with the previously sent and shared values $b_j$ and $r_j$.

5. Conclusions

In this work, we have presented a quantum multiparty delegated protocol that provides security for clients with limited quantum abilities, therefore extending previous results on two-party [5] and multiparty [7] computation while using recent work on delegated blind computing [10,11,22]. Our protocol requires no quantum memory, entangling operations or measurement devices for the clients, only the ability to perform X gates and Z rotations. We prove security against a dishonest server or a coalition of malicious clients; it remains to study whether the proposed protocol remains secure against a dishonest coalition between clients and the server or if there is an unavoidable leakage of information. One equivalent way of studying this problem would be by extending the results of [12] in the multiparty setting, where both the parties and the server have inputs in the computation. An even more interesting question is whether we can enhance our protocol to include verifiability in a similar way as is done in [11].

The specific protocol presented here uses the measurement-based quantum computing framework, to extend the delegated blind protocol of [10] into the multiparty setting. As such, it inherits the key advantage of using MBQC over gate teleportation approaches; once the preparation phase is finished (all qubits are sent to the server and entangled in a graph state), the rest of the communication is classical. The scheme has low round complexity, both quantum and classical. The quantum communication required is linear to the number of elementary gates required to decompose the unitary that we want to apply (see Appendix of [10]). Concerning classical communication, it is not straightforward to compute the necessary bits of communication that are required to perform the VSS scheme and the computation of the angles, since they depend on the cryptographic assumptions that we make (e.g., the number of malicious parties, physical infrastructure); however, we consider that classical communication is less expensive than quantum communication, and since it seems to be growing at a worse polynomial with the parameters of the protocol [23], our scheme remains efficient. Our scheme could also be adapted to any blind computing model, for example the measurement-only model [24], since as mentioned in [22], all protocols with one-way communication from the server to a client are inherently secure due to no-signalling. We have also assumed that the clients choose to act passively maliciously, since any active dishonest activity would be detected with high probability; however, a quantitative proof of security, assuming more extensive attacks from the side of the clients would be a natural extension of this work.

Finally, a similar approach to ours has been explored for two-party computation, which uses recent advances in classical Fully Homomorphic Encryption (FHE). In [25] and in follow-up work [26], it is shown how to evaluate quantum circuits using quantum FHE; it would be very interesting to see how they can be adapted in the case of multiple parties and whether the computational and communication requirements are different from our work.