The Poetics of Physics
Abstract
1. Introduction

Structure of the Paper
2. Meaning as Poetry
When we start explaining the language of famous scientists as examples of ‘poetic diction’ … [it is no] waste of time [if it helps anyone to be convinced] how essentially parochial is the fashionable distinction between Poetry and Science as modes of experienceOwen Barfield, Poetic Diction VIII:6 (1928) [27]
… James Clerk Maxwell would urge mathematicians to formulate their thinking in ‘words without the aid of symbols’, not because he would sympathize with the lingualists, but because he knew the creative force of communicating ideasTom McLeish (2019) p. 243 [7]
The formulation of the fruitful question, posed in the right way, constitutes the great imaginative act in scienceTom McLeish The Poetry and Music of Science p. 10 (2019) [7]
Metaphors are not merely peripheral decoration or even useful models, they are fundamental forms of the awareness of our condition … it seems to me impossible to discuss certain kinds of concepts without the resort to metaphor, since the concepts are themselves deeply metaphorical and cannot be analysed into non-metaphorical components without a loss of substance.Iris Murdoch, The Sovereignty of Good over other Concepts (1967) [57]
το πνευμα οπου θελει πνει … που υπαγει ουτως εστιν πας
ο γεγεννημενος εκ του πνευματος
Spiritus ubi vult spirat … sic est omnis qui natus est ex spiritutransl: Jerome (c.400 CE) [68]
The wynde bloweth where he listeth [where it wills] …
so is every man that is boren of the sprete [born of the spirit]
3. The Thinginess of Things
procul dubio non est mundus factus in tempore, sed cum tempore … nullum autem posset esse praeteritum, quia nulla erat creatura, cuius mutabilibus motibus ageretur
verily the world was made with time, and not in time … no time passed before the world, because no creature was made by whose course it might pass. But it was made with time, if motion be time’s conditionAugustine, City of God XI:6, c.420 CE [93]
The testimony of Holocaust survivors is the modern context in which we most readily recognise that authentic testimony from participants is completely indispensable to acquiring real understanding of historical events, at least events of such exceptionality.Bauckham, 2006 §18 (p. 499) [101]
Traditional philosophy has accustomed us to regard language as something secondary, and reality as something primary. [Niels] Bohr considered this attitude toward the relation between language and reality inappropriate. When one said to him that it cannot be language that is fundamental, but that it must be reality that, so to speak, lies beneath language, and of which language is a picture, he would reply, “We are suspended in language in such a way that we cannot say what is up and what is down. The word ‘reality’ is also a word, a word we must learn to use correctly.”
… the intuition of rationality in nature [must] be acknowledged as a justifiable and indeed essential part of scientific theory. That is why scientific theory … [can be] represented as a mere economical description of facts … or as a working hypothesis … [but these are] interpretations that all deliberately overlook the rational core of science.
… great theories are rarely simple in the ordinary sense of the term. Both quantum mechanics and relativity are very difficult to understand; it takes only a few minutes to memorize the facts accounted for by relativity, but years of study may not suffice to master the theory and see these facts in its context.
… We understand the meaning of the term ‘simple’ only by recalling the meaning of the terms ‘rational’ or ‘reasonable’ or ‘such that we ought to assent to it’, which the term ‘simple’ was supposed to replace. The term ‘simplicity’ functions then merely as a disguise for another meaning than its own. It is used for smuggling an essential quality into our appreciation of a scientific theory which a mistaken conception of objectivity 40 forbids us to acknowledge.Polanyi, Personal Knowledge 1958 [38], §1:4 (emphasis added)
What is the true lesson of the Copernican revolution? Copernicus gave preference to man’s delight in abstract theory, at the price of rejecting the evidence of our senses, which present us with the irresistible fact of the sun, the moon, and the stars rising daily in the east to travel across the sky to their setting in the west.Polanyi, 1958 [38], §1:1
Rules have been stated to formalise the object theory, but now we must understand without rules how those rules work. An intuitive mathematics is necessary even to define the formal mathematics.Polanyi, 1958 [38], §8:8
Die Analogie dieses Schlusses mit der Antinomie Richard springt in die Augen; auch mit dem ,,Lügner” besteht eine nahe Verwandtschaft, denn der unentscheidbare Satz [R(q); q] besagt ja, daß q zu K gehört, [das heißt] nach (1), daß [R(q); q] nicht beweisbar ist. Wir haben also einen Satz vor uns, der seine eigene Unbeweisbarkeit behauptet.
13 Man beachte, daß ,,[R(q); q]” … bloß eine metamathematische Beschreibung des unentscheidbaren Satzes ist.
The analogy between this result and Richard’s antinomy leaps to the eye; there is also a close relationship with the “Liar”, since the undecidable proposition [R(q); q] states precisely that q belongs to K, that is according to Equation (1), [R(q); q] is not provable. We are therefore confronted with a proposition that asserts its own unprovability.
(footnote #13:) Note that “[R(q); q]” … is merely a metamathematical description of the undecidable proposition.Gödel, 1931 [43]
Et certe id quo maius cogitare nequit, non potest esse in solo intellectu. Si enim vel in solo intellectu est, potest cogitare esse et in re, est in solo intellectu: id ipsum quo maius cogitare non potest, est quo maius cogitare potest. Sed certe hoc esse non potest.
And surely that-than-which-a-greater-cannot-be-thought cannot exist in the mind alone. For if it exists solely in the mind even, it can be thought to exist in reality also, which is greater. If then that-than-which-a-greater-cannot-be-thought exists in the mind alone, this that-than-which-a-greater-cannot-be-thought is that-than-which-a-greater-can-be-thought. But this is obviously impossible.Anselm, 1078 [116], II
Gratias tibi, bene dominum, gratias tibi, quia quod prius credidi te donante, iam sic intelligo te illuminante, ut si te esse nolim credere, non possim non intelligere.
I give thanks, good Lord, I give thanks to you, since what I believed before through your free gift I now so understand through your illumination, that [even] if I did not want to believe that you existed, I should nevertheless be unable not to understand it.Anselm, 1078 [116], IV
καλουντος τα μη οντα ως οντα(Romans 4:17, Textus Receptus [67])
calleth thoſe things which be not as though they were(transl: Tyndale, 1526 [69])
This book will rely primarily on natural language (about which there is nothing particularly natural) … There is no substitute for natural language when it comes to expressing social identities or defining political ideologies. … Those who believe that we will one day be able to rely on a mathematical formula, algorithm, or econometric model to determine the “socially optimal” level of inequality are destined to be disappointed. … I do not contend that “truth” is found only in numbers or certainty only in “facts”.Picketty, 2019 [34], Introduction
4. Entropy and Information
4.1. Early Work on the Concept of Entropy
It is interesting that, although this field [entropy] has long been regarded as one of the most puzzling and controversial parts of physics, the difficulties have not been mathematical. … It is the enormous conceptual difficulty of this field which has retarded progress for so long.Jaynes, 1965 [129] (emphasis original)
Clausius assumed that (German) Energie literally meant ‘work content‘ (Werkinhalt) and devised the term Entropie as a corresponding designation for the ‘transformation content’ (Verwandlungsinhalt) of a system.Oxford English Dictionary, 3rd Edition (September 2018)
Entropy was first defined by the German physicist Rudolf Clausius (1822–1888). Scottish physicists Peter Guthrie Tait (1831–1901) and James Clerk Maxwell (1831–79) were the first to interpret entropy as a measure of the unavailability of energy for work.
The modern mathematical definition of entropy, in terms of the possible microstates … of a thermodynamic system, first appears in the work of Austrian physicist Ludwig Boltzmann (1844-1906), who viewed entropy as a measure of the disorder of a system.
[Sense 3 “Statistics and Information Theory”)] … mathematician Claude Shannon (1916–2001) coined the term in the context of information theory (see sense 3b)Oxford English Dictionary, 3rd Edition (September 2018)
es kann nie Wärme aus einem kälteren in einen wärmeren Körper übergehen, wenn nicht gleichzeitig eine andere damit zusammenhängende Aenderung eintritt.
Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.Clausius, 1854 [35]
Bei dieser Bestimmungsweise kann man den Satz von der Aequivalenz von Wärme und Arbeit, welcher nur einen speciellen Fall der allgemeinen Beziehung zwischen lebendiger Kraft und mechanischer Arbeit bildet, kurz so aussprechen:
Es läſst sich Arbeit in Wärme und umgekehrt Wärme in Arbeit verwandeln, wobei stets die Gröſse der einen der der anderen proportional ist.
… Betrachten wir nun die bei einer Zustandsänderung gethane innere und äuſsere Arbeit zusammen, so können sich beide, wenn sie von entgegengesetzten Vorzeichen sind, theilweise gegenseitig aufheben, und dem Reste muſs dann die gleichzeitig eintretende Aenderung der Wärmequantität aequivalent seyn. Für die Rechnung aber kommt es auf dasselbe hinaus, wenn man für jede von beiden einzeln eine aequivalente Wärmeänderung annimmt.
Sey daher Q die ganze Wärmemenge, welche man einem Körper, während er auf einem bestimmten Wege aus einem Zustande in einen andern übergeht, mittheilen müſs, (wobei eine entzogene Wärmemenge als mitgetheilte negative Wärmemenge gerechnet wird), so zerlegen wir diese in drei Theile, von denen der erste die Vermehrung der wirklich in dem Körper vorhandenen Wärme, der zweite die zu innerer und der dritte die zu äuſserer Arbeit verbrauchte Wärme begreift.
Von dem ersten Theile gilt dasselbe, was schon vom zweiten gesagt ist, daſs er von der Art, wie die Ver-änderung stattgefunden hat, unabhängig ist, und wir können daher beide Theile zusammen durch eine Function U darstellen, von der wir, auch wenn wir sie sonst noch nicht näher kennen, wenigstens soviel im Voraus wissen, daſs sie durch den Anfangs- und Endzustand des Körpers vollkommen bestimmt ist.
Der dritte Theil dagegen, das Aequivalent der äuſseren Arbeit, kann, wie diese selbst, erst dann bestimmt werden, wenn der ganze Weg der Veränderungen gegeben ist. Nennen wir die äuſsere Arbeit W, und das Wärmeaequivalent für die Einheit der Arbeit A, so ist der Werth des dritten Theiles A∙W, und wir erhalten daher als Ausdruck des ersten Hauptsatzes folgende Gleichung:
(I) Q = U + A∙W
With this means of determination, one can now concisely express the relation between the equivalence of heat and work (which is only a special case of the general relationship between active power and mechanical work) by the following saying:
Work can be turned into heat and vice versa heat can be turned into work, so that the magnitude of the one is always proportional to the other.
… Let us now consider, in the event of a change of state, the internal and external work together. These both, taken together, can partially compensate each other if they are of opposite signs. Then the remainder must be equivalent to the change of the quantity of heat that occurs at the same time [i.e., during the change of state event]. For the calculation however, it comes back to the same thing, if one assumes an equivalent change in heat from the two separate entities [i.e., for each of internal work and external work separately, one takes the heat equivalent].
Let Q be the entire quantity of heat that must be imparted to a body, while going on a certain path from one state to another (where heat removed is counted as a negative quantity of heat imparted) [this is in the context of the Carnot cycle]. This can be broken into three parts, of which the first is the increase in heat actually present in the body, the second is the heat used for internal work and the third the heat used for external work.
Of the first part one can say the same as has already been said about the second part: that it is independent of the way that the change of state happened. We can therefore combine both parts together into a function U, for which we know in advance (regardless of how little knowledge we otherwise have) that it is completely (sufficiently) defined by the initial and final states of the body.
On the other hand, the third part, i.e., the equivalent of the external work, can only be calculated when the whole path of change is given. We call the external work W, and the heat equivalent for the unit of work A, so that the value of this third part is the product A∙W, and we come into view of the resulting first law in the following equation: (I) Q = U + A∙WClausius, 1854 [35] (emphasis original)
4.2. Entropy and Statistical Mechanics
Entropy is just as much, and just as little, extensive in classical statistics as in quantum statistics … entropy stands strongly contrasted to energy.Jaynes, 1992 [130]
[Gibbs] had perceived that, when two systems interact, only the entropy of the whole is meaningful. Today we would say that the interaction induces correlations in their states which makes the entropy of the whole less than the sum of entropies of the parts; and it is the entropy of the whole that contains full thermodynamic information. This reminds us of Gibbs’ famous remark, made in a supposedly (but perhaps not really) different context: “The whole is simpler than the sum of its parts.” How could Gibbs have perceived this long before the days of quantum theory?Jaynes, 1992 [130] (emphases original)
… not only in the well-known statistical sense that it measures the extent of human ignorance as to the microstate [but also] [e]ven at the purely phenomenological level, entropy is an anthropomorphic concept. For it is a property, not of the physical system, but of the particular experiments you or I choose to perform on it.Jaynes, 1965 [129] (emphasis original)
… we can … appreciate … [that] Boltzmann’s formula … put forward in 1875 … represented an enormous advance on what had gone before … There are, nevertheless, still certain aspects of vagueness in this definition, associated, primarily, with the notion of what is to be meant by a “macroscopic parameter”.Penrose, 2010 [142], §1.4
Thermodynamics … is a description of these variables of the system: those through which we assume we are able to interact with the systemRovelli, 2017 [143] (ch.10, n.4; emphasis original)
4.3. Information
When one compares the generality and power of explanation of Shannon’s [146] paper “A Mathematical Theory of Communication” to alternative theories at the time, one can hardly disagree with J.R.Pierce [147] who states that it “came as a bomb”.Lundheim, 2002 [145]
In this connection it is essential to note the following. The mere fact that the same mathematical expression −∑pi log pi occurs both in statistical mechanics and in information theory does not in itself establish any connection between these fields. This can be done only by finding new viewpoints from which thermodynamic entropy and information-theory entropy appear as the same concept.Jaynes, 1957 [150] (emphasis original)
Landauer’s principle, while perhaps obvious in retrospect, makes it clear that information processing and acquisition have no intrinsic, irreducible thermodynamic cost whereas the seemingly humble act of information destruction does have a cost, exactly sufficient to save the Second Law from [Maxwell’s] Demon.Bennett, 2003 [152]
4.4. The Entropy of Black Holes
[here] we attempt a unification of black-hole physics with thermodynamics. In Sec. II we point out a number of analogies between black-hole physics and thermodynamics, all of which bring out the parallelism between black-hole area and entropy. In Sec. III, after a short review of elements of the theory of information, we discuss some features of black-hole physics from the point of view of information theory. We take the area of a black hole as a measure of its entropy—entropy in the sense of inaccessibility of information about its internal configuration 59.Bekenstein, 1973 [158]
4.5. Geometric Entropy: Holography and Entanglement
The holographic principle … implies that the number of fundamental degrees of freedom is related to the area of surfaces in spacetime. Typically, this number is drastically smaller than the field theory estimate. Thus the holographic principle calls into question not only the fundamental status of field theory but the very notion of locality. … Quantum gravity has imprinted few traces on physics below the Planck energy. Among them, the information content of spacetime may well be the most profound.Bousso, 2002 [168]
we have shown that the [double logarithmic spiral] structure of the … Milky Way … is consistent with a holomorphic representation in geometric algebra. In particular, we have shown that the [calculated] galactic shape, aspect ratio, and structural stability (which are all highly constrained by the algebra) are consistent with observation; and we have also shown that the total galactic [virial] mass is also consistent with observation. Note that this is a simplified (“zeroth order”) analytical approximation to reality: … the dynamics driving the galactic evolution [are neglected … but] this treatment gives the proper weight to the effect of the [central supermassive] black hole entropyParker and Jeynes, 2019 [28]
[a property] of the thermodynamics of the system: [which is] a significant methodological advance since a detailed treatment of the energetics may be avoidable. … The spherical C60 fullerene molecule therefore represents a least exertion or Maximum Entropy (most likely) topology … For C60 the double-spiral trajectories have been proved holomorphic and maximum entropy in an exact Euler-Lagrange analytical treatment (given the approximation to a true spherical geometry).Parker and Jeynes, 2020 [167]
The geometric entropy of both the sphere and the double-helix are clearly holographic in nature, since they are proportional to the surface areas of enclosed volumes. …
… consideration of the geometric entropy of systems ranging … from the molecular … through to [cosmic] scales yields a common holographic interpretation … The holographic principle itself … is a consequence of the holomorphism … of the things considered.
The close relationship between quantum mechanics … and statistical mechanics … is well known ... However, using geometric entropy and the entropic version of Liouville’s Theorem … we have shown not only how the entropy of a MaxEnt system is holographic in nature, but also that there exists an associated entropic version of the uncertainty principle, based on the Boltzmann constant as the appropriate entropic counterpart to the Planck constant.Parker and Jeynes, 2021 [160]
4.6. The Arrow of Time, and Teleology
One claimed virtue [of this approach] … is the ability … to provide time-asymmetry. … Why then do we not observe [entropy decreasing]? To answer this question … [and by] translating their conception of entropy into information-theoretic language [they] showed that their formulation of the second law requires infinite information for specifying the initial states of a singular distribution evolving in the negative [time] direction, but only finite information for specifying the initial states for evolution in the positive [time] direction.
This would render the initial conditions for systems to approach equilibrium along the negative t-axis physically unrealizable … Since singular probability distributions are supposedly operationally unrealizable, they argue it is physically impossible for unstable systems to evolve to equilibrium in the negative [time] direction. Hence, their version of the second law acts as a selection rule for initial states.
This argument is supposed to show why anti-thermodynamic behavior in the real world is impossible … Nevertheless, the argument is problematic. The most fundamental difficulty is that it conflates epistemic concepts (e.g., information, empirical accessibility of states) with ontic concepts (e.g., actual states and behaviors of systems).Bishop, 2004 [176]
[Parker and Jeynes, 2019] have shown that the principle of least action has the entropic analogue of a principle of least exertion: where “action” is the path integral of the kinematic Lagrangian, “exertion” is the path integral of the entropic Lagrangian—which still satisfies the various canonical conjugate-pairing relationships. Roughly speaking, in the energy domain where the Hamiltonian represents the total energy of a system (that is, the sum of potential and kinetic terms), the Lagrangian represents an energy balance (the difference of potential and kinetic terms). The entropic Hamiltonian-Lagrangian treatment emerges from a consideration of information as the orthogonal complement to entropyParker and Jeynes, 2020 [157]
Both its staunchest advocates and those remaining silent about the PLA shared the conviction that final causation, material or organismic teleology, and analogies with human behavior had to be kept out of physics.Stöltzner, 2003 [178]
Moreover, none of the protagonists of the debate under investigation considered the PLA as an instance of backward causation. The history of physical teleology might alternatively suggest a relationship between the PLA and the problem of determinism. … neither PLA-advocates nor logical empiricists contemplated any relation between the PLA and the second law of thermodynamics [except Boltzmann]. Rather, they explicitly restricted the validity of the PLA to reversible phenomena regardless of their views on causality.Stöltzner, 2003 [178]
It is worth pointing out that Bohm’s recognition of a “quantum-mechanical” potential U(x) exerting a “quantum-mechanical” force “analogous to, but not identical with” the conventional strong force on a nucleon ([Bohm 1952] his Equation (8)), can now be understood to be a prescient anticipation of our entropic force, familiar from our previous discussion of galactic geometry ([Parker and Jeynes 2019, their Equation (23)).Parker, Jeynes and Catford (2022) [161]
5. Knowledge of Meaning
5.1. The problem of Definition
… our mental processes, which constitute our being and our life, are not just abstract and mechanical, but personal, as well—and, as such, involve not just classifying and categorising, but continual judging and feeling also.Oliver Sacks, The Man who mistook his Wife for a Hat (1985)[191]
5.2. Metaphysics and Metanarratives
Der im System PM unentscheidbare Satz wurde also durch metamathematische Überlegungen doch entschieden.
So the proposition which is undecidable in the PM system yet turns out to be decidable by metamathematical considerationsGödel, 1931 [43]
5.3. Ambiguity and Coherence
οι ουρανοι διηγουνται δοξαν θεου … ο νομος του κυριου αμωμος επιστρεφων ψυχας … τα δικαιωματα κυριου ευθεια ευφραινοντα καρδιαν
The heauens declare the glorie of God … the law of the Lord is perfite [perfect], conuerting the ſoule … the ſtatutes of the Lord are right, and reioice the heartPs.19:1,7,8 (Geneva, 1560 [184])
ιδου ημεραι ερχονται φησιν κυριος και διαθησομαι τω οικω ισραηλ και τω οικω ιουδα διαθηκην καινην … ουτως ειπεν κυριος ο δους τον ηλιον εις φως της ημερας σεληνην και αστερας εις φως της νυκτος … εαν παυσωνται οι νομοι ουτοι απο προσωπου μου φησιν κυριος και το γενος ισραηλ παυσεται γενεσθαι εθνος κατα προσωπον μου πασας τας ημερας
Beholde, the daies come, ſaith ye Lord, that I wil mak a newe couenant with the houſe of Iſraél, and with the houſe of Iudáh … Thus ſaith the Lord, which giueth the ſunne for a light to the day, and the courſes of ye moone and of the ſtarres for a light to the night ... If theſe ordinances departe out of my ſight, ſaith the Lord, then ſhall the ſeed of Iſraél ceaſe from being a nation before me, for euer.Jeremiah 31:31,35,36 (Geneva, 1560 [184])
5.4. Meaning in Poetry
| Lo giorno se n’andava, e l’aere bruno toglieva li animai che sono in terra da le fatiche loro; e io sol uno | The day was dying, and the darkening air Brought all the working world of living things To rest. I, only, sweated to prepare For war, the way ahead, the grind that brings |
| m’apparecchiava a sostener la guerra si` del cammino e si de la pietate, che ritrarra la mente che non erra. | The battler to hot tears for each yard gained: To bitter tears, and memories more real Than what was real and which is thus retained Unblunted, edged with even sharper steel. |
| O muse, o alto ingegno, or m’aiutate; o mente che scrivesti cio ch’io vidi, qui si parra la tua nobilitate. | My Muse, my schooled and proven gift, help me: It’s now or never. Fortify my mind With the vivifying skills of poetry, For what I saw needs art of a great kind. I saw great things. Give them nobility. |
| Dante Alighieri, Divina Commedia, 1320 (transl. Clive James, 2013); Canto II | |
Dante was one of the most educated men of his time even in the conventional sense, quite apart from the proto-scientific sense in which he was original without parallel. But [Byron and other translators] couldn’t, or wouldn’t, get down to the level where syllables met each other and generated force. That had to be the aim, impossible as it seemed; to generate the force, both semantic and phonetic: the force of both meaning and sound. Indeed, in the original, some of the meaning was in the sound. Unless the translator did something to duplicate how the poem sounded, he, or she, wouldn’t get near what it meant.James, 2013 [198] (emphasis original)
6. Image and Knowledge: Seeing and Knowing


7. The Poetics of Physics
8. Conclusions
The necessity of the good is then an aspect of the kind of necessity involved in any technique for exhibiting factMurdoch, On ‘God’ and ‘Good’, 1966 [78]
Let us consider the case of conduct. What of [Jesus’] command, ‘Be ye therefore perfect’ [Matt.5:48]? Would it not be more sensible to say, ‘Be ye therefore slightly improved’?Murdoch, On ‘God’ and ‘Good’, 1966 [78]
9. Epilogue
God is One
Man is two: woman is too
Love is three: binding mankind whole
Right is four-square: breath of man and breath of woman
Mercy is prime five: both two summed with three and one summed with four
Mankind’s number is six: love’s mutuality
God’s number is prime seven: the resting of creation
The first perfect cube conquers death: man and woman joining in life© 2020 C.Jeynes
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
| 1 | This strongly suggests Basarab Nicolescu’s idea of “Transdisciplinarity” [4] which has many merits (including both the very clear assertion that “knowledge is open” and also the recognition that disciplinary boundaries are essentially arbitrary, as we say here) but from our point of view it does not treat the “subject-object” distinction satisfactorily. Nicolescu correctly attacks the idea that it is possible to completely separate “subject” from “object”, but still thinks that the “three axioms of the methodology of transdisciplinarity” may establish his (transdisciplinary) discipline. Clearly, his is a valuable contribution, but here we are saying something different: that meaning is necessarily poetic. |
| 2 | A.N.Whitehead is famous for saying, “the safest general characterisation of the European philosophical tradition is that it consists of a series of footnotes to Plato” [14]. Everyone (including Whitehead himself) who comments on this aphorism hedges it about with qualifications, but nevertheless the Socratic analytical style is thought to be properly “philosophical” where the poetical (or “mystical” or “religious”) styles of other ancient peoples is not. We think this is misleading, and will adduce evidence for this long predating the Hellenic period. |
| 3 | At one point in a detailed monograph on unconscious and/or unexamined bias, Jessica Nordell says, “It may be that I did not even see [the operation of bias]” [15]. We see only what we believe, to an extent that is surprising (and often shocking). In another place she comments: “We have to develop the ability to truly recognize what we see” (ibid, p. 164, citing Kahneman and Klein 2009) [16]. As a STEM Ambassador I regularly play the “how many eyes have you got” game with 9-year-olds. To do science you have to see with your mind’s eye (so you must have at least three eyes). St.Paul, writing to the Ephesians in 58 CE (using the conveniently definite dating of Robinson, 1976 [17]) wishes that their “eyes of the understanding be enlightened”: πεφωτισμένους τοὺς ὀφθαλμοὺς τῆς καρδίας ὑμῶν (pephōtismenous tous ophthalmous tēs kardias hymōn; literally, “being-enlightened the eyes of-the heart of-you”: Eph.1:18). Note that the old authors considered that we feel with our heads but think with our hearts; they would consider the modern head-heart dichotomy deranged. Classically, the mind is located in the heart, which is why we speak of “the heart of the matter”. |
“Seeing” is a central idea in this essay—John Berger’s contribution, “Ways of Seeing”, [18] is now iconic, but is equally applicable even in physics. Bohm and Hiley (1993 [19], §14.1, p. 323) say “Our theories are not primarily forms of knowledge about the world but rather, they are forms of insight that arise in our attempts to obtain a perception of a deeper nature of reality as a whole … new concepts … serve as ways of looking at reality”. They go on to speak of “unbroken wholeness” (ibid. §15.2, p. 352). Michael Berry points out to me (private communication 5 December 2022) that Bohm’s formalism was anticipated in detail by Erwin Madeling [20], but Bohm apparently was unaware of this. Berry himself [21] (§4) has noticed “a germ” of the same idea in the treatment of caustics in optics going back to Newton himself. | |
| 4 | So Odin plucked out an eye to gain knowledge, and when Jesus said, “seeing they see not” (Matthew 13:13 passim; 1st century CE) he was quoting the pre-Hellenic seer (Isaiah 6:9f; 7th century BCE) who wanted the people to “understand with their hearts”. This saying of Jesus is one of the few attested in all four Gospels, underlining its central importance in European culture of the last two millennia: this attitude to seeing also underlies (almost invariably tacitly) the European philosophical tradition. |
| 5 | A Reviewer has suggested that since Jorge Wagensberg [23] and others “affirm the metaphorical foundation of sciences” one can hardly treat the “unity of truth” as a given. This is an error. It is true that science (along with all knowledge, as we here insist) does have a metaphorical foundation, but here metaphor does not denote a mere “figure of speech”: on the contrary, metaphor is fundamental to all language, as we will show in detail (this indeed is a commonplace of the poets). And if truth is not unitary then we may feel many things, but we can know nothing at all. Note that saying “truth is one” is not the same as saying “truth is simple”. Reality is elusive. |
| 6 | The ontology of “physical law” is well-trodden ground (see for example Bird [29]) and out of our present scope. |
| 7 | Barfield says of this dictum: “The use of them [the terms] is left to the Logician, who, in his endeavour to keep them steady and thus fit them to his laws, is continually seeking to reduce their meaning. I say seeking to do so, because logic is essentially a compromise. He could only evolve a language, whose propositions would really obey the laws of thought by eliminating meaning altogether. But he compromises before this zero-point is reached” (ibid., emphases original). This is entirely consistent with our view, mutatis mutandis. |
The idea that the “poet’s vocation … [is as] a maker of words” (emphasis original) is now a cliché—this quote is taken randomly (from Oliver O’Donovan’s 2021 essay [30] on Psalm 119). | |
In a subtle work now largely overlooked, Barfield (1957 [31]) also investigates the “modern” attitude to hypotheses in a treatment close to ours here in certain important respects. He says that the post-Copernican attitude is that “if a hypothesis saves all the appearances it is identical with truth” (ibid. Ch.VII) where of course his debt to Pierre Duhem (1908 [32]) is clear and explicit in his treatment. Much has happened since 1957 (including the establishment of the reality of both black holes and the cosmic microwave background), and this description of hypotheses (which characterisation does not adequately represent the breadth of Barfield’s argument) is clearly a version of naïve realism, which is no longer tenable (if it ever was). In our terms he claims that the modern (post-Copernican) view confuses the formalism with the reality (for further on “reality” see below, note#31). | |
Moreover, his gloss on the Hebrew Scriptures, not only regarding the (temporal) priority of Hebrew thought over Greek, but also underlining both the otherness of the Hebrew mode of thought and the metaleptic nature of the Christian (Greek) Scriptures’ dependence on the Hebrew Scriptures, is entirely consistent with our view (see §6 below). | |
| 8 | We will quote Thomas Piketty (2019, [34]) saying “there is nothing ‘natural’ about language” (§3): by “natural language” we mean the language we use every day without any special technical vocabulary. This is the same language used for novels and the same language used for poetry, although in both cases the authors or poets may use a register of language that can hardly be called “everyday”. We always compose (or write) for an audience: this will determine our style. But composition for a general audience cannot use any special language. We will call this, for want of a better term, “natural” language. |
Note that this is not a “definition”, and is not intended to be one. We are not attempting to construct any sort of “analytical metaphysics” (on “metaphysics” see note#17 below). Formal definitions use analytic (not poetic) language, but we here merely explain informally which meaning we intend. | |
| 9 | Martin Edwardes treats the idea of “negotiating meaning” at length, but for convenience we summarise it here with an example. If, driving down a single track road, I meet another car, who has priority? We both have right of way, but neither of us has priority, and we have to “negotiate” who backs up to the nearest passing place. Without agreement, we cannot move. If I want to say something straightforward so that you understand me, we already know how to do that. But if I want to say something new, you may not at first know what I mean: then we have to together “negotiate the meaning” until you are satisfied. |
This idea of “negotiating” meaning is far-reaching. Sidney Dekker [36] (p. 16), in a deep and influential discussion of systematic ways to avoid disasters in various industrial processes, points out that “Systems are not basically safe. People create safety while negotiating multiple system goals”. He continues: “Human errors do not come unexpectedly. They are the other side of human expertise—the human ability to conduct these negotiations while faced with ambiguous evidence and uncertain outcomes. | |
| 10 | The “scientific method” itself has been discussed in detail recently by Jorge Wagensberg [23], who proposes a well-defined (“unique”) programme which is supposed to distinguish what is properly “scientific”. We cannot digress to adequately critique this paper here, but we point out that he relies on concepts such as “objectivity” (and he calls Popper’s “falsifiability” idea “sublime”). Whatever the merits of these, our discussion includes the ontology of “objectivity” where his does not. |
| 11 | Kahneman and Klein in their classic paper investigate this intuition in detail: “expert intuition is sometimes remarkably accurate and sometimes off the mark” [16], of course they are considering real technical (“expert”) knowledge. They explicitly point out that the cues experts use to make their judgments “involve tacit knowledge [which is] difficult for the expert to articulate”. On tacit knowledge of course see Polanyi 1958 [38] (and our discussion below §3). On the proper use of (and limits to) expertise see also Collins and Evans (2007) [39]. |
| 12 | This is evidenced by all the physics papers cited in this work, including Gödel, 1931 [43]. Interested readers could also look at the historical papers collected in translation by Stephen Hawking [44], in particular the seminal work of George Boole, Richard Dedekind, Kurt Gödel himself, and Alan Turing (Hawking’s other selections are mostly extracts). The introductory sections of these major papers have no equations: but they are not “wordy”—diffuse and vague—far from it! They are crucial to understanding the mathematical arguments that follow. |
| 13 | Interestingly, the dancer Emily Coates [46] has recently written about “The Poetics of Physics in Dance”. She points out that a simple “translation” of physical ideas into dance terms cannot succeed either in effectively communicating the scientific ideas or of creating effective art: she says, “science is not art … as historians of science have been noting for some time, the practices of science and art have more in common than many have assumed, and using the framework of translation doesn’t allow for their overlap.” Instead, she speaks of “intensification” and (particularly relevant to our purposes here) “an intensification of our encounter with time … dance has the power to perceive and move with its subjects to such a degree as to reveal scientific ontologies that would otherwise be inaccessible” (my emphasis). She speaks of “ideas in motion: scientific laws made hyper-perceptible”. She cites Steve Paxton [47], in whose “alluring poetics, physics is social, and sociality is expressed through physics”. We are engaged in something rather different here, but in her conclusion Coates underlines our guiding principle in this essay, that physics is irreducibly personal: she says, “When scientific knowledge assumes bodily form … the unavoidable human source of science becomes poignantly clear” (emphasis original). |
| 14 | |
| 15 | We are not here concerned with how much animals know: so far as we are aware, science is human. Here we are interested only in how we know things, not in how other creatures may possibly know things. |
| 16 | |
| 17 | We use “metaphysics” as a term cognate to (e.g.,) “metanarrative”, “metamathematics”, “metadata”: that is, a “natural” language (see note#8) in which one may speak of the underlying features of the language or activity in question (the art of narrative, mathematics, the structure of the dataset). Note that Graeber and Wengrow [11] (p. 31) refer to “a standard historical metanarrative” in their important work. So here we use “metaphysics” to mean “the metanarrative of physics”. See below §5.2. |
We do not intend the conventional (often pejorative) range of meanings normally associated with “metaphysics”. In particular we will in this essay directly address (as “ontology” or “epistemology”) what is usually spoken of as metaphysics, the first meaning of which is given by the Oxford English Dictionary: “The branch of philosophy that deals with the first principles of things or reality … theoretical philosophy as the ultimate science of being and knowing” (OED 3rd Edition 2001) [53]. | |
As Rasmus Jaksland points out, “there is no univocal definition of metaphysics” [54], although he proceeds on the basis that metaphysics ought to be “naturalised” with a subject matter essentially indistinguishable from physics proper, except that the proper physical treatment has not yet become clear. We think that this approach is overcomplicated as well as apparently begging the basic ontological and epistemological questions: even the scaled back proposal of “Moderately naturalistic metaphysics” (Morganti & Tahko [55] acknowledges that “metaphysics” (in the OED meaning) may explore “a basic possibility space in such a way that the grounds for the interpretation of scientific theories are laid” in just the way we will describe here. We wish to speak of metaphysics simply as the (“natural”) language used to set up the model of the physical system (with entropy as an example: §4.1). | |
Therefore, we think that James Ladyman’s suggestion that “The first task of the metaphysician, like the scientist, is to construct a hypothesis that accounts for the phenomena in question” [56] is beside the point. It is the job of the scientists to account for the phænomena, but what terms are available to them? New terms for the new science must be constructed (“negotiated”, [26]) out of existing language in a way comparable to how Clausius did it for “entropy” in 1854 [35] (see §4.1). In any case, as Karen Barad says: “the primary ontological unit is the phenomenon” [24](p. 333). We will discuss this further in §5.1 below. | |
In the context of a discussion of the unity of truth, Michael Polanyi criticises an eminent professor who, attempting to escape positivism, creates “a labyrinth of subterfuges in order to say (“scientifically”) that [certain people] regard the seeking of the truth to be their right and duty”, calling such pseudo-scientific circumlocutions a “perversion”, and saying that the positivists were “repudiating metaphysics along with dogma” [22] (Ch2). Here Polanyi uses “metaphysics” in our sense. | |
| 18 | Charlotte Higgins (2022)[59] quotes Daryna Gladun (a Ukrainian poet based in Bucha before the Russian invasion on 24 February 2022): “[my work] sits at the boundary between literature and journalism. It is poetry in uniform. I set aside metaphors to speak about the war in clear words.” Higgins comments on this: “It interests me that she uses metaphor to describe this process at the same time as apparently eschewing it: in the end metaphor will out. If war involves a fracturing of language, it is poetry that will eventually creep in to fill the gaps”. Metaphor will out! We cannot say what is close to our hearts without “metaphor”. Metaphor is not merely a “figure of speech”, it is itself the very lifeblood of speech. |
| 19 | The writer to the Hebrews says, Ἔστιν δὲ πίστις ἐλπιζομένων ὑπόστασις (Heb.11:1; “faith is the substance of things hoped for”): ὑπόστασις (hypostasis) is a deep idea explained in theological (Trinitarian) terms by Lienhard, 2002 [60]: the point here is that the idea of substance is intrinsically metaphorical, just as Iris Murdoch says. |
| 20 | Our thesis is very restrained: it uses only the English, Palikur, German, Italian, Latin, Greek and Hebrew languages (although also alluding to Portuguese, Náhuatl, Spanish, Gaelic, French and Welsh). The comparative linguistics, which are pregnant with ontological implications (Perunović 2021 [61]), are here only hinted at. These implications exist in an attenuated way even for “simple” data handling (Forkel 2018 [62]). |
| 21 | “Standard empiricism”, believed to be “objective”, has its usual meaning (Maxwell 2020 [63]). Nicholas Maxwell shows how the usual treatment smuggles our own ideas in in the same way that Polanyi (1958 [38]) shows that knowledge is personal (the unavoidable subjectivity is smuggled in by how we speak of “simplicity”—see §3). That is, our understanding is idealistic: it depends on our own personal (or “subjective”) ideas. |
Note that measurement itself is now acknowledged by the metrologists to have an irreducibly subjective element, see in particular §5.1 and note#75. Note also that the subjectivity of our knowledge (that is, its necessarily personal nature) does not undermine it in any way, since it is socially validated by the peer review system (Hicks 2016 [64]). | |
| 22 | One sort of “naïve realist” might be what Timothy Lyons (2006 [65]) calls the “deployment realist” who says essentially that scientific theories are true because they work. Lyons explains in detail the multiple problems of this view, also confronting the literature at length. Michael Berry (2020 [66]) wittily contrasts the “idealist” and the “realist” with his aphorism “True but not real” (applied to scientific explanations) contrasting with the opposite idea (“real but not true”) applicable to our (real enough, if possibly misleading) perceptions of the phӕnomena. The example is the table—we push the explanation down to the quantum level—all true enough, but where has the table gone? |
| 23 | We give dates for the New Testament texts (conveniently but anachronistically reproduced in a miniscule Greek script with word spacing) as authoritatively discussed by John Robinson (1976 [17]). |
| 24 | Tyndale’s translations were printed in a blackletter font, but for convenience we transcribe here in a Latin font. German texts were usually printed in a blackletter font (known in German as “Fraktur”) until it was discontinued in 1941. But the German texts of Gödel and Clausius (§§3,4.1) were printed in a Latin font. |
| 25 | Ambiguity has been explored in detail in an important monograph (Anthony Ossa-Richardson, 2019 [73]), showing that although our modern appreciation of poetic ambiguity can be traced back to William Empson’s seminal work (Empson 1930 [74]), it has a long prehistory in Europe reaching back to Augustine and the Christian understanding of the Hebrew Scriptures. Ossa-Richardson underlines our point here when he quotes Eugen Bleuler (1914 [75]) approvingly as “seeing in ambivalence … ‘one of the most important mainsprings of poetry’ [Die Ambivalenz is eine der wichtigsten Triebfedern der Dichtung]” (op.cit. p. 373). Ossa-Richardson (ibid.) comments that Robert Graves would later agree with this judgment. |
| 26 | “Wovon man nicht sprechen kann, darüber muss man schweigen.” (Wittgenstein 1921 [76], §7) |
| 27 | “Man kann für eine große Klasse von Fällen der Benützung des Wortes »Bedeutung«—wenn auch nicht für alle Fälle seiner Benützung—dieses Wort so erklären: Die Bedeutung eines Wortes ist sein Gebrauch in der Sprache” (Wittgenstein 1953 [77], §43; emphasis original). This is translated as “For a large class of cases—though not for all—in which we employ the word “meaning” it can be defined thus: the meaning of a word is its use in the language.” Wittgenstein died in 1951: the Philosophical Investigations was published posthumously. |
| 28 | … although Wittgenstein is usually spoken of either as a positivist (early) or a pragmatist (late) of the sort that Iris Murdoch takes aim at. So he says, “Wie haben wir denn die Bedeutung dieses Wortes (»gut« zum Beispiel) gelernt? An was für Beispielen; in welchen Sprachspielen?” (“How then did we learn the meaning of this word (“good”, for example)? What examples are there; which language games are being played?”; Wittgenstein 1953 [77], §77) but Murdoch specifically attacks this point of view in her essay “On ‘God’ and ‘Good’ ” (Murdoch 1966 [78]). |
| 29 | So when one young Palikur man saw a large city for the very first time (from an airplane) he shouted, “Babamnamnapadmin!”, which means, literally, “repeated protrusions, many, tall, widespread, vast beyond comprehension”. It would take an English speaker a paragraph to describe a city to someone who had never seen one before, but a Palikur speaker can pack it all into one adjective. This entire word was coined on the spot and likely had never been spoken before, yet any Palikur speaker would immediately understand it, and they would have a good idea of what a city looked like from the air. Impressive! (Private communication, email from Diana Green 9 September 2022.) |
| 30 | Course and MacMillan (2021 [85]) have similarly observed, speaking of the threatened loss of the Gaelic language: “The culture, the people, everything would disappear forever”. |
| 31 | This is strictly correct if we include the language of music or art (McLeish 2019 [7]), and if we note that Polanyi’s “tacit knowledge” is predicated on students picking up this tacit knowledge in the lab by doing things in collaboration with (and talking with) supervisors and colleagues (Polanyi 1958 [38]). |
| 32 | “Thingification” is an interesting word whose first usage the Oxford English Dictionary (OED) attests in 1935; the OED lists thinghood as used by A.N.Whitehead, but sadly does not list the (better) synonym thinginess (philosophers might speak instead of “reification”, a Latinist neologism of the mid-19th century). The OED also attests all of thingly (adjective), thingy (both as a noun and an adjective), thingness, and thingliness (respectively 1450, 1787, 1891, 1840, 1662). Bruno Latour (2004 [81]) also spoke of “thinginess”. We are not much concerned here with Bill Brown’s “Thing Theory” (Brown, 2004 [87]), which is interested more in our relation with things than the things-in-themselves. |
| 33 | Of course, Augustine was thinking about “massive” things, not mass-less ones like the photon. It is an elementary result of special relativity that the closer one’s speed is to the speed of light the slower “time” passes: thus for photons “time” stops altogether. This very simple and straightforward result is entirely counter-intuitive which remains very shocking however familiar it is: see further on the individuality of things in general (and electrons in particular) at note#92 below. |
| 34 | “Real” is another nice word whose extensive cluster of connotations includes royalty—well known today by the many followers of premier-ranked Real Madrid: monotheists would say that the idea of reality derives from God the ‘King of kings’ (that is, God the Creator). See also the discussion of “Wigner’s friend” scenarios in note#38. |
| 35 | This point of view was famously proposed by Herbert Butterfield in his The Origins of Modern Science (1957 [96]), which remains important as is discussed (for example) by Regis Cabral (1996 [97]) and Cunningham and Williams (1993 [98]). Butterfield’s style of argument may appear dated, but it seems to remain uncontentious that his substantive points remain valid. |
| 36 | Charlotte Higgins (2022 [59]) reports the Ukrainian writer Oleksandr Mykhed as saying: “It is true that when Russia’s full-scale invasion started, on 24th February, literature was the last thing on people’s minds—you could not protect your family from a rifle with a poem.” Higgins continues: “But as the conflict has continued, the power of writing to record, to testify and to witness has seemed more and more important … diaries …able to gather experience and emotion in its rawest form.” Higgins reports the Ukrainian scholar Oksana Maksymchuk speaking of poetry’s ability to “crystallise a particular moment in time, or an emotion that is fleeting.” If poetry flourishes even in war, does that not underline our desire—and need—to know things truly? And true knowledge is essentially poetic. |
| 37 | It is today a commonplace that we see only what we believe (for an experimental example of this see Zhaoping 2007 [103]). Of course this is an exaggeration, but it is always an effort to allow for our biasses (and we never completely succeed). So in the line after “meeting the universe halfway” Alice Fulton [102] says (as it were in explanation), “nothing will unfold for us unless we move towards what looks to us like nothing.” We creep towards knowledge in ignorance. But however fallible and incomplete, we may still know truly, we may still touch reality. Fulton concludes: “let my glance be passional towards the universe and you.” Note that for the poets knowledge is always personal. On bias, Caroline Criado-Perez (2019 [104]) draws attention to what surely is an unforgivable bias expressed in the systematic disregarding of differences between men and women in medical research. Richard Douglas Fields (2014 [105]) opines that “Testing Males and Females in Every Medical Experiment Is a Bad Idea”, and Sarah Richardson (and others, 2015 [106]) opine more subtly that focussing “on preclinical sex differences will not address women’s and men’s health disparities” which may be true but the main issue that Criado-Perez is drawing attention to is the enormous and systematic data-gap regarding sex-based differences in medical outcomes. |
| 38 | Such “Wigner’s friend” scenarios mean that observer-independent “facts” cannot be determined in these cases, but this does not mean that these experimenters are thereby not realists. Just because an idea of “objective reality” can be shown to be illusory in at least some cases does not mean that the reality itself is illusory. Instead we should conclude that our ideas of it may be mistaken. As Karen Barad points out, such experiments are seriously difficult and to successfully carry them out one must be pretty sure that Nature really is there and will play ball. Barad says, quoting from Greenstein and Zajonc (1997 [110]): “it is not trivial to detect the extant quantum behaviour in quantum eraser experiments. The experimenters must be clever enough to design an experiment that can detect the entanglement” (Barad 2007 [24] p. 348). But asserting (in our terms) that the thinginess of the phænomena being investigated is ontologically secure is not asserting even that we can know it! So Barad asserts, citing Bohr himself, that “things” cannot be taken as “ontologically basic entities” (ibid. p. 138). The thinginess of things is ontologically secure precisely because it is phænomena that are “ontologically primitive” (ibid. p. 333). |
| 39 | “Subject” and “object” are primarily terms of grammar. In the phrase “objective knowledge” the adjective “objective” is being used as a (grammatical) metaphor which we here regard as empty: with Polanyi and Barad, we regard the philosophical conception of “objectivity” as being essentially mistaken. To minimise confusion we will therefore avoid the use of the terms “subjective” and “objective”. |
| 40 | “Objectivity” is a strangely slippery idea, for all that it is supposed to straighforwardly underlie the “scientific method” (and see note#10). Caroline Criado Perez (2019 [104]) gives an interesting example when she criticises the Bank of England’s (allegedly) “objective selection criteria” for choosing “key figures from the past” to grace British banknotes. |
Michael Polanyi says further: “Thus the ideal of pure objectivity in knowing and in science has been shown to be a myth” (Polanyi and Prosch, 1975 [22], Ch.3). He insists: “the processes of knowing (and so also of science) in no way resemble an impersonal achievement of detached objectivity … Scientific inquiry is accordingly a dynamic act of the imagination and is rooted in commitments and beliefs about the nature of things. It is a fiduciary act … Its method is not that of detachment but involvement.” | |
| 41 | |
| 42 | Poets that is, and anyone using poetic language such as the novelist: “We must be ruled by the situation itself and this is unutterably particular. Indeed this is something to which we can never get close enough, however hard we may try to as it were crawl under the net.” (Murdoch,1954 [91]; ch.6, p. 90). This is “Annandine” (Hugo’s alter ego) speaking. The novelist (who identifies with Hugo’s point of view) makes her point by indirection: going “under the net”. |
| 43 | Using the conveniently definite dating of Robinson (1976 [17]). |
| 44 | This recursive form of logic remains of interest today (Leonard, 2021 [117]) |
| 45 | |
| 46 | And we may grasp this illumination by the “leap of faith” (properly, the “leap by faith” over Lessing’s “ditch”) proposed by Søren Kierkegaard explicitly in his “Unscientific Postscript” (Kierkegaard 1846 [122]) and implicitly in his discussion of Abraham’s faith in “Fear and Trembling” (Kierkegaard 1843 [123]). It has been heavily debated ever since; Kierkegaard was very influential in 20th century philosophy. Earlier we called the same thing an “intuitive leap”. |
| 47 | To be precise, where Gödel proves a tautology (all theorems are formal manipulations in logic) Anselm asserts something about the real world. I think nobody believes that the reality of any thing can be established merely by “the analysis of concepts” (Ward 2008 [12], ch.6), however, as Keith Ward [124] points out, the Ontological Argument “shows that God is either necessary or impossible (that is, either cannot fail to exist, or that the concept is incoherent). But we cannot, simply by thinking, establish which.” (ibid.) Here we are interested in the analysis and epistemology of concepts in general (including scientific concepts), but not in the theological or ethical discussion of them. Such discussion is of course important, but outside our present scope. |
| 48 | “consistent” means that no false proposition can be proved in the system; “complete” means that there exists a proof in the system for every true proposition. Gödel cites the 1925 edition of Russell and Whitehead’s monumental work Principia Mathematica, and also David Hilbert’s work in arithmetic (Russell and Whitehead 1910 [125], Hilbert and Ackermann 1928 [126]): note that “arithmetic” is emphatically not “child’s play”! |
| 49 | where by “ideological” we intend to mean merely “of ideas”. Of course there is a difference between the ideology of economics (which is is highly political), and the ideology of physics (which is mostly philosophical). We are not here alluding to the politics of science, which is not our present focus important though power relationships are in the development of science. |
| 50 | The following summary is given by Velazquez, Parker and Jeynes (Velazquez et al., 2022 [72]), although it is still not entirely clear how to interpret this thermodynamically: |
“Before 1956, physicists believed that the so-called parity P, charge C and time T symmetries were unbreakable in quantum field theories. However, different experiments concerning weak forces confirmed along the years the violation of P-symmetry (Lee and Yang Phys.Rev., 1956; Wu et al. Phys.Rev., 1957), the violation of C symmetry (Ioffe et al. JEPT 1957, Lee et al. Phys.Rev., 1957), as well as the violation of the combined CP-symmetry (Christenson et al. Phys.Rev.Letts., 1964, Alavi-Harati et al. Phys.Rev.Letts., 1999, Fanti et al. Phys.Letts.B, 1999). | |
“Nowadays, the standard model of particle physics only admits the combined CPT-symmetry (Schwinger Phys.Rev., 1951), in which the effect of time reversal is equivalent to renaming particles as antiparticles (and vice versa: see Lüders Dan.Med.Fys.Med., 1954). By itself, the existing violations of the CP-symmetry requires the violation of T-symmetry to complete the CPT-symmetry. The direct observation of a time-reversal violation (but maintenance of the CPT-symmetry) was confirmed by the experiment conducted by the “BaBar” collaboration in 2012 (Lees et al. Phys.Rev.Letts., 2012). This experiment took advantage of entangled B0 and 0 mesons in the U(4s) resonance produced in positron-electron collisions with the goal of determining the proper time difference between the decay of the two B states. These were indeed directly observed, showing that the laws of microphysics are not identical whether time runs forwards or backwards, even though CPT-symmetry is maintained. | |
“In conjunction with the detection of both the Higgs boson (Chatrchyan et al. Phys. Letts. B, 2012, Aad et al. Phys.Letts.B, 2012) and gravitational waves (Abbott et al. Phys.Rev.Letts., 2016), the direct observation of a time-reversal violation was a crucial breakthrough of the past decade which showed that the laws of microphysics may also describe irreversible processes without invoking a loss of information. For the first time, irreversibility appeared as a fundamental property of the physical realm and not as an emergent feature. The subtle CP violations (and corresponding T violation) of particle physics experiments can be expected to have a significant impact at the macroscopic level, the evidence for which seems to be everywhere. For example, according to Sakharov (Sov.Phys.Uspekhi, 1991) the CP-violation could explain the imbalance of matter and anti-matter abundance in the present-day Universe, and the previous possibility could be connected (via CPT-symmetry) with the irreversible accelerating expansion of the Universe (in accordance with the T violation).” | |
| 51 | So Roger Penrose speaks specifically of “the principles that actually underlie the behaviour of our physical world” (2004 [133], Preface). Clearly, if pressed everyone will say that the reality is one thing and our ideas of it are something else, but in actual practice we do not tend to distinguish the two things very sharply. This becomes very obvious when string theorists (and others) speak of “before the Big Bang” as a sensible idea (which it cannot be since time itself started then), or of “inflation” or “dark matter” (or the “multiverse”) as realities. So here Penrose has apparently made a reality of the principles, where strictly speaking our formalisms cannot ever completely capture reality. And Penrose’s book is a brilliant and seminal tour de force! |
Additionally, Carlo Rovelli believes of “the world” that it “does not exist in space and does not develop in time” (Rovelli 2014 [134], ch.13). Instead he speaks, rapturously and persuasively (like a “poet”), of a “world made up solely of interacting quantum fields the swarming of which generates—through a dense network of reciprocal interactions—space, time, particles, waves and light” (ibid.). He does not explicitly distinguish the reality itself from our ideas of it, even if he does emphasise that our ideas may be mistaken. Ordinary readers (also including most scientists) are not in a position to judge the strengths and weaknesses of Rovelli’s position, and therefore how Rovelli himself may be mistaken (and what shape a more correct view might take). | |
Then Frank Wilczek (2021 [92]) says in his Afterword: “I have been at pains to be clear that science teaches us what is …” This really sounds like an ontological statement. I am sure that Wilczek himself distinguishes the reality from our formalisms, but it is too easy for the ordinary reader to slide from a strict view into a comfortable (and mistaken) approximation. | |
As examples of (apparent) confusion beween symbols and reality, I have mentioned three books by by renowned physicists (two of them Nobel prizewinners: Wilczek 2004 [135], Penrose 2020 [136]), all with “Reality” in their titles. Physicists really do believe that they touch reality: we are here enquiring into what this means. It seems that a correct view is not very simple. | |
| 52 | Actually, Sadi Carnot’s seminal treatment in 1824 relied on the false idea of caloric: it was Clausius who found the correct interpretation we still use (see Paul Sen, 2021 [45]). It was also Clausius who recognised that the change in the internal energy U of the system is path-independent and therefore that U is what we would now call a “function of state” (for a close discussion of this see Jennifer Coopersmith, 2015 [137]). |
| 53 | The symbol “S” (denoting entropy) originated with Clausius, possibly indicating the integral (“Summe”: ∫ dQ/T) he introduced to define the “second law” (Paul Sen, 2021 [45] p. 68, mentions “a charming unsubstantiated story that he did so in honour of Sadi Carnot”). In modern terms S has the unit Joules per Kelvin (energy/temperature), where the idea of “absolute temperature” was clear to Clausius who already knew in 1854 that 0 °C = 273 K (accepting the 1848 value of William Thomson—later Lord Kelvin). “W” (supposedly from “Wahrscheinlichkeit”, probability) denotes the number of different states the system can have. From this formula Boltzmann could derive the ideal gas law in what is now a textbook treatment. |
| 54 | This statement appears to be controversial since conventional (simple) physics treatments hold that entropy is extensive (meaning, roughly, “double the size, double the entropy”; for example, mass is extensive, colour is intensive). However, it is very clear that this is an error. Entropy may indeed be extensive but only for certain sorts of systems. In principle it is intensive in general, as explained in detail by Walter Grandy (2008 [138], ch.5: “The Presumed Extensivity of Entropy”), who points out (as we also do) not only the anthropomorphic (“subjective”) nature of the Partition Function, but also the necessity of considering the indistinguishability of states (not particles). This latter is also asserted by Karen Barad who insists (from an entirely different point of view) that “the primary ontological unit is the phenomenon” (Barad 2007 [24], p. 333). |
Grandy (ibid.) also points out, citing Wolfgang Pauli’s famous Lectures at ETH Zurich (conducted in 1952 [139]), that Boltzmann’s equation for entropy (see Equation (1)) is determined up to f(N), an arbitrary function (not merely a constant) of the number of states N in the state space: “S = k {lnW + f(N)}”. Note that the entropic Liouville Theorem still applies (Parker and Jeynes 2021 [140]), meaning that N does not necessarily have to be defined in statistical mechanics terms: it may instead be defined in terms of “degrees of freedom” which may also apply to small systems. Benoit Mandelbrot (1989 [141]) has elegantly explained some basic thermodynamic ideas which have bedevilled the discussion of small systems. | |
Grandy says, “The effect … is to convince us that a proper definition of entropy should at bottom be theoretical … It is not an empirical question but a conceptual one” (ibid. p. 68). There are of course many incorrect ways to think, but there is no mechanical method of finding a correct way. | |
| 55 | The Partition Function of a system is an abstract representation of how the system shares out the total energy between its constituent parts. |
| 56 | His argument involves a calculation of the entropy of the system of resonators, and therefore also involves Boltzmann’s relation (which he gives correctly, that is, up to a constant factor and using the natural logarithm: “S = k lnW + constant”). He obtains the values of both eponymous constants (the “Planck” and the “Boltzmann” constants, h and k, which he calls “universal” or “natural” constants) by considering the accurate measurements of what we now call Wien’s displacement constant, b = 2.94 mm.K, that had then recently appeared: he obtains k = 1.346.10−23 J/K and h = 6.55.10−34 J.sec. Today’s accepted values are, b = 2.90 mm.K; k = 1.381.10−23 J/K; h = 6.63.10-34 J.sec. Note that Planck recognised that ħc/k has the same unit as b (where ħ ≡ h/2π is Dirac’s “reduced” Planck constant and c is the speed of light), and in fact ħc/k ≈ b. |
| 57 | It is germane to mention that there remains an ongoing technical debate surrounding the meaning of Landauer’s Principle, which John Norton alleges to be “unproved”, and indeed based on “circular reasoning” (Norton 2013 [154]). The issues are intricate, but involve debate over the applicability to fluctuation theory and to systems not representable by statistical ensembles (such as black hole event horizons). The latest summary of this debate (Ladyman and Robertson, 2014 [155]) criticises Norton’s results but also allows that at least some of his analysis appears to be valid. However, everyone believes that Maxwell’s Demon fails, and the the Second Law remains valid (whether or not it is fundamental). |
| 58 | Parker and Jeynes (2019 [28]) also show that information and entropy should be considered (contra Brillouin) not as opposites, but as complementary (that is, orthogonal in complex Minkowski 4-space). And indeed, Parker and Jeynes (2020 [157]) use the Shannon information entropy explicitly to discuss the stability of fullerenes: “for example, for C60 … we can calculate an entropy … using the Shannon fragmentation metric”. |
| 59 | But note that treating the black hole in QGT as unitary (than which exists nothing simpler; Parker and Jeynes 2021 [160])—that is, ontologically primary—implies that NO “internal configuration” exists at that scale of description. That the alpha particle is also unitary in QGT (Parker et al. 2022 [161]) is not a contradiction (considering that the “constituents” of the alpha are 2 protons and 2 neutrons) since to give a QGT account of those constituents would require a change of scale. Of course, the black hole already has the scale of the Planck length (than which exists nothing smaller). |
| 60 | Here, the ideas of “holomorphic”, “maximum entropy”, and “unitary” are closely related: holomorphic (literally “the shape of wholeness”) has its full mathematical meaning even though it is applied to physical entities; unitary (than which exists nothing simpler) on the other hand is related to philosophical ideas of monadology (Leibniz 1714 [163]; see also Thomas 2015 [164]), not to (for example) the mathematical idea of an Hermitian adjoint. |
| 61 | Parker and Jeynes (2019 [28]) have shown that the double-logarithmic spiral (DLS) is an eigenfunction of the entropic Hamiltonian, and that spiral galaxies are well-modelled (at zeroth order) by the DLS. Moreover, Parker and Jeynes (2021 [160]) have used the QGT formalism to show (i) that this (idealised) DLS system conforms to the entropic Euler-Lagrange equations; (ii) that its entropy production is therefore Noether-conserved; and (iii) that its entropy production is necessarily non-zero, having two components: one component is small and comparable to the Hawking radiation of the supermassive black hole at the galactic centre, and the other component is many orders of magnitude larger (and presumably comparable to the entropy created by the accretion behaviour of the black hole). |
| 62 | These include problems in the definition of the (presumed) holographic “surface” of the galaxy (see Parker and Jeynes 2019 [28]). That is, how big it is supposed to be. The astrophysicists treat this problem heuristically, by calculating how much “dark matter” is required as a function of distance from the galactic centre. However, it should be noted that the stability of spiral galaxies (which are ubiquitous in the Universe) is an immediate consequence of QGT. This geometrical stability is not easy to account for in standard treatments since the distances involved (105 light years for the Milky Way) preclude normal feedback mechanisms. But QGT is defined in hyperbolic space, and non-locality is built into it—see §4.5. |
| 63 | Joseph Liouville (Liouville 1838 [165]) obtained a result whose importance was recognised only subsequently: in 1844 Augustin-Louis Cauchy proved the related result for complex analysis that every bounded entire function must be constant, which follows from the fact (important in QGT) that holomorphic functions are analytic. But it was J.W.Gibbs who was the first to recognise the importance of this equation as the “fundamental equation” of statistical mechanics (Gibbs 1884 [166]) |
| 64 | Arno Keppens (Keppens 2018 [167]) also independently derives the Bekenstein–Hawking expression by considering the consequences of the underpinning of Raphael Bousso’s “holographic principle” (Bousso 2002 [168]) by the quantisation of space-time. Keppens proposes “viewing the conjectured pre-geometric atoms of quantum space as the ontological micro-constituents of our emergent reality”, although QGT represents ontology as (if anything) scale-less—that is, unitary entities (which either have no “micro-constituents” or do not depend on them ontologically) may be found at any scale including the alpha particle (see Parker et al., 2022 [161]) and black holes (see Parker and Jeynes 2021 [160]). Moreover, Barad (2007 [24]) denies even the existence of “ontological micro-constituents”. This emphasis on ontology is relevant to Keppens’ work since he wishes to aim “getting as close as possible to the very nature of reality”. |
| 65 | It is worth pointing out that Karen Barad approaches this from a fundamental point of view, by denying that “objects have inherent properties” (Barad 2007 [24], p. 293), explaining that this is a consequence of the BKS Theorem (Bell 1966 [169], Kochen and Specker 1967 [170]). That is, simple “individual entities” do not really exist as such, even if it is often very convenient to pretend they do. The way the local and non-local interact is yet to be described in detail, although Velazquez (2022 [71]) and Velazquez et al. (2022 [72]) coherently treat reversibility and irreversibility together in a novel way: they rely on a complexification of the analytical approach (“analytical continuation”). This is not to deny our own personal individualities (heaven forbid!), but to point out with the poet that “no man is an island” and that we are nothing if we are isolated, notwithstanding our individuality. We are locally ourselves even if we are also (non-locally) entangled with everyone else. We make our own (local) decisions, even if those decisions are strongly constrained by our (non-local) circumstances. |
| 66 | Note that QGT is defined in hyperbolic space: this is a necessary consequence of the logarithmic dependence expressed in Equation (1). It is hyperbolic space that generates the scale-independence of QGT expected from a thermodynamics which must be true at all scales if it is fundamental to physics. |
| 67 | Of course, none of these eminent scientists could have taken the recent developments in thermodynamics into account. But however eminent they are, no one really believes them when they claim that the arrow of time is unreal. So Iris Murdoch, speaking of “simple and obvious facts” (and referring to the prominent philosophers John M.E. McTaggart and George E. Moore), observes that “McTaggart says that time is unreal, Moore replies that he’s just had his breakfast” (Murdoch 1962 [100]). Emily Thomas (2015 [164]) points out that the little-known British idealist Hilda Oakeley (1867–1950) had previously also criticised McTaggart (and by implication, Leibniz and other idealist monadologists). Matyáš Moravec (2022 [174]) traces the influence of Henri Bergson (1859–1941) on Oakeley and others, and the reception of Bergson’s ideas after Bertrand Russell’s ferocious attack on them in 1912. Russell’s views on time have been very influential in the physics community to this day but may not survive contact with the new thermodynamics. |
| 68 | “Cause-and-effect” is a central feature of science: experiments are specifically designed to show that certain causes have certain effects. Nevertheless, in principle “cause-and-effect” is necessarily an approximation since everything is entangled with everything else (how do we determine the boundary between the “local” and the “non-local”?). As Graeber and Wengrow (2021 [11], p. 21) say, “One must simplify the world in order to discover something new about it” (my emphasis). This, surprisingly, is directly addressed by Sidney Dekker (2006 [36], p. 73) when, speaking of the attribution of “human error” in investigations of disasters, he asks “What is the cause of the mishap?”, saying “Cause is something we construct”. He goes on to insist (p. 78) “there are no such things as … causes … In fact, there is no … origin [cause] anywhere (other than the Big Bang)” precisely because everything is entangled with everything else—especially when things go wrong! Dekker quotes James Reason’s (1990 [177]) analysis of the infamous Bhopal accident in 1984 as a prime example of “latent errors” buried in the system. What “caused” this disaster? It makes little sense (and is less use) to say that Union Carbide’s management system “caused” it. Certain events triggered it, but viewed correctly these should be seen as “effects” themselves since they were built into the system already. |
| 69 | We should point out that QGT has surprising and surprisingly far-reaching consequences, such as the demonstration that DNA must be right-handed because of the Second Law (Parker and Walker 2010 [180]), a result later formally proved in a general treatment (Parker and Jeynes 2019 [28]; see Appendix A in Supplementary Materials). |
| 70 | Bohm’s proposal is considered by Rovelli to violate his Hypothesis 2 (completion) of his Relational Quantum Mechanics (Rovelli 1996 [182]). However, neither Bohm nor Rovelli take account of Parker’s Principle of Least Exertion (Parker and Jeynes, 2019 [28]) in any way, even though both of them give significant weight to the (physical) quantity Information in their different treatments. But Parker has shown that a physical system cannot be treated completely unless its info-entropy is also considered. |
| 71 | Velazquez et al. (2022 [72]) also treat the 2nd Law as axiomatic in a fundamental approach to reversible/irreversible processes (explicitly considering the Loschmidt Paradox). |
| 72 | Although in Biblical Hebrew there is no equivalent impersonal word for “meaning”: [בִינָ֔ה] (ḇî·nāh) is invariably used specifically of someone’s understanding; it is used only once in the Hebrew Bible as syntactically impersonal at Daniel 8:15 (translated “meaning” by Geneva 1560 [184]), but even in this late text it refers semantically to Daniel’s understanding of the vision. |
| 73 | Charlotte Higgins (2022 [59]) comments: “Ukrainian writers often tell me that now is not the time for literary experimentation, but rather for directness and documentary. What is clear though, is that they are experimenting almost despite themselves, as they edge towards the impossible task of expressing the inexpressible.” True documentary involves speaking meaningfully of what may very well be ineffable when the circumstances are extreme. But it is when the circumstances are extreme that we most seek meaningful expression! Poetry (or poetic speech) is existentially fundamental. |
| 74 | Ariel Caticha (2021 [185]) takes an entirely different line here, commenting that the “search for the meaning of entropy has proved so elusive” precisely because we do not need to “know what ‘entropy’ means—we only need to know how to use it”. In fact he says that “entropy needs no interpretation” (italics original). Additionally, Caticha treats “information” not as something strictly physical, as we do here, but effectively in anthropological terms, that is: as “defined in terms of its effects on the beliefs of rational agents” (underlining the complexity of the philosophical position), although it is clear that Caticha’s purpose is to recast “information” as a model-making category. He considers information mathematically as a synthesis of Bayesian and Maximum Entropy methods of correct inference in the context of changing “information” (interpreted as constraints on the model). |
| 75 | JCGM: Joint Committee for Guides in Metrology; BIPM: Bureau International des Poids et Mesures (International Bureau of Weights and Measures). The JCGM is responsible for the GUM (the Guide to the Expression of Uncertainty in Measurement: JCGM 2008 [189]) and the VIM (the Vocabulaire international de métrologie: JCGM 2012 [190]). The essentially human nature of measurement is underlined by the insistence in the latest revisions of the GUM and the VIM that the measurement is not aimed at determining the “true value” (whose very existence is philosophically debatable) but instead seeks to specify a “process of experimentally obtaining one or more quantity values that can reasonably be attributed to a quantity” (JCGM 2012). This makes it very plain that, as Karen Barad says, it is the phænomenon (not the presumed entity) that is ontologically primitive (Barad 2007 [24], p. 333) |
| 76 | There is a very large literature on “realism” which we can only touch on here. Barad (2007 [24]) is as good an entry as any into the philosophical literature since the book opens with a detailed account and discussion of Bohr’s physics-philosophy. But “reality” is regularly presented as a preoccupation of leading scientists: “Process and Reality” (Whitehead 1929 [14]), “The Road to Reality” (Penrose 2004 [133]), “Reality is not what it seems” (Rovelli 2014 [134]), “Fundamentals: Ten Keys to Reality” (Wilczek 2021 [92]). Although all these authors are realists, none of them are “naïve realists”: as Rovelli observes, reality is not what it seems—it is elusive! |
| 77 | It might be thought that an argument from mathematics cannot be used for or against any doctrine of materialism. But Gödel proved what Whitehead suspected, that not even maths is a strictly necessary thing (since it is Gödel-incomplete). Nevertheless, maths is indispensible to our knowledge of physics (and much else besides). The strict materialist would claim knowledge is ultimately thought, and thought must ultimately be physical (neurons firing and suchlike) since nature is all there is. But this position looks irrational, given that our knowledge is necessarily Gödel-incomplete. Materialists should claim instead that “thought may (or may not) ultimately be physical” (and they believe that it is physical). However, we suspect not only that mind is immaterial, but also that such a position accords best with the evidence. |
| 78 | This usage of “meta” and “metameta” has been analysed logically in some detail for this context: as Masahiko Sato says, it “plays a fundamental role when we define formal systems such as logical and computational calculi” (Sato 2003 [192]). |
| 79 | “Indivisible” is a neologism of Henry More (More 1647 [193], see Gorman 2021 [128]), as is also “indiscerpible” (that is, physically indivisible, from the Latin discerpere—to tear asunder; now obsolete). We can now recognise the alpha particle as indiscerpible (since it is naturally very stable indeed) although it is not strictly indivisible, being composed of two protons and two neutrons. But the Quantitative Geometrical Thermodynamics (QGT) discussed at §4.4 above treats it as a unitary entity—in other words, an atom in 17th century terms! |
| 80 | It is hard to overestimate the importance of the advent of the microscope to natural philosophy. Suddenly things became much more complex and beautiful than anyone had imagined. This is excellently reviewed and described by Kevin Killeen (Killeen 2017 [194]), who thus provides a corrective to our ideas of the emergence of “scientific modernity” which (as he puts it) “is often still viewed as a sad but necessary putting aside of the poetic”. |
| 81 | The Ontological Argument (Anselm 1078 [116]) has puzzled philosophers for a millennium, and was written as a prayer, which is also a form of poetical speech. The poet recognises that not everything can be explained, and the philosopher should recognise that this ineffability is a property of logic. Logical arguments are necessarily incomplete, but the coherence of all effective poetry is a property of rationality. The philosophers should take more account of the poetical properties of the Ontological Argument. |
| 82 | E.R.Dodds’ influential idea of “irrational intuition” in his famous book of a generation ago (Dodds 1951 [121], p. 217 passim) is in our terms quite mistaken since it is rationality itself that guides, structures and mediates intuition (see for example Polanyi 1958 [38]). Intuition may or may not be well-directed, but calling it either rational or irrational is a category error. |
| 83 | We give the ancient (koine) Greek text rendering the ancient Hebrew (Hebrew Bible c.500 BCE [195]; see §6) because the Hebrew original (with its vocalisation remembered separately) was not a text as we now understand it: the Masoretic text (“MT”: essentially the “pointed” Hebrew text of Samuel ben Jacob) was only completed in modern times (1010 CE: the “Leningrad Codex”). The unpointed (original) Hebrew text is an abjad, that is, a very highly compressed mnemonic (consonantal) text: the vowels are preserved separately by the oral tradition (known as the Masorah). The MT encodes this vocalisation into the text itself by a sophisticated “pointing” system. |
| 84 | The Greek translation of the Hebrew (the Septuagint, “Lxx” [196]) was started in the 3rd century BCE by the Jewish scholars in Alexandria at the request of the Pharaoh (Ptolemy II, 285-247 BCE), and probably essentially finished by the 2nd century BCE. Note that the chapter numbering varies between the MT and Lxx for Jeremiah and Psalms. The Lxx is itself a canonical text for Christians since the (Greek) New Testament quotes it verbatim in many places. |
We use the English of the Geneva translation (1560 [184]) since this was widely reprinted and used in England up to and beyond the Restoration of Charles II (1660), remaining very influential through the substantial dependence on it of the King James Version (1611, originally printed in a blackletter font) which became the dominant text in English until the mid-20th century. Verse numbers were first introduced by the Geneva scholars. The 1560 Geneva Bible was printed in a clear Latin (not blackletter) font. The New Testament of both Geneva and KJV are heavily dependent on Tyndale’s 1526 [69] (blackletter) New Testament. | |
| 85 | Bohm and Hiley (1993 [19], §14.1,p. 320) discuss this in some detail: “Heisenberg … said very explicitly that the essential truth was in the mathematics. This view has become the common one among most modern theoretical physicists who now regard the equations as providing their most immediate contact with nature … without an equation there is really nothing to talk about. On the other hand, in the past we began talking about our concept of physical reality and used the equations to talk about them.” They go on to speak of a “new creative approach” which may start either from (informal) physical ideas or from formal mathematical ones. |
| 86 | Observation shows that Parker and Jeynes (2019 [28]) correctly calculate an energy of 1.2 × 10−15 J required to transform a DNA molecule to a different form: they also reasonably calculate an energy-equivalent galactic mass of the Milky Way as 2.3×1059 J, an energy 74 orders of magnitude larger. Parker et al. (2022 [161]) also correctly calculate nuclear sizes: the atomic nucleus is some nine orders of magnitude smaller than the DNA molecule treated previously. But exactly the same (thermodynamic) methods are in use, as expected since the Laws of Thermodynamics are expected to apply at all scales. |
| 87 | The scalelessness in time has not yet been explicitly demonstrated in quantitative examples by QGT methods: these very new methods have not yet been developed to treat dynamical systems. However, Parker et al. (2022 [161]) point out that radioactive decay (the beta-decay process, which is logarithmic in time) is apparently correctly accounted for in their heuristic treatment of 6He decaying to 6Li. |
| 88 | “Conjugate quantities” are those related by the “Uncertainty Relations” (position and momentum, time and energy etc.). These relations are discussed in considerable depth by Karen Barad, both of the position/momentum (x and p) and the time/energy (t and E) conjugate pairs are given explicitly in terms of the Planck constant h: ΔxΔπ ≥ h/4π; ΔtΔE ≥ h/4π (Barad 2007 [24], p. 300: as Equation (2) and an inline equation). Note that Barad draws a sharp philosophical distinction (reinterpreting the Δ operator) between Heisenberg’s “Uncertainty Relations” (which are epistemological) and Bohr’s “Indeterminacy Relations” (which are ontological). |
| 89 | If we only know our ideas of the thing (rather than the thing-in-itself) why should we believe that the thing-in-itself has any reality independent of us? This gives rise to what is known as (some version of) “external world skepticism”. Grace Helton discussed this in detail, commenting: “if solipsism is in fact refutable, it is at least not obvious what form its refutation might take … My aim is … showing that it is not a straightforward matter to see how these difficulties might be overcome, with the result that solipsism cannot be dismissed out of hand” (Helton 2021 [199]). |
| 90 | Physicists who claim to be solipsists do exist. Professor Joan Vaccaro’s position is subtle, but she asserts (in part): ““I” do not exist objectively ... This is the fundamental absurdity of life.” She goes on to “recite” the “Solipsist’s Plea”: Oh Universe!/I assume that you exist./Let me feel your far flung matter, / so that your illusion may persist (Vaccaro 2022 [200]). But she was not willing to debate this with me (private communication, 9 March 2022). |
| 91 | Barad criticises Frayn, but does not note that Frayn’s device of a triple rendering of the Heisenberg-Bohr meeting is a nod to Kierkegaard’s similar (quadruple) device in his terrifying account of Abraham and Isaac in Fear and Trembling (Kierkegaard 1843 [123]) that was so influential in the 20th century. |
Kierkegaard was translated into English rather late (1930s and later). But he was translated into German repeatedly from the later 19th century. Christoph Schrempf had translated Kierkegaard’s complete works into German by 1922, but these were renowned as being rather free. Parts of Fear and Trembling and other works were published by Hermann Ulrich in 1925 in a much closer German rendering (Ulrich 1925 [203]). | |
| 92 | The reason that we cannot say what “an electron” is is that all electrons are entangled with each other (being indistinguishable) so that “an electron” does not exist at all as an individual entity. Karen Barad insists on this, observing (in the context of a discussion of the implications of Bell’s Theorem) “that it is no longer possible to embrace the metaphysics of individualism” (Barad 2007 [24], p. 292). |
Surprisingly, this was underlined by the poet some three millennia ago, who asserted to God silence is praise “[דֻֽמִיָּ֬ה תְהִלָּ֓ה] ḏu·mî·yāh ṯə·hil·lāh” (Psalm 65:2, using the Masoretic Text 1010CE, and following the English translation of Alter 2007 [204]) in the context of God’s power both over his Creation (he “stills the roar of the sea ”) and also over “the tumult of nations” (ibid. v.8) but starting with the poet’s own shortcomings (“crimes”) on which God is silent (he “covers” them: [תְכַפְּרֵֽם] ṯə·ḵap·pə·rêm, ibid.v.4). Here the personal and indeterminate nature of the ontology of knowledge is explicit, and the poem is undoubtedly early: David was c.1000 BCE and he or one of his musicians (also called “seers”) may well be the poet. Note that this is the indeterminacy (or silence) of the eloquent poet, not of the baffled philosopher (Wittgenstein 1921 [76], §7). | |
This is not an isolated instance. Psalm 19 juxtaposes the wordless praise of the Creator by the cosmos (“day after day they pour forth speech … they use no words … yet their line goes out into all the earth”, v.3) with the delight of the poet in God’s law (“the law of the Lord is perfect, refreshing the soul ”, v.7). The physicist knows the same delight. There are also other examples. The via negativa has ancient roots. | |
It is not only the ancient poets who notice the apparent entanglement of everything. Jessica Nordell, in the context of a discussion of police bias, also points out that people’s very health itself may be measurably compromised by an inability to recognise our entanglement with each other as social beings: “Bias requires a firm division between the self and the other. But if the distinction beween the concept of ‘I’ and the concept of ‘you’ is not so clear, bias loses its meaning.” (Nordell 2021 [15], p. 128). | |
| 93 | It is only rarely that we manage to see things we do not recognise. Michael Berry lauds Newton, saying that he “was a very careful observer, and paid particular attention to phenomena that resisted his attempts to explain them” (Berry 2002 [21]). |
| 94 | For convenience we follow the dating of New Testament texts by J.A.T.Robinson (1976 [17]). |
| 95 | The Creation narrative in Genesis in the form we have it almost certainly dates from around the Temple reforms of Josiah in the 7th century BCE: see II Kings 23 and Margaret Barker’s gloss on this (Barker 1987 [205], p. 142). The modern Hebrew script we use today was introduced in the early 5th century BCE by Ezra the Scribe. It has been widely thought that this Creation narrative represented a theological innovation at that time, since comparable tropes had not been found in the surrounding cultures. But this position is certainly mistaken, since a reanalysis (Korpel and de Moor 2014 [206], see Jeynes 2014 [207]) of two tablets from the Ugarit tell at Ras Shamra confidently dated late 13th century BCE show that the Ugaritic creation story has many remarkably close similarities with the Hebrew one. Therefore, the traditional ascription of the Hebrew story to Moses (perhaps 16th century BCE or earlier) cannot be rejected out of hand. |
| 96 | For convenience, and to be definite, we accept the traditional account of the genesis of the Hebrew text of the Hebrew Scriptures that we have in our hands as being the work of Ezra the Scribe working in Babylon around 500 BCE, although nothing much rests on this dating in this present work. Ezra introduced (or restored) the “Assyrian script” that is used to this day in Israel: previously the common (Canaanite) script was completely different. All this is discussed in detail in the Appendix (see Supplementary Materials). |
| 97 | To repeat: “Modern” Hebrew here means the unpointed script that Ezra the Scribe introduced a mere two and a half millennia ago. This script is still today in everyday use in Israel. If modern Israelis wish to use an “archaic” script, they use the Masoretic pointing system introduced by Samuel ben Jacob (and the Masoretic scholars) only a thousand years ago. |
| 98 | The alternative possibility that such artefacts were created for the antiquities market is considered in the Appendix (see Supplementary Materials) and ruled out on the grounds that the palaeo-Hebrew is meaningful. |
| 99 | It is necessary to limit the scope of this work to exclude questions of ethics, but these persistently obtrude whenever poetics and our basic approach to knowledge are in view. Where is Justice? Jon Cruddas (2021 [213], p. 20) analyses the political consequences of “epochal technological change” in a deep treatment that insists on the necessity of an “ethical orientation” capable of addressing the central political questions of “justice and human labour” (p. 26f). The revolutionary advances in thermodynamics we have described in §4 are indeed expected to result in the “epochal technological change” Cruddas speaks of: and therefore our exclusion of ethical questions is in principle unrealistic. Nevertheless, we leave such questions for further work. |
References
- McLuhan, M. Understanding Media: The Extensions of Man; McGraw Hill: New York, NY, USA, 1964. [Google Scholar]
- Landau, L.; Lifshitz, E. Course of Theoretical Physics; Fizmatgiz: Moscow, Russia, 1940; (multiple volumes written in Russian published from 1940: English translations published from the 1950s). [Google Scholar]
- Webb, R. Carlo Rovelli’s New Book: Eclectic Essays on Physics, History and More (New Scientist, 28 October 2020). Available online: https://www.newscientist.com/article/mg24833060-600-carlo-rovellis-new-book-eclectic-essays-on-physics-history-and-more/#ixzz7EG6FK1Zx (accessed on 10 December 2022).
- Nicolescu, B. Methodology of Transdisciplinarity—Levels of reality, logic of the included middle and complexity. Transdiscipl. J. Eng. Sci. 2010, 1, 19–38. [Google Scholar] [CrossRef]
- Carson, R. Silent Spring; Houghton Mifflin: Boston, MA, USA, 1962. [Google Scholar]
- Keats, J. La Belle Dame Sans Merci (Original Version in a Letter to Keats’s Brother George dated 21st April 1819; Joseph Appleyard: London, UK, 1820. [Google Scholar]
- McLeish, T. The Poetry and Music of Science; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Popper, K. Unended Quest: An Intellectual Autobiography; Routledge: London, UK, 1976. [Google Scholar]
- Snow, C.P. The Two Cultures; Cambridge University Press: Cambridge, UK, 1959. [Google Scholar]
- Sacks, O. Greetings from the Island of Stability; New York Review of Books, 8 February 2004; Republished in Sacks: 2019; Picador: London, UK, 2004. [Google Scholar]
- Graeber, D.; Wengrow, D. The Dawn of Everything: A New History of Humanity; Allen Lane: London, UK, 2021; Penguin Books, 2022. [Google Scholar]
- Szpiro, G. Poet of the infinite. Nature 2012, 492, 38–39. Available online: https://www.nature.com/articles/492038a (accessed on 10 December 2022). [CrossRef]
- Gray, J. Henri Poincaré: A Scientific Biography; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Whitehead, A.N. Process and Reality. An Essay in Cosmology; Gifford Lectures Delivered in the University of Edinburgh During the Session 1927–1928; Macmillan: New York, NY, USA; Cambridge University Press: Cambridge, UK, 1929; Corrected edition; Griffin, D.R., Sherburne, D.W., Eds.; The Free Press: New York, NY, USA, 1979; Page numbers are given for the corrected edition. [Google Scholar]
- Nordell, J. The End of Bias: How We Change Our Minds; Metropolitan Books; Henry Holt & Co.: New York, NY, USA; Granta Books: London, UK, 2021. [Google Scholar]
- Kahneman, D.; Klein, G. Conditions for Intuitive Expertise: A Failure to Disagree. Am. Psychol. 2009, 64, 515–526. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.A.T. Redating the New Testament; SCM Press: London, UK, 1976. [Google Scholar]
- Berger, J. Ways of Seeing; BBC: London, UK, 1972. [Google Scholar]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Appreciation of Quantum Theory; Routledge: Abingdon, UK, 1993. [Google Scholar]
- Madelung, E. Quantentheorie in hydrodynamischer Form. Z. für Phys. 1927, 40, 322–326. [Google Scholar] [CrossRef]
- Berry, M.V. Exuberant interference: Rainbows, tides, edges, (de)coherence …. Philos. Trans. R. Soc. Lond. A 2002, 360, 1023–1037. [Google Scholar] [CrossRef]
- Polanyi, M.; Prosch, H. Meaning; University of Chicago Press: Chicago, IL, USA, 1975. [Google Scholar]
- Wagensberg, J. On the Existence and Uniqueness of the Scientific Method. Biol. Theory 2014, 9, 331–346. [Google Scholar] [CrossRef][Green Version]
- Barad, K. Meeting the Universe Halfway: Quantum Physics and the Entanglement of Matter and Meaning; Duke University Press: Durham, NC, USA, 2007. [Google Scholar]
- Williams, W.C. Paterson; A New Directions Book: New York, MY, USA, 1926; corrected edition New Directions Publishing, New York, 1993. [Google Scholar]
- Edwardes, M.P.J. The Origins of Self; UCL Press: London, UK, 2019. [Google Scholar] [CrossRef]
- Barfield, O. Poetic Diction: A Study in Meaning; Faber & Dwyer: London, UK, 1928. [Google Scholar]
- Parker, M.C.; Jeynes, C. Maximum Entropy (Most Likely) Double Helical and Double Logarithmic Spiral Trajectories in Space-Time. Sci. Rep. 2019, 9, 10779. [Google Scholar] [CrossRef]
- Bird, A. Laws and essences. Ratio 2005, 18, 437–461. [Google Scholar] [CrossRef]
- O’Donovan, O. The Long Psalm. In From Words to Meaning; Samuel, H., Kurtis, R., Peters, E.N., Eds.; Ortlund, Sheffield Phoenix Press: Sheffield, UK, 2021. [Google Scholar]
- Barfield, O. Saving the Appearances: A Study in Idolatry, 3rd ed.; Faber and Faber: London, UK, 2011; Barfield Press: Oxford, UK, 1957. [Google Scholar]
- Duhem, P. SOZEIN TA PHAINOMENA (σῴζειν τὰ φαινόμενα), Essai sur la Notion de Théorie Physique de Platon à Galilée (Hermann, Paris, 1908); Transl. Edmund Dolan and Chaninah Maschler: To Save the Phenomena: An Essay on the Idea of Physical Theory from Plato to Galileo; University of Chicago Press: Chicago, IL, USA, 1969. [Google Scholar]
- Sacks, O. Humphrey Davy, Poet of Chemistry; New York Review of Books, 4 November 1993; Republished in Sacks; Picador: London, UK, 2019. [Google Scholar]
- Piketty, T. Capital et Idéologie, Capital and Ideology; Éditions du Seuil: Paris, France, 2019. [Google Scholar]
- Clausius, R. Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie. Ann. der Phys. und Chem. 1854, 169, 481–506. [Google Scholar] [CrossRef]
- Dekker, S. The Field Guide to Understanding Human Error; Ashgate: Aldershot, UK, 2006. [Google Scholar]
- Weinreb, R.; Tzvi, H. Rabbi Weinreb’s Parsha Column, Korach: “Two Jews, Three Opinions”. 2021. Available online: https://outorah.org/p/19574/ (accessed on 16 December 2021).
- Polanyi, M. Personal Knowledge: Towards a Post-Critical Philosophy; University of Chicago Press: Chicago, IL, USA, 1958. [Google Scholar]
- Collins, H.; Evans, R. Rethinking Expertise; University of Chicago Press: Chicago, IL, USA, 2007. [Google Scholar]
- Whorf, B.L. The Relation of Habitual Thought and Behavior to Language, ETC: A Review of General Semantics, 1(4) (Summer 1944) 197–215 (reprinted from Language, Culture and Personality: Essays in Memory of Edward Sapir; Menasha, Wisconsin, 1941). Available online: https://www.jstor.org/stable/42581315 (accessed on 14 December 2022).
- Hadamard, J. The Psychology of Invention in the Mathematical Field; Princeton University Press: Princeton, NJ, USA, 1945. [Google Scholar]
- Maxwell, J.C. VIII. A dynamical theory of the electromagnetic field. Philos. Trans. 1865, 155, 459–512. [Google Scholar] [CrossRef]
- Gödel, K. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I (On Formally Undecidable Propositions of Principia Mathematica and Related Systems I). Mon. für Math. und Phys. 1931, 38, 173–198, (reprinted in English in Hawking, 2005). [Google Scholar] [CrossRef]
- Hawking, S. God Created the Integers; Running Press: Philadelphia, PA, USA, 2005. [Google Scholar]
- Sen, P. Einstein’s Fridge: The Science of Fire, Ice and the Universe; William Collins: London, UK, 2021. [Google Scholar]
- Coates, E. The Poetics of Physics in Dance. PAJ A J. Perform. Art 2017, 39, 7–21. [Google Scholar] [CrossRef]
- Paxton, S. Fall after Newton. Contact Q. 1988, 13, 38. Available online: https://contactquarterly.com/contact-editions/title/fall-after-newton-1987#$ (accessed on 14 December 2022).
- Nye, M.J. Michael Polanyi: Science as Personal Knowledge and Social Practice. Angew. Chem. Int. Ed. 2017, 56, 3426–3433. [Google Scholar] [CrossRef]
- Sacks, O. Everything in its Place: First Loves and Last Tales; Alfred A. Knopf: New York, NY, USA, 2019. Republished 2020; Picador: London, UK, Page numbers given are to the 2020 paperback edition. [Google Scholar]
- Damasio, H.; Grabowski, T.; Frank, R.; Galaburda, A.M.; Damasio, A.R. The Return of Phineas Gage: Clues About the Brain from the Skull of a Famous Patient. Science 1994, 264, 1102–1105. [Google Scholar] [CrossRef]
- Damasio, A. Descartes’ Error: Emotion, Reason and the Human Brain; G.P.Putnam’s Sons: New York, NY, USA, 1994. [Google Scholar]
- Macmillan, M. Restoring Phineas Gage: A 150th Retrospective. J. Hist. Neurosci. 2000, 9, 46–66. [Google Scholar] [CrossRef]
- Oxford English Dictionary. 3rd (online) edition. Available online: https://www.oed.com/ (accessed on 14 December 2022).
- Jaksland, R. An apology for conflicts between metaphysics and science in naturalized metaphysics. Eur. J. Philos. Sci. 2021, 11, 74. [Google Scholar] [CrossRef]
- Morganti, M.; Tahko, T.E. Moderately naturalistic metaphysics. Synthese 2017, 194, 2557–2580. [Google Scholar] [CrossRef]
- Ladyman, J. Science, metaphysics and method. Philos. Stud. 2012, 160, 31–51. [Google Scholar] [CrossRef]
- Murdoch, I. The Sovereignty of Good over Other Concepts; The Leslie Stephen Lecture; Cambridge University Press: Cambridge, UK, 1967; reprinted in The Sovereignty of Good, Routledge & Kegan Paul: Abingdon, Oxon, 1970. [Google Scholar]
- Yeats, W.B. The Symbolism of Poetry (The Dome: An Illustrated Magazine and Review of Literature, Music, Architecture and the Graphic Arts; Open Court Publishing Co.: La Salle, IL, USA, 1900; pp. 249–257. [Google Scholar]
- Higgins, C. “For Ukrainians Now, Poetry is a Shelter from War’s Horrors” (The Guardian Newspaper, Friday 9th December 2022). Available online: https://www.theguardian.com/commentisfree/2022/dec/09/for-ukrainians-poetry-isnt-a-luxury-its-a-necessity-during-war (accessed on 9 December 2022).
- Lienhard, J.T. Ousia and Hypostasis: The Cappadocian Settlement and the Theology of ‘One Hypostasis’. In The Trinity: An Interdisciplinary Symposium on the Trinity; Stephen, T., Davis, D.K.S.J., Gerald O’Collins, S.J., Eds.; Oxford University Press: Oxford, UK, 2002; Chapter 5; pp. 99–122. [Google Scholar] [CrossRef]
- Perunović, A. From Devotion to Commitment: Towards a Critical Ontology of Engagement. Philos. Soc. 2021, 32, 261–281. [Google Scholar] [CrossRef]
- Forkel, R.; List, J.-M.; Greenhill, S.J.; Rzymski, C.; Bank, S.; Cysouw, M.; Hammarström, H.; Haspelmath, M.; Kaiping, G.A.; Gray, R.D. Cross-Linguistic Data Formats, advancing data sharing and re-use in comparative linguistics. Sci. Data 2018, 5, 180205 (10p). [Google Scholar] [CrossRef] [PubMed]
- Maxwell, N. Aim-Oriented Empiricism and the Metaphysics of Science. Philosophia 2020, 48, 347–364. [Google Scholar] [CrossRef]
- Hicks, D.J. Bibliometrics for Social Validation. PLoS ONE 2016, 11, e0168597. [Google Scholar] [CrossRef]
- Lyons, T.D. Scientific Realism and the Stratagema de Divide et Impera. Br. J. Philos. Sci. 2006, 57, 537–560. [Google Scholar] [CrossRef]
- Berry, M.V. True, But not Real, Physics World. 2020, p. 56. Available online: https://physicsworld.com/a/true-but-not-real/ (accessed on 14 December 2022).
- Greek New Testament: “Textus Receptus” 1550/1894, Unbound Bible), imported from The Sword Project (CrossWire Bible Society). Available online: http://unbound.biola.edu (accessed on 14 November 2020).
- Jerome of Stridon (c.400 CE). Translation into Latin (382–405 CE) of the Bible from Greek and Hebrew texts: Authoritative editions now recognised are the Vulgata Clementina (1592) published after the Council of Trent, and the Nova Vulgata (1979) published after the Second Vatican Council. Available online: https://archive.org/details/Vulgata_Clementina (accessed on 14 September 2020).
- Tyndale, W. The New Testament; Peter Schoeffer of Worms: Stuttgard, Germany, 1526; (Reprinted by The British Library, London, UK 2008). [Google Scholar]
- Dolan, B. Soul searching: A brief history of the mind/body debate in the neurosciences. Neurosurg. Focus 2007, 23, E2. [Google Scholar] [CrossRef] [PubMed]
- Velazquez, L. Thermo-statistical analogues of Hamilton-Jacobi and Einstein field equations. Phys. Rev. D 2022. preprint submitted. [Google Scholar] [CrossRef]
- Velazquez, L.; Parker, M.C.; Jeynes, C. Irreversibility in Geometrical Thermodynamics, preprint submitted to Entropy (Special Issue on ‘The Geometry of Thermodynamics III’). Gen. Theor. Phys. 2022. [Google Scholar] [CrossRef]
- Ossa-Richardson, A. A History of Ambiguity; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Empson, W. Seven Types of Ambiguity: A Study of its Effects on English Verse; Chatto & Windus: London, UK, 1930. [Google Scholar]
- Bleuler, E. Die Ambivalenz. In Festgabe zur Einweihung der Neubauten; der Universität Zurich, 6 parts in 1, part III; Schulthess Druck AG: Zürich, Switzerland, 1914; p. 102. [Google Scholar]
- Wittgenstein, L. Logisch-Philosophische Abhandlung; Ostwald’s Annalen der Naturphilosophie XIV Band, 3/4 Heft; Suhrkamp Verlag: Berlin, Germany, 1921; pp. 185–262, (transl. Frank P. Ramsey and Charles Kay Ogden: Tractatus Logico Philosophicus; Routledge & Kegan Paul Ltd.: London, UK, 1922). [Google Scholar]
- Wittgenstein, L. Philosophische Untersuchungen; Suhrkamp Verlag: Frankfurt am Main, Germany, 1922; (transl. G.E.M.Anscombe: Philosophical Investigations; Macmillan: London, UK, 1953). [Google Scholar]
- Murdoch, I. On ‘God’ and ‘Good’, Lecture at the 1966 meeting at Bowdoin College (Brunswick, Maine), of the ‘Study Group on the Foundations of Cultural Unity’, published in The Anatomy of Knowledge; Marjorie, G., Ed.; University of Massachusetts Press: Amherst, MA, USA, 1966; reprinted in The Sovereignty of Good, Routledge & Kegan Paul: Abingdon, Oxon, 1970. [Google Scholar]
- Rorty, R. Consequences of Pragmatism; University of Minnesota Press: Minneapolis, MN, USA, 1982. [Google Scholar]
- Rorty, R. “Response to Ramberg”: Essay in Robert Brandom (ed), Rorty and His Critics; Wiley Blackwell: New York, NY, USA, 2000. [Google Scholar]
- Latour, B. Why Has Critique Run out of Steam? From Matters of Fact to Matters of Concern. Crit. Inq. 2004, 30, 225–248. [Google Scholar] [CrossRef]
- Green, D.; Green, H. Yuwit Kawihka Dicionário Palikúr—Português; Associação Internacional de Linguística–SIL Brasil; SIL International: Dallas, TX, USA, 2010. [Google Scholar]
- Green, L.; Green, D. Knowing the Day, Knowing the World: Engaging Amerindian Thought in Public Archaeology; University of Arizona Press: Tucson, Arizona, 2013. [Google Scholar]
- Green, D.R.; Green, D.M. Topology-Based Classification in the Palikur Language. Lincom Europa GmbH: München, Germany, 2023. [Google Scholar]
- Course, M.; MacMillan, G. Fishing, Gaelic and Environment in the Outer Hebrides. In C`anan & Cultar/Language & Culture; McLeod, W., Gunderloch, A., Dunbar, R., Eds.; Book Series: Rannsachadh na Gàidhlig 10 (“Gaelic research #10”); Aberdeen University Press: Aberdeen, Scotland, 2021. [Google Scholar]
- Frayn, M. The Human Touch; Faber: London, UK, 2006. [Google Scholar]
- Brown, B. A Sense of Things; University of Chicago Press: Chicago, IL, USA, 2004. [Google Scholar]
- Stevens, W. “Not Ideas About the Thing But the Thing Itself”. In The Collected Poems of Wallace Stevens; Alfred, A., Ed.; Knopf: New York, NY, USA, 1954. [Google Scholar]
- Finch, A. A Place for Abstraction: Revisiting “No Ideas But in Things” (First published in A Poet’s Craft: A Comprehensive Guide to Making and Sharing Your Poetry. University of Michigan Press, 2013. Available online: https://anniefinch.com/place-for-abstraction/ (accessed on 15 May 2022).
- Jordan, J. ‘A Thingy World’: Iris Murdoch’s stuff. Mod. Lang. Rev. 2012, 107, 364–378. [Google Scholar] [CrossRef]
- Murdoch, I. Under the Net; Chatto & Windus: London, UK, 1954; Page Numbers Quoted from the Vintage Classics edition (Penguin, London, 2019). [Google Scholar]
- Wilczek, F. Fundamentals: Ten Keys to Reality; Penguin: London, UK, 2021. [Google Scholar]
- Augustine of Hippo (c.420 CE). De Civitate Dei; 413–426 CE; transl. John Healy 1610: “City of God”; Tasker, R.V.G., Ed.; for Everyman’s Library, J.M.Dent & Sons: London, UK, 1945; Available online: https://web.archive.org/web/20130619130438/http://www.abbaye-saint-benoit.ch/saints/augustin/citededieu/ (accessed on 14 September 2022).
- Augustine of Hippo (c.400 CE). Confessiones. (397–400 CE). transl.R.S.Pine Coffin “Confessions”. Penguin Classics: London, UK, 1961. Available online: https://www.stoa.org/hippo/ (accessed on 10 September 2022).
- Hawking, S.W.; Penrose, R. The singularities of gravitational collapse and cosmology. Proc. R. Soc. A 1970, 314, 529–548. [Google Scholar] [CrossRef]
- Butterfield, H. The Origins of Modern Science, 2nd ed.; Cambridge Lectures, 1948; G.Bell & Sons: London, UK; Free Press: New York, NY, USA, 1949. [Google Scholar]
- Cabral, R. Herbert Butterfield (1900-79) as a Christian Historian of Science. Stud. Hist. Philos. Sci. 1996, 21, 547–564. [Google Scholar] [CrossRef]
- Cunningham, A.; Williams, P. De-Centring the ‘Big Picture’: “The Origins of Modern Science” and the Modern Origins of Science. Br. J. Hist. Sci. 1993, 26, 407–432. [Google Scholar] [CrossRef]
- Schroeder, G.L. The Science of God; Simon & Schuster: New York, NY, USA, 1997. [Google Scholar]
- Murdoch, I. The Idea of Perfection. Yale Rev. 1962, 53, 342–380, (based on the Ballard Matthews lecture at University College of North Wales, 1962; reprinted in The Sovereignty of Good, Routledge & Kegan Paul, Abingdon, Oxon, 1970). [Google Scholar]
- Bauckham, R. Jesus and the Eyewitnesses: The Gospel as Eyewitness Testimony; Wm. B. Eerdmans Publishing Co.: Cambridge, UK, 2006. [Google Scholar]
- Fulton, A. Cascade Experiment. In Powers of Congress; David Godine: Boston, MA, USA, 1990. [Google Scholar]
- Zhaoping, L.; Jingling, L. Filling-in and suppression of visual perception from context: A Bayesian account of perceptual biases by contextual influences. PLoS Comput. Biol. 2008, 4, e14. [Google Scholar] [CrossRef]
- Criado-Perez, C. Invisible Women; Chatto & Windus: London, UK, 2019; Vintage: London, UK, 2020. [Google Scholar]
- Fields, R.D. Testing Males and Females in Every Medical Experiment Is a Bad Idea. Sci. Am. 2014, 311, 14. [Google Scholar] [CrossRef]
- Richardson, S.; Reiches, M.; Shattuck-Heidorn, H.; LaBonte, M.L.; Consoli, T. Focus on preclinical sex differences will not address women’s and men’s health disparities. Proc. Natl. Acad. Sci. USA 2015, 112, 13419–13420. [Google Scholar] [CrossRef]
- Coleridge, S.T. General Introduction: Or Preliminary Treatise on Method, Encyclopædia Metropolitana, 1st ed.; Coleridge; Rest Fenner: London, UK, 1818. [Google Scholar]
- Fedrizzi, A.; Proietti, M. “Objective Reality Doesn’t Exist, Quantum Experiment Shows” LiveScience, 16 November 2019. Available online: https://www.livescience.com/objective-reality-not-exist-quantum-physicists.html (accessed on 14 December 2022).
- Proietti, M.; Pickston, A.; Graffitti, F.; Barrow, P.; Kundys, D.; Branciard, C.; Ringbauer, M.; Fedrizzi, A. Experimental test of local observer independence. Sci. Adv. 2019, 5, eaaw9832. [Google Scholar] [CrossRef]
- Greenstein, G.; Zajonc, A.G. The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics; Jones & Bartlett: Sudbury, MA, USA, 1997. [Google Scholar]
- Petersen, A. The Philosophy of Niels Bohr, in Niels Bohr: A Centenary Volume; Kennedy, A.P., French, C.J., Eds.; Harvard University Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Klarreich, E. A Mathematician Who Dances to the Joys and Sorrows of Discovery, Quanta Magazine, 20 November 2017. Available online: https://www.quantamagazine.org/mathematician-federico-ardila-dances-to-the-joys-and-sorrows-of-discovery-20171120/ (accessed on 22 December 2021).
- Ravetz, J.R. Scientific Knowledge and its Social Problems; Oxford University Press: Oxford, UK, 1971. [Google Scholar]
- Kleene, S.C. Introduction to Metamathematics; North-Holland: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Read, S. The Liar Paradox from John Buridan back to Thomas Bradwardine. Vivarium 2002, 40, 189–218. [Google Scholar] [CrossRef]
- Anselm of Bec (1078). Proslogion; Charlesworth, M.J., Ed.; Oxford University Press: London, UK, 1965. [Google Scholar]
- Leonard, N. Belief and rational indeterminacy. Synthese 2021, 199, 13523–13542. [Google Scholar] [CrossRef]
- Descartes, R. Discours de la Méthode Pour bien Conduire sa raison, et Chercher la Vérité Dans les Sciences; Jan Maire: Leiden, The Netherlands, 1637. [Google Scholar]
- Descartes, R. Principia Philosophiae; Louis Elzevir: Amsterdam, The Netherlands, 1644. [Google Scholar]
- Berkeley, G. A Treatise Concerning the Principles of Human Knowledge; Jeremy Pepyat, Skinner Row: Dublin, Ireland, 1970. [Google Scholar]
- Dodds, E.R. The Greeks and the Irrational; University of California Press: Berkeley, CA, USA, 1951. [Google Scholar]
- Kierkegaaard, S. Afsluttende Uvidenskabelig Efterskrift Til de Philosophiske Smuler; Concluding Unscientific Postscript to Philosophical Fragments; Hos, C.A., Ed.; Reitzel: Copenhagen, Denmark, 1843; transl.; Hong, H.V.; Hong, E.H., Translators; Princeton University Press: London, UK, 1992. [Google Scholar]
- Kierkegaaard, S. Frygt og Bæven; Herman, H.J., Ed.; Lynge & Son: Copenhagen, Denmark, 1843; Fear and Trembling transl; Alastair Hannay Penguin: London, UK, 1985. [Google Scholar]
- Ward, K. Why There Almost Certainly Is a God; Lion Hudson PLC.: Oxford, UK, 2008. [Google Scholar]
- Russell, B.; Whitehead, A.N. Principia Mathematica, 1st ed.; 1910; 2nd edi.; 1925; Cambridge University Press: Cambridge, UK, 1910. [Google Scholar]
- Hilbert, D.; Ackermann, W. Grundzüge der Theoretischen Logik; Springer: Berlin, Germany, 1928. [Google Scholar]
- Kuhn, T.S. The Structure of Scientific Revolutions; University of Chicago Press: Chicago, IL, USA, 1962. [Google Scholar]
- Gorman, C. The Atom in Seventeenth-Century Poetry; Studies in Renaissance Literature; D.S.Brewer: Cambridge, UK, 2021; Volume 39. [Google Scholar]
- Jaynes, E.T. Gibbs vs Boltzmann Entropies. Am. J. Phys. 1965, 33, 391–398. [Google Scholar] [CrossRef]
- Jaynes, E.T. The Gibbs Paradox. In Maximum Entropy and Bayesian Methods; Smith, C.R., Erickson, G.J., Neudorfer, P.O., Eds.; Kluwer Academic Publishers: Dordrecht, Holland, 1992; pp. 1–22. [Google Scholar]
- Christenson, J.H.; Cronin, K.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the K20 Meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Ann. der Phys. und Chem. 1865, 201, 353–400. [Google Scholar] [CrossRef]
- Penrose, R. The Road to Reality: A Complete Guide to the Laws of the Universe; Jonathan Cape: London, UK, 2004. [Google Scholar]
- Rovelli, C. La Realtà non è Come ci Appare; Raffaello Cortina Editore: Milano, Italy, 2014; transl. Simon Carnell & Erica Segre: Reality is not what it seems; Allen Lane: London, UK, 2016. [Google Scholar]
- Wilczek, F. Facts. 2004. Available online: https://www.nobelprize.org/prizes/physics/2004/wilczek/facts/ (accessed on 14 December 2022).
- Penrose, R. Black Holes, Cosmology, and Space-Time Singularities. 2020. Available online: https://www.nobelprize.org/prizes/physics/2020/penrose/lecture/ (accessed on 14 December 2022).
- Coopersmith, J. Energy, the Subtle Concept; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Grandy, W.T. Entropy and the Time Evolution of Macroscopic Systems; Oxford University Press: Oxford, UK, 2008. [Google Scholar] [CrossRef]
- Wolfgang, P. Thermodynamics and the Kinetic Theory of Gases, in Pauli Lectures on Physics, Volume 3; MIT Press: Cambridge, MA, USA, 1973; republished by Dover Books: New York, NY, USA, 2003; this lecture was c.1952. [Google Scholar]
- Parker, M.C.; Jeynes, C. Entropic Uncertainty Principle, Partition Function and Holographic Principle derived from Liouville’s Theorem. Phys. Open 2021, 7, 100068. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Temperature Fluctuation: A well-defined and unavoidable notion. Phys. Today 1989, 42, 71–72. [Google Scholar] [CrossRef]
- Penrose, R. Cycles of Time; The Bodley Head: London, UK, 2010. [Google Scholar]
- Rovelli, C. L’ordine del Tempo; Adelpho Edizione: Milano, Italy, 2017; transl. Simon Carnell & Erica Segre: The Order of Time; Allen Lane: London, UK, 2018. [Google Scholar]
- Planck, M. Ueber das Gesetz der Energieverteilung im Normalspectrum. Ann. Phys. 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Lundheim, L. On Shannon and “Shannon’s Formula”. Telektronikk 2002, 98, 20–29. Available online: https://www.researchgate.net/profile/Lars_Lundheim/publication/251375021_On_Shannon_and_Shannon’s_formula/links/59a3fa29aca272a6461b918b/On-Shannon-and-Shannons-formula.pdf (accessed on 14 December 2022).
- Shannon, C.E. “A Mathematical Theory of Communication”. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Pierce, J.R. The Early Days of Information Theory. IEEE Trans. Inf. Theory 1973, 19, 3–8. [Google Scholar] [CrossRef]
- Tolman, R.C. Principles of Statistical Mechanics; Clarendon Press: Oxford, UK, 1936. [Google Scholar]
- Brillouin, L. The Negentropy Principle of Information. J. Appl. Phys. 1953, 24, 1152. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Landauer, R. Computation: A Fundamental Physical View. Phys. Scr. 1987, 35, 88–95. [Google Scholar] [CrossRef]
- Bennett, C.H. Notes on Landauer’s principle, reversible computation, and Maxwell’s Demon. Stud. Hist. Philos. Mod. Phys. 2003, 34, 501–510. [Google Scholar] [CrossRef]
- Parker, M.C.; Walker, S.D. A Unified Carnot Thermodynamic and Shannon Channel Capacity Information-Theoretic Energy Efficiency Analysis. IEEE Trans. Commun. 2014, 62, 3552–3559. [Google Scholar] [CrossRef]
- Norton, J.D. All Shook Up: Fluctuations, Maxwell’s Demon and the Thermodynamics of Computation. Entropy 2013, 15, 4432–4483. [Google Scholar] [CrossRef]
- Ladyman, J.; Robertson, K. Going Round in Circles: Landauer vs. Norton on the Thermodynamics of Computation. Entropy 2014, 16, 2278–2290. [Google Scholar] [CrossRef]
- Parker, M.C.; Walker, S.D. Is computation reversible? Opt. Commun. 2007, 271, 274–277. [Google Scholar] [CrossRef]
- Parker, M.C.; Jeynes, C. Fullerene Stability by Geometrical Thermodynamics. ChemistrySelect 2020, 5, 5–14. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes and thermodynamics. Phys. Rev. D 1976, 3, 191–197. [Google Scholar] [CrossRef]
- Parker, M.C.; Jeynes, C. A Relativistic Entropic Hamiltonian–Lagrangian Approach to the Entropy Production of Spiral Galaxies in Hyperbolic Spacetime. Universe 2021, 7, 325. [Google Scholar] [CrossRef]
- Parker, M.C.; Jeynes, C.; Catford, W.N. Halo Properties in Helium Nuclei from the Perspective of Geometrical Thermodynamics. Ann. Phys. 2022, 534, 2100278. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Leibniz, G.W. La Monadologie (MS, 1714; Lehrsätze über die Monadologie, 1720; “Principia philosophiae”, Acta Eruditorum 1721; Leibniz: Philosophical Writings, transl. Mary Morris, Everyman’s Library, Dent, London 1934). Available online: https://www.plato-philosophy.org/wp-content/uploads/2016/07/The-Monadology-1714-by-Gottfried-Wilhelm-LEIBNIZ-1646-1716.pdf (accessed on 14 October 2020).
- Thomas, E. British Idealist Monadologies and the Reality of Time: Hilda Oakeley Against McTaggart, Leibniz, and Others. Br. J. Hist. Philos. 2015, 23, 1150–1168. [Google Scholar] [CrossRef]
- Liouville, J. Sur la Théorie de la Variation des constantes arbitraires. J. Mathématiques Pures Appl. 1838, 3, 342–349. [Google Scholar]
- Gibbs, J.W. On the Fundamental Formula of Statistical Mechanics, with Applications to Astronomy and Thermodynamics. Proc. Am. Assoc. Adv. Sci. 1884, 33, 57–58. [Google Scholar]
- Keppens, A. What Constitutes Emergent Quantum Reality? A Complex System Exploration from Entropic Gravity and the Universal Constants. Entropy 2018, 20, 335. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2022, 74, 825–874. [Google Scholar] [CrossRef]
- Bell, J.S. On the Problem of Hidden Variables in Quantum Mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The Problem of Hidden Variables in Quantum Mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Lucia, U. Macroscopic irreversibility and microscopic paradox: A Constructal law analysis of atoms as open systems. Sci. Rep. 2016, 6, 2045–2322. [Google Scholar] [CrossRef]
- Earman, J. The ‘‘Past Hypothesis’’: Not even false. Stud. Hist. Philos. Mod. Phys. 2006, 37, 399–430. [Google Scholar] [CrossRef]
- Prigogine, I. La Fin des Certitudes in Collaboration with Isabelle Stengers. Éditions Odile Jacob: Paris, France, 1996. [Google Scholar]
- Moravec, M. Taking time seriously: The Bergsonism of Karin Costelloe-Stephen, Hilda Oakeley, and May Sinclair. Br. J. Hist. Philos. 2022, 24p. [Google Scholar] [CrossRef]
- Prigogine, I. Time, Structure and Fluctuations; Royal Swedish Academy of Sciences: Lecture accepting the Nobel Prize for Chemistry 1977. Science 1978, 201, 777–785. [Google Scholar] [CrossRef] [PubMed]
- Bishop, R.C. Nonequilibrium statistical mechanics Brussels–Austin style. Stud. Hist. Philos. Mod. Phys. 2004, 35, 1–30. [Google Scholar] [CrossRef]
- Reason, J. Human Error; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Stöltzner, M. The principle of least action as the logical empiricist’s Shibboleth. Stud. Hist. Philos. Mod. Phys. 2003, 34, 285–318. [Google Scholar] [CrossRef]
- Coopersmith, J. The Lazy Universe: An Introduction to the Principle of Least Action; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Parker, M.C.; Walker, S.D. A Dynamic Model of Information and Entropy. Entropy 2010, 12, 80–88. [Google Scholar] [CrossRef]
- Bohm, D. A suggested interpretation of the Quantum Theory in terms of hidden variables I. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Rovelli, C. Relational Quantum Mechanics. Int. J. Theor. Phys. 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
- Rae, A. Quantum Physics: Illusion or Reality? 2nd ed.; Cambridge University Press: Cambridge, UK, 1986; reprinted with updates 2009, 6th printing 2018; p. 137. [Google Scholar]
- The Geneva Bible (Rowland Hall, Geneva, 1560), Facsimile of The Geneva Bible from the Copies in the Chapin Library (Columbia University) and the Scheide Library (Princeton University); Wisconsin Press: Madison, WI, USA, 1969; and republished by Hendrickson Publishers, Peabody, Mass, USA, 2007; Available online: https://www.gla.ac.uk/myglasgow/archivespecialcollections/digitisedcollections/divinewritethekingjamesbibleandscotland/thegenevabible/ (accessed on 14 October 2021).
- Caticha, A. Entropy, Information, and the Updating of Probabilities. Entropy 2021, 23, 895. [Google Scholar] [CrossRef]
- Landauer, R. Information is Physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Mari, L.; Maul, A.; Irribarra, D.T.; Wilson, M. Quantification is Neither Necessary Nor Sufficient for Measurement. J. Phys. Conf. Ser. 2013, 459, 012007. [Google Scholar] [CrossRef]
- Maul, A.; Irribarra, D.T.; Wilson, M. On the philosophical foundations of psychological measurement. Measurement 2016, 79, 311–320. [Google Scholar] [CrossRef]
- JCGM, Joint Committee for Guides in Metrology. Guide to the Expression of Uncertainty in Measurement (GUM), 1st ed.; JCGM: Paris, France, (2010: 2008 version with minor corrections); 2008 is 1995 version with minor corrections; JCGM 100:2008 (BIPM: Paris); Available online: https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf/cb0ef43f-baa5-11cf-3f85-4dcd86f77bd6 (accessed on 14 October 2022).
- JCGM, Joint Committee for Guides in Metrology. International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM), 3rd ed.; JCGM: Paris, France, 2008 version with minor corrections, Joint Committee for Guides in Metrology; JCGM 200:2012; BIPM: Paris, 2008; Available online: https://www.oiml.org/en/files/pdf_v/v002-200-e07.pdf (accessed on 15 December 2021).
- Sacks, O. The Man Who Mistook his Wife for a Hat; Gerald Duckworth: London, UK, 1985; new edition in Picador Classics, London, 2015. [Google Scholar]
- Sato, M.; Sakurai, T.; Kameyama, Y.; Igarashi, A. Calculi of Meta-variables. In Computer Science Logic; Baaz, M., Makowsky, J.A., Eds.; CSL 2003. Lecture Notes in Computer Science; Springer: Berlin, Heidelberg, 2003; Volume 2803. [Google Scholar] [CrossRef]
- More, H. Philosophicall Poems; Platonick Song of the Soul: Cambridge, UK, 1647. [Google Scholar]
- Killeen, K. Microscopy, Surfaces and the Unknowable in Seventeenth-Century Natural Philosophy (from Lucretius to Margaret Cavendish), Journal of the Northern Renaissance (Issue 8, Spring 2017—Scrutinizing Surfaces). Available online: https://jnr2.hcommons.org/issues/issue-8-2017/ (accessed on 14 December 2022).
- Hebrew Bible (c.500 BCE). BHS Hebrew Bible (Masoretic text in “Leningrad Codex” by Samuel ben Jacob, Egypt, 1010 CE, now held in the Russian National Library, St. Petersburg, catalogued as “Firkovich B19A”) in Unicode with Ketib & Qere, distributed by CCAT (University of Pennsylvania): Transcribed from: Biblia Hebraica Stuttgartensia quae antea cooperantibus (A. Alt, O. Eissfeldt, P. Kahle ediderat R. Kittel; editio funditus renovata, adjuvantibus H. Bardtke et al. cooperantibus H.P. Rüger et J. Ziegler; ediderunt K. Elliger et W. Rudolph; textum Masoreticum curavit H.P. Rüger, Masoram elaboravit G.E. Weil). Deutsche Bibelstiftung: Stuttgart, Germany, 1977; Modern edition (with English translation and helpful Introduction) published by the Jewish Publication Society, Philadelphia, 1985, 2nd ed. 1999, “student pocket ed.” 2003. Unbound Bible; Available online: http://unbound.biola.edu (accessed on 12 November 2020).
- LXX (“Septuagint”, c.250 BCE). Septuaginta, ed. A. Rahlfs (Stuttgart: Württembergische Bibelanstalt, 1935; repr. in 9th ed., 1971), from the Unbound Bible, distributed by the Center for Computer Analysis of Texts (CCAT) at the University of Pennsylvania. Available online: http://unbound.biola.edu (accessed on 12 November 2020).
- Rubin, S.; Crucifix, M. Earth’s Complexity Is Non-Computable: The Limits of Scaling Laws, Nonlinearity and Chaos. Entropy 2021, 23, 915. [Google Scholar] [CrossRef] [PubMed]
- James, C. Dante: The Divine Comedy; Liveright Publishing, W.W.Norton & Co.: New York, NY, USA, 2013. [Google Scholar]
- Helton, G. Epistemological solipsism as a route to external world skepticism. Philos. Perspect. 2021, 35, 229–250. [Google Scholar] [CrossRef]
- Vaccaro, J. Personal Website: The Solipsist’s Plea. Available online: https://joanv.me/solipsists_plea/index.php (accessed on 30 April 2022).
- Meillassoux, Q. Après la Finitude: Essai sur la Nécessité de la Contingence; Editions du Seuil, Paris, France, 2006; transl. Ray Brassier: After Finitude: An Essay on the Necessity of Contingency; Continuum: New York, NY, USA, 2008. [Google Scholar]
- Frayn, M. Copenhagen; first played at the Cottesloe Theatre, London, 21 May 1998; Text Methuen: London, UK, 1998. [Google Scholar]
- Ulrich, H. Sören Kierkegaarde. Erſter Teil Die Werke: Ausgewählt und überſetzt; Hochweg-Verlag: Berlin, Germany, 1925. [Google Scholar]
- Alter, Robert. The Book of Psalms: A Translation with Commentary; W.W.Norton & Co.: New York, NY, USA, 2007. [Google Scholar]
- Barker, M. The Older Testament; SPCK: London, UK, 1987; reprinted Sheffield Phoenix Press: Sheffield, UK, 2005. [Google Scholar]
- Korpel, M.C.A.; de Moor, J.C. Adam, Eve, and the Devil; Sheffield Phoenix Press: Sheffield, UK, 2014. [Google Scholar]
- Jeynes, C. Review of “Adam, Eve, and the Devil” by Marjo Korpel & Johannes de Moor. 2014. Available online: https://www.researchgate.net/publication/265184845_Review_of_Adam_Eve_and_the_Devil_by_Marjo_Korpel_Johannes_de_Moor_Sheffield_2014 (accessed on 15 November 2022).
- Hopwood, M. Singing in Chains; Gomer Press: Llandysul, Wales, 2004. [Google Scholar]
- Eusebius of Caesarea (c.320 CE). Εὐαγγελικὴ προπαρασκευή (Usually Known by the Latin Title: Praeparatio Evangelica); Gifford, E.H., Translator; Oxonii E Typographico Academico: London, UK; New York, NY, USA, 1903; Available online: https://www.tertullian.org/fathers/eusebius_pe_00_intro.htm (accessed on 14 November 2020).
- Barker, M. Great High Priest; T&T Clark Ltd.: London, UK, 2003. [Google Scholar]
- Davies, G.; Aitken, J.K. Ancient Hebrew Inscriptions: Vols 1, Corpus and Concordance; Davies, G.I., Ed.; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Vos, B. Integrated HPS? Formal versus historical approaches to philosophy of science. Synthese 2021, 199, 14509–14533. [Google Scholar] [CrossRef]
- Cruddas, J. The Dignity of Labour; Polity Press: Cambridge, UK, 2021. [Google Scholar]
- Sacks, O. “The Lost Mariner”, New York Review of Books; Republished in The Man Who Mistook His Wife for a Hat; Gerald Duckworth: London, UK, 1985. [Google Scholar]
- Wieseltier, L. Kaddish; Alfred A. Knopf: New York, NY, USA, 1998; Picador: London, UK, 1999. [Google Scholar]
- Shelley, P.B. A Defence of Poetry. In Essays; Shelley, M.W., Ed.; Edward Moxon: London, UK, 1840. [Google Scholar]


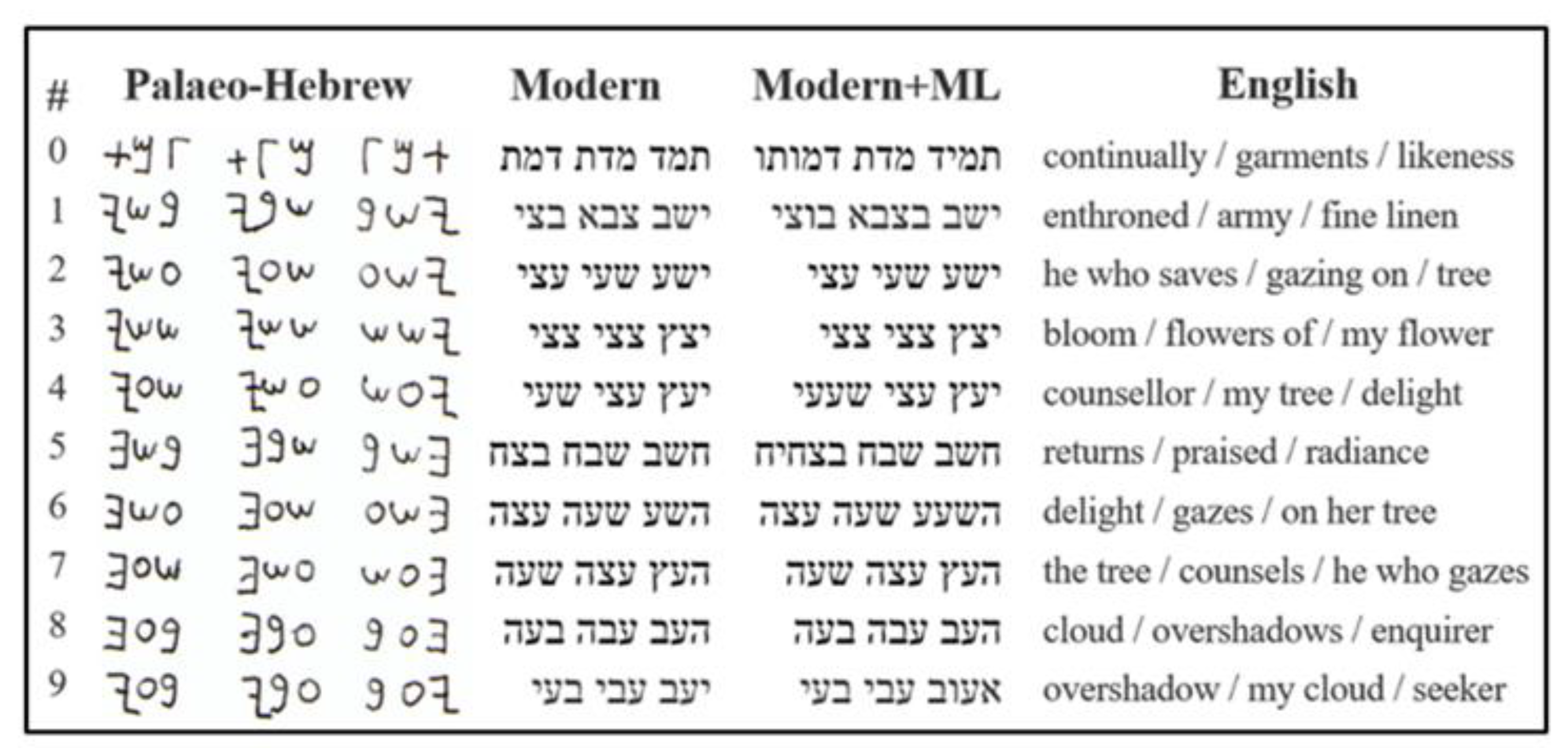
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeynes, C.; Parker, M.C.; Barker, M. The Poetics of Physics. Philosophies 2023, 8, 3. https://doi.org/10.3390/philosophies8010003
Jeynes C, Parker MC, Barker M. The Poetics of Physics. Philosophies. 2023; 8(1):3. https://doi.org/10.3390/philosophies8010003
Chicago/Turabian StyleJeynes, Chris, Michael C. Parker, and Margaret Barker. 2023. "The Poetics of Physics" Philosophies 8, no. 1: 3. https://doi.org/10.3390/philosophies8010003
APA StyleJeynes, C., Parker, M. C., & Barker, M. (2023). The Poetics of Physics. Philosophies, 8(1), 3. https://doi.org/10.3390/philosophies8010003






