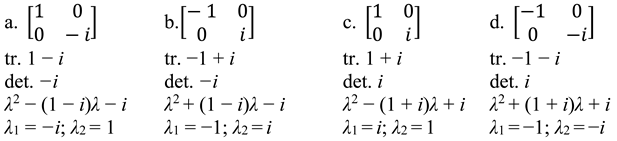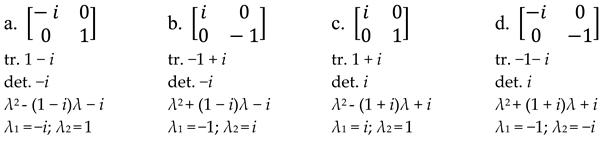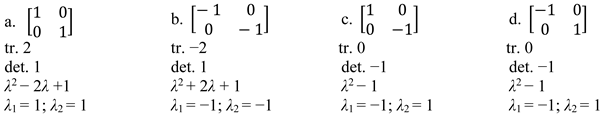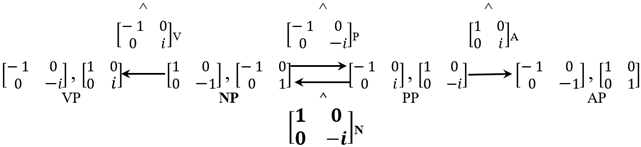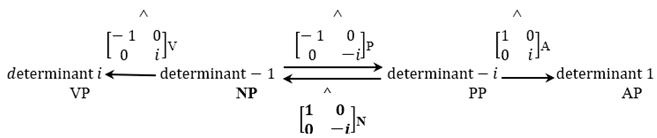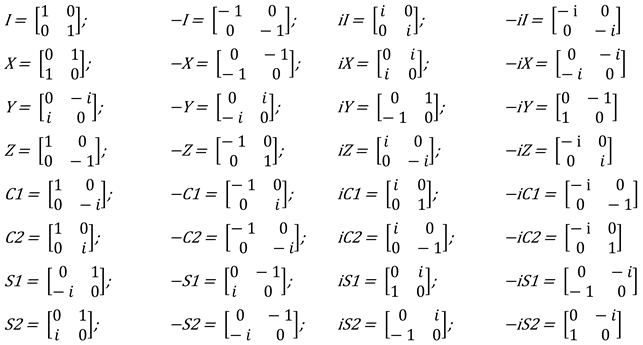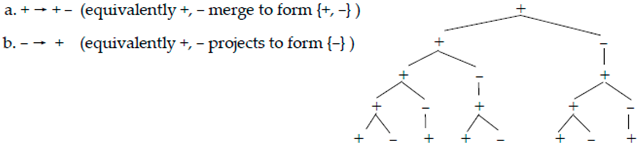1. Featural Specifications as Categorial Dimensions
Let us examine the head-complement relation, which presupposes an understanding of categories that can be heads and what we presume to be their complements.
1 In current parlance, we take those to be instances of External Merge (EM), of the 1
st-Merge type: this is inasmuch as the process is presumed to take an item from the lexicon (the head) and asymmetrically associate it to a projection, its complement. Evidently, that presupposes understanding what is meant by “head” and “projection”, or the presumed “endocentricity” of phrases. Bear in mind that a Chomsky grammar is a 4-tuple [Σ, T, N, P], specifying rules over arbitrary vocabularies of “non-terminals” N and “terminals” T, thus allowing a set of productions P starting on initial axiom Σ. Rules of the sort X → ψ, where X ∈ N and ψ is some arbitrary string of terminals in T*,
2 do not guarantee the endocentricity of phrases, since (by that formalism) one could rewrite a VP, say, as a noun followed by a prepositional phrase only (or any other string of terminals, but no verb). If these constructions do not exist in natural language, the formalism is inadequate [
1].
The problem of endocentricity is intimately related to the problem of selection (e.g., that intransitive, transitive, or ditransitive verb takes different dependents). It is
because a transitive verb takes a complement
that it is immediately dominated by a VP of a (transitive) kind, and similarly with other such dependencies. That is the essence of the “lexicalist” idea behind bottom-up projections, sketched in Chomsky [
2] and then pursued from Jackendoff [
3] to Speas [
4], the bases (together with Muysken [
5] and Kayne [
6]) for Chomsky’s Bare Phrase Structure (BPS) [
7]. To capture such syntagmatic interactions, linguists had to consider systematicities implied not just in the terminal vocabulary (nouns as opposed to verbs, marked vs. default exemplars, etc.), but also the generalizations within the non-terminals (subcategorization restrictions among the former, label endocentricity). The standard treatment of these ideas presumed “distinctive features” of some sort [
8,
9].
Chomsky [
2] extended distinctive phonological features to the noun vs. verb distinction. Just as consonants are taken to be maximally distinct from vowels (which the orthogonality of features [+consonantal, −syllabic] vs. [−consonantal, +syllabic] expresses), so too verbs are seen, in demonstrable senses, as maximally distinct from nouns, as reflected in Chomsky’s equally orthogonal categorial features [−N, +V] vs. [+N, −V]. In fact, Chomsky seems to have been concerned with orthogonality between syntactic “dimensions” of some sort; just as the “vowel dimension” is as different to the “consonant dimension” as can be, so too can nominal expressions in syntax be seen as orthogonal to verbal expressions. This has (arguable) consequences that Varro already emphasized in
De Lingua Latina, Vol 2: Book IX, XXIV-31, when dividing “speech into four parts, one in which the words have cases, a second in which they have indications of time, a third in which they have neither, a fourth in which they have both” (translated by Kent [
10]). It is actually remarkable how similar this is to Chomsky’s categorization for the X’-schema:
- (1)
[±N, ±V]: [+N, −V] = N[oun]; [+N, +V] = A[djective]; [−N, +V] = V[erb],
[−N, −V] = everything else;
- (2)
Xn → … Xn−1…, where xi = [α = N, β = V]i and X1 = X
Let us assume that there are two basic lexical features N and V (
N,
V). Where the language has rules that refer to the categories nouns and adjectives…they will be framed in terms of the feature +N. and where there are rules that apply to the category nouns and adjectives, they will be framed in terms of the feature +V. [
2] (Lecture 3, p. 2)
What is the nature of those “dimensions”? One possibility is to liken them to the underlying “vision maps” that stem from cones and rods (see [
11]). In this view, whatever the nature of features may ultimately be, it is mediated by brain physiology. This approach is promising, for instance, for voice onset time (VOT), associated by Poeppel [
12] to specific “brain events”. That seems just as reasonable for activating vocal folds, upon the appropriate motor commands, as the response of cones of different types is for light of diverse frequencies—if presuming efference vs. afference. For that approach, the project is empirical in a classical sense, and perhaps harder for linguistic features (if not present in other animals we allow ourselves to experiment with) than for vision features one detects even in insects. Much as I respect that line of reasoning, I have little to contribute to it in the present context. But there is a different, though compatible, approach to feature dimensions: that their nature is algebraic and, hence, arguably
prior to any substantive feature system. In phonology, the ± consonantal or ± syllabic dimensions seem more fundamental than, for example, ±continuant or ±labial features, in terms (at least) of universal relevance in articulating morpho-phonemics and the orthogonality conditions presumed for the deeper type. The issue I want to explore here is whether similar fundamental dimensions exist in syntax.
Note that Chomsky could have chosen attributes A or P (for adjectives and prepositions) instead of N or V, since any two binary features obviously yield four distinctions. But he assumed, instead, “that there are two lexical features N and V”, which accords with traditional intuitions: in some sense, nominal and verbal dimensions are more essential than adjectival or prepositional ones.
3 Chomsky [
2] (lecture 3, p. 3) also asserts that the initial phrase-marker, prior to any transformations modifying it, is “projected from the lexical categories uniformally”. He then clarifies his hypothesis that: “in a fundamental way the expansion of major categories like NP, VP, AP is independent of categorial choice of the head…[as] instantiations of the same general schemata.” This presupposes an understanding that syntax is somehow articulated around N and V dimensions. The suggestion I will be pursuing here is that the N vs. V distinction reflects algebraic conditions that also underlie our number system. This is for reasons Chomsky often emphasizes, going back to Alfred Wallace (see [
13]): that mathematical knowledge could not have served any obvious evolutionary purpose—and, thus, is seen as an outgrowth of language. But before developing that point, I would like to reflect on the topological nature of phrases.
2. Lindenmayer Systems in Matrix Representation
A standard Chomsky-grammar involves rewriting mechanisms applying one-at-a time (Chomsky’s [
14] “Traffic Convention”). While rewrite rules were abandoned half a century ago (see [
15,
16]), actually projecting systems still preserve the fundamental properties of a Chomsky-grammar. This is demonstrably the case for string-based systems like those in [
17], but it can also be argued for the BPS system in [
7] or current extensions. A relation like (3a) is equivalent, at the relevant level of abstraction, to one as in (3b):
- (3)
a. The merge of α and β results in {α, β}
b. {α, β} → α, β
Needless to say, it makes good sense to project (whatever that ultimately means) α or β as in (3a), the relation being “bottom-up”, whereas the same is not true about the “top-down” (3b). As will be clear immediately, however, this is immaterial to the topology of the resulting phrasal objects. To see that, we need to consider a phrasal entity that boils down to the maximal expansion of procedures as in (3), literally to infinity because they are (in principle) recursive on all branches.
Lindenmayer [
18] explored the elimination of Chomsky’s Traffic Convention, so that in Lindenmayer (L-)systems each rewritable symbol must rewrite, at whatever derivational line the system is running. This is the reason L-systems, while good at modeling some fractal structures, do not generate formal languages, even though they describe the overall topological space of a certain natural language expansion. For instance, Boeckx, Carnie, & Medeiros [
19] show how the customary syntactic X’-theory, presumed by Speas [
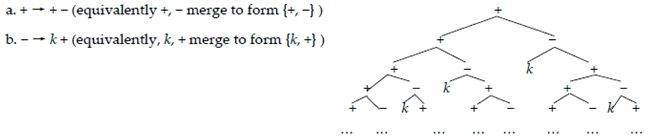
4], yields maximally expanding structures as in (26) (where the “slash” notation is meant to represent an unbounded expansion):
Sending this schema to infinity (imagining all relevant projections that become possible as the structure unfolds), produces an L-tree following the rule-schema in (27) (where k is a constant):
More importantly for our purposes, in this Lindenmayer (maximally expanded) fashion, there is a useful matrix representation for the ensuing phrasal object and its corresponding topology.
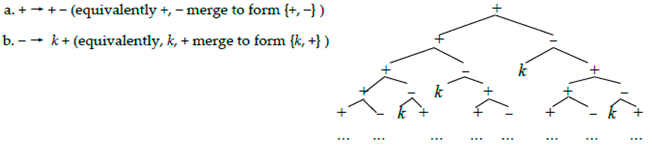
Medeiros [
20] expands on an idea dating back to King [
21], for an L-system like (5), over
n specific symbols (here three: +, −, and
k). The idea is to associate these symbols to entries in square matrix columns 1 to
n, next to represent each rule expansion as corresponding square matrix rows, utilizing a zero for whichever symbol a rule expansion lacks. Uriagereka [
22] represents constants as their own column, albeit with a corresponding row of only zeroes. For (5):
All that (6) encodes is that process (5a) (merging + and −, projecting +) is presented as one token + and one token − in the “+ row” (with zero ks in that row); and process (5b) (merging k and +, projecting −) is coded as 1 token + and one token k in the “− row” (with zero − s in that row); while the k row is all zeroes because k doesn’t expand, as it is “its own projection”. As such, this is just a compact way to pack the relevant information into a square matrix. One such matrix is a particularly elegant mathematical object, with an associated characteristic polynomial calculated from scalars associated to the matrix diagonal (it’s so-called trace and determinant).
While readers can find details about matrices in any standard introduction to linear algebra (even in the Wikipedia entry for “square matrix”), it is worth bearing in mind that the characteristic polynomial for a square matrix is a fundamental invariant across different bases (which keep relations unchanged) for the matrix. Recall that a polynomial is a collection of monomial terms Kx, where constant K is the term’s coefficient and a root of the polynomial turns it to an equation; the root of polynomial P(z) is the number zj such that P(z)j = 0. P(z) is of degree n if it has n roots, its degrees of freedom. Thus, the characteristic polynomial of a matrix can be thought of as its numerical description. The polynomial roots (solutions to the polynomial when construed as equating zero) constitute fundamental elements in the matrix diagonal, its eigenvalues. From those, one can compute the matrix eigenvectors, or characteristic vectors of the linear transformation the matrix represents, which changes by a scalar factor when the linear transformation is applied—the factor in point being the eigenvalue. Aside from having the eigenvalues as roots, among the polynomial coefficients are the matrix trace (sum of the elements in the diagonal) and determinant (here, a product of the elements in the diagonal minus the product of those in the off-diagonal, with further caveats for higher-dimensional matrices). It is interesting to note for our purposes that, with Medeiros’s method in place, we can compute how an L-system grows as it expands. The degree n of the characteristic polynomial tells us the dimension n x n of its corresponding square matrix and, therefore, the number of rewrite or Merge type applications that correspond to it in an L-system. In turn, one matrix eigenvalue, often called its spectral radius, can be defined as in (7a), a quantity related to the topological derivational entropy hT of a matrix A, (7b):
- (7)
Derivational entropy
a. For spectral radius ρ(A), square matrix A’s largest absolute value λmax of A’s eigenvalues,
b. A’s topological derivational entropy hT = log2 λmax
So relevant to this calculation of “how the system grows” is the magnitude of the highest eigenvalue of its associated matrix. The systems that interest us are “fractal” in that the recursive application of their constituent rules, when maximally applied, correspond to square matrices whose repetitive effect on the system is tracked by self-multiplication (a matrix power), as shown for related systems in Ott [
23]. We can see this idea at work by simply running the successive powers of an L-system interpreted through its Medeiros-matrix (henceforth M-matrix) as in (6):
- (8)
1 = ; 2 = ; 3 = ; …
With each successive power we obtain, in the matrix top row, the number of symbols of a given kind in a new derivational line in the L-tree, as readers can check by simply counting them in (5) (one can also try as an exercise the next power, to see how the next top row will be 5, 3, 2, etc.).
4 Slightly more technically, for any two successive matrix powers A
n and A
n+1, the ratio between the spectral radiuses
ρ(A
n+1)/
ρ(A
n) is the initial spectral radius
ρ(A
1) for the seed matrix.
5Note: the claim is not that an object like (4), its abstract version in (5), or its square matrix representation in (6), are anything like “syntactic trees” that users parse in the performance of their grammatical knowledge. It is, instead, that the underlying
topological representation of the (X’-theoretic) phrasal scheme has the “shape” implied in (6), whose derivational entropy, in the sense in (7), can be simply calculated—this quantity, again, telling us “how the system grows”. Here is not the place to demonstrate this, but actually the X’-theoretic representation in (4) is one among infinitely many that branch, albeit in binary fashion (or presuming binary Merge) and involving “self-projecting” constants (or absolute terminals) like
k there. Indeed, among such binary structures, it is provably the most elegant in terms of its potential to pack the largest amount of structure (see Uriagereka [
24]). One can think of the general topology of a phrasal system as the equivalent of a terrain over which to ride a bike. Thus, Tour de France stages are characterized by a “profile”, which can be “flat”, “mountainous”, “hilly”, “potentially windy”, and so on—characteristics that obviously affect how fast and safely cyclist ride, in a peloton or otherwise, with likely breakaways or a final sprint, etc. So too, the phrasal topology is basically determining what sorts of parse-trees are possible within a given (grammatical) system, at this point merely worrying about constituency conditions (note also that the matrix representation ignores linear order). In the present paper, I will be concentrating on only head-complement relations (see Note 1).
3. The Fundamental Assumption and its Fundamental Corollary
After having completed that excursus into phrasal topologies represented as M-matrices, we can now return to the issue of Chomsky’s 1974 system as presented in (1) and (2) above. One could soundly express the substantive intuitions we discussed in the following formal fashion:
- (9)
Fundamental Assumption
The V dimension is a (mathematical) transformation over an orthogonal N dimension.
If we instantiate (5) in the complex plane, we could conclude:
- (10)
Fundamental Corollary
The N dimension has unit value 1; the V dimension, unit value i; [±N, ±V] = [±1, ±i].
Before being tempted to ask “what that even means”, in substantive terms, note an immediate consequence of the Fundamental Corollary: it allows us to operate with Chomsky’s matrices. Clearly, [±N, ±V] makes no claim different from [±V, ±N], in that alternative order, whereas [±1, ±i] can be entirely different from [±i, ±1]. That may matter much, formally, which we need to delve into, so as to seriously (attempt to) answer what (10) might imply, entail, and in the end mean.
Chomsky [
2], in the same section quoted in
Section 1 above, raised the following issue:
There will also be subsidiary features, that are necessary to distinguish auxiliaries from main verbs and adverbials from adjectives for example. So there will be a hierarchy of categories, super-lexical categories, super-super-lexical categories…In other words it ought to be in essence the case that the structure of NP’s, S’s, and AP’s should be about the same… and this will be true of higher order endocentric categories.
Now: in what sense are lexical projections, like noun phrases, and grammatical projections, like sentences, “about the same”? And what are “higher order endocentric categories”? One can always introduce more dimensions, for instance calling A/P dimensions ±A and ±P, playing the substantive game already alluded to for color and cones, VOT, and so on. But a direct alternative is to argue that further formal conditions emerge by algebraically operating with the fundamental ones in (10)/(11) only—that is, by taking our formalism seriously.
Once again, on p. 2 (his number (38)), Chomsky
orders his features in the familiar fashion of [±N, ±V]. This, as such, may be quite different from expressing the mere
presence of ±N and ±V features, if the brackets imply order—one different from that in [±V, ±N]. The theorist needs then to decide whether that is a notational variant, a matter that arises with ±1 and ±
i, as well as expressions combining these: [±1, ±
i] and [±
i, ±1] could be equivalent ways of expressing a complex number, indicating some value in the
x axis (for ±1) and the
y axis (for ±
i); but these two could also be different vectors. Indeed, Orús et al. [
25], presuming (5)/(6), argue for the relevance of representing these notions in terms of the diagonal of 2 × 2 square matrices as follows:
- (11)
a. b.
It is entirely possible that these square matrices have little to do with the Medeiros square matrices discussed in
Section 2 to represent L-trees. But because one should try bold hypotheses to test their validity, I will be working towards a system in which, in the end, the ontology of the objects in (11) is actually the same one as the ones for L-trees already discussed. I will not argue that point, however, until
Section 7 of this paper.
Once again, the advantage of matrices is that we can treat them as linear operators with standard properties,
6 for traces and determinants, characteristic polynomials, or eigenvalues:
7Just by examining the algebraic characteristics of these Chomsky objects (through the lens of (10)), we know the categories stand in specific formal relations with regards to one another. In fact—because multiplying matrices with identical real or inverse complex entries result in the identity matrix
, and multiplying any of the objects in (8)/(9) among themselves, or among the eight possible
results of multiplication among the combinations as in
Table 1—one can prove that the Chomsky matrices align into
an Abelian (commutative) group for matrix multiplication (see Note 7).
That basically means the multiplication in point is a very stable scaling, always staying within the algebraic space that could be characterized as involving objects of the following form:
- (14)
One way to interpret such matrices as linear operators (see Note 6) is through column vectors:
- (15)
a. , b.
Matrix (14) operates on whatever vector space it transforms by carrying its “horizontal” or x unit vector to (15a) and its “vertical” or y unit vector to (15b), to scale that space from those initial conditions. This may be harder to visualize for the complex entries, with these column vectors:
- (16)
, b.
But we just have to imagine a “rotation” of the plane where the x and y unit vectors exist onto a more abstract hyper-plane, as it were “popping out of the page”, to intuit further dimensions of transformation that we allow ourselves to contemplate, when considering the effect of operating by way of the combinations that (16) implies. To be sure, not having given any “meaning” (of any kind) to these numbers, such considerations are purely abstract—but I return to that shortly.
4. The Jarret Graph
To relate those abstract ideas to grammaticality, consider self-products in the Chomsky group (
Table 2):
For matrices with just real entries, the result is the identity matrix, while for those with complex entries only, the result is its negative counterpart,
, also in the group. The result of self-multiplying matrices with mixed entries is
and
, depending on whether the complex entries are. This is a well-known matrix, called
σ
Z, first systematically studied by Wolfgang Pauli while analyzing electron spin, around 1924 (see
https://en.wikipedia.org/wiki/Pauli_matrices (accessed on 28 August 2022)). This matrix is remarkably elegant, as shown through relevant formal characteristics:
Note how the matrix trace (sum of entries in the matrix diagonal) is zero for both (17c) and (17d) (the negative counterpart of (17c)), as a consequence of which the characteristic polynomial results in the elimination of the λ term and, therefore, an identical polynomial for σZ and -σZ. This is unlike what we see for the identity (17a) and its negative counterpart (17b), each with its characteristic polynomial. Consequently, the eigenvalues (roots of the polynomial) are the same for σZ and -σZ (again, unlike for the identity and its negative). There is no other pair of matrices in the Chomsky group for which this is true; so suppose we build on this elegant formal fact.
The reason for that is not algebraic but informational, since what we should be seeking, in any linguistic organization, is a formal system for which syntactic computations can be grounded with reasonable priors—then to build semantic and phonological nuances “on top”. If nature’s job is to decide on initial conditions for a computational system deploying the Chomsky matrices, there is no better formal solution, in terms of matrix elegance, than to have the base step in the system land on “the most elegant” (symmetric, orthonormal) matrix. Curiously, as we see from
Table 2, precisely all the original Chomsky matrices (in the sense of literally interpreting his 1974 [±N, ±V] as in (1), with the items listed, in that order, in the matrix diagonal) land on Pauli’s σ
Z after squaring them. This is arguably significant too, under certain assumptions about Merge.
As mentioned already in
Section 1, (external 1
st) Merge, EM, is inherently asymmetrical for a head and the projection of its complement. That works directly for the operation after it has started. But it is computationally impossible to merge a head
to a projection if we do not have, yet, any projection formed in a given derivation—in the pristine moment in which just two heads are selected for assembly. A natural way to address this is the idea in Guimarães [
26] of allowing the self-merger of heads, at the base of a derivation. Then we can characterize EM as an operation resulting in an anti-symmetrical relation (i.e.: asymmetrical in all instances but the relation of an element to itself). But once again note that the results in
Table 3 obtain for
all Chomsky matrices:
Table 3.
Self-products for the original (reinterpreted) Chomsky matrices.
Table 3.
Self-products for the original (reinterpreted) Chomsky matrices.
| 2 = | 2 = | 2 = | 2 = |
In other words, self-merging (here understood as self-multiplication) of the nouns, verbs, adjectives, and prepositional representations results in σ
Z, obviously collapsing the formal results into identical representations. While algebraically this is entirely fine, for a symbolic system it is the equivalent of Paul Revere’s famous code having been the senseless “One if by land, one if by sea!”
8 The whole point of a simple code is to have different signals representing
different events, which is precisely what the self-multiplication in
Table 3 denies, since matrix multiplication is not a structure-preserving operation. Is there a solution to this information impasse?
Actually, there is a simple one: phrasal axioms. We routinely take syntactic representations to map to some meaning, which we customarily do by axioms to establish relevant representations; e.g., mapping noun phrases to entities or sentences to truth values. So suppose we assume this:
- (18)
Anchoring Axiom
Only nouns self-merge.
While obviously (18) is not algebraic, it is as straightforward, as such, as stipulating that NPs map to entities. It is, of course, cognitively interesting why (18) should be, and one could imagine that the alien heptapodes in the movie Arrival, let’s say, had a different anchoring axiom in their cyclic view of time—perhaps for them only verbs self-merge. The point is that any information system with associated meaning must presume axioms of this sort, and this, as we see shortly, does work.
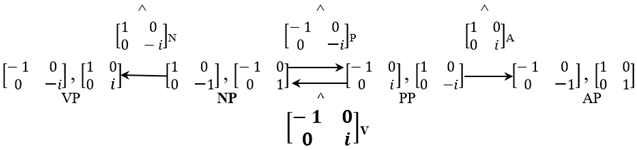
For initiating the computation in the self-merger of nouns—as the first product in
Table 3, in Chomsky’s terms—limits the next steps in direct ways. This is best seen by considering the following graph, helpfully proposed to me by physicist Michael Jarret. In (19), the notation is algebraic, linguistic codes tracking the presumed substance. The Chomsky matrices come with a “hat” ^, indicating their being taken as operators on the vector space of the Chomsky group. By the Anchoring axiom, this means a self-merging noun
(
boldfaced in (19)) plays a dual role: as an operator on itself, with an argument of identical formal characteristics.
- (19)
Note, also, how the Jarret graph only relates the categories within the Chomsky group that involve real entries in the top row, and how the Chomsky operators take one of two “twin” matrices—in the sense that they (NP, VP, PP, AP) share the same eigenvalues and determinant (−1 for NP, i for VP, −i for PP, 1 for AP projections). This is a consequence of the Anchoring axiom and “semiotic” assumptions: the idea that the computational system seeks to maximize the connections among categories in the Chomsky group, and thus even if other mappings are algebraically viable, they lead to disconnected graphs, or graphs without the recursive condition that (19) presupposes.
As just discussed, the Jarret graph could be more succinctly expressed as follows:
The original Chomsky matrices can be seen as operators on “projections” within the Chomsky group, whose “labels” are the determinants listed in (20) (there are no other possible determinants for objects in the Chomsky group). I am using those words in quotes because, algebraically, the “projections” are simply matrices within the group that are not being treated as operators, while their “label” is nothing but their determinant (which is equivalent for “twin” matrices with the same trace and eigenvalues). The graph makes the following categorial generalization:
- (21)
“Selection” conditions for operators in the Jarret Graph:
- a.
Nouns may either self-merge or take PPs to NPs
- b.
Verbs take NPs to VPs
- c.
Prepositions take NPs to PPs
- d.
Adjectives take PPs to APs
What is remarkable about (19) is that the statements in (21), substantive though they may seem, have no semantic cause to them: they follow from the algebra, once the Anchoring Axiom is established and “semiotic” conditions (e.g., about involving all categories into a connected, recursive, graph) are presumed. These may map to the semantics, but not
because of meaning.
9 5. Non-Algebraic Assumptions in the Jarret Graph
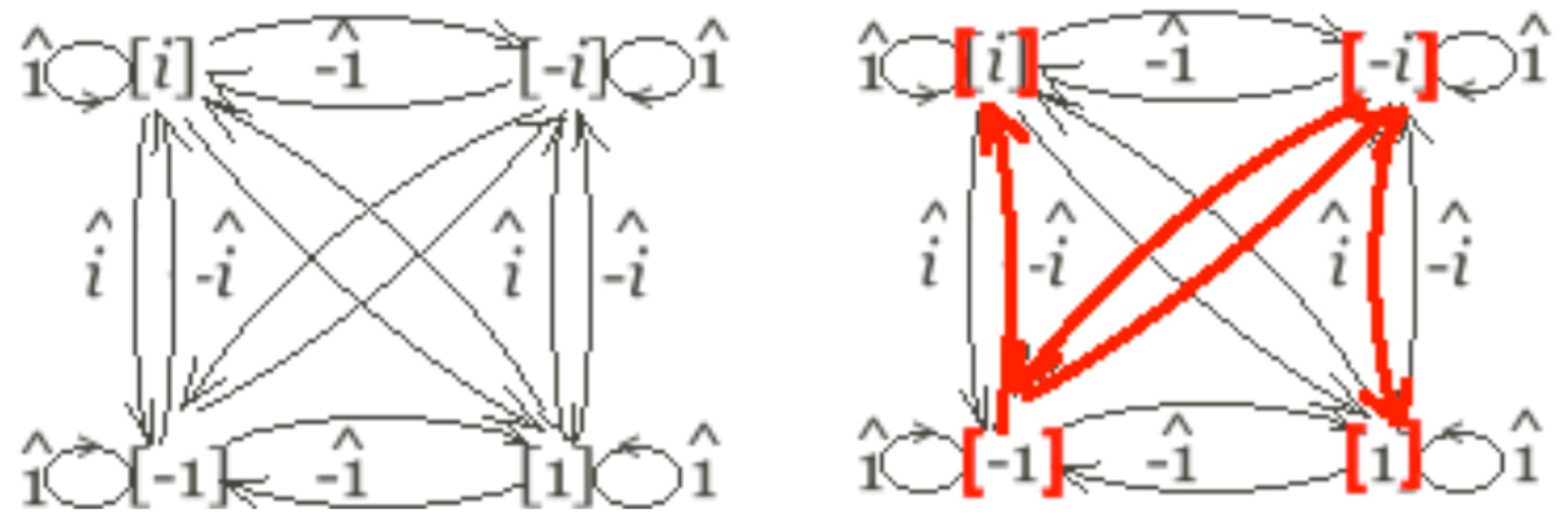
To see the basic algebraic possibilities presumed in the Jarret Graph, consider the determinant products in
Figure 1, where the graph, expressed in terms of the matrix determinants as in (20), correspond to the highlighted possibilities to the right of the table. Of course, one needs to consider why the other algebraic possibilities in
Figure 1 (covering the entire space of combinations) do not result in a graph equivalent to the Jarret Graph, with grammatical reality.
Figure 1.
Determinant products for the matrices in the Chomsky group.
Figure 1.
Determinant products for the matrices in the Chomsky group.
The answer is substantive: the Anchoring Axiom—plus semiotic/information assumptions about to be specified—yields the Jarret Graph as what the language faculty found within this algebraic space. A different species (anchoring the system on verbs, prepositions, or adjectives) would yield a different solution, as could a system that is not meant to be used to encode and share information.
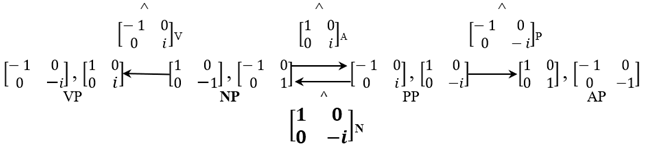
To ponder why other possibilities do not arise, consider (22),
10 which would wreak havoc on the “selection” generalizations in (21) (vis-à-vis the descriptively adequate graph in (19)):
Here we have swapped the A in the Jarret Graph for the P element, preserving the rest. Note, however, that (22) cannot be obtained under the assumption of the Anchoring Axiom and the fact that the Chomsky category for nouns is . What we obtain under those presuppositions is (23):
This is because, after Chomsky’s self-merges, it yields Pauli’s . In the present exercise, we are swapping the next operator (using an A , instead of a P ); then the ensuing product is not the “twin” category but, rather, again the initial . This graph is as algebraically fine as the Jarret Graph, but it does not cover all eight categories in the Abelian subset of the Chomsky group: only six of them are involved. If the point of these combinatorics is to find ways to maximally involve them all, then (23) is simply invalid.
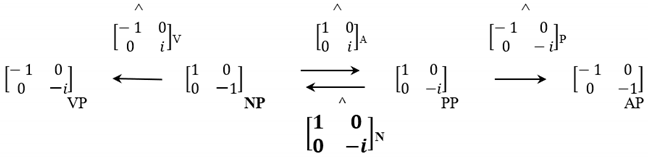
One could also consider a related problem as in (24), where we swap the V and the N in the Jarret graph. Although algebraically there is nothing wrong with this either, (24) directly violates the Anchoring Axiom, for the only way in which the system could start by assuming the highlighted matrix as an initial operator if Chomsky verbs, , not nouns, , self-merge.
To be explicit about our non-algebraic, information-driven, assumptions, we stipulate:
- (25)
Semiotic assumptions for algebraic syntactic matrices:
- (i)
Univocal.
- (ii)
Complete.
- (iii)
Recursive.
- (iv)
Fully connected.
For the relevant portion of the Chomsky group (with real entries in the top row), and presuming an Anchoring Axiom as in (18), this results in the Jarret Graph, whose consequence is to indirectly describe (many) “selection” restrictions we find across languages (and see Note 9).
Although the empiricist may find nitpickings about (21), this is the empirical payoff:
- (26)
Exemplars covered by the Jarret Graph:
- a.
[NP pictures [PP of [NP war]]]
- b.
[VP hate [NP war]]]
- c.
[PP of [NP war]]]
- d.
[NP proud [PP of [NP science]]]
And, obviously, some recursiveness (involving the core of the graph) is directly expressible, as a consequence yielding so-called tail-recursion:
- (27)
a. [VP hear [NP stories [PP about [NP pictures [PP of [NP students [PP of …]]]]]]]
b. [AP proud [PP of [NP stories [PP about [NP pictures [PP of [NP students [PP of …]]]]]]]]]
I hasten to add the hopefully evident: that (21)/(26) is not meant to cover all selection restrictions in natural language (more on this shortly) and one can certainly raise issues about various nuances. Here are some, beyond covering further territory. Note that the Jarret graph forces adjectives to emerge only via taking a PP argument, which poses the issue of what to do with isolated adjectives (not proud of science, but proud period). Although I will not pursue this now, it is clear that classes of adjectives can be easily specified this way, since all adjectives can be (often redundantly) expressed in terms of a complement realizing the adjectival dimension:
- (28)
a. red (in/of color) b. tall (in/of stature) c. large (in/of size) d. pitiful (in/?of nature)
The graph fares well for both bare (self-merged) nouns and relational nouns, and directly describes simple PPs (more generally adpositions, although it is a delicate issue whether postpositional phrases involve displacement). On the matter of (syntactic) “linearization”, the graph takes no stand as to whether complements precede their head, but contentious disputes in that regard (involving the order of complements across languages) would have to be resolved to determine whether, in particular, complement-head orders directly accord with the graph or need to be resolved involving displacement and, as discussed below, further structure. One thing is overwhelmingly clear even for VPs across language, though: the vast majority are not just transitive, but indeed they normally first involve NP direct objects—all of which the graph covers. Evidently, the issue is to ponder in/di-transitives or clausal dependents, which is not a matter of the graph overgenerating.
11Ultimately, more important than such considerations are further consequences the present approach affords. Note that only two matrix pairs in the Jarret Graph involve only real entries: those corresponding to ±σZ and ±I. Matrices of that kind—with real values in the diagonal and also real or conjugate symmetrical values elsewhere, here zero—are called Hermitian and present particularly elegant properties, vis-à-vis non-Hermitian counterparts. In comparable situations in particle physics, these same operators, equipped with positive inner products (the central metric in a vector space), have real eigenvalues. This is key to representing physical quantities, since measurements correspond to real quantities. Interestingly, this separates what “exists” (is mathematically necessary for a system to work) from what is “observable” (definitely identified for measurement). If we suppose the way for the abstract syntax in that mathematical existence to interface with concrete external systems, or definite internal thought, is through equal certainty, then only Hermitian points in the Jarret Graph yield “interpretations”:
Only Hermitian matrices are legible at the interfaces.
While not (logically) necessary, (29) makes sense and has architectural consequences: primitive semantic types—like “entity” or “predicate”—correspond to the “legible” (read: real) matrix projections.
12 None of the Chomsky matrices (lexical operators) are “legible” in that sense, so their meaning is entirely contextual: it becomes viable in the domain of sentence grammar. Interpretive Axiom (29) should be seen in the same light as Anchoring Axiom (18): neither is a piecemeal statement about the syntax/semantics interface, though they both have radical consequences.
6. Beyond the Jarret Graph
The discussion in the previous section pertains only to the four Chomsky matrices and their “projections” via matrix multiplication, yielding the Abelian group that the Jarret Graph lives on. As noted, we also have a larger group, involving extensions of the Chomsky matrices, obtained by flipping around the attributes. Indeed, once Pauli’s σ
Z is invoked, it is natural to ask whether the other Pauli matrices (σ
X =
and σ
Y =
) should also play a role in the system. Multiplication by either one of those yields an interesting group of 32 matrices, 16 positive and their negative counterparts, that Orús et al. [
25] dubbed the Chomsky-Pauli group
GCP. Readers will be easily able to spot here the Abelian group arrayed into the Jarret Graph, as well as the entire Chomsky group (all of them using diagonal matrices only;
Z and
I, the identity, are two of Pauli’s matrices and the mnemonic
C is a shorthand for the Chomsky objects). In addition to that, the
GCP contains also non-diagonal matrices; inasmuch as these are symmetrical with the Chomsky objects, they are notated in (30) with an
S, and they align with Pauli’s
X and
Y.
- (30)
Chomsky-Pauli Group GCP
What I am calling “the Chomsky group” contains only diagonal matrices with mixed (real and complex) entries (the portion arrayed into the Jarret graph also being a group, indeed an Abelian one); the entire set of matrices with mixed entries is actually not a group. However, readers can check (see Note 7) how the extension of the vector space in (14) as in (31) does yield a multiplicative group:
- (31)
a. b.
Although the present exercise is not the place to try this, one needs to determine how, by the same methods and results, we can use the matrices in the
GCP as operators to cover some “grammatical category” space (for T, Det, C, and so on). Bear in mind that the “grammatical structure” never starts a derivation, it is presumed to be added on “lexical structure”—which the Jarret graph grounds. Ideally, the way to connect the Jarret graph to a Super Jarret Graph is by applying the extended-Chomsky categories (“grammatical” elements) to the Jarret Graph, in the process yielding a related object with “more structure”, targeting each of the projections in (16). We should not need more than that, the super-graph preserving the basic symmetries of the Jarret Graph, including the determinats/labels we have established for basic “projection”—which, in this sense, could be seen as an “extended projection” into a layer of functional structure. One should also not need further phrasal axioms beyond the already stipulated Anchoring and Interpretive axioms, so that whatever semantics ensues follows from, rather than determine, the algebraic fate of the graph.
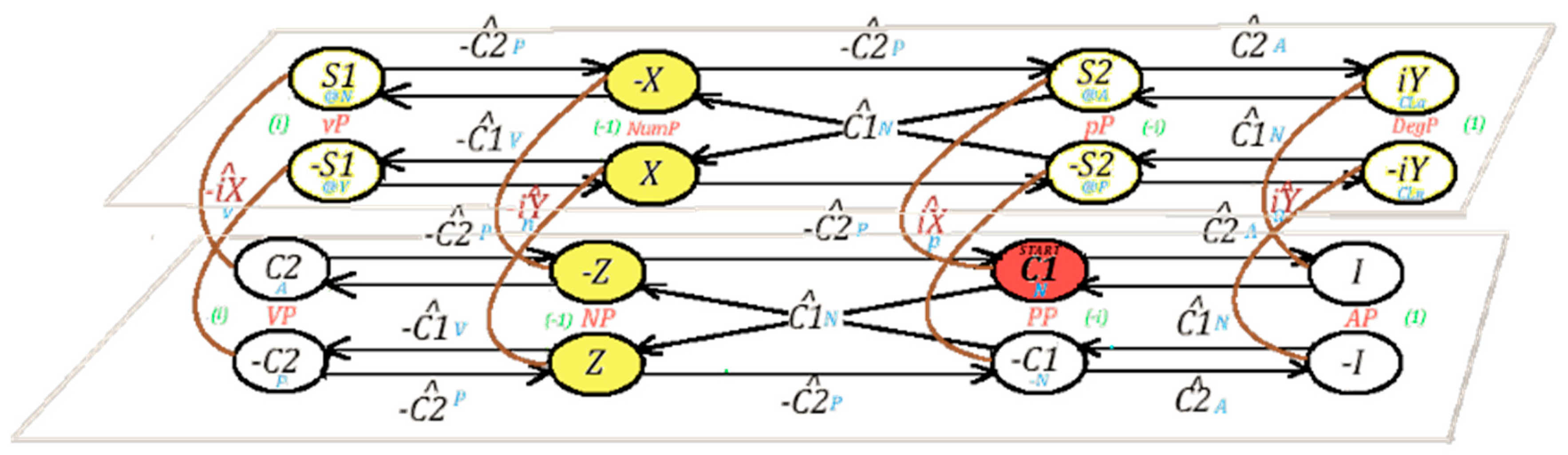
Figure 2 shows a cartoon version of the SJG from work in progress.
The Super Jarret Graph contains the Jarret Graph as a sub-graph (in the lower tier), so that the information flow can start in the emphasized node and go from any of the nodes in the more basic “lexical” graph to this extension, where the observable/interpretable categories (all Hermitian) are highlighted. Bear in mind that the super-graph contains only sixteen of the categories in the G
CP, presupposing further nuances if the entire group has grammatical significance. The super-graph should be seen as an empirical claim based on the formalism deployed, presuming the Jarret graph with all the implications above. The goal, as a result of the various dynamics, should be to obtain a “periodic table” of categorial elements of this elementary sort, ideally without having to invoke new dimensions or higher orders.
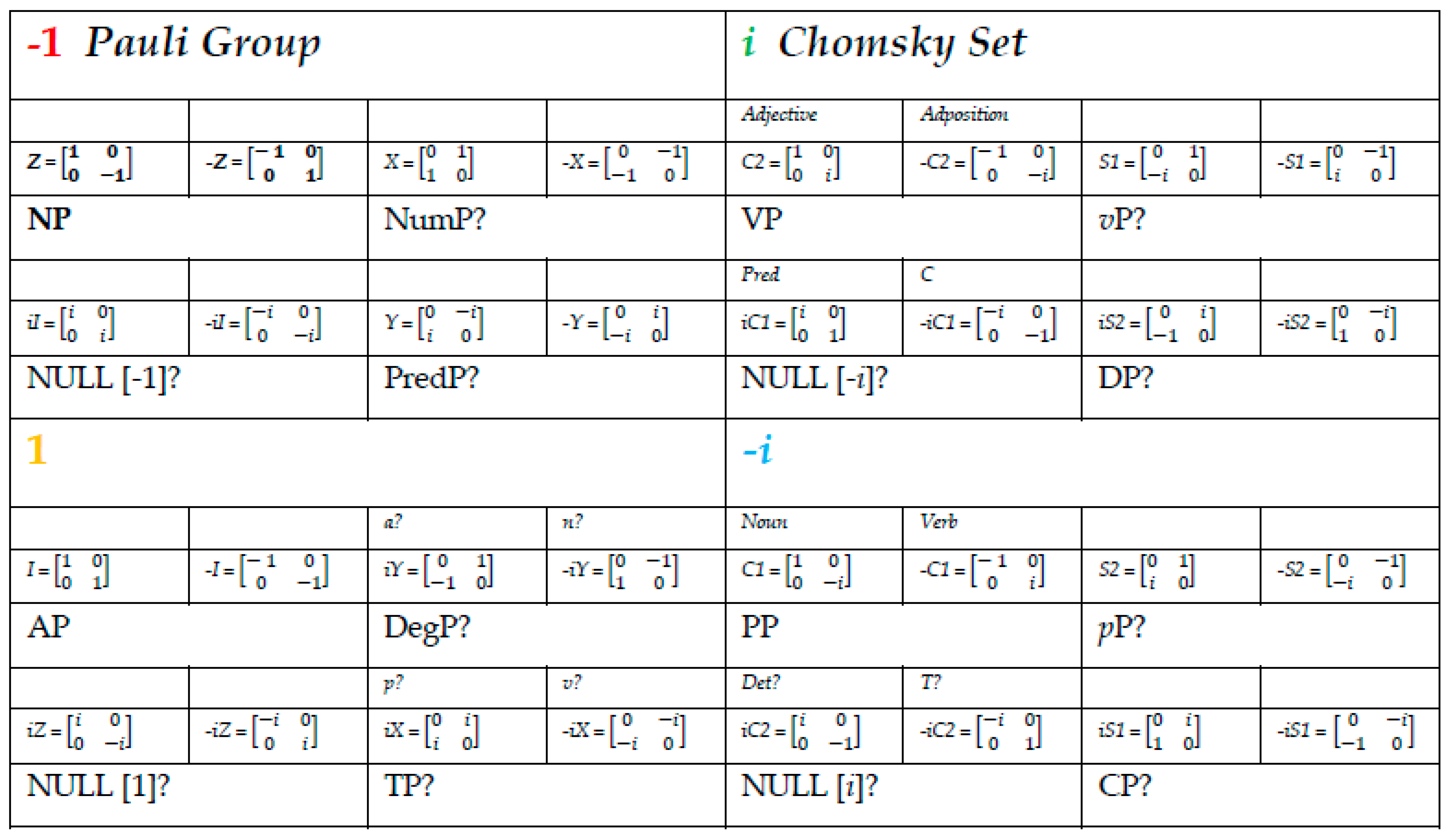
Figure 3 below is based on the Jarret Graph as already discussed, as well as
Table 3 and extensions from the presuppositions behind it: semiotic and phrasal axioms, together with “churning calculations” in the way any “categorial grammar” of this sort may function, applying “type changing” rules—here, matrix multiplication. The question marks in the table are meant to suggest that we haven’t discussed here any specificities for those categories or associated projections. In general, with any “periodic table” of this sort, one either needs to predict why a given gap exists in the paradigm or otherwise argue for a given underlying category “fitting the bill”.
Note that superposing objects in the GCP and normalizing the results (to entries ±1, ±i) has a consequence for what one may think of as “phrasalization” of the categories under discussion:
- (32)
If this sort of matrix-superposition is grammatically relevant (through the M-matrices in
Section 2), it may have a dramatic effect on the interactions of the ensuing system.
Let’s start by recalling the self-products in
Table 3, generalizing them for the matrices in (32), as follows:
- (33)
a. 2 = 3 = 4 = … = n =
b. 2 = ; 3 = ; 4 = ; 5 = ; …
c. 2 = ; 3 = ; 4 = ; 5 = ; …
Observe how only the successive powers for matrices as in (33c) “grow”, not those as in either (33a) or (33b). The difference between each condition is easy to state through the spectral radius ρ(A) defined in (7a), from which the system’s derivational entropy is calculated, as repeated now:
- (34.)
Derivational entropy
a. For spectral radius ρ(A), square matrix A’s largest absolute value λmax of A’s eigenvalues,
b. A’s topological derivational entropy hT = log2 λmax.
For either (33a), (33b)—or any of the matrices in the
GCP—for A matrix in the sequence of powers,
ρ(A) is always 1. In contrast, some of the superposed matrices (arising from summing matrices within G
CP) have
ρ(A) larger than 1.
13 Consequently, the topological derivational entropy
hT of the matrices in (33a) or (33b) is log
2 λ
max = log
2 1 = 0; in contrast, for
hT of the matrices in (33c) log
2 λ
max = log
2 2 = 1. This topological entropy matters for interpreting systems’ growth as they (try to) expand in L-system fashion, via rewrite or EM merge processes.
7. Categories & Interactions Redux
At the end of
Section 3 I promised to consider the bold hypothesis that the ontology of the Chomsky/Pauli 2 × 2 objects is ultimately related, if not equatable, to the Medeiros interpretation of L-trees topologies in square matrix fashion. Intuitively, just as it is obviously relevant for a power sequence of the sort in (33c) to grow, one may take it to be equally relevant for the power sequence of a related matrix to stay “cyclic”, as in (33a) or (33b). The latter condition arises for a matrix A with spectral radius
ρ(A) = 1, whose topological derivational entropy is zero and, thus, the subsequent powers of A fall into a multiplicative group. Computationally, the group in point could be seen as Markovian, “stable” in that very repetition, perhaps like “earworms” in the stuck song syndrome (
https://en.wikipedia.org/wiki/Earworm (accessed on 28 August 2022)). While this is meant just as a metaphor for now, the idea is that the formal representation of certain matrices arising from multiplication of a computational seed disallows growth into a phrasal topology that could permit an associated phrasing. Again, all matrices within the
GCP have the formal condition of their power sequences being “cyclic” in this sense, while some of their (normalized) superpositions can be shown to allow for the fractal growth the standard L-systems imply—starting with the simple (33c), which corresponds to a trivial Lindenmayer expansion as in (35):
From this perspective, while elements in the GCP need to be necessarily categorial in the Markovian cyclicity of corresponding powers, the mere superposition of its elements is enough, under the right conditions, to allow for the phrasalization of corresponding categories—via the same algebra.
For concreteness, consider the sum of three Pauli matrices in (36a), normalized to (36b):
14- (36)
a. b.
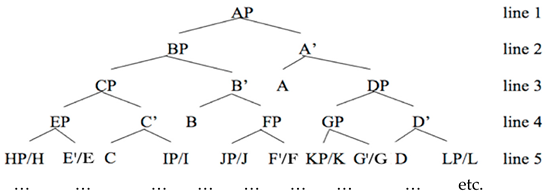
The first two of these are part of the Jarret Graph, and the third is in the Super Jarret Graph, so it is easy, both algebraically and computationally, to see how to obtain a result that can be normalized to the matrix in (36b) (though see Note 14). In turn, (36b) is at the core of the X’-theoretic 3 × 3 matrix in (28), representing the variable elements in the L-system, per the Medeiros method “in reverse”:
Ordered context-sensitive manipulations (expressed in rewrite fashion for concreteness) turn objects that (38a)/(38b) describes into the familiar X’-theoretic object in (5), repeated below. (38a) makes a chunk of structure […]+ in (37) that happens to be sister to and daughter to a “-” into a constant k that does not rewrite any further; while subsequently (38b) prunes the “-” (whose “purpose” is only to contextualize the atomization) out of existence:
- (38)
a. […]+ → k/[… __− …] −
b. − → Ø
This is to say that well-known computational methods yield the observables, although how to go from (37) to (39) in algebraic fashion, no matter how indirectly, is a more interesting question.
15Differently put: the distinction between categories and interactions may actually be algebraically subtler than anticipated. The Jarret Graph or its super-graph extension are meant as involving matrices whose corresponding power sequences are cyclic, as “earworms” of the grammar. Being stuck in one’s mind would allow these objects—and corresponding vector specifications that linguistic experience may associate to their various phonological and semantic nuances—to be identifiable in a mental lexicon. A superposition in the algebraic bedrock, however, yields a fractal topology of the phrasal sort, in ways we cannot explore here. This is in part because there are 2
32 ways of superposing (summing) the categories in the
GCP, and if the empirically observed X’-schema in (39) is any indication, we need a further dimension for the system’s constants. That presupposes, together with the phrasalization (via superposition), some mechanism like (38a) for the atomization of phrasal chunks into lexical idioms, perhaps akin to whatever goes on in idiomatization more generally, as discussed in Lasnik & Uriagereka [
27].
To visualize these algebraic gymnastics, readers may imagine a lexicon as a network of relations built on what objects in the
GCP operate on: its own formal scaffolding “rotating” in four dimensions.
16 Those should express the categorial distinctions Chomsky [
2] was after: nouns, verbs, and so on, all the way “up” to determiners, inflectional categories, or wherever else may be syntactically needed. The (ultimately mental) states this allows ought to be the support for the lexical and grammatical categories we have been using in a text like this (and see Note 16). To be sure, that alone will not distinguish, let’s say,
write from
read,
page from
noun, or any of the thousands of instantiations one carries in one’s head—worse: anyone
could carry in one’s head, in principle, and for any language in the past or the future. But just as assigning categorial features [+N, -V] does not, in itself, distinguish all possible nouns there could be, so too the implied algebra is meant to combine with whatever system may be in place for the further nuances one may want to add to the relevant vector space.
17 Once we establish the vectorial units of said space as priors, whatever substantive dimensions are added to the foundations are as immaterial (to the structure itself) as the notes of a melody one can deploy within a given harmony. Importantly—while there are grammatical processes that depend on the implementation of the features this system presupposes (by changing values and attributes as relevant, to distinguish nouns from verbs, etc.)—there is no syntactic process that depends on the exact implementation of the relevant vector spaces. Thus, there are syntactic operations that target nouns
or verbs, but none that target the noun
page as opposed to any other or the verb
write, but not the verb
read, etc.
18 What we are attempting to establish now is just the algebraic foundation of the vector space where syntax lives.
19 8. Conclusions
Verbs and, especially, nouns are fundamental. These elements are not just the cognitive back-bone of the grammatical system, they also feature prominently in the main processes the grammar instantiates: θ-dependencies, Case, agreement, or construal relations. Here I have made nouns axiomatically start a derivational system based on matrix multiplication, instantiating a reflexive base condition. That algebraic system can be accessed by formally pursuing an intuition dating back to antiquity, which has an abstract “nominal” dimension “at right angles” to a maximally distinct “verbal” dimension. In the system proposed, operating on nouns yields a measurable/observable (Hermitian matrix), which in turn limits other potential combinations with abstract lexical categories; this is what I have been calling the Jarret Graph, which was argued to underlie complement interactions for lexical heads.
There are two ways in which that decision is not enough. First, there are obvious categories in grammar that do not reduce to the basic lexical four; second, equally obviously, there are relations beyond head-complement dependencies. The first issue can be dealt with within our formalism by exploring it to its fullest: literally turning entries around; this is how we went from the Abelian group of categories within the Jarret Graph, first, into the Chomsky group (flipping the entries in the diagonal) and, next, into the GCP, which includes all of the Pauli group and extends it (by mixing real and complex entities, or vertically flipping the elements in the Chomsky group into their symmetrical counterparts). Although this short paper cannot fulfill the promise of distributing the formal entities in that group into a full-fledged “periodic table” of grammatical categories, mapping them within the formal system amounts to a dissertation exercise, with familiar categorial-grammar methods (we know the input, suspect the output, have an excellent sense of the phonetics and an informed idea of the semantics, so it is all a matter of “aligning the Rubik cube”). A harder—more interesting—question is how to go beyond head-complement relations, in particular into head-specifier relations and the long-range correlations they afford.
That one shouldn’t trivially align head-complement and head-specifier relations ought to need not argument, in syntactic, semantic, and phonological terms. In minimalist parlance, head-complement relations define the so-called
domain D of a phase, the rest being its
edge E. As emphasized in Uriagereka [
30] (chapter 5), there are several grammatical conditions taking place within Ds, from theme selection with projection consequences to agreement probing, including partitive case and head-to-head dependencies (incorporation, affixation, light verbs, etc.). In contrast, Es determine everything from external argument taking to structural Case, together with all sorts of (successive) displacements and entanglements (see [
27]). Such E-related super-configurational conditions are decidedly more complex than the corresponding D ones, of a (phrasal) configurational sort. These distinctions have dramatic consequences, also, for the mapping to the interfaces, from intonational units to event-participation and the convoluted gymnastics of generalized quantification, or intertwined construals and ellipses too numerous to mention here, with consequences for pragmatic conditions and the articulation of Familiar/Novel information. In this exercise, we just looked at the configurational relations, which is only a stepping stone towards understanding the more elaborate ones that presuppose them.
A novel idea explored here is that the presumed difference between categories and interactions—in a context of the head-complement sort—are less dramatic than it may seem, before analyzing the matter algebraically. The formal intuition is no different from why the powers for any number
kn growing exponentially with the size of
n do not for the subcase
k = 1. We are dealing with matrices, but they too have powers, and their effect on their spectral radius (per (7)) does depend on whether it is 1 or more, thereby affecting the system’s topological derivational entropy. In the former instance the power sequence “cycles back” to the origin, after hitting the identity matrix, while in the latter the power series yields fractal growth instead.
20 We have capitalized on that distinction to separate “cyclic/Markovian” categories from derivational topologies that may carry phrasal combinations. To go on with the Tour metaphor in
Section 2, the “earworm” stages would have to be designed by M.C. Escher, to cycle back after a topological trick involving a Möbius Strip! In contrast, all other stages would shoot out to infinitude, creating a space for exploration of the relevant terrain that can take arbitrarily many twists and turns, within the restricted topology. Algebraically, the difference is small: mere symmetry within the underlying square matrices vs. breaking that symmetry into some result that could be chaotic.
Although I have not sketched the idea beyond the programmatic, it reduces to linguistic knowledge being accumulated in a (mental?) lexicon by way of the presuppositional effect of depleting words. Although this has a Hebbian ring to it, which connectionist networks have taken to new depths through state-of-the-art algorithms, the issue is what could the complex entries be that I have crucially introduced. These cannot relate to “neurons that fire together wiring together”, if that is being presupposed as some sort of (distant) underlying brain physiology to carry some version of the system… That said, by now there are non-obvious conditions neurons are known to perform, which have little to do with the usual firing in the direction of the axon. Neurons, for instance, “fire backwards” while mammals sleep (for reasons that might relate to the consolidation of memories—see [
31]). Also, there appear to be physiological dependencies “at right angles” with standard neuronal firing. At a neuronal level, one can imagine modeling the balance between excitatory postsynaptic potentials vs. inhibitory postsynaptic potentials in terms of negative vs. positive scalars in a network; at the same time, Hebbian plasticity is known to amplify correlations in neural circuits, creating a positive feedback loop that renders circuits unstable, which needs to be constrained. Heterosynaptic plasticity apparently serves a central homeostatic role to cause pathway unspecific synaptic changes in the opposite direction as Hebbian plasticity (see, e.g., [
32]).
21 The scope of these changes appear to be global in the dendrites, suggesting that, aside from positive/negative interactions among neurons, to yield standard Hebbian learning and some inhibitory correlate, something else entirely, and orthogonal to such interactions (though still numerical in their own right) may also be at play.
Those comments are meant within the relatively new, but entirely classical, domain of neuroscience. Even more radically, Fisher [
33], Straub et al. [
34], speculate with quantum processing with nuclear spins in the brain, identifying phosphorus as “the unique biological element with a nuclear spin that can serve as a qubit for such putative quantum processing—a neural qubit—while the phosphate ion is the only possible qubit-transporter.” This is presupposing that central quantum-processing requires quantum entanglement, which Fisher argues can happen as a result of an enzyme-catalyzed reaction that breaks a pyrophosphate ion into two phosphate ions. The admittedly drastic idea is that multiple entangled relevant molecules “triggering non-local quantum correlations of neuron firing rates, would provide the key mechanism for neural quantum processing”. Evidently, if anything this dramatic were at stake, much of what is known about neuroscience in general would have to be rethought. I mention it here simply as an indication that all bets probably should be off when it comes to interpreting the relatively simple observables discussed here, which need not go into such old chestnuts as awareness, consciousness, morality, and the like. Ordinary syntax poses related and more tractable questions.
Be that as it may, an individual “use” of language by any speaker may be seen as relevant to convey some truths (or lies!) about the world. However, the social effect seems to be to create an ensemble of weighted concepts that get harbored in categories transmitted from a generation to the next. In this sense, while (obviously) there is a portion of that repository that I happen to store in my head, you in yours, etc., there is also a societal entity that persists, probably the way economies or social systems may, drifting away as the case may be. For those structures, it is immaterial what I or you may be saying or how it affects our lives, as it is the fact that we are using it. This even allows for the possibility of some of the complex algebraic possibilities explored here having nothing to do with what gets literally “recorded” in actual brains, possibly existing in a reality that one may wish to call Platonic—but with relatively little added value to such a claim. Unless, of course, economies and social systems “evolving” in history are also Platonic.
My concrete claims boil down to two. One, that while syntactic deployment requires an open-ended topology (with non-zero topological derivational entropy) to allow for recursive thoughts, lexical storage demands, instead, a cyclical scaffolding (with zero entropy) to let ideas repetitively cohere into entities stable enough to last one’s lifetime and, ideally, get passed on, in some simple Markovian fashion. Here we have only studied what amounts to the hypothesized priors of such a system: its underlying scaffolding—therein the second claim. For the symmetries and asymmetries studied here to make any sense, that scaffolding must involve complex (non-observable) dimensions. While these are not obvious to relate to brain interactions (even with hand-waving), they are one of the most interesting aspects of the proposal.
The final ace in the sleeve for this sort of proposal is how it relates to ideas in Smolensky & Legendre [
35], starting from (vastly) different presuppositions, since the latter work is coming from a connectionist tradition, while the present one is explored within symbolic conventions. Interestingly, in some regards the present approach, upon tensorizing the
GCP in ways sketched in Orús et al. [
25], is entirely compatible with that model, and thus can preserve its virtues, including a way to directly map the relevant representations to actual phrase-markers (not just L-trees). More importantly, both systems present the ability to (formally) state entanglements upon relevant superpositions—what syntacticians customarily call “chains of occurrences”. While this idea is only offered as a proof of concept in the connectionist instance, and without obvious connections to actual observables across languages, I intend to show in a sequel to this piece how the present formulation has the same mathematical result as a direct consequence, moreover tracking grammatical facts in a more direct fashion (e.g., allowing us to state differences between voice and information questions). It is interesting that one should converge in a similar math from very different assumptions (in the present instance, asking how to generalize from the most modest formal objects to matrices combining them, step by step). While data-driven analyses involve the same math that can be deployed over the group we have begun to formally analyze, we “got there” from first principles that we still teach in our introductory linguistics classes, dating back to the dawn of linguistics. While this could certainly be mere coincidence, it may also be an indication that some progress may be at hand as these matters are further explored.