The Impact of Meta-Induction: From Skepticism to Optimality

Abstract

In the first section, five major attempts to solve the problem of induction and their failures are discussed. In the second section, an account of meta-induction is introduced. It offers a novel solution to the problem of induction, based on mathematical theorems about the predictive optimality of attractivity-weighted meta-induction. In the third section, how the a priori justification of meta-induction provides a non-circular a posteriori justification of object-induction, based on its superior track record, is explained. In the fourth section, four important extensions and refinements of the method of meta-induction are presented. The final section, summarizes the major impacts of the program of meta-induction for epistemology, the philosophy of science and cognitive science.

1. The Problem of Induction: Solution Attempts and Their Failures

The aim of this paper is to give an overview of the problem of induction, to present and develop the meta-inductive approach to this problem, and in particular to highlight the impact of this approach. Thereby, the notion of induction is always in the usual, narrow sense of transferring observed patterns to future or unobserved cases. Some philosophers understand induction in a wider sense, covering all kinds of non-deductive and uncertain inferences, including abductions or inferences regarding the best explanation [1] (p. 42), [2], and [3] (p. 13). The justification of theory-generating abduction involves additional complications that are not considered in this paper.

The problem of induction, otherwise known as Hume’s problem, consists of the apparent impossibility of providing a non-circular justification of the truth-conduciveness of inductive inferences. Hume’s major skeptical arguments [4] (ch. 4, ch. 6) can be summarized as follows:

• It is impossible to justify the reliability of induction by logical demonstration, because induction is not logically valid.
• The reliability of induction cannot be justified by observation either, because its conclusion speaks about unobserved (future) cases.
• Most importantly, the reliability of induction cannot be justified by induction using its past success, as this argument would be circular.
• These skeptical objections do not merely show that induction is not strictly valid; they also undermine a demonstration of the probabilistic reliability of induction, since such a demonstration would have to be based on the inductive transfer of past success frequencies to the future, which would be a circular argument.

These arguments led Hume to the skeptical conclusion that induction cannot be rationally justified but is merely the result of psychological habit [4] (part 5). Since all sorts of human prejudice and superstition are likewise based on "psychological habit", Hume’s skeptical conclusion would imply that there is no substantial difference between the irrational practices of men of the Stone Age and the inductive methods of modern science. If that were true, then the enterprise of enlightenment rationality is bound to fail and, as Russell [5] (p. 699) once remarked, there would be “no intellectual difference between sanity and insanity”.

There have been several attempts in the analytic philosophy of the 20th century to find solutions to Hume’s problem. In this section, we give a brief overview of five major attempts and their failures. These negative insights will help to identify the direction that allows for a positive solution.

1.1. Is Induction Rational “by Definition”?

Defenders of the analytic account have argued that induction is simply part of the meaning of the word “rational” [6] (p. 74f), [7] (p. 204), and proponents of common-sensism have argued in similar ways [8], [9] (p. 29ff.) The major objection against this account is the following: for a justification of induction, it is clearly insufficient that inductive reasoning accords with our semantic intuitions about the meaning of “rationality”. Rather, a genuine justification of induction has to demonstrate that induction serves the epistemic goal of cognitive success (attaining content-rich truths and avoiding errors). It is not possible to guarantee the cognitive success of a method by a mere definition, since success expresses a relationship between a method and its domain of application.

A more refined argument for the analytic account has been developed by Strawson [10] (p. 249). He argued that the justification of induction faces a similar problem as the justification of deduction, namely, that a justificational circle is unavoidable because we cannot imagine a situation in which the rules of logic fail. However, even if we grant Strawson the point that possible worlds falsifying laws of logic are hardly conceivable, his argument fails since, for inductive inferences, the situation is entirely different: we can easily imagine possible worlds in which inductive reasoning goes wrong and familiar “laws of nature” are suddenly broken, just as happens in Lewis Carroll’s Alice’s Adventures in Wonderland.

It is not only theoretically conceivable that inductive methods fail or are inferior to non-inductive methods. Millions of people do in fact believe in superior non-inductive prediction methods, be it based on God-guided intuition, clairvoyance or on other purported paranormal abilities. Therefore, a satisfying justification of induction would not only be of fundamental epistemological importance but also of fundamental cultural importance, as part of the philosophical program of enlightenment.

1.2. Can Induction Be Justified by Induction or by Assumptions of Uniformity?

The inductive justification of induction has been proposed by several philosophers [11,12] as a kind of stopgap to the problem of induction. The justification is circular—more precisely, “rule-circular”, since the reliability of the inference rule underlying this argument presupposes the truth of its conclusion. Both Braithwaite and Black thought that rule-circular justifications could be epistemically valuable. However, the problem of circular justifications is that with their help, mutually contradictory conclusions can be justified from the same or equivalent premises. This was first demonstrated by Salmon [13] (p. 46), who showed that the same type of rule-circular argument can also be used to “justify” the rule of counter-induction. The rule of counter-induction predicts the opposite of what has been observed in the past; thus, it predicts the opposite of what is predicted by the rule of induction:

(1a) Rule-circular justification of induction:	(1b) Rule-circular justification of counter-induction:
Premise: Past inductions have been successful.	Premise: Past counter-inductions have not been successful.
Therefore, by rule of induction: Future inductions will be successful, i.e., induction is reliable.	Therefore, by rule of counter-induction: Future counter-inductions will be successful, i.e., counter-induction is reliable.

Both “justifications” have precisely the same structure, the premises of both arguments are true, and yet they have conclusions that are in mutual contradiction, because it is impossible that both future inductions and future counter-inductions are reliable, in the “minimal” probabilistic sense of having a success-probability of more than 50%. This shows that the rule-circular arguments are pseudo-justifications that cannot have epistemic value.

Mill [14] (III.3.1) and Russell [15] proposed that induction should be justified by the metaphysical assumption of the uniformity of nature. This assumption implies the uniformity of past and future, observed and unobserved; thus, it implies the reliability of induction. The problem of this account is, again, that it leads into a justification circle, because every attempt to justify the assumption that nature is uniform must involve an inductive inference from past observations to future expectations.

A “localized” version of the uniformity account has been proposed by Norton [16]. According to Norton, inductive reasoning is not governed by formal and general rules, such as, “If all observed As are Bs, then probably all As are Bs”, but by “local” material inferences, such as, “If some samples of bismuth melt at 271 °C, then all samples of bismuth do so”. Local inductions are, in turn, justified by local uniformity assumptions, such as, “Samples of the same element agree in their physical properties”. The fundamental problem of Norton’s localized account is the same as that of the Mill–Russell account: domain-specific uniformity assumptions are generalizations and must be justified by inductive inferences; thus, Norton’s justification ends up in a circle or in an infinite regress. Norton argues that this circle or infinite regress is less harmful for local than for general inductive inferences, but this argument is not convincing [17] (p. 762), [18].

1.3. Can Induction Be Justified by Abduction or Inference to the Best Explanation?

Several authors [19], [20] (sec. 6); [21] (p. 69) have proposed that inductive inferences are justified because they can be regarded as inferences to the best explanation (IBEs), or abductive inferences. An inductive generalization—so the argument goes—is an instance of an IBE because the best (available) explanation of a hitherto observed regularity (e.g., “So far, all observed ravens were black”) is the corresponding lawlike generalization (“It is a law that all ravens are black”).

It is certainly true that, whenever we are willing to project or generalize our observations inductively, we assume that the observed regularity was not accidental but is instead backed up by a non-accidental lawlike regularity. What this shows is that inductive projections are semantically more or less equivalent to implicit assumptions of lawlikeness. It is doubtful whether this almost analytical connection constitutes an explanation. Even if we call it a weak form of explanation, two fundamental questions remain: (i) why are lawlikeness-explanations the best explanation of observed regularities? and (ii) why are IBEs justified at all? Attempts to answer these questions run into the following two problems.

Problem 1, regarding question (i): the justification of induction by means of an IBE seems to presuppose that we already believe in the inductive uniformity of nature. Otherwise, it is unclear why one should regard the statement, “Because it’s a law that all Fs are Gs” as being the best explanation of the fact that, “So far, all observed Fs have been Gs”. If one assumes that, from time to time, nature’s laws undergo radical changes, the explanation, “Because so far it was lawlike that Fs are Gs” seems to be the better explanation. In conclusion, the IBE justification of induction is indirectly circular, as it can only work if inductive uniformity assumptions are presupposed.

Problem 2, concerning question (ii): analogous justification strategies, such as the ones proposed for induction, have been proposed for IBEs and they are beset with analogous problems [22], [23] (sec. 2.5). Generally speaking, the problem of justifying abduction is even harder than that of justifying induction: all challenges involved in the latter problem arise for the former, but the former problem is beset with the additional challenge that, in theory-generating abductions, new theoretical concepts are introduced into the conclusion.

1.4. Can the Problem of Induction Be Circumvented by Externalism?

Externalists [24] attempt to circumvent the problem of induction by identifying the justification of a prediction method with its (past and future) reliability by definition, independently of whether and how human beings can find out whether a method is reliable (i.e., that it will be successful in the future). The major problem of this externalist move is that purely externalist justifications—those that are not backed up by “internalist” justifications, i.e., arguments—are cognitively inaccessible. Only the past track record of a prediction method is cognitively accessible, and the reasoning from this track record to the method’s reliability is an inference. Let us illustrate this problem at hand of the rule-circular “justification” of induction and counter-induction, discussed above. Externalists accept the (rule-) circular justifications in (1a) in the following conditional sense: if the world is inductively uniform, then the inductive justification of induction is externalistically acceptable. However, for reasons of parity, the same argument applies to the conditional justification of counterinduction in (1b): if the world is anti-uniform, the counter-inductive justification of counter-induction is externalistically acceptable. The externalist qua externalist cannot give an unconditional argument that favors induction over counter-induction [25] (p. 562).

Some philosophers have doubted that counter-inductive prediction rules can be successful [25] (p. 561), [26,27]. However, this can easily be the case: most oscillatory sequences are friendly to counter-induction. Consider, for example, the simple inductive rule BI for “binary induction” over random sequences of binary events, e_i ∈{0,1} (“∈” for “is an element of”). The rule predicts e_n+1 = 1 if f_n(1) ≥ 1/2 (or n = 0) and e_n+1 = 0, otherwise, where f_n(1) is the frequency of 1s in the first n members of the sequence. The corresponding binary counter-induction rule, BCI, predicts e_n+1 = 0 if f_n(1) ≥ 1/2 (or n = 0) and e_n+1 = 1 otherwise. It is well known that over random sequences with a limiting frequency of r, BI has a limiting success rate of max ({r,(1 − r)}) and BCI of 1−max({r,1 − r}). Thus, whenever r ≠ 0.5, BI is more successful than BCI. Now consider the non-randomly oscillating event sequence (0, 1, 0, 1,…). Its finite frequencies, f_n(1), are 0, 1/2, 1/3, 1/2, 2/5, 1/2, 3/7,…. For this sequence, the success rate of BCI is 1, while that of BI is 0 (more on the predictive success of counter-induction in Schurz [23] (p. 246ff.).

In conclusion, the recognition of the reliability of a prediction method requires that past success records are inductively transferrable to the future. Whether this is the case is cognitively inaccessible, as long as we do not have what externalists want to circumvent: namely, an internalist justification of induction.

1.5. Are Inductions Truth-Preserving with High Probability?

Probabilistic accounts of induction attempt to show that inductive inferences are truth-preserving with high probability. However, the basic probability axioms do not entail any inductive consequences. In order to support inductive inferences, probabilistic accounts have to make additional inductive assumptions that are in need of justification.

There are (at least) two kinds of probabilities, objective-statistical and subjective-epistemic. Subjective-epistemic probabilities are abbreviated by an uppercase “P” and express rational degrees of belief, satisfying the basic probability axioms. Objective-statistical probabilities are abbreviated by a lowercase “p” and denote the limits of frequencies in infinite random sequences, provided that these limits exist [28]. Formally, p(F) = lim_n→∞f_n(F), where f_n(F) denotes the relative frequency of property F in the first n elements of a given random sequence (a₁, a₂,…), and the existence-of-a-limit condition asserts that ∀ε > 0∃n∀m ≥ n: |f_n(F)−p(F)| < ε. In a more contemporary view, statistical probabilities are understood as dispositions (“generic propensities”) of random experiments to generate outcome sequences converging towards these frequency limits1.

Concerning statistical probabilities, the assumption of the existence of a frequency limit is already a weak inductive uniformity assumption. The convergence of finite frequencies to limits is not necessary. For illustration, Example (2) presents a 0–1 sequence whose frequencies do not converge but oscillate permanently between values ≥2/3 (converging to the “limit superior” 2/3) and the value 1/3:

(2) Binary sequence without frequency limit (“n:1” stands for a subsequence of n 1s, and analogously for “n:0”):

Sequence:   2⁰:1,  2¹:0,  2²:1, 2³:0, 2⁴:1,… 2^2⋅n:1    2^{2⋅n +1}:0 …

Frequency of 1’s: 1   1/3,   5/7,  1/3,   21/31,… ≥ 2/3  1/3  …

Even sequences that possess frequency limits can be complex and irregular. To compute the statistical probabilities of their convergence properties via the Binomial formula, one assumes the principle of statistical independence, which is an even stronger inductive uniformity assumption (see below).

Epistemic probabilities are explicated via Bayesian probability theory. In this account, too, inductive reasoning cannot be justified without additional inductive assumptions. Howson [30] (p. 279) argued to the contrary: that, already, the basic probability axioms would yield a “weak” inductive logic because every hypothesis with non-extreme probability (P(H) ≠ 0,1) that entails a piece of evidence, E, is confirmed by this evidence in the Bayesian sense of probability-raising: P(H|E) > Pr(E). However, without further inductive assumptions, E increases H’s probability only because E is a content part of H and increases its own probability to 1 (P(E|E) = 1), but E does not increase the probability of any content part of H that logically transcends E, i.e., it is not entailed by E. In contrast, for a genuine confirmation of a hypothesis, H, it seems to be intuitively mandatory that E also raises the probability of the E-transcending content parts of H [2] (pp. 98,242Fn. 5), [31,32]. This requires additional induction assumptions (see below).

A confirmation of H that does not transfer to the evidence-transcending parts of H is called a pseudo-confirmation. An example of a pseudo-confirmation discussed in the confirmation literature is that of tackings by conjunctions. Here, an irrelevant conjunct, X, (e.g., that the moon is made of green cheese) is “tacked” onto the evidence, E, with the result that E “confirms” E∧X [33] (p. 128), [34] (p. 67). One special case of the tacking problem is the Bayesian version of Goodman’s paradox, in which a counter-inductive projection of the evidence is “tacked” onto the evidence, as follows.

(3) Goodman’s paradox for Bayesian confirmation:

Evidence E: All emeralds observed until now are green.

Inductive projection H₁*: All unobserved emeralds are green.

Counter-inductive projection H₂*: All unobserved emeralds are blue.

Inductive generalization H₁: All emeralds are green; this is logically equivalent with E∧H₁*.

Counter-inductive generalization H₂: All emeralds are green if observed until now and blue if otherwise; this is logically equivalent with E∧H₂*.

Paradox: Both H₁ and H₂ are confirmed by E in the Bayesian sense.

The “paradox” (3) shows clearly that Bayesian confirmation is not intrinsically inductive—a conclusion that has later been drawn by Howson himself [35] (p. 134). The evidence-transcending content parts of H₁ and H₂ are H₁* and H₂*, but neither for H₁* nor for H₂* does there follow a probability increase from the basic probability axioms.

Goodman’s paradox, as described above, seems to be just a special case of Hume’s problem. Goodman [36] (sec. 3.4), however, tightened his paradox: he disguised the counterinduction by introducing the strangely defined predicate grue as follows: “Something is grue if it is green and observed before a future time-point t and blue otherwise”. In the result, a counter-induction over color properties is transformed into an induction over the positional predicate “grue”. If one now applies induction simultaneously to the predicates “green” and “grue” of emeralds, one obtains contradictory predictions, namely, that unobserved emeralds will be green versus blue. Goodman-type predicates have been called positional (or “pathological”) predicates because their meaning involves an analytic dependence on time and observation, in contrast to ordinary qualitative predicates. The moral to be drawn from Goodman’s “new riddle of induction” (as he called it) is that even if rules of induction can be justified, they must not be applied to positional predicates, only to qualitative predicates [37] (p. 211).

The reason why we should inductively project only qualitative and not positional properties is the following: induction consists of transferring the same properties from the observed to the unobserved. Thus, to formulate the rules of induction, we must know what has remained invariant in our observations and what has changed. This depends on the qualitative predicates, since we assume that different instances of the same qualitative predicate refer ontologically to the same property. However, Goodman objected to this plausible solution that the qualitativity of a predicate is language-dependent: it is relative to a given choice of primitive predicates that are assumed as being qualitative. One may equally choose a language with “grue” and “bleen” (blue if observed before t and green otherwise) as primitive predicates; in the latter language, the predicates “green” and “blue” could be defined. The treatment of this aspect of Goodman’s problem requires a solution to the problem of language dependence that cannot be addressed here. In this paper, we assume that methods of prediction are always applied to qualitative predicates; it can be proved that under this assumption, Goodman’s problem cannot arise [23] (p. 54).

In Example (3) above, it was shown that the basic probability axioms do not contribute to a solution of the problem of induction. Only for probability distributions that satisfy additional inductive assumptions does it follow that H₁* is inductive-probabilistically confirmed and H₂* disconfirmed by E. A weak inductive assumption that is assumed in Bayesian statistics is de Finetti’s [38] principle of exchangeability (or symmetry, as Carnap [39] (p. 117f) called it). Assuming a first-order language with an infinite sequence of (non-identical) individual constants, I = (a₁, a₂, …), then a probability distribution, P, is defined as exchangeable if P is invariant with regard to arbitrary permutations of the constants in I, i.e., P(A(a₁, …, a_n)) = P(A(a_π(1), …, a_π(n))) holds for every permutation of the indices π [2] (p. 89), [40] (p. 71). Informally speaking, the condition of exchangeability asserts that, independent of their particular properties, the probabilistic tendencies of all individuals are the same. If we think of “property-less” individuals as positions in space-time, this amounts to an inductive uniformity assumption over space and time. Probability functions that are exchangeable and non-dogmatic (assigning a non-zero probability to all possible propositions) enable inductive learning [2] (p. 141ff), [23] (sec. 12.2), [41]:

(4) Theorem: Assume P is exchangeable and non-dogmatic. Then (a) the posterior probability of a prediction “Fa_n+1” increases continuously with the number of confirming instances (“instantial relevance”) and (b) converges against Fx’s observed frequency, f_n(Fx), when the sample size n goes to infinity. Formally:

(a) P(Fa_n+1 | f_n(Fx) = $\frac{\mathrm{k}+1}{\mathrm{n}+1}$) > P(Fa_n+1 | f_n(Fx) = $\frac{\mathrm{k}}{\mathrm{n}}$) > P(Fa_n+1 | f_n(Fx) = $\frac{\mathrm{k}}{\mathrm{n}+1}$), and

(b) lim_n→∞ P(Fa_n+1 | f_n(Fx) = $\frac{[\mathrm{r}\cdot \mathrm{n}]}{\mathrm{n}}$) = r

([r] = the integer-rounding of the real number, r).

However, inductive convergence in the sense of (4) is too weak for practical implications, because it holds only in the long run and has no implications for the short run. The distance between the posterior probability and the observed frequency may still be maximal after any finite number of times because—in contrast to the results about meta-induction in the next section—there are no guaranteed upper bounds for this distance that quickly converge to zero. Formally, this means that:

(4-Addendum): For every event-sequence (±Fa_i: i∈ℕ), ε > 0 and n∈ℕ, there is a non-dogmatic but biased prior, such that P(Fa_n+1 | f_n(Fx) = $\frac{[\mathrm{r}\cdot \mathrm{n}]}{\mathrm{n}}$) is ε-close to 0 if r > 0.5 (and ε-close to 1 if r < 0.5).

For example, no finite set of counterexamples can convince a Bayesian agent who believes strongly enough in the existence of a benevolent God to give up his faith.

Objective Bayesianism assumes a stronger principle that regulates the choice of priors: the principle of indifference. The principle goes back to Laplace; more contemporary defenders of this principle are Jaynes [42] and Williamson [43]. The principle of indifference asserts that in the absence of experience, the same prior probability should be assigned to every possibility. The question is, however, what counts as a possibility—depending on that decision, the indifference principle may give opposite results. First, assume that one chooses an indifferent distribution over all possible words or (linguistically) over all complete state descriptions. Such a distribution is called state-indifferent. For binary events, a state description corresponds to an infinite 0-1 sequence. With this prima facie natural prior, one obtains a maximally induction-hostile prior distribution:

(5) Theorem: For a state-indifferent prior probability distribution, P, over binary events (±Fx), the posterior probability is always 1/2, independently from the so-far observed events. Formally: P(Fa_n+1|±Fa₁∧…∧±Fa_n) = 1/2 (for all n ∈ ℕ and choices of “±”).

Thus, a state-indifferent P makes inductive learning impossible. Result (5) is well known; a state-indifferent P coincides with Carnap’s confirmation function c^† [44] (p. 564–566), [45] (p. 64–66). Wolpert’s [46] famous no-free lunch theorem in computer science is a generalization of this result [47].

In conclusion, objective Bayesianism breaks down for state-indifferent priors. One obtains a radically different result if one assumes a prior distribution that is frequency-indifferent, i.e., flat over the possible frequency limits of infinite binary sequences. A frequency-indifferent prior is highly induction-friendly and validates Laplace’s rule of induction, P(Fa_n+1 | f_n(Fx) =$\frac{\mathrm{k}}{\mathrm{n}}$) = $\frac{\mathrm{k}+1}{\mathrm{n}+2}$; its generalization leads to Carnap’s c* function, = $\frac{\mathrm{k}+\mathrm{w}}{\mathrm{n}+\mathrm{\mu }}$, with w/μ as the logical width of Fx [40] (p. 72ff.). Solomonoff [48] (§4.1) proved that a frequency-indifferent prior has a strong bias toward inductive regularity: the frequency-uniform probability of a sequence, s, decreases exponentially with its Kolmogorov complexity.

To summarize: different choices of the possibility space (or partition) over which indifference is assumed lead to radically different results with regard to problem induction. The preference for induction-friendly priors needs a justification, but without a solution to Hume’s problem, one cannot give such a justification.

2. The Optimality of Meta-Induction

One solution strategy remains that is not affected by the objections of the previous section, namely, the method of optimality justification that is the topic of this section. A predecessor of this method is Reichenbach’s best alternative account of induction. Reichenbach [49] (sec. 91) attempted to show that induction is the best we can do, in order to achieve success in predictions. Reichenbach [50] (p. 363) draws the picture of a fisherman sailing to the sea and not knowing whether he will find fish (= find regularities). Yet, it is clearly more reasonable for him to carry his fishing net (= induction) with him than not to do so, because by carrying it he can only win (catch fish), but not lose anything.

Reichenbach’s best-alternative account failed because it was developed for object-induction (induction applied to events) in relation to all possible prediction methods. For proving object-level optimality, one would have to find a method of induction that predicts in every environment at least as well as does every other prediction method. There is a famous result of formal learning theory going back to Putnam [51] that proves the impossibility of Reichenbach’s project. For every (non-clairvoyant) prediction method, M, one can construct an M-adversarial event-sequence, s, for which M’s predictions fail, and an alternative method, M*, that predicts the sequence, s, perfectly [52] (p. 263). This abstract argument is made concrete by the objection that one cannot exclude the possibility of a clairvoyant, for example, a God-guided soothsayer who perfectly predicts the random tossing of a coin, while a scientific inductivist can only have a success rate of 0.5 in this case.

Reichenbach saw these objections and tried to escape their force, without success [53]. For example, in one place [49] (p. 474), Reichenbach switched the goal of his intended optimality justification from predictive success to approximating the frequency limit in the long run, i.e., for n → ∞. With respect to this goal, the justification of the simplest object-inductive generalization rule that projects the observed frequency to the limit is almost trivial: if a limit exists, this rule must approximate the limit, while if no limit exists, no rule can find it. The problem of this move of Reichenbach is that finding a true statistical generalization “in the limit” is predictively and practically insignificant because, after any finite number of observations, however large, the observed frequency may still be maximally distant from the true frequency limit. Thus, the object-inductivist has no clue when he or she has approximated the limit within tight bounds—which is a crucial difference to the meta-inductive optimality theorem below that provides tight, short-run bounds. Moreover, many other object-inductive rules (for example, the lambda-rules of Carnap [44]) are equally guaranteed to approximate the limit, and a general optimality argument for one of these rules with regard to speed of convergence does not exist2.

For these reasons, Reichenbach withdraws the above-mentioned switch over to the goal of long-run approximation and switched back to the goal of predicting events or event-frequencies in finite future time spans [49] (pp. 351,47f.), with the result of being confronted with the possibility of a predictively superior, non-inductive method. Struggling with this objection, Reichenbach remarked that if a successful future-teller existed, then that would already be “some uniformity” that the inductivist would recognize by applying induction to the success of the prediction methods [49] (p. 476f), [50] (p. 353f). However, Reichenbach did not make anything out of this observation; in particular, he did not try to show that, by this meta-inductive observation, the inductivist could have an equally high predictive success as the future-teller [56] (ch. III.4).

Precisely at this point, the meta-inductive account hooks in. The major innovation of this account is to apply optimality at the level of meta-methods. These are methods that have the outputs or even the algorithms of other methods as their inputs. Similar to universal Turing machines, they attempt to construct optimal methods out of these inputs. Generally speaking, a meta-inductive prediction method tracks the success rates of all accessible prediction methods. Based on this information, it tries to select or construct a method that is optimal among all those methods that are accessible to the meta-inductive agent. Thereby, a method, M, is called accessible to a meta-inductive agent, X, if X has information about M’s past successes and about M’s actual prediction (either because M announces its prediction or because X knows M’s prediction algorithm). The methods that are accessible to X are called X’s candidate methods. A set of methods, 𝓜, is called simultaneously accessible to the meta-inductive agent X if X has access to all methods in 𝓜 and can observe and compare their success.

A meta-method that is optimal among all accessible prediction methods is called access-optimal. Can a meta-inductive method be designed that is universally access-optimal, i.e., in every possible environment being at least as good (or possibly better) than every accessible method? This constitutes the leading question of the research program of meta-induction, as developed by Schurz3 [23,57], based on mathematical results in machine learning [64]. As an appetizer, observe that Putnam’s above-mentioned refutation of the optimality of method M holds true only if method M is not a meta-inductive method that has cognitive access to the superior method M*; in the latter case, M will base its predictions on M* and could be equally successful as M. Thus, by restricting optimality to accessible methods, the optimality account may succeed. The restriction to accessible methods implies no epistemic disadvantage because inaccessible methods are irrelevant to the epistemic decision. However, even under this restriction, the question is highly non-trivial, because every meta-inductive method bases its prediction of the next instance on the past success records of the accessible method. This may involve losses because the hitherto best methods may perform badly in the prediction of the next event. These losses have to be kept limited, in order to avoid a breakdown of the idea.

Technically, the meta-inductive account is based on the notion of a prediction game, defined as follows [23] (ch. 5–6):

(6) A prediction game is a pair ((e), 𝓜) consisting of:

(1) An infinite sequence (e): = (e₁, e₂,…) of events e_i, whose possible values are coded by real numbers (possibly rounded) in the interval [0,1]; for example, a sequence of daily weather conditions, stock values, weekly football results, etc.

(2) A finite set of simultaneously accessible prediction methods (or “players”) where 𝓜 = {M₁,…, M_m, MI}. MI represents the meta-inductive method, and the M_i are the candidate methods of MI. They may be computational algorithms, real-life experts or even (purported or real) clairvoyants.

Each prediction game constitutes a possible world. Apart from the above definition, no further assumptions about these possible worlds are made. The sequence of events can be arbitrary; its events may be graded or binary, where binary events are coded by their truth-values of 1 and 0. The finite event frequencies can but need not converge to limits. The class of methods may vary from world to world; even “paranormal” worlds hosting “clairvoyants” are admitted. To avoid an infinite regress of meta-levels, not only independent methods but also other meta-methods are allowed as MI’s candidate methods. MI is assumed to have internal access to some independent “fallback” method that MI uses if no other candidate methods are present.

In each round n of the game, it is the task of each method to deliver a prediction pred_n+1 of the next event (e_n+1) of the sequence. In real-valued prediction games, it is allowed to predict “mixtures” (weighted averages) of events; thus, the value space of possible predictions (Val_pred) may extend the space of possible events (Val_e): Val_e ⊆ Val_pred ⊆ [0,1]. The deviation of the prediction pred_n from the event e_n is measured by a normalized loss function, loss(pred_n,e_n) ∈ [0,1]. The natural (or absolute) loss-function is defined as the absolute distance |pred_n−e_n|. However, the optimality theorem for real-valued prediction games holds for all convex loss functions (meaning that the loss of a weighted average of two predictions is not greater than the weighted average of the losses of two predictions), and the optimality theorem for discrete games holds even for all loss functions (see Section 3). Based on the given loss function, the predictive success of method M is evaluated by the following notions:

-

score(pred_n,e_n) = _def 1 − loss(pred_n,e_n) is the score obtained by prediction, pred_n, measuring the prediction’s closeness to the truth.

-

Suc_n(M) = _def Σ_1≤i≤n score(pred_i(M),e_i) is the absolute success achieved by method M until time n,

-

suc_n(M) = _def Suc_n(M)/n is the success rate of method M at time n, and

-

maxsuc_n is the maximal success rate of all methods at time n.

Object-methods or “independent” methods base their predictions on observed events. The simplest independent methods are OI for linear and OI² for quadratic loss functions (the latter are important for probabilistic predictions). OI predicts the median value of the observed events, which for binary events means that OI predicts e_n+1 = 1 if f_n(e_i = 1) ≥ 0.5, and e_n+1 = 0 otherwise (the “maximum rule”). In contrast, OI² predicts the observed mean value, which for binary events means that OI² predicts the observed frequency. It is well known that for IID sequences, OI maximizes the predictive long-run success for linear and OI² for squared loss functions [23] (sec. 5.9).

Meta-methods or “dependent” methods base their predictions on observations of their candidate methods. Non-inductive meta-methods select or weigh candidate methods independent of their success; one example is authority-based meta-methods. In contrast, meta-inductive methods select or weigh candidate methods in a positive correlation with their past success. The simplest meta-inductive strategy is Imitate-the-best, abbreviated as ITB. This predicts what the presently best non-MI method will predict (resolving ties according to a given ordering of candidate methods). Interestingly, ITB is not universally access-optimal; its success rate can only be optimal if, after some finite time, there is a unique best method that ITB imitates forever [23] (sec. 6.1). 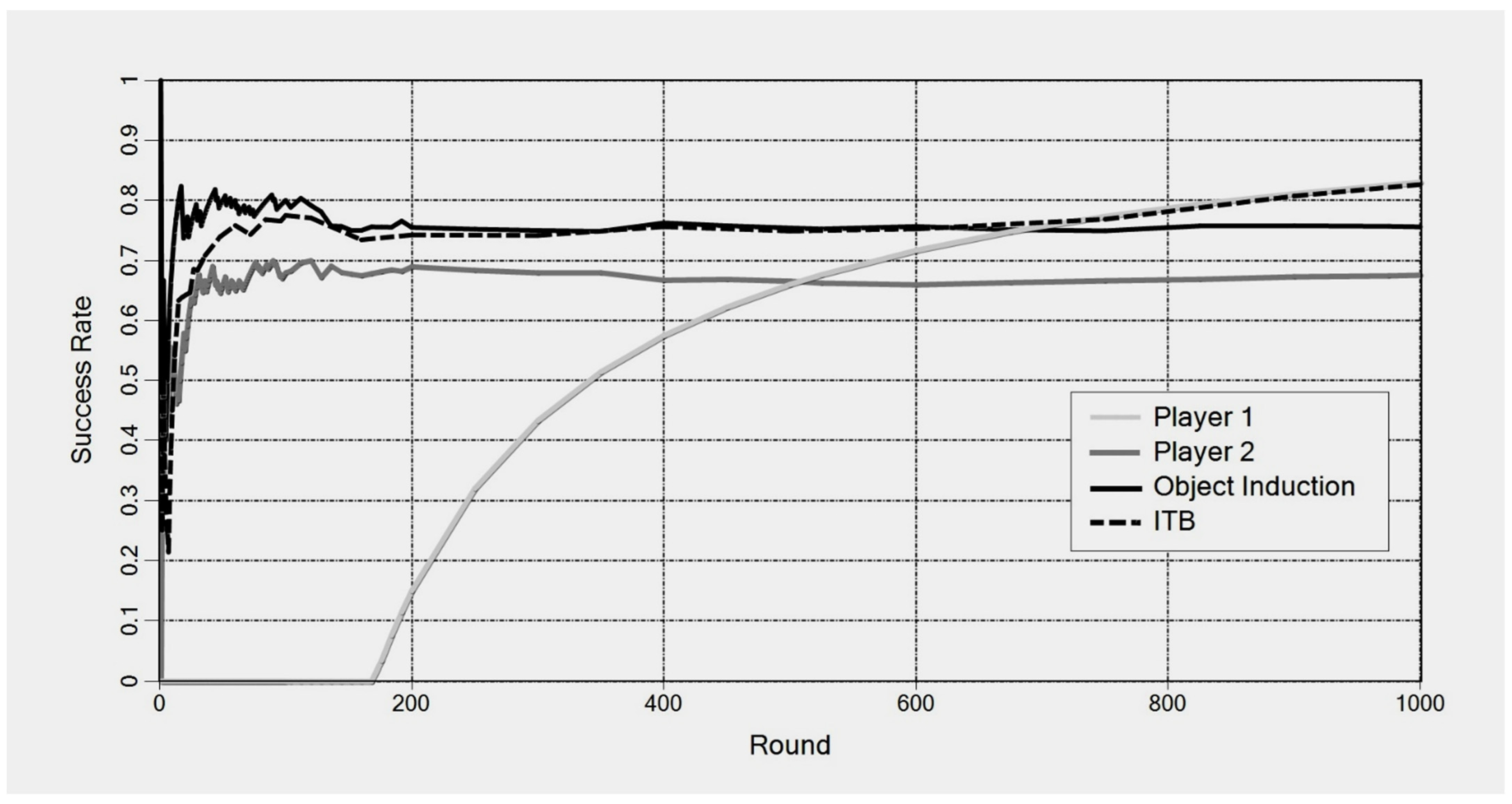Figure 1 shows a computer simulation of such a scenario: ITB always favors the best player and its success rate converges against that of the best method, which is “player 1” after round 170.

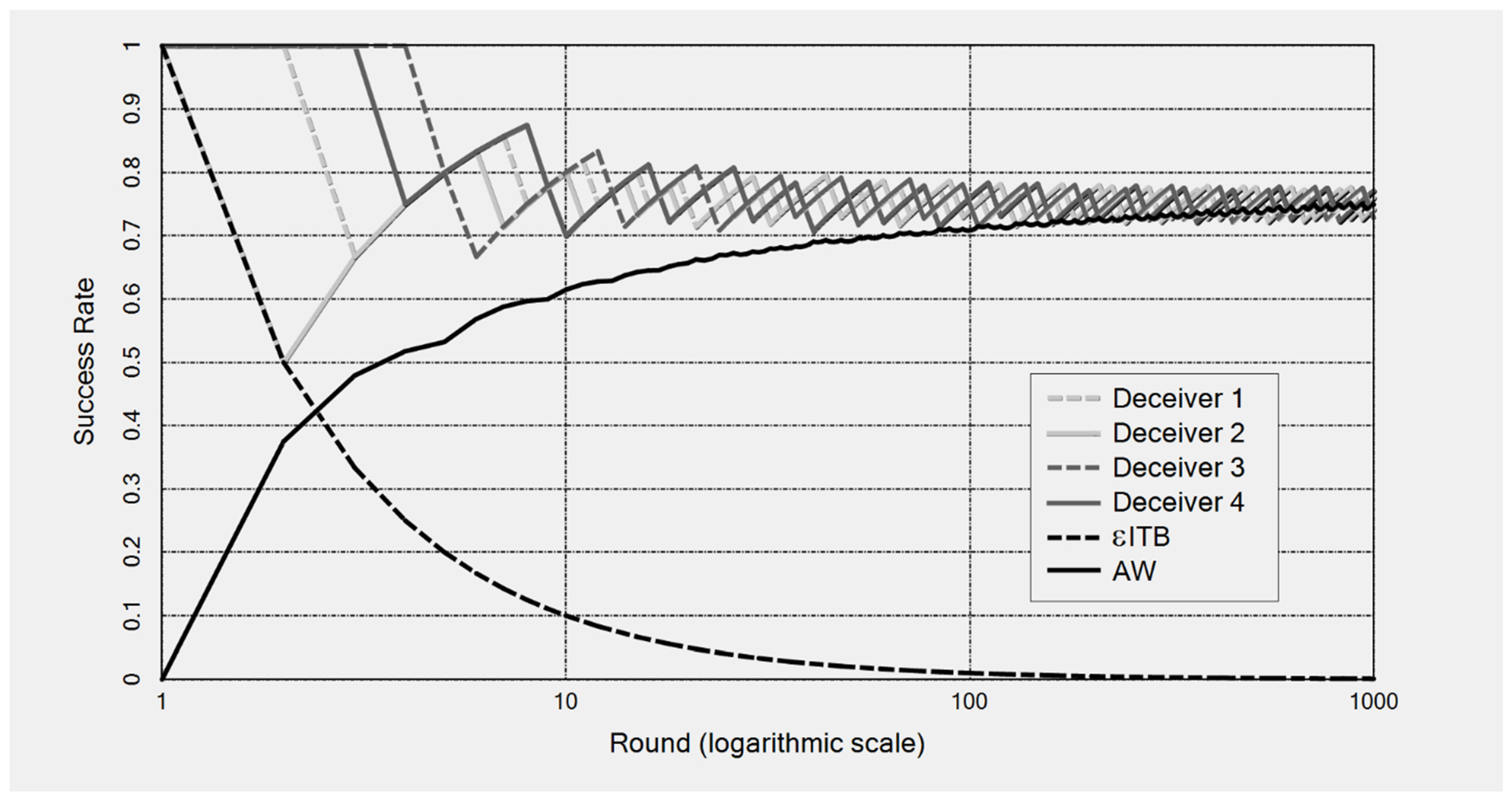
ITB’s optimality breaks down when ITB plays against “deceiving” methods that lower their success rate as soon as their predictions are imitated [57] (sec. 4). A realistic example is the predictions of stock values in a “bubble economy”: here, the prediction that a given stock will yield a high rate of return leads many investors to put their money into that stock, thereby causing it to crash (since the stock lacks sufficient economic support). The susceptibility of ITB to deceptions cannot be prevented by a cautious version, called εITB, that switches to a new favorite only if its success rate exceeds that of the previous favorite by a small value, ε. Figure 2 presents a computer simulation of a prediction game in which εITB tries to imitate four deceiving players (“deceivers”) that oscillate in their success rates with an amplitude of ε = 0.05. εΙΤΒ guesses the first event correctly but then makes wrong predictions forever because each of the four deceivers predicts wrongly if, and only if, they are imitated by εITB. In the resulting simulation, εITB’s success rate is driven to zero, while the deceivers’ mean success rate is 3/4.

Nevertheless, there exists a meta-inductive strategy that can handle deceivers. This strategy is called attractivity-weighted meta-induction, abbreviated as AW. AW predicts a weighted average of the predictions of all accessible methods. The weight of a given method, M, at time n, w_n(M), correlates with M’s attractivity for AW.

(7) Predictions of AW: pred_n+1(AW) = _def $\frac{{\displaystyle {\sum }_{1\le \mathrm{i}\le \mathrm{m}}\mathrm{wn}\left(\mathrm{Mi}\right)\cdot {\mathrm{pred}}_{\mathrm{n}+1}\left({\mathrm{M}}_{\mathrm{i}}\right)}}{{\displaystyle {\sum }_{1\le \mathrm{i}\le \mathrm{m}}{\mathrm{W}}_{\mathrm{n}}\left({\mathrm{M}}_{\mathrm{i}}\right)}}$

(if n = 0 or ${\displaystyle {\sum }_{1\le \mathrm{i}\le \mathrm{m}}{\mathrm{W}}_{\mathrm{n}}\left({\mathrm{M}}_{\mathrm{i}}\right)}$ = 0, AW predicts by its own fallback method).

In Figure 2 above, besides εITB, AW also plays against the four deceiving methods. Apparently, AW does not let itself be deceived, because it never only favors one method but instead takes a weighted average of all four of them, whence it predicts on average equally well as the four methods. In terms of the example of predicting stock values, AW would correspond to the strategy of distributing one’s money over several stocks in the form of a stock portfolio, with cleverly designed weights, instead of putting all the money in the stock that is presently most successful.

The attractivity of method M for AW at a given time, at_n(M), is defined as the surplus success rate of M over AW, i.e., as suc_n(M) − suc_n(AW), which is negative if M performs worse than AW. In machine learning, at_n(M) is also called a regret (from the viewpoint of AW). Based on these attractivities, weight-functions can be defined in different ways that all grant long-run optimality but have different short-run properties [23] (sec. 6.6–6.8). A definition that minimizes the upper bounds of short-run regrets are exponential attractivities: w_n(M) = _def e^{η⋅n⋅at_n(P)}, with η = $\sqrt{8\cdot \ln \left(\mathrm{m}\right)/(\mathrm{n}+1)}$. The following universal optimality theorem for AW has been proved [23] (theorem 6.9, appendix 12.24), based on Cesa-Bianchi and Lugosi [64]:

(8) Theorem: Universal access-optimality of AW:

For every prediction game ((e), {M₁,…,M_m, AW}) with convex loss function:

(i) (Short-run:) (∀n ≥ 1:) suc_n(AW) ≥ maxsuc_n − 1.78⋅$\sqrt{\ln \left(\mathrm{m}\right)/\mathrm{n}}.$

(ii) (Long-run:) suc_n(AW) converges to maxsuc_n as n→∞.

According to theorem (8), attractivity-weighted meta-induction is universally optimal in the long run for arbitrary finite sets of accessible prediction methods. In the short run, weighted meta-induction may suffer from a possible loss (or “regret”), compared to the leading method. As explained, this loss is caused by the fact that AW must base its prediction on the past success rates of the candidate methods. However, theorem (8)(i) states a worst-case upper bound for this loss, which is small if the number of rounds, n, is not fewer than the number of candidate methods, m, and which quickly converges to zero when n grows large. For example, with 10 candidate methods, the worst-case regret after 1000 rounds is $\sqrt{\ln \left(10\right)/1000}$ = 0.0023. Empirical evaluation studies show that the average loss of AW in realistic scenarios is about 5% of this worst-case loss, i.e., 0.00011 [23] (tab. 6.1).

An important feature of attractivity weighting is that AW tends to forget methods that are constantly worse than itself, since exponential weights with negative attractivities quickly converge to zero. This forgetting ability is necessary for AW’s long-run optimality and a crucial distinction of AW compared to success-weighted meta-induction, which uses simple success rates as weights and is provably non-optimal [23] (sec. 6.8.1). In games in which one method dominates its competitors, the weights of the best method will quickly converge to 1 and AW’s behavior will converge to that of ITB.

The optimality result (8) holds in all possible worlds—including random worlds, chaotic worlds without convergent frequencies, “adversarial” event sequences producing the opposite of the prediction of a particular method, worlds hosting clairvoyants, deceivers, etc. Result (8) is still exposed to certain restrictions, namely:

-

The assumption of a fixed finite set of candidate methods;

-

The assumption that predictions can be mixed; and

-

The convexity of the loss function.

In Section 4, we present ways to overcome these restrictions.

The optimality theorem (8) asserts merely the optimality but not the dominance of AW. There exist different variants of attractivity-weighted meta-induction that are equally long-run optimal [23] (sec. 6.6); thus, AW cannot be universally dominant. However, the following restricted dominance theorems have been proved [23] (sec. 8.3.1–8.3.2), where an access-optimal method, M, dominates a method M* if M’s long-run success outperforms that of M* in at least one world:

(9) Theorem: Dominance results for AW:

(a) AW dominates all independent methods and all meta-methods that are not universally access-optimal.

(b) Among others, the following meta-methods are not access-optimal:

(b1) all one-favorite methods (which at each time point imitate the prediction of one accessible method);

(b2) success-based weighting (using success rates as weights); and

(b3) linear regression for a linear loss function.

A final remark: the optimality (and partial dominance) of meta-induction must not be misunderstood as if meta-induction in isolation were the best possible strategy. Without competent candidate methods as well, meta-induction cannot be successful. What the optimality theorem justifies is merely that meta-induction is universally recommendable ceteris paribus, as a strategy applied on top of one’s toolbox of candidate methods. At the same time, it is always reasonable to improve one’s pool of candidate methods, which is, however, no objection against the a priori justification of meta-induction.

3. The A-Posteriori Justification of Object-Induction

The meta-inductive optimality theorem establishes a non-circular justification of attractivity-weighted meta-induction: in all possible worlds, it is reasonable for the epistemic agent, X, to apply the strategy, AW, to all prediction methods accessible to X, since this can only improve but not worsen X’s success in the long run, and the possible short-run regrets are negligible. This justification of meta-induction is analytic and a priori, insofar as it does not make any assumptions about contingent facts. Moreover, the justification is non-circular because it does not rest on any inductive inference or assumption of uniformity.

The given optimality justification is only a justification of meta-induction. By itself, it does not entail the rationality of object-induction. Object-induction cannot be justified a priori: it may well be that we live in a world in which not object-induction but (e.g.,) clairvoyance is predictively superior. In this case, meta-induction would prefer clairvoyance over object-induction. Yet, the a priori justification of meta-induction gives us the following a posteriori justification of object-induction in our hands:

(10) A posteriori justification of object-induction:

Premise 1: So far, object-inductive prediction methods were significantly more successful than all accessible non-inductive prediction methods.

Premise 2: Meta-induction is a priori rational.

Conclusion: Therefore, it is justified, by meta-induction, to continue favoring object-inductive prediction methods in the future.

Different from the rule-circular justification of induction in argument (1) in Section 1.2, argument (10) is not circular, because premise 1 rests on observation and premise 2 has been independently established by mathematical-analytic demonstration.

In summary, our account of the problem of induction proposes a two-step solution: Step 1 consists of the a priori justification of meta-induction, on which step 2 bases an a posteriori justification of object-induction. The latter justification is contingent on and relative to the presently available evidence, which could change over time. This accords with Hume’s insight that superior clairvoyants cannot be logically excluded.

The a posteriori justification of object-induction does not answer the question of which particular method of object-induction should be used for which particular domain (e.g., ITB, multilinear regression, simple or full Bayes estimation, time series analysis). Many scientific debates concern this question. For this purpose, meta-inductive success evaluation is also a highly appropriate tool.

The a posteriori argument not only justifies the prediction of the next instance but also the entire method by which predictions are generated. Our notion of “method” is very broad, covering not only prediction algorithms but also generalization methods, theories, or probability distributions. Therefore, the a posteriori argument also gives us a justification of generalizations, theories and probability distributions. Given that successful probability distributions are weakly inductive, in the sense of satisfying exchangeability and non-dogmatism (recall Section 1.5), meta-induction also justifies these principles.

4. Generalizations of the Optimality Theorem

4.1. Discrete Prediction Games

The events of a real-valued prediction game need not be real-valued; they may also be discrete, for example, binary, coded by 0 or 1. Even in this case, AW’s predictions may be properly real-valued, since AW predicts the weighted averages of 0s and 1s. In contrast, in discrete prediction games, the prediction of mixtures of events is impossible or forbidden. In these games, there is a finite set of possible event values, Val = {v₁…,v_q}, and predictions have to select an event in Val. For example, in a binary game with two methods predicting 0 and 1, respectively, where the first method has a weight of 0.6, AW would predict 0.6 × 0 + 0.4 × 1 = 0.4 but, in a discrete game, the meta-inductivist would have to choose between 0 and 1. Nevertheless, the optimality result (8) can be transferred to discrete games. There are two methods by which this can be done:

(i) Randomization (RAW): the RAW method chooses between predictions of possible event values, according to the following probability distribution: each possible event value is predicted with a probability P_n equaling the sum of the normalized weights of all candidate methods predicting this value (at the given time). The optimality theorem for RAW in discrete prediction games is formulated in terms of RAW’s cumulative expected success rate, abbreviated as $\overline{\mathrm{sucn}}$(RAW), which is the sum of the probabilistically expected scores of RAW until time n, divided by n. The achieved optimality theorem for $\overline{\mathrm{sucn}}$(RAW) has the same upper bounds for short-run regrets as for AW4 [23] (sec. 6.7.1). The advantage of the optimality result for RAW is that it holds for all (not only for convex) loss functions, due to the linearity of probabilistic expectation values. It also has a disadvantage: RAW’s optimality presupposes that RAW’s choice of predicted event values is probabilistically independent of the actual event values (conditional on the past). This excludes “Humean demons” in the form of adversarial event sequences that always produce the opposite of what RAW has predicted. For a solution to Hume’s problem, this restriction is unacceptable. Therefore, Schurz [57] (sec. 8) developed an alternative solution that works without this restriction and is truly access-universal, namely:

(ii) Collective meta-induction (CAW): here, a collective of k meta-inductivists, CAW₁,…, CAW_k, approximates the predictive probabilities of RAW by the frequencies of their discrete predictions as closely as possible. The optimality theorem for CAW is formulated in terms of the actual average success rate of the CAW_i’s, denoted as $\widehat{\mathrm{s}u{c}_n}\left(CAW\right)$. The obtained upper bound for the short-run regret of $\widehat{\mathrm{s}u{c}_n}\left(CAW\right)$ is, again, given by the term 1.78⋅$\sqrt{\ln \left(\mathrm{m}\right)/\mathrm{n}}$ of theorem (8), plus an additional term of $\frac{\mathrm{q}-1}{2\cdot \mathrm{k}}$ that is due to the rounding of RAW’s ideal probabilities by the finite frequencies of k meta-inductivists [65] (theorem 3). The additional regret term can be driven toward zero by increasing the number, k, of CAWs. The approximate access-optimality of $\widehat{\mathrm{s}u{c}_n}\left(CAW\right)$ is universal and holds for arbitrary loss functions. The objection may be raised against this result that it grants access-optimality only for the average success of the collective but not for every individual meta-inductivist. However, if the CAWs cooperate and share their success equally, then every individual CAW earns average success and is guaranteed to be access-optimal. At this point, the game-theoretic requirement of cooperation achieves fundamental importance for a problem of epistemology.

4.2. Action Games

A further important generalization is the application of meta-induction to action games—an application going back to the research about “multi-armed bandits” [66]. Action games are based on a set of possible methods of action and in each round, each method (or “player”) chooses a particular action upon which the environment reacts with a certain “payoff” (score). The payoff function is unknown to the methods and may change dynamically over time. All results about prediction games are transferrable to action games by (i) identifying each choice of action in a given round, with the prediction that the chosen action will yield maximal payoff (among all payoffs yielded by accessible actions), (ii) identifying the maximal payoff with the event (in the given round), and (iii) equating the loss function with (a function of) the difference between the achieved actual payoff and the maximal payoff. As for prediction games, one can define the methods AW, RAW and CAW: AW properly mixes actions (which is possible if those actions involve a continuous parameter), RAW mixes actions probabilistically, and CAW realizes RAW’s probability by action frequencies in the collective. It can be proved that attractivity-weighted meta-induction over possible actions is universally access-optimal, with the same bounds as for prediction games [23] (sec. 7.5).

4.3. Growing Sets of Candidate Methods

A further restriction of theorem (8) is the assumption of a finite and fixed pool of candidate methods. It has been objected that the finiteness restriction is a disadvantage [67]. However, humans are finite cognitive beings who can simultaneously represent and compare only a certain, finite, number of methods. Therefore, the finiteness assumption is justified5. What is problematic, however, is the restriction to a fixed pool of candidate methods. Sterkenburg [59] objected that in real-life situations, new methods may be invented “on the fly” and the set of candidate methods may grow. In reply to this objection, an extension of the optimality theorem has been developed that applies to sets of candidate methods that may grow unboundedly in time. A universal optimality theorem has been proved for unboundedly growing sets of methods, under the mild restriction that the number of accessible methods, m(n), grows less than exponential in time, or formally, lim_n→∞ m(n)/eⁿ = 0 [65] (theorem 4).

4.4. Bayesian Prediction Games

If the circumstances of one’s possible actions are uncertain, it becomes important for maximizing one’s expected utility to predict correct probabilities of those events that make up the possible circumstances, C, of one’s actions. The prediction of probabilities constitutes the topic of probabilistic or Bayesian prediction games. The events of such a game are given by a discrete space. Val = {v₁,…,v_q}. of possible event values, but now. each candidate method predicts a probability distribution over these event values. Therefore. (in spite of the discrete values) Bayesian games are a subcase of real-valued prediction games. Abstractly speaking, each method M_i is identified with a probability function, P_i, over Val and Val’s Cartesian products. For example, if the value space of stock value predictions is {Goes up, Goes down, Stays}, then a Bayesian stock forecaster predicts, for example, “Goes up: 20%, Goes down: 50%, Stays: 30%” for tomorrow’s stock value. Reasonable probabilistic forecasters will conditionalize the predicted probabilities of possible values of the next event on the observed preceding events, P_i(e_n+1 = v_j|e₁,…, e_n) but they may additionally conditionalize them according to method-specific information that is not transparent to the meta-inductivist or to other predictors. The score of a probabilistic prediction is determined in relation to the actual event that occurred and is represented by the truth value, 1. Thus, if the event v_k ∈ Val occurred at time n+1, then only the predicted probability of the event value v_k counts and its distance to 1 determines the loss function6.

It is a well-known fact that linear loss functions (including the natural loss) are not suitable for probabilistic prediction since the success of predicting a binary event is maximized if the event probabilities are rounded to 1 or 0 (according to the method OI mentioned in Section 2). So, if probabilistic forecasters were rewarded by a linear scoring function, they would not be incentivized to predict their actual degrees of beliefs, but their roundings would be to 0 or 1. Therefore, non-linear scoring functions have been devised, having the property that the expected success of real-valued predictions in IID (or Markov) sequences is maximal exactly if the forecasters predict their event probabilities. Scoring and loss functions having this property are called proper. For binary events, the expected loss of predicting a real value, r, under the probability function P is given as E(loss(R)) = _def P(v = 1)⋅loss(r,1) + P(v = 0)⋅loss(r,0). If the loss function is proper, this function becomes minimal exactly if r equals P(v = 1). According to a famous result of Brier [68], the quadratic loss function, loss(r,e) = (r − e)², constitutes a proper scoring rule. Another proper loss function is the logarithmic one [59]. However, we do not think that proper loss functions are generally preferable, as some philosophers have argued; we consider their advantages as being confined to probabilistic predictions [69] (p. 113).

The probabilistic meta-inductivist, P_AW, computes its probability function as the attractivity-weighted average of the P_i,ns as defined in (7), or formally: P_AW,n(e_n+1 = v_k|e₁,…,e_n) = _def Σ_1≤i≤mw_n(P_i)⋅P_i,n(e_n+1 = v_k |e₁,…,e_n). It follows from theorem (8) that AW’s degrees of belief are universally long-run optimal, with tight short-run regrets converging quickly to zero. Since the weighted averages of probability functions are again probability functions, meta-induction over Bayesian forecasters provides a strategy of optimal probability aggregation that can be employed as a method of establishing group opinions. Moreover, meta-inductive probability aggregation offers a new solution to the Bayesian problem of selecting an appropriate prior distribution. As we know from Section 1.5, Bayesian convergence fails if one does not restrict the class of admissible priors to those that prefer simple over complex states of the world. In contrast, it is unproblematic to include into one’s candidate set induction-hostile prior distributions (recall theorem (5) in Section 1.5); yet, meta-inductive probability aggregation works and will produce an optimal meta-inductive distribution, P_AW. If the event sequence is induction-friendly, then, with increasing amounts of evidence, P_AW will assign almost all weight to induction-friendly priors and forget the induction-hostile priors.

5. Conclusions: The Impact of Meta-Induction

The immediate impact of meta-induction for epistemology and the philosophy of science consists in proposing a novel solution to the problem of induction, based on the method of optimality justifications; a method that seems to work and can stop justificational regress. Optimality justifications have been further generalized to the domain of theory-generating abductions [70] and the domain of logic [71]. The method of optimality justification promises to supply new foundations for foundation-theoretic epistemology (I prefer “foundation-theoretic” over “foundationalist” because it avoids negative connotations). Foundation-theoretic epistemology was born in the philosophical era of Enlightenment in the 16th century. It is based on the idea that, in order to reach knowledge, we should not legitimize our beliefs by external authorities but justify them by reason—by means of a system of arguments through which all our beliefs can be soundly derived from a small class of basic beliefs and principles that are immediately evident to everyone. The foundation-theoretic program of epistemology came increasingly under attack through the development of philosophical (post)modernity following the Enlightenment era. The major challenge of foundation theory was the problem of finding a means to stop the justificational regress, resulting from the supposed necessity to base each justification upon premises that are themselves in need of justification—which must either lead into a circle or into an infinite regress of reasons.

Alternative epistemologies have been developed, such as coherentism, externalism and common-senseism (or dogmatism), the major motivation of which is based on the supposition that the regress problem is unsolvable and the foundation-theoretic program is illusory. Coherentism allows circular justifications, which makes justifications easy; however, as we have seen in Section 1.2, circular justifications lead to epistemological relativism because they make it possible to justify opposite beliefs. Externalism identifies justifiedness with reliability “by definition”; this avoids the regress problem but makes justifications cognitively inaccessible and deprives externalism from ameliorative applications. Common-senseism and dogmatism assume non-evident principles as given, which stops the justificational regress but makes this epistemology susceptible of relapsing to pre-Enlightenment forms of belief stabilization, based on authority. The dissatisfying consequences of these alternative positions may be endurable if one assumes that a solution to the regress problem is impossible. However, given that the regress problem is solvable, and the foundation-theoretic program works, these disadvantages can be avoided and these alternative accounts lose their motivation.

Beyond its general impact on epistemology and the philosophy of science, the meta-inductive optimality program has fruitful applications in neighboring disciplines such as Bayesian probability theory (as worked out in Section 4.4), cognitive science, social epistemology and cultural evolution theory. In cognitive science, the success rate of prediction methods is tested by means of computer and real-life experiments, in the form of prediction tournaments. It has turned out that the success records of most methods are highly sensitive to the “environment” within which they are applied. This insight led to the approach of ecological (or adaptive) rationality [72]. It has been found that in environments that are less induction-friendly, simpler prediction methods can yield equally good or sometimes even better results than complex prediction methods, for the reason that the latter ones are “overfitting”, which means that they adapt themselves to random accidentalities of the sample [73] (pp. 36, 44f.), [74]. However, in real-life applications (e.g., predictions of the stock market) the “environment” that one is in is typically unknown. Thus, one does not know which of the “locally adapted” methods one should apply—a problem that has been called the “revenge of ecological rationality” [75]. Meta-induction, when applied to a toolbox of locally adapted methods, offers an ideal solution to this problem because it grants access-optimality without presupposing information about the environment one is in. The success of meta-induction has been confirmed in a series of experiments [61].

Meta-induction can also be employed as a method of social learning, i.e., learning from other persons, based on their success records. In this interpretation, meta-induction becomes fruitful for problems in social epistemology and the theory of cultural evolution. Social learning should not be based on unreflected or untested authority but instead on the track records of one’s informants, by applying the method of meta-induction. The well-known problem therein is that, in an information society with a high division of epistemic labor, the track records of most informants or experts are unknown. However, at least in one’s local “epistemic community”, it can be assumed that track records are accessible. Based on the computer simulations of Paul Thorn, it has been shown that local meta-induction over small epistemic neighborhoods is sufficient to produce global propagation and the spreading of reliable information in the entire society, even if reliable information was initially rare, provided only that the local epistemic neighborhoods are overlapping [23] (sec. 10.2), [76]. The same simulations show that success-independent methods of social learning, such as blind authority-imitation or peer-aggregation, are not able to propagate reliable information.

Last but not least, social learning is the basis of cultural evolution. As remarked at the end of Section 3, meta-inductive learning is optimal only in the ceteris paribus sense: one should always choose one’s ultimate methods of prediction or action by meta-induction, but this is not the only thing needed to be successful; at the same time, one should constantly try to improve one’s pool of independent methods that are the input of meta-inductive learning. In the context of cultural evolution, this means that social learning can only be advantageous for a society if there are enough individual learners in the society who search for new and possibly more successful methods of prediction or action, at the risk of higher costs for themselves. Since society can profit by imitating those individual learners who were successful, individual learners that pass on their knowledge will play the role of “altruists” in epistemic game theory. Based on a simulation study by Rendell et al. [77], it can be argued that an optimally mixed society consists of a small percentage (10–20%) of individual learners and a majority of social learners [23] (sec. 10.3).