Abstract
The game of Go was the last great challenge for artificial intelligence in abstract board games. AlphaGo was the first system to reach supremacy, and subsequent implementations further improved the state of the art. As in chess, the fall of the human world champion did not lead to the end of the game. Now, we have renewed interest in the game due to new questions that emerged in this development. How far are we from perfect play? Can humans catch up? How compressible is Go knowledge? What is the computational complexity of a perfect player? How much energy is really needed to play the game optimally? Here, we investigate these and related questions with respect to the special properties of Go (meaningful draws and extreme combinatorial complexity). Since traditional board games have an important role in human culture, our analysis is relevant in a broader context. What happens in the game world could forecast our relationship with AI entities, their explainability, and usefulness.
1. Introduction
Humans have been playing the game of Go for thousands of years, and will continue to play it for long time, since it remains entertaining and educational. It is a way of self-development: while we progress our understanding of the game, we also learn something about ourselves. In this sense, the game is surely not over yet. The appearance of superhuman Go AI engines changed several things, but we still have many reasons to play. This might hold until the widespread use of direct brain to digital computer neural interfaces, at which point the question of whether humans want to play the game or not becomes meaningless.
Here, we investigate the more technical problem of assessing the possibility and feasibility of human players catching up with the AI engines. We do not have a hidden agenda of finding proof for human superiority; we simply go through the logical possibilities which may be overshadowed by the stunning success of deep reinforcement learning methods. We think that Go as a game is deep enough that we still have some interesting twists and turns ahead of us. We are also convinced that the way we use and relate to AI tools in Go can become a formative example for our future society.
This paper has the following structure. First, we briefly introduce the game itself; then, we summarize the three milestones in the development of Go AIs. This historical overview takes us to the present, where we examine how superhuman AIs are used in the Go community. This is followed by an analysis on the AIs’ impact on human players. The investigation prompts the central question: How much can humans improve? Can we catch up with the AI players? The logical possibility depends on the distance of the superhuman AI engines from perfect play. Indirect, circumstantial evidence is sought after for the proximity of perfect play by an empirical study in the next section, where we produce game records of handcrafted AI self-plays. This investigation then leads us to the question: How compressible is Go knowledge? Finally, we conclude our investigation with a positive outlook, based on the new possibilities we now have for improving our understanding of the game.
2. The Idea of Go
Go is a two-person perfect-information game with no random factor. It is played on a grid with black and white stones, with the players taking turns to place one stone at a time on an empty intersection of the grid. Originally, the goal might have been simply to have more stones of one’s color on the board than the opponent [1] (Appendix B). Stones fully surrounded (that have no empty neighboring intersections) are captured and removed from the board. This is one possible way of getting to place more stones on the board than the opponent, but the more common method is to surround parts of the board with one’s stones, making it impossible for the opponent to enter. Therefore, Go is often defined as the game of surrounding territory. The same whole-board position cannot be repeated (ko rule), so games are guaranteed to finish in finite time. Although the stones do not move, the game is very dynamic: any played stone can tip the balance of the forces on the board.
It is interesting that, while the core concept of the game is clear, many interpretations of Go rulesets and scoring methods exist. The winner can be determined by either counting the number of stones, or the sum of a player’s stones and the empty intersections they surround, or the sum of the stones a player has captured and the empty intersections their stones surround. While these scoring methods are considerably different, they describe the same game and (with a few exceptions) lead to the same result. The first of these methods is no longer widely in use, but the second method is implemented in the Chinese rules and the third method in the Japanese rules of Go.
Komi
There is one aspect of the differences in rulesets crucial to our discussion. The komi is a compensation given to White for not making the first move. Since the objective of the game is to get more stones on the board than the opponent, it is clear that the player who goes first has an advantage. However, the need for komi was not recognized until the 20th century. Before that, Black’s first-move advantage was considered a feature of the game, and the game was made fair by having the players play several games against each other, alternating colors [2]. Komi was gradually instated in tournament Go when it became necessary to more quickly tell the winner of a match-up in a fair fashion. Values of the komi have historically varied from 2.5 points to 8 points, with 7.5 points under Chinese rules and 6.5 points under Japanese rules being the currently used values.
The komi shows that ultimately we want to define Go as a game in which perfect play gives a draw. In practice, komi is usually not set to an integer value to prevent tied games: this is more about game management and tournament organization than the nature of the game.
3. Go AI Short History
The development of AIs in Go went through three phases. The first one was dominated by explicitly coding human expertise, the second one by random sampling of games, and now we have deep reinforcement learning.
3.1. Programming Human Expertise
Due to the high branching factor of the game tree of Go, using classical AI search is not feasible; it only works for solving local tactical problems [3,4]. Instead of a tree search, direct coding of high-level human expertise was applied first [5]. GnuGo is the culmination of this approach; we mention two of its components. It uses pattern matching to select good moves with the help of a database of useful patterns. These encode tactical ideas (see Figure 1) in a convenient human-readable and editable format. Whenever a tactical mistake was found, a corresponding pattern was added, attempting to strengthen the engine. This led to a common problem in knowledge-based systems, colloquially referred as the knowledge acquisition bottleneck. The strict rules represented in the patterns start to interact in unpredictable ways and make the engine play weaker than before. Furthermore, it is difficult to prepare patterns that work for all situations; Figure 2 shows two examples of a pattern gone wrong. For strategic decisions, an influence function is used, which is similar to calculating the strength of some force field radiated by groups of stones—a mathematical characterization of an intuitive idea.
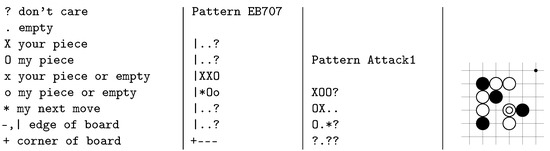
Figure 1.
Patterns in GnuGo are stored in text files. These are two examples with explanation on the left. The first example is about blocking a possible incursion. The second is a standard tactical move, a net. The configuration on the right is a possible match for the second pattern.
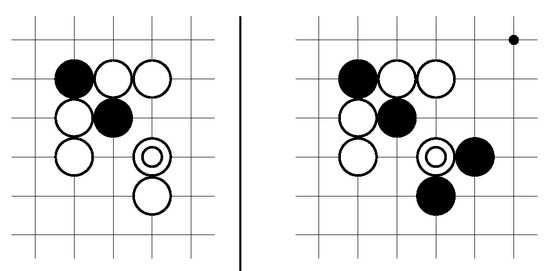
Figure 2.
White’s play in this figure follows Pattern Attack1 in Figure 1. However, in the first diagram, White’s move is unnecessary and inefficient, and, in the second diagram, the move does not work because of the combined effect of Black’s stones below and to the right. These two examples showcase one of the main challenges in preprogramming Go patterns into an AI.
3.2. Monte Carlo Methods
In problems where we cannot examine all possibilities, random sampling can give us an approximate, ‘good enough’ solution. In Go, the toughest problem is positional judgement. Given a board position, can we tell who is ahead? Can we compute the probability of winning? By the elementary definition of probability, we could do an empirical experiment for finding the winning chances. We can imagine gathering many human players, pairing them according to their rankings, and letting them continue play from the position in question. We then record the wins and losses for a player, and their ratio will tell us the winning probabilities for both sides. However, it turned out that we do not even need the clever human players: it is enough to just have random plays. The computer can make legal moves with little computation. Consequently, it can quickly play a large number of random games from any board position. This is an example of a Monte Carlo simulation.
The Monte Carlo methods in Go did not shock the Go community. They did not get an AI to the professional level even when it was combined with the tree search, so not many people took notice. However, we argue that even the somewhat limited success is really surprising from the human perspective. The computer appears to play cleverly, playing at a strong amateur level [6]. It can also read life-and-death positions correctly, although it may need the help of an opening pattern dictionary. However, looking under the hood reveals something rather silly: the engine spends most of its time playing random moves, akin to the proverbial monkeys banging on a typewriter, eventually producing the works of Shakespeare. Except that, in the case of board position evaluation, the randomized method does work. This is different from what many would consider intelligent activity—but how different is it, really? Advances in cognitive neuroscience actually suggest a similar picture for the brain: “neurons not only tolerate noise but even amplify it—probably because some degree of randomness is helpful in many situations where we search for an optimal solution to a complex problem.” [7].
3.3. Deep Reinforcement Learning
The breakthrough of AG was due to a well-engineered blend of several ideas, most notably the combination of learning algorithms with neural networks.
Explicitly coding human expertise fails on two accounts. On the one hand, we do not know exactly how we play the game. It is difficult to verbalize our Go knowledge. Explanations for a move often get replaced by an ‘it felt right’ statement. On the other hand, there is the knowledge acquisition bottleneck problem. Even if we can formalize explicit rules, they grow in number and they start contradicting each other in some board positions. The solution is to let the computer learn from data, guided by a reward signal (wins in board games). Reinforcement learning [8] has become the main method in artificial intelligence for solving complex problems.
The second idea is using a deep neural network. Modeled after our visual information processing, convolutional neural networks produce more and more abstract representations of their inputs. In Go, the board position is treated as a bitmap image, and as in image processing, where we apply filters for detecting features of the images (e.g., edges), successive layers of neurons work with higher level representations of the position. The output of the network is a probability distribution of the suggested moves, which can also serve as an evaluation of the board position. Neural networks without search can already be very strong, but combined with a Monte Carlo tree search they can reach superhuman level.
Why does deep learning work? When we contemplate the hill-climbing algorithms, it seems unavoidable to get stuck at some local maximum. However, this intuition comes from low-dimensional thinking. We already have problems seeing the Klein-bottle as it really is without intersecting itself. The search space of neural networks, however, has millions of dimensions, and so there is always some dimension to move away from a local maximum.
4. Using AIs
The grand challenge of AI as a research field was to produce a Go-playing program that can beat the best human player. What is the next step? We now have a variety of Go engines at that level. What can we do with them?
4.1. Playing against AIs
Before AG, beginners of the game were advised not to play too much against AIs, as they often made strange and inefficient moves, possibly causing humans to learn bad habits. Currently, we have the same advice for a different reason. It is hopeless and frustrating to play against an AI, since it is practically impossible to win. To help this, we can:
- Play handicap games: One of the best features of Go is its natural handicap system that works by allowing Black to place extra stones on the board in the beginning.
- Limit the AIs: There are numerous attempts to tweak AI engines to play weaker, or one can also play an earlier network. Both of these methods may suffer from the problem of the AIs making strange, unreasonable moves.
4.2. Analysis
Modern AIs are not very suitable as sparring partners, but they are useful as analysis tools. Learning from one’s mistakes is one of the best ways for improving. Reviewing games is the recommended method for developing playing skills, but how can we identify our mistakes? How can we find the alternative, better variations? The AIs’ analysis tools solve this problem, giving a probability distribution of good moves and their evaluations. One can easily compare the game move with the predicted good moves. When the difference between the game move and the AI move is big, a mistake is found.
The AI’s principal variation (the most advantageous sequence of play) can give information about a better way of playing, but how much a human can infer from it depends on the player. An AI cannot explain why it plays its moves beyond giving an estimated winning probability and possibly a score estimation, but humans cannot generate these numbers on their own. The AI’s output is generally the most useful for a human if the AI’s idea was originally conceivable for the human, but depends on an important key move or realization later in the sequence to truly work. More often, however, an AI chooses its moves by its superior whole-board judgement, which is difficult to explain in human terms.
What can strong players learn from analyzing their games against the AI? A primary obstacle may be that the human moves are good, but the AI’s moves are simply just a little bit better each time. If this difference is caused by the AI’s moves being better in a complicated whole-board context, there may be no way for the human to infer new knowledge from the AI’s suggestions. Thereby, the reward signal is not useful, the end result of a game is always a loss, and the individual moves are not bad either—they are just slightly less good than the AI’s.
One way for a human to start circumventing this problem is to learn and memorize long sequences that have been shown to be fair in a local context, and to learn how to match a particular sequence for a particular whole-board position. This way, by playing prestudied sequences, a player can effectively reduce the number of loss-making exchanges, improving their result against the AI. However, it can be argued that this way a player is ‘playing the opponent, rather than the game’; a single deviation from the pattern by the opponent would leave the player unsure of what to play next.
Generally, Go players are the most interested in analyzing games that they lost. After winning a game, the Dunning–Kruger effect [9] and the confirmation bias join hands to make a player think that everything went according to plan, and that there is nothing more to learn from the game. However, examining won games in detail is often revealing, and sometimes even shocking: in the majority of games, the case is that the player made a lot of mistakes, and simply won due to more mistakes by the opponent. This finding follows the traditional wisdom of Go teachers that there is a lot to learn from every game.
5. Impact
A game as a cultural phenomenon is a dynamical entity. The rules may remain the same, but how the game appears in society is constantly changing. Who are the players and what motivates them to play? What collective knowledge do they have about the game? The appearance of superhuman AI engines is a large perturbation in this development.
5.1. Shifting View of Strong Play
How is the perception of strong play changing? Note that we are not defining strong play here, but the perception of it. We contrast two polarized views that span the spectrum of different ways of thinking about playing strength.
The traditional view of skill in board games is defined by a player having a flash of insight, an unexpected idea to turn the game for the better. This can be labeled as the ‘romantic genius’ viewpoint, where the player’s innate talent and the inspiration create something new and admirable on the spot. In a sublimated form, this is still with us. For instance, probably the most famous played game of Go, the Ear-reddening game (played in 1846), is remembered by Black’s move 127, an exceptional move in the center of the board that caused White’s ears to flush red [2]. As a more recent example, in the Hikaru No Go comic and animation series [10], the ‘divine move’ is sought after by the top players.
As the quality of preparation for games improves and accumulated wisdom expands, there is less room for this out-of-the-blue type of creativity. Computer programs further accelerated this natural progress. Therefore, the current viewpoint of strong play is rather different. It is the ability of not making mistakes, just exploiting the faults in the opponent’s play, no matter how small. ‘You can’t win a game unless the opponent makes a mistake. The trick is in creating a position where there is more opportunity for the opponent to go wrong.’ [11]. Stated even more succinctly: You cannot win a game, but you can wait for the opponent to lose it. Solid, sustained performance became the indicator of strong play. Deep learning AIs excel in faultless play so much that measuring consistency of the performance of a player move by move is a way to detect possible cheating in online play [12].
5.2. Social Changes
How do the changes ushered by the appearance of superhuman AIs affect players? Big media events, such as the historical AG vs. Lee Sedol match in 2016, can have big emotional impacts either way, but they do not change the everyday life of the Go community. On the contrary, the subsequent development is revolutionary: the technology became widely available and accessible. AG was never released as a software package, but the published papers [13,14,15] contain enough information to reimplement the engine. Open-source projects with distributed training (the computation-intensive, but embarrassingly parallel self-plays) could reproduce the results [16,17]. By themselves, they had limited impact. These software packages required software engineering expertise to install on computers. Therefore, other open-source projects concentrated on user interfaces and usability. The graphical analysis tools became widely available, even on mobile devices or simply on the web. They display realtime information about the engine’s ‘thinking’ process (e.g., win rate, estimated score lead, etc.) both numerically and visually integrated in the board view.
As a first-hand experience, we describe how teaching changed recently in an integrated AI/Mathematics university course. In early 2019, students could see a demonstration of an AI game analysis, prepared by the instructor on a single dedicated computer. A year later, most student games were routinely analyzed by an AI. Less than a year later, in the second half of 2020, immediate AI analysis has been built into the game server (OGS) used for the course. In short, superhuman Go knowledge became accessible by everyone in our current information society.
There are many ways a human being can be engaged with the game of Go, and they can have many different motivations for playing. Keeping this in mind, we try to identify two basic profiles: the player and the scholar of the game:
- player: somebody who enjoys the competition and is motivated by winning games and climbing the ranking ladder; and
- scholar: somebody who enjoys the game as an intellectual challenge, derives pleasure from the game content and learning itself and not directly from the fact of winning.
By this dichotomy, it is clear that no pure players or scholars exist; everyone familiar with the game has a dynamically changing blend of these two extremes. Go as a sport fits into the player profile, while Go as art and science can be associated with the scholar’s view. The reason we describe these profiles is that the changes induced by AIs affect the profiles differently.
Top players may experience the sense of a lost mission, since ’becoming the best’ has become impossible. This sentiment may not be shared by the whole community, since most players are used to the existence of better players. However, with the wide availability of strong Go programs, cheating has become rampant in the online Go world, affecting negatively many of the players who play Go for the exciting matches against other human players [12].
Scholars of the game benefit more clearly from the existence of good AI engines, as the computer can just ‘tell the truth’ about a debated board position. Previously, players would have to pay for teaching to get the same effect, but now it is enough to simply have a strong computer—or, in fact, even just a modern smartphone. Consequently, many Go teachers are now facing the danger of losing their jobs, even though they can still provide a big value that AIs cannot: they can explain why particular moves are good or bad.
6. Can Humans Catch Up?
At the moment, the almost unanimous answer is no. The succession of AG, AGZ, and AZ was so quick and impressive that it left no room for doubt. Some might tentatively mention the possible ‘delusions’ that the modern AIs may still have. Due to the statistical process inside, they might get a position’s evaluation wrong, as happened in the fourth game of the AG vs. Lee Sedol match. However, these are specific to particular networks, and they do not appear deterministically. Another possibility is that the deep learning AIs might be plateauing as the pure Monte-Carlo engines did, albeit at a higher level.
If the AIs are not at perfect play, then by definition there are counterstrategies. We also do not have evidence for humans reaching their limit. The development of mathematics shows that concepts that were extremely difficult to grasp in the beginning (e.g., complex numbers) are now easy textbook material. It is imaginable that our knowledge about the game will advance by similar conceptual leaps. Understanding the output of current AIs could be the key to that development. For that purpose, we can compare our studying method to the AIs’ learning algorithms.
6.1. Human versus AI Learning
How do we learn? How long does it take? Who do we learn from? What does AG do? The technical details are precisely described [13,14,15], but they do not sufficiently answer the question on a conceptual level. Here is one way to think about it: Go knowledge is not given by a few strict rules, but a large set of mini skills [18] that are not too easy to express verbally. Making these skills more explicit and explainable is very much the process of becoming a professional player. A human player learns these skills from their masters, from historical game records, and from their own games. It takes a long time to build up expertise, and every player has a unique selection, a subset of all available mini skills. AG does the same: it learns from existing game records. It goes through games of strong players and remembers the good ideas. Not the moves directly, since the exact same board position has a near-zero probability of occurring again, but the statistical patterns of good moves. There are clear differences between actual implementations of this learning process. The brain learns by forming and adjusting connections between neurons. AG learns by updating numerical values in a large table. Why is AG stronger? It learns more quickly, therefore it can acquire more of the mini skills in a short amount of time. AG can be understood as a search engine that has access to all previous knowledge, not with a rigid, but with a flexible, statistical pattern matching. In effect, playing against AG is playing against many strong players at the same time, while a human player has a more limited collection of master players to learn from. If the human player could go through all the 30,000,000 positions AG learned from [19], could we expect the same kind of performance from the human as well? This is not possible simply due to the lifespan of a human being and due to personal and social constraints. However, where the upper knowledge limit of the human brain lies is an interesting open question.
Another advantage the AI engines enjoy is that they do not need other players to learn from: self-plays are sufficient. They were used in AG, but AGZ took it to the next step, not learning from expert games at all. For humans, self-play seems psychologically impossible: one example is from the novel by Zweig [20], and the story ends badly. Chess and Go teachers almost invariably advise against playing against oneself, but for example Bobby Fischer, who played himself as a child [21], is an exception to the rule.
On the other hand, human players have a big advantage: the ability to reason about causes and effects, as opposed to the model-blind, purely associative deep learning systems [22]. Is it possible to improve our planning skills when we have access to high-quality statistical patterns as board-position-to-good-move associations? With planning, we can group together moves that help in achieving the same goal. It is unclear whether some representations of plans are present in deep learning AIs. They take the board position as an input image, and the subsequent layers of the neural networks produce more and more abstract representations of the configuration of the stones. What are these abstract representations? This is still a research question, but it is unlikely that they correspond to plans. This is suggested by top human players’ reports that playing with AIs does not create an experience of a ‘dialogue’, which usually results from the players fitting and executing their plans against each other. In any case, the crucial question is the compressibility of Go knowledge. Is it possible to have higher-level representations of the ideas and mini skills, or is the large list of the weights of neural connections the ultimate way of describing playing skills?
Let us examine what happens if we postulate the impossibility of humans catching up with the current deep learning AIs. Turning the logic around, that entails that humans reached their limits. More precisely, this means either that human cleverness, i.e., using high-level rules in an efficient and flexible manner, has an inherent limitation or that Go knowledge is not compressible.
6.2. Taboos and Dogmas
In its learning process, AGZ recreated and then surpassed human knowledge [14]. It is humbling that a simple learning algorithm with enough computational power found the same pieces of knowledge that many humans produced collectively during the history of the game. It is also reassuring to find that humans did things right up to a certain point.
It appears now that knowledge generation and transmission have constraints in human culture. Before AG and AGZ, we all agreed on some principles that turned out not to be universally valid. They were passed on from masters to newer generations of players, and no one had the playing strength and perseverance to prove them wrong. The new AIs broke some taboos, making us face our dogmatic way of thinking. Starting from the famous Move 37, the AG Master series made this increasingly obvious. Figure 3 shows a couple of examples.
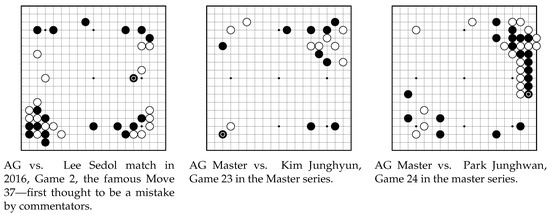
Figure 3.
Shoulder hit on the 5th line goes against the previous wisdom of the balance of the 3rd (secures territory) and 4th line (creates influence). Early 3-3 invasion was considered to be a weak move, until strong AIs started to play it earlier and earlier (now as early as the 2nd move). Crawling on the second line again contradicts the idea of 3rd–4th line balance, but in this example it worked very well.
Did the AIs free us from dogmatic thinking? Certainly, now people are willing to try more ideas. However, there is an increasing tendency of mimicking AI moves without properly understanding them. This is probably just a newer version of dogmatic thinking.
7. Perfection: Mathematical and Relative
The ultimate goal for a player is being invincible in the game, i.e., being maximally efficient and error-free. This is the final endpoint of the learning process. In Go, perfection is theoretically possible, but it is unclear whether it is realizable or not.
7.1. Solved Games
There is a negative relationship between the complexity of a game and human interest. If it is easy to solve, it does not hold human interest for long. For example, tic-tac-toe can amuse small children, but only until they find the optimal strategy. Roughly speaking, there are the small games we can solve, and the big games we cannot and which we therefore are fascinated by. Checkers is in the intersection of solved and interesting games [11].
People sometimes refer to AG with the phrase of Go being solved. This is not correct, since creating a superhuman Go playing entity is not the same as mathematically solving the game. To be precise, there are different levels of a game being solved [23]:
- Ultra-weakly solved: The result of perfect play is known, but not the strategy. For example Hex, where a simple mathematical proof shows that the first player wins, but we do not know how to achieve that result.
- Weakly solved: Perfect result and strategy are known from the starting position. Checkers is solved this way; therefore, there are still positions for which we do not know the perfect result.
- Strongly solved: For all legal board positions, we know the perfect result and we can demonstrate a sequences of moves leading to that.
Solving Go was possible only for small boards, up to 30 intersections [24,25]. Figure 4 shows what it means to be solved in Go: we can see the best available result for each opening move. We also know that to balance the game we need to choose komi to be 25 (assuming area scoring). Beyond these small boards, solving Go becomes hopeless. The game’s combinatorial complexity is prohibitively high [26]. Moreover, Go is a constructing game. In checkers and chess, the board position eventually evolves into well-known and solved endgame positions, simply due to the reduced number of pieces. In Go, we end up in unique board positions that are crystallized summaries of the game moves.

Figure 4.
Best available results on the board for the first move of Black [24], assuming area scoring. Color indicates winner and the number is the score lead.
Perfect games are paths in the game tree where every branching (every move) leads to a maximal possible score. In other words, none of the players make a mistake. If we have the full game tree, the standard minimax algorithm can find these paths [27].
Having access to the complete game tree would allow us to answer questions that mathematicians like to ask. What is the length of the shortest perfect game(s)? How about the longest? Is there a perfect game without a capture? What is the maximum number of captures in a perfect game? In high-level play, there is no need to play capturing races out, since both players can see the end result; thus, an invisible threat guides their moves. In beginner games, on the other hand, it is often an issue that the players run out of stones due to the high number of captures and recaptures. However, we cannot conclude that perfect games should not have captures, as in superhuman AI self-plays we often see large groups given up if there is a big enough compensation. The AIs do not show the same type attachment to territories already staked out or to established groups as humans do [28]. Extensive ko fights also generate a large number of captured stones.
The combinatorial complexity of the game prohibits us from having answers to these questions with a brute-force method. How far are the current Go engines from perfect play? There are some indirect ways to measure that distance, e.g., the added value of the tree search to the raw output of the policy network [12]. The current AIs are certainly not at perfect play yet, as omniscient neural networks would have only three distinct output win rate probabilities of 0%, 50%, and 100% for all board positions. Talking in terms of probabilities other than these three values is admitting ignorance.
7.2. Relative Perfection
A game can be perfect relative to a playing entity: the entity chooses all the moves to its best knowledge. Does such a balanced self-play lead to a draw? Assuming that the ultimate result in perfect Go is a draw, this can separate engines into two groups: ones that produce draws and ones that do not. Alternatively, this criterion can classify them along a spectrum by the probability of producing draws. Logically, if we have perfect play, then we get draws. If we get draws, perfect play is not guaranteed, but not getting draws guarantees suboptimal play. We produced handcrafted AI self-plays, i.e., we used engines to do continuous analysis and chose the next move manually when a clear choice emerged. Although relative perfection is not easy to define precisely, we used the following conditions in the experiments.
- Winning chances are balanced in the beginning, as close to 50% as possible. This is achieved by evaluating the empty board adjusting komi to a suitable integer value.
- The game has to end in a draw (for a given ruleset).
- At each turn, the playing entity chooses the best known moves, thus it is not allowed to choose a weaker move in order to attain a draw artificially.
The summary of the observations is that strong AI engines can reliably produce drawn games while weaker ones cannot. GnuGo can probably achieve a draw in self-play only by pure luck. Even then, the game is full of mistakes that happen to cancel each other. Using pure Monte Carlo tree search with millions of playouts, Pachi [6] can maintain balance for a while, but then one side slips a bit, and then the difference steadily grows. Interestingly, Leela Zero (network 276, 40 × 256) also has trouble achieving draws. Analyzing it with KataGo v1.6.1 (network g170-b40c256 × 2-s5095420928-d1229425124, 40 × 256), it becomes clear that Leela Zero’s network does not see that the predicted scores are far away from zero. On the other hand, Leela Zero has a different opinion about KataGo’s balanced self-plays. It is easy to decide who is more in the right in this case: KataGo reliably wins matches against Leela Zero.
7.2.1. Motivations for Relative Perfection
In game analysis, we observed that Go AIs can keep the winning probability and the score lead constant from any board position. This was contrasted with human play (including professional games to some extent) with some amount of zigzagging, gains and losses move by move.
Traditionally, aspiring professional players and players who want to improve are recommended to study games played by strong players. Logically, the stronger the players are, the more there is one can learn from their play. Weaker play by definition has more and stronger counterstrategies available, and is therefore less efficient as learning material. However, there is also a practical limitation of comprehension ability: similarly to how elementary school children cannot understand differential calculus, weaker players may not be able to follow what is going on in professional games. Traditionally, this problem is solved by including human-made commentaries along with game records.
Relatively perfect games by AIs are arguably the most optimal study material, since they involve moves that have the relatively smallest amount of weaknesses and counterstrategies. However, it remains an open question whether such study material is efficient for human players, who learn to play the game by attaching meaning to stones on the board and moves they make. An AI chooses its move by its superior policy network and whole-board view for which a human cannot compensate; a human player, instead, creates a narrative for a game and judges more constrained positions against each other. If an AI’s play cannot be explained in these terms, it may be difficult for a human to infer useful knowledge from its games.
It is a special feature of Go that draws are meaningful, i.e., they fulfill the goal of the game, surrounding territory. In chess, the goal is to checkmate the opponent’s king, so in a draw the players mutually admit the inability to do so.
If for nothing else, these game records are good intellectual exercises for refuting them as ‘perfect’ games. A human paired with an AI can look for mistakes, the existence of which would show that it is not a perfect game.
7.2.2. Creating ‘Perfect’ Games
Relatively perfect game records can be created by AI self-plays by two different methods:
- Extremely long thinking times: While the raw policy output of the deep neural networks in modern AIs already has superhuman strength, the Monte Carlo tree search can further refine the policy and yield even better moves. Theoretically, Monte Carlo search methods converge to an optimal solution given enough time [29]. Therefore, giving long thinking times to the engines can approximate perfect play.
- Handcrafted self-plays: A human observer can do an ongoing analysis on the board positions, restart the search if the position has several good moves, and choose between equally good options. This way the human acts as a meta level for the search algorithm.
7.2.3. Observations in Handcrafting
In the following, we describe some observations during the handcrafting process.
- ‘Priming the pump’: One easy method to produce a flat winning percentage graph is to build up a large search tree by allowing millions of visits in a position, preferably at a position with a forced move, so all simulations go into one move. Then, one can relatively quickly make the moves by following the most visited move until the built-up visit count disperses, usually when there are two moves with equivalent values. On the board, building up the search tree in the opening almost takes the game to its endgame. However, the search can become biased, and somehow the choices are not as good as they look.
- Restarting the search: The Monte Carlo tree search is a randomized process. Therefore, it should not be surprising that restarting the search gives different recommendations for the next move.
- Making the endgame sensible: The neural networks we use now were trained to maximize the winning percentage and to some extent the score lead. They do not value the aesthetics of the moves. This becomes a problem in the endgame, when the engines suggest moves that actually do not change the score. The theory of endgame can be discussed with mathematical precision [1] and can even be played perfectly [30]. There is probably room for developing an engine that switches from the neural network to a coded algorithm to play the endgame with no unnecessary moves. In the meantime, we can use the human observer to select aesthetic moves.
- The engine changes its mind: It is a frequent phenomenon that, after millions of visits, well after a best move has been established, a better option emerges. The engine ‘changes its mind’. Clearly, this is due to the discovery of a better variation somewhere deeper in the search tree. This does not matter much when playing against human players, but in self-play this leads to a more balanced game.
8. How Compressible Is Go Knowledge?
We can accelerate the human learning process by making it faster (which we do not know much about) or by reducing the learning material. Can we do a lossless compression of the knowledge required to play Go perfectly? First, we need to look at the uncompressed data.
8.1. OmegaGo
If the story started with AlphaGo, then it will end with OmegaGo, which will make a perfect move in each legal board position. There is a simple (imaginary) implementation of OmegaGo. We know that there are approximately legal board positions on the board [26]. For comparison, the number of particles in our observable universe is in the order of . This means that even if we could somehow convince an elementary particle to store a board position worth of information, using up all of our universe for data storage, we still would not be able to call it a good start. Without access to many other parallel words, this remains a thought experiment. However, let us not focus on the practical problems for now.
The legal positions are all accessible from the starting position (empty board), if the ruleset allows arbitrary many passes during the game. This implies that we have all handicap games as well. We generate the whole game tree and, by using the standard minimax algorithm [27], we can figure out the maximal guaranteed score, let us say, for Black. With enough patience for the game tree traversal, we can finally build OmegaGo.
OmegaGo is just a database, a map from board positions to moves. Each position is associated with an optimal move. There may be more moves that guarantee the optimal value, but for realizing perfect play it is sufficient to have one. (This leaves the possibility for an updated version, OmegaGo+, in case there is a market for a perfect engine that plays with more variety). The program operates as a lookup table: it takes a board position, finds it in the database, and returns the corresponding perfect move. There is no planning and reasoning present in OmegaGo. Thus perfect play is possible without those skills, but it may not be realizable.
The size of the code for the database lookup is dominated by the size of the dataset. Therefore, we only need to calculate the storage requirement of the database in order to get the size of the OmegaGo software package. We need 573 bits to define the configuration of stones, 9 bits for denoting an illegal move (ko), and another one for whose turn is it, 9 bits for the perfect move, 592 in total. OmegaGo needs bits, megabytes. In contrast, the current Leela Zero network size is about 90 MB (compressed). How far is it from perfect play? Certainly the distance is not proportional to the storage requirements, as that would imply that AIs made near zero progress.
8.2. Which Complexity Measure?
What is the smallest code size that can provide exactly the same information as the complete table? In other words, what’s the Kolmogorov complexity of the game? We require a program that takes a string—a board position—and produces another string—a perfect move. What is the length of a minimal size program that can do this? The answer is simple. It takes very little to write a tree search algorithm that goes through all possible continuations of the board position and picks the first move of a maximal sequence. This is again OmegaGo; we simply traded a large memory bank for a long computation.
A similar approach was suggested by Rhodes [31], using algebraic automata theory. The player is modeled as a finite state automaton (algebraically as a transformation semigroup), and its complexity is defined by the number of hierarchical levels in the structure of the automaton. This corresponds to the number of intermeshing loops in the state transition diagram of the automaton. It is conjectured that this complexity is roughly the average length of games.
Unfortunately, we are nowhere near having such precise mathematical models of players, such as Turing-machines for Kolmogorov complexity or finite state automata for algebraic complexity. However, we have some results in complexity theory. Finding the winner in an arbitrary position is PSPACE-hard [32], and the same is true when restricted to endgame positions [33]. However, a perfect player for the weakly solved game might be able to avoid the difficult positions. In other words, are there perfect strategies that keep the games simple? Can a perfect player playing only from the empty board position have smaller computational complexity?
Alternatively, we can compare power consumption. The human brain is said to be operating on 20 watts, while a standard PC with a good GPU requires at least 200 watts. On the other hand, some of the engines are capable of running (albeit very slowly) on CPUs only, so a Raspberry Pi 4 computer can have superhuman strength, which is definitely under 10 watts. This calculation does not take into account the training process, which is larger by several magnitudes.
In practice, we use the size of a neural network as a proxy for the theoretical complexity. We know that a 40 blocks network is stronger than one with 20 blocks. However, a bigger network takes longer to train; therefore, with more computational power, we could probably produce even stronger AIs. Continuing computer Go competitions may eventually shed light on the optimal size of the network.
9. Conclusions
The rise of superhuman AIs in Go was a historical event. It brought many changes in how we play and in how we study the games—both good and bad. The game is more accessible than ever, but we have online cheating and some Go teachers may lose their livelihoods. The consequences are not played out yet; we live in a transitional period. The point we want to make here is that the game is not over yet. Until the game is solved, or there is clear evidence that AI engines are close to perfect play, we cannot exclude the possibility of human players reaching the level of the AI engines. Young players starting now take the AIs for granted. Are they going to be free of dogma, will they get caught in the new dogma defined by the AIs, or will they reach perfection? This depends on how compressible perfect Go knowledge is, and whether it fits into the human mind or high-performance computers.
We have now better opportunities in learning, understanding and improving in the game of Go, since:
- we are free from the previously unknown constraints of thinking;
- we have better analysis tools and access to high-quality statistical patterns; and
- we have causal reasoning abilities.
The next task for the Go community is to find new narratives for winning plans informed by the output of deep learning AIs, no matter whether these plans are present in the AIs or not.
Author Contributions
All authors contribute equality to the article. All authors have read and agreed to the published version of the manuscript.
Funding
The hardware equipment for the computational experiments was provided by internal research funds at Akita International University.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | the field of artificial intelligence, or a software package with artificial intelligence capabilities |
| AG, AGZ, AZ | AlphaGo, AlphaGo Zero, Alpha Zero |
| OGS | Online-Go Server |
References
- Törmänen, A.; Verlag, H. Rational Endgame; Hebsacker Verlag: Scheeßel, Germany, 2019. [Google Scholar]
- Power, J. Invincible, the Game of Shusaku; Game Collections Series; Kiseido Publishing Company: Kanagawa-Ken, Japan, 1998. [Google Scholar]
- Wolf, T. The program GoTools and its computer-generated tsume go database. In Proceedings of the Game Programming Workshop in Japan’94, Hakone, Japan, 21–23 October 1994; pp. 84–96. [Google Scholar]
- Kishimoto, A.; Müller, M. Search versus knowledge for solving life and death problems in Go. In Proceedings of the AAAI, Pittsburgh, PA, USA, 9–13 July 2005; pp. 1374–1379. [Google Scholar]
- Millen, J.K. Programming the game of Go. In Byte Magazine; UBM Technology Group: San Francisco, CA, USA, 1981; Volume 6. [Google Scholar]
- Baudiš, P.; Gailly, J.L. PACHI: State of the Art Open Source Go Program. In Advances in Computer Games; van den Herik, H., Plaat, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7168, pp. 24–38. [Google Scholar] [CrossRef]
- Dehaene, S. Consciousness and the Brain: Deciphering How the Brain Codes Our Thoughts; Penguin Publishing Group: New York, NY, USA, 2014. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Kruger, J.; Dunning, D. Unskilled and unaware of it: How difficulties in recognizing one’s own incompetence lead to inflated self-assessments. J. Personal. Soc. Psychol. 1999, 77, 1121. [Google Scholar] [CrossRef]
- Hotta, Y.; Obata, T. Hikaru No Go; Original Japanese Version Published in 1998; VIZ: San Francisco, CA, USA, 2004; Volume 23. [Google Scholar]
- Schaeffer, J. One Jump Ahead: Computer Perfection at Checkers, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Egri-Nagy, A.; Törmänen, A. Derived metrics for the game of Go—Intrinsic network strength assessment and cheat-detection. arXiv 2020, arXiv:2009.01606. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. Available online: https://science.sciencemag.org/content/362/6419/1140.full.pdf (accessed on 12 November 2020). [CrossRef] [PubMed]
- Leela Zero, G.C.P. Go Engine with No Human-Provided Knowledge, Modeled after the AlphaGo Zero Paper. 2019. Available online: https://zero.sjeng.org (accessed on 12 November 2020).
- Wu, D.J. Accelerating Self-Play Learning in Go. arXiv 2019, arXiv:1902.10565. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Törmänen, A.; Verlag, H. Invisible—The Games of AlphaGo; Hebsacker Verlag:: Scheeßel, Germany, 2017. [Google Scholar]
- Zweig, S.; Gay, P.; Rotenberg, J. Chess Story; New York Review Books Classics; Also known as The Royal Game, Published in 1943; New York Review Books: New York, NY, USA, 2011. [Google Scholar]
- Brady, F. Endgame: Bobby Fischer’s Remarkable Rise and Fall—From America’s Brightest Prodigy to the Edge of Madness; Crown: New York, NY, USA, 2011. [Google Scholar]
- Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect; Penguin Books: New York, NY, USA, 2018. [Google Scholar]
- Schaeffer, J.; Burch, N.; Björnsson, Y.; Kishimoto, A.; Müller, M.; Lake, R.; Lu, P.; Sutphen, S. Checkers Is Solved. Science 2007, 317, 1518–1522. [Google Scholar] [CrossRef] [PubMed]
- Werf, E.; Herik, H.; Uiterwijk, J. Solving Go On Small Boards. ICGA J. 2003, 26. [Google Scholar]
- Werf, E.; Winands, M. Solving Go for Rectangular Boards. ICGA J. 2009, 32, 77–88. [Google Scholar] [CrossRef]
- Tromp, J.; Farnebäck, G. Combinatorics of Go. In Computers and Games; Springer: Berlin/Heidelberg, Germany, 2007; pp. 84–99. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall Press: Englewood Cliffs, NJ, USA, 2009. [Google Scholar]
- Cobb, W. Reflections on the Game of Go: The Empty Board 1994–2004; Slate and Shell: Richmond VA, USA, 2005. [Google Scholar]
- Kocsis, L.; Szepesvári, C. Bandit Based Monte-Carlo Planning. In Machine Learning: ECML 2006; Fürnkranz, J., Scheffer, T., Spiliopoulou, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–293. [Google Scholar]
- Berlekamp, E.; Wolfe, D. Mathematical Go: Chilling Gets the Last Point; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Rhodes, J.; Nehaniv, C. Applications of Automata Theory and Algebra: Via the Mathematical Theory of Complexity to Biology, Physics, Psychology, Philosophy, and Games; World Scientific: Singapore, 2010. [Google Scholar]
- Lichtenstein, D.; Sipser, M. GO Is Polynomial-Space Hard. J. ACM 1980, 27, 393–401. [Google Scholar] [CrossRef]
- Wolfe, D. Go endgames are PSPACE-hard. In More Games of No Chance; MSRI Publications: Cambridge, UK, 2002; Volume 42, pp. 125–136. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).