Thinking the Unthinkable: An Alternative Route to a Unified Theory

Abstract

One of the greatest quests in physics in current times is the search for a grand unified theory—to bring all the forces of nature into one coherent explanatory framework. Despite two centuries of progress, both in comprehending the individual forces and formulating mathematical constructs to explain the existence and operation of such forces, the final step to unify the localised atomic and subatomic forces with gravity has proven to be elusive. Whilst recognising that there are arguments for and against the unification of all the forces of nature, the pursuit for unity has been driving many physicists and mathematicians to explore increasingly extraordinary ideas, from string theory to various other options requiring multiple dimensions. Can process philosophy ride to the rescue? By changing our perspective, it might be possible to derive a provocative and compelling alternative way to understand basic (and advanced) physics. This process approach would see all matter objects, at whatever scale, as energetic systems (inherently dynamic). Through the use of game theory, there is a way to appreciate the combination of entropy together with all the apparent forces of nature, being gravity and the more localised forces, within a singular, metaphysically consistent, construct. The outcome, however, challenges our whole understanding of the universe and fundamentally changes our relationship with matter.

1. Introduction

Given the immense costs of building and running scientific apparatuses such as CERN, and given the manner in which the search for unification of the forces of nature is reported in popular scientific press, one could be forgiven for thinking that the concept of unity is universally accepted. It remains, however, a matter of philosophical debate as to whether the notion of unity is valid. There are other philosophical perspectives, such as pluralism [1,2], empirical pragmatism [3,4] and category error or misplaced unity [5,6,7], which lean away from unity. These alternatives would suggest that all the effort and investment to find an all-encompassing model is in vain. However, these philosophical counter arguments against unity remain marginalised, at least from the perspective of many scientists, with a large proportion of physicists seemingly assuming without question that unification of the physical forces (strong, weak, electromagnetic and gravity) of some form exists; we just have to find it.

Looking beyond the world of physics, with the scientific world split into numerous silos, the largest being the physical, life and social sciences, in contrast only a very few scientists (such as Nicholson and Dupre [8]) contemplate whether there could be some way of understanding nature, other than the scientific research method itself, that encompasses all these scientific fields—a process oriented unity of sciences, not just the physical forces of nature. At this higher level, most scientists remain happy for their different interests in the ways of the universe to remain fully separated and appreciated through disparate rules and laws.

Whilst recognising the philosophical arguments against unity, we now know that living objects (the subject matter of the life sciences) are indubitably formed from atoms and molecules (the subject matter of the physical sciences). And, as we gain more and more understanding of biochemical processes and larger molecular objects (such as RNA, proteins, and viruses), the line between physics and biology is becoming increasingly blurred. An artificial separation between these fields of science (such as notions of living or inert, animate or inanimate) is progressively harder to justify.

This paper should be read in the spirit of a thought experiment that reformulates the question of unification from the perspective of process philosophy and game theory. The paper explores a tantalizing glimpse of a possible way of understanding the universe that could unify our approach to all the forces of nature and potentially encompass all the different sciences within a consistent metaphysical framework. The outcome does not lead to a singular equation, such as the Standard Model of Particle physics. But it does suggest a possible metaphysical approach to appreciating the physical, life and social worlds in the same unified way. It should, however, be emphasized that such a unifying framework will not alone necessarily solve all scientific questions. But it could enable scope for real analogies across the sciences, providing an opportunity to increase and deepen understanding without seeking to diminish the complexity and emergence of phenomena that can arise at larger scales, such as the appearance of life, beauty, intelligence and culture in living and social systems. If the possibility of a consistent metaphysical approach is deemed to have merit, then it may provide direction for new avenues of research, especially within cross-disciplinary areas such as systems science.

2. Background

Ever since James Clerk Maxwell formulated his unified theory of electromagnetism [9,10], physicists have been on the hunt for a broader theoretical framework embracing gravity—the original force of nature, as deduced by Isaac Newton [11,12]. Since Maxwell’s day, we have become aware of additional forces, notably the subatomic weak and strong forces [13,14]. Progress has been made to unify these short-range forces within what has become known as the Standard Model of Particle Physics [15,16]. At the same time, our comprehension of the forces of nature has fundamentally changed. Albert Einstein’s general theory of relativity has altered how we appreciate gravity [17,18], while quantum mechanics has given us a completely new perspective on the nature of matter and how particles interact [19,20].

Quantum field theory is a theoretical framework that combines classical field theory, special relativity and quantum mechanics to describe the interactions of subatomic particles [21,22]. Through several iterations, a singular construct has been formulated, which combines electromagnetism with the strong and weak forces, giving rise to the Standard Model [13,16]. This has been successful in predicting the behaviour of subatomic particles. It does not, however, include gravity [23,24]. One of the major challenges for integrating gravity with the other forces is that gravity seems to operate over much longer distances and is relatively very weak [25,26].

The search for a grand unified theory has to date been tackled in various ways [27], including but not limited to:

▪

Supersymmetry (referred to as SUSY) attempts to extend the success of the Standard Model. This approach proposes a symmetry between fermions (matter particles) and bosons (force carriers) [28]. It involves postulating the existence of a higher symmetry group and treating the short-range forces as a singular force. Such a force would then break down into the known combination of forces at lower energies [29].

▪

Quantum Gravity (also known as Loop Quantum Gravity) builds upon the general success of quantum mechanics and seeks to treat spacetime itself as quantised [30,31].

▪

Theories of Everything represent substantially different approaches, including String Theory [32] as the most notable contender. String Theory encompasses various formulations, all of which are based on the idea that particles are vibrating strings. M-theory [33] seeks to unify string theories by making use of an 11-dimensional framework.

▪

Holographic Theory emerges from a combination of string theory and black hole physics, suggesting that all information within a volume of space can be described by information on the boundary of that space [34].

▪

Emergent Gravity explores whether gravity is an emergent phenomenon arising from more fundamental quantum processes [35,36].

None of these attempts have been experimentally confirmed [21]. A solution remains elusive, and the search continues to integrate gravity into some wider framework [22,37,38]. This quest to find a broader theory tends to be tackled with mathematics, seeking out new or extended mathematical constructs that can accommodate all the forces. All these approaches, though recognising the probabilistic character of quantum mechanics, fall within the ontological framework of mechanistic determinism [39,40,41], also known in philosophy as substance physics. The working presumption in all the above models is that the fundamental constants of nature (such as the Gravitational Constant), the particles that we observe and their characteristics (such as electrons, their mass and charge) and the various forces were all pre-determined. Whilst they may not (could not) have existed before the universe began, their values are deemed to have been essentially fixed from the very outset—at the start of the Big Bang.

Other unifying concepts have been proposed over the years, including vitalism, panpsychism, animism, and, of course, the variety of historic religious narratives. But none of these are deemed to be truly scientific. Alternative propositions, which seek to be consistent with mainstream thinking, have come forward in the last half-century, including, but not limited to, evolutionary cosmology [42,43,44], cosmological natural selection [45,46,47], and emergent naturalism [48,49,50]. However, these ideas remain marginal positions within the physical sciences. They have been held back because they all lack any practical explanations for the basic physics that we experience in the world around us.

Alongside these alternatives to the mainstream, there is a growing cohort of process philosophers who are seeking to challenge the doctrine of substance physics. Process philosophy, as a line of inquiry, can be traced back to Heraclitus (c. 535–475 BCE), who saw the world in terms of constant change. The classic analogy is that of a river, where, as the water flows, he stated that you can never step into the same river twice. In the twentieth century, it was Alfred North Whitehead [51] who first championed a return to process philosophy. Thereafter, a variety of thinkers have progressed process philosophy, some leaning towards a theological line of inquiry and others taking a more naturalist (or secular) approach. Key proponents of the more naturalist process philosophy have included: Hartshorne [52], Rescher [53], Ulanowicz [54], Eastman [55], Thompson [56], Seibt [57] and Connolly [58]. It is, however, recognised that this categorisation of current process philosophy into non-secular and secular strands may be deemed an over-simplification by those closer to this area of philosophical discourse. Furthermore, alongside process philosophers, there have been other thinkers who have sought to challenge the doctrine of mechanistic materialism (or determinism) but who are not generally deemed to be process philosophers; Hans Jonas [59] is one of the better known; others include: Cassirer [60], Hartmann [61], Heidegger [62], Marcel [63], Merleau-Ponty [64], Teilhard de Chardin [65], Tillich [66].

Process philosophy has, however, remained sidelined from mainstream physics [53,54,57,67,68,69]. It has been hampered by several notable impediments. Firstly, leading process philosophers, such as Whitehead [51], Bergson [70], James [71,72] and Peirce [73,74,75], have tended to be abstract and metaphysical, and not provided pragmatic, practical explanations for everyday phenomena. Secondly, despite various attempts, no process-oriented solution has been satisfactorily provided to explain basic phenomena such as the forces of nature or the 2nd Law of Thermodynamics [39,46,51,53,54,55,70,76,77,78,79,80,81,82,83]. And, equally importantly, process philosophers have struggled to provide sufficiently convincing explanations on how seemingly stable systems, such as atoms and molecules (otherwise understood as substances), can arise from the inherently dynamic, ever-changing universe, which they are seeking to advocate [51,53,70,75,80,82,84]. Simply put, if an atom or a chair is a river, then how?

The approach proposed in this paper represents a provocative process-oriented solution to these conundrums. It provides a means to place all the forces of nature into a single framework. This alternative way sees particles of matter as energetic systems, which are inherently dynamic, and all the forces of nature as emergent manifestations of repetitive interactions.

3. Addicted to Mechanistic Determinism

The groundwork for 20th-century physics and the formulation of quantum mechanics was laid during the 19th-century. Scientists of that era inhabited an atomistic, materialistic, and reductionist universe, following the substance perspective. They saw everything around them in terms of objects (substances) and forces following deterministic laws [85,86,87,88]. It was a Cartesian form of mechanism, where substances are seen as inert without external forces. As a generality, to 19th-century scientists, the wider universe, in analogy to a clock, followed pre-determined rules and mathematical formulae. Objects within that universe were invariably seen as passive substances, the movements of which were dictated by the forces applied to them.

As reductionists, they could see that if you grind down any solid, you just get smaller stuff—rocks, stones, gravel, sand, dust, powder—until you end up with atoms—the smallest objects, from which to build things (a Lego brick notion of the universe). Atoms were seen as miniature ball-bearings—small, indivisible particles—as originally envisaged by the Ancient Grecians, Democritus and Leucippus. Layered onto this were Isaac Newton’s ideas that these particles could be attracted to each other through a universal invisible force, called gravity. Once they had gained a better understanding of electricity through the contributions of Maxwell, amongst others, the notion of electric charge, positive and negative attracting, became a further layer onto this construct [89], providing the basis for short-range forces which hold those particles tightly together, thereby creating molecules and solid substances.

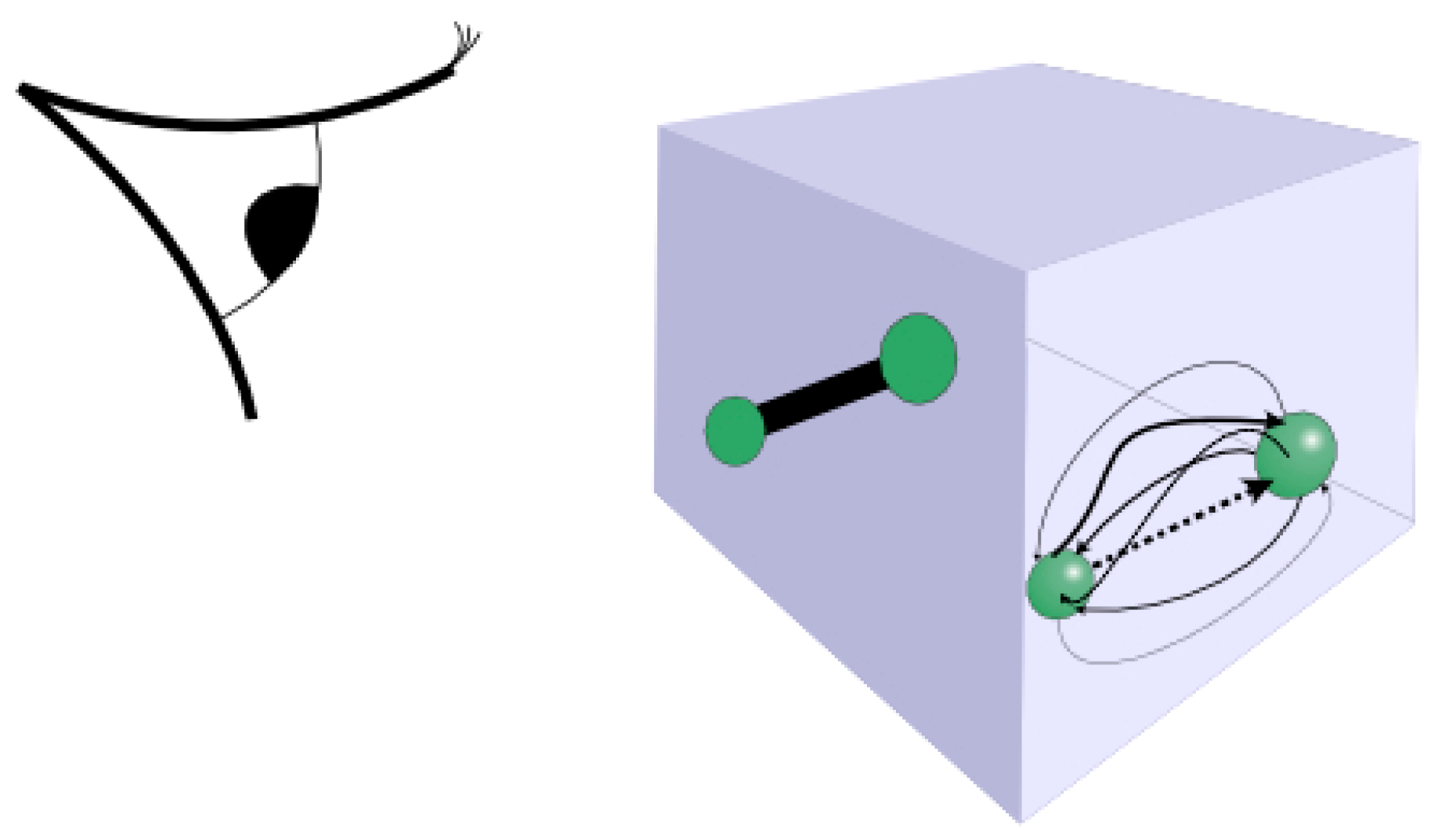
Winding forward to today, we find ourselves in a rather odd situation. The physics that is taught in a school environment aligns with this substance physics mentality, and collectively, we remain addicted to the same materialistic and reductionist approach. Atoms, and particles generally, are seen in terms of inert objects bound by invisible springs (however conceived), which we call forces (see Figure 1). Object (mass) and spring (force) are envisaged as being conceptually distinct phenomena, where the motions of objects are entirely dictated by the forces applied to them. Yet both relativity and quantum mechanics conceive the universe otherwise. Einstein’s general theory of relativity can be summed up as follows: “matter tells spacetime how to curve, and curved spacetime tells matter how to move”. It is a chicken-and-egg concept with no clear reasoning for the underlying cause of the apparent force of gravity, other than simply accepting that all matter seems somehow to be attracted to other matter. In contrast, the Standard Model of Particle Physics now sees the other forces of nature (strong, weak and electromagnetic) as being mediated by exchanges of energy in the form of sub-atomic particles.

Over the course of the last 100 years, as quantum mechanics has matured both theoretically and practically, through iterations such as Quantum Electrodynamics (QED) and Quantum Chromodynamics (QCD), the fundamental forces of nature are indeed now seen in terms of energetic exchanges. In quantum field theory, the known short-range forces (electromagnetic, weak and strong) are all described as being mediated by force-carrying particles known as gauge bosons [21,90]. The perceived forces arise from emission and absorption by the objects of matter (fermions, such as quarks, nucleons, electrons, etc.) of these force-carrying particles, which allow for a transfer of energy and momentum. These force-carrying particles include gluons, W and Z bosons, and, of course, photons. In this construct, the force is a manifestation (a consequence) of the interaction between the particles (see Figure 2).

The Standard Model of Particle Physics is therefore based on a fundamentally different metaphysical understanding of matter compared to general relativity. And, neither quantum mechanics nor relativity aligns with the other major plank of our physical sciences, being the Second Law of Thermodynamics, which is derived from a strictly 19th-century substance perspective.

4. Entropy

As they gained expertise in converting heat energy into motion through steam engines, one of the 19th-century scientists’ most intractable puzzles became how to explain the expansion and mixing of gases, and the concordant loss of useful energy. To them, gaseous atoms (those indivisible ball-bearings) obeyed Newton’s laws of motion, undergoing elastic collisions. But applying Newton’s laws to large populations of atoms does not lead to rapidly mixing or expanding gases, from which the original energy is seemingly lost. Various attempts were made to explain these observations. This mystery was eventually resolved in a rather unconventional way by the ground-breaking work of the Austrian mathematician, Ludwig Boltzmann, whose contribution came at the dawn of the 20th-century, presaging the formulation of quantum mechanics. Boltzmann decided to apply statistics to the problem and, through this, formulated statistical mechanics [91]. His function entropy, generally denoted with the sign ‘S’, provides both a quantification and a seeming rationale for the loss of useful energy in a system.

Boltzmann started out with the assumption that atoms were, in essence, miniature inanimate ball bearings. He then crafted a mathematical construct which can provide a quantifiable estimate for the difference between two states, say Temperature 1 and Temperature 2, for an isolated gaseous system (that is, a system which is, as far as is possible, closed off with no inputs or outputs of energy or matter—absolutely no interaction with its surroundings). His solution could be likened to time-lapse photography, providing a reel of snapshot solutions for each delta change in temperature or pressure, showing a system transitioning from an initial state towards a final equilibrium, in which all parts of the chosen system have the same temperature, or pressure, or level of mixing of atoms, or all of these. But, whilst the mathematics provides a means to calculate a function, which provides a very good fit against observed availability (or apparent loss) of energy, especially in nearly isolated systems, it does not in any way explain the process by which a system has progressed from one state to the next—how it evolves towards equilibrium, what happens between those time-lapse shots? So, in the spirit of that era, Boltzmann’s solution was assumed to be a universal law (a force, of sorts), applicable to all substances, in the same way that gravity appears to be.

Though Boltzmann’s work was originally received with scepticism, it has now become a mainstay of modern science. It represents the theory that is seen to explain the observed dispersal of energy and gaseous matter in simple systems, providing the mathematical foundations for the 2nd Law of Thermodynamics. It has proven to be an incredibly useful tool, contributing to many collective successes, allowing us to manipulate elements and compounds to produce all sorts of useful chemical processes, generating more complex chemicals from plastics to medicines to silicon chips. Yet it is not a simple concept to comprehend and causes many people to tie themselves in knots trying to understand how best to apply it [92]. Boltzmann’s mathematics tells us what happens, but not how or why.

Statistical mechanics is now used to explain the banal to the fantastic, from cups of tea cooling to black holes hypothetically evaporating. The concept is so powerful that many have construed it to provide the arrow of time itself [93,94]. And through extrapolating the 2nd Law from discrete isolated systems to everything (the whole cosmos), it is now generally thought that the universe will ultimately undergo some form of heat death as all energy and matter eventually disperse and mix [95].

By dint of its success, Boltzmann’s work has locked in atomistic and reductionist expectations that all particles of matter represent (or at least act like) inanimate objects (substances, akin to miniature ball bearings) dictated by the forces applied to them. From this perspective, we see matter deterministically obeying some cosmic law, in which energy always escapes and things always become more mixed up, messy and disordered, the universe travelling unerringly towards ubiquitous uniformity. This disordering process is as ever-present as the gravity keeping our feet firmly planted on the ground.

In this regard, the 2nd Law of Thermodynamics is derived from a completely different metaphysical conceptualisation of the universe compared to both Einstein’s general relativity and the Standard Model of Particle Physics. Furthermore, we now know through the formulation of quantum mechanics that matter particles, say atoms, are very definitely not, nor do they behave like, miniature non-interacting ball bearings—as was Boltzmann’s starting point.

5. What Do We Know About Atoms?

Firstly, thanks to Rutherford’s experiments firing alpha particles at gold foil, we know that atoms have internal structure—a nucleus surrounded by a shell of electrons [96]. Secondly, thanks to varied contributors, including Schrodinger, through quantum mechanics, we now appreciate the configurations of that electronic shell [97]. This has aided understanding of the structure and characteristics of objects that we can see and touch, such as snowflakes and diamonds. And, thirdly, we know that atoms are continuously interacting with their environment, as evidenced through observations such as black body radiation [98]. Your ability to see the world around you is dependent on every atom on every surface within your field of vision constantly absorbing and emitting energy—a constant flow of energy—perhaps, a river of energy.

It was Albert Einstein who realised that energy comes in the form of photons—being particles, not rays as his predecessors thought. Each photon has its own discrete, quantifiable amount of energy. This paved the way for the formulation of quantum mechanics [99]. And, in a nutshell, the original conception of quantum mechanics arose from appreciating that atoms are rather choosy about which photons they absorb and emit [100]—as exhibited through their electromagnetic spectra (Figure 3). Furthermore, for each type of free gaseous atom or molecule, above a certain wavelength (or below a certain energy), any radiation will simply pass straight through and cannot be absorbed [101].

6. What Else Do We Now Know About Matter?

We now know that there are three constitutional impossibles within our universe:

▪

energy in a closed system (whether in the form of matter or energy) cannot be created or destroyed (1st Law of Thermodynamics);

▪

you cannot go below the lowest temperature, being zero Kelvin (3rd Law of Thermodynamics); and

▪

matter cannot travel faster than the speed of light (that is, Einstein’s most notable contribution).

These three conjectures have a fundamental connection. From them, one can infer that it is impossible to completely isolate any particle or lumps of matter from the wider universe [102,103]. Even the 19th-century scientists knew this experimentally, despite their precise theoretical definition of the 2nd Law of Thermodynamics as pertaining specifically to an isolated system.

The notion of complete isolation can be likened to a variation on Schrodinger’s Cat thought experiment. If you were to create a truly isolated system, a perfect thermos flask, you would have effectively removed an item of matter from the universe, thereby violating the 1st Law of Thermodynamics (assuming that the whole universe is itself in effect an isolated system). Such a laboratory-created isolated system would have to involve the particle(s) of matter floating in a vacuum surrounded by genuinely zero Kelvin with no physical contact, no interaction with any fields and no black body radiation to or from the outside world—absolutely no interaction, effectively removed from the universe. When you peaked back inside this perfect thermos, would your atom, cat or cup of tea still be there?

Turning this inference on its head, we must conclude that all particles of matter MUST constantly interact with their surroundings. It is an inherent nature of matter to continuously interact either through direct contact with other matter or through directly absorbing/emitting radiation. No particle in the universe can truly stand alone and be isolated… ever [39,62,80,104,105,106,107]. This idea of the non-separability of objects has been argued as consistent with quantum mechanics by authors such as Schaffer [108,109].

Energy particles, Einstein’s photons, get around this. In travelling at the speed of light, they experience no time. So, from their frame of reference (drawing on Einstein’s relativity), despite us observing them travelling as individual particles or waves across billions of light-years, photons never in fact lose contact with the universe of which they are a part (emission from a star and absorption by the human eye is instantaneous). Further, we know that photons are always an interacting part of the universe because the path of those particles bends around massive objects, such as galaxies. But as soon as any energy becomes effectively stationary, wrapped up as a piece of matter, it experiences time and, so it would seem, must, in some way, remain in constant contact with ambient energy or other local matter, and thereby the wider universe.

Following this line of thinking, our universe can be viewed as being an immense network of interactions and material connections—“everything is connected”. It is a single system. Anything not coupled in some way with that web is not part of our universe. And everything which is part of that network, whilst able to change from one thing to another (matter to energy, etc.), must forever remain a part of the whole—”energy cannot be created or destroyed”. What is part of the universe cannot cease to be part of the universe. What is not part of the universe cannot become part of the universe.

7. What, Then, Are Atoms and What Are Forces?

This question can be asked of any particle at the molecular through to subatomic scales. But for simplicity, we will stick with atoms.

Atoms are very definitely not the equivalent of miniature ball bearings. They have an internal structure and necessarily constantly interact with their surroundings—absorbing and emitting energy. They are, by deduction, energetic systems. In our everyday lives, we experience many other more familiar such systems—all those living things around us, including houseplants, pets, and other people. These larger energetic systems are also all completely dependent on continuously interacting with their surroundings in order to survive and remain coherent entities within our universe—to exist as part of that universal web of interactions. Drawing on systems thinking [110,111,112], all energetic systems, no matter how small, have the following factors in common: (1) they have internal structure, (2) they are inherently dynamic, with energy constantly flowing through them, and (3) they are differentiable from, yet in constant interaction with, their surroundings.

Let us put aside for a moment the concepts of animate and inanimate as being distracting notions. Instead, let us be radical and try out thinking purely in terms of energetic systems, which must interact with their surroundings. With this alternative mindset, the idea of animation is a matter of degree, rather than a binary, is or is not. We recognise already that there is a wide variety of living systems from ourselves, capable of seemingly complex thought and intentions, all the way down to bacteria, which we perceive instead as energetic systems that simply respond to their energetic and chemical environments, such as swimming up a sugar gradient. So, atoms and molecules could be understood as even simpler agents—energetic systems which respond spontaneously to their material and energetic environment.

Seeing atoms (or particles generally) as inherently energetic systems gives us a new way to understand forces—those invisible connecting springs, which we construe to bind particles together. As already noted, short-range forces are now understood within the Standard Model of Particle Physics to arise as a consequence of exchanges of particles (energy) between interacting systems.

The Standard Model has proven to be very effective in explaining experimental results in particle accelerators and has enabled various predictions, which have then proven correct [113]. However, it embeds a fundamental change in our perception of the forces of nature. If the forces involved are actually the manifestation of energetic interactions, then the particles involved, even electrons, can no longer be reduced to indivisible atomistic objects of matter dictated by forces applied to them. They are inherently energetic systems, capable of absorbing and emitting energy, having internal structure and constantly interacting with their environment. This is a completely different starting point from the one originally envisaged by Boltzmann and suggests that the fundamental premise of substance physics is wrong, thereby putting in question Boltzmann’s starting assumptions, which underpin the 2nd Law of Thermodynamics.

So, where do we go next? This is treacherous ground; many have become shipwrecked in the process of trying to challenge or rethink entropy. Boltzmann’s mathematics has proven its worth time and time again. Furthermore, elements of Boltzmann’s work now form a mainstay of quantum mechanics, being also strongly grounded in statistics. The answer may lie not in trying to dispute entropy nor statistical mechanics, but rather in understanding afresh what the process is behind them. This may seem a circuitous route to addressing the challenge to unify the forces of nature, but the journey is worth it.

8. A New Process-Oriented Way to Envisage Basic Physics

If objects in our experience, such as atoms, are energetic systems and depend on constant interaction with their environment, then this forces the question to be considered: should we be treating basic matter systems as agents? If we were to consider basic matter objects as agents, then, given their dependence on energy for interaction (they cannot be isolated), when there are multiple systems and limited energy, these systems should be seen to inevitably compete for such energy. The outcome is apparent agency, even if such agency is very minimal (i.e., spontaneously responding to changes in energetic circumstances). This idea that atoms might be treated as agents is beginning to be explored by others [114,115].

Turning to process philosophy, this takes as its starting point that being is dynamic, not static. It presupposes that the fundamental underlying nature of all matter and substance is change, and that this should be the primary focus of any comprehensive philosophical account of reality. This contrasts with the foundational assumptions of Western metaphysics, which implicitly assume a static description of reality, onto which any dynamic behaviour is either taken as mere appearance or the consequence of some other motivation. For example, according to substance physics, changes in movement (i.e., acceleration) of any otherwise static objects (or objects moving with constant velocity) are attributed to the existence of fields and forces (such as the gravitational field).

Conventional physics, drawn from Newton and others, sees the universe in terms of Lego bricks stuck together by forces, thereby creating larger objects. Process philosophers do not deny that there are temporally stable aspects of reality—such as the chair you might be sitting on. But they take such apparently static persistent systems to be the regular behaviour of dynamic organisations that arise due to the continuously ongoing processes within those objects. To the process mindset, despite the static appearance of objects, such as chairs, dynamism is the natural state of things.

The fundamental units within process philosophy are events and interactions (originally referred to by Whitehead [51] as ‘actual occasions’). Things that appear stationary or inert are not, therefore, static objects but are inherently dynamic, in which actual occasions are constantly taking place. Phenomena, such as the forces conceived by conventional Western physics, are understood from a process philosophy stance as arising from the constant repeated interactions between component parts. An apparent bond or force—say, two atoms fused together to create a molecule—is then the consequence, not the cause, of the two objects, the atoms, holding together (which is consistent with the modern interpretation of the Standard Model).

This notion of agency is essentially unthinkable when working from a substance starting point (as did Boltzmann), with conventional Western philosophy struggling, for instance, to explain emergent properties such as life [49,54,56,79,116,117,118,119,120]. But from a process philosophical standpoint, nothing is truly inert, agency is inherent and emergence is a natural consequence of the behaviour of component parts [51,84,121,122,123].

9. If We Were to Treat Atoms as Agents…

If atoms were to be treated as agents, then we can turn to the biological sciences for assistance in explaining their behaviour. This parallelization between the physical and biological sciences relies on a high degree of abstraction—simply considering all systems as agents. This ignores many variances between these scientific fields, which may in practice arise in part because of huge differences in the population numbers involved, together with the scalar difference at which we are able to observe such systems.

There is now a growing body of knowledge concerning interactions between conspecific organisms (that is, identical organisms, or members of the same species). Being identical living systems, conspecifics are, according to Darwin [124], inherently competitive, especially when available food is limited. But if self-same organisms are intrinsically in competition with each other, then how come we observe many species creating cooperative systems? Darwin himself commented on this in relation to eusocial species—ants, bees, etc.—but there are many more cooperative examples from herds and pods to troops and tribes, and, of course, ourselves creating human society. This conundrum—intrinsically competitive entities engaging in cooperative behaviour—has remained an unresolved part of evolutionary theory.

During the latter part of the 20th-century, headway has been made to resolve the question of social (cooperative) evolution through the use of game theory, in particular a strand of thinking that has become known as evolutionary game theory. Leading thinkers in this area have been Maynard Smith [125,126,127], Axelrod [128], and, more recently, Nowak [129,130,131]. Our modern understanding of game theory as a mathematical discipline originated with Jon von Neumann’s groundbreaking paper on the minimax theorem in 1928 [132], and has now become a mature area of mathematics. A wide variety of game types (one of the best known being the Prisoner’s Dilemma) have been identified over the years [133].

Out of the broad array of ways that agents can compete or cooperate, it has been resolved that there are only four evolutionary stable game strategies [85,93,94,95]. These are the ways of competing or cooperating that will endure within large populations. No matter what game strategy any individual agent might start out playing, it will end up being forced to fall into line with the evolutionary stable game strategy that all other agents are pursuing. Or, turning this on its head, the evolutionary stable game strategies cannot be invaded by an alternative strategy without most members of the population switching at the same time. So, despite mathematical game theory identifying a wide selection of potential game strategies, in practice, in large populations of interacting agents (humans, ants or atoms), only four will actually be observed.

These four game strategies are depicted in Figure 4 and hereafter referred to as Forms of Interaction. Treating systems as agents, spontaneously responding to their energetic environment, the question that emerges is how we would expect a population of such agents to behave when following each of these four different game strategies and what type of larger system (the behaviour of the whole population) does that give rise to. To deduce this, it is first helpful to understand a little better what each of these Forms of Interaction represents. The following set of game strategies pertain specifically to energy acquisition by agents through direct interaction with the wider environment or through interaction with other conspecific agents, and does not include those other identified types of cooperation that have been considered within the field of social evolution, such as inclusive fitness, group selection, and multilevel selection theory, which are applicable to replicating or reproducing energetic systems.

Passive Competition (also denoted selfishness or latent competition) applies where each agent acts independently without any direct consequences to other members of the population, but its behaviour is in any event detrimental to all other parties, because through its very existence it is consuming a limited common good (using the economic interpretation of the term “common good”), thereby reducing energy availability to all others. Being that organisms are generally quite picky as to what food they can eat, food availability within any ecosystem for any particular species is limited. So, an example would be a dispersed population of non-territorial, non-interacting foraging animals—each additional animal causes a marginal reduction in the amount of food available for every other animal.

Active Competition (also referred to as spite or conflict) corresponds to circumstances where there is a potential disadvantage from the chosen course of action by each party. Typically, this represents deciding whether to enter into conflict (such as stealing food) with the risk of injury. However, the reward of being able to eat in the present may make the risk worthwhile despite the possible consequences. This is typically seen in nature through mobbing behaviour by, say, seagulls, which readily steal food from each other both sneakily and blatantly.

Active Cooperation (also manifesting as sharing or direct reciprocation) happens where agents choose to cooperate because they can see a benefit arising. This can be expressed through sharing a limited common good (say, two people sharing a fish, which they have caught together) or direct reciprocation. Sharing results in both or all agents obtaining a guaranteed smaller immediate gain (dividing the resource between them) than each could potentially have achieved from a competitive course of action, but now without any consequences such as injury. Game theory suggests that as the likelihood and cost associated with injury increase, a threshold is reached at which it becomes a better course of action to cooperate for a smaller gain. Direct reciprocation manifests as direct exchange of one food for another—say, an apple for an orange. In this case, the same quantum of energy is swapped, thereby ensuring fairness, but it is qualitatively different, allowing each party to have access to a wider range of nutrients.

Passive Cooperation (representing indirect reciprocation or trade) is often referred to as altruism, where one party seemingly contributes to another’s benefit without an obvious immediate return. However, more detailed analysis has shown that there is always an expectation of some reward from another agent or later (say, the altruism cycles round a population, everyone helping and being helped at various times according to their changing circumstances). This might involve everyone contributing to a communal food store, from which they can all take food later. Simple trade, where two parties directly exchange different goods, is direct reciprocation (Active Cooperation)—as noted above. But when trade involves monetary exchange, the practical effect is delayed reciprocation. Exchange or trade is reliant on a commonly accepted currency that can later be translated into energy, a desired material good or service, through a further exchange at a later point in time [134,135,136].

In considering this set of interactions, a key principle to take away is that competition invariably gives rise to a directionality for the flow of energy amongst the agents within a system, whereas cooperation does not necessarily do so. In competitive scenarios, one agent always gains at another’s loss, thereby hindering flows of energy and enforcing localized directionality. In cooperative situations, energy and information can flow back and forth, therefore not enforcing any localized directionality, thereby allowing energy to flow through the larger cooperative system.

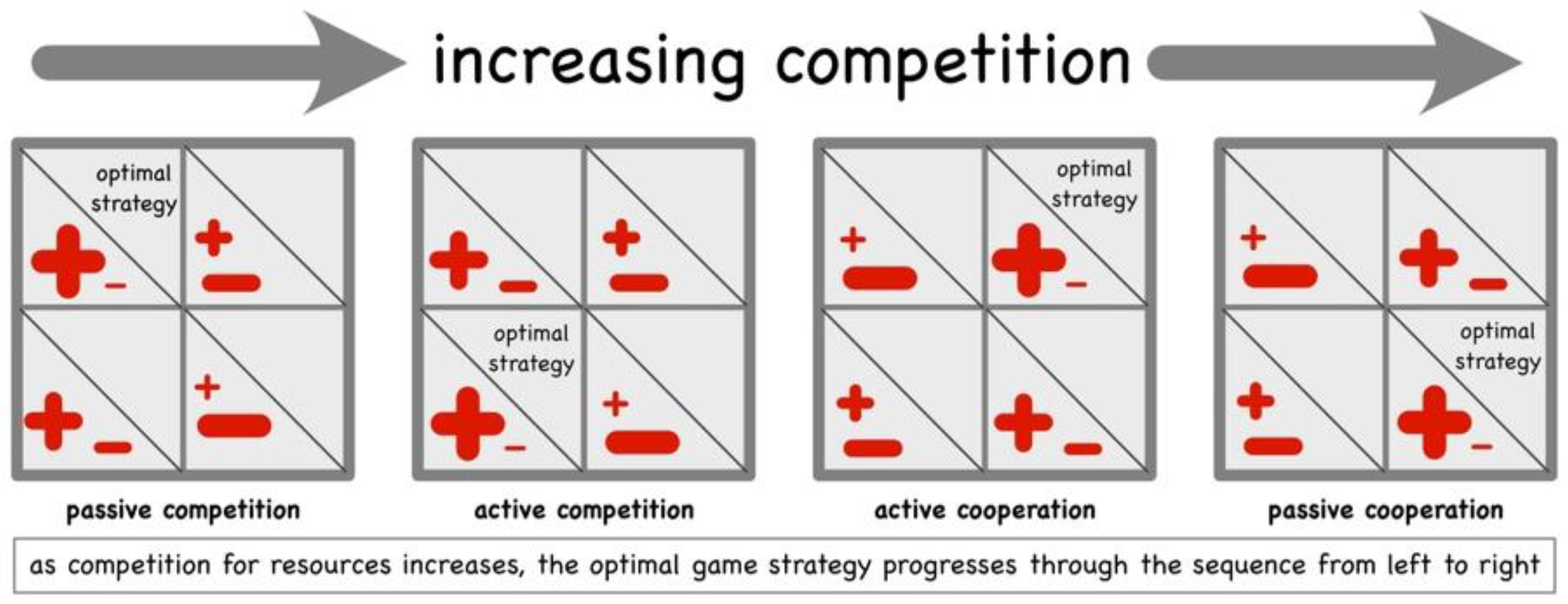
The game theory approach to social evolution, which is now established science, provides an explanation for the emergence of cooperation between conspecifics. The default position is for agents to act competitively; as observed by Darwin, it is an innate tendency for each agent to chase the energy that it needs to exist. However, the mathematics of game theory shows that when the price paid for competition (such as the risk of injury from stealing) becomes too high, then it becomes preferable from the perspective of each agent to turn to cooperation. This can be translated into a general premise that when there is high energetic availability within a system (say, high temperature), then the agents within (the sub-systems) can be expected to adopt competitive strategies. However, when energy is reduced, then threshold points will be reached, at which it becomes better for agents to come together and cooperate (see Figure 5 and Figure 6).

In ecosystems, Passive Competition gives rise to the dispersal of organisms throughout a habitat. With each organism seeking to operate independently, maximise its access to food by minimising experienced competition from its conspecifics, and avoid direct conflict, the population spreads out to all areas where the organisms can acquire the food they need to survive. The end result is that each agent is physically as far apart as possible from every other self-same agent [137]. If, however, food becomes scarce, then this leads to agents changing their behaviour and expressing Active Competition. This manifests as mobbing behaviour (fluctuating dispersal and concentration): for example, sea gulls or pigeons mobbing a food source and stealing fish or breadcrumbs off each other [138,139].

Applying this construct to the physical sciences would see Passive Competition expressed as self-same gaseous atoms dispersing when there is sufficient ambient radiation. Noting from their absorption/emission spectra how selective gaseous particles are for specific wavelengths of energy, each atom will be able to absorb a maximal amount of suitable passing photons by being physically as far apart as possible from any other identical particles (those of the same element or compound). If there were several gases (populations of different conspecifics), then using this construct, it would be predicted that each type of gas would independently disperse into a volume, the combination thereby mixing to create a gaseous ecosystem, each gas expressing its own partial pressure. This is precisely what we observe in everyday physics—in the context of black body radiation, gases expand to fill a volume and different gases spontaneously mix.

Active Competition would manifest as atoms effectively stealing energy from each other, imparting momentum outward away from any energy source. Wherever there is an imbalance of energy, Active Competition would naturally cause it to dissipate, flowing from those atoms who have, to those who have not—dispersing throughout a system and outwards to the environs. This can be readily modelled in any agent-based modelling programme (without any requirement for agents to operate with intent), through which it can be shown that, in a contained system, competition gives rise to an equalising effect, leading to all agents eventually having a similar amount of energy. Again, this is what we observe in simple everyday physics—energy disperses and systems naturally progress towards equilibrium.

In this regard, populations of competing agents, whether these are deemed to be atomic/molecular or composed of organisms, are seen to physically disperse in space and, through the equalising effect of competition, all agents in a population end up with access to a similar amount of energy.

Taken together, both Forms of Competition cause populations to undergo, what are known as, repetitive zero-sum games for all the agents involved. The outcome for a whole population of agents (atoms) is complete mixing of all the different elementary conspecifics together with dispersal of energy, evenly to all parts of an enclosed volume (or enclosed ecosystem). This effects the same end result as we currently describe with the terms equilibrium and maximum entropy and is deemed to be caused by the 2nd Law of Thermodynamics by means of Boltzmann’s statistical mechanics. The mathematics that Boltzmann applied is entirely correct for such a population of competing agents—as predicted through his statistics, competition drives each agent to differentiate itself spatially and energetically from every other agent, and thereby the population progresses towards maximum entropy—complete dispersal and uniformity.

Turning to cooperation, when available energy reduces further and direct competition becomes more intense, then game theory shows that the cost–benefit equation for each agent tips in favour of cooperation [128]. The mathematics of this is tried and tested. Active Competition flips over to Active Cooperation. In ecology, this gives rise to the aggregation of conspecifics, creating herds, troops, packs, pods and other groupings of organisms, which roam the landscape as units, all peacefully sharing food together within their groups, competing at a group level against other similar groups.

Translating this over to the physical sciences, we would predict a lowering of temperature to result in gaseous atoms (or ions) aggregating together to create free-roaming bound groups of atoms, which we otherwise know of as molecules (or smaller molecules giving rise to larger ones). In reducing the temperature, then suitable available photons within the black body radiation, which the original particles could absorb, would become rare. Free atoms in a gas would no longer be able to interact adequately alone directly with their environment. Consequently, to avoid becoming truly isolated, they would spontaneously join up with other atoms, where the subsequent molecules would be large enough to continue to absorb and emit the more readily available, longer wavelength, ambient photons at that lower temperature.

As explored in any undergraduate chemistry course, molecules have additional degrees of freedom (vibration and rotation) and can therefore more readily absorb longer wavelengths of radiation than the individual constituent atoms. Within these molecules, as per the Standard Model, the atoms would be sharing the energy from incident photons and constantly passing energy to and fro between each other, giving rise to an apparent bond. But, as per the Standard Model, what we see as a bond is simply a constant process of sharing or direct reciprocation between the component parts. For each atom, to avoid isolation and achieve that necessary contact with the wider universe, it is now better to be part of some larger system (part of a molecule) than roaming around freely on its own.

That is relatively simple—straightforward alternative ways of describing the physics and chemistry learnt at high school and university first degrees. Now, here is the interesting bit that takes us into new territory.

In the biological world, the reason why a monkey, say, must stay part of its actively cooperating group (a troop) is that it will only benefit from sharing food (Active Cooperation—direct reciprocation) if it is ever-present. None of its peers will save up some spare fruit and hand it over later. Every monkey must be there with all others in the group to benefit from the collective cooperation. Hence, this evolutionary stable game strategy essentially enforced cooperation, causing all the monkeys to stick together out of energetic necessity, roaming the landscape as a group foraging for stuff to eat (sharing, but not trusting).

However, Passive Cooperation does not require such a continued localised presence as Active Cooperation. When it emerges as an evolutionary stable strategy, indirect reciprocation can involve instantaneous exchanges of energy and virtual energy (such as trading using money) or delayed reciprocations, such as contributing to and later accessing a store of food. But, for this game strategy to be successful for the entire population, it requires there to be focal points of collective interaction and some form of common currency [140,141,142,143,144,145,146].

A good example might be leafcutter ants, going out foraging, bringing back leaf cuttings to the nest, in return for which (an exchange) they get some food (being previously mulched and decomposed leaves). Essentially, by being a source of energy—a place to exchange the efforts of their labours for some hard-earned food—the nest provides a centre of attraction for the whole society of ants, to which each ant must constantly return for its own survival—to eat. In the human world, our equivalents are marketplaces—foci of exchange interactions—which lead to agglomeration economics and determine our human and economic geography with towns and cities forming around such trading centres [144,147,148,149,150].

Remember that, in this new way of looking at physics, apparent forces are the manifestation of the behaviour of atoms: the consequence, not the cause. So, translating the behaviour of Passive Cooperation at a population level to the physical sciences, we find ourselves with a simple explanation for the force of gravity! In this alternative way of seeing things, gravity arises from Passive Cooperation. It occurs as an emergent behaviour within large populations through indirect reciprocation and not between pairs of agents. Consequently, it ends up being expressed as a relatively feeble, nebulous force—far weaker than those which appear to hold atoms together and bind molecules (roaming, sharing groups). Further, it does not arise from specific exchanges of energy between pairs of matter objects, as understood in the Standard Model for the other short-range forces of nature. Being a shared locus of exchange for the entire population, gravitational focal points become pegs on the physical map—fixed points in space with an inertia created by all the local participating population of particles—a city, a beehive, a gravitational centre of attraction for basic matter.

The notion of a sense of gravity emerging amongst populations to create centres of attraction can be seen in many parts of nature, especially in the context of eusocial species. More recently, computer programmes running agent-based modelling systems have been shown to generate spontaneous gravitational emergence within populations, which make use of trading or exchange (Passive Cooperation) interactions. This occurs within agent-based systems, where the agents have no agency, as such—operating just like particles might do [140,141,142,143,144,145,146].

To date, we have interpreted the force of gravity as a weak universal force applying to all particles of matter—Newton’s original equation, subsequently re-cast by Einstein. The formation of stars is then seen to arise by means of this weak force, gradually causing large clouds of hydrogen to eventually coalesce. This new way of looking at physics would see things very differently.

Under this alternative perspective, a large cloud of hydrogen atoms/molecules, all of which are at a similar temperature, would experience next-to-no internal gravitational force. It is only when the inner volume of such cloud becomes sufficiently cold—with those particles in the cloud centre starved of energy, denied any incoming suitable photons because these have all been absorbed by the outer layers—and the energy differential between exterior and interior of the cloud has reached a critical point, then passive cooperation interactions (trading energy) kick into effect at scale—the whole population transitioning at once from one evolutionary stable game strategy to another. This would cause a gravitational force to start manifesting, creating a positive feedback process which ultimately leads to the implosion of the cloud and formation of a star. Thereafter, the star represents a source of energy for all surrounding matter within that emergent solar system and beyond. Within this way of looking at things, it is precisely the same evolutionary process as that which gives rise to thunderstorms and cities, and originally caused the evolution of societal nests in the insect world.

We have been describing star formation through an ever-present weak universal force of gravity, and now more sophisticatedly through curvature of spacetime. But could the same thing simply be emergent behaviour within large populations of conspecifics, which are otherwise starved of energy? That curvature of spacetime might instead be an emergent property arising from all the interactions taking place between the component agents—the density of interactions causing those atoms and molecules to perceive localised spacetime to be curved.

So, we have our first few explanations of basic physical phenomena from this new process-oriented approach to physics:

▪

Passive and Active Competition give rise to Entropy. Entropy, as we understand it, would arise from competition between self-same energetic systems. In this construct, Boltzmann’s ‘S’ would essentially be a measure of or proxy for the level of competition between all identical agents within a system. It would thereby be a function of the system (population) in question and not something that can be exported. The mathematics is entirely correct. But we now also have an explanation for the process behind it—what is happening between Boltzmann’s time-lapsed photographs of systems.

▪

Active Cooperation causes Molecular Bonding. Molecular bonding would arise from direct reciprocation between atoms. All other short-range forces likewise would arise from direct reciprocation interactions, enabling participating energetic systems to maximise their interaction with the surrounding matter and energy environment.

▪

Passive Cooperation leads to Gravity. Gravitational effects would arise from indirect reciprocation between atoms (and particles generally). This would explain why it is so different from and so much weaker than those other apparent forces of nature. Furthermore, this way of understanding gravity helps explain why it often appears as an opposite or counterforce, of sorts, to entropy—concentration versus dispersal of populations (and hence the cruciform depiction in Figure 6).

But, if there were to be no originating gravitational force, this seriously messes with our deterministic mindsets—everything we have been taught at school and university is suddenly not quite so… grounded. In this construct, the observation of gravity arises because of the behaviour of umpteen numbers of particles all wanting to be part of the action and participate in exchange interactions so as to avoid becoming isolated—no more or less than human beings gravitate towards cities as a means to generate an income to survive.

10. Lowering the Temperature Further

So far, the focus has been on gaseous systems. What happens when the temperature is lowered further, and ambient (black body) radiation comprises mostly photons with longer and longer wavelengths, with which individual gaseous atoms or molecules can no longer interact in their gaseous state? At face value, one might expect the formation of larger and larger atomic systems. But it is not quite that simple, because the Periodic Table of atoms includes a set of highly stable energetic systems, capable of absorbing and emitting the type of radiation found around the universe outside of the interior of stars. The atomic nuclei are themselves forged in stellar environments. Once outside, they cannot simply merge and convert into larger and larger atoms—no more or less than two single or multi-cellular organisms could merge to create some monstrosity (we see locust swarm, not giant locust).

Being that they are energetic systems, self-same atoms or molecules are seen as innately competitive. So, when the temperature drops, rather than forming larger atomic systems, it might be predicted that they would find interesting new ways to compete and cooperate for available energy. Instead of larger atoms, we observe the formation of composite energetic systems, resulting in the variety of matter structures that we find in the world around us.

In the biological sciences, drawing on life history theory, this same construct is expressed through living systems having a discrete set of needs, giving rise to a hierarchy of needs: Level 1 = survival, Level 2 = safety/security, Level 3 = health maintenance, and Level 4 = information needs. It is difficult to appreciate atoms or molecules as having ‘needs’ as such, even though, as established earlier, they do need to interact.

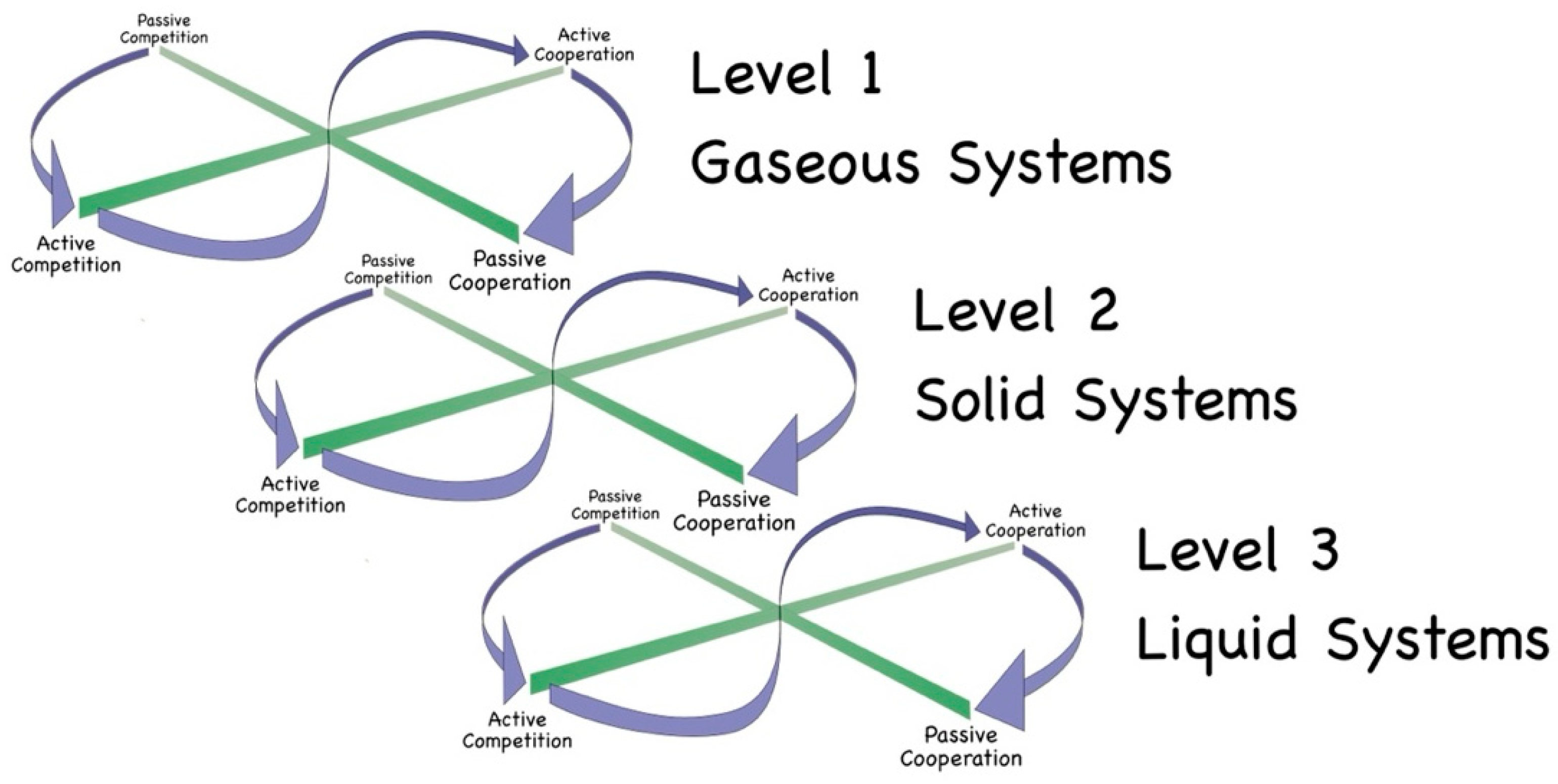
These concepts can be interpreted into the physical sciences as representing competition or cooperation between particles with respect to: Level 1—frequency of acquisition of intermittent energy, Level 2—flow of energy, Level 3—total quantum of energy, and Level 4—spatial information about available energy. These basic energetic requirements give rise to Ideal Type interactions (Level 1 to Level 1, Level 2 to Level 2, etc.) and, according to the logic of this framework, manifest through the basic states of matter—gas, solid and liquid:

▪

Level 1 Systems involving Level 1 to Level 1 interactions—gases occur when there is sufficient ambient radiation for atoms and molecules to operate as free agents, absorbing and emitting photons directly to and from the surrounding vacuum;

▪

Level 2 Systems involving Level 2 to Level 2 interactions—solids occur when the wavelengths of most of the radiation is too long for individual free atoms/molecules to interact with; they can only achieve sufficient interaction through being part of some larger object, which is able to create a surface onto which those long-wavelength photons can be incident; the atoms within the interior of solids access energy through direct contact with other atoms, energy passing from one atom directly to its neighbours or being shared/exchanged across multiple atoms in the form of vibrations;

▪

Level 3 Systems involving Level 3 to Level 3 interactions—liquids occur when the particles can, in part, obtain energy directly from ambient radiation, but need to top this up with intermittent direct-contact interactions with other atoms; hence, liquids sit at the interface between gases and solids, combining interactions observed in both gases and solids; and

▪

Level 4 Systems involving Level 4 to Level 4 interactions—dynamic fluid systems (such as vortices) occur when there is a flow of energy through a liquid system, causing the matter particles to keep responding spontaneously to an ever-changing energetic environment and information about their surroundings.

When the temperature is significantly lowered, then, for each atom to continue to interact with the wider universe, aggregations of atoms/molecules must come together to create larger objects (still being energetic systems). Within such larger systems, the particles compete or cooperate for energy in the same way as already discussed in a gaseous context; hence for each type of competition/cooperation (Levels 1 to 4), there is seen to be the same sequence of game strategy derived interactions running from Passive Competition through to Passive Cooperation (see Figure 7). By way of example, in some solid systems, the atoms can be construed as internally competing, whereas in other solid structures, the component atoms are cooperating. The internal competition or cooperation between atoms/molecules manifests in terms of macroscopic properties, such as insulation (particles keeping absorbed energy to themselves) and conduction (particles readily sharing or exchanging energy within the solid).

This could be construed as manifesting within matter systems (gas, solid, liquid) through creating four fundamental categories of material at each level—as set out in

Table 1. The variety of material structures created by atomic energetic systems.

System	Passive Competition	Active Competition	Active Cooperation	Passive Cooperation
Level 1 Gases	dispersing matter (entropy)	dispersing energy (entropy)	molecules (atomic bonding)	foci of exchange (gravity)
Level 2 Solids	amorphous solids (insulator)	polymers and fractals (growth systems)	crystalline insulating solids (heat conduction)	crystalline conducting solids (electrical conduction)
Level 3 Liquids	emulsions (insulator)	liquid crystals (layered systems)	insulating liquids (heat conduction)	ionic solutions (electrical conduction)
Level 4 Fluid Systems	turbulent flow (chaotic systems)	vortices (dynamic systems)	laminar flow	channelled flows

. The various systems or structures shown have been deduced by looking at how the same competitive and cooperative processes operate within the biological and social sciences domains. The fourth level of this framework corresponds to behaviours of matter systems, which sit beyond our ability to explain through a purely atomistic and reductionist mindset of objects and forces.

Through this new way of looking at physics, the reason for the existence of different states of matter becomes better understood and, further, it can be readily explained why phase changes take place at such precise temperatures. Essentially, each atom is constantly responding to its energetic environment (not forces). When the local energetic environment changes, whether that be vacuum radiation or energy obtained through direct contact with neighbouring atoms, all particles spontaneously flip in terms of type of interactions (Level 1 to 4) or Forms of Interaction (states within phases), responding to their changed circumstances, whether these be optimal to correlate or not correlate, aggregate or disaggregate (compete or cooperate) with neighbours. Underlying all this is the simple mathematics of game theory.

If all the above were to be true, then constructs that we have invented through our deterministic physics to explain the existence of forces, such as the electromagnetic force, may become unnecessary. By way of example, the concept of electric charge can alternatively be explained through appreciating energetic systems competing or cooperating. For instance, at ambient temperatures, electrons compete against other electrons, thereby spontaneously dispersing. The observation that they repel each other is very real, but the notion that this is caused by a negative charge becomes redundant. Within this new physics, attraction between electrons and protons is better understood as a symbiotic relationship to enable each particle type to achieve greater interaction with its environment at low temperatures than by means of the notion of positive and negative attraction.

11. Testability

19th-century science was incredibly successful. By way of example, the various gas laws that were derived make use of mathematical equations to accurately predict how the measurable parameters of gases (temperature, pressure and volume) vary with respect to each other. This gave confidence in a universe that obeys precise rules. But such phenomena could equally arise from the behaviour of vast numbers of atoms and molecules all reacting spontaneously to their energetic environments. The concept of evolutionary game theory, as applied to matter systems, suggests that within any energetic context all atoms or molecules will be forced to adopt similar game strategies, giving rise to macroscopic behaviour, which appears to be very predictable… and conform to precise mathematical formulae.

What we have been learning through the 20th-century is that the microscopic world, which is the subject of consideration of quantum mechanics, is far more fickle. At the microscopic scale, when smaller populations are being considered, molecules and smaller particles do not necessarily follow precise rules. Rather, their behaviour is better understood statistically. Could this be an indication of individual particles each responding spontaneously to their energetic environment, rather than following precise mechanistic rules?

One of the ways that we can try to test out the ideas presented in this paper would be through agent-based modelling. We now have sufficiently powerful computers to model large numbers of agents and observe what macroscopic phenomena might arise from the multiplicity of interactions at a microscopic level. This could be used to explore in more detail the implications of evolutionary game theory and how this might manifest within the physical world of atoms and other microscopic particles. Agent-based models could be used to better explore the circumstances that populations flip from one Form of Interaction to another, especially the change to Passive Cooperation. This could help tease out whether this approach really does provide an alternative causal explanation for the existence of gravity.

12. Our Universe… But Not as We Know It

Our 19th-century forefathers made it their business to deduce the universal laws and constants that make the universal clock tick, so to speak. When thinking about the beginning of things, such as the Big Bang, determinists conceptualise that the rules governing the universe were pre-scripted. Before the universe began, those important constants, such as the gravitational constant, the mass and electric charge of an electron, and numerous others, were all pre-defined. It is an engineer’s way of thinking about a clockwork universe. This has led to a variety of leading thinkers wondering why these constants are what they are: as many note, if these were just the merest fraction altered, the universe would be a very different place, and we probably would not be a part of it [42,151,152,153]. This takes some authors down the road of thinking that there must have been a purposive design to the universe to enable us to exist [154,155].

If you are willing to let go of such a mechanistically deterministic mindset, then you must also leave behind this idea about how things began. Rather, from a process-oriented perspective, everything started with a completely blank sheet, just like life on Earth did. From there, the universe evolved. Everything that we now see arose because of paths being taken. None of the universal constants, which we have measured, existed at the start of the process… no more than our human DNA, nor the laws of the land of modern societies, were anything more than theoretical possibilities when life on Earth first appeared. All the laws of physics, the forces and the various constants could instead be construed to have emerged as a consequence of the interactions between matter systems—an ongoing process whereby the constants and systems evolve together.

By way of example, we do not question that all life on Earth is based on certain chirality rules (chiral molecules are mirror images of each other—almost all biological amino acids have left-hand chirality and biological sugars have right-hand chirality). We appreciate that this arose because of forks in our evolutionary history. Thereafter, the incorrect chirality always caused things to go wrong within biological systems, so evolutionary biological processes selected for only those chemical reactions and processes that led to the correct chirality. Man, of course, had to learn the hard way not to make chemicals with the wrong chirality (witness the thalidomide disaster). Turning to the physical sciences, the question is regularly posed in popular scientific press—‘where’s all the anti-matter?’ The answer is possibly quite simple. The universe chose a path. Thereafter, putting anti-matter into the equation just made a mess of things, tending to destroy all structure. And so (using Darwinian jargon), particle interactions and processes have been selected for, which keep it out.

In putting aside our addiction to mechanistic determinism in the physical sciences, and instead seeing matter in terms of inherently dynamic energetic systems (agents?), there is scope to derive a singular framework which can account for all the forces of nature [8]. The proposals presented here provide a means to understand all those forces within a singular metaphysical way of understanding things. If nothing else, this is a step forward from our current circumstance, in which the major planks of the physical sciences (Einstein’s Relativity, Quantum Mechanics and Entropy) all sit within completely different metaphysical constructs.

13. Conclusions

We return at the end to the question of entropy and Boltzmann’s statistical mechanics. His mathematical construct has been incredibly useful for the last 120 years, helping us to solve all sorts of challenges. But Boltzmann’s mathematics could equally be a statistical description of a population of competing agents, modelling how all agents in a system are driven by competition to differentiate and end up evenly dispersed across all the available microstates. Maximum entropy would thereby represent the outcome of countless repetitive zero-sum competitive games, leading to complete spatial dispersal of agents and even distribution of energy. The 2nd Law, then, could be construed as the result of the innate competition between self-same energetic entities.

If this were the case, then despite starting with an erroneous assumption about the very nature of matter, Boltzmann’s mathematics is genius. It is a wholly correct approach to model a population of competing agents (and not inanimate objects). Consequently, it provides an extremely good fit against measured observation for simple isolated (as far as is possible) gaseous systems, especially when such systems are composed of very large populations of agents, such as atoms in a gas. And, because his mathematics is such a good fit against observation, despite everything that quantum mechanics has tried to tell us since, we have been lured into accepting Boltzmann’s original starting position—that atoms are inanimate objects responding to forces applied to them—despite now knowing full-well that atoms are far from being inanimate objects.

Could it, then, be true that the 2nd Law of Thermodynamics is an example of a questionable-cause logical fallacy argument? The notion of the 2nd Law of Thermodynamics, arising from a universal phenomenon known as entropy, correlates with what we observe. It might not be the cause. The cause could be so much simpler—competition—where, according to evolutionary game theory, intense competition leads to cooperation. And suddenly, the behaviour of all matter systems (breaking apart or coalescing) can be explained through a singular explanatory framework.

Now, if entropy as currently construed is a consequence, not a cause, then many everyday phenomena would be far easier to explain to children and undergraduate students than relying on concepts in statistical mechanics such as macro configurations and microstates. Rather, it turns thermodynamics into fun: “Wonder why your tea cools?” “It’s because those cheeky air molecules literally steal the heat away.” And, in one fell swoop, in the spirit of Copernicus’ heliocentric theory of five hundred years ago, all that was previously complicated becomes simple.

Clearly, if this new physics has any validity, then other questions come to the fore, such as: “how frequent must the interactions of a lone particle be, to not become isolated?” Furthermore, if, as inferred, the gravitational constant is not constant, then our whole comprehension of the cosmos will be thrown into disarray.

If you are willing to think the unthinkable and treat particles as being not quite so inanimate—rather as energetic systems responding spontaneously to their environment (agents)—then an alternative way of understanding our universe is possible. In this alternative construct, all the forces that we perceive, and thence all the structures that we experience in space or time, cutting across all the fields of science, are emergent manifestations of underlying interactions and processes. It may be that the only way to unify all the forces of nature into a theory of everything is to recognise that there are no underlying fundamental forces after all.

This approach to unification may be deeply unsatisfactory for those working from a mechanistic materialism/determinism perspective, chasing some unified mathematical model to explain the whole universe. But coming from a process philosophy perspective, such an approach to unity is possibly the best that can be achieved. Fundamentally, it allows for a comprehensive understanding of our cosmos, covering all scales and types of systems (physical, living or social), which sits within a singular metaphysical construct. It may not alone lead to new discoveries. But, over time, such a unified alternative has scope to deepen our understanding of nature and appreciation of the way things work.