Single Aliquot Regeneration (SAR) Optically Stimulated Luminescence Dating Protocols Using Different Grain-Sizes of Quartz: Revisiting the Chronology of Mircea Vodă Loess-Paleosol Master Section (Romania)
Abstract
1. Introduction
2. Optically Stimulated Luminescence Dating Methodology
2.1. Principles of Luminescence Dating
2.2. Fine (4–11 µm) Versus Coarse (>63 µm) Quartz Grains Dating of Loess
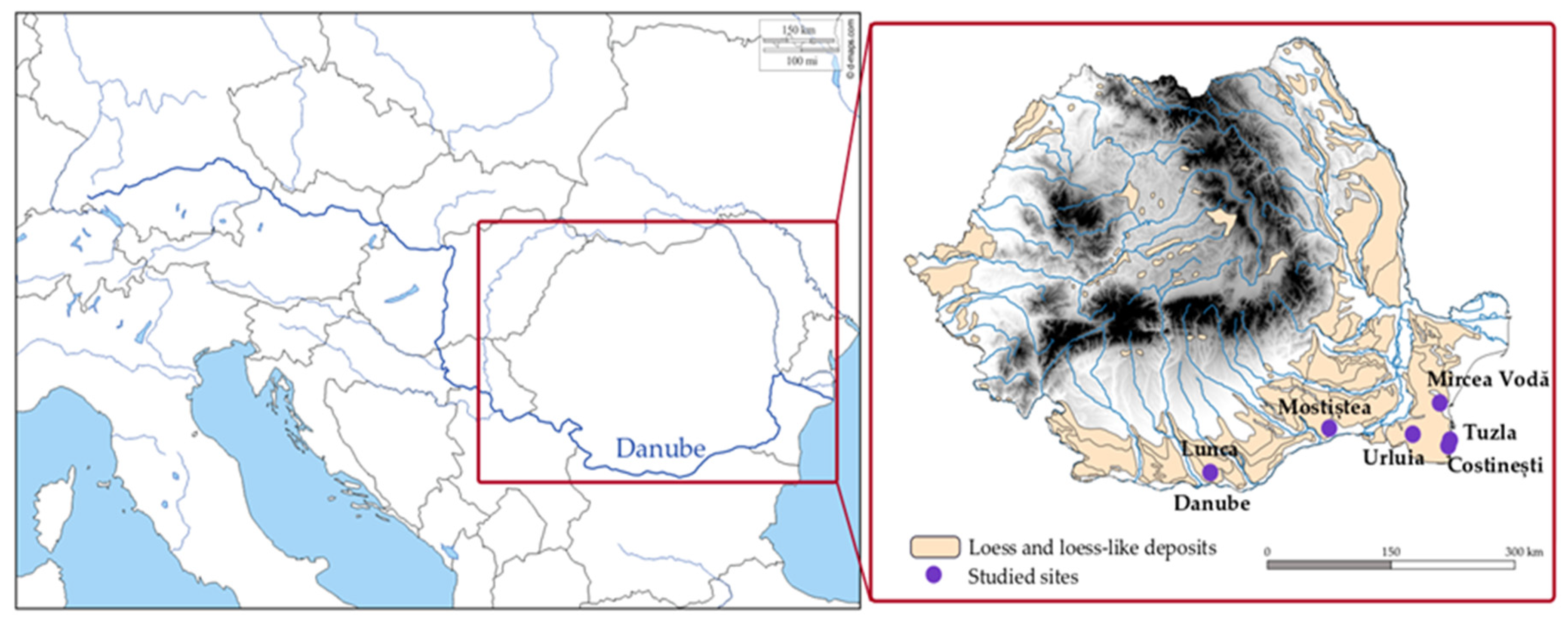
3. Studied Site
3.1. Location and Importance
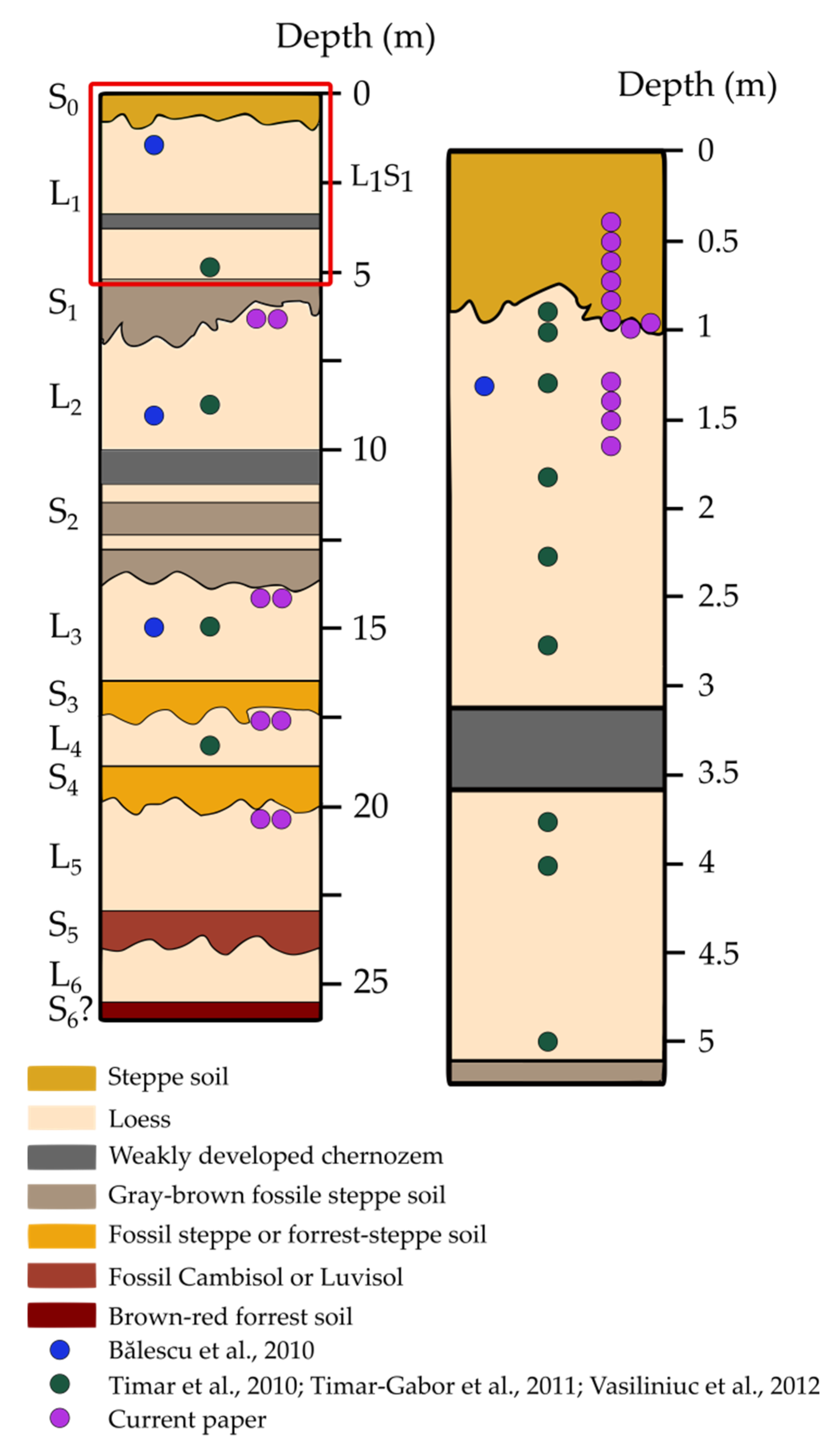
3.2. Stratigraphy
3.3. Previous Studies on Mircea Vodă Section
Luminescence Characteristics and Behavior
3.4. Current Study on Mircea Vodă
3.4.1. Sampling, Preparation and Analytical Facilities
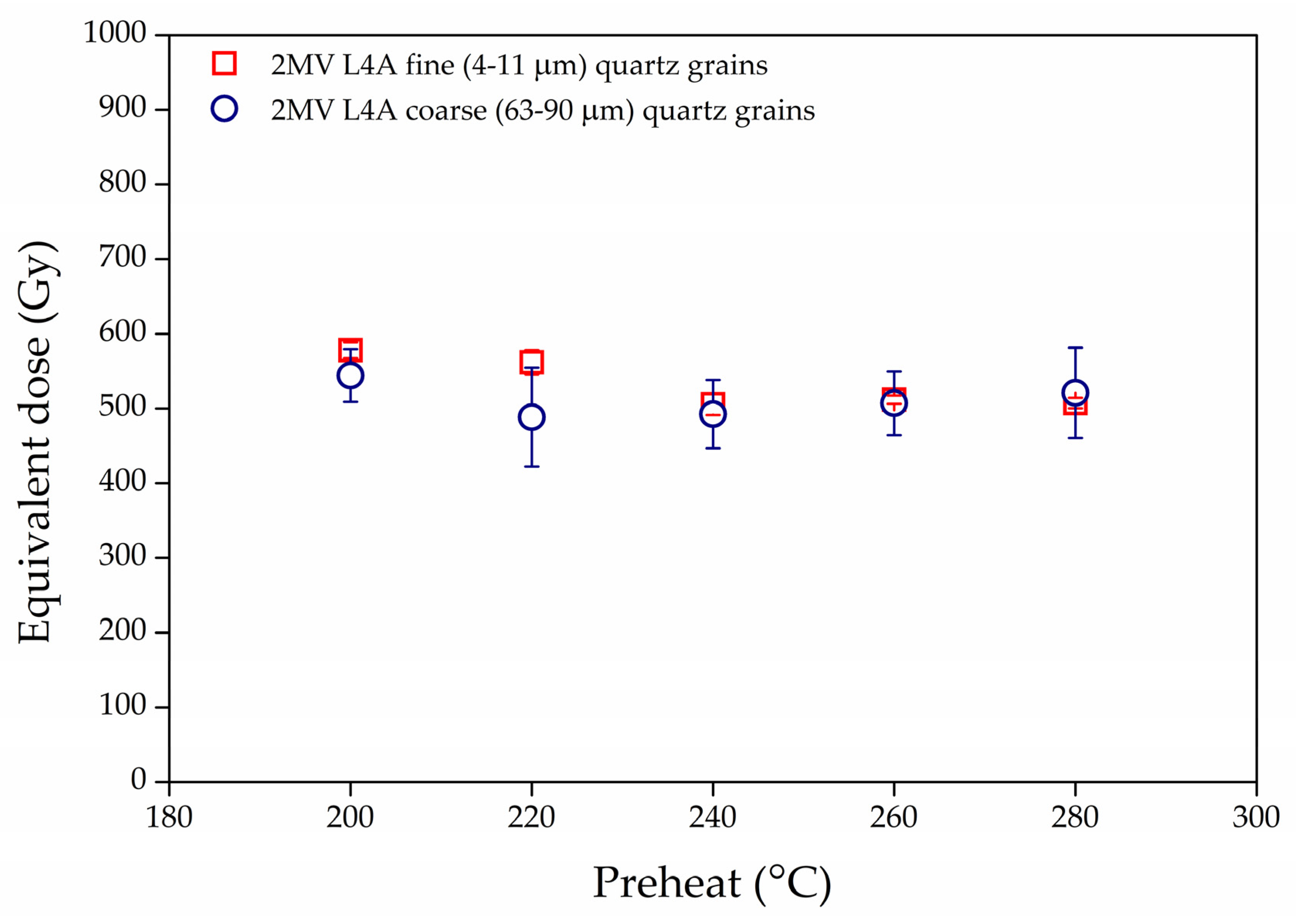
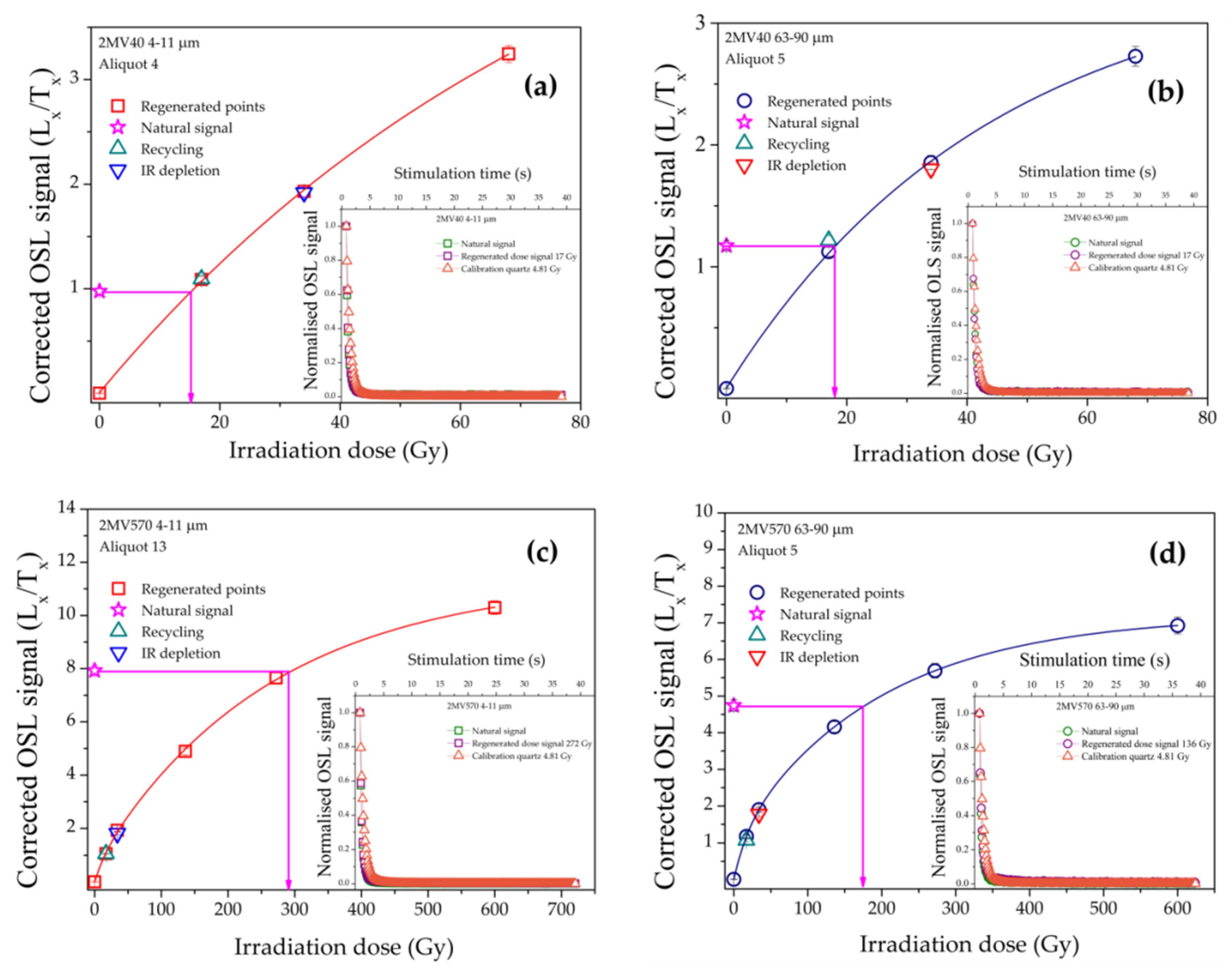
3.4.2. Luminescence Measurements
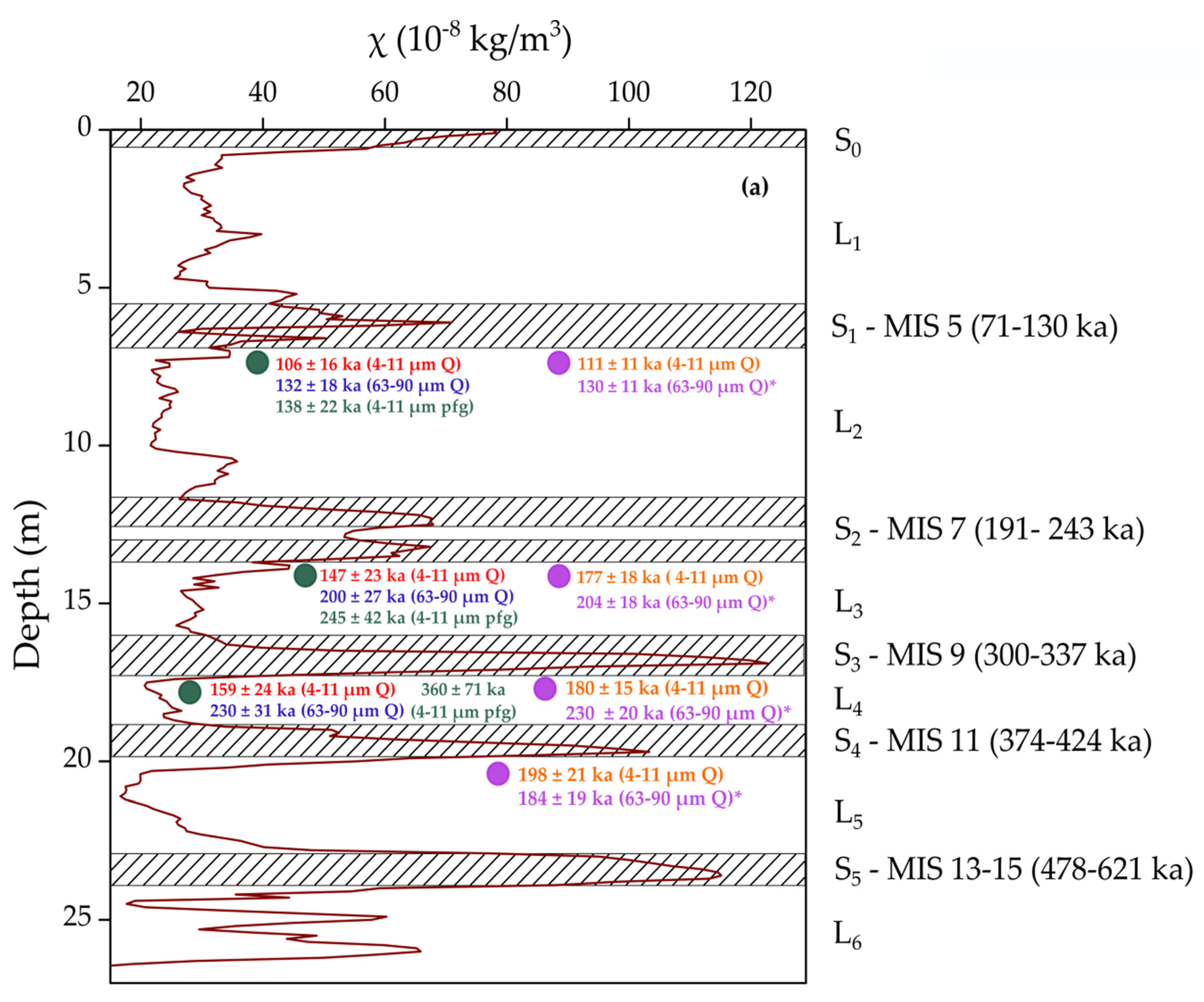
4. Ages and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Murray, A.S.; Wintle, A.G. Luminescence dating of quartz using an improved single-aliquot regenerative-dose protocol. Radiat. Meas. 2000, 32, 57–73. [Google Scholar] [CrossRef]
- Timar, A.; Vandenberghe, D.; Panaiotu, E.C.; Panaiotu, C.G.; Necula, C.; Cosma, C.; van den haute, P. Optical dating of Romanian loess using fine-grained quartz. Quat. Geochronol. 2010, 5, 143–148. [Google Scholar] [CrossRef]
- Buylaert, J.P.; Vandenberghe, D.; Murray, A.S.; Huot, S.; De Corte, F.; Van den Haute, P. Luminescence dating of old (>70 ka) Chinese loess: A comparison of single aliquot OSL and IRSL techniques. Quat. Geochronol. 2012, 10, 75–80. [Google Scholar] [CrossRef]
- Lai, Z.P. Chronology and the upper dating limit for loess samples from Luochuan section in the Chinese Loess Plateau using quartz OSL SAR protocol. J. Asian Earth Sci. 2010, 37, 176–185. [Google Scholar] [CrossRef]
- Buylaert, J.P.; Murray, A.S.; Vandenberghe, D.; Vriend, M.; De Corte, F.; Van den haute, P. Optical dating of Chinese loess using sand-sized quartz: Establishing a time frame for Late Pleistocene climate changes in the western part of the Chinese Loess Plateau. Quat. Geochronol. 2008, 3, 99–113. [Google Scholar] [CrossRef]
- Fleming, S.J. Study of thermoluminescence of crystalline extracts from pottery. Archaeometry 1966, 9, 170–173. [Google Scholar] [CrossRef]
- Zimmerman, D.W. Thermoluminescent dating using fine grains from pottery. Archaeometry 1971, 13, 29–52. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Vandenberghe, D.A.G.; Vasiliniuc, S.; Panaiotu, C.E.; Panaiotu, C.G.; Dimofte, D.; Cosma, C. Optical dating of Romanian loess: A comparison between silt-sized and sand-sized quartz. Quat. Int. 2011, 240, 62–70. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Vasiliniuc, S.; Vandenberghe, D.A.G.; Cosma, C.; Wintle, A.G. Investigations into the reliability of SAR-OSL equivalent doses obtained for quartz samples displaying dose response curves with more than one component. Radiat. Meas. 2012, 47, 740–745. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Constantin, D.; Marković, S.B.; Jain, M. Extending the area of investigation of fine versus coarse quartz optical ages from the Lower Danube to the Carpathian Basin. Quat. Int. 2014, 388, 168–176. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Buylaert, J.-P.; Guralnik, B.; Trandafir-Antohi, O.; Constantin, D.; Anechitei-Deacu, V.; Jain, M.; Murray, A.S.; Porat, N.; Hao, Q.; et al. On the importance of grain size in luminescence dating using quartz. Radiat. Meas. 2017, 106, 464–471. [Google Scholar] [CrossRef]
- Constantin, D.; Begy, R.; Vasiliniuc, S.; Panaiotu, C.; Necula, C.; Codrea, V.; Timar-Gabor, A. High-resolution OSL dating of the Costinești section (Dobrogea, SE Romania) using fine and coarse quartz. Quat. Int. 2014, 334, 20–29. [Google Scholar] [CrossRef]
- Anechitei-Deacu, V.; Timar-Gabor, A.; Fitzsimmons, K.E.; Veres, D.; Hambach, U. Multi-method investigations on quartz grains of different sizes extracted from a loess section in Southeast Romania interbedding the Campanian Ignimbrite ash layer. Geochronometria 2013, 41, 1–14. [Google Scholar] [CrossRef]
- Vasiliniuc, Ș.; Vandenberghe, D.A.G.; Timar-Gabor, A.; Panaiotu, C.; Cosma, C.; van den Haute, P. Testing the potential of elevated temperature post-IR IRSL signals for dating Romanian loess. Quat. Geochronol. 2012, 10, 75–80. [Google Scholar] [CrossRef]
- Vasiliniuc, S.; Vandenberghe, D.A.G.; Timar-Gabor, A.; Van Den haute, P. Conventional IRSL dating of Romanian loess using single aliquots of polymineral fine grains. Radiat. Meas. 2013, 48, 60–67. [Google Scholar] [CrossRef]
- Huntley, D.J.; Godfrey-Smith, D.I.; Thewalt, M.L.W. Optical dating of sediments. Nature 1985, 313, 105–107. [Google Scholar] [CrossRef]
- Singhvi, A.K.; Porat, N. Impact of luminescence dating on geomorphological and palaeoclimate research in drylands. Boreas 2008, 37, 536–558. [Google Scholar] [CrossRef]
- Wintle, A.G. Luminescence dating: Where it has been and where it is going. Boreas 2008, 37, 471–482. [Google Scholar] [CrossRef]
- Mejdahl, V. Thermoluminescence dating: Beta-dose attenuation in quartz grains. Archaeometry 1979, 21, 61–72. [Google Scholar] [CrossRef]
- Aitken, M.J. Thermoluminescence Dating; Academic Press: London, UK, 1985; pp. 252–262. [Google Scholar]
- Schmidt, C.; Bösken, J.; Kolb, T. Is there a common alpha-efficiency in polymineral samples measured by various infrared stimulated luminescence protocols? Geochronometria 2018, 45, 160–172. [Google Scholar] [CrossRef]
- Constantin, D.; Timar-Gabor, A.; Veres, D.; Begy, R.; Cosma, C. SAR-OSL dating of different grain-size quartz from a sedimentary section in southern Romania interbedding the Campanian Ignimbrite/Y5 ash layer. Quat. Geochronol. 2012, 10, 81–86. [Google Scholar] [CrossRef]
- Lomax, J.; Fuchs, M.; Preusser, F.; Fiebig, M. Luminescence based loess chronostratigraphy of the Upper Palaeolithic site Krems-Wachtberg, Austria. Quat. Int. 2014, 351, 88–97. [Google Scholar] [CrossRef]
- Trandafir, O.; Timar-Gabor, A.; Schmidt, C.; Veres, D.; Anghelinu, N.; Hambach, U.; Simon, S. OSL dating of fine and coarse quartz from a Palaeolithic sequence on the Bistrița Valley (Northeastern Romania). Quat. Geochronol. 2014, 30, 487–492. [Google Scholar] [CrossRef]
- Fuchs, M.; Kreutzer, S.; Rousseau, D.-D.; Antoine, P.; Hatté, C.; Lagroix, F.; Moine, O.; Gauthier, C.; Svoboda, J.; Lisá, L. The loess sequence of Dolní Věstonice, Czech Republic: A new OSL-based chronology of the Last Climatic Cycle. Boreas 2013, 42, 664–677. [Google Scholar] [CrossRef]
- Kreutzer, S.; Fuchs, M.; Meszner, S.; Faust, D. OSL chronostratigraphy of a loess-palaeosol sequence in Saxony/Germany using quartz of different grain sizes. Quat. Geochronol. 2012, 10, 102–109. [Google Scholar] [CrossRef]
- Constantin, D.; Veres, D.; Panaiotu, C.; Anechitei-Deacu, V.; Groza, S.M.; Begy, R.; Kelemen, S.; Buylaert, J.P.; Hambach, U.; Marković, S.B.; et al. Luminescence age constraints on the Pleistocene-Holocene transition recorded in loess sequences across SE Europe. Quat. Geochronol. 2019, 49, 71–77. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Constantin, D.; Buylaert, J.P.; Jain, M.; Murray, A.S.; Wintle, A.G. Fundamental investigations of natural and laboratory generated SAR dose response curves for quartz OSL in the high dose range. Radiat. Meas. 2015, 81, 150–156. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Wintle, A.G. On natural and laboratory generated dose response curves for quartz of different grain sizes from Romanian loess. Quat. Geochronol. 2013, 18, 34–40. [Google Scholar] [CrossRef]
- Chapot, M.S.; Roberts, H.M.; Duller, G.A.T.; Lai, Z.P. A comparison of natural-and laboratory-generated dose response curves for quartz optically stimulated luminescence signals from Chinese Loess. Radiat. Meas. 2012, 47, 1045–1052. [Google Scholar] [CrossRef]
- Buggle, B.; Glaser, B.; Zöller, L.; Hambach, U.; Marković, S.; Glaser, I.; Gerasimenko, N. Geochemical characterization and origin of Southeastern and Eastern European loesses (Serbia, Romania, Ukraine). Quat. Sci. Rev. 2008, 27, 1058–1075. [Google Scholar] [CrossRef]
- Fitzsimmons, K.E.; Marković, S.B.; Hambach, U. Pleistocene environmental dynamics recorded in the loess of the middle and lower Danube basin. Quat. Sci. Rev. 2012, 41, 104–118. [Google Scholar] [CrossRef]
- Codrea, V. Geologia Cuaternarului: Notiuni de Baza; (Quaternary Geology. Basic Notions); Litographed course; Babes-Bolyai University: Cluj Napoca, Romania, 1998. [Google Scholar]
- Conea, A. Profils de loess en Roumanie. La stratigraphy des loess d’Europe. In Bulletin de l’Association Française Pour L’étude du Quaternaire; Fink, J., Ed.; Suppl. INQUA: Budapest, Hungary, 1986; pp. 127–134. [Google Scholar]
- Conea, A. Formatiuni Cuaternareîn Dobrogea (Loessuri si Paleosoluri) (Quaternary Units in Dobrogea), 1st ed.; Editura Academiei RSR: Bucuresti, Romania, 1970; p. 234. [Google Scholar]
- Panaiotu, C.G.; Panaiotu, E.C.; Grama, A.; Necula, C. Paleoclimatic Record from a Loess-Paleosol Profile in Southeastern Romania. Phys. Chem. Earth A 2001, 26, 893–989. [Google Scholar] [CrossRef]
- Necula, C.; Panaiotu, C. Application of dynamic programming to the dating of a loess-paleosol sequences. Rom. Rep. Phys. 2008, 60, 157–171. [Google Scholar]
- Bălescu, S.; Lamothe, M.; Panaiotu, C.; Panaiotu, C. La chronologie IRSL des séquences loessiques de l’est de la Roumanie. Quaternaire 2010, 21, 115–126. [Google Scholar] [CrossRef]
- Constantin, D.; Cameniță, A.; Panaiotu, C.; Necula, C.; Codrea, V.; Timar-Gabor, A. Fine and coarse-quartz SAR-OSL dating of Last Glacial loess in Southern Romania. Quat. Int. 2015, 357, 33–43. [Google Scholar] [CrossRef]
- Rădan, S.C.; Rădan, M. Study of the geomagnetic field structure in Tertiary in the context of magnetostratigraphic scale elaboration. I—The Pliocene. Anu. Inst. Geol. României 1998, 70, 215–231. [Google Scholar]
- Buggle, B.; Hambach, U.; Glaser, B.; Gerasimenko, N.; Marković, S.; Glaser, I.; Zöller, L. Stratigraphy, and spatial and temporal paleoclimatic trends in Southeastern/Eastern European loess-paleosol sequences. Quat. Int. 2009, 196, 86–106. [Google Scholar] [CrossRef]
- Bălescu, S.; Lamothe, M.; Mercier, N.; Huot, S.; Bălteanu, D.; Billardd, A.; Hus, J. Luminescence chronology of Pleistocene loess deposits from Romania: Testing methods of age correction for anomalous fading in alkali feldspars. Quat. Sci. Rev. 2003, 22, 967–973. [Google Scholar] [CrossRef]
- Fitzsimmons, K.E.; Hambach, U. Loess accumulation during the last glacial maximum: Evidence from Urluia, southeastern Romania. Quat. Int. 2014, 334, 74–85. [Google Scholar] [CrossRef]
- Buggle, B.; Hambach, U.; Müller, K.; Zöller, L.; Marković, S.B.; Glaser, B. Iron mineralogical proxies and Quaternary climate change in SE-European loess-paleosol sequences. Catena 2014, 117, 4–22. [Google Scholar] [CrossRef]
- Necula, C.; Panaiotu, C. Rock magnetic properties of a loess-paleosols complex from Mircea Vodă (Romania). Rom. Rep. Phys. 2012, 64, 516–527. [Google Scholar]
- Necula, C.; Panaiotu, C.; Heslop, D.; Dimofte, D. Climatic control of magnetic granulometry in the Mircea Vodă loess/paleosol sequence (Dobrogea, Romania). Quat. Int 2013, 293, 5–14. [Google Scholar] [CrossRef]
- Heslop, D.; Langereis, C.G.; Dekkers, M.J. A new astronomical timescale for the loess deposits of Northern China. Earth Planet. Sci. Lett. 2000, 184, 125–139. [Google Scholar] [CrossRef]
- Buggle, B.; Hambach, U.; Kehl, M.; Marković, S.B.; Zöller, L.; Glaser, B. The progressive evolution of a continental climate in southeast-central European lowlands during the Middle Pleistocene recorded in loess paleosol sequences. Geology 2013, 41, 771–774. [Google Scholar] [CrossRef]
- Lisiecki, L.E.; Lisiecki, P.A. Application of dynamic programming to the correlation of paleoclimate records. Paleoceanography 2002, 17, 1049. [Google Scholar] [CrossRef]
- Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records. Paleoceanography 2005, 20, PA1003. [Google Scholar] [CrossRef]
- Vasiliniuc, Ș.; Vandenberghe, D.A.G.; Timar-Gabor, A.; Cosma, C.; van den Haute, P. Combined IRSL and post-IR OSL dating of Romanian loess using single aliquots of polymineral fine grains. Quat. Int. 2013, 293, 15–21. [Google Scholar] [CrossRef]
- Wallinga, J.; Murray, A.; Duller, G. Underestimation of equivalent dose in single-aliquot optical dating of feldspars caused by preheating. Radiat. Meas. 2000, 32, 691–695. [Google Scholar] [CrossRef]
- Wacha, L.; Frechen, M. The geochronology of the “Gorjanović loess section” in Vukovar, Croatia. Quat. Int. 2011, 240, 87–99. [Google Scholar] [CrossRef]
- Thiel, C.; Buylaert, J.P.; Murray, A.; Terhorst, B.; Hofer, I.; Tsukamoto, S.; Frechen, M. Luminescence dating of the Stratzing loess profile (Austria)—Testing the potential of an elevated temperature post-IR IRSL protocol. Quat. Int. 2011, 234, 23–31. [Google Scholar] [CrossRef]
- Stevens, T.; Marković, S.B.; Zech, M.; Hambach, U.; Sümegi, P. Dust deposition and climate in the Carpathian Basin over an independently dated last glacial-interglacial cycle. Quat. Sci. Rev. 2011, 30, 662–681. [Google Scholar] [CrossRef]
- Lang, A.; Lindauer, S.; Kuhn, R.; Wagner, G.A. Procedures used in optically and infrared stimulated luminescence dating of sediments in Heidelberg. Anc. TL 1996, 14, 7–11. [Google Scholar]
- Frechen, M.; Schweitzer, U.; Zander, A. Improvements in sample preparation for the fine grain technique. Anc. TL 1996, 14, 15–17. [Google Scholar]
- Thomsen, K.J.; Bøtter-Jensen, L.; Jain, M.; Denby, P.M.; Murray, A.S. Recent instrumental developments for trapped electron dosimetry. Radiat. Meas. 2008, 43, 414–521. [Google Scholar] [CrossRef]
- Hansen, V.; Murray, A.S.; Buylaert, J.-P.; Yeo, E.-Y.; Thomsen, K. A new irradiated quartz for beta source calibration. Radiat. Meas. 2015, 81, 123–127. [Google Scholar] [CrossRef]
- Murray, A.S.; Wintle, A.G. The single aliquot regenerative dose protocol: Potential for improvements in reliability. Radiat. Meas. 2003, 37, 377–381. [Google Scholar] [CrossRef]
- Cunningham, A.C.; Wallinga, J. Selection of integration intervals for quartz OSL decay curves. Quat. Geochronol. 2010, 5, 657–666. [Google Scholar] [CrossRef]
- Prescott, J.R.; Hutton, J.T. Cosmic ray contributions to dose rates for luminescence and ESR dating: Large depths and long-term time variations. Radiat. Meas. 1994, 23, 497–500. [Google Scholar] [CrossRef]
- Vandenberghe, D.; De Corte, F.; Buylaert, J.-P.; Kučera, J.; Van den haute, P. On the internal radioactivity of quartz. Radiat. Meas. 2008, 43, 771–775. [Google Scholar] [CrossRef]
- Rees-Jones, J. Optical dating of young sediments using fine-grain quartz. Anc. TL 1995, 13, 9–14. [Google Scholar]
- Murray, A.S.; Svendsen, J.I.; Mangerund, J.I.; Astakhov, V.I. Testing the accuracy of quartz OSL dating using a known-age Eemian site on the river Sula, northern Russia. Quat. Geochronol. 2007, 2, 102–109. [Google Scholar] [CrossRef]
- Pawley, S.M.; Toms, P.; Armitage, S.J.; Rose, J. Quartz luminescence dating of Anglian Stage (MIS 12) fluvial sediments: Comparison of SAR age estimates to the terrace chronology of the Middle Thames valley, UK. Quat. Geochronol. 2010, 5, 569–582. [Google Scholar] [CrossRef]
- Lowick, S.E.; Preusser, F. Investigating age underestimation in the high dose region of optically stimulated luminescence using fine grain quartz. Quat. Geochronol. 2011, 6, 33–41. [Google Scholar] [CrossRef]
- Lowick, S.E.; Preusser, F.; Wintle, A.G. Investigating quartz optically stimulated luminescence dose-response curves at high doses. Radiat. Meas. 2010, 45, 975–984. [Google Scholar] [CrossRef]
- Duller, G.A.T. Distinguishing quartz and feldspar in single grain luminescence measurements. Radiat. Meas. 2003, 37, 161–165. [Google Scholar] [CrossRef]

| Authors/Year | Mineral | Stratigraphical Units Investigated | Measurement Protocol |
|---|---|---|---|
| Bălescu, S.; Lamothe, M.; Panaiotu, C.; Panaiotu, C. (2010) [38] | alkali feldspars (60–80 µm) |
| Multiple aliquot additive dose method (MAAD) |
| Timar, A.; Vandenberghe, D.; Panaiotu, E.C.; Panaiotu, C.G.; Necula, C.; Cosma, C.; van den haute, P. (2010) [2] | quartz (4–11 µm) |
| SAR (CW-OSL) |
| Timar-Gabor, A.; Vandenberghe, D.A.G.; Vasiliniuc, Ș.; Panaiotu, E.C.; Panaiotu, C.G.; Dimofte, D.; Cosma, C. (2011) [8] | quartz (63–90 µm) |
| SAR (CW-OSL) |
| Timar-Gabor, A.; Vasiliniuc, S.; Vandenberghe, D.A.G.; Cosma, C.; Wintle, A.G.; (2012) [14] | quartz (4–11 and 63–90 µm) |
| SAR (CW-OSL) Dose response curves constructed up to 1200 Gy using LM-OSL signals |
| Vasiliniuc, Ș.; Vandenberghe, D.A.G.; Timar-Gabor, A.; Panaiotu, C.; Cosma, C.; van den Haute, P. (2012) [14] | polymineral grains (4–11 µm) |
| Post- IR IR225, 300 |
| Vasiliniuc, Ș.;Vandenberghe, D.A.G.;Timar-Gabor, A.;Cosma, C.; Van Den haute, P. (2013) [51] | polymineral grains (4–11 µm) |
| Double SAR (CW-OSL) |
| Vasiliniuc, Ș.;Vandenberghe, D.A.G.;Timar-Gabor, A.; van den Haute, P. (2013) [15] | polymineral grains (4–11 µm) |
| Modified SAR -IRSL at 115°C and 250°C |
| Timar-Gabor, A.; Constantin, D.; Buylaert, J.P.; Jain, M.; Murray, A.S.; Wintle, A.G. (2015) [28] | quartz (63–90 µm) |
| SAR (CW-OSL) Dose response curves constructed up to 15 kGy |
| Unit Code | Sampling Depth (m) | Laboratory Code | Grain Size (µm) | Equivalent Dose (Gy) | Recycling Ratio | Recuperation (%) | IR depletion Ratio | Total dose Rate (Gy/ka) | Cosmic dose Rate (Gy/ka) | Age (ka) | Random Error (%) | Systematic Error (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
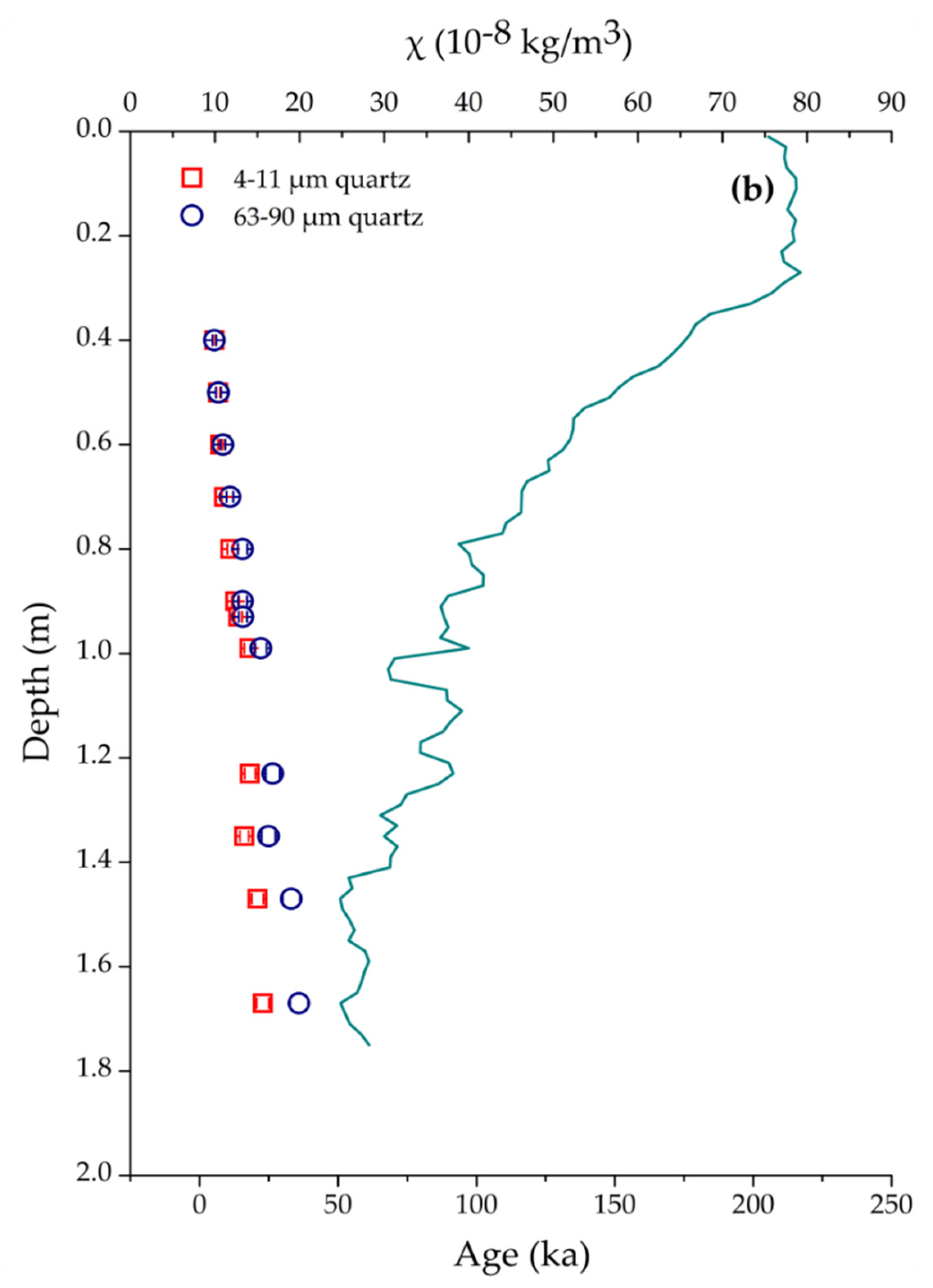
| S0/L1 | 0.4 | 2MV 40 | 4–11 | 15.4 ± 0.2 | 1.02 ± 0.01 | 0.11 ± 0.03 | 0.99 ± 0.01 | 2.91 ± 0.05 | 0.22 ± 0.03 | 5.3 ± 0.5 | 2.3 | 9.9 |
| 63–90 | 12.9 ± 1.5 | 1.03 ± 0.01 | 0.15 ± 0.07 | 0.98 ± 0.01 | 3.44 ± 0.05 | 5.3 ± 0.7 | 11.8 | 7.6 | ||||
| S0/L1 | 0.5 | 2MV 50 | 4–11 | 20.3 ± 0.3 | 1.02 ± 0.01 | 0.07 ± 0.03 | 0.95 ± 0.01 | 3.05 ± 0.07 | 0.21 ± 0.03 | 6.7 ± 0.7 | 2.7 | 9.9 |
| 63–90 | 17.3 ± 1.9 | 1.05 ± 0.01 | 0.14 ± 0.04 | 0.98 ± 0.01 | 2.55 ± 0.06 | 6.8 ± 0.9 | 11.2 | 7.6 | ||||
| S0/L1 | 0.6 | 2MV 60 | 4–11 | 23.6 ± 0.5 | 1.04 ± 0.01 | 0.05 ± 0.05 | 0.99 ± 0.01 | 3.15 ± 0.05 | 0.21 ± 0.03 | 7.5 ± 0.8 | 2.7 | 9.9 |
| 63–90 | 22.1 ± 1.6 | 1.02 ± 0.01 | 0.21 ± 0.10 | 0.98 ± 0.01 | 2.64 ± 0.05 | 8.4 ± 0.9 | 7.4 | 7.6 | ||||
| S0/L1 | 0.7 | 2MV 70 | 4–11 | 25.6 ± 0.3 | 1.03 ± 0.01 | 0.07 ± 0.03 | 0.98 ± 0.01 | 2.88 ± 0.05 | 0.20 ± 0.03 | 8.9 ± 0.9 | 2.1 | 9.9 |
| 63–90 | 26.6 ± 2.1 | 1.03 ± 0.01 | 0.09 ± 0.02 | 0.98 ± 0.01 | 2.41 ± 0.05 | 11.0 ± 1.2 | 8.1 | 7.6 | ||||
| S0/L1 | 0.8 | 2MV 80 | 4–11 | 31.2 ± 0.4 | 1.00 ± 0.01 | 0.07 ± 0.03 | 0.95 ± 0.01 | 2.81 ± 0.05 | 0.20 ± 0.03 | 11.1 ± 1.1 | 2.0 | 10.0 |
| 63–90 | 36.4 ± 2.9 | 1.02 ± 0.01 | 0.09 ± 0.03 | 0.95 ± 0.01 | 2.35 ± 0.05 | 15.5 ± 1.7 | 8.2 | 7.6 | ||||
| S0/L1 | 0.9 | 2MV 90 | 4–11 | 35.9 ± 0.6 | 0.99 ± 0.01 | 0.19 ± 0.04 | 0.98 ± 0.01 | 2.77 ± 0.05 | 0.19 ± 0.03 | 12.9 ± 1.3 | 2.5 | 10.0 |
| 63–90 | 36.0 ± 2.5 | 1.03 ± 0.01 | 0.05 ± 0.02 | 0.97 ± 0.01 | 2.32 ± 0.05 | 15.5 ± 1.6 | 7.2 | 7.6 | ||||
| S0/L1 | 0.93 | MV 2.1 | 4–11 | 28.3 ± 0.6 | 1.04 ± 0.01 | 0.03 ± 0.03 | 0.94 ± 0.01 | 2.75 ± 0.04 | 0.19 ± 0.03 | 14.0 ± 1.4 | 2.3 | 9.7 |
| 63–90 | 36.1 ± 2.0 | 1.02 ± 0.01 | 0.11 ± 0.03 | 0.98 ± 0.01 | 2.31 ± 0.04 | 15.6 ± 1.5 | 5.8 | 7.6 | ||||
| S0/L1 | 0.99 | MV 2.2 | 4–11 | 51.7 ± 0.6 | 0.99 ± 0.01 | 0.04 ± 0.01 | 0.98 ± 0.01 | 2.88 ± 0.05 | 0.19 ± 0.03 | 18.0 ± 1.8 | 2.2 | 9.7 |
| 63–90 | 53.6 ± 2.6 | 1.01 ± 0.01 | 0.04 ± 0.02 | 0.97 ± 0.01 | 2.42 ± 0.05 | 22.1 ± 2.1 | 5.2 | 7.7 | ||||
| S0/L1 | 1.23 | MV 2.3 | 4–11 | 51.2 ± 0.9 | 1.02 ± 0.02 | 0.04 ± 0.02 | 0.90 ± 0.01 | 2.81 ± 0.06 | 0.18 ± 0.03 | 18.2 ± 1.9 | 2.8 | 9.9 |
| 63–90 | 62.1 ± 3.0 | 1.01 ± 0.01 | 0.15 ± 0.07 | 0.97 ± 0.01 | 2.53 ± 0.05 | 26.4 ± 2.5 | 5.3 | 7.6 | ||||
| S0/L1 | 1.35 | MV 2.4 | 4–11 | 46.8 ± 0.8 | 1.03 ± 0.02 | 0.04 ± 0.02 | 0.98 ± 0.01 | 2.92 ± 0.04 | 0.18 ± 0.03 | 16.1 ± 1.6 | 2.2 | 9.9 |
| 63–90 | 60.8 ± 3.8 | 1.02 ± 0.01 | 0.09 ± 0.03 | 0.97 ± 0.01 | 2.44 ± 0.04 | 24.9 ± 2.5 | 6.4 | 7.7 | ||||
| S0/L1 | 1.47 | MV 2.5 | 4–11 | 59.7 ± 1.0 | 1.03 ± 0.01 | 0.04 ± 0.02 | 0.92 ± 0.01 | 2.85 ± 0.05 | 0.18 ± 0.03 | 20.9 ± 2.1 | 2.3 | 9.9 |
| 63–90 | 79.0 ± 4.1 | 1.00 ± 0.01 | 0.06 ± 0.02 | 0.97 ± 0.01 | 2.39 ± 0.04 | 33.1 ± 3.1 | 5.5 | 7.7 | ||||
| S0/L1 | 1.67 | MV 2.6 | 4–11 | 67.4 ± 0.6 | 1.00 ± 0.01 | 0.05 ± 0.01 | 0.98 ± 0.01 | 2.91 ± 0.05 | 0.17 ± 0.03 | 22.8 ± 2.3 | 2.0 | 10.1 |
| 63–90 | 86.9 ± 3.5 | 1.00 ± 0.01 | 0.06 ± 0.03 | 0.98 ± 0.01 | 2.42 ± 0.04 | 35.9 ± 3.2 | 4.4 | 7.7 | ||||
| L2 | 5.70 | 2MV 570A | 4–11 | 331 ± 6 | 0.96 ± 0.01 | 0.10 ± 0.01 | 0.95 ± 0.01 | 3.03 ± 0.06 | 0.11 ± 0.02 | 109 ± 11 | 2.6 | 10.0 |
| 63–90 | 303 ± 13 | 0.97 ± 0.01 | 0.06 ± 0.02 | 0.96 ± 0.01 | 2.54 ± 0.05 | 120 ± 11* | 4.7 | 7.8 | ||||
| L2 | 5.70 | 2MV 570B | 4–11 | 331 ± 3 | 0.96 ± 0.01 | 0.09 ± 0.01 | 0.96 ± 0.01 | 2.95 ± 0.06 | 0.11 ± 0.02 | 112 ± 12 | 2.2 | 10.1 |
| 63–90 | 353 ± 13 | 0.97 ± 0.01 | 0.05 ± 0.02 | 0.95 ± 0.01 | 2.46 ± 0.05 | 143 ± 13* | 4.2 | 7.8 | ||||
| L3 | 13.70 | 2MV L3A | 4–11 | 514 ± 16 | 0.98 ± 0.01 | 0.06 ± 0.01 | 0.98 ± 0.01 | 2.88 ± 0.05 | 0.06 ± 0.01 | 179 ± 19 | 2.4 | 10.3 |
| 63–90 | 475 ± 19 | 0.96 ± 0.01 | 0.010 ± 0.02 | 0.94 ± 0.01 | 2.39 ± 0.04 | 199 ± 18* | 4.3 | 8.0 | ||||
| L3 | 13.70 | 2MV L3B | 4–11 | 501 ± 11 | 0.98 ± 0.01 | 0.05 ± 0.01 | 0.99 ± 0.01 | 2.86 ± 0.06 | 0.06 ± 0.01 | 175 ± 18 | 2.2 | 10.2 |
| 63–90 | 501 ± 23 | 0.95 ± 0.01 | 0.11 ± 0.02 | 0.94 ± 0.01 | 2.38 ± 0.05 | 210 ± 20* | 5.0 | 8.0 | ||||
| L4 | 17.70 | 2MV L4A | 4–11 | 567 ± 9 | 0.99 ± 0.01 | 0.05 ± 0.002 | 1.00 ± 0.01 | 3.14 ± 0.05 | 0.04 ± 0.01 | 180 ± 19 | 2.3 | 10.4 |
| 63–90 | 577 ± 23 | 0.97 ± 0.01 | 0.13 ± 0.02 | 0.97 ± 0.01 | 2.60 ± 0.05 | 222 ± 20* | - | - | ||||
| L4 | 17.70 | 2MV L4B | 4–11 | 477 ± 6 | 1.00 ± 0.01 | 0.07 ± 0.004 | 0.91 ± 0.01 | 3.41 ± 0.06 | 0.04 ± 0.01 | 140 ± 13 | 2.2 | 8.8 |
| 63–90 | 555 ± 26 | 0.98 ± 0.01 | 0.17 ± 0.03 | 0.95 ± 0.01 | 2.31 ± 0.05 | 240 ± 23* | - | - | ||||
| L5 | 20.50 | 2MV L5A | 4–11 | 566 ± 8 | 0.98 ± 0.01 | 0.07 ± 0.003 | 0.98 ± 0.01 | 2.66 ± 0.06 | 0.04 ± 0.01 | 213 ± 22 | 2.5 | 10.2 |
| 63–90 | 425 ± 39 | 0.98 ± 0.01 | 0.21 ± 0.09 | 0.98 ± 0.01 | 2.22 ± 0.05 | 192 ± 24* | - | 8.0 | ||||
| L5 | 20.50 | 2MV L5B | 4–11 | 556 ± 13 | 0.99 ± 0.01 | 0.06 ± 0.01 | 0.98 ± 0.01 | 2.98 ± 0.06 | 0.04 ± 0.01 | 187 ± 20 | 2.9 | - |
| 63–90 | 443 ± 35 | 0.94 ± 0.02 | 0.43 ± 0.10 | 0.97 ± 0.03 | 2.48 ± 0.05 | 179 ± 20* | 8.1 | 8.0 |
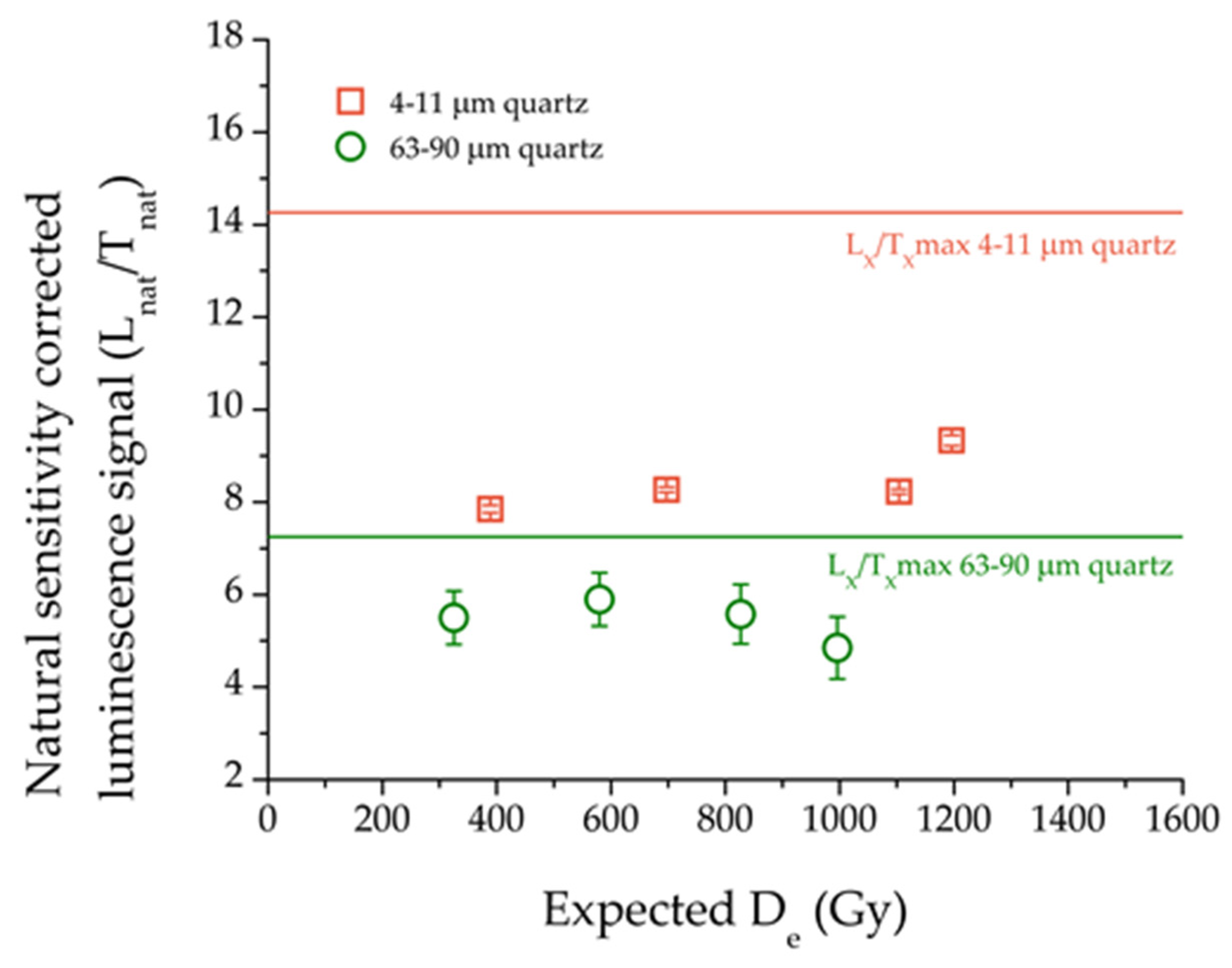
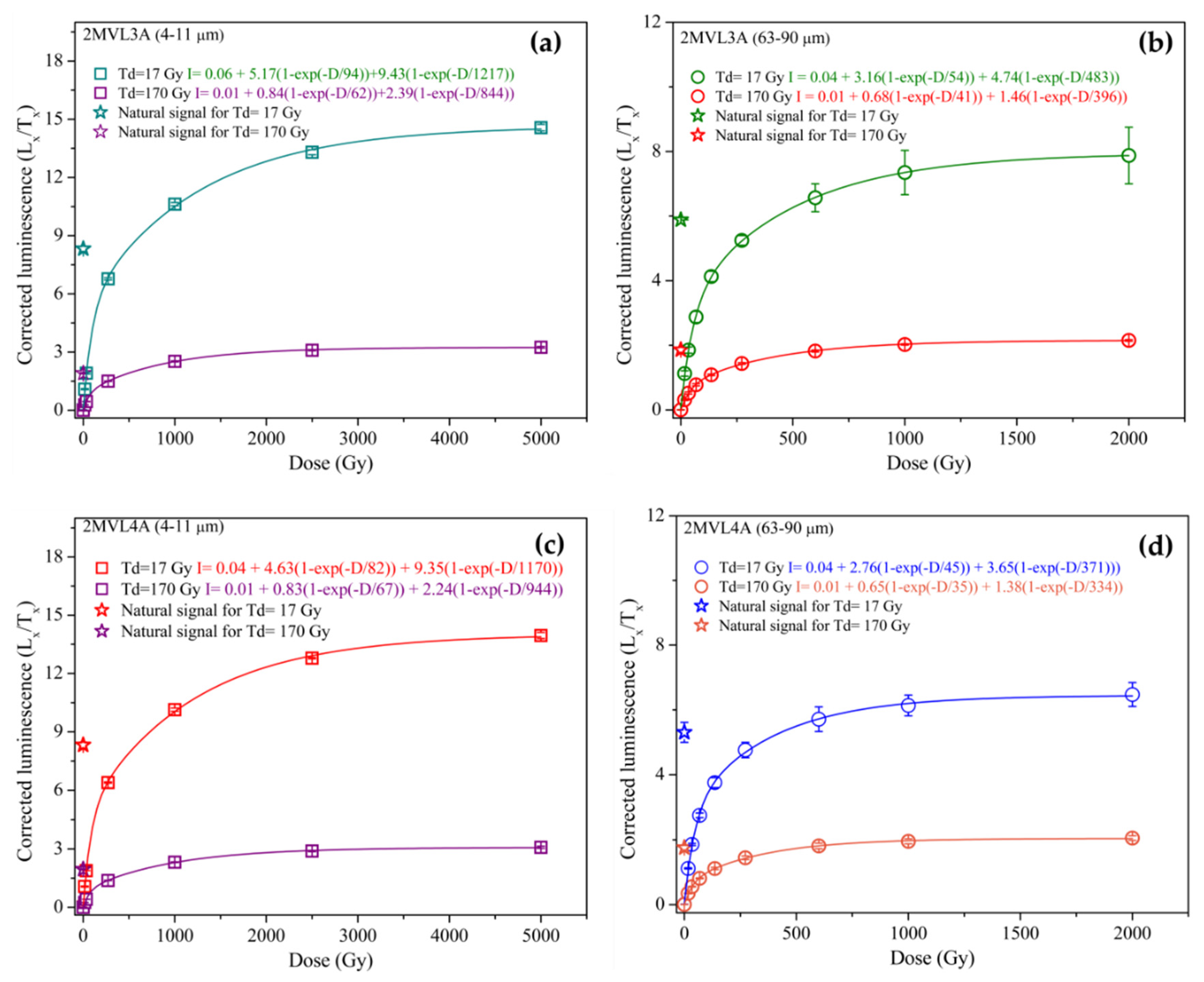
| Sample | Test Dose (Gy) | y0 | y0Error | A1 | A1 Error | D01 | D01Error | A2 | A2 Error | D02 | D02Error | Reduced χ2 | R2 | De (Gy) | Closeness of Natural Signal to Laboratory Saturation Level (%) |
| 4–11 μm 2MV L3A | 17 | 0.06 | 0.14 | 5.2 | 0.4 | 94 | 18 | 9.4 | 0.4 | 1217 | 112 | 0.022 | 0.999 | 493 ± 28 | 57 |
| 170 | 0.01 | 0.02 | 0.8 | 0.06 | 62 | 8 | 2.4 | 0.06 | 844 | 42 | 0.05 × 10−2 | 0.999 | 505 ± 26 | 59 | |
| 4–11 μm 2MV L4A | 17 | 0.04 | 0.12 | 4.6 | 0.3 | 82 | 13 | 9.4 | 0.3 | 1170 | 88 | 0.017 | 0.999 | 584 ± 29 | 60 |
| 170 | 0.01 | 0.03 | 0.8 | 0.08 | 67 | 12 | 2.2 | 0.07 | 944 | 63 | 0.09 × 10−2 | 0.999 | 604 ± 47 | 63 | |
| Sample | Test Dose (Gy) | y0 | y0 Error | A1 | A1 Error | D01 | D01 Error | A2 | A2 Error | D02 | D02 Error | Reduced χ2 | R2 | De (Gy) | |
| 63–90 μm 2MV L3A | 17 | 0.04 | 0.05 | 3.2 | 0.2 | 54 | 4 | 4.7 | 0.2 | 483 | 30 | 0.002 | 0.999 | 584 ± 29 | 74 |
| 170 | 0.01 | 0.02 | 0.7 | 0.05 | 41 | 5 | 1.5 | 0.05 | 396 | 25 | 0.03 × 10−2 | 0.999 | 560 ± 73 | 86 | |
| 63–90 μm 2MV L4A | 17 | 0.04 | 0.07 | 2.8 | 0.3 | 45 | 6 | 3.7 | 0.2 | 371 | 41 | 0.005 | 0.999 | 440 ± 27 | 83 |
| 170 | 0.01 | 0.02 | 0.7 | 0.06 | 35 | 5 | 1.4 | 0.05 | 334 | 24 | 0.3 × 10−2 | 0.999 | 628 ±89 | 89 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groza-Săcaciu, Ș.-M.; Panaiotu, C.; Timar-Gabor, A. Single Aliquot Regeneration (SAR) Optically Stimulated Luminescence Dating Protocols Using Different Grain-Sizes of Quartz: Revisiting the Chronology of Mircea Vodă Loess-Paleosol Master Section (Romania). Methods Protoc. 2020, 3, 19. https://doi.org/10.3390/mps3010019
Groza-Săcaciu Ș-M, Panaiotu C, Timar-Gabor A. Single Aliquot Regeneration (SAR) Optically Stimulated Luminescence Dating Protocols Using Different Grain-Sizes of Quartz: Revisiting the Chronology of Mircea Vodă Loess-Paleosol Master Section (Romania). Methods and Protocols. 2020; 3(1):19. https://doi.org/10.3390/mps3010019
Chicago/Turabian StyleGroza-Săcaciu, Ștefana-M., Cristian Panaiotu, and Alida Timar-Gabor. 2020. "Single Aliquot Regeneration (SAR) Optically Stimulated Luminescence Dating Protocols Using Different Grain-Sizes of Quartz: Revisiting the Chronology of Mircea Vodă Loess-Paleosol Master Section (Romania)" Methods and Protocols 3, no. 1: 19. https://doi.org/10.3390/mps3010019
APA StyleGroza-Săcaciu, Ș.-M., Panaiotu, C., & Timar-Gabor, A. (2020). Single Aliquot Regeneration (SAR) Optically Stimulated Luminescence Dating Protocols Using Different Grain-Sizes of Quartz: Revisiting the Chronology of Mircea Vodă Loess-Paleosol Master Section (Romania). Methods and Protocols, 3(1), 19. https://doi.org/10.3390/mps3010019





