Head and Neck Cancer Segmentation in FDG PET Images: Performance Comparison of Convolutional Neural Networks and Vision Transformers
Abstract
:1. Introduction
- (a)
- The use of a clinically relevant HNC PET data set with 650 lesions;
- (b)
- Inclusion of primary and secondary lesions;
- (c)
- The use of a high-quality expert-generated ground truth;
- (d)
- Assessment of differences regarding their significance by utilization of statistical tests.
- Machine-learning-based models like CNNs and Transformers have different inductive biases, which influence a model’s ability to learn from a given data set with certain image characteristics, data set size, etc., and also affect its performance on new data. Thus, to inform method development and optimization efforts, it is worthwhile to investigate the performance of ViT networks in the context of HNC segmentation in PET scans on a reasonably sized image data set.
- A current shortcoming of existing studies is that secondary lesions are ignored in algorithm performance assessment but are of clinical relevance. Consequently, existing performance estimates could be biased. Secondary lesions are typically harder to segment due to potentially smaller size and lower contrast, but they are used for radiation treatment planning. Furthermore, primary and secondary lesions combined are utilized to calculate indices like MTV and TLG, which are often used as quantitative image features for outcome prediction.
- To assess systematic over- or under-segmentation, adequate error metrics are required, because this knowledge is relevant for selecting segmentation methods in the context of radiation treatment.
2. Materials and Methods
2.1. Image Data and Pre-Processing
2.2. Convolutional Neural Networks (CNNs)
2.2.1. U-Net
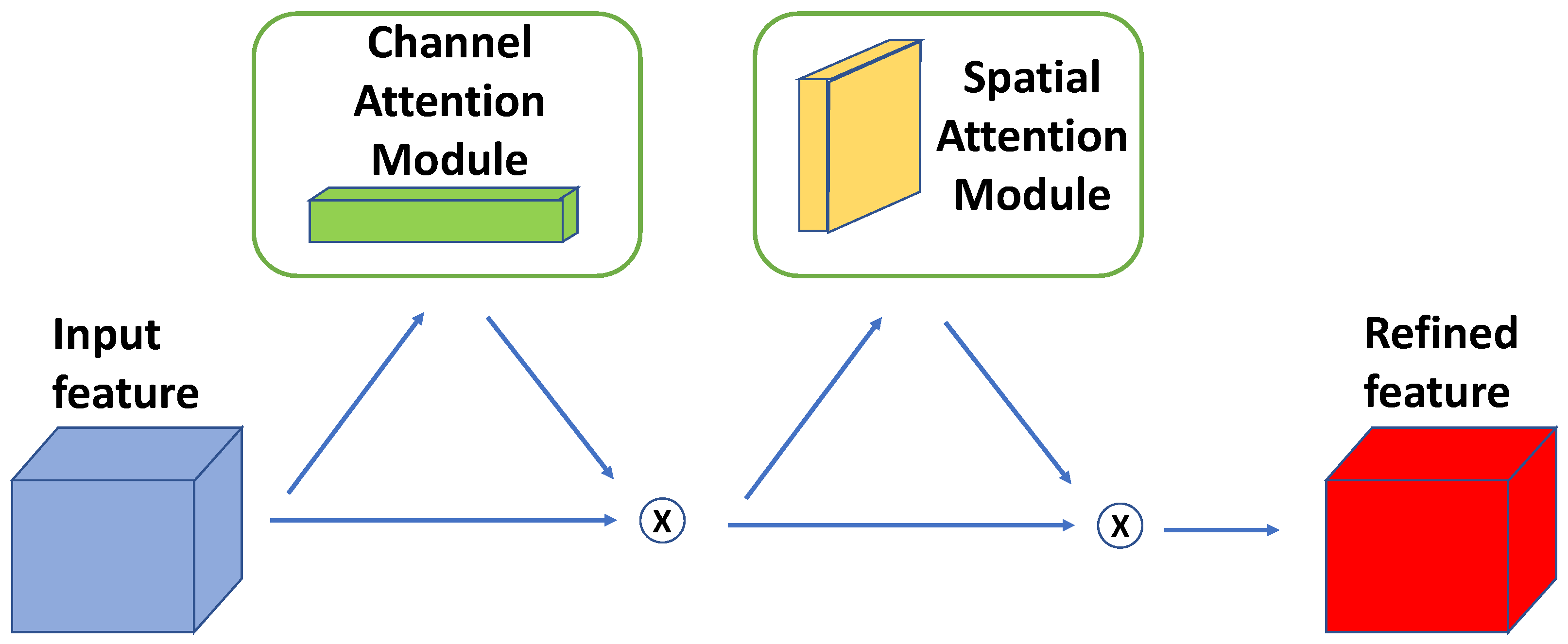
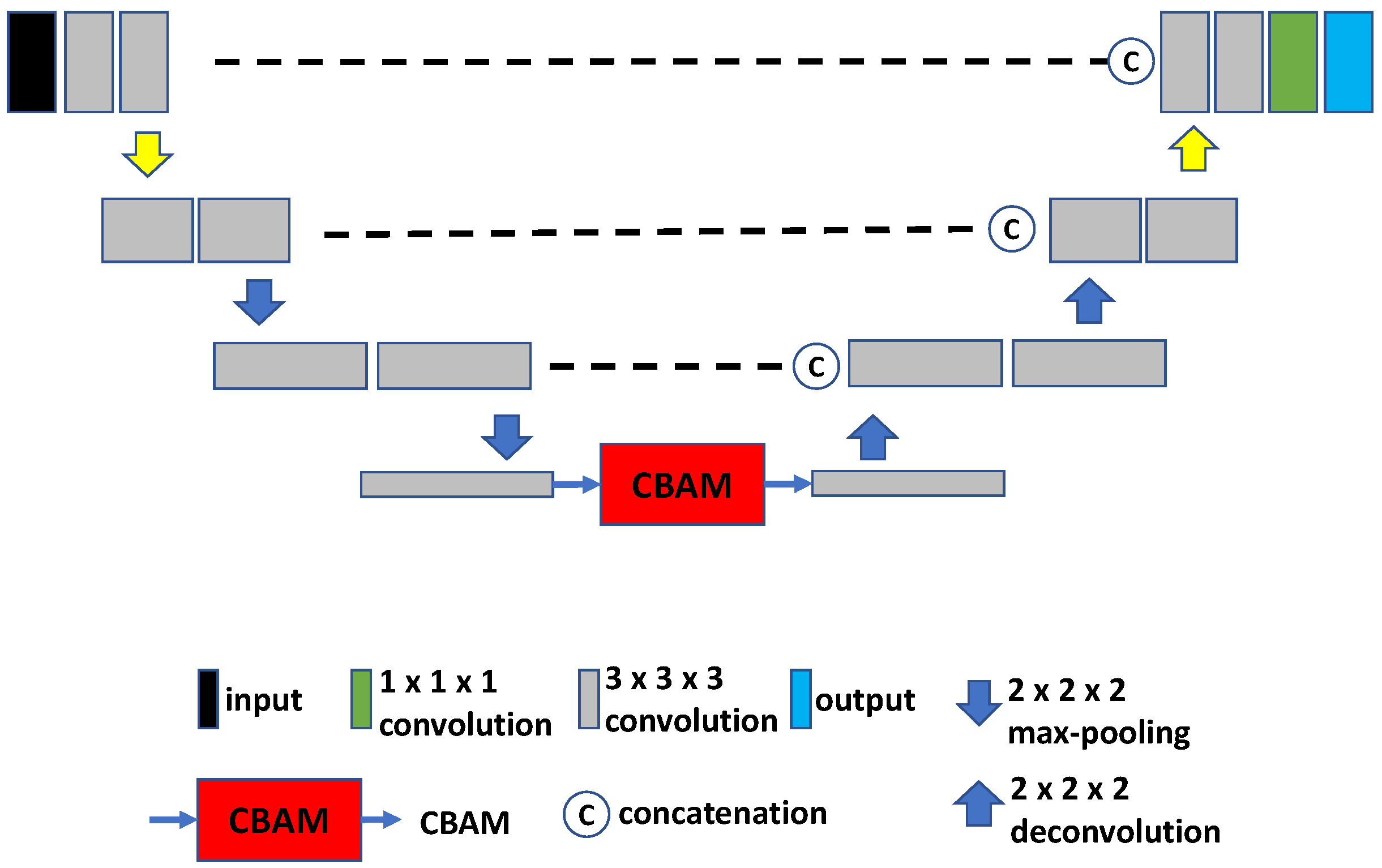
2.2.2. U-Net with CBAM
2.3. Vision Transformer-Based Models
- (a)
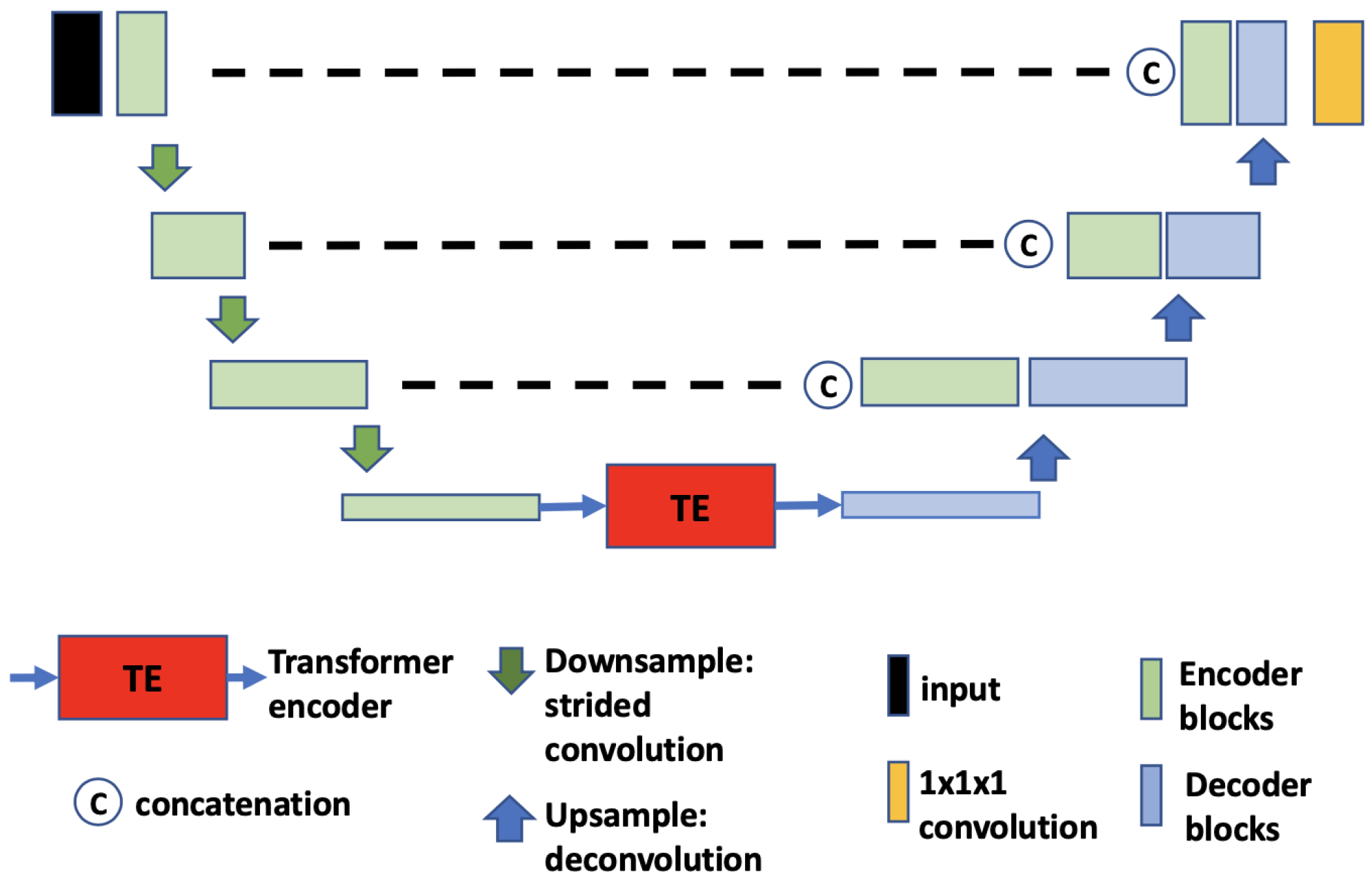
- TransBTS. The core idea of TransBTS [30] (Figure 4) is to replace the bottleneck part of the 3D U-Net with a set of Transformer encoders to model the long-distance dependency in a global space [30]. The contraction–expansion structure from the U-Net is mainly utilized because splitting the data into 3D patches following the ViT makes the model unable to capture the local context information across the whole spatial and depth dimensions for volumetric segmentation. Using convolution blocks with downsampling before the Transformer encoder allows it to learn long-range correlations with a global receptive field with relatively small computational complexity.
- (b)
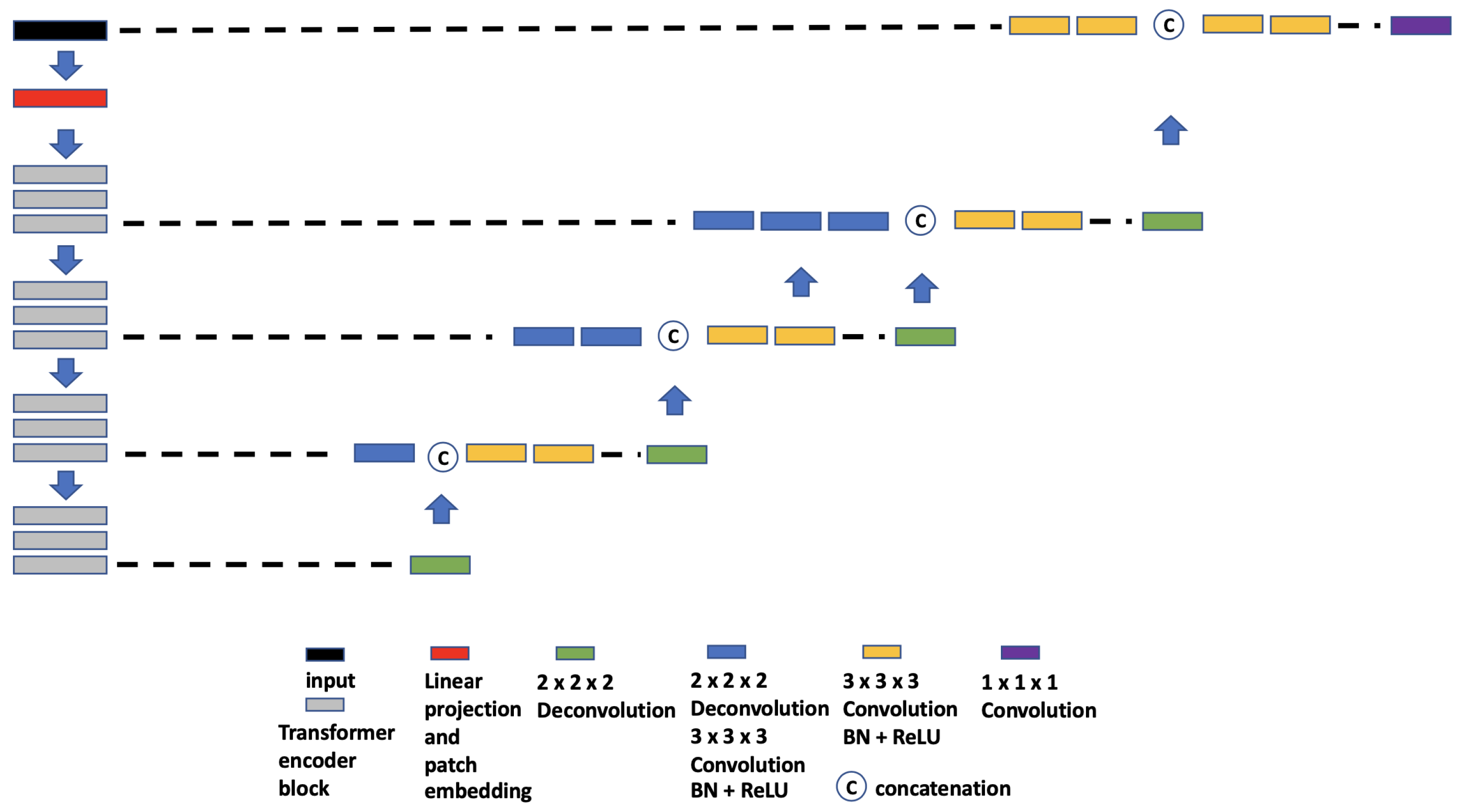
- UNETR. UNETR (Figure 5), proposed by Hatamizadeh et al. [31], is another example of the combination of CNN and ViT. In contrast to TransBTS, UNETR does not use convolution blocks and downsampling to reduce the feature size of the whole data; instead, it splits the data into 3D volume patches and then employs the Transformer as the main encoder and connects it directly to the decoder via skip connections. More specifically, as shown by Hatamizadeh et al. [31], feature representations are extracted from several different layers of the Transformer decoder and reshaped and projected from the embedding space into the input space via deconvolutional and convolutional layers. At the last Transformer layer, a deconvolutional layer is applied to upsample the feature map size by 2, and then it is concatenated with the projected Transformer output from the upper tier. The concatenated feature map is fed to consecutive convolutional layers and subsequently upsampled with a deconvolutional layer. The process is repeated until the original input resolution is reached.
- (c)
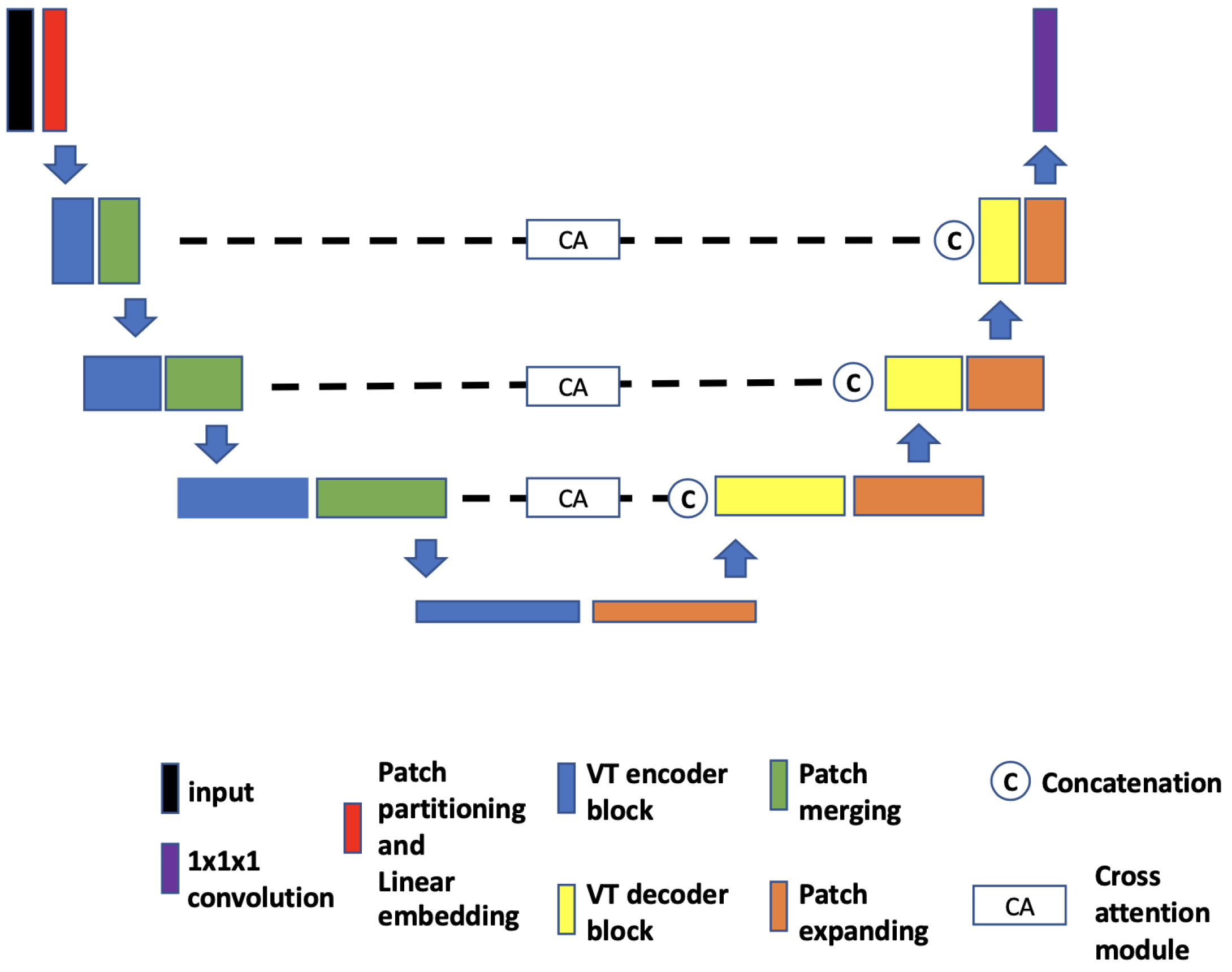
- VT-UNet. The VT-UNet (Figure 6) proposed by Peiris et al. [32] also built on the encoder–decoder-based U-Net architecture. However, instead of trying to combine the CNN with Transformers like TransBTS and UNETR, VT-UNet is purely based on Transformers. This is achieved by two specially-designed Transformer blocks. In the encoder, a hierarchical Transformer block is used to capture both local and global information. It is similar to Swin Transformer blocks [33]. In the decoder, a parallel cross-attention and self-attention module is utilized. It enables creating a bridge between queries from the decoder and keys/values from the encoder. This architecture enables preserving global information during the decoding process [32]. More specifically, the Swin Transformer-based encoder expands the original 2D Swin Transformer to create a hierarchical representation of the 3D input by starting from small volume patches, which are gradually merged with neighboring patches in deeper Transformer layers. Then, the linear computational complexity with input size is achieved by computing SA locally within non-overlapping windows that partition an input. In addition, a shift of the window partition between consecutive SA layers provides connections among windows and significantly enhances the model power [33]. The idea of parallelization in the decoder is to mimic the skip connections in the U-Net and serve the same purpose, enabling a connection between lower-level spatial features from lower layers and higher-level semantic features from upper layers.
2.4. Post-Processing
2.5. Experimental Setup
2.5.1. Network Training
2.5.2. Network Application
2.5.3. Performance Metrics
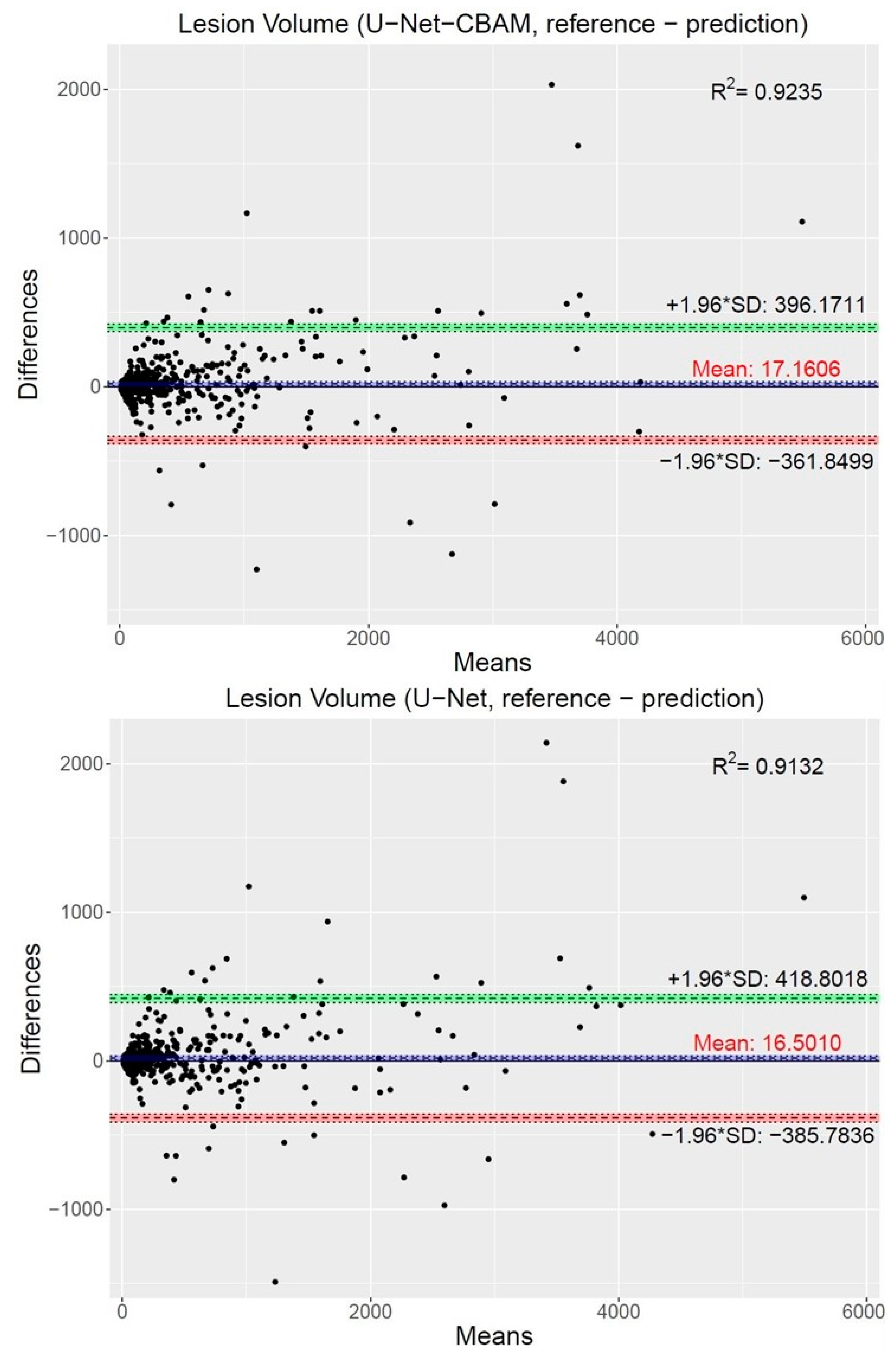
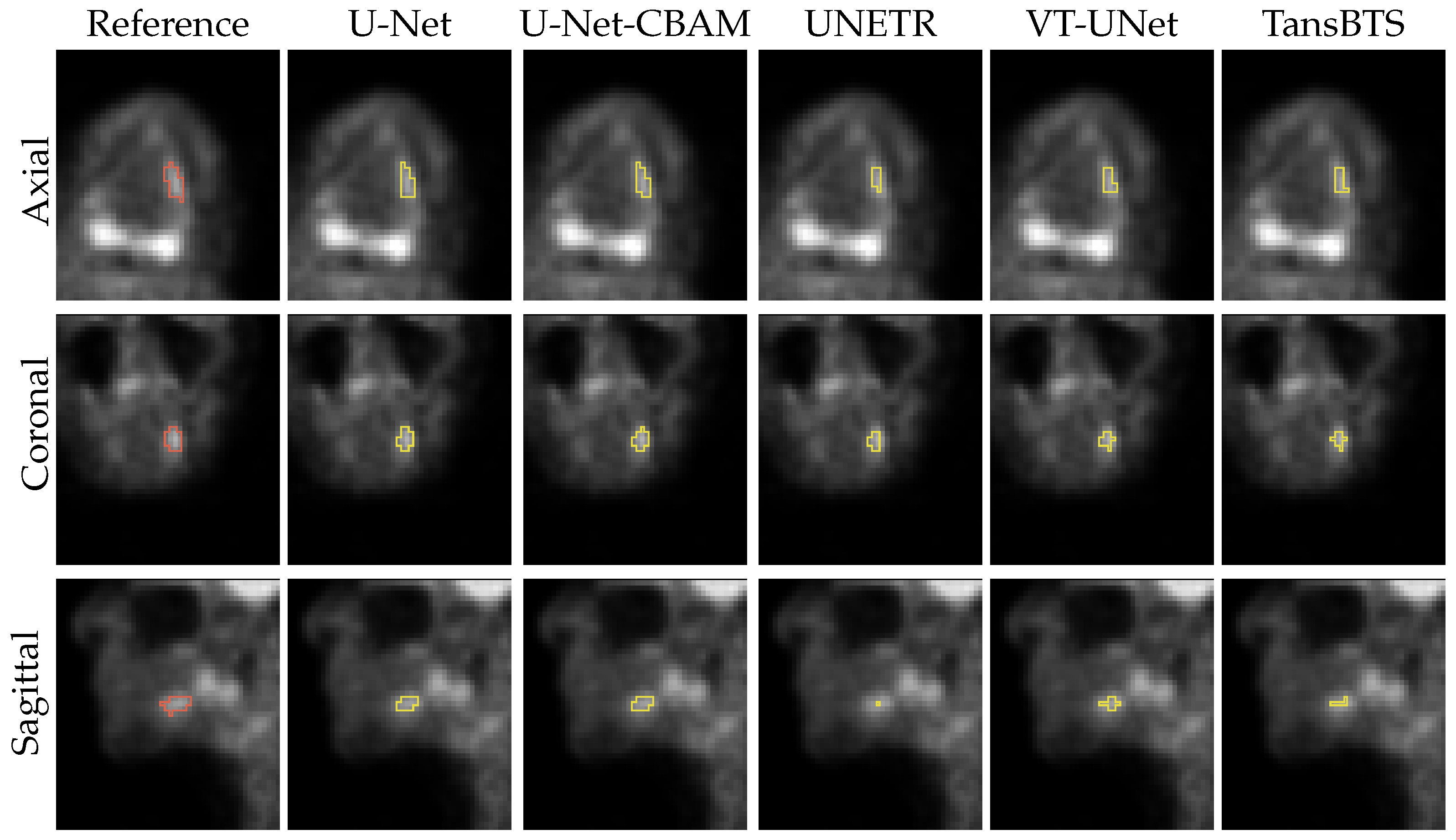
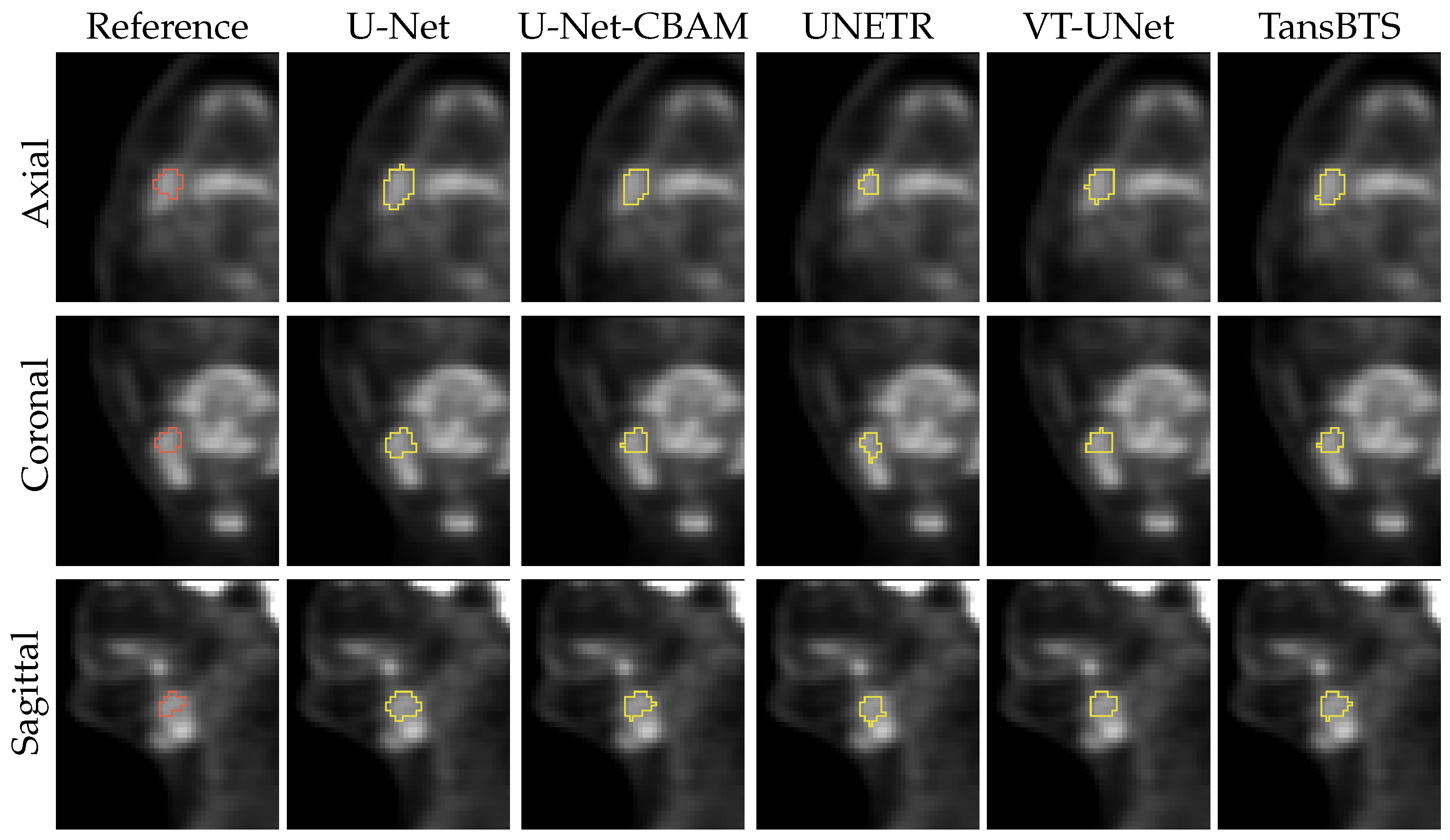
3. Results
4. Discussion
4.1. Segmentation Performance
4.2. Current Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Castelli, J.; De Bari, B.; Depeursinge, A.; Simon, A.; Devillers, A.; Roman Jimenez, G.; Prior, J.; Ozsahin, M.; de Crevoisier, R.; Bourhis, J. Overview of the predictive value of quantitative 18 FDG PET in head and neck cancer treated with chemoradiotherapy. Crit. Rev. Oncol. Hematol. 2016, 108, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Im, H.J.; Bradshaw, T.; Solaiyappan, M.; Cho, S.Y. Current Methods to Define Metabolic Tumor Volume in Positron Emission Tomography: Which One is Better? Nucl. Med. Mol. Imaging 2018, 52, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Beichel, R.R.; Van Tol, M.; Ulrich, E.J.; Bauer, C.; Chang, T.; Plichta, K.A.; Smith, B.J.; Sunderland, J.J.; Graham, M.M.; Sonka, M.; et al. Semiautomated segmentation of head and neck cancers in 18F-FDG PET scans: A just-enough-interaction approach. Med. Phys. 2016, 43, 2948–2964. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Caldwell, C.; Mah, K.; Mozeg, D. Coregistered FDG PET/CT-based textural characterization of head and neck cancer for radiation treatment planning. IEEE Trans. Med. Imaging 2009, 28, 374–383. [Google Scholar]
- Yang, J.; Beadle, B.M.; Garden, A.S.; Schwartz, D.L.; Aristophanous, M. A multimodality segmentation framework for automatic target delineation in head and neck radiotherapy. Med. Phys. 2015, 42, 5310–5320. [Google Scholar] [CrossRef]
- Berthon, B.; Evans, M.; Marshall, C.; Palaniappan, N.; Cole, N.; Jayaprakasam, V.; Rackley, T.; Spezi, E. Head and neck target delineation using a novel PET automatic segmentation algorithm. Radiother. Oncol. 2017, 122, 242–247. [Google Scholar] [CrossRef]
- Visvikis, D.; Cheze Le Rest, C.; Jaouen, V.; Hatt, M. Artificial intelligence, machine (deep) learning and radio(geno)mics: Definitions and nuclear medicine imaging applications. Eur. J. Nucl. Med. Mol. Imaging 2019, 46, 2630–2637. [Google Scholar] [CrossRef]
- Huang, B.; Chen, Z.; Wu, P.M.; Ye, Y.; Feng, S.T.; Wong, C.O.; Zheng, L.; Liu, Y.; Wang, T.; Li, Q.; et al. Fully Automated Delineation of Gross Tumor Volume for Head and Neck Cancer on PET-CT Using Deep Learning: A Dual-Center Study. Contrast Media Mol. Imaging 2018, 2018, 8923028. [Google Scholar] [CrossRef]
- Guo, Z.; Guo, N.; Gong, K.; Zhong, S.; Li, Q. Gross tumor volume segmentation for head and neck cancer radiotherapy using deep dense multi-modality network. Phys. Med. Biol. 2019, 64, 205015. [Google Scholar] [CrossRef]
- Groendahl, A.R.; Skjei Knudtsen, I.; Huynh, B.N.; Mulstad, M.; Moe, Y.M.M.; Knuth, F.; Tomic, O.; Indahl, U.G.; Torheim, T.; Dale, E.; et al. A comparison of fully automatic segmentation of tumors and involved nodes in PET/CT of head and neck cancers. Phys. Med. Biol. 2021, 66, 065012. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Oreiller, V.; Andrearczyk, V.; Jreige, M.; Boughdad, S.; Elhalawani, H.; Castelli, J.; Vallières, M.; Zhu, S.; Xie, J.; Peng, Y.; et al. Head and neck tumor segmentation in PET/CT: The HECKTOR challenge. Med. Image Anal. 2021, 77, 102336. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Sobirov, I.; Nazarov, O.; Alasmawi, H.; Yaqub, M. Automatic Segmentation of Head and Neck Tumor: How Powerful Transformers Are? In Proceedings of the 5th International Conference on Medical Imaging with Deep Learning, Zurich, Switzerland, 6–8 July 2022; Volume 172, pp. 1149–1161. [Google Scholar]
- Li, G.Y.; Chen, J.; Jang, S.I.; Gong, K.; Li, Q. SwinCross: Cross-modal Swin Transformer for Head-and-Neck Tumor Segmentation in PET/CT Images. arXiv 2023, arXiv:2302.03861. [Google Scholar] [CrossRef]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; et al. The Cancer Imaging Archive (TCIA): Maintaining and operating a public information repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Khanh, T.L.B.; Dao, D.P.; Ho, N.H.; Yang, H.J.; Baek, E.T.; Lee, G.; Kim, S.H.; Yoo, S.B. Enhancing U-Net with Spatial-Channel Attention Gate for Abnormal Tissue Segmentation in Medical Imaging. Appl. Sci. 2020, 10, 5729. [Google Scholar] [CrossRef]
- Tong, X.; Wei, J.; Sun, B.; Su, S.; Zuo, Z.; Wu, P. ASCU-Net: Attention Gate, Spatial and Channel Attention U-Net for Skin Lesion Segmentation. Diagnostics 2021, 11, 501. [Google Scholar] [CrossRef]
- Guo, C.; Szemenyei, M.; Yi, Y.; Wang, W.; Chen, B.; Fan, C. SA-UNet: Spatial Attention U-Net for Retinal Vessel Segmentation. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 1236–1242. [Google Scholar] [CrossRef]
- Kazaj, P.M.; Koosheshi, M.; Shahedi, A.; Sadr, A.V. U-Net-based Models for Skin Lesion Segmentation: More Attention and Augmentation. arXiv 2022, arXiv:2210.16399. [Google Scholar]
- Xu, Y.; Hou, S.K.; Wang, X.Y.; Li, D.; Lu, L. C+ref-UNet: A novel approach for medical image segmentation based on multi-scale connected UNet and CBAM. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Xiong, X.; Smith, B.J.; Graves, S.A.; Sunderland, J.J.; Graham, M.M.; Gross, B.A.; Buatti, J.M.; Beichel, R.R. Quantification of uptake in pelvis F-18 FLT PET-CT images using a 3D localization and segmentation CNN. Med. Phys. 2022, 49, 1585–1598. [Google Scholar] [CrossRef]
- Xiong, X. Deep Convolutional Neural Network Based Analysis Methods for Radiation Therapy Applications. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2022. [Google Scholar]
- Shamshad, F.; Khan, S.; Zamir, S.W.; Khan, M.H.; Hayat, M.; Khan, F.S.; Fu, H. Transformers in Medical Imaging: A Survey. arXiv 2022, arXiv:2201.09873. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gan, C.; Li, Z.; Rekik, I.; Yin, Z.; Ji, W.; Gao, Y.; Wang, Q.; Zhang, J.; Shen, D. Transformers in Medical Image Analysis: A Review. Intell. Med. 2022, 3, 59–78. [Google Scholar] [CrossRef]
- Wang, W.; Chen, C.; Ding, M.; Yu, H.; Zha, S.; Li, J. TransBTS: Multimodal Brain Tumor Segmentation Using Transformer. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2021, Strasbourg, France, 27 September–1 October 2021; de Bruijne, M., Cattin, P.C., Cotin, S., Padoy, N., Speidel, S., Zheng, Y., Essert, C., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 109–119. [Google Scholar]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. UNETR: Transformers for 3D Medical Image Segmentation. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; IEEE Computer Society: Washington, DC, USA, 2022; pp. 1748–1758. [Google Scholar]
- Peiris, H.; Hayat, M.; Chen, Z.; Egan, G.; Harandi, M. A Volumetric Transformer for Accurate 3D Tumor Segmentation. arXiv 2021, arXiv:2111.13300. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Zhao, X.; He, L.; Wang, Y.; Chao, Y.; Yao, B.; Hideto, K.; Atsushi, O. An Efficient Method for Connected-Component Labeling in 3D Binary Images. In Proceedings of the 2018 International Conference on Robots and Intelligent System (ICRIS), Changsha, China, 26–27 May 2018; pp. 131–133. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing: Analysis and Machine Vision; CL Engineering: New York, NY, USA, 2007. [Google Scholar]
- Baker, N.; Lu, H.; Erlikhman, G.; Kellman, P.J. Deep convolutional networks do not classify based on global object shape. PLoS Comput. Biol. 2018, 14, e1006613. [Google Scholar] [CrossRef]
- Tuli, S.; Dasgupta, I.; Grant, E.; Griffiths, T.L. Are Convolutional Neural Networks or Transformers More Like Human Vision? arXiv 2021, arXiv:2105.07197. [Google Scholar]



| U-Net | UNETR | U-Net-CBAM | TransBTS | VT-UNet | ||
|---|---|---|---|---|---|---|
| Successful segmentations | (%) | 82.0 | 73.2 | 82.8 | 83.5 | 82.2 |
| Failed segmentations | (%) | 18.0 | 26.8 | 17.2 | 16.5 | 17.8 |
| U-Net | UNETR | U-Net-CBAM | TransBTS | VT-UNet | ||
|---|---|---|---|---|---|---|
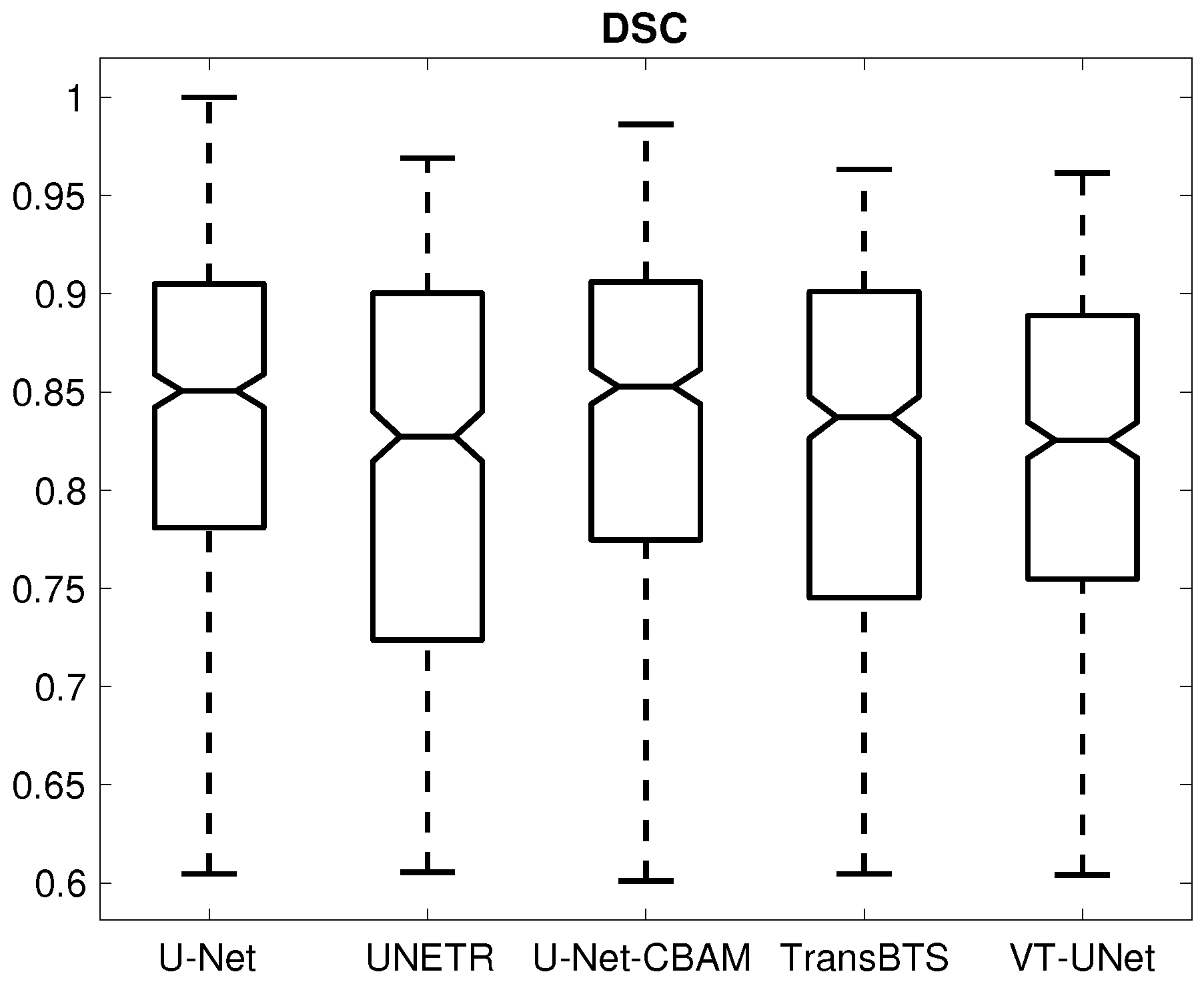
| DSC | (-) | 0.833 ± 0.091 | 0.809 ± 0.101 | 0.833 ± 0.092 | 0.819 ± 0.098 | 0.813 ± 0.090 |
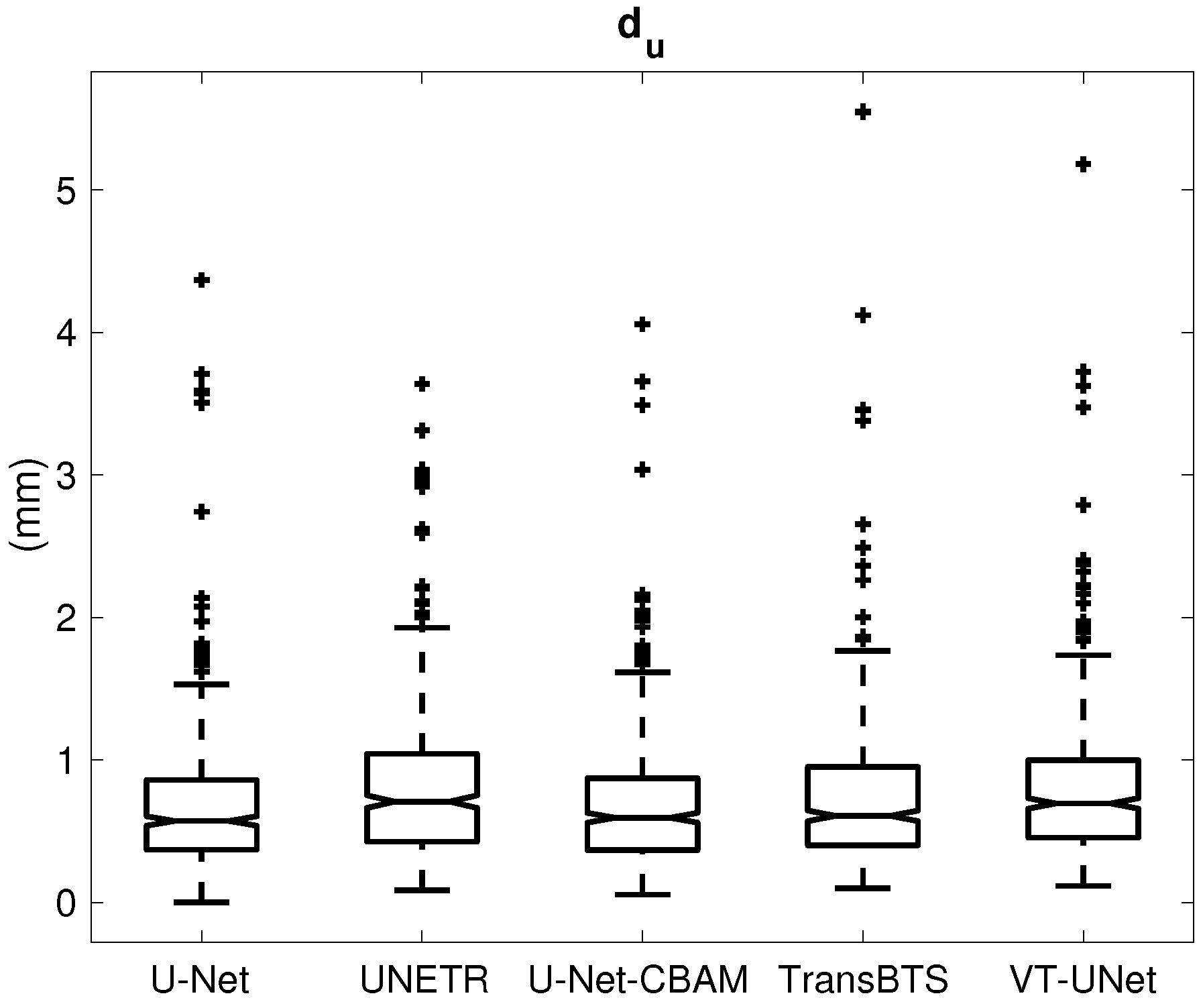
| (mm) | 0.684 ± 0.489 | 0.806 ± 0.530 | 0.682 ± 0.464 | 0.740 ± 0.556 | 0.785 ± 0.510 | |
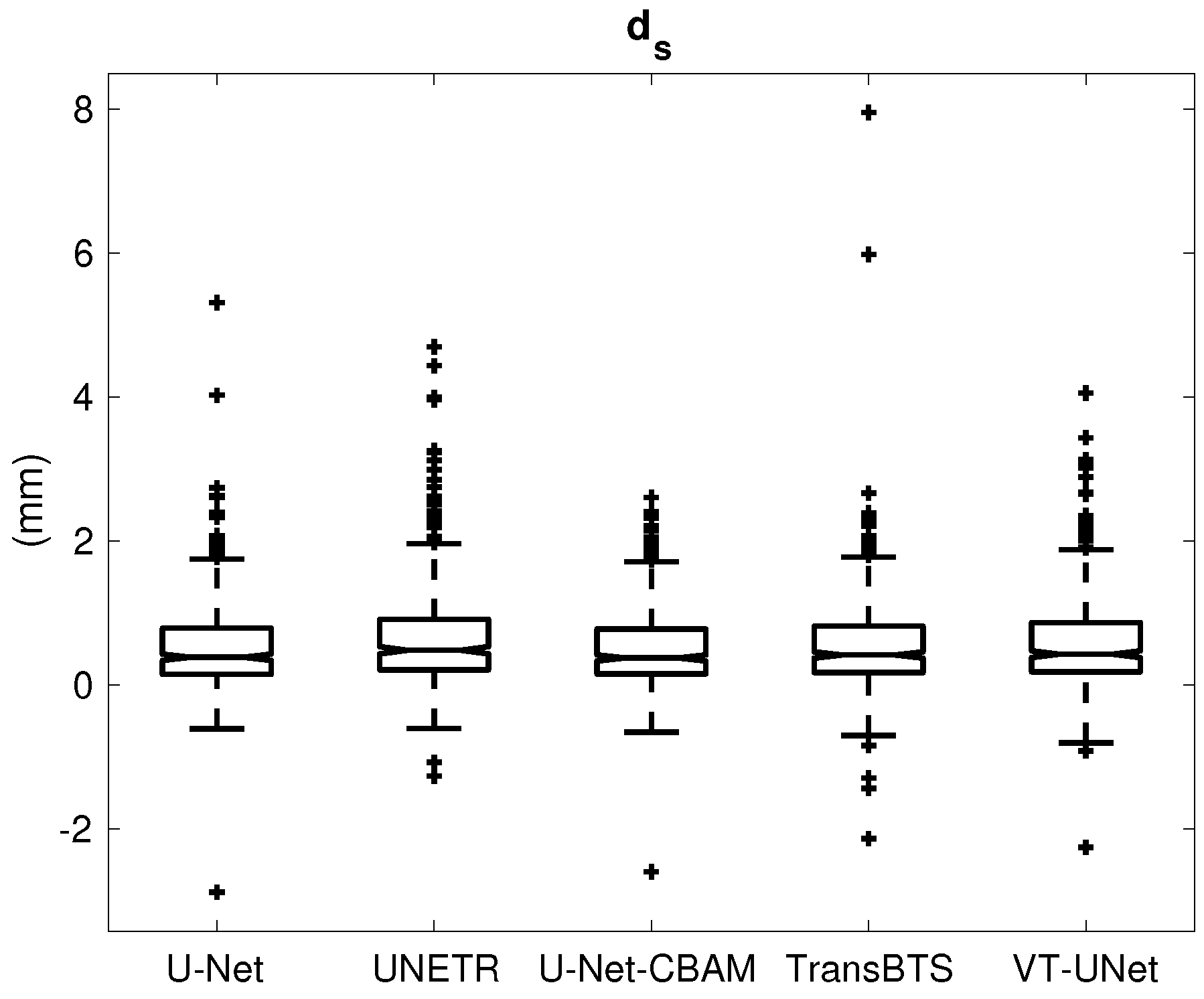
| (mm) | 0.538 ± 0.623 | 0.663 ± 0.734 | 0.504 ± 0.550 | 0.559 ± 0.688 | 0.574 ± 0.636 |
| U-Net | UNETR | U-Net-CBAM | TransBTS | VT-UNet | ||
|---|---|---|---|---|---|---|
| Difference | (%) | −19.78 | −24.57 | −19.39 | −7.66 | −20.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, X.; Smith, B.J.; Graves, S.A.; Graham, M.M.; Buatti, J.M.; Beichel, R.R. Head and Neck Cancer Segmentation in FDG PET Images: Performance Comparison of Convolutional Neural Networks and Vision Transformers. Tomography 2023, 9, 1933-1948. https://doi.org/10.3390/tomography9050151
Xiong X, Smith BJ, Graves SA, Graham MM, Buatti JM, Beichel RR. Head and Neck Cancer Segmentation in FDG PET Images: Performance Comparison of Convolutional Neural Networks and Vision Transformers. Tomography. 2023; 9(5):1933-1948. https://doi.org/10.3390/tomography9050151
Chicago/Turabian StyleXiong, Xiaofan, Brian J. Smith, Stephen A. Graves, Michael M. Graham, John M. Buatti, and Reinhard R. Beichel. 2023. "Head and Neck Cancer Segmentation in FDG PET Images: Performance Comparison of Convolutional Neural Networks and Vision Transformers" Tomography 9, no. 5: 1933-1948. https://doi.org/10.3390/tomography9050151
APA StyleXiong, X., Smith, B. J., Graves, S. A., Graham, M. M., Buatti, J. M., & Beichel, R. R. (2023). Head and Neck Cancer Segmentation in FDG PET Images: Performance Comparison of Convolutional Neural Networks and Vision Transformers. Tomography, 9(5), 1933-1948. https://doi.org/10.3390/tomography9050151






