Effects of Path-Finding Algorithms on the Labeling of the Centerlines of Circle of Willis Arteries
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
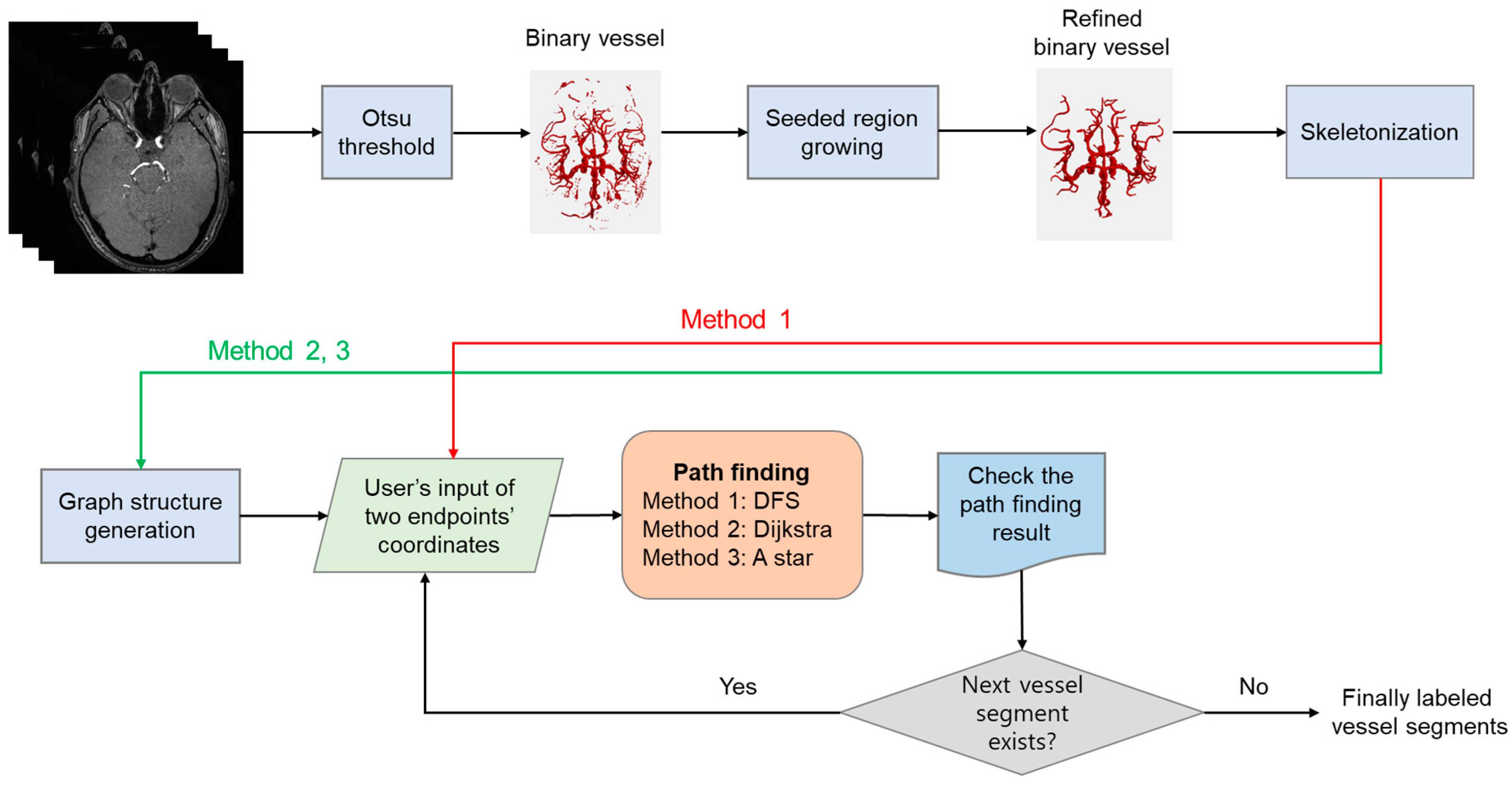
2.2. Vessel Segmentation and Skeletonization
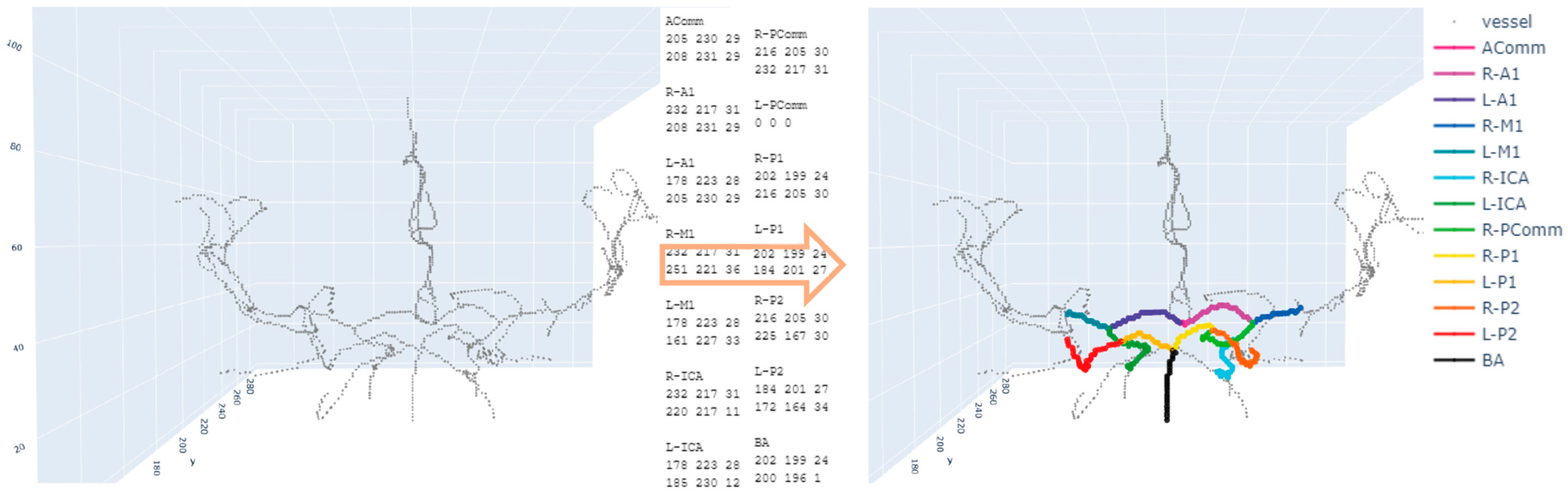
2.3. Annotation of Two Endpoints
2.4. Path-Finding Algorithms
2.5. Evaluation
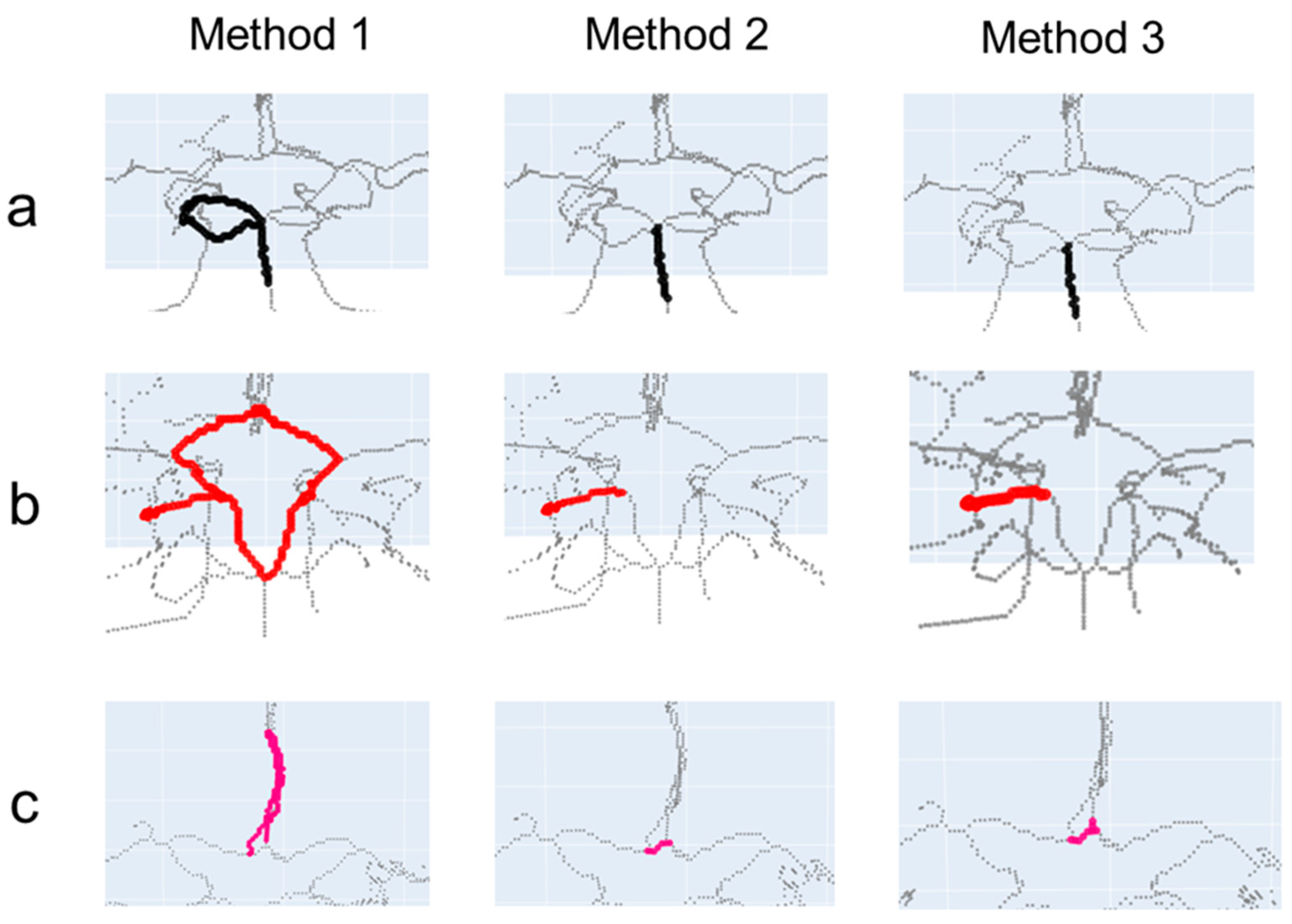
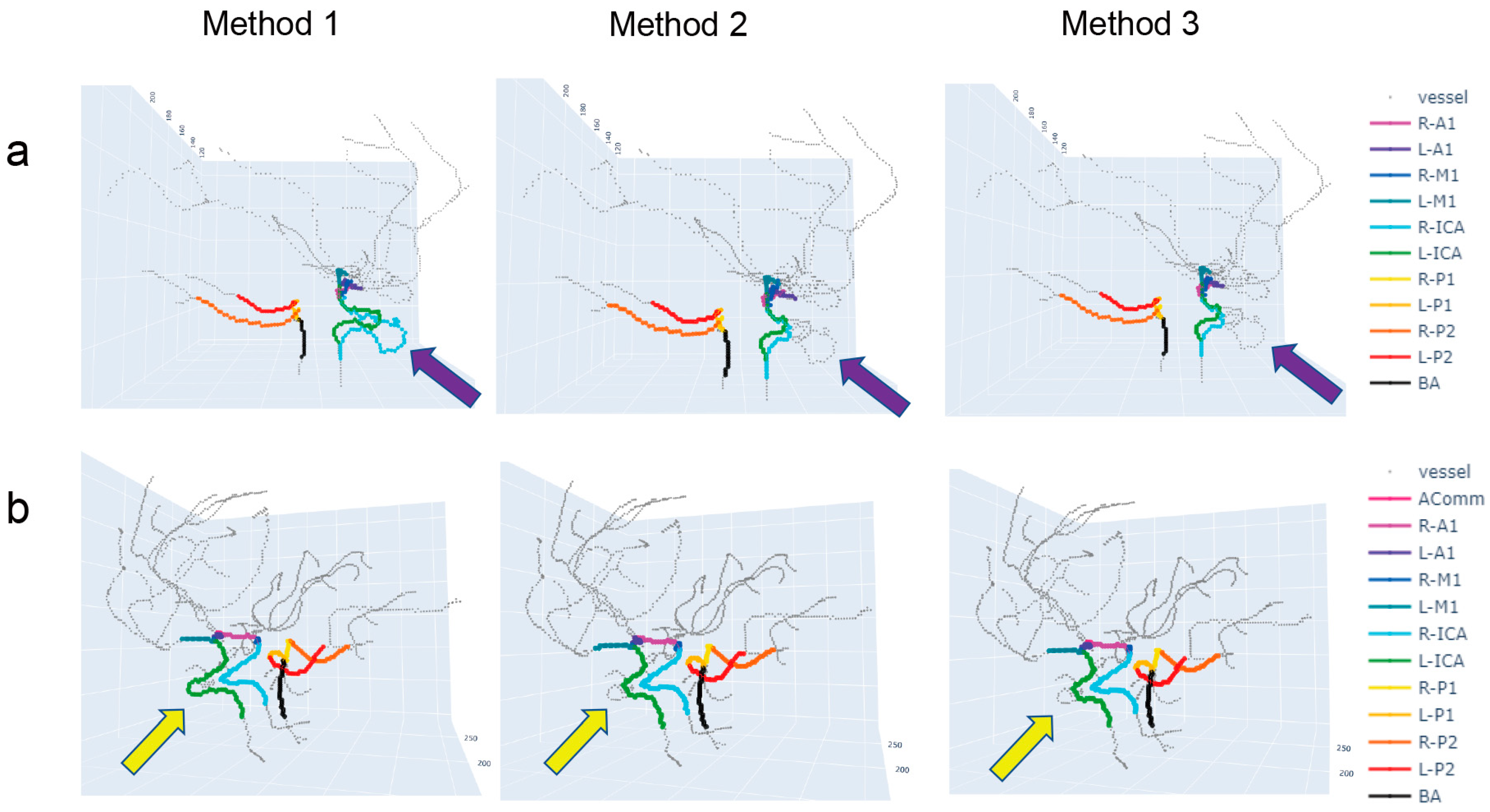
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ritz, K.; Denswil, N.P.; Stam, O.C.; van Lieshout, J.J.; Daemen, M.J. Cause and mechanisms of intracranial atherosclerosis. Circulation 2014, 130, 1407–1414. [Google Scholar] [CrossRef]
- Hu, X.; De Silva, T.M.; Chen, J.; Faraci, F.M. Cerebral Vascular Disease and Neurovascular Injury in Ischemic Stroke. Circ. Res. 2017, 120, 449–471. [Google Scholar] [CrossRef] [PubMed]
- Krzyzewski, R.M.; Klis, K.M.; Kwinta, B.M.; Gackowska, M.; Gasowski, J. Increased tortuosity of ACA might be associated with increased risk of ACoA aneurysm development and less aneurysm dome size: A computer-aided analysis. Eur. Radiol. 2019, 29, 6309–6318. [Google Scholar] [CrossRef] [PubMed]
- Jeong, W.; Rhee, K. Hemodynamics of cerebral aneurysms: Computational analyses of aneurysm progress and treatment. Comput. Math. Methods Med. 2012, 2012, 782801. [Google Scholar] [CrossRef]
- Magid-Bernstein, J.; Girard, R.; Polster, S.; Srinath, A.; Romanos, S.; Awad, I.A.; Sansing, L.H. Cerebral Hemorrhage: Pathophysiology, Treatment, and Future Directions. Circ. Res. 2022, 130, 1204–1229. [Google Scholar] [CrossRef]
- Cirillo, M.; Scomazzoni, F.; Cirillo, L.; Cadioli, M.; Simionato, F.; Iadanza, A.; Kirchin, M.; Righi, C.; Anzalone, N. Comparison of 3D TOF-MRA and 3D CE-MRA at 3T for imaging of intracranial aneurysms. Eur. J. Radiol. 2013, 82, e853–e859. [Google Scholar] [CrossRef] [PubMed]
- Lell, M.M.; Anders, K.; Uder, M.; Klotz, E.; Ditt, H.; Vega-Higuera, F.; Boskamp, T.; Bautz, W.A.; Tomandl, B.F. New techniques in CT angiography. Radiographics 2006, 26 (Suppl. 1), S45–S62. [Google Scholar] [CrossRef]
- Han, H.C. Twisted blood vessels: Symptoms, etiology and biomechanical mechanisms. J. Vasc. Res. 2012, 49, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Kandil, H.; Soliman, A.; Ghazal, M.; Mahmoud, A.; Shalaby, A.; Keynton, R.; Elmaghraby, A.; Giridharan, G.; El-Baz, A. A Novel Framework for Early Detection of Hypertension using Magnetic Resonance Angiography. Sci. Rep. 2019, 9, 11105. [Google Scholar] [CrossRef]
- Kim, H.J.; Song, H.N.; Lee, J.E.; Kim, Y.C.; Baek, I.Y.; Kim, Y.S.; Chung, J.W.; Jee, T.K.; Yeon, J.Y.; Bang, O.Y.; et al. How Cerebral Vessel Tortuosity Affects Development and Recurrence of Aneurysm: Outer Curvature versus Bifurcation Type. J. Stroke 2021, 23, 213–222. [Google Scholar] [CrossRef]
- Klis, K.M.; Krzyzewski, R.M.; Kwinta, B.M.; Lasocha, B.; Brzegowy, P.; Stachura, K.; Popiela, T.J.; Borek, R.; Gasowski, J. Increased tortuosity of basilar artery might be associated with higher risk of aneurysm development. Eur. Radiol. 2020, 30, 5625–5632. [Google Scholar] [CrossRef] [PubMed]
- Sodi, A.; Guarducci, M.; Vauthier, L.; Ioannidis, A.S.; Pitz, S.; Abbruzzese, G.; Sofi, F.; Mecocci, A.; Miele, A.; Menchini, U. Computer assisted evaluation of retinal vessels tortuosity in Fabry disease. Acta Ophthalmol. 2013, 91, e113–e119. [Google Scholar] [CrossRef] [PubMed]
- Klis, K.M.; Krzyzewski, R.M.; Kwinta, B.M.; Stachura, K.; Gasowski, J. Tortuosity of the Internal Carotid Artery and Its Clinical Significance in the Development of Aneurysms. J. Clin. Med. 2019, 8, 237. [Google Scholar] [CrossRef] [PubMed]
- Bogunovic, H.; Pozo, J.M.; Cardenes, R.; San Roman, L.; Frangi, A.F. Anatomical labeling of the Circle of Willis using maximum a posteriori probability estimation. IEEE Trans. Med. Imaging 2013, 32, 1587–1599. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Mossa-Basha, M.; Balu, N.; Canton, G.; Sun, J.; Pimentel, K.; Hatsukami, T.S.; Hwang, J.N.; Yuan, C. Development of a quantitative intracranial vascular features extraction tool on 3D MRA using semiautomated open-curve active contour vessel tracing. Magn. Reson. Med. 2018, 79, 3229–3238. [Google Scholar] [CrossRef]
- Robben, D.; Turetken, E.; Sunaert, S.; Thijs, V.; Wilms, G.; Fua, P.; Maes, F.; Suetens, P. Simultaneous segmentation and anatomical labeling of the cerebral vasculature. Med. Image Anal. 2016, 32, 201–215. [Google Scholar] [CrossRef]
- Dumais, F.; Caceres, M.P.; Janelle, F.; Seifeldine, K.; Ares-Bruneau, N.; Gutierrez, J.; Bocti, C.; Whittingstall, K. eICAB: A novel deep learning pipeline for Circle of Willis multiclass segmentation and analysis. Neuroimage 2022, 260, 119425. [Google Scholar] [CrossRef]
- Nazir, A.; Cheema, M.N.; Sheng, B.; Li, H.T.; Li, P.; Yang, P.; Jung, Y.Y.; Qin, J.; Kim, J.M.; Feng, D.D. OFF-eNET: An Optimally Fused Fully End-to-End Network for Automatic Dense Volumetric 3D Intracranial Blood Vessels Segmentation. IEEE Trans. Image Process. 2020, 29, 7192–7202. [Google Scholar] [CrossRef]
- Suran, S.; Pattanaik, V.; Malathi, D. Discovering shortest path between points in cerebrovascular system. In Proceedings of the 6th IBM Collaborative Academia Research Exchange Conference (I-CARE) on I-CARE 2014, Bangalore, India, 9–11 October 2014; pp. 1–3. [Google Scholar]
- Shen, M.; Wei, J.; Fan, J.; Tan, J.; Wang, Z.; Yang, Z.; Qiao, P.; Liao, F. Automatic cerebral artery system labeling using registration and key points tracking. In Proceedings of the Knowledge Science, Engineering and Management: 13th International Conference, KSEM 2020, Hangzhou, China, 28–30 August 2020; pp. 355–367. [Google Scholar]
- Thamm, F.; Jurgens, M.; Taubmann, O.; Thamm, A.; Rist, L.; Ditt, H.; Maier, A. An algorithm for the labeling and interactive visualization of the cerebrovascular system of ischemic strokes. Biomed. Phys. Eng. Express 2022, 8, 065016. [Google Scholar] [CrossRef]
- Kroon, D.-J. Region Growing, MATLAB Central File Exchange; The MathWorks, Inc.: Natick, MA, USA, 2021. [Google Scholar]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Kim, Y.C.; Kim, K.R.; Lee, H.; Choe, Y.H. Fast calculation software for modified Look-Locker inversion recovery (MOLLI) T1 mapping. BMC Med. Imaging 2021, 21, 26. [Google Scholar] [CrossRef] [PubMed]
- Nunez-Iglesias, J.; Blanch, A.J.; Looker, O.; Dixon, M.W.; Tilley, L. A new Python library to analyse skeleton images confirms malaria parasite remodelling of the red blood cell membrane skeleton. PeerJ 2018, 6, e4312. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.D.; Lee, K.D.; Steve Hubbard, S.H. Data Structures and Algorithms with Python; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Schrijver, A. Combinatorial Optimization: Polyhedra and Efficiency; Springer: Berlin/Heidelberg, Germany, 2003; Volume 24. [Google Scholar]
- Russell, S.J. Artificial Intelligence a Modern Approach; Pearson Education, Inc.: London, UK, 2010. [Google Scholar]
- Chen, Y.; Jin, D.; Guo, B.; Bai, X. Attention-Assisted Adversarial Model for Cerebrovascular Segmentation in 3D TOF-MRA Volumes. IEEE Trans. Med. Imaging 2022, 41, 3520–3532. [Google Scholar] [CrossRef]
- Livne, M.; Rieger, J.; Aydin, O.U.; Taha, A.A.; Akay, E.M.; Kossen, T.; Sobesky, J.; Kelleher, J.D.; Hildebrand, K.; Frey, D.; et al. A U-Net Deep Learning Framework for High Performance Vessel Segmentation in Patients With Cerebrovascular Disease. Front. Neurosci. 2019, 13, 97. [Google Scholar] [CrossRef] [PubMed]
- Wozniak, T.; Strzelecki, M.; Majos, A.; Stefanczyk, L. 3D vascular tree segmentation using a multiscale vesselness function and a level set approach. Biocybern. Biomed. Eng. 2017, 37, 66–77. [Google Scholar] [CrossRef]
- Lell, M.M.; Ruehm, S.G.; Kramer, M.; Panknin, C.; Habibi, R.; Klotz, E.; Villablanca, P. Cranial computed tomography angiography with automated bone subtraction: A feasibility study. Investig. Radiol. 2009, 44, 38–43. [Google Scholar] [CrossRef]
- van Straten, M.; Venema, H.W.; Streekstra, G.J.; Majoie, C.B.; den Heeten, G.J.; Grimbergen, C.A. Removal of bone in CT angiography of the cervical arteries by piecewise matched mask bone elimination. Med. Phys. 2004, 31, 2924–2933. [Google Scholar] [CrossRef]
- Fu, F.; Wei, J.; Zhang, M.; Yu, F.; Xiao, Y.; Rong, D.; Shan, Y.; Li, Y.; Zhao, C.; Liao, F.; et al. Rapid vessel segmentation and reconstruction of head and neck angiograms using 3D convolutional neural network. Nat. Commun. 2020, 11, 4829. [Google Scholar] [CrossRef]
- Payer, C.; Stern, D.; Bischof, H.; Urschler, M. Integrating spatial configuration into heatmap regression based CNNs for landmark localization. Med. Image Anal. 2019, 54, 207–219. [Google Scholar] [CrossRef]
- Alansary, A.; Oktay, O.; Li, Y.; Folgoc, L.L.; Hou, B.; Vaillant, G.; Kamnitsas, K.; Vlontzos, A.; Glocker, B.; Kainz, B.; et al. Evaluating reinforcement learning agents for anatomical landmark detection. Med. Image Anal. 2019, 53, 156–164. [Google Scholar] [CrossRef] [PubMed]
- Xue, H.; Artico, J.; Fontana, M.; Moon, J.C.; Davies, R.H.; Kellman, P. Landmark Detection in Cardiac MRI by Using a Convolutional Neural Network. Radiol. Artif. Intell. 2021, 3, e200197. [Google Scholar] [CrossRef] [PubMed]
| Method 1 (DFS Algorithm) | Method 2 (Dijkstra Algorithm) | Method 3 (A* Algorithm) | p-Value * | p-Value † | p-Value ‡ | No. of Undetected Paths | Total | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of Correct Paths | No. of Incorrect Paths | No. of Correct Paths | No. of Incorrect Paths | No. of Correct Paths | No. of Incorrect Paths | |||||||
| AComm | 19 | 25 | 44 | 0 | 36 | 8 | <0.001 | <0.001 | 0.006 | 16 | 60 | |
| ACA A1 | R | 51 | 9 | 60 | 0 | 60 | 0 | 0.003 | 0.003 | 1 | 0 | 60 |
| L | 49 | 10 | 59 | 0 | 59 | 0 | 0.001 | 0.001 | 1 | 1 | 60 | |
| MCA M1 | R | 55 | 5 | 60 | 0 | 60 | 0 | 0.057 | 0.057 | 1 | 0 | 60 |
| L | 58 | 2 | 60 | 0 | 59 | 1 | 0.496 | 1 | 1 | 0 | 60 | |
| PComm | R | 8 | 6 | 14 | 0 | 14 | 0 | 0.016 | 0.016 | 1 | 46 | 60 |
| L | 10 | 8 | 18 | 0 | 18 | 0 | 0.003 | 0.003 | 1 | 42 | 60 | |
| PCA P1 | R | 52 | 8 | 57 | 3 | 58 | 2 | 0.204 | 0.095 | 1 | 0 | 60 |
| L | 51 | 9 | 60 | 0 | 60 | 0 | 0.003 | 0.003 | 1 | 0 | 60 | |
| PCA P2 | R | 55 | 5 | 60 | 0 | 60 | 0 | 0.057 | 0.057 | 1 | 0 | 60 |
| L | 51 | 9 | 60 | 0 | 60 | 0 | 0.003 | 0.003 | 1 | 0 | 60 | |
| BA | 53 | 7 | 60 | 0 | 60 | 0 | 0.013 | 0.013 | 1 | 0 | 60 | |
| ICA | R | 51 | 9 | 50 | 10 | 50 | 10 | 1 | 1 | 1 | 0 | 60 |
| L | 51 | 9 | 52 | 8 | 52 | 8 | 1 | 1 | 1 | 0 | 60 | |
| Total | 614 | 121 | 714 | 21 | 706 | 29 | 105 | 840 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-O.; Kim, Y.-C. Effects of Path-Finding Algorithms on the Labeling of the Centerlines of Circle of Willis Arteries. Tomography 2023, 9, 1423-1433. https://doi.org/10.3390/tomography9040113
Kim S-O, Kim Y-C. Effects of Path-Finding Algorithms on the Labeling of the Centerlines of Circle of Willis Arteries. Tomography. 2023; 9(4):1423-1433. https://doi.org/10.3390/tomography9040113
Chicago/Turabian StyleKim, Se-On, and Yoon-Chul Kim. 2023. "Effects of Path-Finding Algorithms on the Labeling of the Centerlines of Circle of Willis Arteries" Tomography 9, no. 4: 1423-1433. https://doi.org/10.3390/tomography9040113
APA StyleKim, S.-O., & Kim, Y.-C. (2023). Effects of Path-Finding Algorithms on the Labeling of the Centerlines of Circle of Willis Arteries. Tomography, 9(4), 1423-1433. https://doi.org/10.3390/tomography9040113








