Can Machine Learning Be Better than Biased Readers?
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Problem Setting
- Random error: readers accidentally introduce wrong labels.
- Systematic error: readers make mistakes when interpreting an image due to a bias.
2.3. Model and Loss Functions
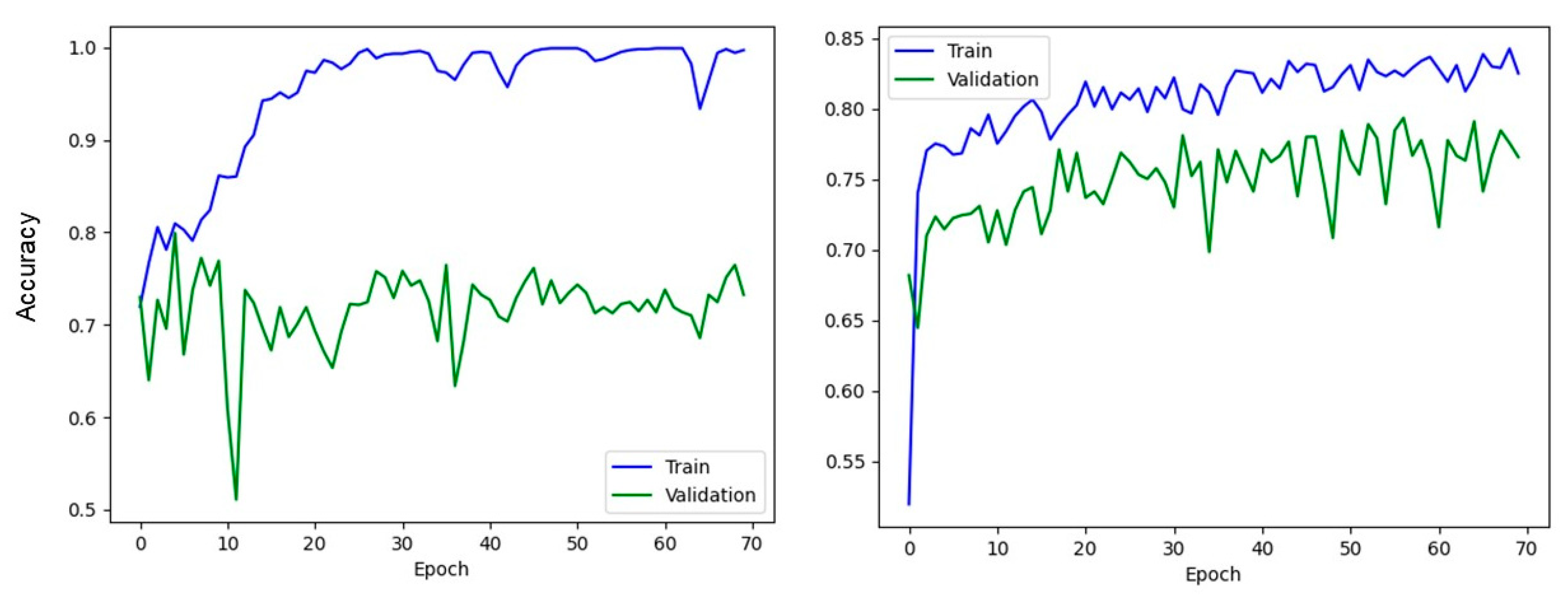
2.4. Environment and Implementation Details
2.5. Experimental Methodology
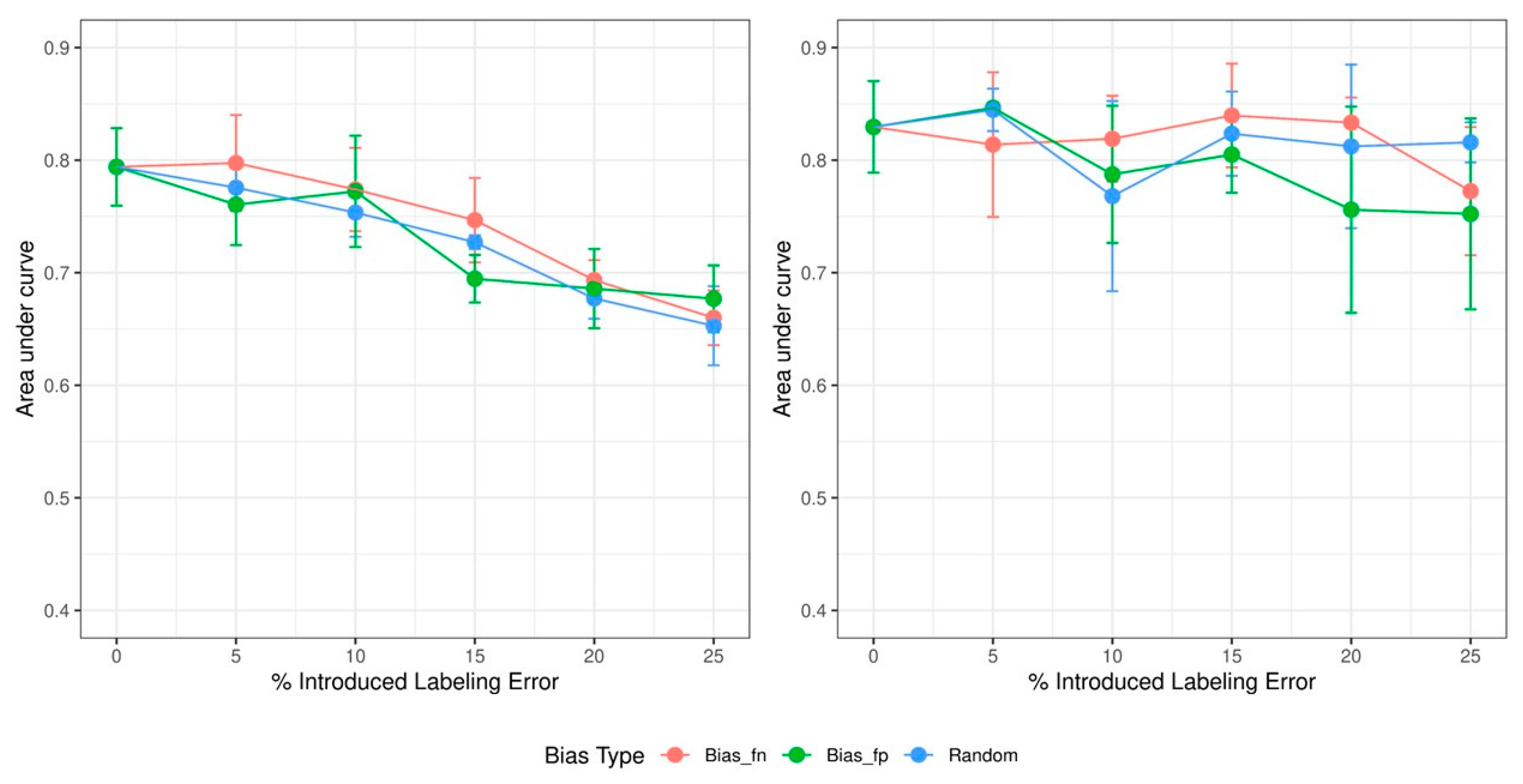
3. Results
4. Discussion
4.1. Dose Effect of Increasing Errors
4.2. Effects of Different Types of Biases
4.3. Limitations
4.4. Recommendation for Amending Biases
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rädsch, T.; Reinke, A.; Weru, V.; Tizabi, M.D.; Schreck, N.; Kavur, A.E.; Pekdemir, B.; Roß, T.; Kopp-Schneider, A.; Maier-Hein, L. Labelling instructions matter in biomedical image analysis. Nat. Mach. Intell. 2023, 5, 273–283. [Google Scholar] [CrossRef]
- Asman, A.J.; Landman, B.A. Robust statistical label fusion through COnsensus Level, Labeler Accuracy, and Truth Estimation (COLLATE). IEEE Trans. Med. Imaging 2011, 30, 1779–1794. [Google Scholar] [CrossRef] [PubMed]
- Brady, A.P. Error and discrepancy in radiology: Inevitable or avoidable? Insights Imaging 2017, 8, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Stec, N.; Arje, D.; Moody, A.R.; Krupinski, E.A.; Tyrrell, P.N. A systematic review of fatigue in radiology: Is it a problem? Am. J. Roentgenol. 2018, 210, 799–806. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, J.R.; Pereira, L.M.; Iversen, M.D.; Ramos, A.L. What is gold standard and what is ground truth? Dental Press J. Orthod. 2014, 19, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Tanno, R.; Saeedi, A.; Sankaranarayanan, S.; Alexander, D.C.; Silberman, N. Learning From Noisy Labels by Regularized Estimation of Annotator Confusion. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 11236–11245. [Google Scholar]
- Chen, P.; Liao, B.; Chen, G.; Zhang, S. A Meta Approach to Defend Noisy Labels by the Manifold Regularizer PSDR. arXiv 2019, arXiv:1906.05509. [Google Scholar]
- Kermany, D.S.; Goldbaum, M.; Cai, W.; Valentim, C.C.S.; Liang, H.; Baxter, S.L.; McKeown, A.; Yang, G.; Wu, X.; Yan, F.; et al. Identifying Medical Diagnoses and Treatable Diseases by Image-Based Deep Learning. Cell 2018, 172, 1122–1131.e9. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Yang, J.; Shi, R.; Ni, B. MedMNIST Classification Decathlon: A Lightweight AutoML Benchmark for Medical Image Analysis. In Proceedings of the IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021; pp. 191–195. [Google Scholar]
- Cordeiro, F.R.; Carneiro, G. A Survey on Deep Learning with Noisy Labels: How to train your model when you cannot trust on the annotations? In Proceedings of the 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 7–10 November 2020; IEEE Computer Society: Los Alamitos, CA, USA; pp. 9–16. [Google Scholar]
- Yan, Y.; Rosales, R.; Fung, G.; Schmidt, M.; Hermosillo, G.; Bogoni, L.; Moy, L.; Dy, J. Modeling annotator expertise: Learning when everybody knows a bit of something. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, PMLR, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; Teh, Y.W., Titterington, M., Eds.; Volume 9, pp. 932–939. [Google Scholar]
| Error Type | % Level of Introduced Error | |||||
|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | ||
| Random error | 5% each | 10% each | 15% each | 20% each | 25% each | |
| Systematic error | False positive labeling | 10% fp | 20% fp | 30% fp | 40% fp | 50% fp |
| False negative labeling | 10% fn | 20% fn | 30% fn | 40% fn | 50% fn | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hibi, A.; Zhu, R.; Tyrrell, P.N. Can Machine Learning Be Better than Biased Readers? Tomography 2023, 9, 901-908. https://doi.org/10.3390/tomography9030074
Hibi A, Zhu R, Tyrrell PN. Can Machine Learning Be Better than Biased Readers? Tomography. 2023; 9(3):901-908. https://doi.org/10.3390/tomography9030074
Chicago/Turabian StyleHibi, Atsuhiro, Rui Zhu, and Pascal N. Tyrrell. 2023. "Can Machine Learning Be Better than Biased Readers?" Tomography 9, no. 3: 901-908. https://doi.org/10.3390/tomography9030074
APA StyleHibi, A., Zhu, R., & Tyrrell, P. N. (2023). Can Machine Learning Be Better than Biased Readers? Tomography, 9(3), 901-908. https://doi.org/10.3390/tomography9030074







