Statistical Interior Tomography via L1 Norm Dictionary Learning without Assuming an Object Support
Abstract
1. Introduction
2. Materials and Methods
2.1. Statistical Iterative Reconstruction
2.2. L1Norm Sparse Representation Based on Learned Dictionary
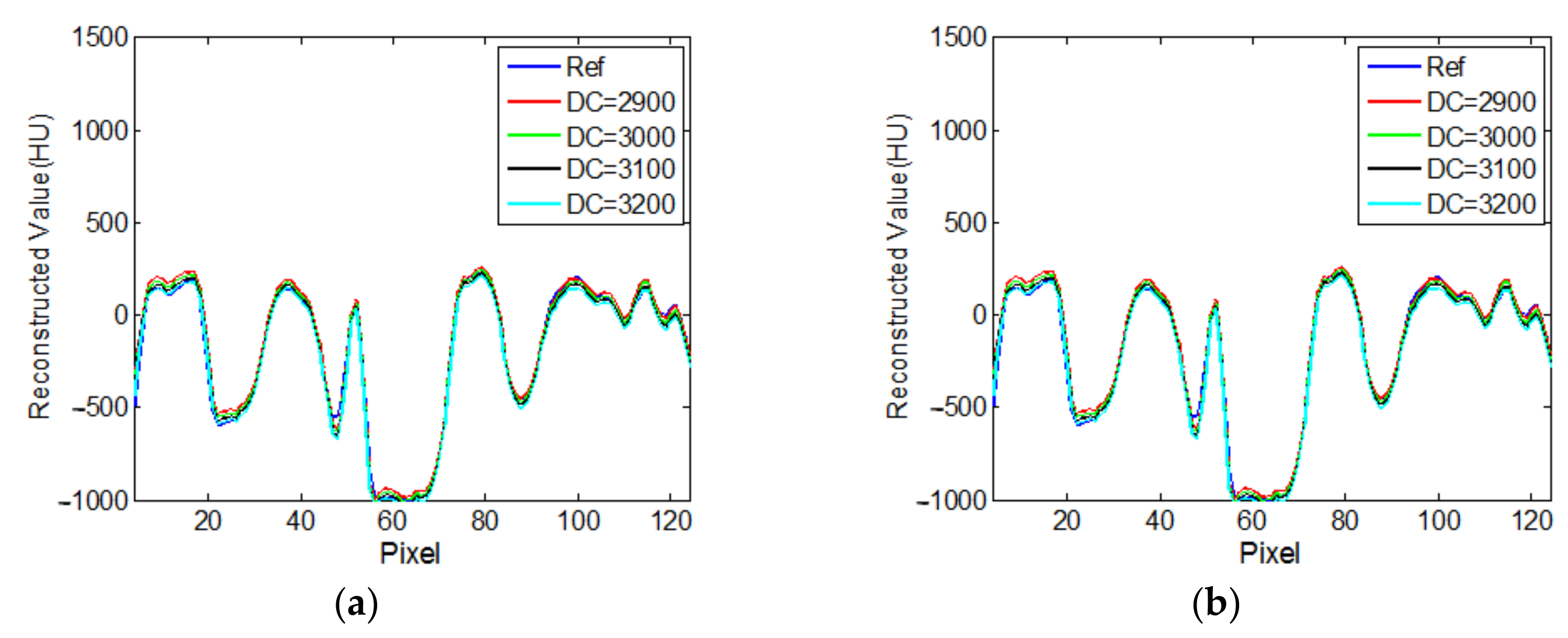
2.3. Direct Current Priors
2.4. Optimization of SIRDL + HL Method
| Algorithm 1: The outline of the optimization algorithm. |
| 1. 8 × 8 size image blocks are extracted from selected CT images to construct training samples, then we train dictionary D using an online learning method and estimate the value of direct component C using projected data. 2. Given:,,,C, K. 3. Initialize: . 4. Repeat: 5. Update the using (8) and LASSO algorithm. 6. Update the reconstructed image using (10). 7. Until: the stop criteria are met. 8. Output: |
3. Experiments and Results
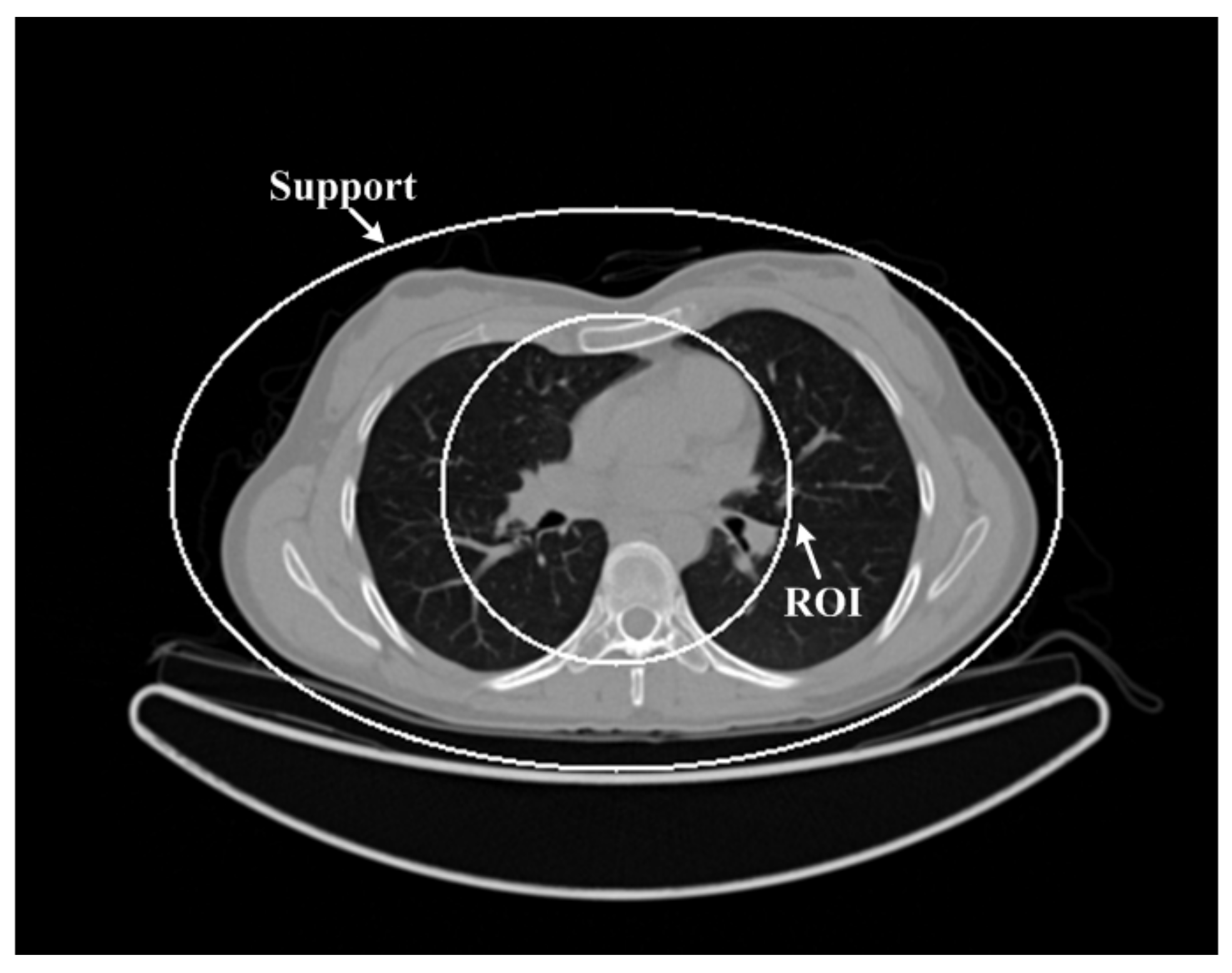
3.1. Human Chest Simulation
3.1.1. The Simulated Low-Dose Projection
3.1.2. Global Dictionary Learning
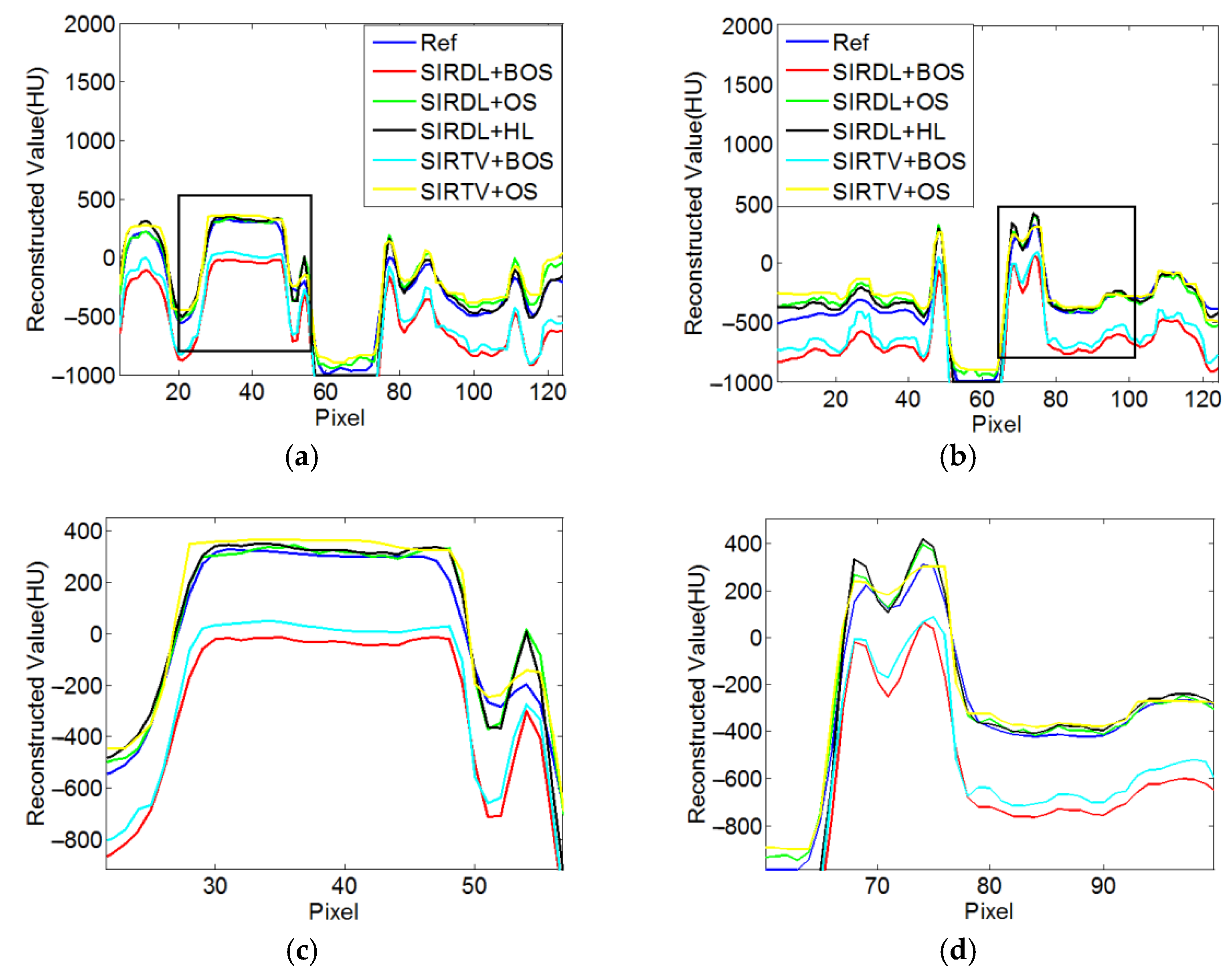
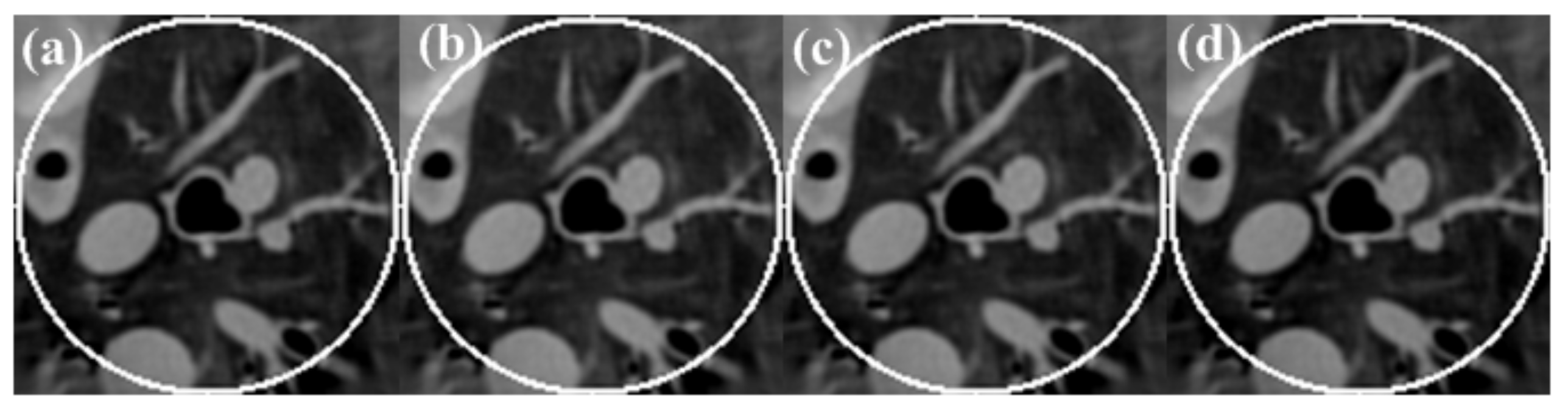
3.1.3. Reconstruction Results
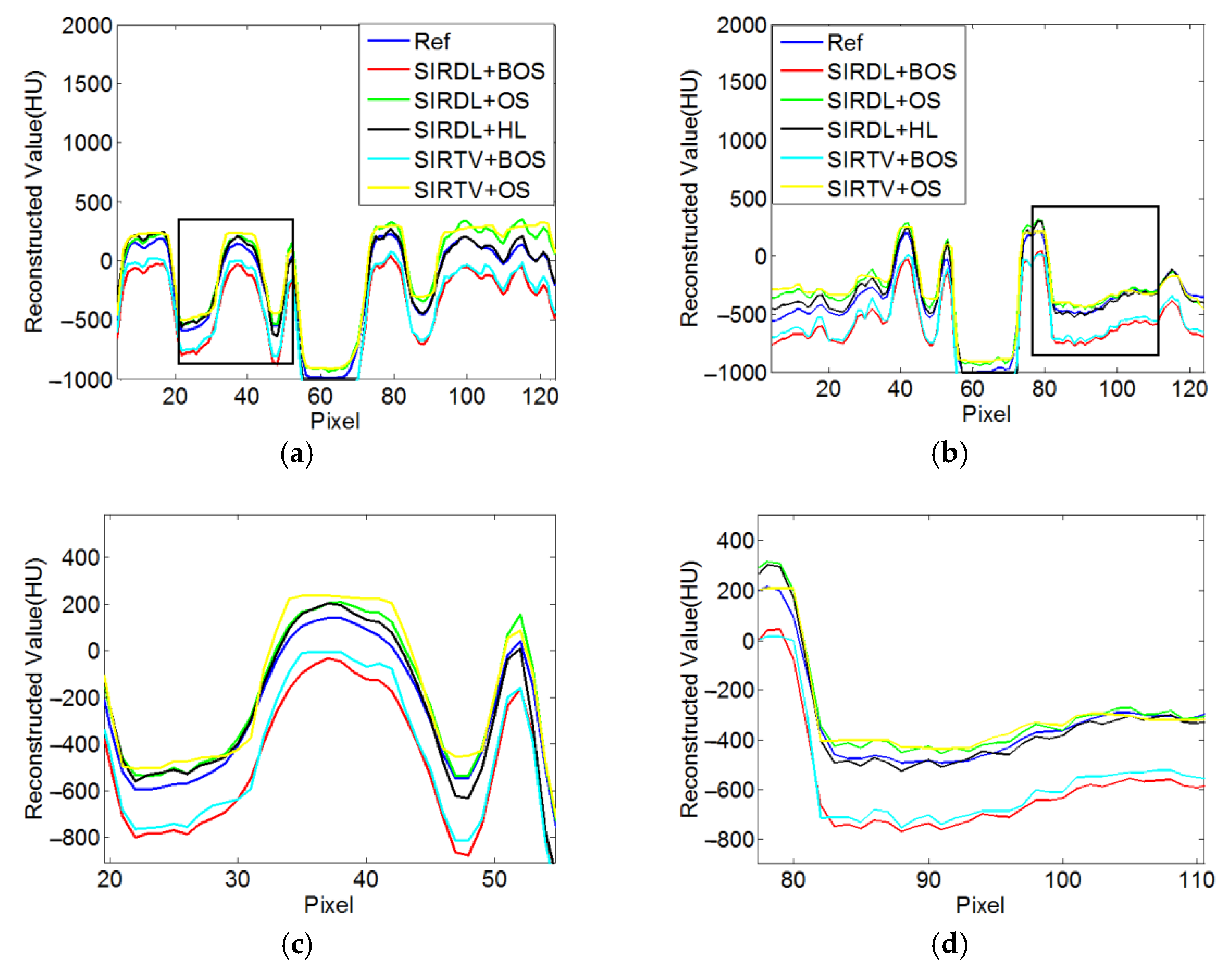
3.1.4. Quantitative Analysis
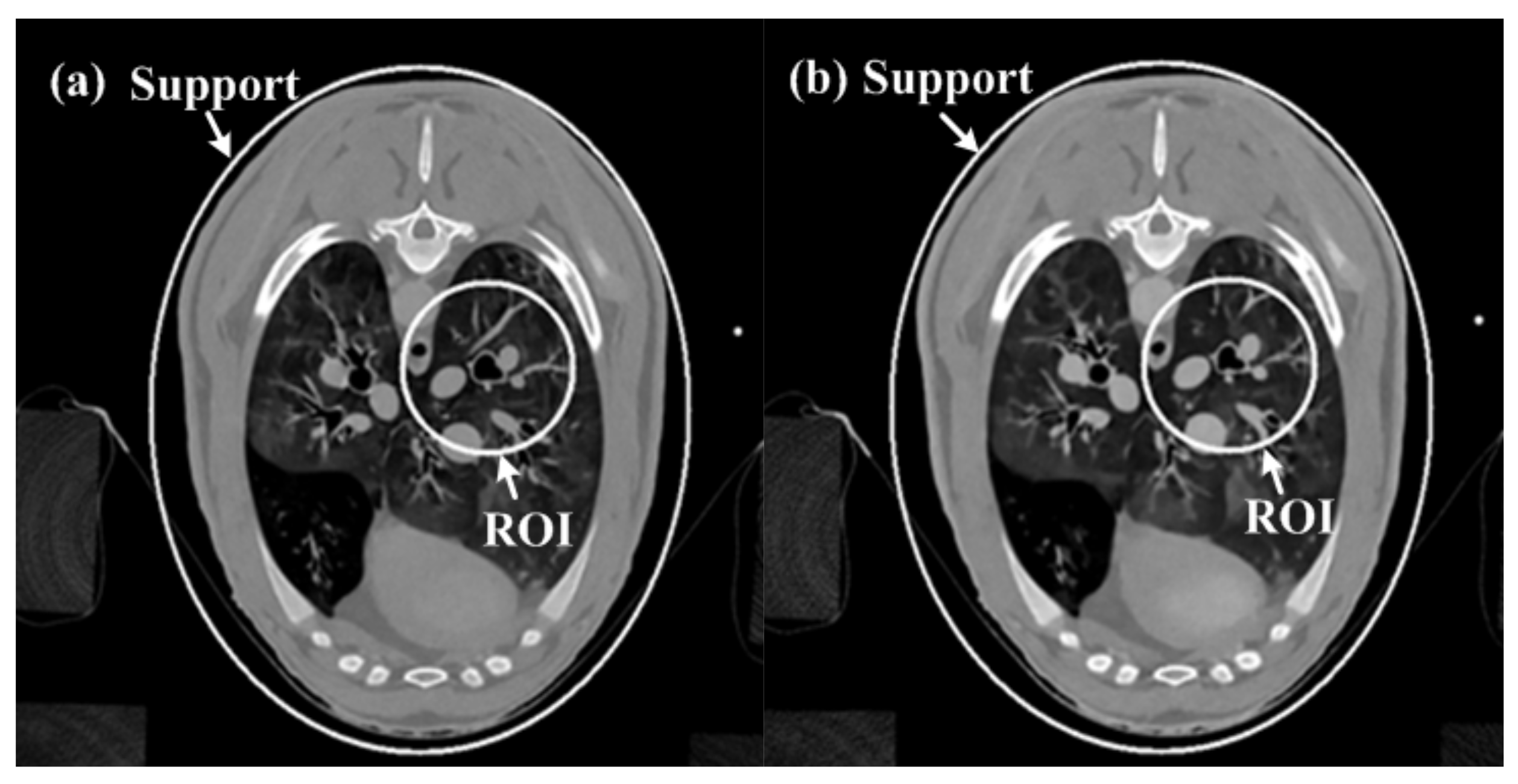
3.2. Real CT Projection
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, G.; Yu, H. The meaning of interior tomography. Phys. Med. Biol. 2013, 58, R161. [Google Scholar] [CrossRef]
- Natterer, F. The Mathematics of Computerized Tomography; Society for Industrial Mathematics: Philadelphia, PA, USA, 2001; Volume 32. [Google Scholar]
- Courdurier, M.; Noo, F.; Defrise, M.; Kudo, H. Solving the interior problem of computed tomography using a priori knowledge. Inverse Probl. 2008, 24, 065001. [Google Scholar] [CrossRef]
- Kudo, H.; Courdurier, M.; Noo, F.; Defrise, M. Tiny a priori knowledge solves the interior problem in computed tomography. Phys. Med. Biol. 2008, 53, 2207. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Yu, H.; Wang, G. Exact interior reconstruction from truncated limited-angle projection data. J. Biomed. Imaging 2008, 2008, 5. [Google Scholar] [CrossRef]
- Yu, H.; Ye, Y.; Wang, G. Interior reconstruction using the truncated hilbert transform via singular value decomposition. J. X-ray Sci. Technol. 2008, 16, 243–251. [Google Scholar]
- Katsevich, A. Singular value decomposition for the truncated hilbert transform. Inverse Probl. 2010, 26, 115011. [Google Scholar] [CrossRef]
- Jin, X.; Katsevich, A.; Yu, H.; Wang, G.; Li, L.; Chen, Z. Interior tomography with continuous singular value decomposition. IEEE Trans. Med. Imaging 2012, 31, 2108–2119. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yu, H.; Wang, G. Compressed sensing based interior tomography. Phys. Med. Biol. 2009, 54, 2791–2805. [Google Scholar] [CrossRef]
- Yu, H.; Yang, J.; Jiang, M.; Wang, G. Supplemental analysis on compressed sensing based interior tomography. Phys. Med. Biol. 2009, 54, N425. [Google Scholar] [CrossRef]
- Yang, J.; Yu, H.; Jiang, M.; Wang, G. High-order total variation minimization for interior tomography. Inverse Probl. 2010, 26, 035013. [Google Scholar] [CrossRef]
- Klann, E.; Quinto, E.T.; Ramlau, R. Wavelet methods for a weighted sparsity penalty for region of interest tomography. Inverse Probl. 2015, 31, 025001. [Google Scholar] [CrossRef]
- Ward, J.P.; Lee, M.; Ye, J.C.; Unser, M. Interior tomography using 1d generalized total variation. Part I: Mathematical foundation. SIAM J. Imaging Sci. 2015, 8, 226–247. [Google Scholar] [CrossRef]
- Lee, M.; Han, Y.; Ward, J.P.; Unser, M.; Ye, J.C. Interior tomography using 1d generalized total variation. Part II: Multiscale implementation. SIAM J. Imaging Sci. 2015, 8, 2452–2486. [Google Scholar] [CrossRef]
- Liu, B.; Katsevich, A.; Yu, H. Interior tomography with curvelet-based regularization. J. X-ray Sci. Technol. 2017, 25, 1–13. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, Y.; Yang, J.; Jiang, M. Mumford-shah-tv functional with application in x-ray interior tomography. Inverse Probl. Imaging 2018, 12, 331. [Google Scholar] [CrossRef]
- Bubba, T.A.; Porta, F.; Zanghirati, G.; Bonettini, S. A nonsmooth regularization approach based on shearlets for poisson noise removal in roi tomography. Appl. Math. Comput. 2018, 318, 131–152. [Google Scholar] [CrossRef]
- Xu, Q.; Mou, X.; Wang, G.; Sieren, J.; Hoffman, E.A.; Yu, H. Statistical interior tomography. IEEE Trans. Med. Imaging 2011, 30, 1116–1128. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, H.; Mou, X.; Zhang, L.; Hsieh, J.; Wang, G. Low-dose x-ray ct reconstruction via dictionary learning. IEEE Trans. Med. Imaging 2012, 31, 1682–1697. [Google Scholar]
- Wu, J.; Dai, F.; Hu, G.; Mou, X. Low dose ct reconstruction via l1 norm dictionary learning using alternating minimization algorithm and balancing principle. J. X-ray Sci. Technol. 2018, 26, 603–622. [Google Scholar] [CrossRef]
- Xu, M.; Hu, D.; Luo, F.; Liu, F.; Wu, W. Limited angle x ray ct reconstruction using image gradient 0 norm with dictionary learning. IEEE Trans. Radiat. Plasma Med. Sci. 2021, 5, 78–87. [Google Scholar] [CrossRef]
- Kong, H.; Lei, X.; Lei, L.; Zhang, Y.; Yu, H. Spectral ct reconstruction based on piccs and dictionary learning. IEEE Access 2020, 8, 133367–133376. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Available online: http://spams-devel.gforge.inria.fr/ (accessed on 5 March 2011).
- Yan, X.; Martin, B.; Sebastian, B.; Hu, S.; Andre, A.; Andreas, M. An improved extrapolation scheme for truncated ct data using 2d fourier-based helgason-ludwig consistency conditions. Int. J. Biomed. Imaging 2017, 2017, 1867025. [Google Scholar]
- Yu, H.Y.; Mou, X.Q.M.; Cai, Y.L. Calibration of cone beam rotational x-ray image sequence. Chin. J. Electron. 2004, 13, 5. [Google Scholar]
- Elbakri, I.A.; Fessler, J.A. Statistical image reconstruction for polyenergetic x-ray computed tomography. IEEE Trans. Med. Imaging 2002, 21, 89–99. [Google Scholar] [CrossRef]
- Available online: http://wiki.kek.jp/pages/viewpage.action?pageId=13667347 (accessed on 10 May 2021).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]

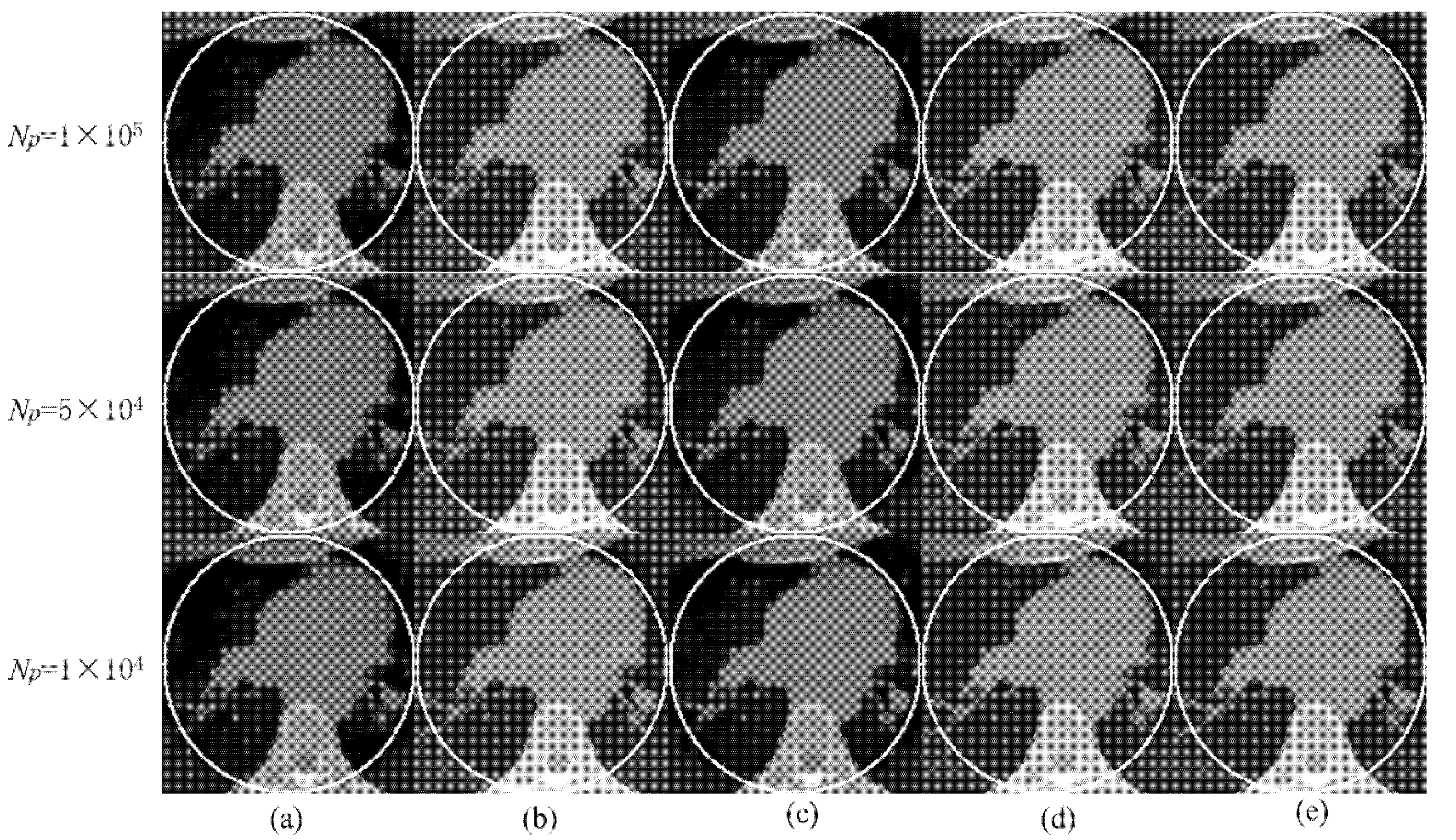



| Algorithm | 1 × 105 | 5 × 104 | 1 × 104 | |||
|---|---|---|---|---|---|---|
| RMSE | SSIM | RMSE | SSIM | RMSE | SSIM | |
| SIRTV + BOS | 258.2 | 0.3617 | 258.4 | 0.3629 | 259.4 | 0.3482 |
| SIRTV + OS | 139.2 | 0.6971 | 139.6 | 0.6829 | 142.3 | 0.6076 |
| SIRDL + BOS | 200.0 | 0.3903 | 201.1 | 0.3861 | 205.0 | 0.3746 |
| SIRDL + OS | 131.3 | 0.7108 | 132.3 | 0.6913 | 134.3 | 0.6238 |
| SIRDL + HL | 128.6 | 0.7204 | 134.3 | 0.7101 | 127.2 | 0.7021 |
| The Number of View | ε | γ | The Number of Subset | The Number of Iteration | |
|---|---|---|---|---|---|
| 1160 | 0.015(0.020) | 40 | 50 | ||
| 580 | 0.022(0.030) | 20 | 80 | ||
| 290 | 0.033(0.060) | 10 | 150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, X.; Mou, X. Statistical Interior Tomography via L1 Norm Dictionary Learning without Assuming an Object Support. Tomography 2022, 8, 2218-2231. https://doi.org/10.3390/tomography8050186
Wu J, Wang X, Mou X. Statistical Interior Tomography via L1 Norm Dictionary Learning without Assuming an Object Support. Tomography. 2022; 8(5):2218-2231. https://doi.org/10.3390/tomography8050186
Chicago/Turabian StyleWu, Junfeng, Xiaofeng Wang, and Xuanqin Mou. 2022. "Statistical Interior Tomography via L1 Norm Dictionary Learning without Assuming an Object Support" Tomography 8, no. 5: 2218-2231. https://doi.org/10.3390/tomography8050186
APA StyleWu, J., Wang, X., & Mou, X. (2022). Statistical Interior Tomography via L1 Norm Dictionary Learning without Assuming an Object Support. Tomography, 8(5), 2218-2231. https://doi.org/10.3390/tomography8050186






