Magnetic Susceptibility Source Separation Solely from Gradient Echo Data: Histological Validation

Quantitative susceptibility mapping (QSM) facilitates mapping of the bulk magnetic susceptibility of tissue from the phase of complex gradient echo (GRE) MRI data. QSM phase processing combined with an

R_{2}^{*}

model of magnitude of multiecho gradient echo data (

R_{2}^{*} Q S M

) allows separation of dia- and para-magnetic components (e.g., myelin and iron) that contribute constructively to

R_{2}^{*}

value but destructively to the QSM value of a voxel. This

R_{2}^{*} Q S M

technique is validated against quantitative histology—optical density of myelin basic protein and Perls’ iron histological stains of rim and core of 10 ex vivo multiple sclerosis lesions, as well as neighboring normal appearing white matter. We found that

R_{2}^{*} Q S M

source maps are in good qualitative agreement with histology, e.g., showing increased iron concentration at the edge of the rim+ lesions and myelin loss in the lesions’ core. Furthermore, our results indicate statistically significant correlation between paramagnetic and diamagnetic tissue components estimated with

R_{2}^{*} Q S M

and optical densities of Perls’ and MPB stains. These findings provide direct support for the use of

R_{2}^{*} Q S M

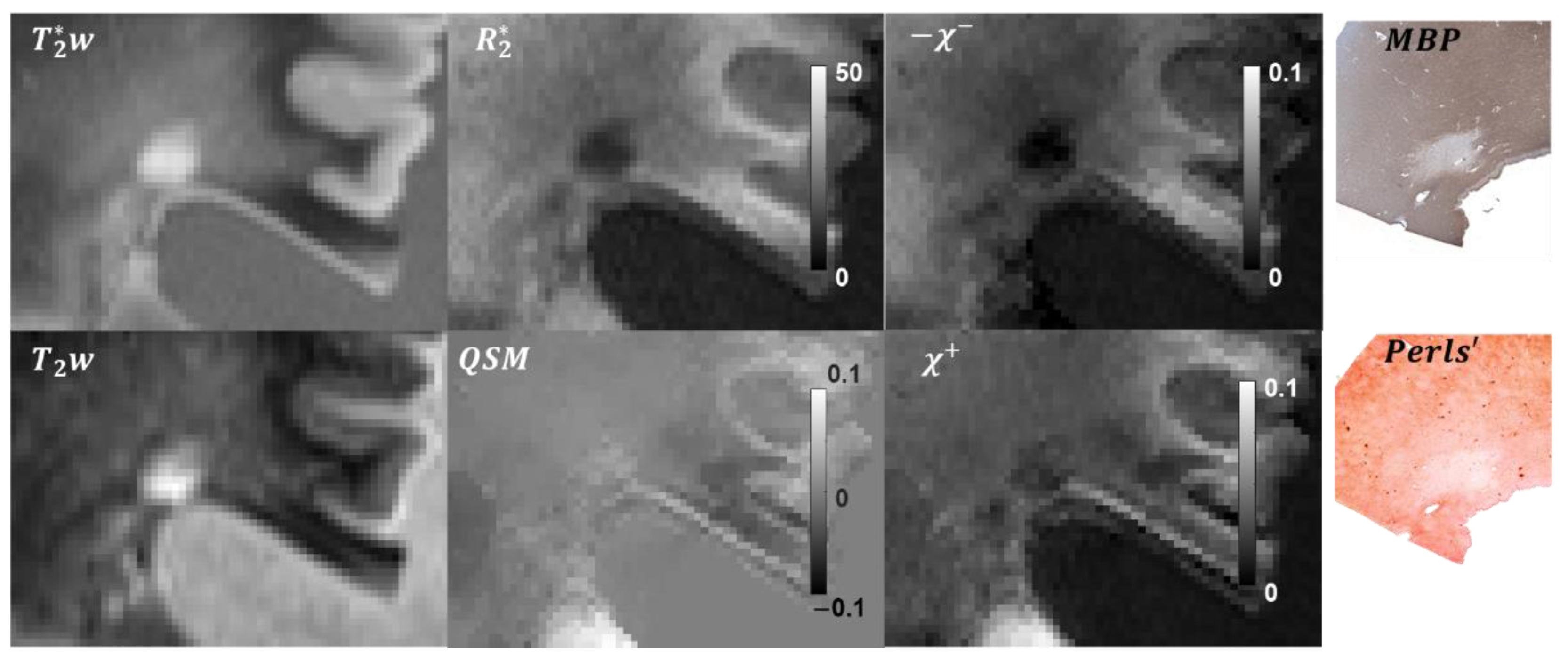
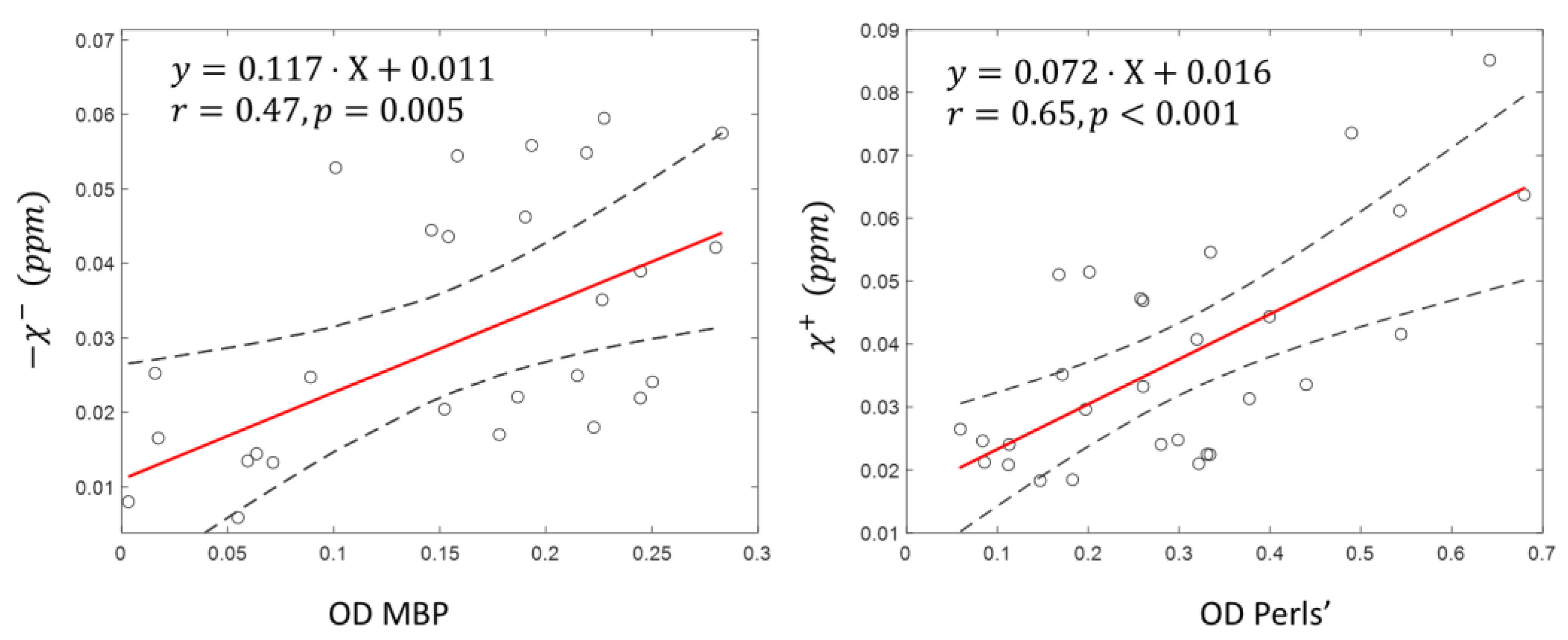
magnetic source separation based solely on GRE complex data to characterize MS lesion composition. View Full-Text

Keywords: quantitative susceptibility mapping; susceptibility source separation; myelin quantification; iron quantification

▼ Show Figures

Figure 1

This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited

Share and Cite

MDPI and ACS Style

Dimov, A.V.; Gillen, K.M.; Nguyen, T.D.; Kang, J.; Sharma, R.; Pitt, D.; Gauthier, S.A.; Wang, Y. Magnetic Susceptibility Source Separation Solely from Gradient Echo Data: Histological Validation. Tomography 2022, 8, 1544-1551. https://doi.org/10.3390/tomography8030127

AMA Style

Dimov AV, Gillen KM, Nguyen TD, Kang J, Sharma R, Pitt D, Gauthier SA, Wang Y. Magnetic Susceptibility Source Separation Solely from Gradient Echo Data: Histological Validation. Tomography. 2022; 8(3):1544-1551. https://doi.org/10.3390/tomography8030127

Chicago/Turabian Style

Dimov, Alexey V., Kelly M. Gillen, Thanh D. Nguyen, Jerry Kang, Ria Sharma, David Pitt, Susan A. Gauthier, and Yi Wang. 2022. "Magnetic Susceptibility Source Separation Solely from Gradient Echo Data: Histological Validation" Tomography 8, no. 3: 1544-1551. https://doi.org/10.3390/tomography8030127

Find Other Styles

Article Metrics

Abstract views Pdf views Html views

Article Menu

Magnetic Susceptibility Source Separation Solely from Gradient Echo Data: Histological Validation

Abstract

Share and Cite

Article Metrics

Article Access Statistics

Article Access Map by Country/Region

Further Information

Guidelines

MDPI Initiatives

Follow MDPI