SNR-Enhanced, Rapid Electrical Conductivity Mapping Using Echo-Shifted MRI
Abstract
:1. Introduction
2. Materials and Methods
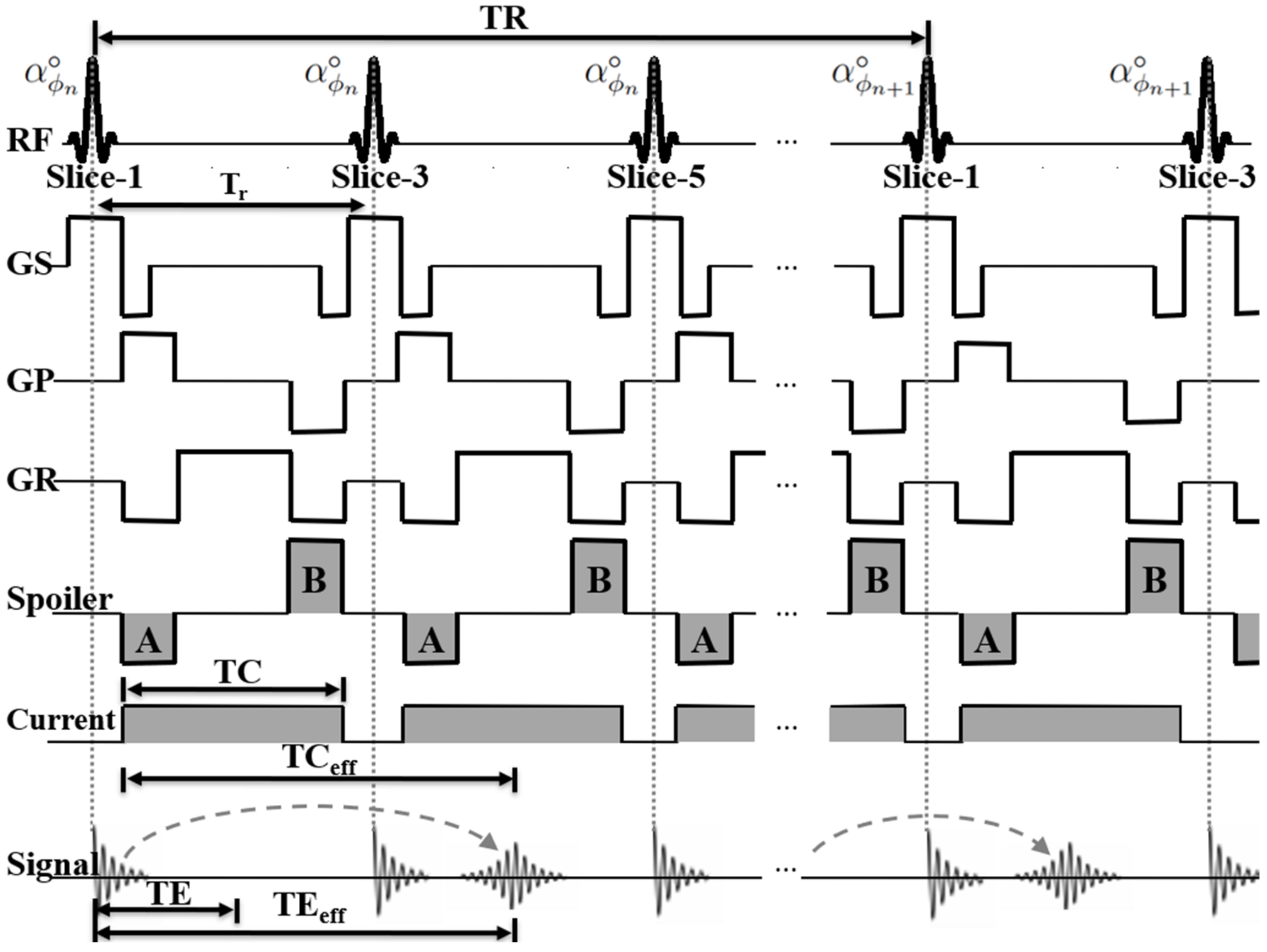
2.1. Multi-Slice ESSSI Imaging with Current Injection
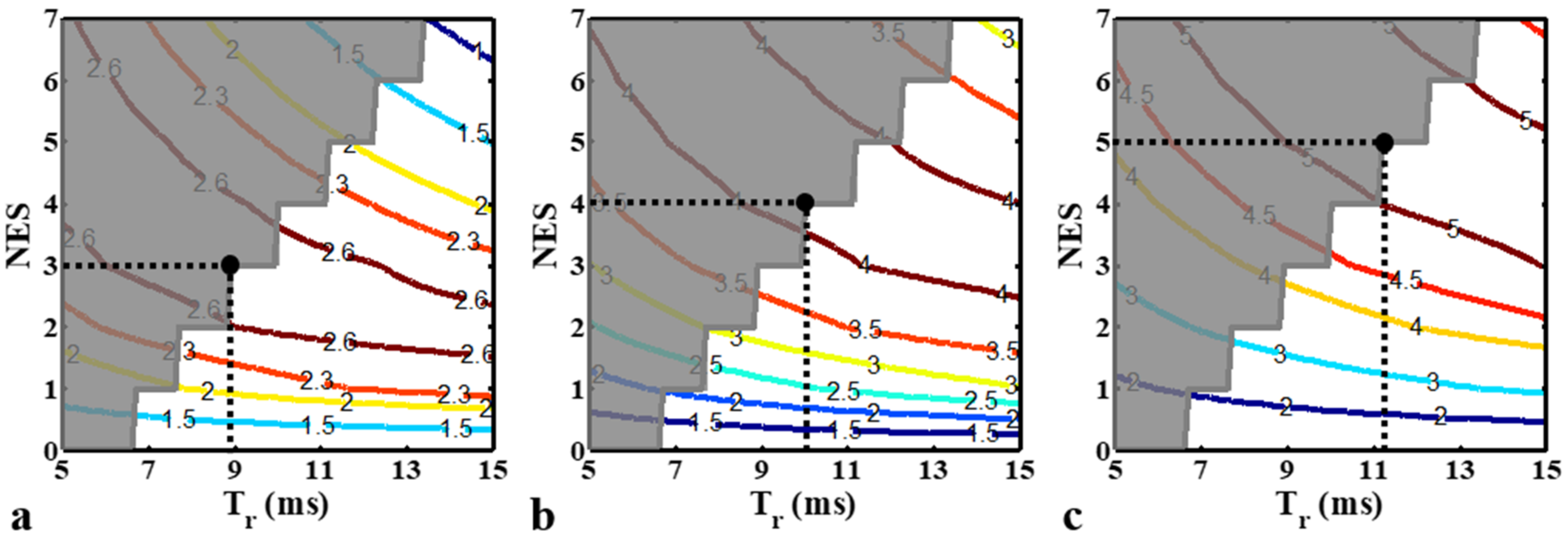
2.2. Bz Estimation and SNR Analysis
2.3. Numerical Simulations
2.4. Experimental Studies
3. Results
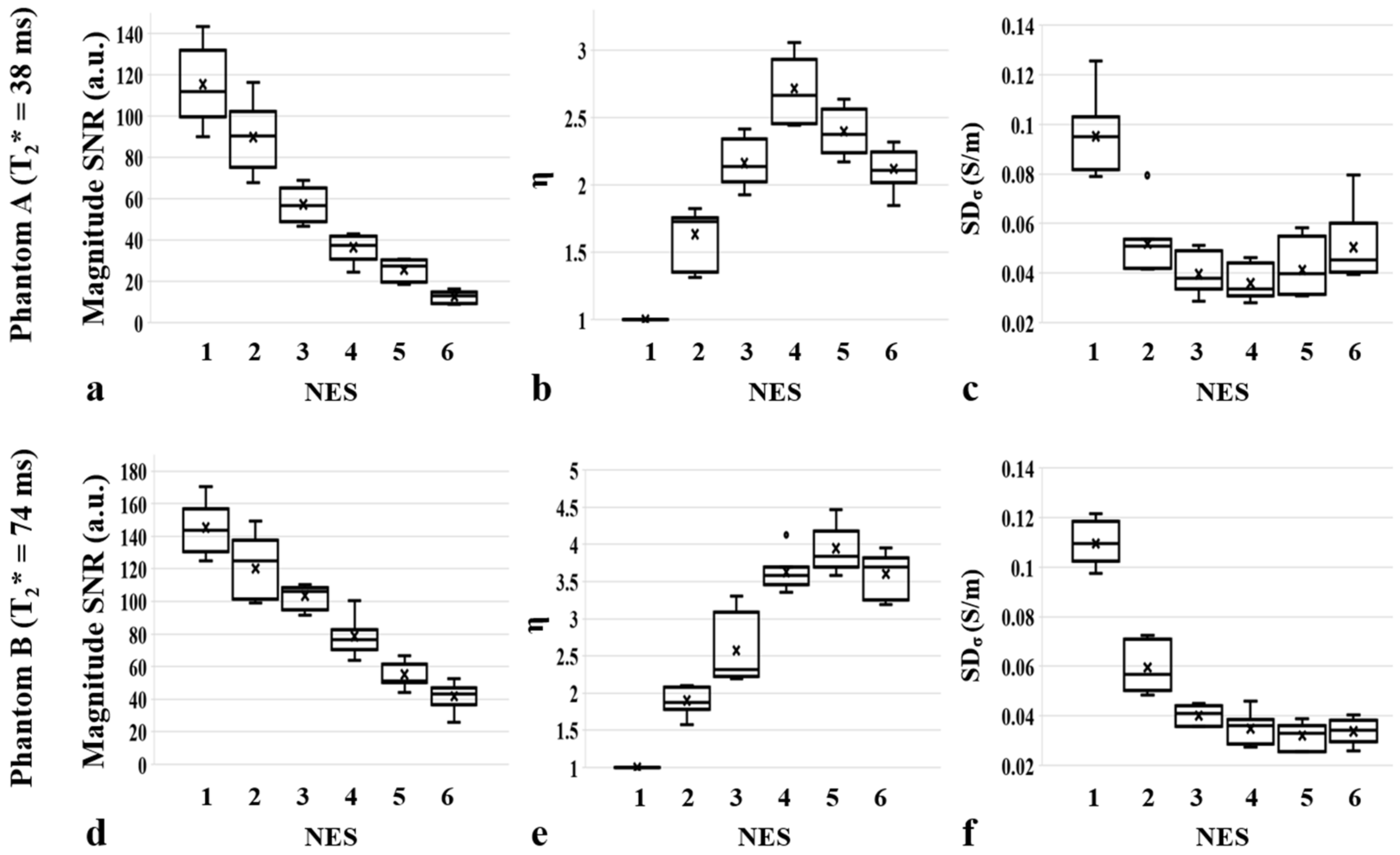
3.1. Numerical Simulations
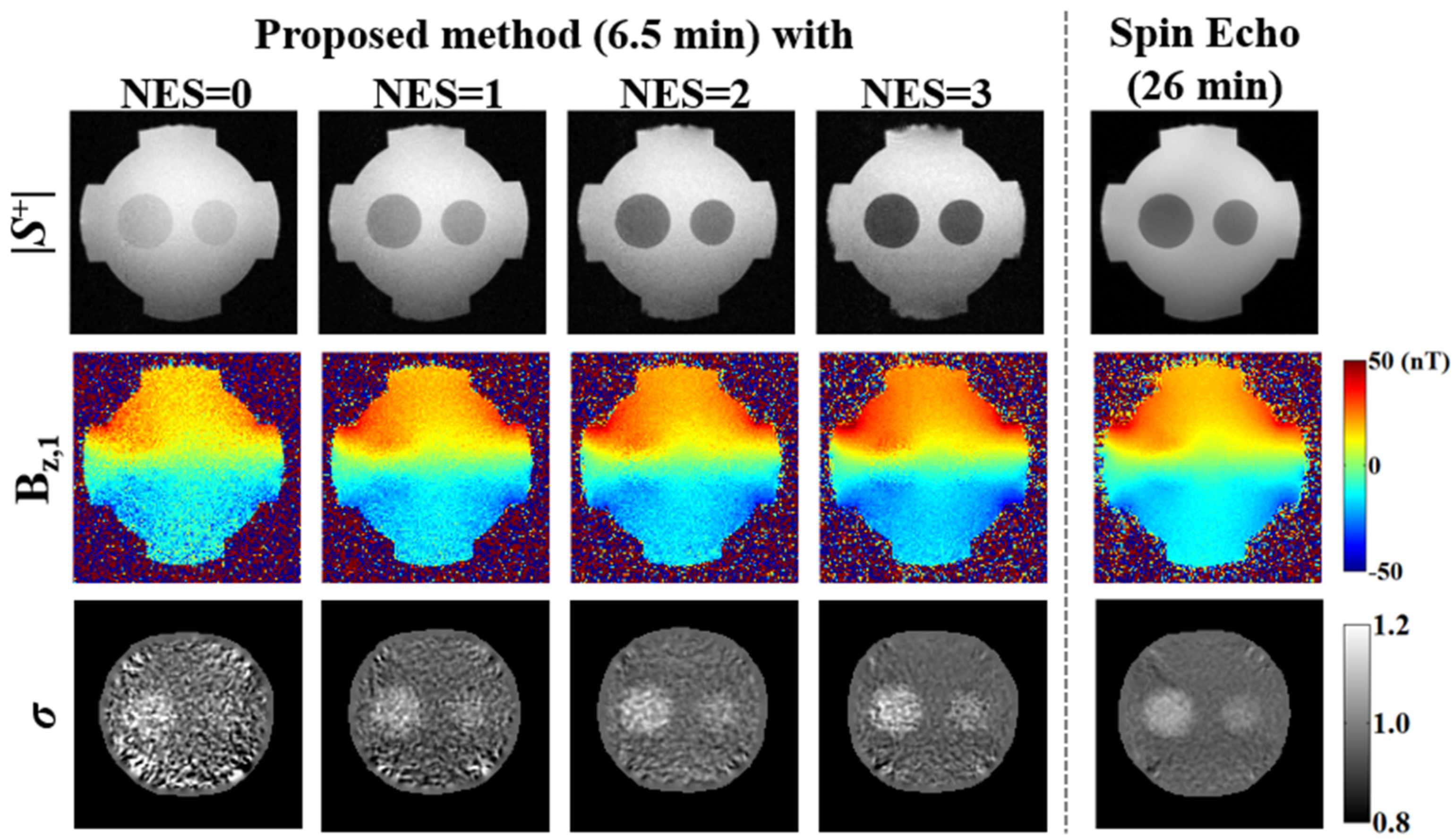
3.2. Experimental Studies
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabriel, C.; Gabriel, S.; Corthout, Y.E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gençer, N.G.; Acar, C.E. Sensitivity of EEG and MEG measurements to tissue conductivity. Phys. Med. Biol. 2004, 49, 701. [Google Scholar] [CrossRef] [PubMed]
- Güllmar, D.; Haueisen, J.; Reichenbach, J.R. Influence of anisotropic electrical conductivity in white matter tissue on the EEG/MEG forward and inverse solution. A high-resolution whole head simulation study. Neuroimage 2010, 51, 145–163. [Google Scholar] [CrossRef]
- Sadleir, R.J.; Fu, F.; Chauhan, M. Functional magnetic resonance electrical impedance tomography (f MREIT) sensitivity analysis using an active bidomain finite-element model of neural tissue. Magn. Reson. Med. 2019, 81, 602–614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beravs, K.; Frangež, R.; Gerkis, A.N.; Demsar, F. Radiofrequency current density imaging of kainate-evoked depolarization. Magn. Reson. Med. 1999, 42, 136–140. [Google Scholar] [CrossRef]
- Hamamura, M.J.; Muftuler, L.T.; Birgul, O.; Nalcioglu, O. Measurement of ion diffusion using magnetic resonance electrical impedance tomography. Phys. Med. Biol. 2006, 51, 2753. [Google Scholar] [CrossRef] [PubMed]
- Oh, T.I.; Kim, Y.T.; Minhas, A.; Seo, J.K.; Kwon, O.I.; Woo, E.J. Ion mobility imaging and contrast mechanism of apparent conductivity in MREIT. Phys. Med. Biol. 2011, 56, 2265. [Google Scholar] [CrossRef]
- Choi, B.K.; Katoch, N.; Kim, H.J.; Park, J.A.; Ko, I.O.; Kwon, O.I.; Woo, E.J. Validation of conductivity tensor imaging using giant vesicle suspensions with different ion mobilities. BioMedical Eng. OnLine 2020, 19, 35. [Google Scholar] [CrossRef]
- Joy, M.L.; Lebedev, V.P.; Gati, J.S. Imaging of current density and current pathways in rabbit brain during transcranial electrostimulation. IEEE Trans. Biomed. Eng. 1999, 46, 1139–1149. [Google Scholar] [CrossRef]
- Khang, H.; Oh, S.; Han, B.; Lee, S.; Cho, M.; Woo, E. A preliminary study on temperature change monitoring using the MR current density imaging technique. Meas. Sci. Technol. 2002, 13, N42. [Google Scholar]
- Chauhan, M.; Indahlastari, A.; Kasinadhuni, A.K.; Schär, M.; Mareci, T.H.; Sadleir, R.J. Low-frequency conductivity tensor imaging of the human head in vivo using DT-MREIT: First study. IEEE Trans. Med. Imaging 2017, 37, 966–976. [Google Scholar] [CrossRef] [PubMed]
- Göksu, C.; Hanson, L.G.; Siebner, H.R.; Ehses, P.; Scheffler, K.; Thielscher, A. Human in-vivo brain magnetic resonance current density imaging (MRCDI). NeuroImage 2018, 171, 26–39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H.J.; Oh, T.I.; Kim, Y.T.; Lee, B.I.; Woo, E.J.; Seo, J.K.; Lee, S.Y.; Kwon, O.; Park, C.; Kang, B.T. In vivo electrical conductivity imaging of a canine brain using a 3 T MREIT system. Physiol. Meas. 2008, 29, 1145. [Google Scholar] [CrossRef]
- Cheney, M.; Isaacson, D.; Newell, J.C. Electrical impedance tomography. SIAM Rev. 1999, 41, 85–101. [Google Scholar] [CrossRef] [Green Version]
- Holder, D.S. Electrical Impedance Tomography: Methods, History And Applications; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Woo, E.J.; Seo, J.K. Magnetic resonance electrical impedance tomography (MREIT) for high-resolution conductivity imaging. Physiol. Meas. 2008, 29, R1. [Google Scholar] [CrossRef] [Green Version]
- Kwon, O.; Woo, E.J.; Yoon, J.-R.; Seo, J.K. Magnetic resonance electrical impedance tomography (MREIT): Simulation study of J-substitution algorithm. IEEE Trans. Biomed. Eng. 2002, 49, 160–167. [Google Scholar] [CrossRef]
- Woo, E.J.; Lee, S.Y.; Mun, C.W. Impedance tomography using internal current density distribution measured by nuclear magnetic resonance. In Proceedings of the Mathematical Methods in Medical Imaging III, San Diego, CA, USA, 8 July 1994; pp. 377–385. [Google Scholar]
- Oh, S.H.; Lee, B.I.; Woo, E.J.; Lee, S.Y.; Cho, M.H.; Kwon, O.; Seo, J.K. Conductivity and current density image reconstruction using harmonic Bz algorithm in magnetic resonance electrical impedance tomography. Phys. Med. Biol. 2003, 48, 3101. [Google Scholar] [CrossRef] [Green Version]
- Seo, J.K.; Yoon, J.-R.; Woo, E.J.; Kwon, O. Reconstruction of conductivity and current density images using only one component of magnetic field measurements. IEEE Trans. Biomed. Eng. 2003, 50, 1121–1124. [Google Scholar]
- Sadleir, R.; Grant, S.; Zhang, S.U.; Lee, B.I.; Pyo, H.C.; Oh, S.H.; Park, C.; Woo, E.J.; Lee, S.Y.; Kwon, O. Noise analysis in magnetic resonance electrical impedance tomography at 3 and 11 T field strengths. Physiol. Meas. 2005, 26, 875–884. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, W.C.; Kim, H.J.; Woo, E.J.; Park, J. Alternating steady state free precession for estimation of current-induced magnetic flux density: A feasibility study. Magn. Reson. Med. 2016, 75, 2009–2019. [Google Scholar] [CrossRef]
- Nam, H.S.; Kwon, O.I. Optimization of multiply acquired magnetic flux density Bz using ICNE-Multiecho train in MREIT. Phys. Med. Biol. 2010, 55, 2743. [Google Scholar] [CrossRef] [PubMed]
- Minhas, A.S.; Jeong, W.C.; Kim, Y.T.; Han, Y.; Kim, H.J.; Woo, E.J. Experimental performance evaluation of multi-echo ICNE pulse sequence in magnetic resonance electrical impedance tomography. Magn. Reson. Med. 2011, 66, 957–965. [Google Scholar] [CrossRef]
- Lee, H.; Sohn, C.H.; Park, J. Current-induced alternating reversed dual-echo-steady-state for joint estimation of tissue relaxation and electrical properties. Magn. Reson. Med. 2017, 78, 107–120. [Google Scholar] [CrossRef]
- Zur, Y.; Wood, M.; Neuringer, L. Spoiling of transverse magnetization in steady-state sequences. Magn. Reson. Med. 1991, 21, 251–263. [Google Scholar] [CrossRef]
- Chung, Y.C.; Duerk, J.L. Signal formation in echo-shifted sequences. Magn. Reson. Med 1999, 42, 864–875. [Google Scholar] [CrossRef]
- Jeon, K.-W.; Lee, C.-O.; Kim, H.-J.; Woo, E.-J.; Seo, J.-K. CoReHA: Conductivity reconstructor using harmonic algorithms for magnetic resonance electrical impedance tomography (MREIT). J. Biomed. Eng. Res. 2009, 30, 279–287. [Google Scholar]
- Association, N.M.E. MS1-2001 Determination of Signal-to-Noise Ratio (SNR) in Diagnostic Magnetic Resonance Images; NEMA: Washington, DC, USA, 2001. [Google Scholar]
- Moonen, C.T.; Liu, G.; Gelderen, P.V.; Sobering, G. A fast gradient-recalled MRI technique with increased sensitivity to dynamic susceptibility effects. Magn. Reson. Med. 1992, 26, 184–189. [Google Scholar] [CrossRef]
- Liu, G.; Sobering, G.; Olson, A.W.; Van Gelderen, P.; Moonen, C.T. Fast echo-shifted gradient-recalled MRI: Combining a short repetition time with variable T2* weighting. Magn. Reson. Med. 1993, 30, 68–75. [Google Scholar] [CrossRef]
- Moonen, C.T.; Barrios, F.A.; Zigun, J.R.; Gillen, J.; Liu, G.; Sobering, G.; Sexton, R.; Woo, J.; Frank, J.; Weinberger, D.R. Functional brain MR imaging based on bolus tracking with a fast T2*-sensitized gradient-echo method. Magn. Reson. Imaging 1994, 12, 379–385. [Google Scholar] [CrossRef]



| Imaging Parameters | Phantoms A and B (Homogeneous) | Phantom C (Non-Homogeneous) | |
|---|---|---|---|
| Proposed Method | Proposed Method | Conventional SE | |
| Field-of-view (mm2) | 180 × 180 | 150 × 150 | 150 × 150 |
| Slice thickness (mm) | 4 | 4 | 4 |
| Matrix size | 128 × 128 | 128 × 128 | 128 × 128 |
| Number of slices | 6 | 8 | 8 |
| TR (ms) | 50–68 | 72 | 1000 |
| TE (ms) | 5.5 | 4 | 40 |
| Flip angle (degree) | 25 | 15 | 90 (excitation)/ 180 (refocusing) |
| Averages | 2 | 10 | 3 |
| Approximate scan time (min) | 0.9–1.2 | 6.5 | 26 |
| NES examined | 0, 1, 2, 3, 4, 5 | 0, 1, 2, 3 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Park, J. SNR-Enhanced, Rapid Electrical Conductivity Mapping Using Echo-Shifted MRI. Tomography 2022, 8, 376-388. https://doi.org/10.3390/tomography8010031
Lee H, Park J. SNR-Enhanced, Rapid Electrical Conductivity Mapping Using Echo-Shifted MRI. Tomography. 2022; 8(1):376-388. https://doi.org/10.3390/tomography8010031
Chicago/Turabian StyleLee, Hyunyeol, and Jaeseok Park. 2022. "SNR-Enhanced, Rapid Electrical Conductivity Mapping Using Echo-Shifted MRI" Tomography 8, no. 1: 376-388. https://doi.org/10.3390/tomography8010031
APA StyleLee, H., & Park, J. (2022). SNR-Enhanced, Rapid Electrical Conductivity Mapping Using Echo-Shifted MRI. Tomography, 8(1), 376-388. https://doi.org/10.3390/tomography8010031





