Initial Condition Assessment for Reaction-Diffusion Glioma Growth Models: A Translational MRI-Histology (In)Validation Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Clinical Case
2.2. MR Image Acquisitions
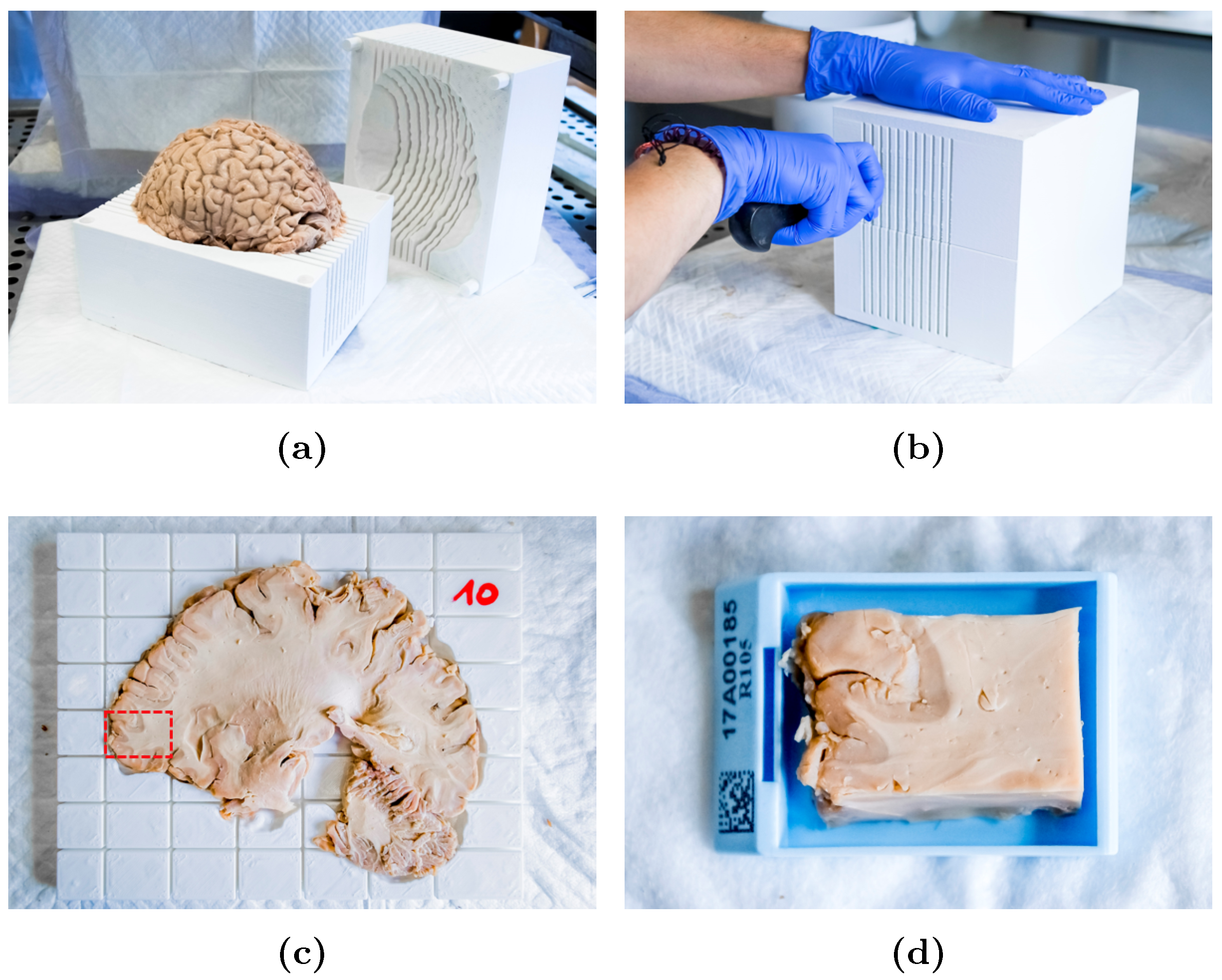
2.3. Slicer Design and Tissue Sampling
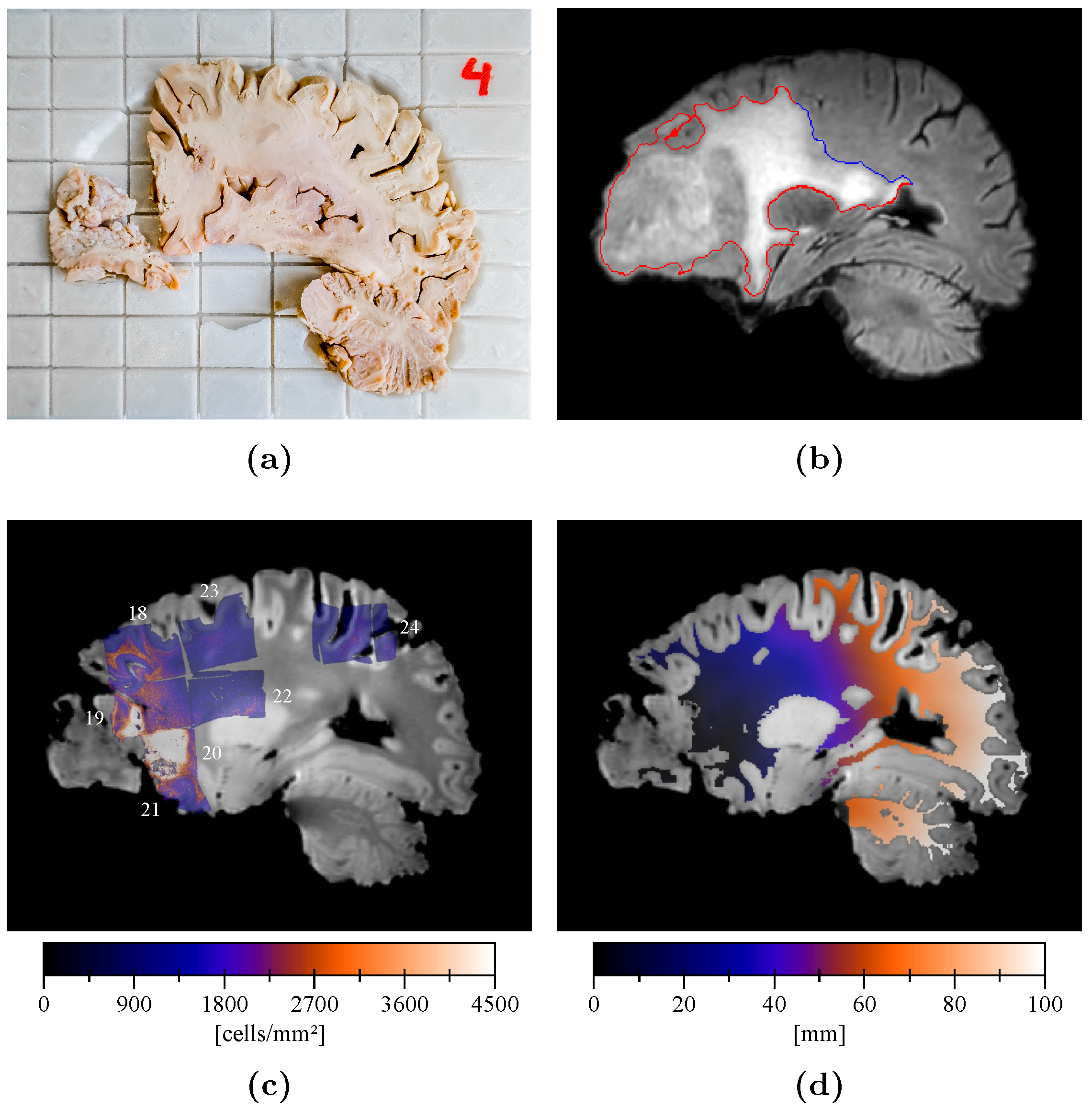
2.4. Sample Processing and Analysis
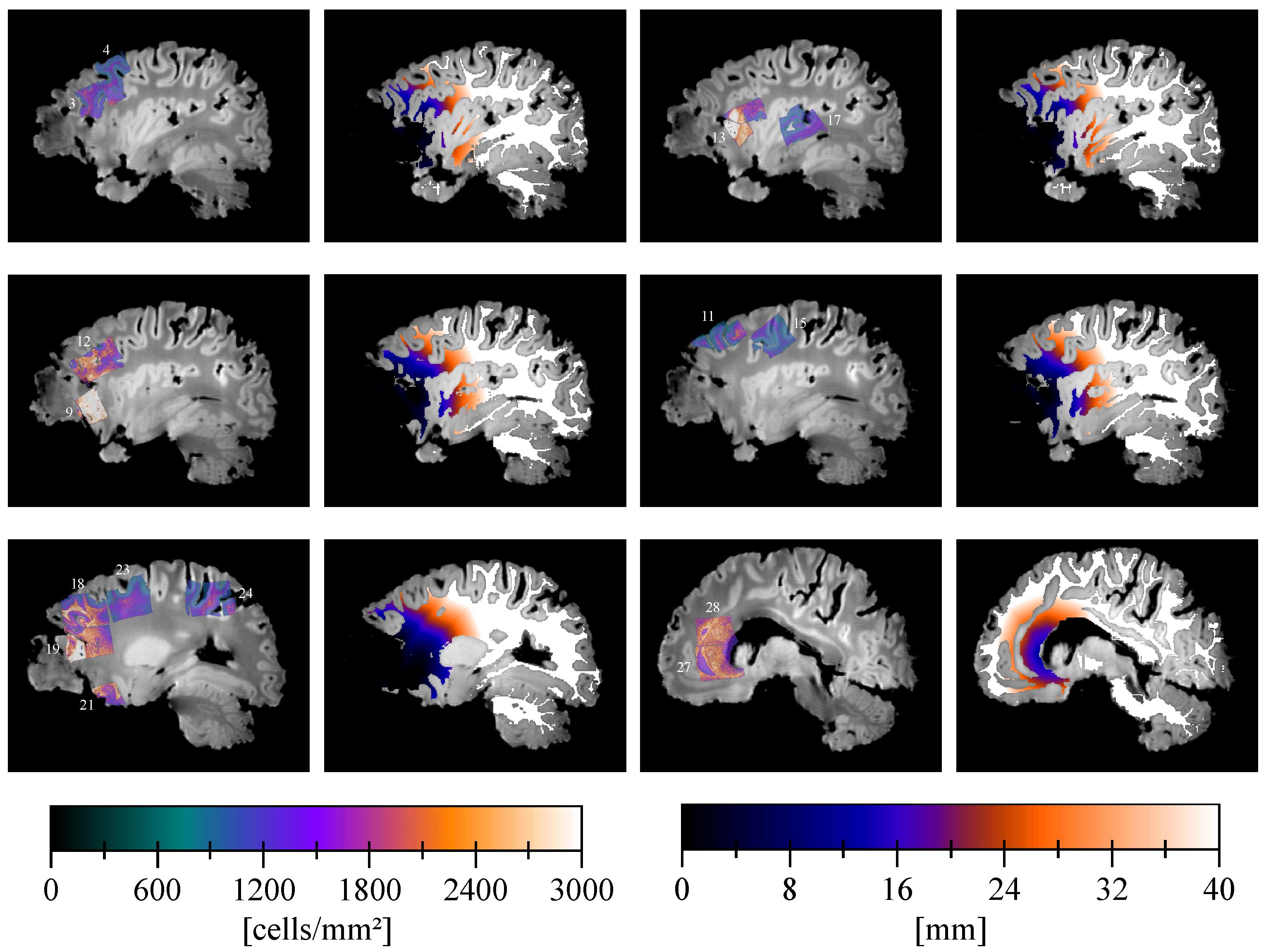
2.5. Cell Density Maps
- cell nuclei are approximately spherical;
- cell nuclei distribution is locally isotropic;
- tile dimensions are sufficiently large to contain multiple cells;
- tile dimensions are sufficiently small for the cell density to be considered homogeneous and isotropic;
2.6. Cell Density Maps to Ex Vivo T1 Registration
2.7. Edema Delineation
2.8. Distance Map
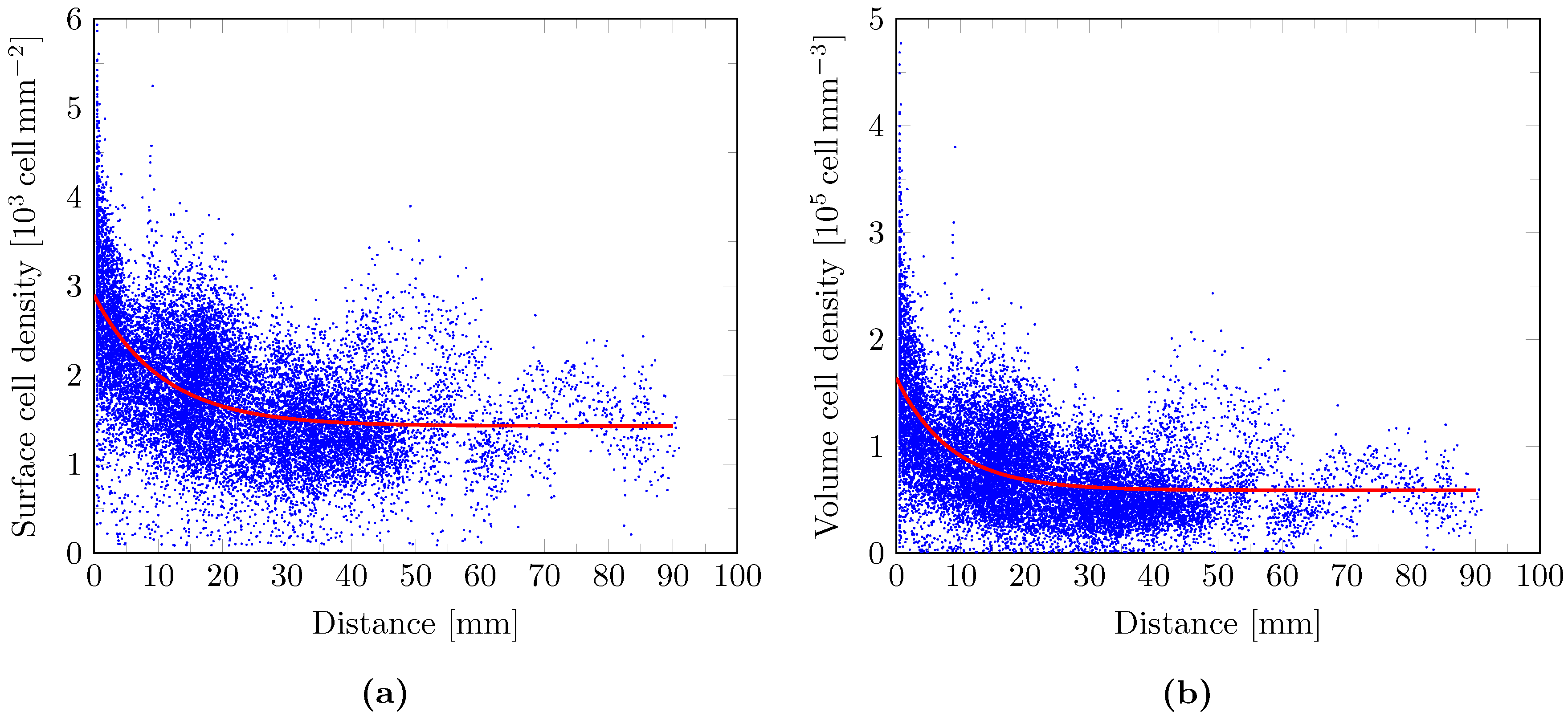
2.9. Cell Density Model
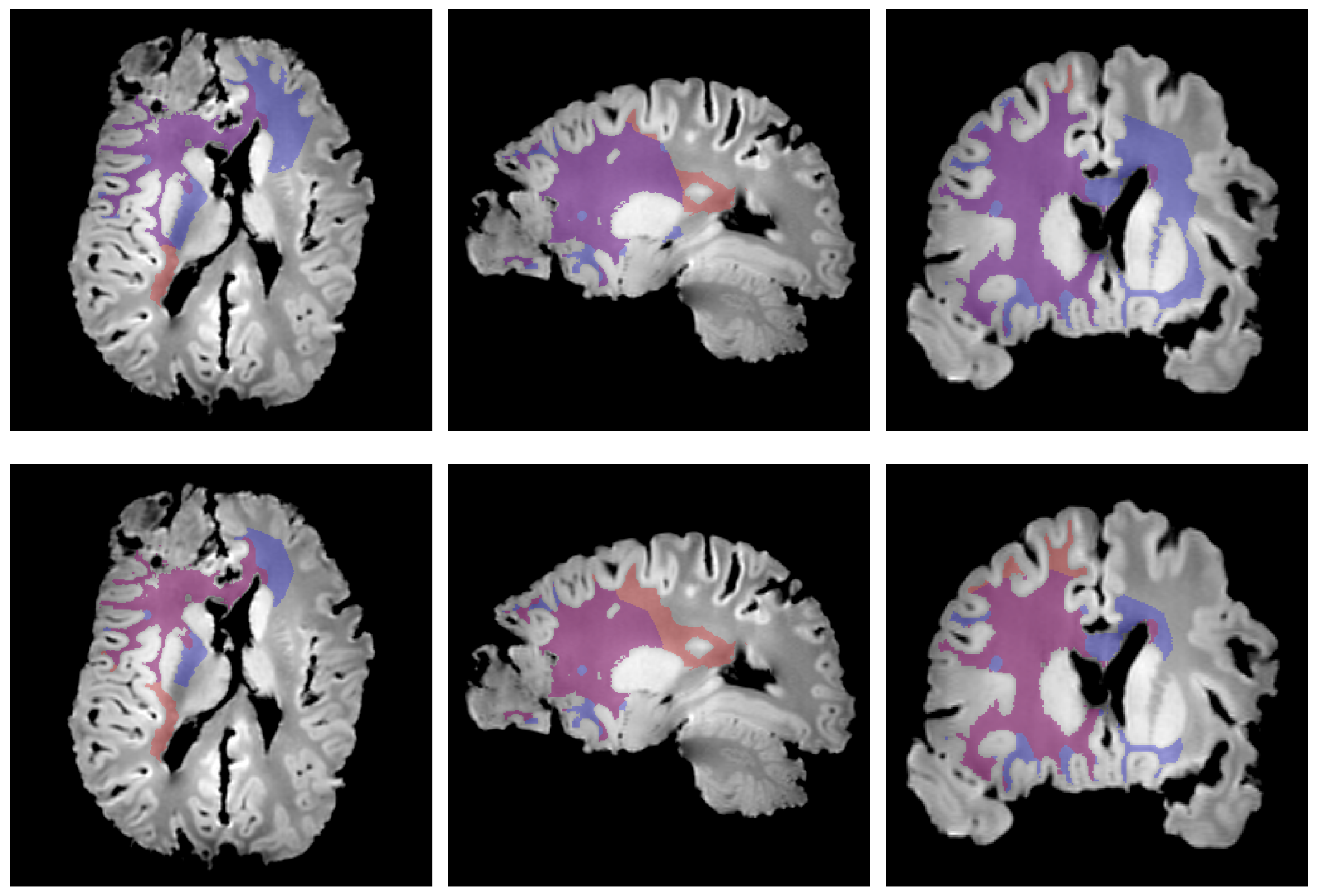
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Average diffusion coefficient |
| AFM | Anisotropic fast marching |
| ASSD | Average symmetric surface distance |
| BBB | Blood–brain barrier |
| DTI | Diffusion tensor imaging |
| DW | Diffusion-weighted |
| FA | Flip angle |
| GBM | Glioblastoma |
| GVP | Glomeruloid vascular proliferation |
| HE | Hematoxylin and eosin |
| IHC | Immunohistochemistry |
| MR(I) | Magnetic resonance (imaging) |
| PD | Proton density |
| PET | Positron emission tomography |
| PPN | Pseudo-palisading necrosis |
| ReLU | Rectified linear unit |
| Susp. | Suspected |
| T1Gd | T1-weighted sequence with injection of gadolinium-based contrast agent |
| T2-FLAIR | T2-weighted sequence with fluid-attenuated inversion recovery |
| TE | Echo time |
| TI | Inversion time |
| TMZ | Temozolomide |
| TR | Repetition time |
| VEGF | Vascular endothelial growth factor |
| WHO | World Health Organization |
Appendix A. Slicer Design
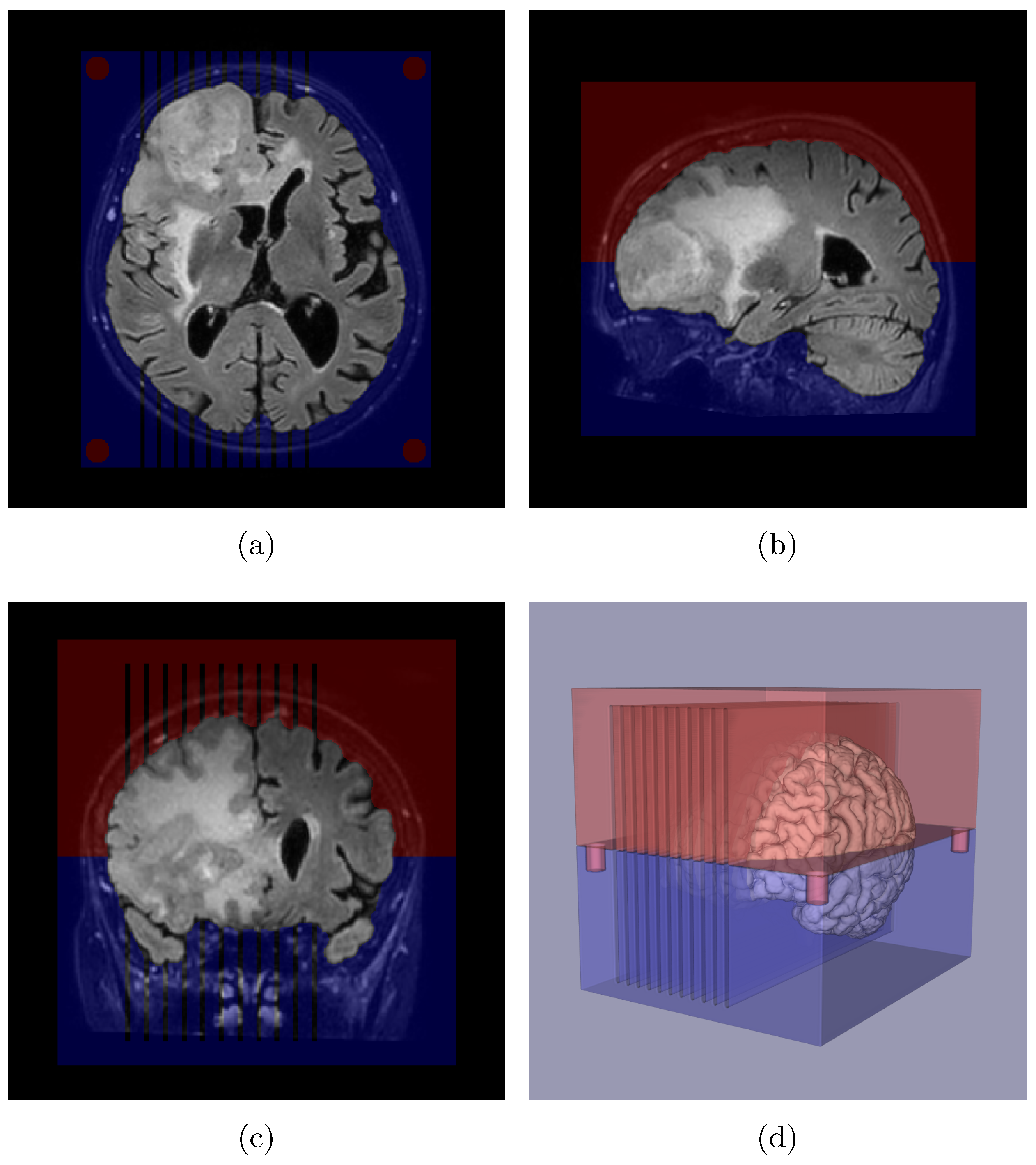
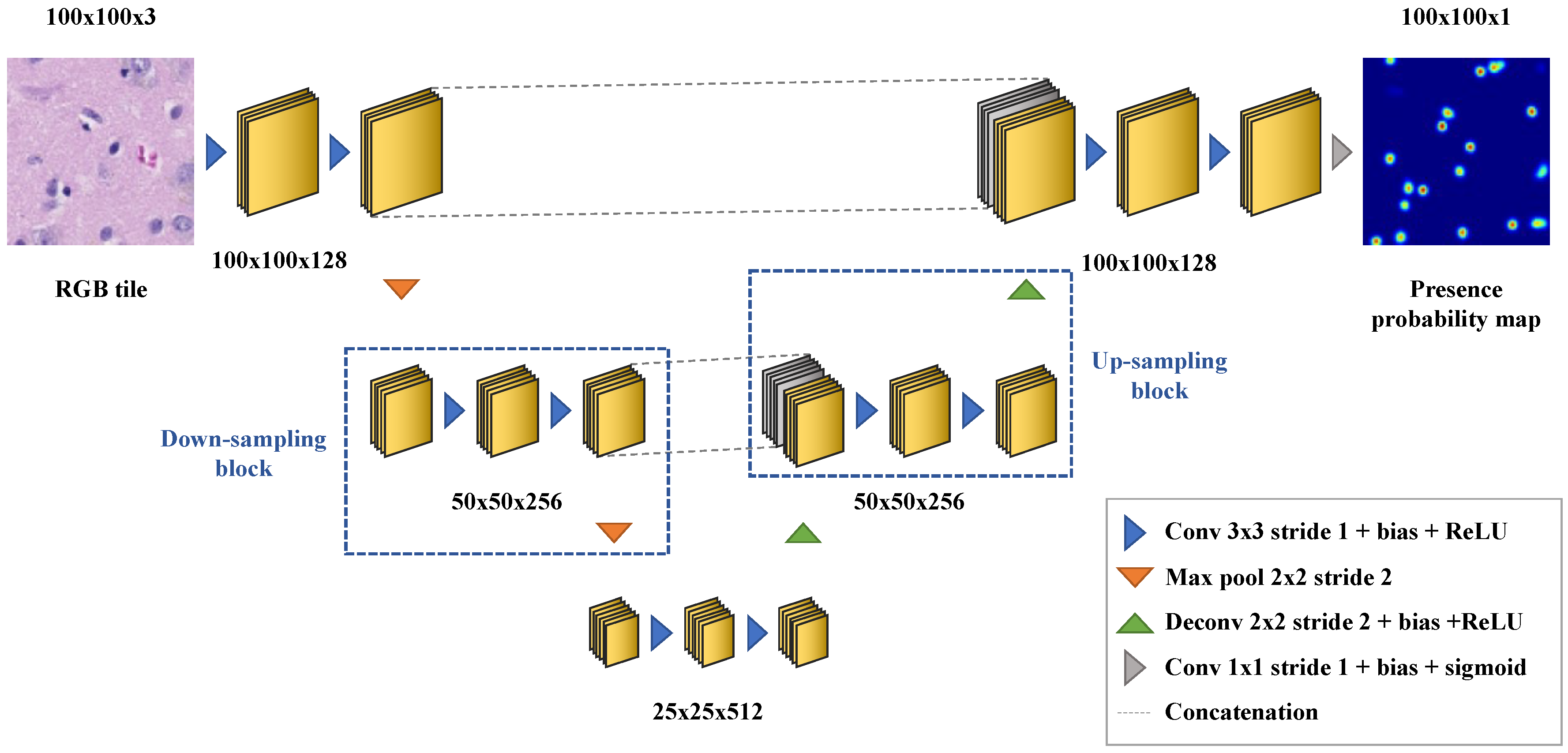
Appendix B. Deep Learning-Based Nuclei Counting
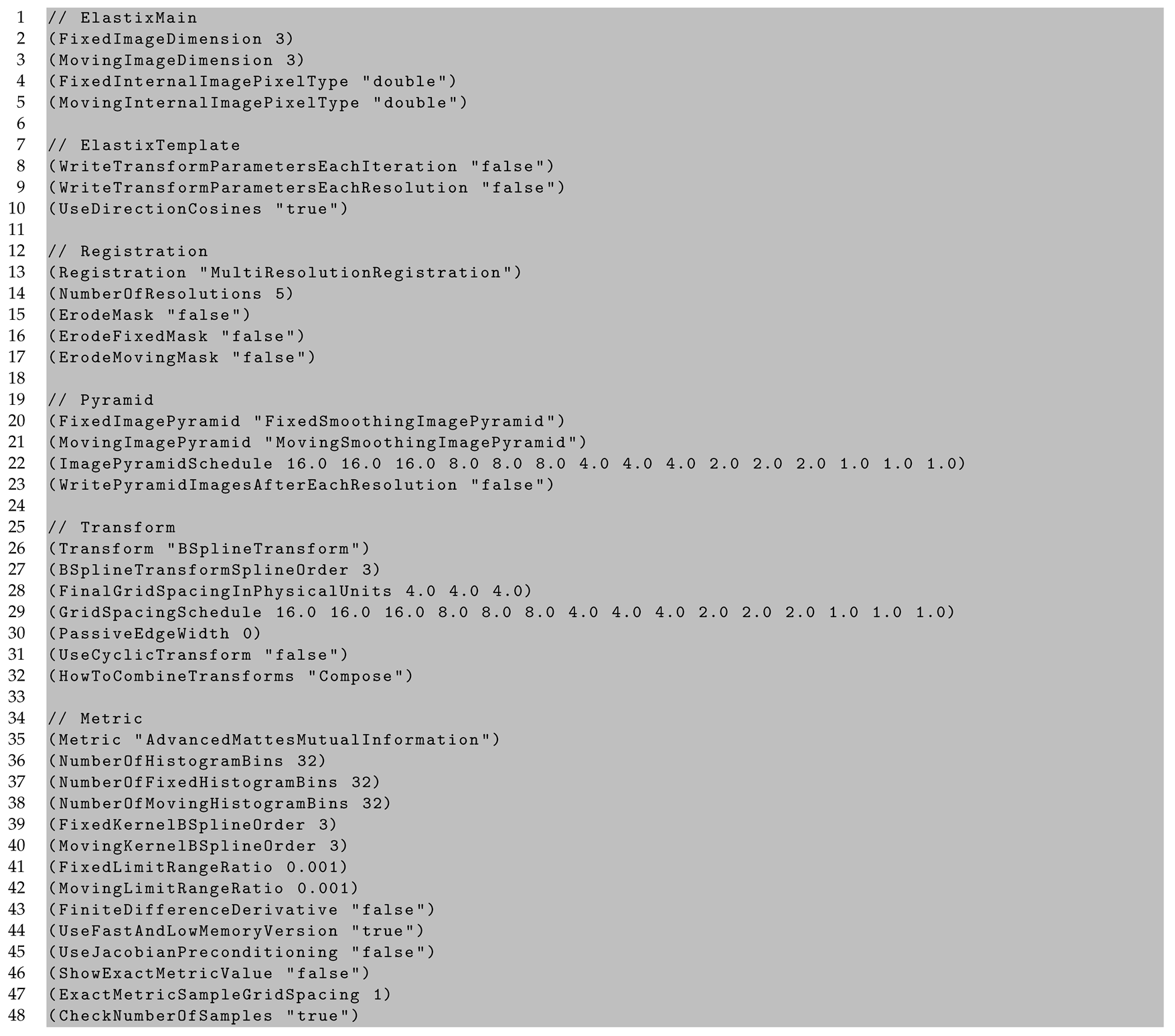
Appendix C. In Vivo to Ex Vivo Registration



Appendix D. Pathological Results
| Cell Density [ ] | Distance [] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Block | PPN | Tumor Cells | GVP | Edema | Min | Max | Mean | Min | Max | Mean |
| 1 | No | No | No | No | 1.08 | 20.46 | 11.77 | 33.40 | 40.40 | 34.95 |
| 2 | No | No | No | No | 2.25 | 23.88 | 13.80 | 35.05 | 46.76 | 40.12 |
| 3 | No | Infiltrative (susp.) | No | Yes | 1.52 | 25.25 | 14.96 | 7.24 | 21.18 | 14.00 |
| 4 | No | No | No | No | 1.36 | 20.64 | 12.50 | 29.36 | 41.66 | 36.84 |
| 5 | No | No | No | Yes | 1.19 | 24.85 | 15.40 | 11.74 | 30.27 | 21.57 |
| 6 | No | Infiltrative (susp.) | No | No | 3.72 | 28.44 | 18.70 | 32.92 | 40.35 | 36.52 |
| 7 | No | Infiltrative (susp.) | No | Yes | 0.89 | 38.95 | 21.44 | 38.59 | 61.70 | 49.04 |
| 8 | Yes | Block | Yes | No | 3.37 | 37.29 | 23.65 | 0.50 | 5.17 | 2.71 |
| 9 | Yes | Infiltrative | Yes | Yes | 1.02 | 44.37 | 31.71 | 0.50 | 4.72 | 1.91 |
| 10 | No | Infiltrative (susp.) | No | Yes | 5.52 | 37.15 | 25.53 | 0.50 | 3.71 | 1.06 |
| 11 | No | No | No | No | 1.73 | 25.68 | 15.21 | 19.85 | 38.74 | 30.74 |
| 12 | No | Infiltrative | Yes | Yes | 0.89 | 36.08 | 19.70 | 0.50 | 31.46 | 14.24 |
| 13 | Yes | Block | Yes | No | 1.40 | 52.46 | 21.69 | 0.50 | 22.85 | 9.72 |
| 14 | No | No | No | No | 1.10 | 19.25 | 11.78 | 17.73 | 32.20 | 25.51 |
| 15 | No | No | No | Yes | 2.08 | 22.90 | 11.41 | 28.63 | 54.74 | 40.14 |
| 16 | No | No | No | No | 0.99 | 26.47 | 13.52 | 20.37 | 48.79 | 35.91 |
| 17 | No | No | No | No | 1.42 | 23.69 | 13.10 | 28.30 | 56.12 | 42.88 |
| 18 | No | No | Yes | Yes | 2.46 | 39.29 | 20.71 | 7.94 | 27.01 | 16.83 |
| 19 | Yes | Block | Yes | Yes | 0.99 | 44.12 | 19.82 | 0.50 | 18.50 | 6.92 |
| 20 | Yes | Block | Yes | No | 6.25 | 61.05 | 28.40 | 0.50 | 7.37 | 2.06 |
| 21 | No | Infiltrative | Yes | Yes | 4.75 | 34.20 | 23.05 | 0.50 | 14.62 | 7.70 |
| 22 | No | No | No | Yes | 0.86 | 30.37 | 10.79 | 2.99 | 36.87 | 21.39 |
| 23 | No | No | No | No | 0.94 | 25.61 | 13.23 | 21.14 | 49.61 | 34.48 |
| 24 | No | No | No | No | 1.37 | 26.72 | 13.72 | 57.27 | 90.93 | 71.08 |
| 25 | No | Infiltrative (susp.) | No | Yes | 0.87 | 39.07 | 21.03 | 1.71 | 21.41 | 10.87 |
| 26 | Yes | Block | Yes | Yes | 6.21 | 54.24 | 22.79 | 0.50 | 8.81 | 2.96 |
| 27 | No | No | No | Yes | 0.93 | 37.96 | 21.33 | 12.74 | 30.35 | 18.40 |
| 28 | No | No | No | No | 0.95 | 34.79 | 20.76 | 14.35 | 35.85 | 22.57 |
Appendix E. Isotropic vs. Anisotropic Metric Tensor
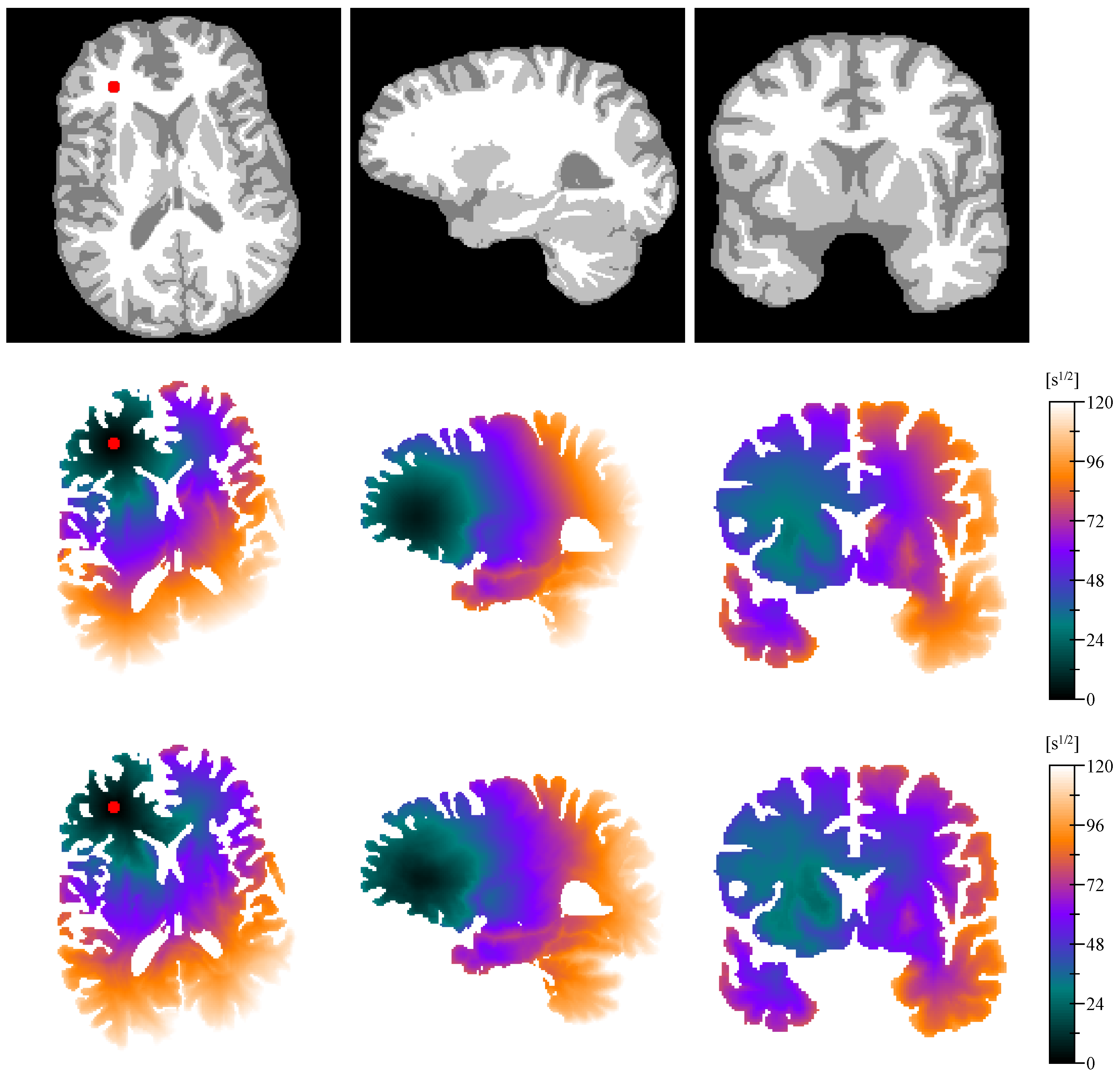
References
- Ostrom, Q.T.; Cioffi, G.; Gittleman, H.; Patil, N.; Waite, K.; Kruchko, C.; Barnholtz-Sloan, J.S. CBTRUS Statistical Report: Primary Brain and Other Central Nervous System Tumors Diagnosed in the United States in 2012–2016. Neuro-Oncol. 2019, 21, 1–100. [Google Scholar] [CrossRef] [PubMed]
- Silbergeld, D.L.; Chicoine, M.L. Isolation and Characterization of Human Malignant Glioma Cells from Histologically Normal Brain. J. Neurosurg. 1997, 86, 525–531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hawkins-Daarud, A.; Rockne, R.C.; Anderson, A.R.A.; Swanson, K.R. Modeling Tumor-Associated Edema in Gliomas during Anti-Angiogenic Therapy and Its Impact on Imageable Tumor. Front. Oncol. 2013, 3, 66. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.X. Glioma-Related Edema: New Insight into Molecular Mechanisms and Their Clinical Implications. Chin. J. Cancer 2013, 32, 49–52. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Ahn, D.; Johnson, G.; Law, M.; Zagzag, D.; Grossman, R.I. Diffusion-Tensor MR Imaging of Intracranial Neoplasia and Associated Peritumoral Edema: Introduction of the Tumor Infiltration Index. Radiology 2004, 232, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Weller, M.; van den Bent, M.; Preusser, M.; Le Rhun, E.; Tonn, J.C.; Minniti, G.; Bendszus, M.; Balana, C.; Chinot, O.; Dirven, L.; et al. EANO Guidelines on the Diagnosis and Treatment of Diffuse Gliomas of Adulthood. Nat. Rev. Clin. Oncol. 2021, 18, 170–186. [Google Scholar] [CrossRef] [PubMed]
- Unkelbach, J.; Menze, B.H.; Konukoglu, E.; Dittmann, F.; Le, M.; Ayache, N.; Shih, H.A. Radiotherapy Planning for Glioblastoma Based on a Tumor Growth Model: Improving Target Volume Delineation. Phys. Med. Biol. 2014, 59, 747–770. [Google Scholar] [CrossRef] [Green Version]
- Wesseling, P.; Kros, J.M.; Jeuken, J.W.M. The Pathological Diagnosis of Diffuse Gliomas: Towards a Smart Synthesis of Microscopic and Molecular Information in a Multidisciplinary Context. Diagn. Histopathol. 2011, 17, 486–494. [Google Scholar] [CrossRef] [Green Version]
- Tracqui, P.; Cruywagen, G.C.; Woodward, D.E.; Bartoo, G.T.; Murray, J.D.; Alvord, E.C. A Mathematical Model of Glioma Growth: The Effect of Chemotherapy on Spatio-Temporal Growth. Cell Prolif. 1995, 28, 17–31. [Google Scholar] [CrossRef]
- Cencini, M.; Lopez, C.; Vergni, D. Reaction-Diffusion Systems: Front Propagation and Spatial Structures. In The Kolmogorov Legacy in Physics; Livi, R., Vulpiani, A., Eds.; Lecture Notes in Physics, Springer: Berlin/Heidelberg, Germany, 2003; pp. 328–341. [Google Scholar]
- Konukoglu, E.; Clatz, O.; Bondiau, P.Y.; Delingette, H.; Ayache, N. Extrapolating Glioma Invasion Margin in Brain Magnetic Resonance Images: Suggesting New Irradiation Margins. Med. Image Anal. 2010, 14, 111–125. [Google Scholar] [CrossRef] [Green Version]
- Clatz, O.; Sermesant, M.; Bondiau, P.Y.; Delingette, H.; Warfield, S.K.; Malandain, G.; Ayache, N. Realistic Simulation of the 3-D Growth of Brain Tumors in MR Images Coupling Diffusion with Biomechanical Deformation. IEEE Trans. Med. Imag. 2005, 24, 1334–1346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuang, Y.; Nagy, J.D.; Eikenberry, S.E. Chapter 2—Introduction to Cancer Modeling. In Introduction to Mathematical Oncology; CRC Press: Abingdon, UK, 2016; pp. 45–92. [Google Scholar]
- Jbabdi, S.; Mandonnet, E.; Duffau, H.; Capelle, L.; Swanson, K.R.; Pélégrini-Issac, M.; Guillevin, R.; Benali, H. Simulation of Anisotropic Growth of Low-Grade Gliomas Using Diffusion Tensor Imaging. Magn. Reson. Med. 2005, 54, 616–624. [Google Scholar] [CrossRef]
- Swanson, K.R.; Rostomily, R.C.; Alvord, E.C. A Mathematical Modelling Tool for Predicting Survival of Individual Patients Following Resection of Glioblastoma: A Proof of Principle. Br. J. Cancer 2008, 98, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Martens, C.; Metens, T.; Debeir, O.; Goldman, S.; Van Simaeys, G. Initial Condition Assessment from Patient MRI Data for Reaction-Diffusion Glioma Growth Models. Proc. Intl. Soc. Mag. Reson. Med. 2019, 27, 2852. [Google Scholar]
- Tovi, M.; Ericsson, A. Measurement of T1 and T2 Over Time in Formalin-Fixed Human Whole-Brain Specimens. Acta Radiol. 1992, 33, 400–404. [Google Scholar] [CrossRef] [PubMed]
- Raman, M.R.; Shu, Y.; Lesnick, T.G.; Jack, C.R.; Kantarci, K. Regional T1 Relaxation Time Constants in Ex Vivo Human Brain: Longitudinal Effects of Formalin Exposure. Magn. Reson. Med. 2017, 77, 774–778. [Google Scholar] [CrossRef]
- Absinta, M.; Nair, G.; Filippi, M.; Ray-Chaudhury, A.; Reyes-Mantilla, M.I.; Pardo, C.A.; Reich, D.S. Postmortem Magnetic Resonance Imaging to Guide the Pathologic Cut: Individualized, 3-Dimensionally Printed Cutting Boxes for Fixed Brains. J. Neuropathol. Exp. Neurol. 2014, 73, 780–788. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W.; Martin, K.; Lorensen, B. The Visualization Toolkit, 4th ed.; Kitware: Clifton Park, NY, USA, 2010. [Google Scholar]
- Yoo, T.; Ackerman, M.; Lorensen, W.; Schroeder, W.; Chalana, V.; Aylward, S.; Metaxas, D.; Whitaker, R. Engineering and Algorithm Design for an Image Processing API: A Technical Report on ITK—The Insight Toolkit. Stud. Health Technol. Inform. 2002, 85, 586–592. [Google Scholar]
- Klein, S.; Staring, M.; Murphy, K.; Viergever, M.A.; Pluim, J. elastix: A Toolbox for Intensity-Based Medical Image Registration. IEEE Trans. Med. Imaging 2010, 29, 196–205. [Google Scholar] [CrossRef]
- Konukoglu, E.; Sermesant, M.; Clatz, O.; Peyrat, J.M.; Delingette, H.; Ayache, N. A Recursive Anisotropic Fast Marching Approach to Reaction Diffusion Equation: Application to Tumor Growth Modeling. In Information Processing in Medical Imaging; Springer: Berlin/Heidelberg, Germany, 2007; pp. 687–699. [Google Scholar]
- Yeghiazaryan, V.; Voiculescu, I. Family of Boundary Overlap Metrics for the Evaluation of Medical Image Segmentation. J. Med. Imaging 2018, 5, 015006. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Von Bartheld, C.S.; Bahney, J.; Herculano-Houzel, S. The Search for True Numbers of Neurons and Glial Cells in the Human Brain: A Review of 150 Years of Cell Counting. J. Comp. Neurol. 2016, 524, 3865–3895. [Google Scholar] [CrossRef] [Green Version]
- Jbabdi, S.; Bellec, P.; Toro, R.; Daunizeau, J.; Pélégrini-Issac, M.; Benali, H. Accurate Anisotropic Fast Marching for Diffusion-Based Geodesic Tractography. Int. J. Biomed. Imaging 2007, 15, 320195. [Google Scholar] [CrossRef]
- Johnson, J.; Nowicki, M.O.; Lee, C.H.; Chiocca, E.A.; Viapiano, M.S.; Lawler, S.E.; Lannutti, J.J. Quantitative Analysis of Complex Glioma Cell Migration on Electrospun Polycaprolactone Using Time-Lapse Microscopy. Tissue Eng. Part C Methods 2007, 2009, 531–540. [Google Scholar] [CrossRef] [PubMed]
- Armento, A.; Ehlers, J.; Schötterl, S.; Naumann, U. Molecular Mechanisms of Glioma Cell Motility. In Glioblastoma; De Vleeschouwer, S., Ed.; Codon Publications: Brisbane, Australia, 2017; pp. 73–94. [Google Scholar]
- Gee, J.C.; Alexander, D.C. Diffusion-Tensor Image Registration. In Visualization and Processing of Tensor Fields; Weickert, J., Hagen, H., Eds.; Mathematics and Visualization; Springer: Berlin/Heidelberg, Germany, 2006; pp. 328–341. [Google Scholar]
- Kelly, P.J.; Daumas-Duport, C.; Kispert, D.B.; Kall, B.A.; Scheithauer, B.W.; Illig, J.J. Imaging-Based Stereotaxic Serial Biopsies in Untreated Intracranial Glial Neoplasms. J. Neurosurg. 1987, 66, 865–874. [Google Scholar] [CrossRef]
- Sahm, F.; Capper, D.; Jeibmann, A.; Habel, A.; Paulus, W.; Troost, D.; von Deimling, A. Addressing Diffuse Glioma as a Systemic Brain Disease with Single-Cell Analysis. Arch. Neurol. 2012, 69, 523–526. [Google Scholar] [PubMed] [Green Version]
- Ganslandt, O.; Stadlbauer, A.; Fahlbusch, R.; Kamada, K.; Buslei, R.; Blumcke, I.; Moser, E.; Nimsky, C. Proton Magnetic Resonance Spectroscopic Imaging Integrated into Image-guided Surgery: Correlation to Standard Magnetic Resonance Imaging and Tumor Cell Density. Neurosurgery 2005, 56, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Roberts, T.A.; Hyare, H.; Agliardi, G.; Hipwell, B.; d’Esposito, A.; Ianus, A.; Breen-Norris, J.O.; Ramasawmy, R.; Taylor, V.; Atkinson, D.; et al. Noninvasive Diffusion Magnetic Resonance Imaging of Brain Tumour Cell Size for the Early Detection of Therapeutic Response. Sci. Rep. 2020, 10, 9223. [Google Scholar] [CrossRef]
- Bobholz, S.A.; Lowman, A.K.; Brehler, M.; Kyereme, F.; Duenweg, S.R.; Sherman, J.; McGarry, S.; Cochran, E.J.; Connelly, J.; Mueller, W.M.; et al. Radio-Pathomic Maps of Cell Density Identify Glioma Invasion Beyond Traditional MR Imaging Defined Margins. bioRxiv 2021. [Google Scholar] [CrossRef]
- Gates, E.D.H.; Weinberg, J.S.; Prabhu, S.S.; Lin, J.S.; Hamilton, J.; Hazle, J.D.; Fuller, G.N.; Baladandayuthapani, V.; Fuentes, D.T.; Schellingerhout, D. Estimating Local Cellular Density in Glioma Using MR Imaging Data. AJNR Am. J. Neuroradiol. 2021, 42, 102–108. [Google Scholar] [CrossRef]
- Atuegwu, N.C.; Colvin, D.C.; Loveless, M.E.; Xu, L.; Gore, J.C.; Yankeelov, T.E. Incorporation of Diffusion-Weighted Magnetic Resonance Imaging Data into a Simple Mathematical Model of Tumor Growth. Phys. Med. Biol. 2012, 57, 225–240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hormuth, D.A.; Al Feghali, K.A.; Elliott, A.M.; Yankeelov, T.E.; Chung, C. Image-Based Personalization of Computational Models for Predicting Response of High-Grade Glioma to Chemoradiation. Sci. Rep. 2021, 11, 8520. [Google Scholar] [CrossRef] [PubMed]
- McHugh, D.J.; Hubbard Cristinacce, P.L.; Naish, J.H.; Parker, G.J.M. Towards a ‘Resolution Limit’ for DW-MRI Tumor Microstructural Models: A Simulation Study Investigating the Feasibility of Distinguishing between Microstructural Changes. Magn. Reson. Med. 2019, 81, 2288–2301. [Google Scholar] [CrossRef] [PubMed]
- Szczepankiewicz, F.; Lasič, S.; van Westen, D.; Sundgren, P.C.; Englund, E.; Westin, C.; Ståhlberg, F.; Lätt, J.; Topgaard, D.; Nilsson, M. Quantification of Microscopic Diffusion Anisotropy Disentangles Effects of Orientation Dispersion from Microstructure: Applications in Healthy Volunteers and in Brain Tumors. NeuroImage 2015, 104, 241–252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stockhammer, F.; Plotkin, M.; Amthauer, H.; van Landeghem, F.K.H.; Woiciechowsky, C. Correlation of F-18-Fluoro-Ethyl-Tyrosin Uptake with Vascular and Cell Density in Non-Contrast-Enhancing Gliomas. J. Neuro-Oncol. 2008, 88, 205–210. [Google Scholar] [CrossRef]
- Lipková, J.; Angelikopoulos, P.; Wu, S.; Alberts, E.; Wiestler, B.; Diehl, C.; Preibisch, C.; Pyka, T.; Combs, S.; Hadjidoukas, P.; et al. Personalized Radiotherapy Design for Glioblastoma: Integrating Mathematical Tumor Models, Multimodal Scans and Bayesian Inference. IEEE Trans. Med. Imaging 2019, 38, 1875–1884. [Google Scholar] [CrossRef]
- Kinoshita, M.; Arita, H.; Goto, T.; Okita, Y.; Isohashi, K.; Watabe, T.; Kagawa, N.; Fujimoto, Y.; Kishima, H.; Shimosegawa, E.; et al. A Novel PET Index, 18F-FDG–11C-Methionine Uptake Decoupling Score, Reflects Glioma Cell Infiltration. J. Nucl. Med. 2012, 53, 1701–1708. [Google Scholar] [CrossRef] [Green Version]
- Hodge, R.D.; Bakken, T.E.; Miller, J.A.; Smith, K.A.; Barkan, E.R.; Graybuck, L.T.; Close, J.L.; Long, B.; Johansen, N.; Penn, O.; et al. Conserved Cell Types with Divergent Features in Human Versus Mouse Cortex. Nature 2019, 573, 61–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Sloan, S.A.; Clarke, L.E.; Caneda, C.; Plaza, C.A.; Blumenthal, P.D.; Vogel, H.; Steinberg, G.K.; Edwards, M.S.B.; Li, G.; et al. Purification and Characterization of Progenitor and Mature Human Astrocytes Reveals Transcriptional and Functional Differences with Mouse. Neuron 2016, 89, 37–53. [Google Scholar] [CrossRef] [Green Version]
- Song, H.W.; Foreman, K.L.; Gastfriend, B.D.; Kuo, J.S.; Palecek, S.P.; Shusta, E.V. Transcriptomic Comparison of Human and Mouse Brain Microvessels. Sci. Rep. 2020, 10, 12358. [Google Scholar] [CrossRef]
- Kijima, N.; Kanemura, Y. Mouse Models of Glioblastoma. In Glioblastoma; De Vleeschouwer, S., Ed.; Codon Publications: Brisbane, Australia, 2017; pp. 131–140. [Google Scholar]
- Blumenthal, D.T.; Gorlia, T.; Gilbert, M.R.; Kim, M.M.; Nabors, L.B.; Mason, W.P.; Hegi, M.E.; Zhang, P.; Golfinopoulos, V.; Perry, J.R.; et al. Is More Better? The Impact of Extended Adjuvant Temozolomide in Newly Diagnosed Glioblastoma: A Secondary Analysis of EORTC and NRG Oncology/RTOG. Neuro-Oncol. 2017, 19, 1119–1126. [Google Scholar] [CrossRef]
- Ducray, F.; Benouaich-Amiel, A.; Idbaih, A.; Rousseau, A.; Laigle-Donadey, F.; Delattre, J.; Sanson, M. Complete Response After One Cycle of Temozolomide in an Elderly Patient with Glioblastoma and Poor Performance Status. J. Neuro-Oncol. 2008, 88, 185–188. [Google Scholar] [CrossRef]
- Baldi, D.; Aiello, M.; Duggento, A.; Salvatore, M.; Cavaliere, C. MR Imaging-Histology Correlation by Tailored 3D-Printed Slicer in Oncological Assessment. Contrast Media Mol. Imaging 2019, 2019, 1071453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. Syst. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Available online: https://www.tensorflow.org/ (accessed on 6 September 2021).
- Kingma, D.; Ba, J. ADAM: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Xing, F.; Cornish, T.C.; Bennett, T.; Ghosh, D.; Yang, L. Pixel-to-Pixel Learning with Weak Supervision for Single-Stage Nucleus Recognition in Ki67 Images. IEEE Trans. Biomed. Eng. 2019, 66, 3088–3097. [Google Scholar] [CrossRef]
- Li, C.; Gore, J.C.; Davatzikos, C. Multiplicative Intrinsic Component Optimization (MICO) for MRI Bias Field Estimation and Tissue Segmentation. Magn. Reson. Imaging 2014, 32, 913–923. [Google Scholar] [CrossRef] [Green Version]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.; Woolrich, M.W.; Smith, S.M. FSL. NeuroImage 2012, 62, 782–790. [Google Scholar] [CrossRef] [Green Version]

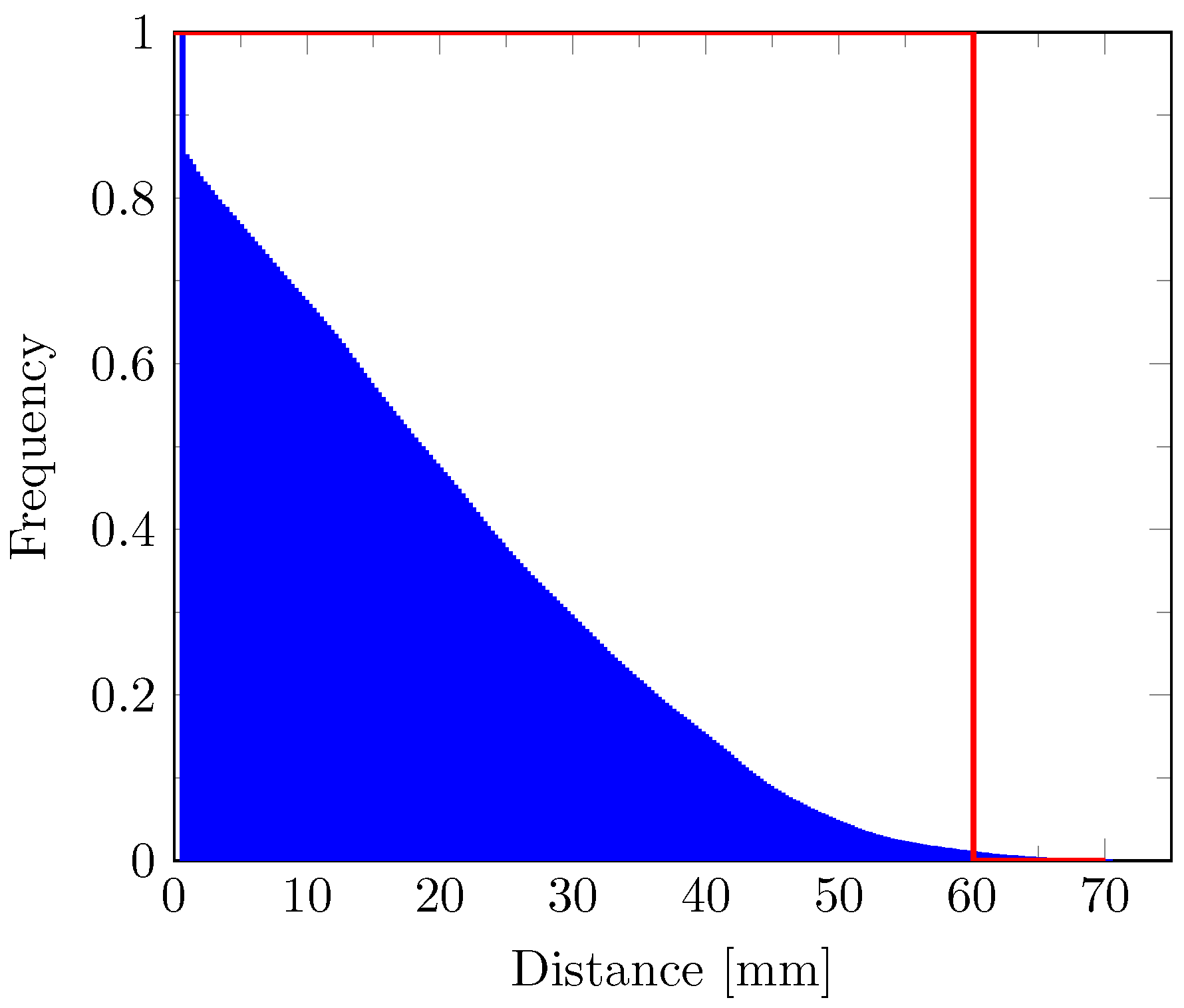
| [ ] | [] | [ ] |
|---|---|---|
| 1.47 | 10.55 | 1.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martens, C.; Lebrun, L.; Decaestecker, C.; Vandamme, T.; Van Eycke, Y.-R.; Rovai, A.; Metens, T.; Debeir, O.; Goldman, S.; Salmon, I.; et al. Initial Condition Assessment for Reaction-Diffusion Glioma Growth Models: A Translational MRI-Histology (In)Validation Study. Tomography 2021, 7, 650-674. https://doi.org/10.3390/tomography7040055
Martens C, Lebrun L, Decaestecker C, Vandamme T, Van Eycke Y-R, Rovai A, Metens T, Debeir O, Goldman S, Salmon I, et al. Initial Condition Assessment for Reaction-Diffusion Glioma Growth Models: A Translational MRI-Histology (In)Validation Study. Tomography. 2021; 7(4):650-674. https://doi.org/10.3390/tomography7040055
Chicago/Turabian StyleMartens, Corentin, Laetitia Lebrun, Christine Decaestecker, Thomas Vandamme, Yves-Rémi Van Eycke, Antonin Rovai, Thierry Metens, Olivier Debeir, Serge Goldman, Isabelle Salmon, and et al. 2021. "Initial Condition Assessment for Reaction-Diffusion Glioma Growth Models: A Translational MRI-Histology (In)Validation Study" Tomography 7, no. 4: 650-674. https://doi.org/10.3390/tomography7040055
APA StyleMartens, C., Lebrun, L., Decaestecker, C., Vandamme, T., Van Eycke, Y.-R., Rovai, A., Metens, T., Debeir, O., Goldman, S., Salmon, I., & Van Simaeys, G. (2021). Initial Condition Assessment for Reaction-Diffusion Glioma Growth Models: A Translational MRI-Histology (In)Validation Study. Tomography, 7(4), 650-674. https://doi.org/10.3390/tomography7040055







