Performance Evaluation of Image Segmentation Using Dual-Energy Spectral CT Images with Deep Learning Image Reconstruction: A Phantom Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Phantom
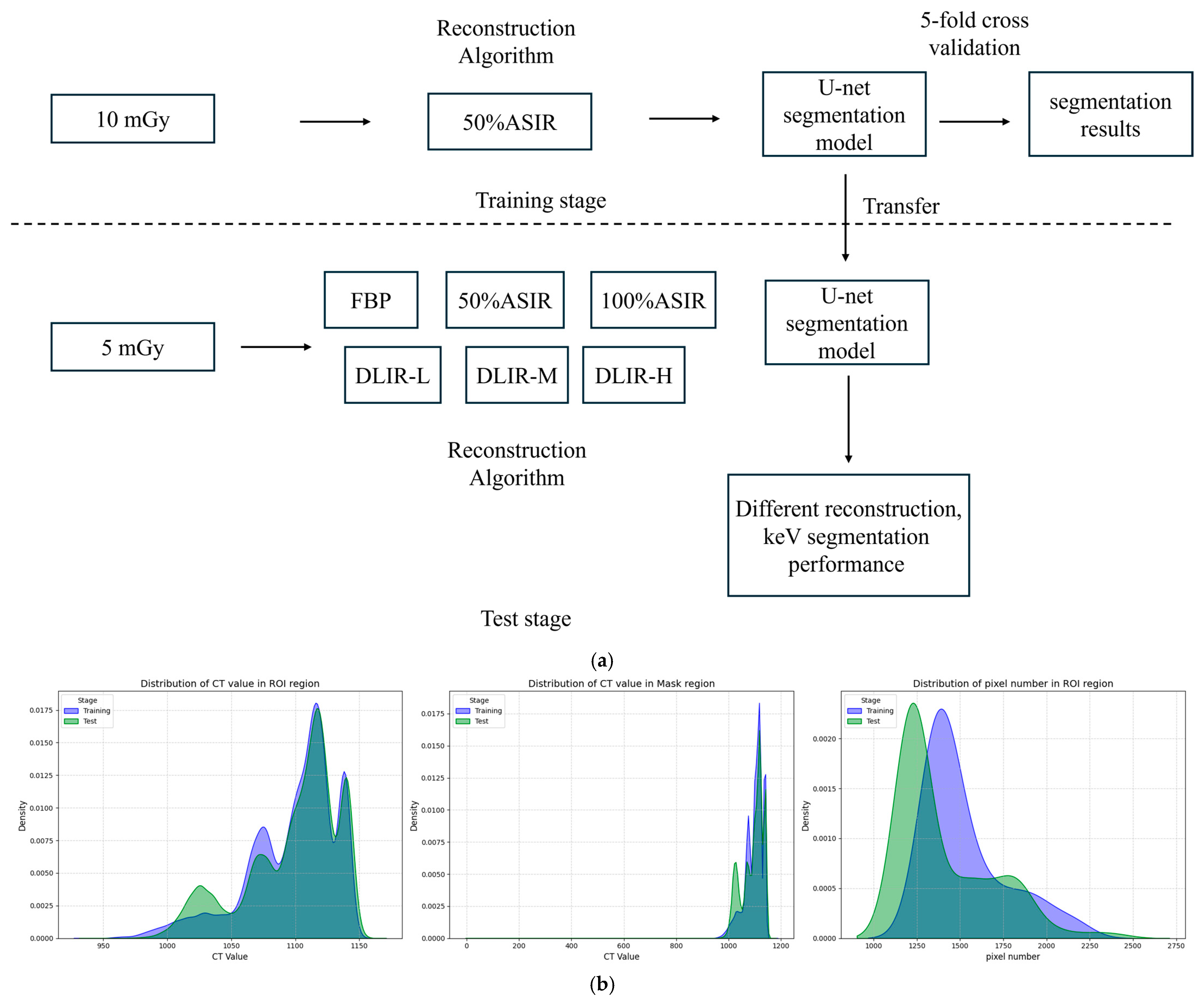
2.2. CT Systems, Parameters for Acquisition and Reconstruction
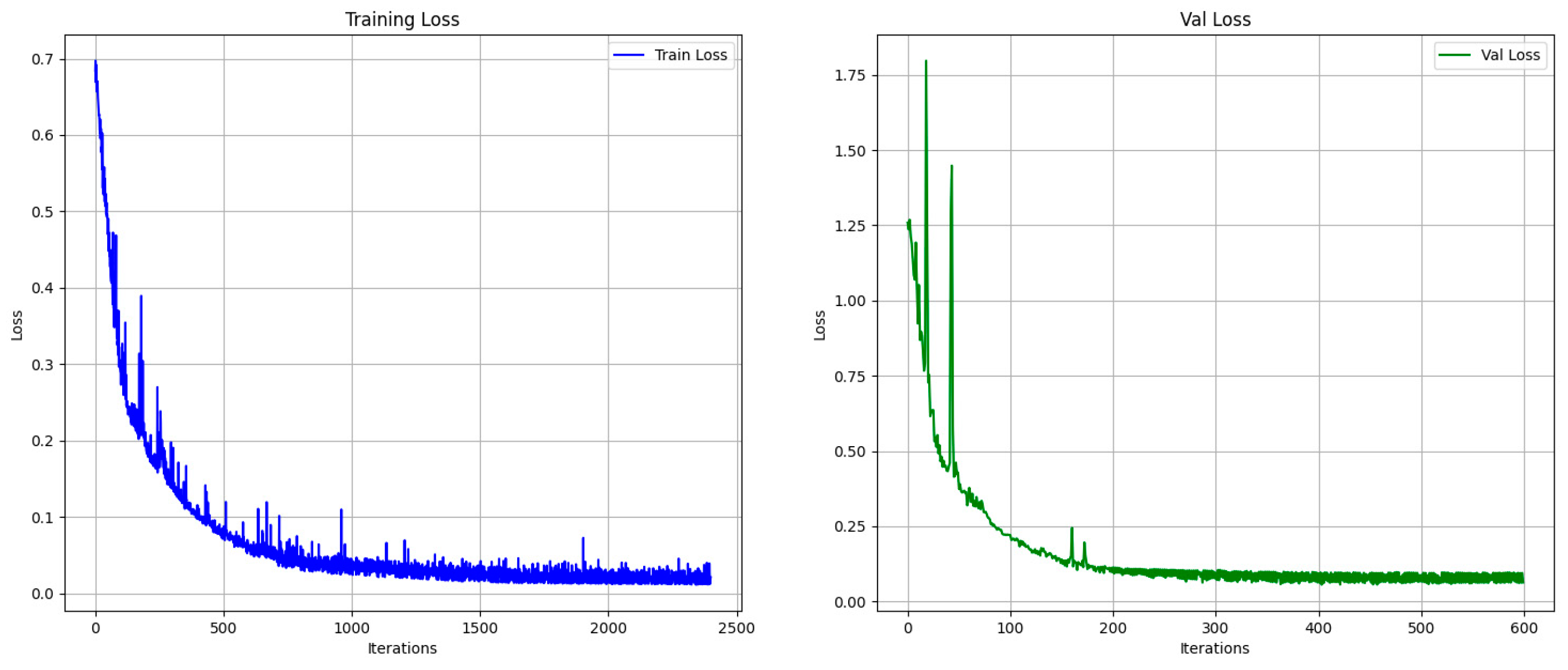
2.3. Deep Learning Model Construction
2.4. Metrics for Deep Learning Automatic Segmentation Evaluation
2.5. Deep Learning Segmentation Model
2.6. Measurement of CT Attenuation and Noise (Standard Deviation, SD)
3. Results
3.1. Metrics for Deep Learning Automatic Segmentation in Validation Set (5 mGy)
3.1.1. Performance Metrics (IOU, DICE, and Sensitivity)
3.1.2. Hausdorff Distance
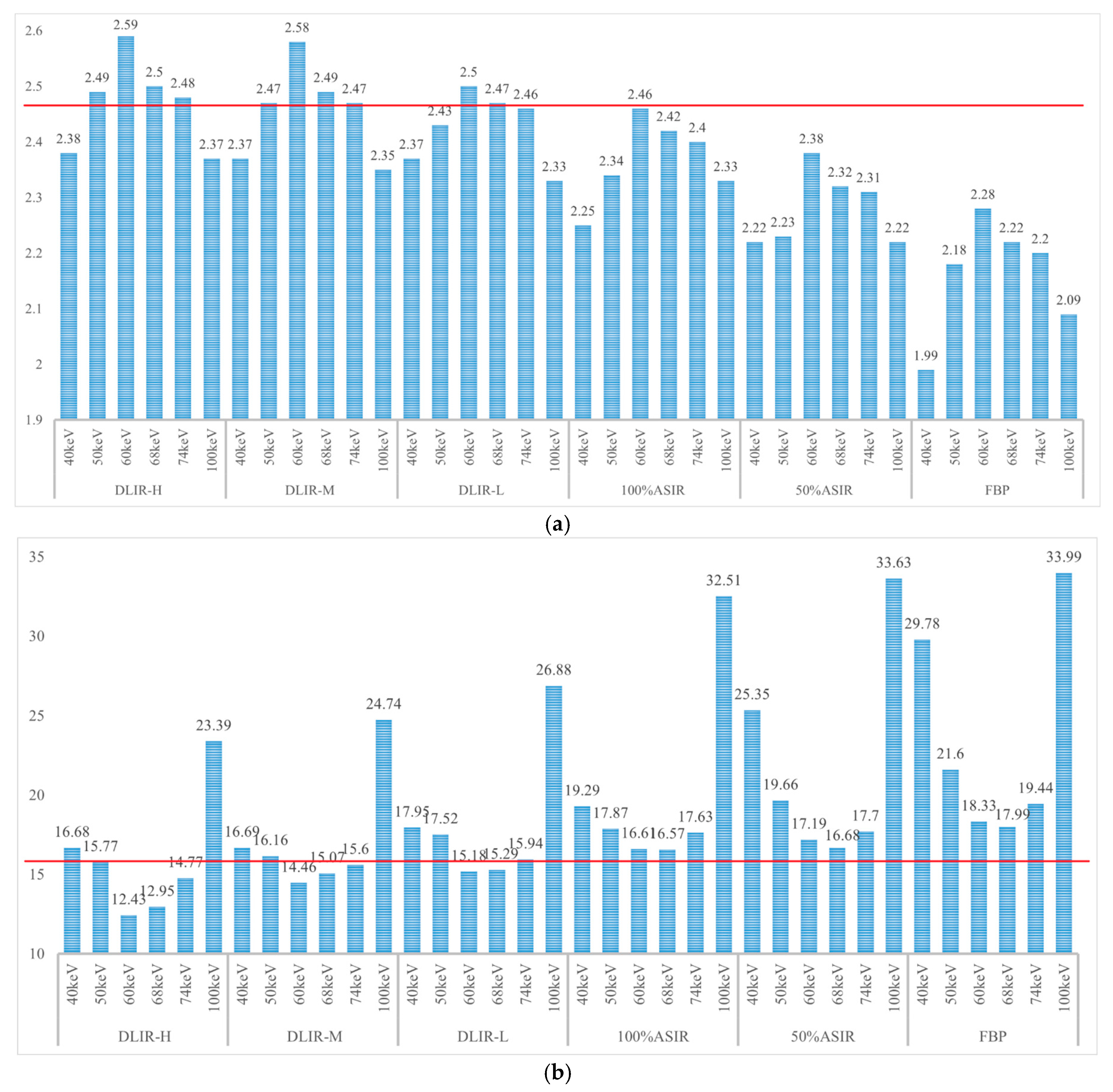
3.2. CT Attenuation and Standard Deviations (SDs) of the Dual-Energy Spectral CT Image
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASIR-V | Adaptive statistical iterative reconstruction-veo |
| CTDIvol | CT dose index |
| DEsCT | Dual-energy spectral computed tomography |
| DICE | DICE coefficient |
| DLIR | Deep learning image reconstruction |
| FBP | Filtered back-projection |
| HU | Hounsfield Unit |
| IOU | Intersection over union |
| IR | Iterative reconstruction |
| keV | Kilo-electron volts |
| NPS | Noise power spectrum |
| ROI | Region of interest |
| SD | Standard deviation |
| U-Net | Convolutional Networks for Biomedical Image Segmentation |
| VMIs | Virtual monochromatic images |
Appendix A. Evaluation Index of the Accuracy of Deep Learning Segmentation Model
Appendix B
| IOU | DICE | Sensitivity | Manhattan_ Distance | Euclidean_ Distance | Cosine_ Distance | ||
|---|---|---|---|---|---|---|---|
| 40 keV | FBP | 0.48 | 0.63 | 0.88 | 24.17 | 4.84 | 0.77 |
| 50% ASIR | 0.57 | 0.72 | 0.93 | 20.25 | 4.42 | 0.68 | |
| 100% ASIR | 0.59 | 0.74 | 0.92 | 14.92 | 3.82 | 0.55 | |
| DLIR-L | 0.63 | 0.77 | 0.97 | 13.75 | 3.69 | 0.51 | |
| DLIR-M | 0.61 | 0.77 | 0.99 | 12.67 | 3.53 | 0.49 | |
| DLIR-H | 0.63 | 0.76 | 0.99 | 12.83 | 3.46 | 0.39 | |
| 50 keV | FBP | 0.59 | 0.74 | 0.85 | 16.92 | 4.07 | 0.61 |
| 50% ASIR | 0.62 | 0.76 | 0.85 | 15.25 | 3.85 | 0.56 | |
| 100% ASIR | 0.65 | 0.78 | 0.91 | 13.75 | 3.70 | 0.42 | |
| DLIR-L | 0.69 | 0.81 | 0.93 | 13.42 | 3.64 | 0.46 | |
| DLIR-M | 0.7 | 0.83 | 0.94 | 12.25 | 3.49 | 0.42 | |
| DLIR-H | 0.72 | 0.82 | 0.95 | 11.92 | 3.42 | 0.43 | |
| 60 keV | FBP | 0.60 | 0.75 | 0.93 | 14.08 | 3.73 | 0.52 |
| 50% ASIR | 0.67 | 0.80 | 0.91 | 13.17 | 3.53 | 0.49 | |
| 100% ASIR | 0.68 | 0.82 | 0.96 | 12.58 | 3.51 | 0.52 | |
| DLIR-L | 0.72 | 0.83 | 0.95 | 11.42 | 3.25 | 0.51 | |
| DLIR-M | 0.75 | 0.85 | 0.98 | 10.92 | 3.19 | 0.35 | |
| DLIR-H | 0.75 | 0.86 | 0.98 | 9.08 | 3.01 | 0.34 | |
| 68 keV | FBP | 0.62 | 0.76 | 0.84 | 13.83 | 3.68 | 0.48 |
| 50% ASIR | 0.67 | 0.80 | 0.85 | 12.92 | 3.27 | 0.49 | |
| 100% ASIR | 0.70 | 0.80 | 0.92 | 12.5 | 3.49 | 0.58 | |
| DLIR-L | 0.71 | 0.83 | 0.93 | 11.35 | 3.42 | 0.52 | |
| DLIR-M | 0.72 | 0.84 | 0.93 | 11.31 | 3.33 | 0.43 | |
| DLIR-H | 0.72 | 0.83 | 0.95 | 9.50 | 3.03 | 0.42 | |
| 74 keV | FBP | 0.62 | 0.75 | 0.83 | 15.08 | 3.79 | 0.57 |
| 50% ASIR | 0.65 | 0.78 | 0.88 | 13.52 | 3.64 | 0.54 | |
| 100% ASIR | 0.67 | 0.80 | 0.93 | 13.53 | 3.53 | 0.57 | |
| DLIR-L | 0.69 | 0.81 | 0.96 | 12.08 | 3.45 | 0.41 | |
| DLIR-M | 0.69 | 0.81 | 0.97 | 11.76 | 3.40 | 0.44 | |
| DLIR-H | 0.69 | 0.81 | 0.98 | 11.08 | 3.31 | 0.38 | |
| 100 keV | FBP | 0.55 | 0.70 | 0.84 | 27.75 | 5.42 | 0.82 |
| 50% ASIR | 0.56 | 0.71 | 0.95 | 27.52 | 5.30 | 0.81 | |
| 100% ASIR | 0.61 | 0.76 | 0.96 | 26.67 | 5.06 | 0.78 | |
| DLIR-L | 0.60 | 0.75 | 0.98 | 21.58 | 4.54 | 0.76 | |
| DLIR-M | 0.62 | 0.76 | 0.97 | 19.67 | 4.34 | 0.73 | |
| DLIR-H | 0.63 | 0.77 | 0.97 | 18.42 | 4.28 | 0.69 |
Appendix C

References
- Lin, H.; Xiao, H.; Dong, L.; Teo, K.B.; Zou, W.; Cai, J.; Li, T. Deep learning for automatic target volume segmentation in radiation therapy: A review. Quant. Imaging Med. Surg. 2021, 11, 4847–4858. [Google Scholar] [CrossRef]
- Lastrucci, A.; Wandael, Y.; Ricci, R.; Maccioni, G.; Giansanti, D. The Integration of Deep Learning in Radiotherapy: Exploring Challenges, Opportunities, and Future Directions through an Umbrella Review. Diagnostics 2024, 14, 939. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Lv, P.; Wang, H.; Cheng, Y. Automatic Liver Segmentation Using EfficientNet and Attention-Based Residual U-Net in CT. J. Digit. Imaging 2022, 35, 1479–1493. [Google Scholar] [CrossRef] [PubMed]
- Walter, A.; Hoegen-Saßmannshausen, P.; Stanic, G.; Rodrigues, J.P.; Adeberg, S.; Jäkel, O.; Frank, M.; Giske, K. Segmentation of 71 Anatomical Structures Necessary for the Evaluation of Guideline-Conforming Clinical Target Volumes in Head and Neck Cancers. Cancers 2024, 16, 415. [Google Scholar] [CrossRef]
- Li, W.; Sun, Y.; Zhang, G.; Yang, Q.; Wang, B.; Ma, X.; Zhang, H. Automated segmentation and volume prediction in pediatric Wilms’ tumor CT using nnu-net. BMC Pediatr. 2024, 24, 321. [Google Scholar] [CrossRef] [PubMed]
- de Margerie-Mellon, C.; Chassagnon, G. Artificial intelligence: A critical review of applications for lung nodule and lung cancer. Diagn. Interv. Imaging 2023, 104, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Cui, Y.; Liu, J.; Sun, Z.; Ma, S.; Zhang, X.; Wang, X. Automated segmentation of kidney and renal mass and automated detection of renal mass in CT urography using 3D U-Net-based deep convolutional neural network. Eur. Radiol. 2021, 31, 5021–5031. [Google Scholar] [CrossRef]
- Hild, O.; Berriet, P.; Nallet, J.; Salvi, L.; Lenoir, M.; Henriet, J.; Thiran, J.P.; Auber, F.; Chaussy, Y. Automation of Wilms’ tumor segmentation by artificial intelligence. Cancer Imaging Off. Publ. Int. Cancer Imaging Soc. 2024, 24, 83. [Google Scholar] [CrossRef]
- Bousse, A.; Kandarpa, V.S.S.; Rit, S.; Perelli, A.; Li, M.; Wang, G.; Zhou, J.; Wang, G. Systematic Review on Learning-based Spectral CT. IEEE Trans. Radiat. Plasma Med. Sci. 2024, 8, 113–137. [Google Scholar] [CrossRef]
- Dabli, D.; Loisy, M.; Frandon, J.; de Oliveira, F.; Meerun, A.M.; Guiu, B.; Beregi, J.P.; Greffier, J. Comparison of image quality of two versions of deep-learning image reconstruction algorithm on a rapid kV-switching CT: A phantom study. Eur. Radiol. Exp. 2023, 7, 1. [Google Scholar] [CrossRef]
- Shapira, N.; Mei, K.; Noël, P.B. Spectral CT quantification stability and accuracy for pediatric patients: A phantom study. J. Appl. Clin. Med. Phys. 2021, 22, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Pérez, G.C.; Fraga Piñeiro, C.; Oñate Miranda, M.; Díez Blanco, M.; Mato Chaín, J.; Collazos Martínez, M.A. Dual-energy CT: Technical considerations and clinical applications. Radiologia 2022, 64, 445–455. [Google Scholar] [CrossRef] [PubMed]
- McCollough, C.H.; Leng, S.; Yu, L.; Fletcher, J.G. Dual- and Multi-Energy CT: Principles, Technical Approaches, and Clinical Applications. Radiology 2015, 276, 637–653. [Google Scholar] [CrossRef]
- Koetzier, L.R.; Mastrodicasa, D.; Szczykutowicz, T.P.; van der Werf, N.R.; Wang, A.S.; Sandfort, V.; van der Molen, A.J.; Fleischmann, D.; Willemink, M.J. Deep Learning Image Reconstruction for CT: Technical Principles and Clinical Prospects. Radiology 2023, 306, e221257. [Google Scholar] [CrossRef]
- Ghasemi Shayan, R.; Oladghaffari, M.; Sajjadian, F.; Fazel Ghaziyani, M. Image Quality and Dose Comparison of Single-Energy CT (SECT) and Dual-Energy CT (DECT). Radiol. Res. Pract. 2020, 2020, 1403957. [Google Scholar] [CrossRef] [PubMed]
- Nagayama, Y.; Sakabe, D.; Goto, M.; Emoto, T.; Oda, S.; Nakaura, T.; Kidoh, M.; Uetani, H.; Funama, Y.; Hirai, T. Deep Learning-based Reconstruction for Lower-Dose Pediatric CT: Technical Principles, Image Characteristics, and Clinical Implementations. Radiogr. A Rev. Publ. Radiol. Soc. N. Am. Inc. 2021, 41, 1936–1953. [Google Scholar] [CrossRef]
- Clark, D.P.; Schwartz, F.R.; Marin, D.; Ramirez-Giraldo, J.C.; Badea, C.T. Deep learning based spectral extrapolation for dual-source, dual-energy X-ray computed tomography. Med. Phys. 2020, 47, 4150–4163. [Google Scholar] [CrossRef]
- Schwartz, F.R.; Clark, D.P.; Ding, Y.; Ramirez-Giraldo, J.C.; Badea, C.T.; Marin, D. Evaluating renal lesions using deep-learning based extension of dual-energy FoV in dual-source CT-A retrospective pilot study. Eur. J. Radiol. 2021, 139, 109734. [Google Scholar] [CrossRef]
- Hlouschek, J.; König, B.; Bos, D.; Santiago, A.; Zensen, S.; Haubold, J.; Pöttgen, C.; Herz, A.; Opitz, M.; Wetter, A.; et al. Experimental Examination of Conventional, Semi-Automatic, and Automatic Volumetry Tools for Segmentation of Pulmonary Nodules in a Phantom Study. Diagnostics 2023, 14, 28. [Google Scholar] [CrossRef]
- Hardie, R.C.; Trout, A.T.; Dillman, J.R.; Narayanan, B.N.; Tanimoto, A.A. Performance of Lung-Nodule Computer-Aided Detection Systems on Standard-Dose and Low-Dose Pediatric CT Scans: An Intraindividual Comparison. AJR Am. J. Roentgenol. 2024, 223, e2431972. [Google Scholar] [CrossRef]
- Groendahl, A.R.; Huynh, B.N.; Tomic, O.; Søvik, Å.; Dale, E.; Malinen, E.; Skogmo, H.K.; Futsaether, C.M. Automatic gross tumor segmentation of canine head and neck cancer using deep learning and cross-species transfer learning. Front. Vet. Sci. 2023, 10, 1143986. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.J.; Ramirez-Giraldo, J.C. Dual-Energy CT in Children: Imaging Algorithms and Clinical Applications. Radiology 2019, 291, 286–297. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.J.; Bhalla, S.; Cullinane, M. Dual-Energy CT Material Decomposition in Pediatric Thoracic Oncology. Radiology. Imaging Cancer 2021, 3, e200097. [Google Scholar] [CrossRef]
- Kamps, S.E.; Otjen, J.P.; Stanescu, A.L.; Mileto, A.; Lee, E.Y.; Phillips, G.S. Dual-Energy CT of Pediatric Abdominal Oncology Imaging: Private Tour of New Applications of CT Technology. AJR Am. J. Roentgenol. 2020, 214, 967–975. [Google Scholar] [CrossRef]
- Gallo-Bernal, S.; Peña-Trujillo, V.; Gee, M.S. Dual-energy computed tomography: Pediatric considerations. Pediatr. Radiol. 2024, 54, 2112–2126. [Google Scholar] [CrossRef] [PubMed]
- Tabari, A.; Gee, M.S.; Singh, R.; Lim, R.; Nimkin, K.; Primak, A.; Schmidt, B.; Kalra, M.K. Reducing Radiation Dose and Contrast Medium Volume with Application of Dual-Energy CT in Children and Young Adults. AJR Am. J. Roentgenol. 2020, 214, 1199–1205. [Google Scholar] [CrossRef]
- Yang, L.; Sun, J.; Li, J.; Peng, Y. Dual-energy spectral CT imaging of pulmonary embolism with Mycoplasma pneumoniae pneumonia in children. Radiol. Med. 2022, 127, 154–161. [Google Scholar] [CrossRef]
- Sun, J.; Li, H.; Yu, T.; Huo, A.; Hua, S.; Zhou, Z.; Peng, Y. Application of metal artifact reduction algorithm in reducing metal artifacts in post-surgery pediatric low radiation dose spine computed tomography (CT) images. Quant. Imaging Med. Surg. 2024, 14, 4648–4658. [Google Scholar] [CrossRef]
- Xie, M.; Wang, H.; Tang, S.; Chen, M.; Li, T.; He, L. Application of dual-energy CT with prospective ECG-gating in cardiac CT angiography for children: Radiation and contrast agent dose. Eur. J. Radiol. 2024, 170, 111229. [Google Scholar] [CrossRef]
- Schicchi, N.; Fogante, M.; Esposto Pirani, P.; Agliata, G.; Basile, M.C.; Oliva, M.; Agostini, A.; Giovagnoni, A. Third-generation dual-source dual-energy CT in pediatric congenital heart disease patients: State-of-the-art. Radiol. Med. 2019, 124, 1238–1252. [Google Scholar] [CrossRef]
- Hudobivnik, N.; Schwarz, F.; Johnson, T.; Agolli, L.; Dedes, G.; Tessonnier, T.; Verhaegen, F.; Thieke, C.; Belka, C.; Sommer, W.H.; et al. Comparison of proton therapy treatment planning for head tumors with a pencil beam algorithm on dual and single energy CT images. Med. Phys. 2016, 43, 495. [Google Scholar] [CrossRef] [PubMed]
- Bruns, S.; Wolterink, J.M.; Takx, R.A.P.; van Hamersvelt, R.W.; Suchá, D.; Viergever, M.A.; Leiner, T.; Išgum, I. Deep learning from dual-energy information for whole-heart segmentation in dual-energy and single-energy non-contrast-enhanced cardiac CT. Med. Phys. 2020, 47, 5048–5060. [Google Scholar] [CrossRef] [PubMed]
- Miller, C.; Mittelstaedt, D.; Black, N.; Klahr, P.; Nejad-Davarani, S.; Schulz, H.; Goshen, L.; Han, X.; Ghanem, A.I.; Morris, E.D.; et al. Impact of CT reconstruction algorithm on auto-segmentation performance. J. Appl. Clin. Med. Phys. 2019, 20, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.J.; Mhlanga, J.C.; Salter, A.; Ramirez-Giraldo, J.C. Comparison of radiation dose and image quality between contrast-enhanced single- and dual-energy abdominopelvic computed tomography in children as a function of patient size. Pediatr. Radiol. 2021, 51, 2000–2008. [Google Scholar] [CrossRef]
- Lee, S.; Choi, Y.H.; Cho, Y.J.; Lee, S.B.; Cheon, J.E.; Kim, W.S.; Ahn, C.K.; Kim, J.H. Noise reduction approach in pediatric abdominal CT combining deep learning and dual-energy technique. Eur. Radiol. 2021, 31, 2218–2226. [Google Scholar] [CrossRef]
- Somasundaram, E.; Taylor, Z.; Alves, V.V.; Qiu, L.; Fortson, B.L.; Mahalingam, N.; Dudley, J.A.; Li, H.; Brady, S.L.; Trout, A.T.; et al. Deep Learning Models for Abdominal CT Organ Segmentation in Children: Development and Validation in Internal and Heterogeneous Public Datasets. AJR Am. J. Roentgenol. 2024, 223, e2430931. [Google Scholar] [CrossRef] [PubMed]
- Bachanek, S.; Wuerzberg, P.; Biggemann, L.; Janssen, T.Y.; Nietert, M.; Lotz, J.; Zeuschner, P.; Maßmann, A.; Uhlig, A.; Uhlig, J. Renal tumor segmentation, visualization, and segmentation confidence using ensembles of neural networks in patients undergoing surgical resection. Eur. Radiol. 2024, 35, 2147–2156. [Google Scholar] [CrossRef]
- Liu, S.; Liang, S.; Huang, X.; Yuan, X.; Zhong, T.; Zhang, Y. Graph-enhanced U-Net for semi-supervised segmentation of pancreas from abdomen CT scan. Phys. Med. Biol. 2022, 67, 155017. [Google Scholar] [CrossRef]
- Delmoral, J.C.; JM, R.S.T. Semantic Segmentation of CT Liver Structures: A Systematic Review of Recent Trends and Bibliometric Analysis: Neural Network-based Methods for Liver Semantic Segmentation. J. Med. Syst. 2024, 48, 97. [Google Scholar] [CrossRef]
- Nadeem, S.A.; Hoffman, E.A.; Sieren, J.C.; Comellas, A.P.; Bhatt, S.P.; Barjaktarevic, I.Z.; Abtin, F.; Saha, P.K. A CT-Based Automated Algorithm for Airway Segmentation Using Freeze-and-Grow Propagation and Deep Learning. IEEE Trans. Med. Imaging 2021, 40, 405–418. [Google Scholar] [CrossRef]
- Ntoufas, N.; Raissaki, M.; Damilakis, J.; Perisinakis, K. Comparison of radiation exposure from dual- and single-energy CT imaging protocols resulting in equivalent contrast-to-noise ratio of lesions for adults and children: A phantom study. Eur. Radiol. 2024. online ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, D.; Kanhere, A.; Doo, F.X.; Zhao, J.; Chan, A.; Welsh, A.; Kulkarni, P.; Trang, A.; Parekh, V.S.; Yi, P.H. Children Are Not Small Adults: Addressing Limited Generalizability of an Adult Deep Learning CT Organ Segmentation Model to the Pediatric Population. J. Imaging Inform. Med. 2024. online ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Holz, J.A.; Alkadhi, H.; Laukamp, K.R.; Lennartz, S.; Heneweer, C.; Püsken, M.; Persigehl, T.; Maintz, D.; Große Hokamp, N. Quantitative accuracy of virtual non-contrast images derived from spectral detector computed tomography: An abdominal phantom study. Sci. Rep. 2020, 10, 21575. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, R.; Kadoya, N.; Nakajima, Y.; Ishii, S.; Shibu, T.; Jingu, K. Impact of CT scan parameters on deformable image registration accuracy using deformable thorax phantom. J. Appl. Clin. Med. Phys. 2023, 24, e13917. [Google Scholar] [CrossRef]
- Jiang, B.; Li, N.; Shi, X.; Zhang, S.; Li, J.; de Bock, G.H.; Vliegenthart, R.; Xie, X. Deep Learning Reconstruction Shows Better Lung Nodule Detection for Ultra-Low-Dose Chest CT. Radiology 2022, 303, 202–212. [Google Scholar] [CrossRef]
- Greffier, J.; Villani, N.; Defez, D.; Dabli, D.; Si-Mohamed, S. Spectral CT imaging: Technical principles of dual-energy CT and multi-energy photon-counting CT. Diagn. Interv. Imaging 2023, 104, 167–177. [Google Scholar] [CrossRef]
- Zeiler, M.D.J.A. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Kingma, D.P.; Ba, J.J.C. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Rajiah, P.; Parakh, A.; Kay, F.; Baruah, D.; Kambadakone, A.R.; Leng, S. Update on Multienergy CT: Physics, Principles, and Applications. Radiogr. A Rev. Publ. Radiol. Soc. N. Am. Inc. 2020, 40, 1284–1308. [Google Scholar] [CrossRef]
- Rapp, J.B.; Biko, D.M.; Siegel, M.J. Dual-Energy CT for Pediatric Thoracic Imaging: A Review. AJR Am. J. Roentgenol. 2023, 221, 526–538. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, Z.; Gao, S.; Hu, J.; Yang, Z.; Peng, Y.; Sun, J. Performance evaluation of deep learning image reconstruction algorithm for dual-energy spectral CT imaging: A phantom study. J. Xray Sci. Technol. 2024, 32, 513–528. [Google Scholar] [CrossRef]
- Steiniger, B.; Lechel, U.; Reichenbach, J.R.; Fiebich, M.; Aschenbach, R.; Schegerer, A.; Waginger, M.; Bobeva, A.; Teichgräber, U.; Mentzel, H.J. In vitro measurements of radiation exposure with different modalities (computed tomography, cone beam computed tomography) for imaging the petrous bone with a pediatric anthropomorphic phantom. Pediatr. Radiol. 2022, 52, 1125–1133. [Google Scholar] [CrossRef] [PubMed]
- McCollough, C.H.; Boedeker, K.; Cody, D.; Duan, X.; Flohr, T.; Halliburton, S.S.; Hsieh, J.; Layman, R.R.; Pelc, N.J. Principles and applications of multienergy CT: Report of AAPM Task Group 291. Med. Phys. 2020, 47, e881–e912. [Google Scholar] [CrossRef]
- Greffier, J.; Hamard, A.; Pereira, F.; Barrau, C.; Pasquier, H.; Beregi, J.P.; Frandon, J. Image quality and dose reduction opportunity of deep learning image reconstruction algorithm for CT: A phantom study. Eur. Radiol. 2020, 30, 3951–3959. [Google Scholar] [CrossRef]



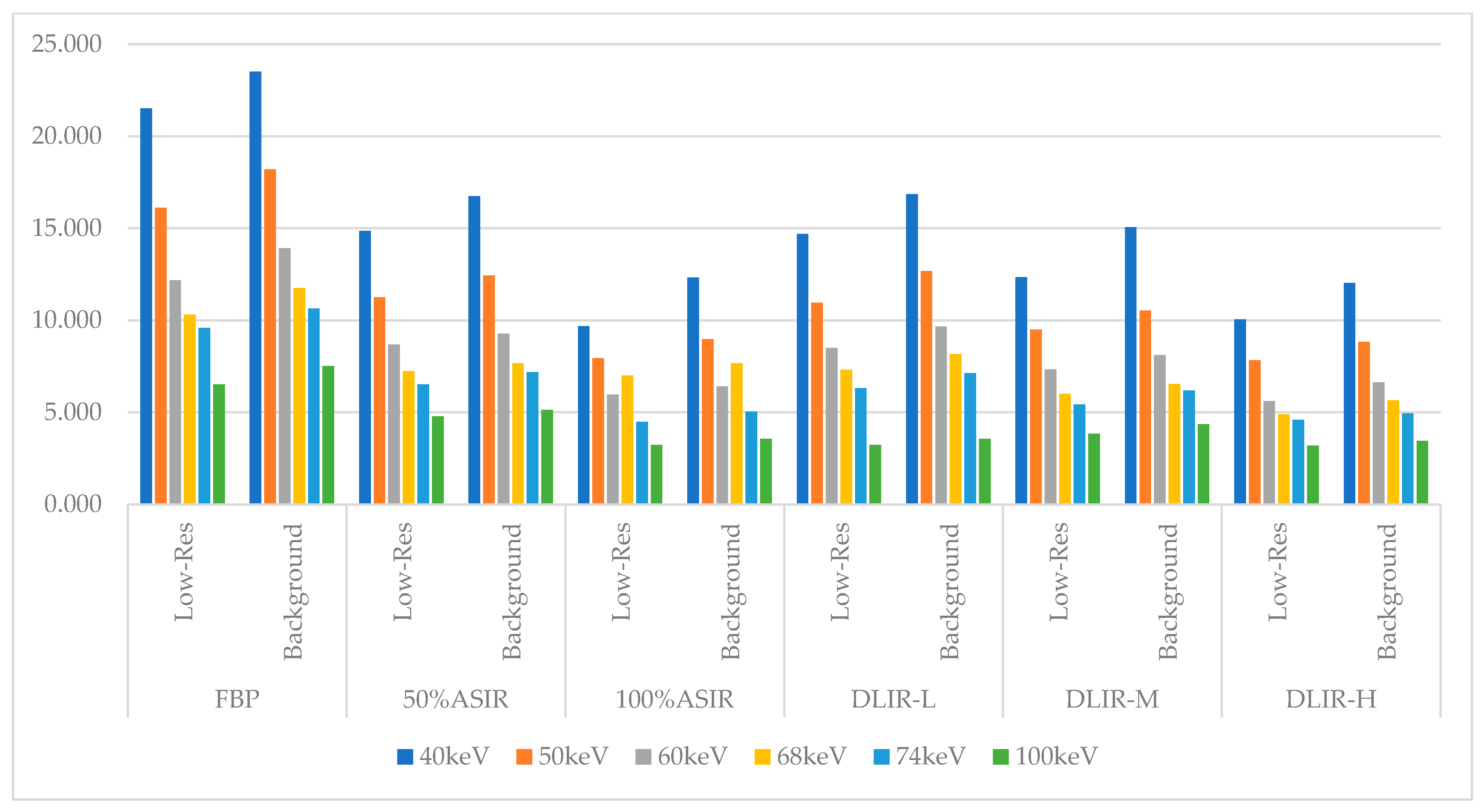
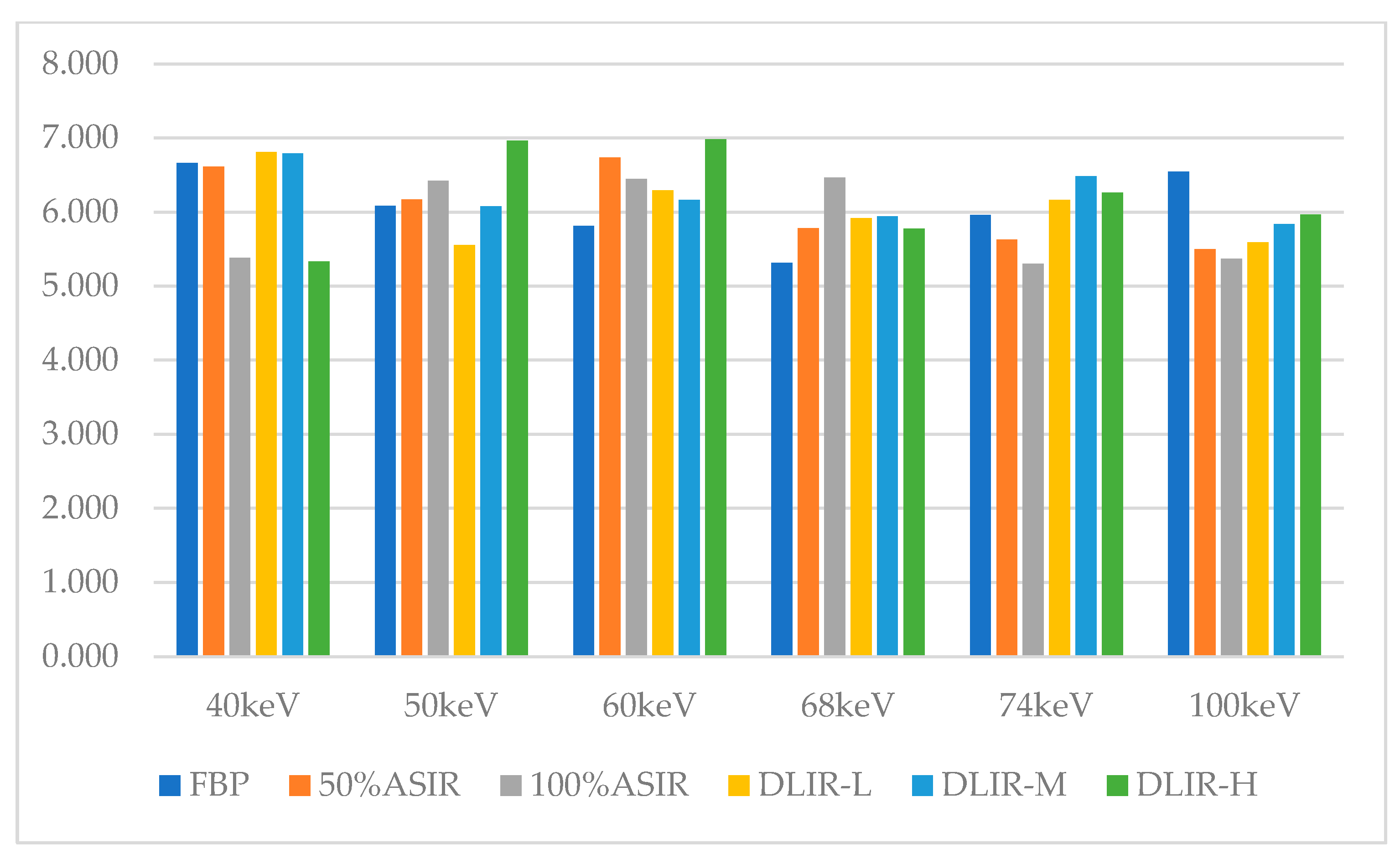
| Recon | FBP | 50% ASIR | 100% ASIR | DLIR-L | DLIR-M | DLIR-H | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | |
| 40 keV | 11.39 | 4.72 | 10.70 | 4.09 | 10.68 | 5.30 | 12.98 | 6.17 | 12.47 | 5.68 | 10.08 | 4.75 |
| 50 keV | 54.18 | 48.10 | 53.59 | 47.42 | 54.10 | 47.68 | 55.20 | 49.64 | 55.31 | 49.23 | 55.65 | 48.68 |
| 60 keV | 80.10 | 74.29 | 80.73 | 73.99 | 83.37 | 76.93 | 81.90 | 75.61 | 82.18 | 76.02 | 82.67 | 75.69 |
| 68 keV | 94.10 | 88.78 | 94.85 | 89.07 | 95.27 | 88.81 | 96.39 | 90.47 | 95.97 | 90.03 | 96.13 | 90.35 |
| 74 keV | 102.28 | 96.32 | 102.03 | 96.41 | 101.68 | 96.38 | 103.63 | 97.46 | 103.75 | 97.26 | 103.59 | 97.33 |
| 100 keV | 119.80 | 113.25 | 119.28 | 113.78 | 120.24 | 114.87 | 121.06 | 115.47 | 121.74 | 115.90 | 120.96 | 114.99 |
| Recon | FBP | 50% ASIR | 100% ASIR | DLIR-L | DLIR-M | DLIR-H | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | Low-Res | Back-Ground | |
| 40 keV | 21.51 | 23.51 | 14.86 | 16.75 | 9.68 | 12.32 | 14.70 | 16.87 | 12.34 | 15.07 | 10.06 | 12.04 |
| 50 keV | 16.12 | 18.20 | 11.26 | 12.44 | 7.94 | 8.98 | 10.95 | 12.67 | 9.50 | 10.53 | 7.84 | 8.84 |
| 60 keV | 12.18 | 13.91 | 8.675 | 9.27 | 7.00 | 6.41 | 8.49 | 9.67 | 7.34 | 8.12 | 5.61 | 6.64 |
| 68 keV | 10.31 | 11.75 | 7.23 | 7.66 | 5.96 | 7.67 | 7.32 | 8.17 | 6.00 | 6.53 | 4.89 | 5.66 |
| 74 keV | 9.59 | 10.65 | 6.52 | 7.19 | 4.48 | 5.04 | 6.31 | 7.14 | 5.43 | 6.18 | 4.60 | 4.95 |
| 100 keV | 6.51 | 7.53 | 4.78 | 5.14 | 3.22 | 3.55 | 4.60 | 3.55 | 3.83 | 4.35 | 3.19 | 3.45 |
| Recon | FBP | 50% ASIR | 100% ASIR | DLIR-L | DLIR-M | DLIR-H |
|---|---|---|---|---|---|---|
| 40 keV | 6.67 | 6.61 | 5.38 | 6.81 | 6.79 | 5.33 |
| 50 keV | 6.09 | 6.17 | 6.42 | 5.56 | 6.08 | 6.97 |
| 60 keV | 5.81 | 6.74 | 6.45 | 6.29 | 6.17 | 6.99 |
| 68 keV | 5.31 | 5.78 | 6.47 | 5.92 | 5.94 | 5.78 |
| 74 keV | 5.96 | 5.63 | 5.30 | 6.16 | 6.48 | 6.26 |
| 100 keV | 6.55 | 5.50 | 5.37 | 5.59 | 5.84 | 5.97 |
| Recon | FBP | 50% ASIR | 100% ASIR | DLIR-L | DLIR-M | DLIR-H |
|---|---|---|---|---|---|---|
| 40 keV | 1.00 | 2.00 | 1.67 | 2.00 | 2.00 | 2.33 |
| 50 keV | 1.50 | 2.50 | 2.33 | 3.00 | 3.33 | 3.33 |
| 60 keV | 2.00 | 3.00 | 2.67 | 3.00 | 3.33 | 3.33 |
| 68 keV | 2.00 | 3.00 | 2.67 | 3.00 | 3.33 | 3.33 |
| 74 keV | 2.00 | 3.00 | 3.00 | 3.00 | 3.33 | 3.67 |
| 100 keV | 1.67 | 2.00 | 2.00 | 2.33 | 2.67 | 3.00 |
| Recon | IOU | DICE | Sensitivity | Manhattan Distance | Euclidean Distance | Cosine Distance | BKG Noise | Quality Score |
|---|---|---|---|---|---|---|---|---|
| FBP | 0.58 | 0.72 | 0.86 | 18.64 | 4.26 | 0.63 | 14.26 | 1.70 |
| 50% ASIR | 0.62 | 0.76 | 0.90 | 17.11 | 4.00 | 0.60 | 9.74 | 2.58 |
| 100% ASIR | 0.65 | 0.78 | 0.93 | 15.66 | 3.85 | 0.57 | 7.33 | 2.39 |
| DLIR-L | 0.67 | 0.80 | 0.95 | 13.93 | 3.67 | 0.53 | 10.01 | 2.72 |
| DLIR-M | 0.68 | 0.81 | 0.96 | 13.10 | 3.55 | 0.48 | 8.46 | 3.00 |
| DLIR-H | 0.69 | 0.81 | 0.97 | 12.14 | 3.42 | 0.44 | 6.93 | 3.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Chen, Z.; Gao, S.; Hu, J.; Yang, Z.; Peng, Y.; Sun, J. Performance Evaluation of Image Segmentation Using Dual-Energy Spectral CT Images with Deep Learning Image Reconstruction: A Phantom Study. Tomography 2025, 11, 51. https://doi.org/10.3390/tomography11050051
Li H, Chen Z, Gao S, Hu J, Yang Z, Peng Y, Sun J. Performance Evaluation of Image Segmentation Using Dual-Energy Spectral CT Images with Deep Learning Image Reconstruction: A Phantom Study. Tomography. 2025; 11(5):51. https://doi.org/10.3390/tomography11050051
Chicago/Turabian StyleLi, Haoyan, Zhenpeng Chen, Shuaiyi Gao, Jiaqi Hu, Zhihao Yang, Yun Peng, and Jihang Sun. 2025. "Performance Evaluation of Image Segmentation Using Dual-Energy Spectral CT Images with Deep Learning Image Reconstruction: A Phantom Study" Tomography 11, no. 5: 51. https://doi.org/10.3390/tomography11050051
APA StyleLi, H., Chen, Z., Gao, S., Hu, J., Yang, Z., Peng, Y., & Sun, J. (2025). Performance Evaluation of Image Segmentation Using Dual-Energy Spectral CT Images with Deep Learning Image Reconstruction: A Phantom Study. Tomography, 11(5), 51. https://doi.org/10.3390/tomography11050051







