A Novel and Reliable Pixel Response Correction Method (DAC-Shifting) for Spectral Photon-Counting CT Imaging
Abstract
1. Introduction
2. Materials and Methods
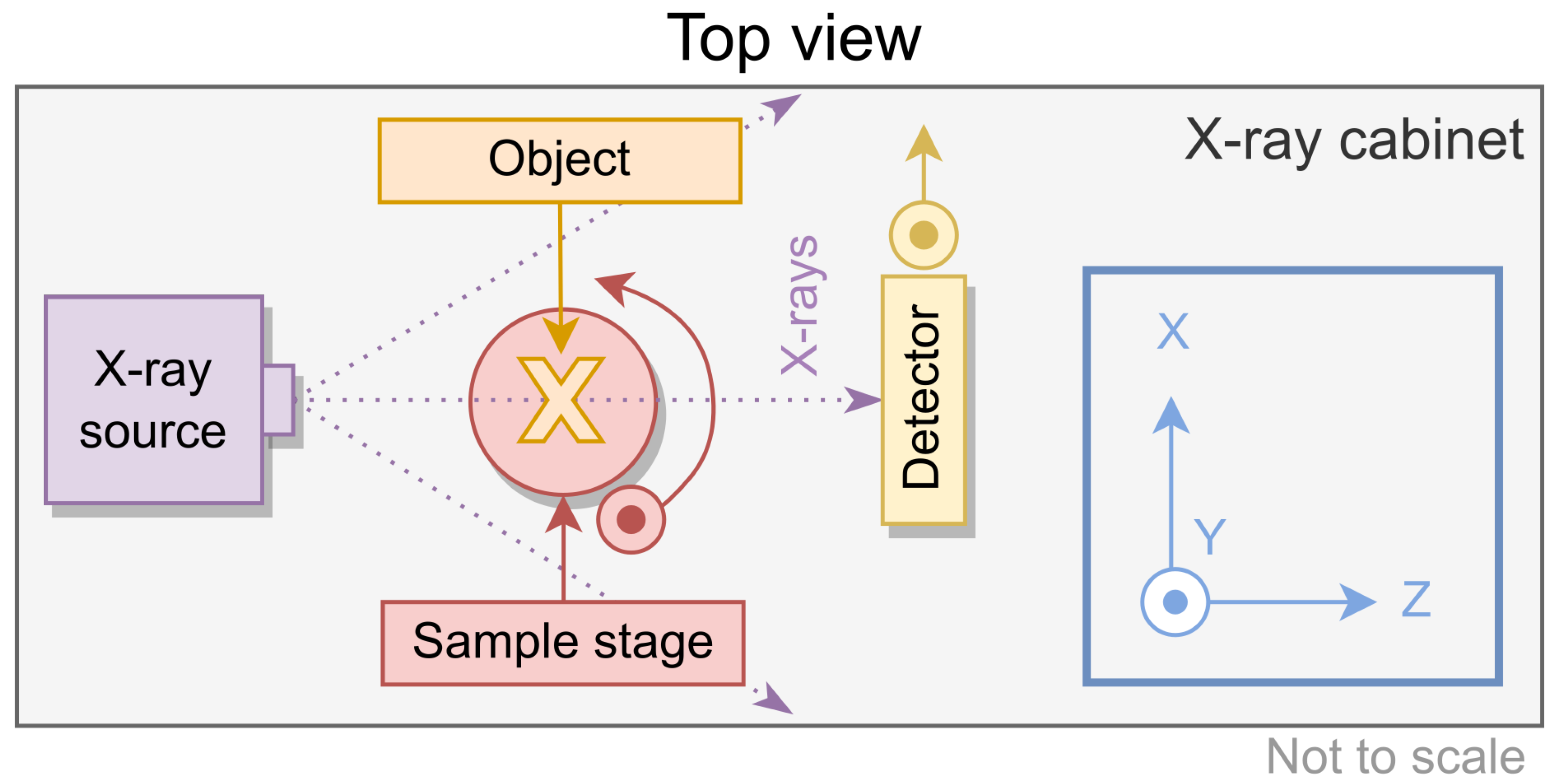
2.1. Experimental Setup
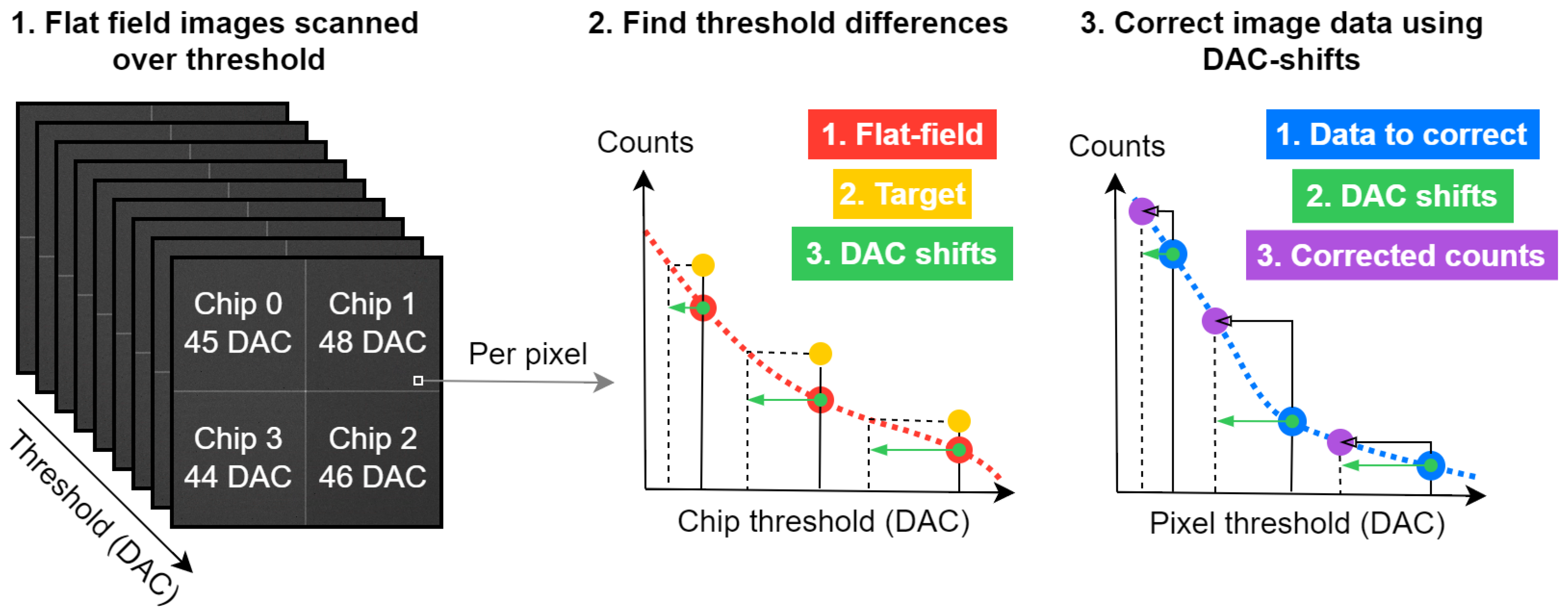
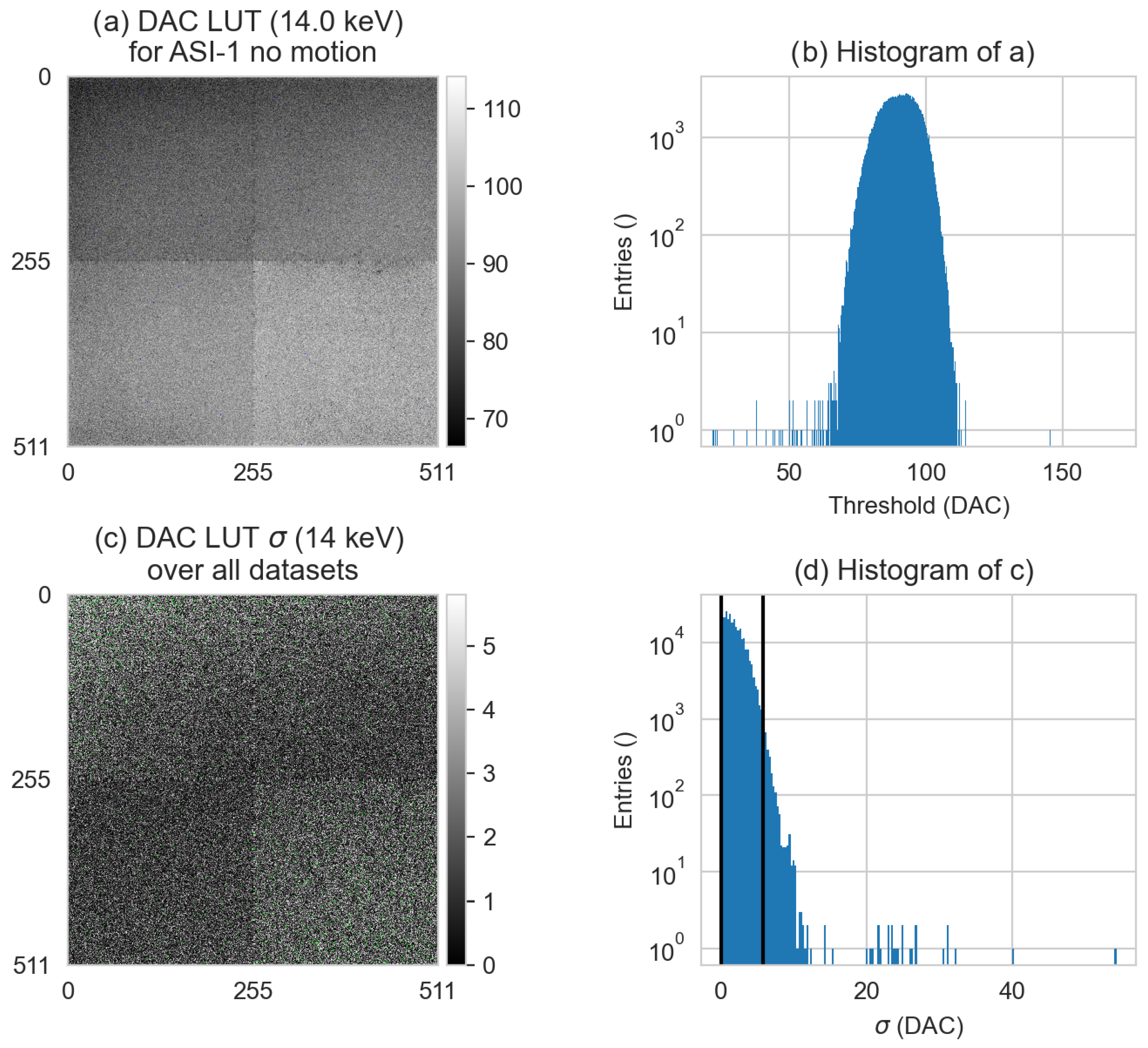
2.2. Image Post-Processing (DAC-Shifting)
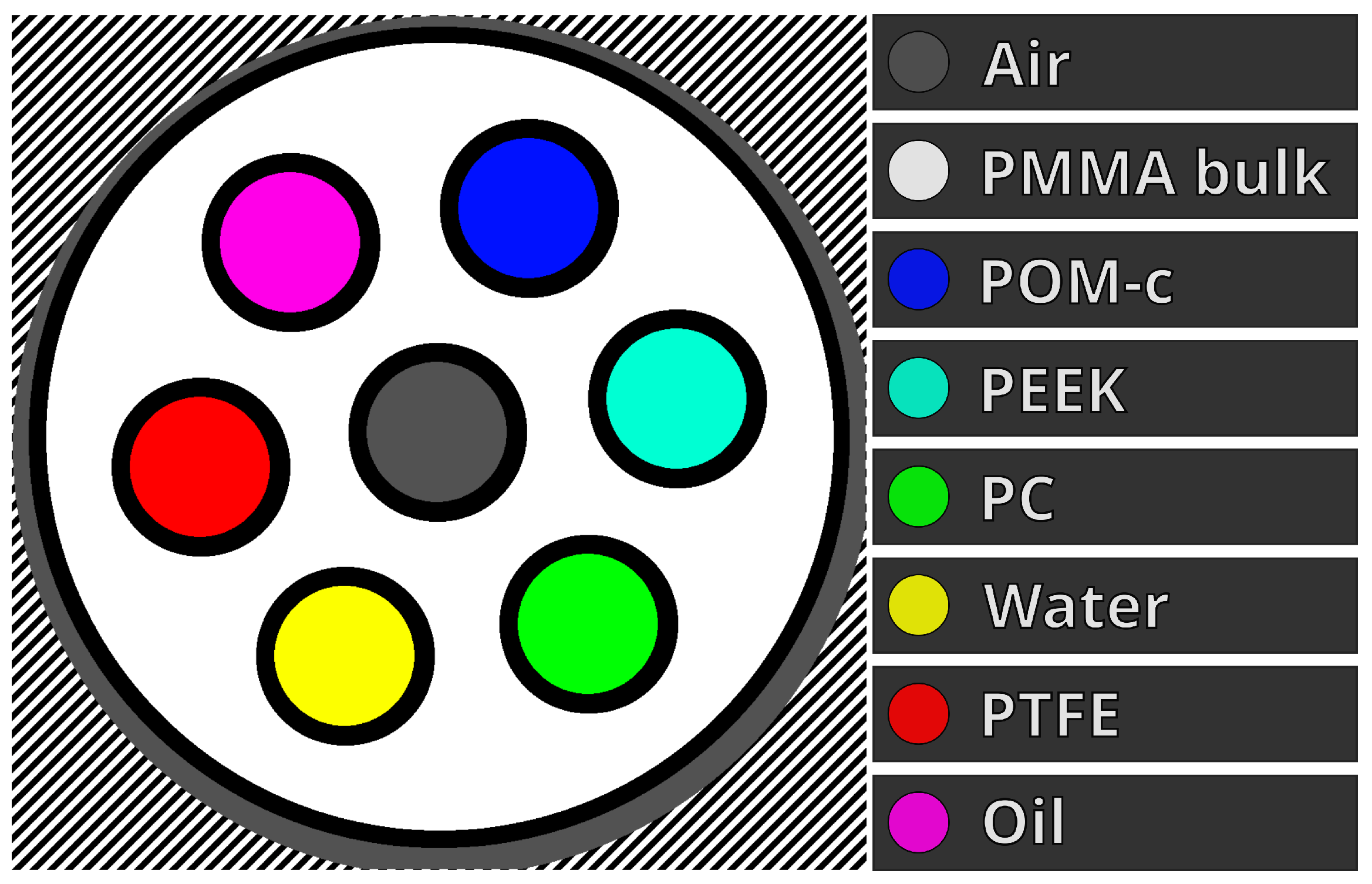
2.3. Phantom Imaging
2.4. Image Reconstruction
2.5. Statistics
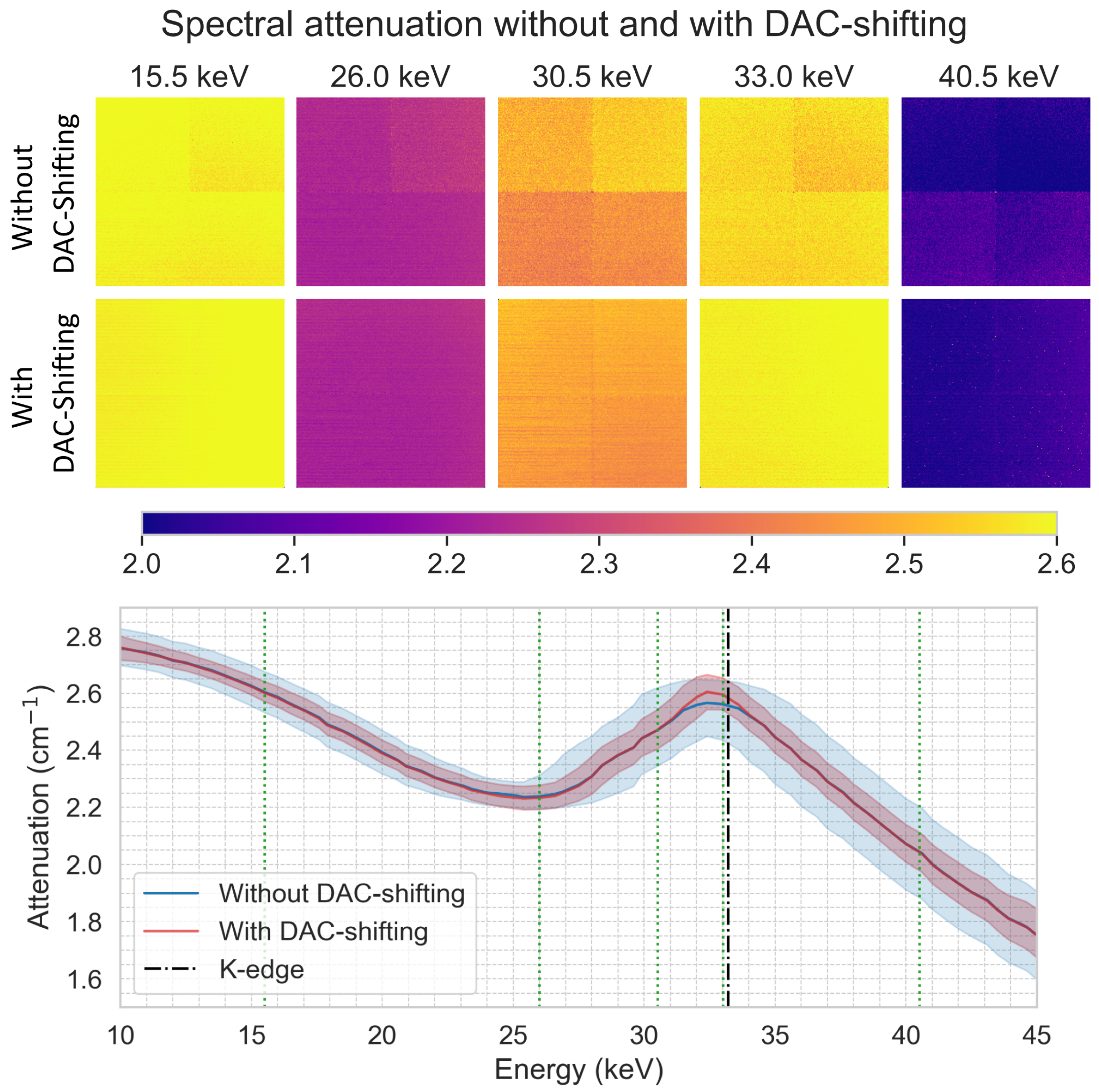
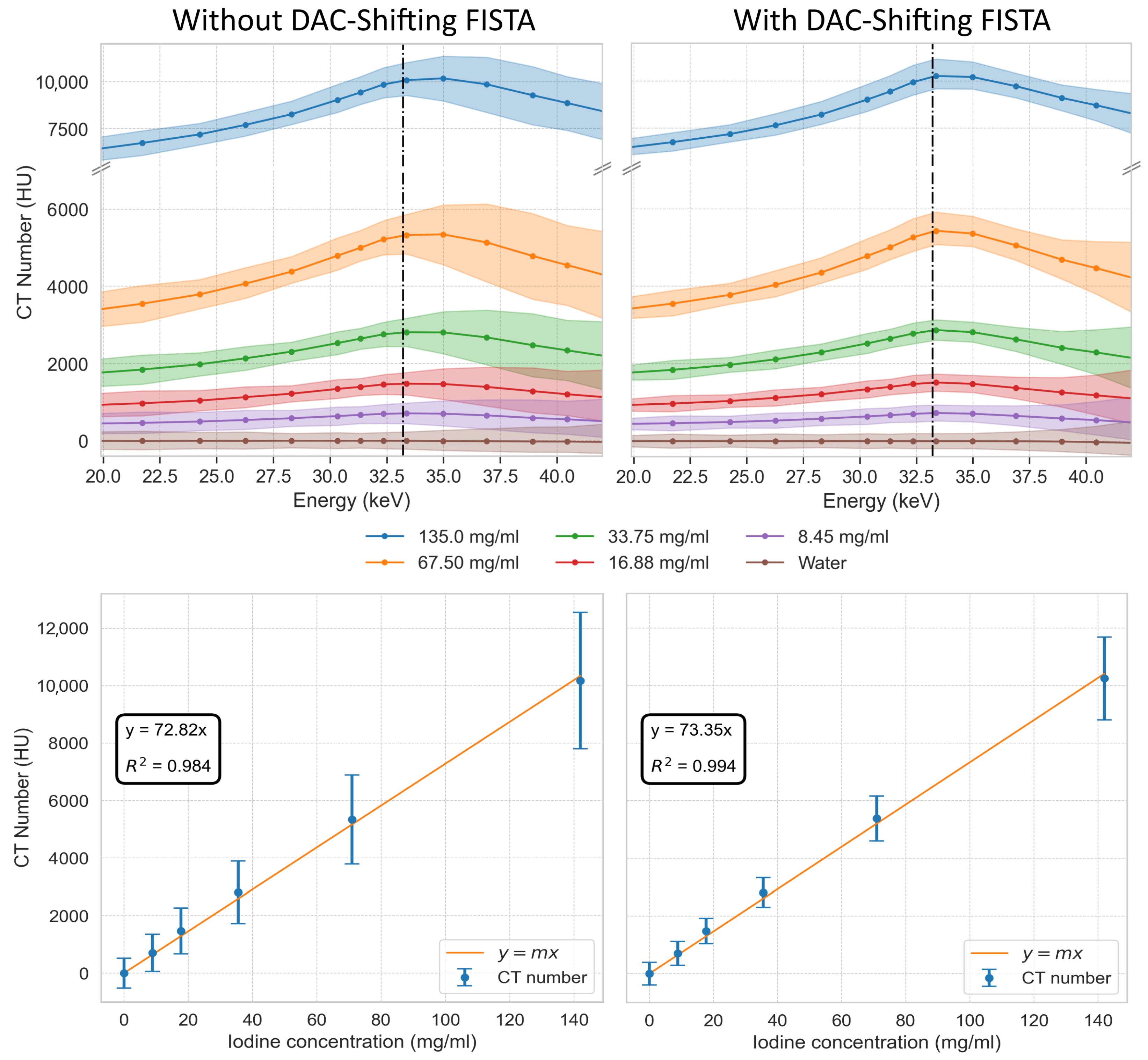
2.6. Spectral K-Edge Experiment with an Iodine Solution
- Tube voltage = 90 kVp;
- Tube current = 89 A;
- DSO (distance source object distance) = 123.0 mm;
- DSD (distance source detector) = 163.0 mm;
- Projections = 720;
- Rotation angle = 360°
- Reconstructed voxel size = 0.0415 mm3.
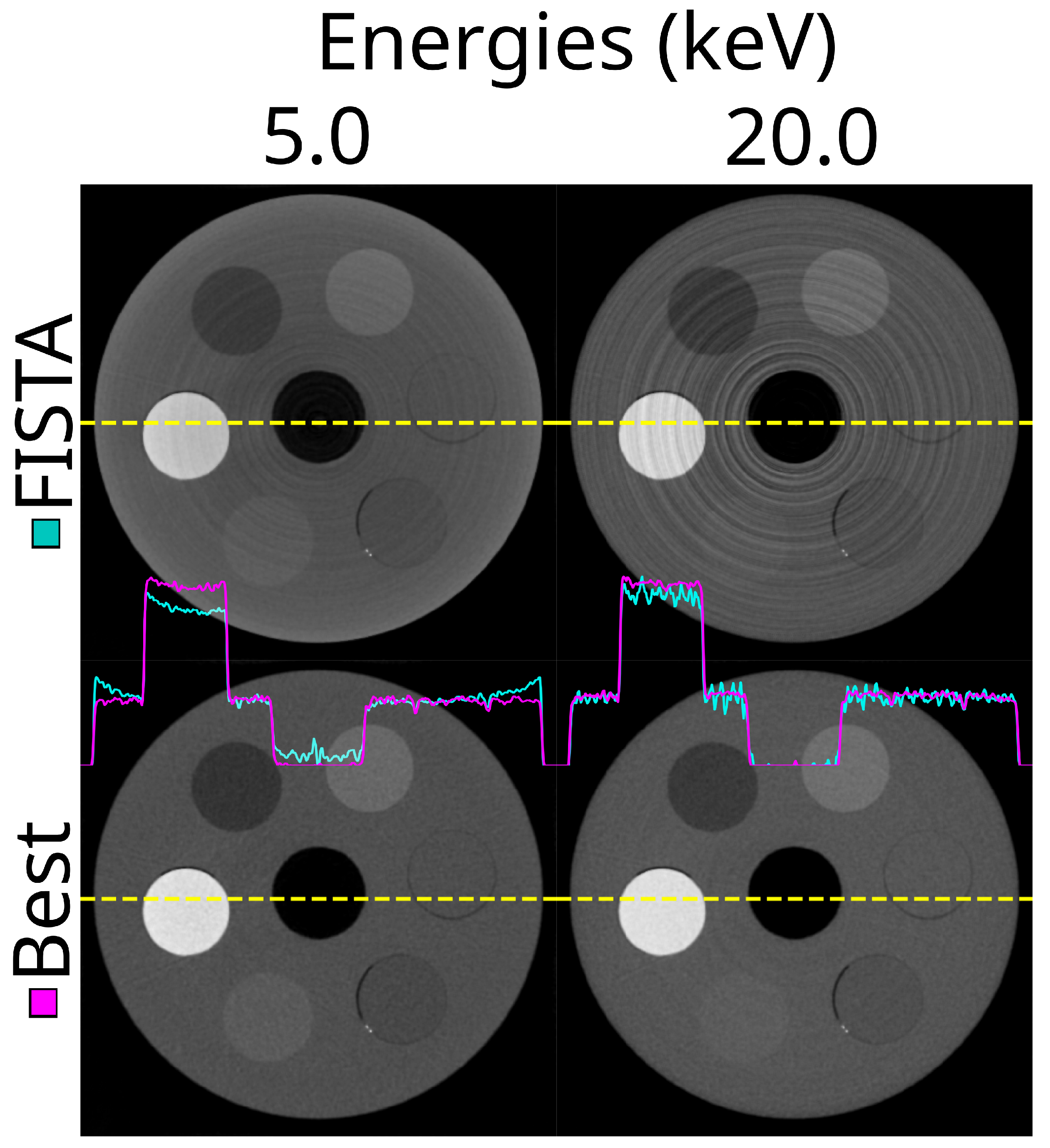
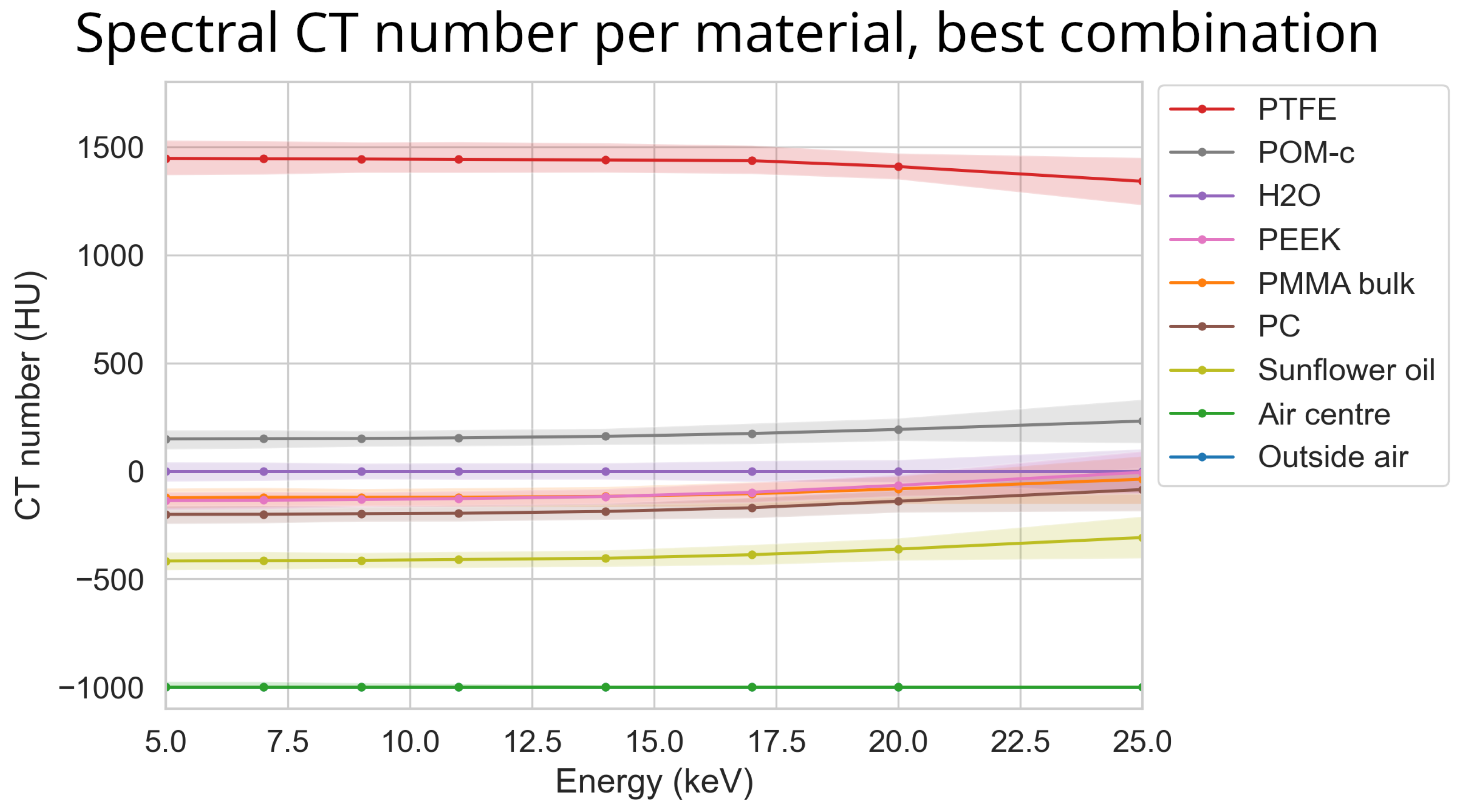
3. Results
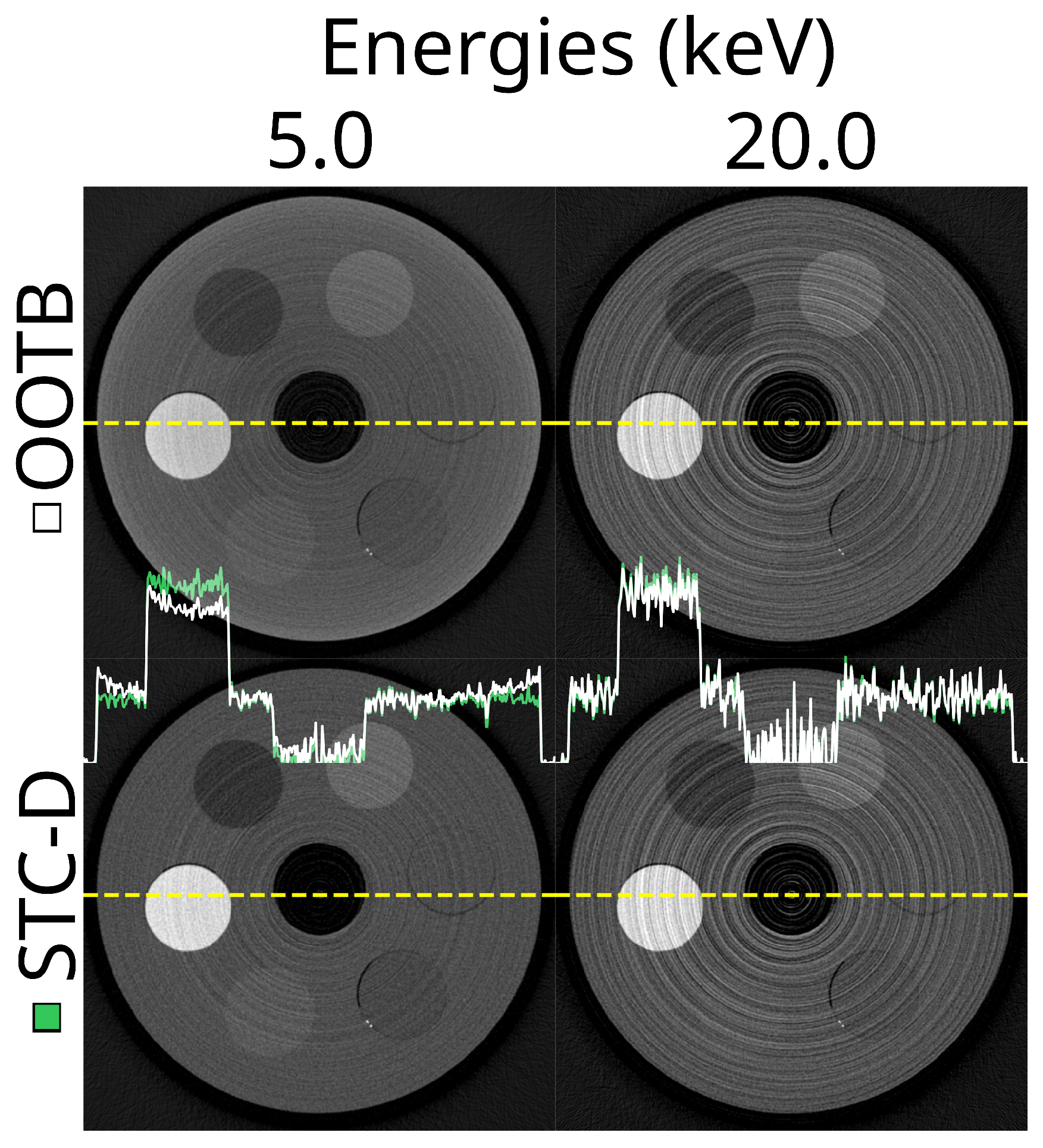
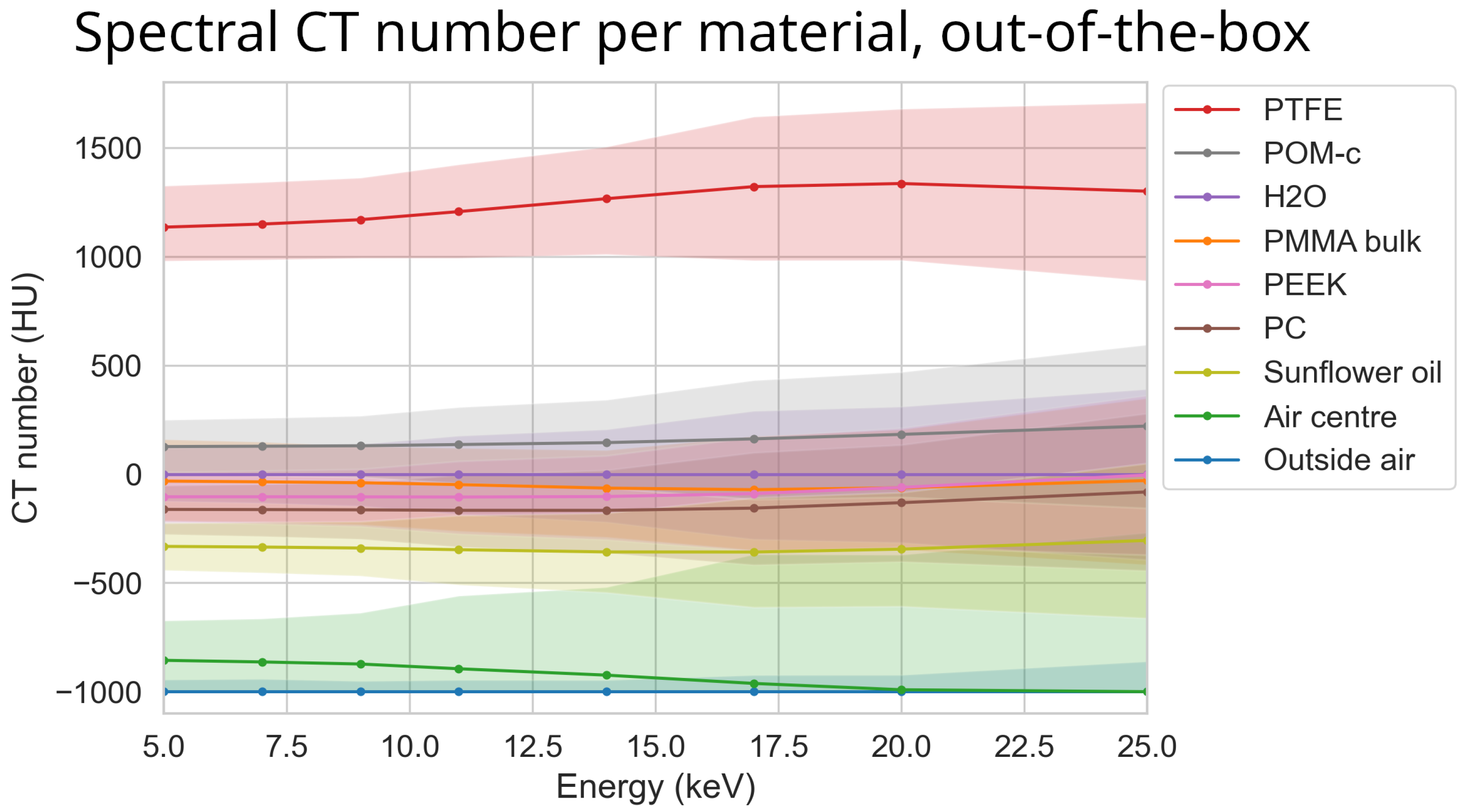
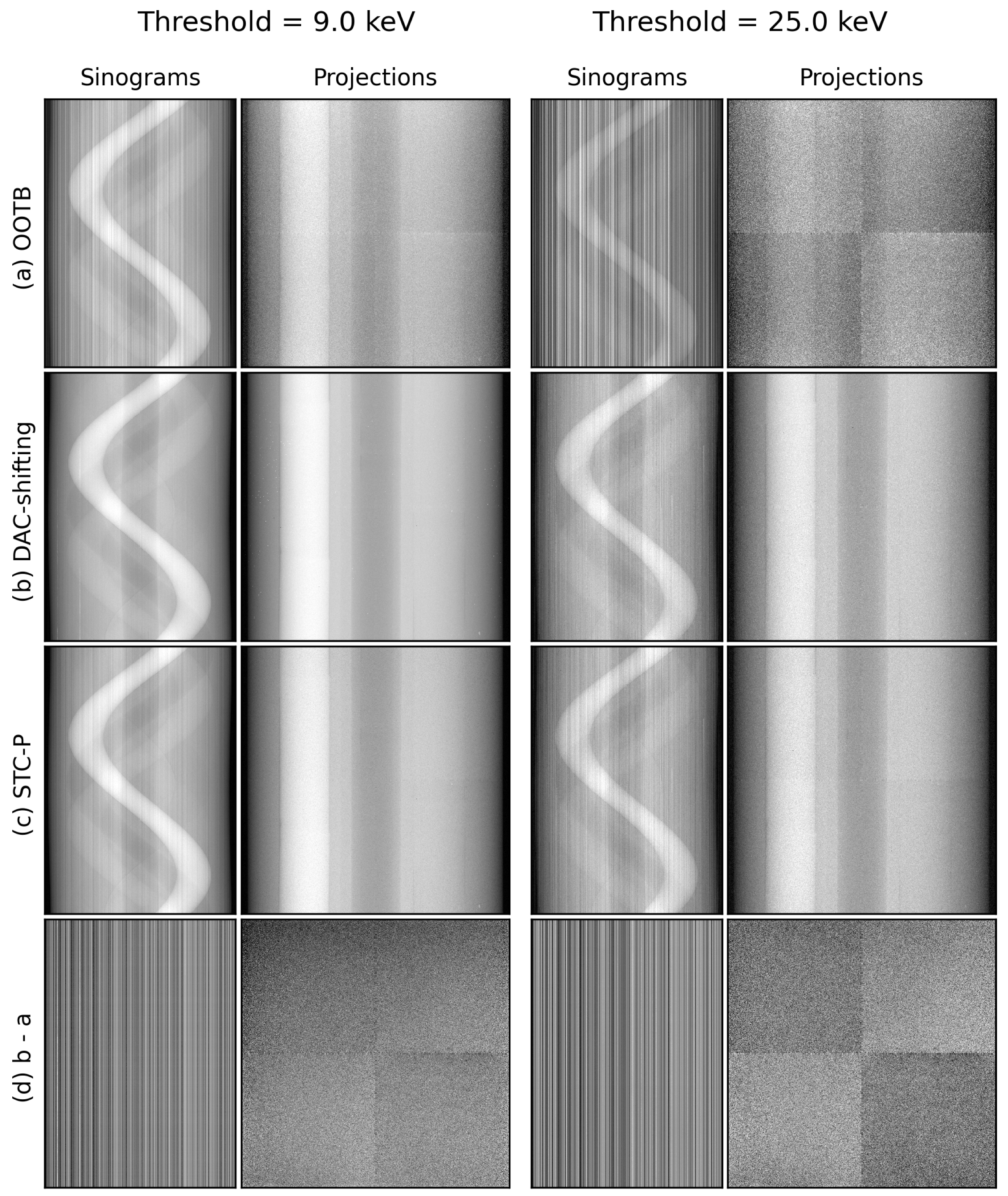
3.1. Out-of-the-Box Imaging
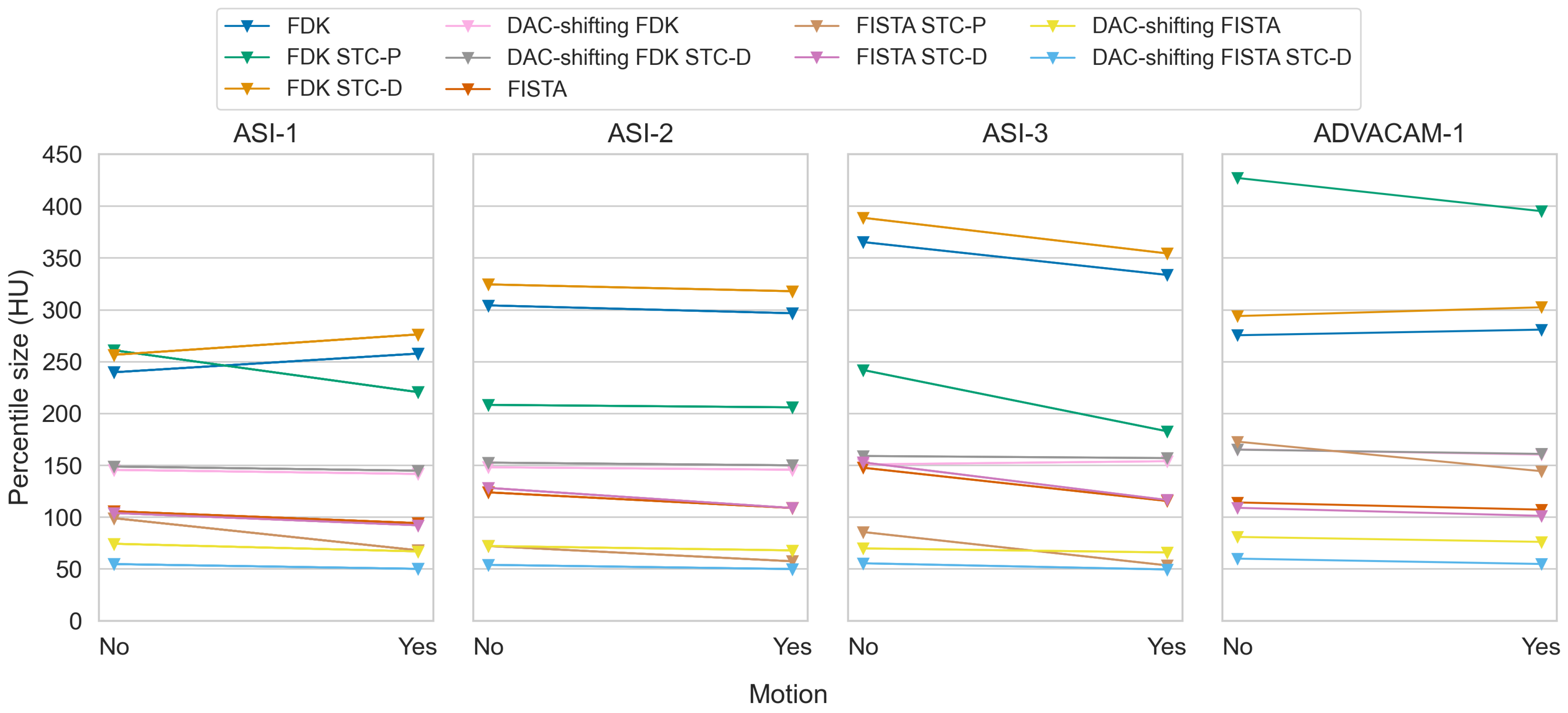
3.2. Effectiveness Scores
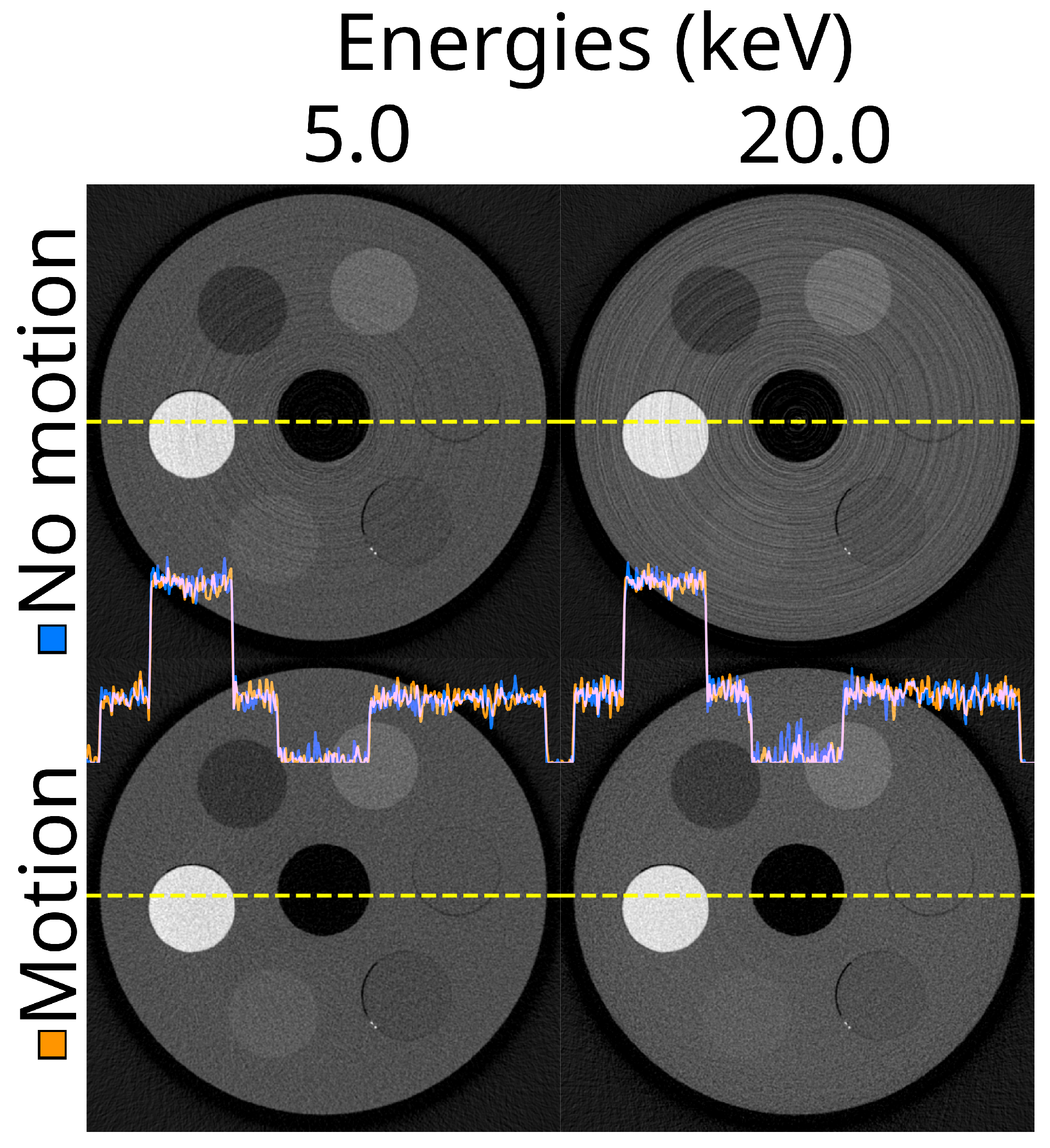
3.3. Stc-D Beam Hardening Correction and Detector Motion
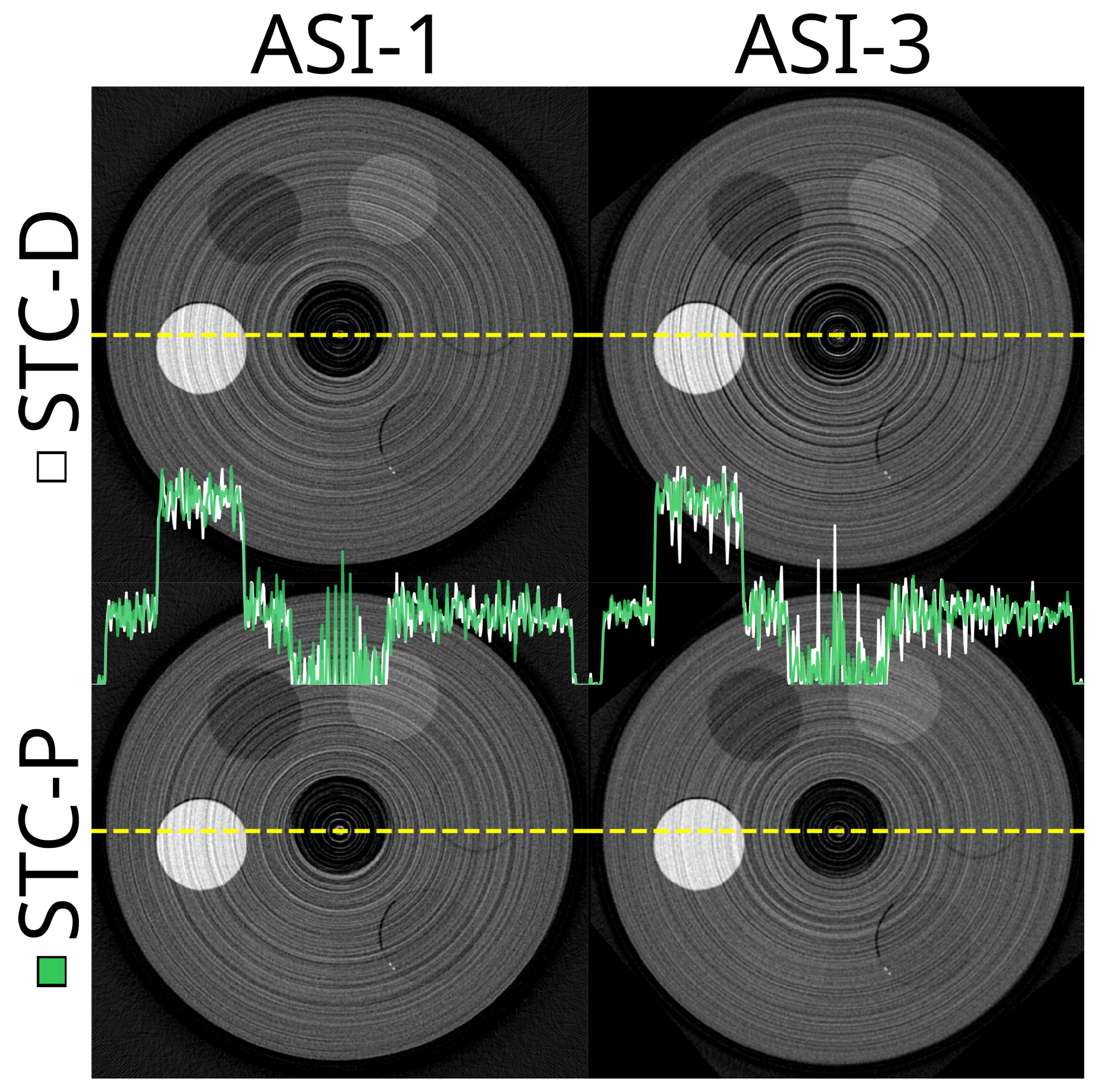
3.4. Stc-P Beam Hardening and Pixel Response Correction
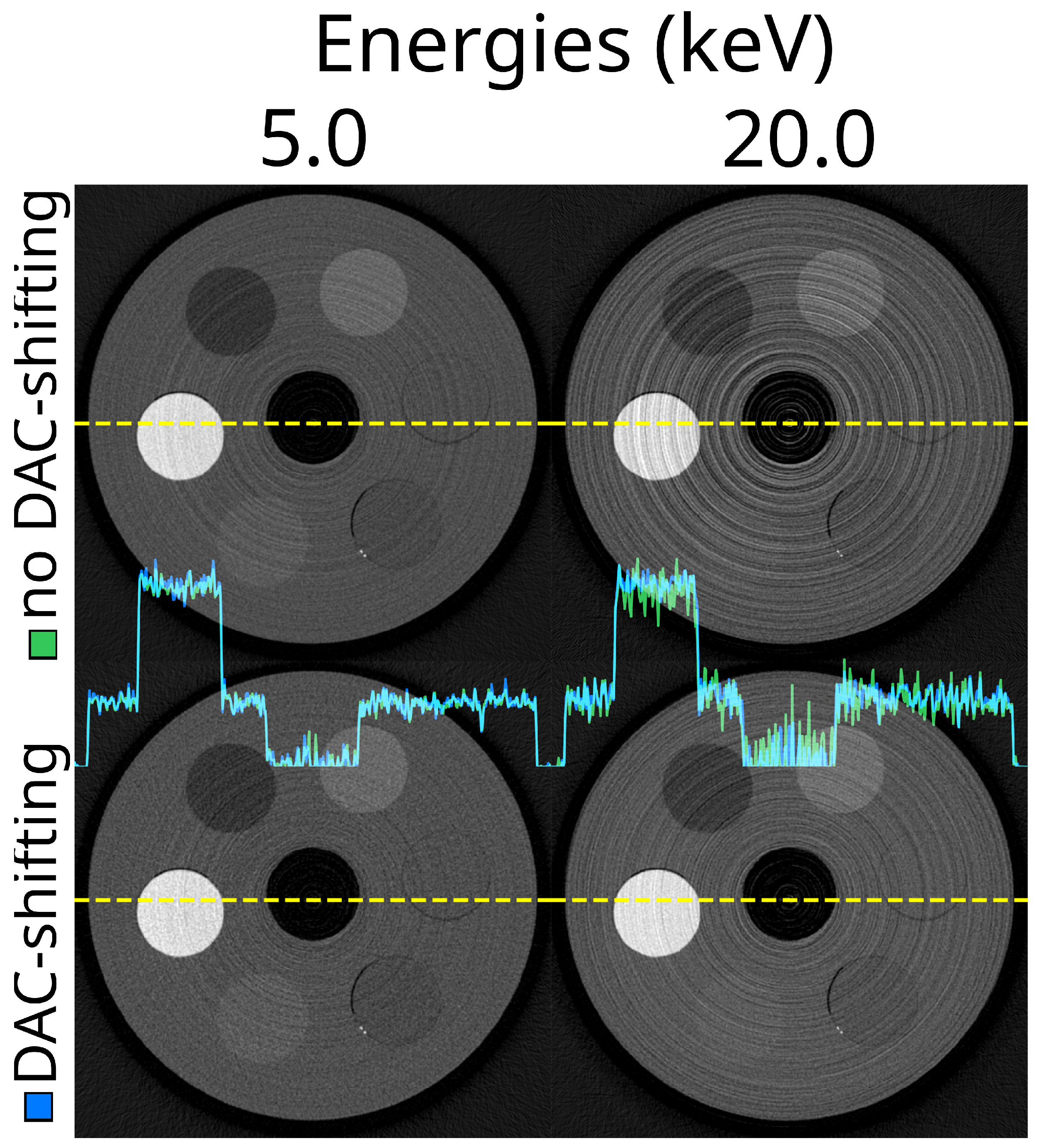
3.5. DAC-Shifting
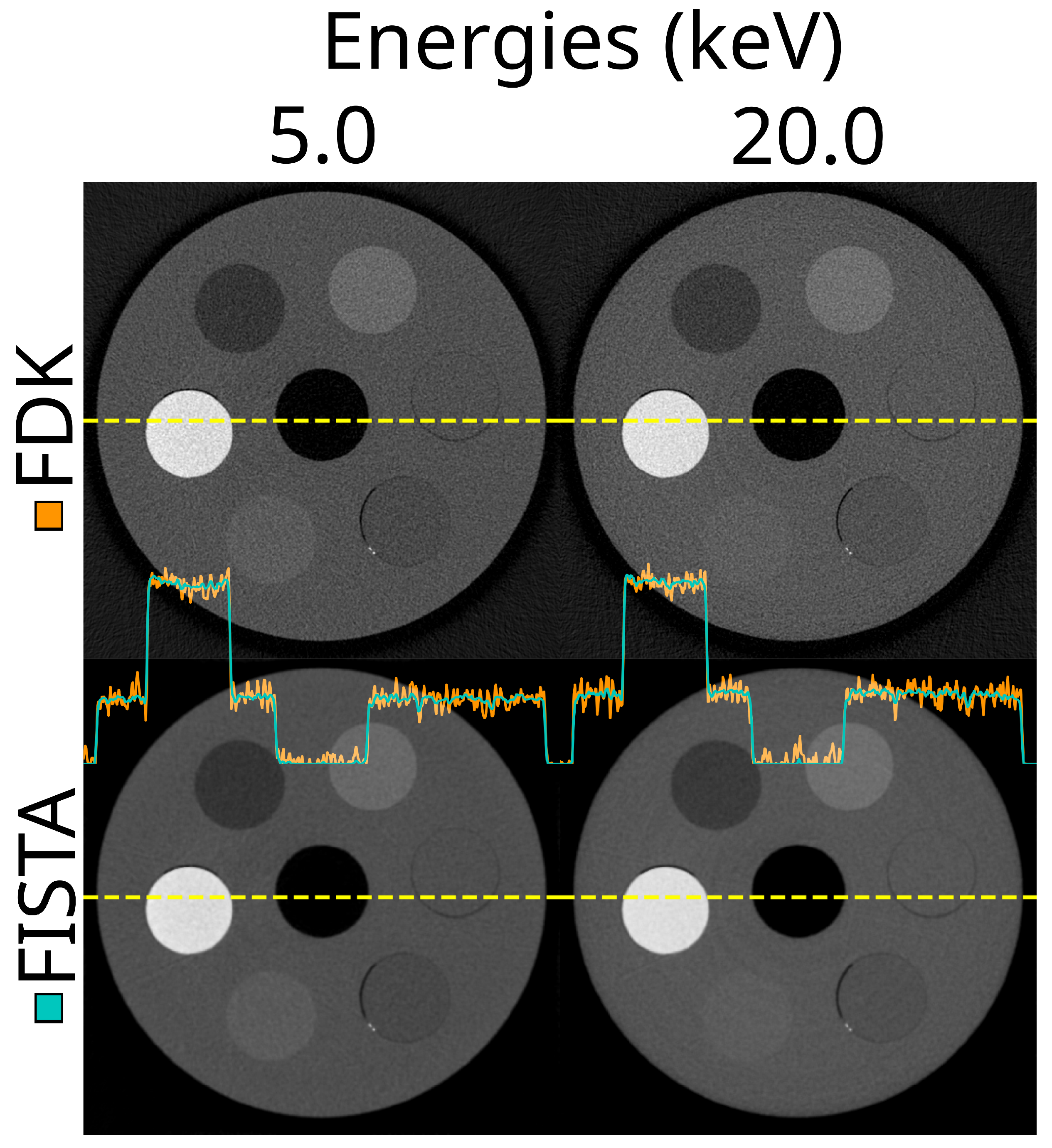
3.6. Reconstruction Methods
3.7. Optimal Settings
3.8. Evaluation of DAC-Shifting Iodine K-Edge Imaging
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Ye, Z.; Chen, J.; Deng, L.; Song, B. Photon Counting CT: Technical Principles, Clinical Applications, and Future Prospects. Acad. Radiol. 2023, 30, 2362–2382. [Google Scholar] [CrossRef] [PubMed]
- Ronaldson, J.P.; Zainon, R.; Scott, N.J.A.; Gieseg, S.P.; Butler, A.P.; Butler, P.H.; Anderson, N.G. Toward quantifying the composition of soft tissues by spectral CT with Medipix3. Med. Phys. 2012, 39, 6847–6857. [Google Scholar] [CrossRef] [PubMed]
- Si-Mohamed, S.; Tatard-Leitman, V.; Laugerette, A.; Sigovan, M.; Pfeiffer, D.; Rummeny, E.J.; Coulon, P.; Yagil, Y.; Douek, P.; Boussel, L.; et al. Spectral Photon-Counting Computed Tomography (SPCCT): In-vivo single-acquisition multi-phase liver imaging with a dual contrast agent protocol. Sci. Rep. 2019, 9, 8548. [Google Scholar] [CrossRef] [PubMed]
- Ballabriga, R.; Alozy, J.; Blaj, G.; Campbell, M.; Fiederle, M.; Frojdh, E.; Heijne, E.H.; Llopart, X.; Pichotka, M.; Procz, S.; et al. The Medipix3RX: A high resolution, zero dead-time pixel detectorreadout chip allowing spectroscopic imaging. J. Instrum. 2013, 8, C02016. [Google Scholar] [CrossRef]
- Marsh, J.F.; Jorgensen, S.M.; Rundle, D.S.; Vercnocke, A.J.; Leng, S.; Butler, P.H.; McCollough, C.H.; Ritman, E.L. Evaluation of a photon counting Medipix3RX cadmium zinc telluride spectral x-ray detector. J. Med. Imaging 2018, 5, 043503. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Yu, H.; Thayer, P.; Jin, X.; Xu, Q.; Bennett, J.; Tappenden, R.; Wei, B.; Goldstein, A.; Renaud, P.; et al. Preliminary experimental results from a MARS Micro-CT system. J. X-ray Sci. Technol. 2012, 20, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Berger, N.; Marcon, M.; Frauenfelder, T.; Boss, A. Dedicated Spiral Breast Computed Tomography With a Single Photon-Counting Detector: Initial Results of the First 300 Women. Investig. Radiol. 2020, 55, 68–72. [Google Scholar] [CrossRef]
- Panta, R.K.; Walsh, M.F.; Bell, S.T.; Anderson, N.G.; Butler, A.P.; Butler, P.H. Energy calibration of the pixels of spectral X-ray detectors. IEEE Trans. Med. Imaging 2015, 34, 697–706. [Google Scholar] [CrossRef] [PubMed]
- Juntunen, M.A.; Inkinen, S.I.; Ketola, J.H.; Kotiaho, A.; Kauppinen, M.; Winkler, A.; Nieminen, M.T. Framework for Photon Counting Quantitative Material Decomposition. IEEE Trans. Med. Imaging 2020, 39, 35–47. [Google Scholar] [CrossRef]
- Persson, M.; Bornefalk, H. A Framework for evaluating threshold variation compensation methods in photon counting spectral CT. IEEE Trans. Med. Imaging 2012, 31, 1861–1874. [Google Scholar] [CrossRef]
- Vavrik, D.; Holy, T.; Jakubek, J.; Pospisil, S.; Vykydal, Z.; Dammer, J. Direct thickness calibration: Way to radiographic study of soft tissues. In Astroparticle, Particle and Space Physics, Detectors and Medical Physics Applications; World Scientific: Singapore, 2006; pp. 773–778. [Google Scholar] [CrossRef]
- Abu Anas, E.M.; Kim, J.G.; Lee, S.Y.; Hasan, M.K. Comparison of ring artifact removal methods using flat panel detector based CT images. Biomed. Eng. Online 2011, 10, 72. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wei, C.; Xu, Q. Detector shifting and deep learning based ring artifact correction method for low-dose CT. Med. Phys. 2023, 50, 4308–4324. [Google Scholar] [CrossRef] [PubMed]
- Biguri, A.; Dosanjh, M.; Hancock, S.; Soleimani, M. TIGRE: A MATLAB-GPU toolbox for CBCT image reconstruction. Biomed. Phys. Eng. Express 2016, 2, 055010. [Google Scholar] [CrossRef]
- Gustschin, N.; Gustschin, A.; Epple, F.M.; Allner, S.; Achterhold, K.; Herzen, J.; Pfeiffer, F. Signal-to-thickness calibration and pixel-wise interpolation for beam-hardening artefact reduction in microCT. Europhys. Lett. 2019, 125, 38003. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Bal, N.J.S.; Fransen, M.; Linde, F.L. Medipix3: Spectral X-ray Micro-CT and Hadron Therapy. Ph.D. Thesis, Universiteit van Amsterdam, Amsterdam, The Netherlands, 2023. [Google Scholar]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet–Fourier filtering. Opt. Express 2009, 17, 34–35. [Google Scholar] [CrossRef] [PubMed]
- Simard, M.; Bouchard, H. One-step iterative reconstruction approach based on eigentissue decomposition for spectral photon-counting computed tomography. J. Med. Imaging 2022, 9. [Google Scholar] [CrossRef] [PubMed]
- Rodesch, P.A.; Si-Mohamed, S.A.; Lesaint, J.; Douek, P.C.; Rit, S. Image quality improvement of a one-step spectral CT reconstruction on a prototype photon-counting scanner. Phys. Med. Biol. 2023, 69, 015005. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, K.C.; Sharma, G.; Parchur, A.K.; Joshi, A.; Schmidt, T.G. Experimental investigation of neural network estimator and transfer learning techniques for K-edge spectral CT imaging. Med. Phys. 2020, 47, 541–551. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Gao, Y.; Xu, Q.; Li, Y.; Zhang, C.; Mou, X.; Liang, Z. Learned Tensor Neural Network Texture Prior for Photon-Counting CT Reconstruction. IEEE Trans. Med. Imaging 2024. early access. [Google Scholar] [CrossRef]
- Nadkarni, R.; Clark, D.P.; Allphin, A.J.; Badea, C.T. A Deep Learning Approach for Rapid and Generalizable Denoising of Photon-Counting Micro-CT Images. Tomography 2023, 9, 1286–1302. [Google Scholar] [CrossRef] [PubMed]
- Di Trapani, V.; Brombal, L.; Brun, F. Multi-material spectral photon-counting micro-CT with minimum residual decomposition and self-supervised deep denoising. Opt. Express 2022, 30, 42995. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Kraft, P.; Bergamaschi, A.; Broennimann, C.; Dinapoli, R.; Eikenberry, E.F.; Henrich, B.; Johnson, I.; Mozzanica, A.; Schlepütz, C.M.; Willmott, P.R.; et al. Performance of single-photon-counting PILATUS detector modules. J. Synchrotron Radiat. 2009, 16, 368–375. [Google Scholar] [CrossRef]
- Hasn, S.; Vavrik, D.; Pichotka, M. Improvement of TimePix energy resolution correcting threshold variations. J. Instrum. 2019, 14, C01010. [Google Scholar] [CrossRef]




| Acquisition Number | Threshold 0 (keV) | Threshold 1 (keV) | Exposure Time (s) |
|---|---|---|---|
| 1 | 5.0 | 7.0 | 2.08 |
| 2 | 9.0 | 11.0 | 2.88 |
| 3 | 14.0 | 17.0 | 4.48 |
| 4 | 20.0 | 25.0 | 9.60 |
| 5 | 25.0 | 30.0 | 9.60 |
| Measurement Number | Date | Manufacturer | Motion | Days from STC Calibration | Dataset Name |
|---|---|---|---|---|---|
| 1 | 29 November 2023 | ASI | No | −22 | ASI-1 |
| 2 | Yes | ||||
| 3 | 30 November 2023 | ADVACAM | No | −21 | ADVACAM-1 |
| 4 | Yes | ||||
| 5 | 19 December 2023 | ASI | No | −1 | ASI-2 |
| 6 | Yes | ||||
| 7 | 23 December 2023 | ASI | Yes | +3 | ASI-3 |
| 8 | 24 December 2023 | No | +4 |
| Acquisition Number | Threshold 0 (keV) | Threshold 1 (keV) | Exposure Time (s) |
|---|---|---|---|
| 1 | 19.5 | 21.5 | 1.10 |
| 2 | 24.0 | 26.0 | 1.66 |
| 3 | 28.0 | 30.0 | 3.04 |
| 4 | 31.0 | 32.0 | 4.00 |
| 5 | 33.0 | 35.0 | 5.10 |
| 6 | 35.0 | 37.0 | 6.04 |
| 7 | 37.0 | 39.0 | 7.44 |
| 8 | 40.5 | 42.5 | 10.0 |
| 9 | 42.5 | 44.5 | 10.0 |
| Datasets | STC-D | Detector Motion | STC-P | DAC-Shifting | Reconstruction Type |
|---|---|---|---|---|---|
| ASI-1 | −4.6 (−7.9: +3.4) p = 0.97 | −7.8 (−11.3: −2.7) p = 0.22 | −10.0 (−17.8: −2.5) p = 0.41 | −40.7 (−46.1: −36.9) p = 0.001 | −60.7 (−64.9: −56.8) p < 0.001 |
| ASI-2 | −3.6 (−6.3: +4.3) p = 0.67 | −7.0 (−11.0: −1.8) p < 0.001 | −37.8 (−43.2: −31.3) p < 0.001 | −50.0 (−53.3: −48.6) p < 0.001 | −62.3 (−65.7: −59.6) p < 0.001 |
| ASI-3 | −2.7 (−4.5: +5.6) p = 0.48 | −14.1 (−23.3: −6.4) p < 0.001 | −43.7 (−47.4: −40.0) p < 0.001 | −55.6 (−58.8: −53.6) p < 0.001 | −63.3 (−66.7: −59.9) p < 0.001 |
| ADVACAM-1 | −6.2 (−10.7: +2.1) p < 0.78 | −5.3 (−7.4: −2.6) p = 0.08 | +45.5 (+39.2: +52.3) p = 0.04 | −40.3 (−45.2: −37.3) p = 0.002 | −60.6 (−63.7: −58.8) p < 0.001 |
| Combined | −4.2 (−7.4: +3.6) p = 0.83 | −8.7 (−13.0: −1.5) p < 0.001 | −13.7 (−16.6: −10.4) p < 0.001 | −47.4 (−51.1: −46.3) p < 0.001 | −61.6 (−66.0: −59.1) p < 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bal, N.J.S.; Chitra Ragupathy, I.; Tramm, T.; Nijkamp, J. A Novel and Reliable Pixel Response Correction Method (DAC-Shifting) for Spectral Photon-Counting CT Imaging. Tomography 2024, 10, 1168-1191. https://doi.org/10.3390/tomography10070089
Bal NJS, Chitra Ragupathy I, Tramm T, Nijkamp J. A Novel and Reliable Pixel Response Correction Method (DAC-Shifting) for Spectral Photon-Counting CT Imaging. Tomography. 2024; 10(7):1168-1191. https://doi.org/10.3390/tomography10070089
Chicago/Turabian StyleBal, Navrit Johan Singh, Imaiyan Chitra Ragupathy, Trine Tramm, and Jasper Nijkamp. 2024. "A Novel and Reliable Pixel Response Correction Method (DAC-Shifting) for Spectral Photon-Counting CT Imaging" Tomography 10, no. 7: 1168-1191. https://doi.org/10.3390/tomography10070089
APA StyleBal, N. J. S., Chitra Ragupathy, I., Tramm, T., & Nijkamp, J. (2024). A Novel and Reliable Pixel Response Correction Method (DAC-Shifting) for Spectral Photon-Counting CT Imaging. Tomography, 10(7), 1168-1191. https://doi.org/10.3390/tomography10070089







