A Hybrid CNN-Transformer Model for Predicting N Staging and Survival in Non-Small Cell Lung Cancer Patients Based on CT-Scan
Abstract
1. Introduction
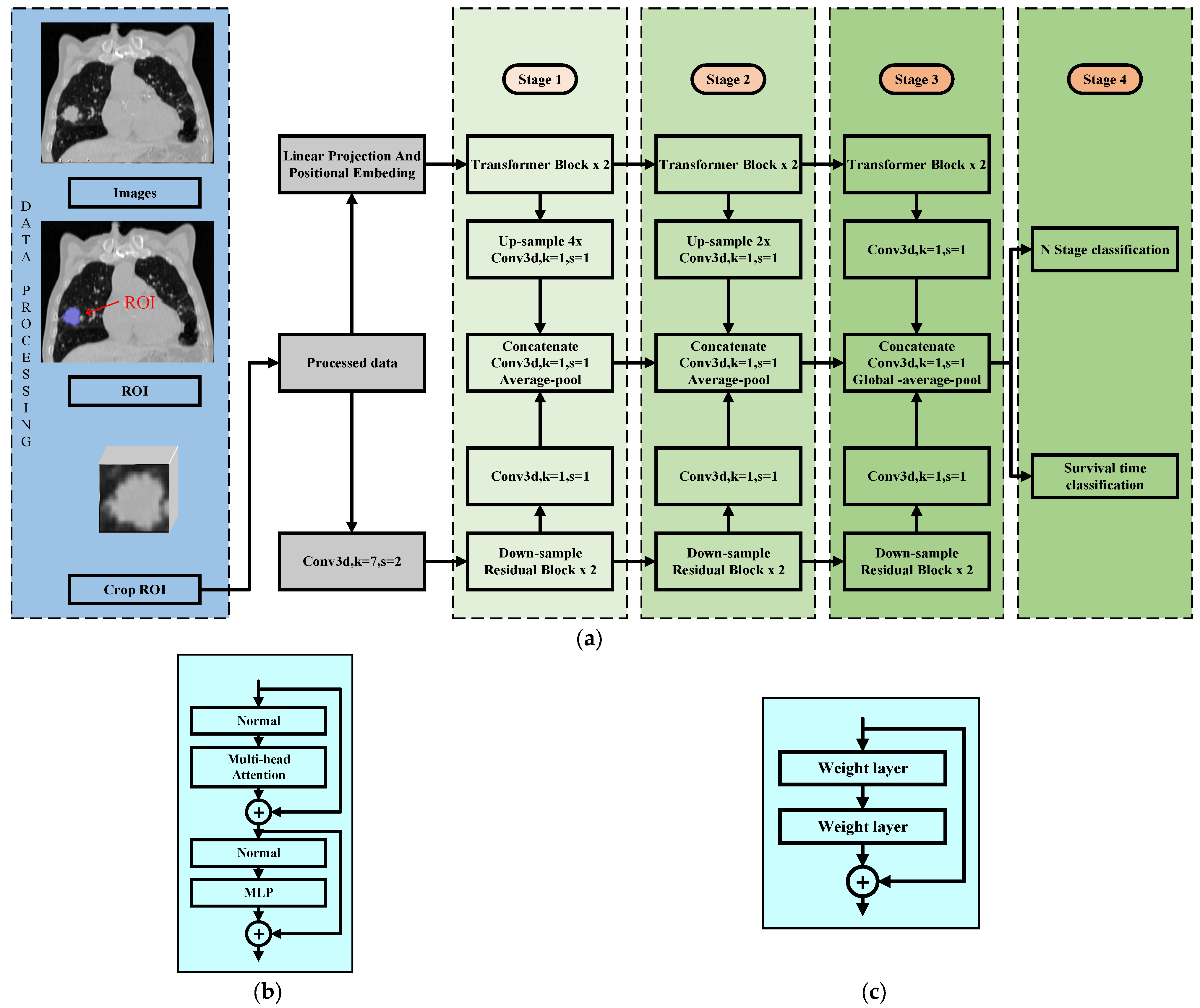
2. Model Description
3. Data Preprocessing and Experimental Parameter Settings
4. Experimental Metrics Explanation
5. Experimental Results
5.1. N Stage Prediction and Survival Analysis
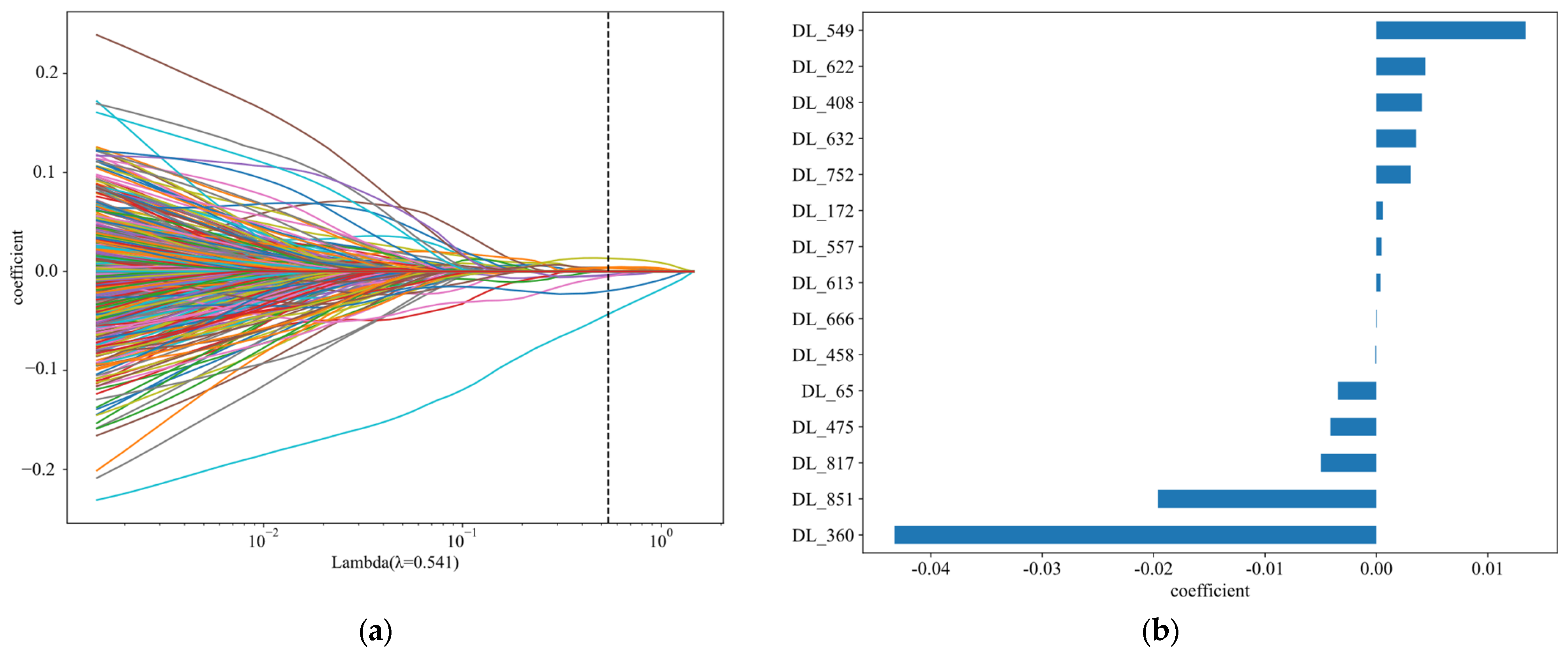
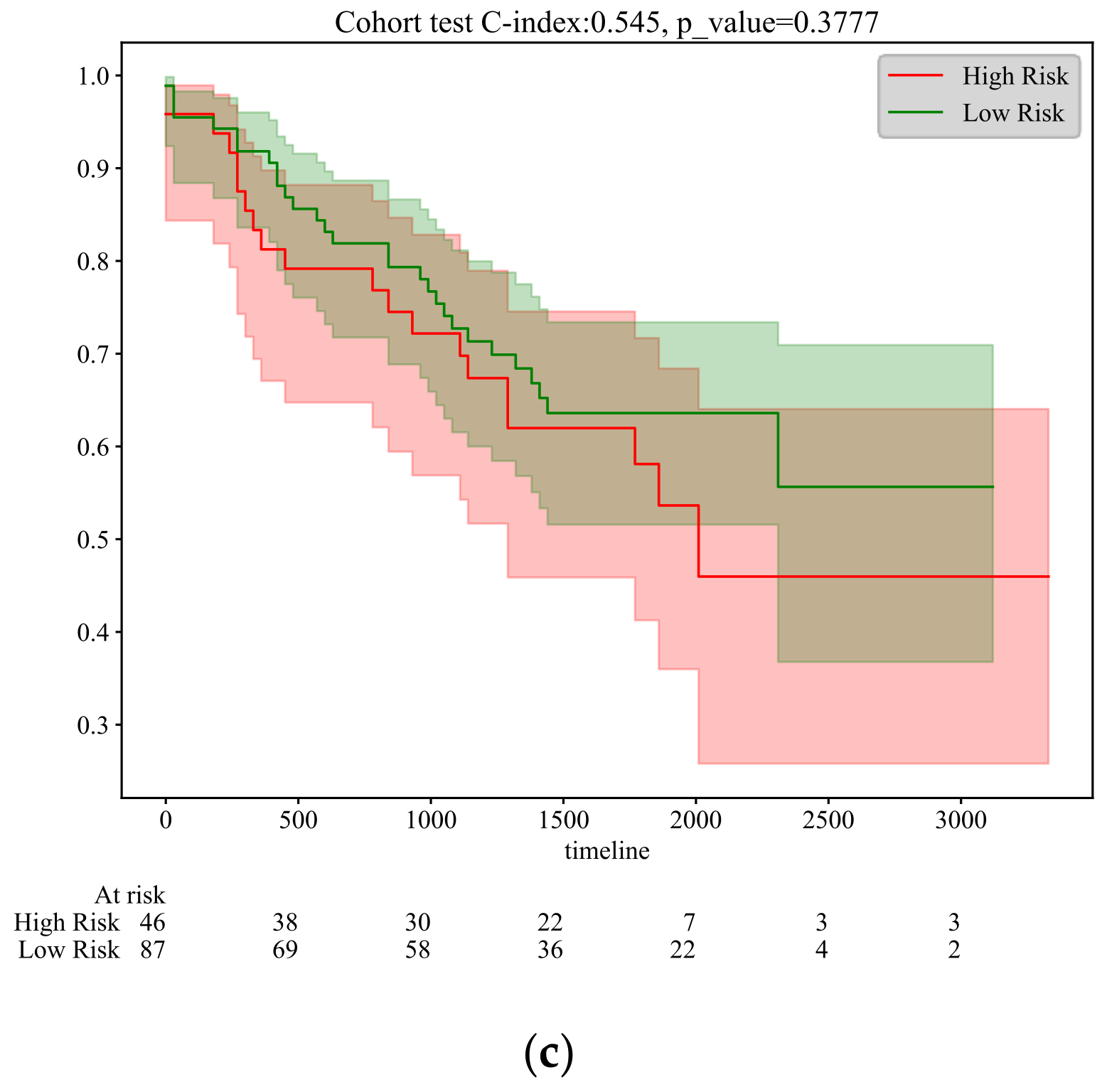
5.2. Survival Time Prediction
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guoqun, C.; Jiaodi, C.A.I. Interpretation of the Clinical Practice Guidelines for Non-small Lung Cancer (version 4 and version 5) of 2022 National Comprehensive Cancer Nerwork (NCCN). J. Diagn. Concepts Pract. 2023, 22, 8. [Google Scholar]
- Pirlog, R.; Chiroi, P.; Rusu, I.; Jurj, A.M.; Budisan, L.; Pop-Bica, C.; Braicu, C.; Crisan, D.; Sabourin, J.; Berindan-Neagoe, I.B. Cellular and molecular profiling of tumor microenvironment and early-stage lung cancer. Int. J. Mol. Sci. 2022, 23, 5346. [Google Scholar] [CrossRef]
- Zhou, W.; Guo, Q.; Wang, H.; Zhang, J. Research advances in the transformation of chronic obstructive pulmonary disease to lung cancer. Acta Pharm. Sin. 2020, 12, 1410–1418. [Google Scholar]
- Bo, Y.; Heng, Z. Revision of the TNM stage grouping in the forthcoming eighth edition of the TNM classification for lung cancer. Zhongguo Fei Ai Za Zhi 2016, 19, 337–342. [Google Scholar]
- Wang, Y.; Zhong, Y.; Deng, J.; She, Y.; Hu, X.; Chen, C. Research progress on prediction of lymph node metastasis in non-small cell lung cancer. Chin. J. Thorac. Cardiovasc. Surg. 2022, 12, 434–440. [Google Scholar]
- Yang, Z.; Wang, Z.; Liu, L. ASO Author Reflections: Comprehensive Comparison of N Staging Subclassification Methods for Non-Small-Cell Lung Cancer. Ann. Surg. Oncol. 2022, 29, 8154–8155. [Google Scholar] [CrossRef]
- Renfang, D.; Yue, Z.; Yue, P.A.N.; Chunhong, H.; Fang, W. Research Progress of Immunotherapy for Non-small Cell Lung Cancer with Drive Gene Mutation. Zhongguo Fei Ai Za Zhi 2022, 25, 201–206. [Google Scholar]
- Chen, Q.; Sun, Z.; Li, J.; Zhang, D.; Guo, B.; Zhang, T. SET domain-containing protein 5 enhances the cell stemness of non-small cell lung cancer via the PI3K/Akt/mTOR pathway. J. Environ. Pathol. Toxicol. Oncol. 2021, 40, 55–63. [Google Scholar] [CrossRef]
- Guo, F.; Guo, L.; Li, Y.; Zhou, Q.; Li, Z. MALAT1 is an oncogenic long non-coding RNA associated with tumor invasion in non-small cell lung cancer regulated by DNA methylation. Int. J. Clin. Exp. Pathol. 2015, 8, 15903. [Google Scholar]
- Xu, W.; Hang, M.; Yuan, C.Y.; Wu, F.L.; Chen, S.B.; Xue, K. MicroRNA-139-5p inhibits cell proliferation and invasion by targeting insulin-like growth factor 1 receptor in human non-small cell lung cancer. Int. J. Clin. Exp. Pathol. 2015, 8, 3864. [Google Scholar]
- Liu, J.; Liu, X. UBE2T silencing inhibited non-small cell lung cancer cell proliferation and invasion by suppressing the wnt/β-catenin signaling pathway. Int. J. Clin. Exp. Pathol. 2017, 10, 9482. [Google Scholar] [PubMed]
- Yanhua, L.I.; Suju, W.E.I.; Junyan, W.; Lei, H.; Lige, C.; Cai, W. Analysis of the factors associated with abnormal coagulation and prognosis in patients with non-small cell lung cancer. Zhongguo Fei Ai Za Zhi 2014, 17, 789–796. [Google Scholar]
- Owens, C.; Hindocha, S.; Lee, R.; Millard, T.; Sharma, B. The lung cancers: Staging and response, CT, 18F-FDG PET/CT, MRI, DWI: Review and new perspectives. Br. J. Radiol. 2023, 96, 20220339. [Google Scholar] [CrossRef]
- Bury, T.; Paulus, P.; Dowlati, A.; Millard, T.; Sharma, B. Staging of the mediastinum: Value of positron emission tomography imaging in non-small cell lung cancer. Eur. Respir. J. 1996, 9, 2560–2564. [Google Scholar] [CrossRef] [PubMed]
- Betancourt-Cuellar, S.L.; Carter, B.W.; Palacio, D.; Reasmus, J.J. Pitfalls and Limitations in Non–Small Cell Lung Cancer Staging[C]//Seminars in Roentgenology. WB Saunders 2015, 50, 175–182. [Google Scholar]
- Chen, D.; She, Y.; Wang, T.; Xie, H.; Li, J.; Jiang, G.; Chen, Y.; Zhang, L.; Xie, D.; Chen, C. Radiomics-based prediction for tumour spread through air spaces in stage I lung adenocarcinoma using machine learning. Eur. J. Cardio-Thorac. Surg. 2020, 58, 51–58. [Google Scholar] [CrossRef]
- Gu, Y.; She, Y.; Xie, D.; Dai, C.; Ren, Y.; Fan, Z.; Zhu, H.; Sun, X.; Xie, H.; Jiang, G.; et al. A texture analysis–based prediction model for lymph node metastasis in stage IA lung adenocarcinoma. Ann. Thorac. Surg. 2018, 106, 214–220. [Google Scholar] [CrossRef]
- Parmar, C.; Leijenaar, R.T.H.; Grossmann, P.; Velazquez, E.R.; Bussink, J.; Rietveld, D.; Rietbergen, M.M.; Haibe-Kains, B.; Lambin, P.; Aerts, H.J.W.L. Radiomic feature clusters and prognostic signatures specific for lung and head & neck cancer. Sci. Rep. 2015, 5, 11044. [Google Scholar]
- Parmar, C.; Grossmann, P.; Bussink, J.; Lambin, P.; Aerts, H.J.W.L. Machine learning methods for quantitative radiomic biomarkers. Sci. Rep. 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Janik, A.; Torrente, M.; Costabello, L.; Calvo, V.; Walsh, B.; Camps, C.; Mohamed, S.; Ortega, A.; Novacek, V.; Massuti, B.; et al. Machine learning–assisted recurrence prediction for patients with early-stage non–small-cell lung cancer. JCO Clin. Cancer Inform. 2023, 7, e2200062. [Google Scholar] [CrossRef]
- Moon, S.; Choi, D.; Lee, J.Y.; Kim, M.H.; Hong, H.; Kim, B.S.; Choi, J.H. Machine learning-powered prediction of recurrence in patients with non-small cell lung cancer using quantitative clinical and radiomic biomarkers. In Proceedings of the Medical Imaging 2020: Computer-Aided Diagnosis, Houston, TX, USA, 16–19 February 2020; Volume 11314, pp. 220–227. [Google Scholar]
- Kim, C.H.; Lee, H.Y.; Kim, H.K.; Choi, J.Y. P2. 01-56 Metastases in Residual PET Uptake of Lymph Nodes After Treatment: Added Value of CT Radiomic Approach for Prediction. J. Thorac. Oncol. 2018, 13, S686. [Google Scholar]
- Ji, G.W.; Zhang, Y.D.; Zhang, H.; Zhu, F.P.; Wang, K.; Xia, Y.X.; Zhang, Y.D.; Jiang, W.J.; Li, X.C.; Wang, X.H. Biliary tract cancer at CT: A radiomics-based model to predict lymph node metastasis and survival outcomes. Radiology 2019, 290, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Cong, M.; Feng, H.; Ren, J.L.; Xu, Q.; Cong, L.; Hou, Z.; Wang, Y.; Shi, G. Development of a predictive radiomics model for lymph node metastases in pre-surgical CT-based stage IA non-small cell lung cancer. Lung Cancer 2020, 139, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.L.; Li, M.M.; Xue, T.; Peng, H.; Shi, J.; Li, Y.Y.; Duan, S.F.; Feng, F. Radiomics nomogram integrating intratumoural and peritumoural features to predict lymph node metastasis and prognosis in clinical stage IA non-small cell lung cancer: A two-centre study. Clin Radiol. 2023, 78, e359–e367. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Z.; Li, Y.; Chen, Z.; Lu, P.; Wang, W.; Liu, W.; Yu, L. Comparison of machine learning methods for classifying mediastinal lymph node metastasis of non-small cell lung cancer from 18 F-FDG PET/CT images. EJNMMI Res. 2017, 7, 11. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, M.; Guo, Q.; Chen, J.; Wang, S.; Liu, S.; Xiao, F. Predicting N2 lymph node metastasis in presurgical stage I-II non-small cell lung cancer using multiview radiomics and deep learning method. Med. Phys. 2023, 50, 2049–2060. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; She, Y.; Deng, J.; Chen, S.; Wang, T.; Yang, M.; Ma, M.; Song, Y.; Qi, H.; Wang, Y.; et al. Deep learning for prediction of N2 metastasis and survival for clinical stage I non–small cell lung cancer. Radiology 2022, 302, 200–211. [Google Scholar] [CrossRef]
- Ouyang, M.; Zheng, R.; Wang, Y.; Zuo, Z.; Gu, L.; Tian, Y.; Wei, Y.; Huang, X.; Tang, K.; Wang, L. Deep learning analysis using 18F-FDG PET/CT to predict occult lymph node metastasis in patients with clinical N0 lung adenocarcinoma. Front. Oncol. 2022, 12, 915871. [Google Scholar] [CrossRef] [PubMed]
- Sibille, L.; Seifert, R.; Avramovic, N.; Vehren, T.; Spottiswoode, B.; Zuehlsdorff, S.; Schäfers, M. 18F-FDG PET/CT uptake classification in lymphoma and lung cancer by using deep convolutional neural networks. Radiology 2020, 294, 445–452. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Xia, W.; Li, Q.; Zhou, L.; Li, Q.; Zhang, R.; Cai, J.; Jian, J.; Fan, L.; et al. A cross-modal 3D deep learning for accurate lymph node metastasis prediction in clinical stage T1 lung adenocarcinoma. Lung Cancer 2020, 145, 10–17. [Google Scholar] [CrossRef]
- Tau, N.; Stundzia, A.; Yasufuku, K.; Hussey, D.; Metser, U. Convolutional neural networks in predicting nodal and distant metastatic potential of newly diagnosed non–small cell lung cancer on FDG PET images. Am. J. Roentgenol. 2020, 215, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Mu, J.; Kuang, K.; Ao, M.; Li, W.; Dai, H.; Ouyang, Z.; Li, J.; Huang, J.; Guo, S.; Yang, J.; et al. Deep learning predicts malignancy and metastasis of solid pulmonary nodules from CT scans. Front. Med. 2023, 10, 1145846. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.; Deng, J.; Hui, E.S.; She, Y.; Chen, C.; Vardhanabhuti, V. Early stage NSCLS patients’ prognostic prediction with multi-information using transformer and graph neural network model. Elife 2022, 11, e80547. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Kuang, H.; Wang, Y.; Wang, J. Hybrid CNN and Low-Complexity Transformer Network with Attention-Based Feature Fusion for Predicting Lung Cancer Tumor After Neoadjuvant Chemoimmunotherapy. In Proceedings of the International Symposium on Bioinformatics Research and Applications, Kunming, China, 19–21 July 2024; Springer Nature: Singapore, 2024; pp. 408–417. [Google Scholar]
- Kou, Y.; Xia, C.; Jiao, Y.; Zhang, D.; Ge, R. DACTransNet: A Hybrid CNN-Transformer Network for Histopathological Image Classification of Pancreatic Cancer. In Proceedings of the CAAI International Conference on Artificial Intelligence, Fuzhou, China, 22–23 July 2023; Springer Nature: Singapore, 2023; pp. 422–434. [Google Scholar]
- Morais, M.; Calisto, F.M.; Santiago, C.; Aleluia, C.; Nascimento, J.C. Classification of Breast Cancer in Mri with Multimodal Fusion. In Proceedings of the 2023 IEEE 20th International Symposium on Biomedical Imaging (ISBI), Cartagena, Colombia, 18–21 April 2023. [Google Scholar]
- Ramezani, H.; Aleman, D.; Létourneau, D. Lung-DETR: Deformable Detection Transformer for Sparse Lung Nodule Anomaly Detection. arXiv 2024, arXiv:2409.05200. [Google Scholar]
- Lin, J.A.; Cheng, Y.C.; Lin, C.K. Towards Enhanced Analysis of Lung Cancer Lesions in EBUS-TBNA-A Semi-Supervised Video Object Detection Method. arXiv 2024, arXiv:2404.01929. [Google Scholar]
- Li, W.; Liu, T.; Feng, F.; Wang, H.; Sun, Y. BTSSPro: Prompt-Guided Multimodal Co-Learning for Breast Cancer Tumor Segmentation and Survival Prediction. IEEE J. Biomed. Health Inform. 2024. [CrossRef]
- Talib, L.F.; Amin, J.; Sharif, M.; Raza, M. Transformer-based semantic segmentation and CNN network for detection of histopathological lung cancer. Biomed. Signal Process. Control 2024, 92, 106106. [Google Scholar] [CrossRef]
- Aerts, H.J.W.L.; Wee, L.; Rios Velazquez, E.; Leijenaar, R.T.H.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; et al. Data from NSCLC-Radiomics (Version 4) [Data Set]; The Cancer Imaging Archive: Maastricht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Bakr, S.; Gevaert, O.; Echegaray, S.; Ayers, K.; Zhou, M.; Shafiq, M.; Zheng, H.; Zhang, W.; Leung, A.; Kadoch, M.; et al. Data for NSCLC Radiogenomics (Version 4) [Data Set]; The Cancer Imaging Archive: Palo Alto VA, USA, 2017. [Google Scholar] [CrossRef]
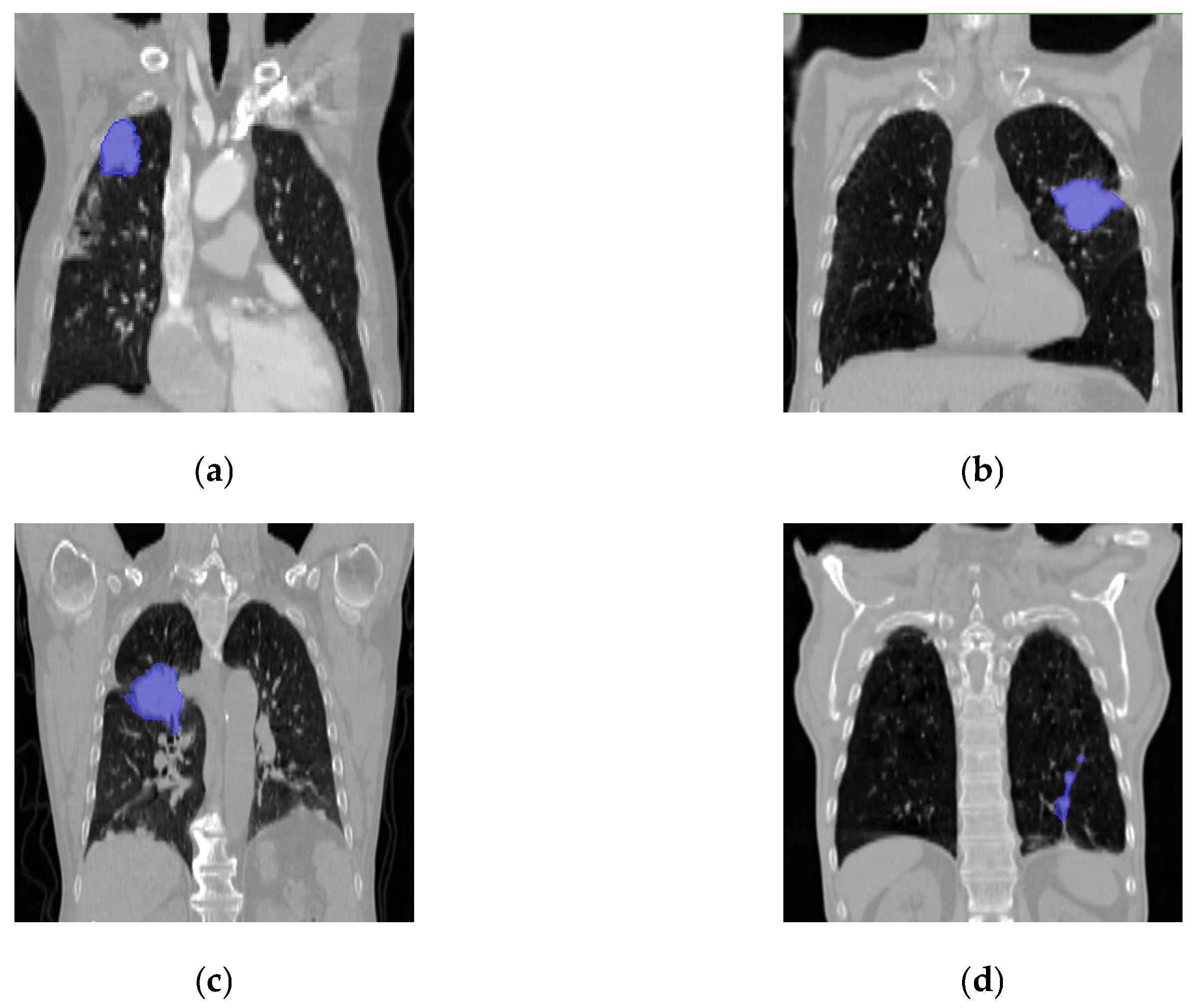

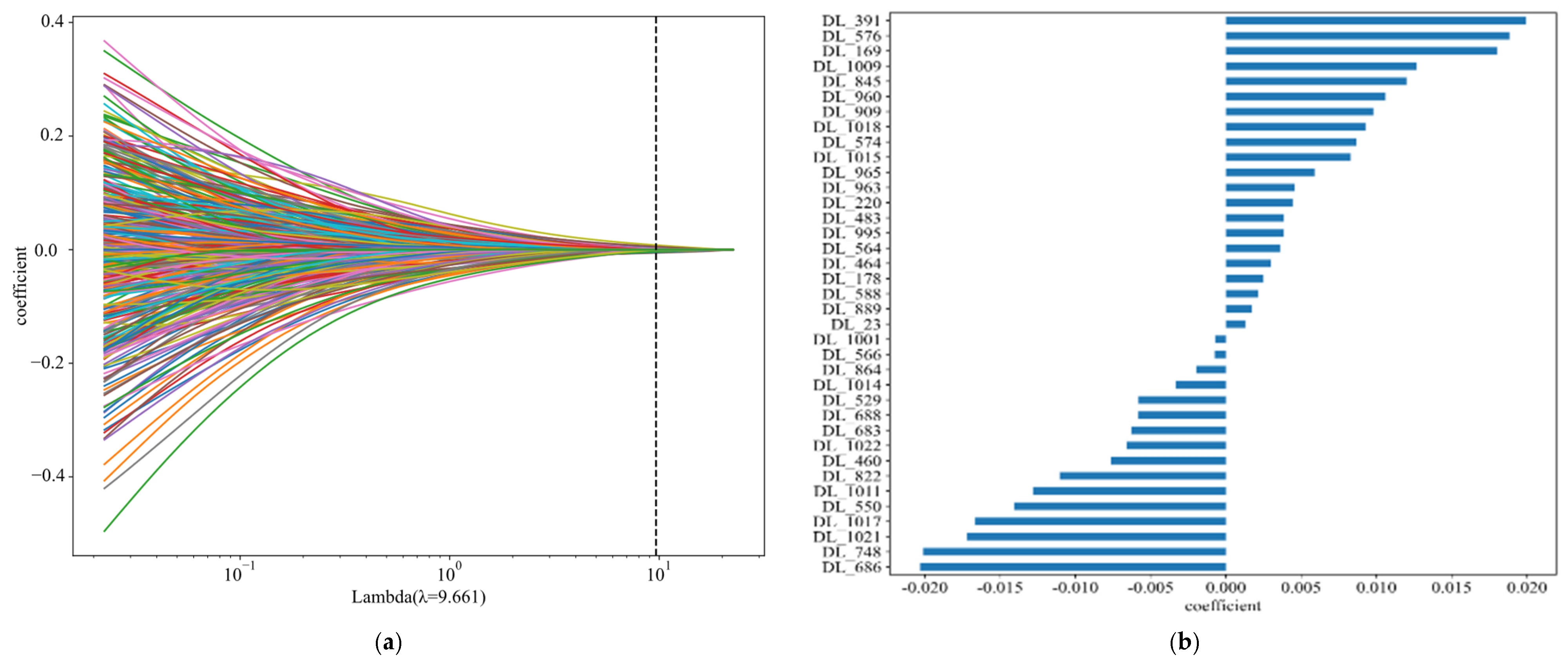
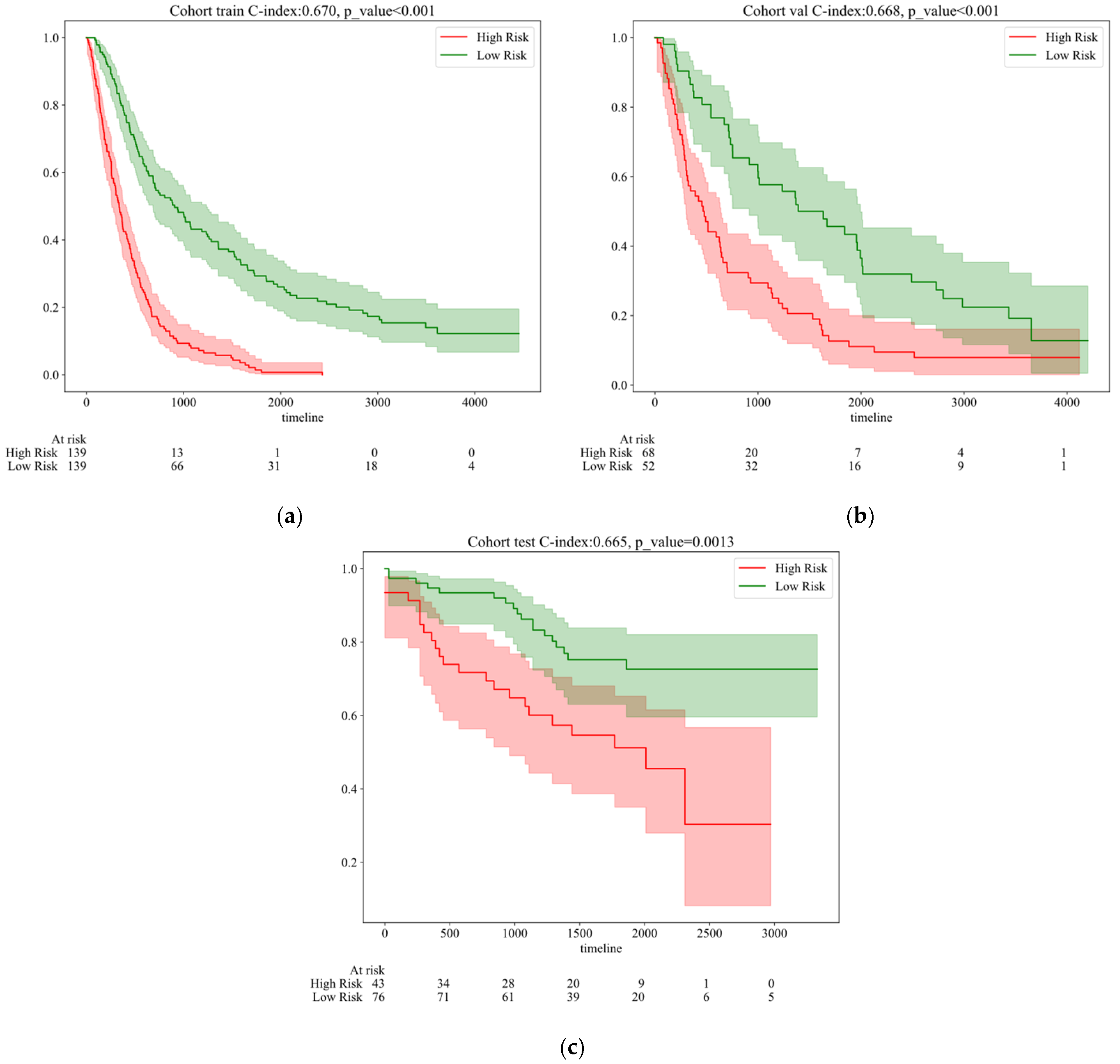

| Feature_Name | ALL | Train | Val | Test | p Value | |
|---|---|---|---|---|---|---|
| Age | 68.33 ± 9.63 | 67.89 ± 10.22 | 68.43 ± 9.24 | 69.23 ± 8.59 | 0.44 | |
| Gender | Female | 154 (29.62) | 90 (32.37) | 32 (26.67) | 32 (26.23) | 0.335 |
| Male | 366 (70.38) | 188 (67.63) | 88 (73.33) | 90 (73.77) | ||
| Model | Acc | Micro-AUC | 95% CI | Sensitivity | Specificity | Cohort |
|---|---|---|---|---|---|---|
| HCT | 0.805 | 0.837 | 0.788–0.845 | 0.757 | 0.817 | Train |
| HCT | 0.828 | 0.813 | 0.750–0.854 | 0.724 | 0.835 | Val |
| HCT | 0.819 | 0.816 | 0.771–0.860 | 0.693 | 0.881 | Test |
| DenseNet121 | 0.773 | 0.862 | 0.838–0.885 | 0.808 | 0.761 | Train |
| DenseNet121 | 0.745 | 0.741 | 0.629–0.753 | 0.613 | 0.710 | Val |
| DenseNet121 | 0.737 | 0.732 | 0.603–0.700 | 0.796 | 0.530 | Test |
| ResNet50 | 0.786 | 0.798 | 0.753–0.832 | 0.728 | 0.721 | Train |
| ResNet50 | 0.773 | 0.766 | 0.649–0.743 | 0.622 | 0.748 | Val |
| ResNet50 | 0.792 | 0.722 | 0.673–0.739 | 0.686 | 0.617 | Test |
| ShuffleNet | 0.713 | 0.784 | 0.754–0.814 | 0.746 | 0.702 | Train |
| ShuffleNet | 0.644 | 0.687 | 0.625–0.748 | 0.663 | 0.638 | Val |
| ShuffleNet | 0.734 | 0.637 | 0.584–0.691 | 0.543 | 0.848 | Test |
| VIT | 0.783 | 0.794 | 0.734–0.824 | 0.716 | 0.792 | Train |
| VIT | 0.764 | 0.767 | 0.695–0.778 | 0.673 | 0.818 | Val |
| VIT | 0.799 | 0.754 | 0.716–0.821 | 0.651 | 0.837 | Test |
| References | Number of Samples | Tasks | Methods | Metrics |
|---|---|---|---|---|
| [17] | 501 | Lymph node metastasis in T1N0M0 stage lung adenocarcinoma patients | Logistic | AUC: 0.808 |
| [18] | 422 | Staging status of non-small cell lung cancer patients | Clustering | AUC: 0.61 ± 0.01 |
| [28] | 140 | N2 lymph node status in stage I-II NSCLC patients | ResNet18 | AUC: 0.83 |
| [30] | 376 | Occult lymph node metastasis in cN0 adenocarcinoma patients | Inception V3 (2D) | AUC: 0.81 |
| [31] | 629 | Suspicious and non-suspicious states of lung cancer lesions | DenseNet | ACC: 0.981 |
| [33] | 264 | Distant metastasis status in NSCLC patients | DenseNet | AUC: 0.65 ± 0.05 |
| [34] | 689 | Malignancy degree of PNs in stage T1 lung cancer patients | ResNet18 | AUC: 0.8037 |
| Model Name | Acc | AUC | 95% CI | Sensitivity | Specificity | Cohort |
|---|---|---|---|---|---|---|
| HCT | 0.745 | 0.772 | 0.7156–0.8281 | 0.726 | 0.756 | train |
| HCT | 0.700 | 0.676 | 0.5711–0.7800 | 0.757 | 0.630 | val |
| HCT | 0.729 | 0.618 | 0.4401–0.7949 | 0.715 | 0.742 | test |
| Survival | Accuracy | AUC | 95% CI | Sensitivity | Specificity | Cohort |
|---|---|---|---|---|---|---|
| 1Y Survival | 0.773 | 0.707 | 0.6433–0.7702 | 0.745 | 0.831 | Train |
| 3Y Survival | 0.808 | 0.779 | 0.7216–0.8362 | 0.762 | 0.845 | Train |
| 5Y Survival | 0.823 | 0.821 | 0.7654–0.8765 | 0.768 | 0.946 | Train |
| 7Y Survival | 0.748 | 0.797 | 0.7337–0.8594 | 0.714 | 1.000 | Train |
| 1Y Survival | 0.763 | 0.749 | 0.6606–0.8373 | 0.758 | 0.806 | Val |
| 3Y Survival | 0.785 | 0.697 | 0.6041–0.7908 | 0.771 | 0.840 | Val |
| 5Y Survival | 0.796 | 0.727 | 0.6242–0.8298 | 0.790 | 0.814 | Val |
| 7Y Survival | 0.785 | 0.726 | 0.6102–0.8422 | 0.780 | 0.822 | Val |
| 1Y Survival | 0.767 | 0.710 | 0.5957–0.8242 | 0.756 | 0.805 | Test |
| 3Y Survival | 0.774 | 0.735 | 0.6379–0.8313 | 0.772 | 0.848 | Test |
| 5Y Survival | 0.759 | 0.663 | 0.5427–0.7826 | 0.766 | 0.795 | Test |
| 7Y Survival | 0.714 | 0.697 | 0.4498–0.9440 | 0.701 | 0.757 | Test |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, C.; Li, J. A Hybrid CNN-Transformer Model for Predicting N Staging and Survival in Non-Small Cell Lung Cancer Patients Based on CT-Scan. Tomography 2024, 10, 1676-1693. https://doi.org/10.3390/tomography10100123
Wang L, Zhang C, Li J. A Hybrid CNN-Transformer Model for Predicting N Staging and Survival in Non-Small Cell Lung Cancer Patients Based on CT-Scan. Tomography. 2024; 10(10):1676-1693. https://doi.org/10.3390/tomography10100123
Chicago/Turabian StyleWang, Lingfei, Chenghao Zhang, and Jin Li. 2024. "A Hybrid CNN-Transformer Model for Predicting N Staging and Survival in Non-Small Cell Lung Cancer Patients Based on CT-Scan" Tomography 10, no. 10: 1676-1693. https://doi.org/10.3390/tomography10100123
APA StyleWang, L., Zhang, C., & Li, J. (2024). A Hybrid CNN-Transformer Model for Predicting N Staging and Survival in Non-Small Cell Lung Cancer Patients Based on CT-Scan. Tomography, 10(10), 1676-1693. https://doi.org/10.3390/tomography10100123




