Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning
Abstract
1. Introduction
- Double adaptive weight strategy: In MIHHO, the convergence accuracy and speed of path planning are effectively improved by enhancing the global search capability in the exploration phase and strengthening the local search capability in the development phase.
- The Dimension Learning-Based Hunting (DLH) search strategy: By introducing the dimensional learning strategy, MIHHO can effectively balance global and local search capabilities and maintain the diversity of the population, thus enhancing the algorithm’s optimization ability.
- Position update strategy based on Dung Beetle Optimizer (DBO) algorithm: A position update strategy based on the DBO algorithm is proposed, which reduces the possibility of the algorithm falling into a local optimal solution in the path planning process.
- Performance test and analysis: The MIHHO algorithm significantly outperforms the other algorithms in terms of optimization-seeking ability, convergence speed, and stability through comparison experiments with 12 classical functions and the CEC2022 test function.
- Path planning experiments: The performance of the MIHHO algorithm was comprehensively evaluated through global path planning simulation experiments in simple and complex environments using the optimal value, mean, and standard deviation of the path length and the number of iterations. The experimental results show that the improved strategy exhibits significant advantages in terms of the solution accuracy, convergence speed, and avoidance of local optima.
2. The Path Planning Optimization Problem
2.1. Environmental Modeling
2.2. Constraints and Fitness Functions
- Map boundary and obstacle constraints:
- 2.
- Path continuity conditions
- 3.
- Path shortest condition
3. Harris Hawk Optimization Algorithm
3.1. Exploration Stage
3.2. Transition from Exploration to Exploitation
3.3. Exploitation Stage
4. Proposed Algorithm
4.1. Double Adaptive Weights Strategy
4.2. Dimension Learning-Based Hunting (DLH) Search Strategy
4.3. Position Update Strategy Based on Dung Beetle Optimizer Algorithm
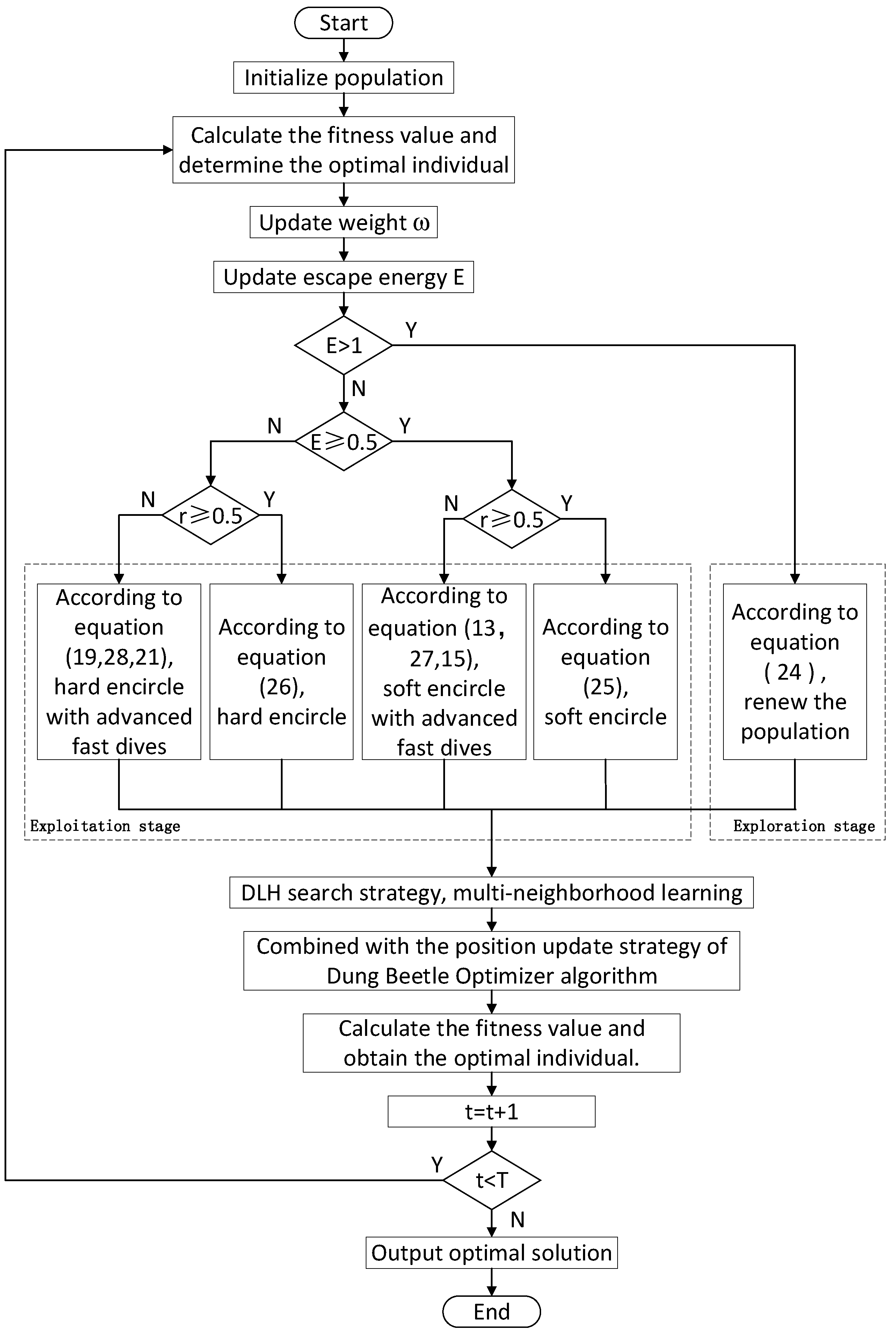
4.4. MIHHO Algorithm Flow
- Step 1: The basic parameters of the Harris hawk population are initialized, including the number of populations , the maximum number of iterations of the algorithm , and the starting position of all individuals in the solution space.
- Step 2: The iteration starts, the fitness value of all individuals in the population is obtained, and the best individual is obtained.
- Step 3: The double adaptive weight strategy (Equations (22) and (23)) is used to dynamically adjust the position of the Harris hawk to improve the search efficiency.
- Step 4: The Harris hawk population updates its position through different strategies. In the exploration phase, two strategies are used to detect prey based on the q-value (Equation (24)). In the exploitation phase, prey are attacked using different strategies based on their escape energy and escape probability, including soft besiege (Equation (25)), hard besiege (Equation (26)), soft besiege with progressive rapid dives (Equations (13), (15) and (27)), and hard besiege with progressive rapid dives (Equations (19), (21) and (28)).
- Step 5: Multi-neighborhood learning is performed according to the DLH search strategy (Equations (30)–(33)).
- Step 6: The fitness value of all individuals in the population is calculated, and the best and worst individuals are obtained.
- Step 7: According to the DBO’s solar ray navigation strategy (Equations (34) and (35)), the positions of individuals caught in localized extremes are updated.
- Step 8: The optimal individual position and fitness value so far are calculated.
- Step 9: The updated new population is returned, and it is determined whether the algorithm terminates. If there is no termination, the second step is followed to continue the execution.
- Step 10: The condition is terminated and the final optimal individual of the population and its fitness value are output.
4.5. Time Complexity Analysis
5. MIHHO Performance Test and Analysis
5.1. Solving the Classical Functions
5.2. Solving the CEC2022 Test Functions
5.3. Comparison with Other Authors Improving HHO
5.4. Ablation Experiment
6. The Application of MIHHO in Path Planning
6.1. Steps in the Path Planning Experiment
- Step 1: Set the initialization parameters. Set the robot start position , goal position , population number , and iteration number , and set the map boundary conditions and obstacle positions.
- Step 2: Initialize the population. Randomly generate paths from the starting point to the endpoint and detect whether they are within the map boundary.
- Step 3: Calculate the degree of adaptation. Evaluate the quality of each path using the objective function (Equation (5)) to determine the best path in the initialization.
- Step 4: Update the weights according to the double adaptive weight formula (Equations (22) and (23)) to improve the probability of finding the optimal path.
- Step 5: In the HHO for path optimization, two strategies are used in the exploration phase to detect the prey through the q-value (Equation (24)). In the exploitation phase, based on the prey’s escape energy and escape probability, different strategies are selected for attacking, including soft besiege (Equation (25)), hard besiege (Equation (26)), soft besiege with progressive rapid dives (Equations (13), (15) and (27)), and hard besiege with progressive rapid dives (Equations (19), (21) and (28)).
- Step 6: Perform multi-neighborhood learning according to the DLH search strategy (Equations (30)–(33)). By searching in different dimensions, the algorithm can find several different paths, increasing the likelihood of finding a better path.
- Step 7: Calculate the fitness values of all individuals of the population and obtain the optimal and worst paths.
- Step 8: Position update strategy based on DBO algorithm (Equations (34) and (35)), update the position of an individual caught in a local extreme to help it jump out of the local optimum and continue searching for a better solution.
- Step 9: Calculate the optimal path and fitness value so far.
- Step 10: Return the updated new population and determine whether the algorithm termination condition is reached; if not, then jump to the second step to continue execution.
- Step 11: Terminate the condition and output the final optimal path of the obtained population and its fitness value.
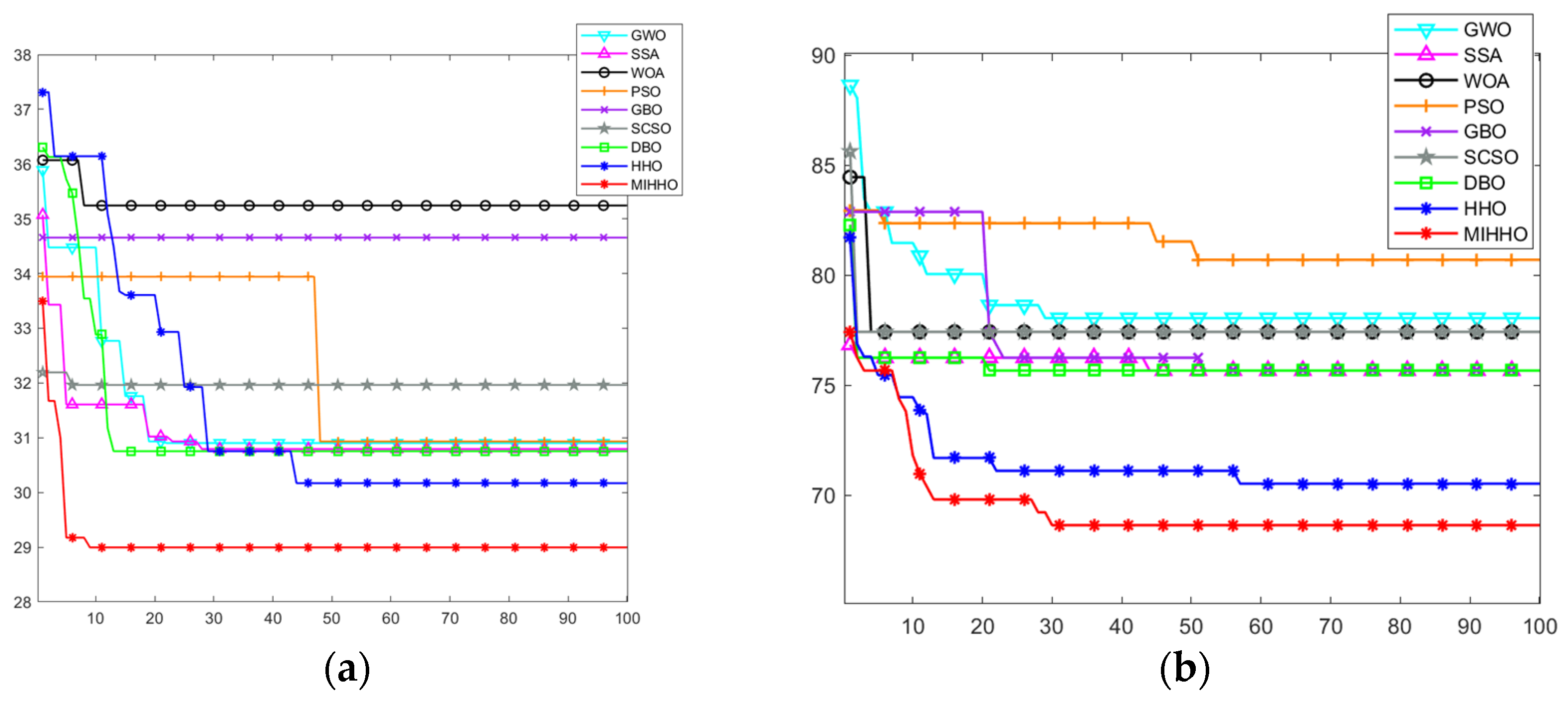
6.2. Analysis of Path Planning Experimental Results
6.2.1. Experimental Simulation in a Simple Environment
6.2.2. Experimental Simulation in Complex Environments
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, X.; Li, R.; Zhao, L.; Wang, K.; Gui, X. Multi-obstacle path planning and optimization for mobile robot. Expert Syst. Appl. 2021, 183, 115445. [Google Scholar] [CrossRef]
- Alshammrei, S.; Boubaker, S.; Kolsi, L. Improved Dijkstra algorithm for mobile robot path planning and obstacle avoidance. Comput. Mater. Contin. 2022, 72, 5939–5954. [Google Scholar] [CrossRef]
- Li, X.; Yu, S.; Gao, X.Z.; Yan, Y.; Zhao, Y. Path planning and obstacle avoidance control of UUV based on an enhanced A* algorithm and MPC in dynamic environment. Ocean Eng. 2024, 302, 117584. [Google Scholar] [CrossRef]
- Gu, X.; Liu, L.; Wang, L.; Yu, Z.; Guo, Y. Energy-optimal adaptive artificial potential field method for path planning of free-flying space robots. J. Frankl. Inst. 2024, 361, 978–993. [Google Scholar] [CrossRef]
- Kar, A.K. Bio inspired computing–a review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Tian, T.; Liang, Z.; Wei, Y.; Luo, Q.; Zhou, Y. Hybrid Whale Optimization with a Firefly Algorithm for Function Optimization and Mobile Robot Path Planning. Biomimetics 2024, 9, 39. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, N.; Wang, X.; Li, M. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst. Appl. 2023, 215, 119327. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Yong, H.; Mingran, W. An improved chaos sparrow search algorithm for UAV path planning. Sci. Rep. 2024, 14, 366. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Liu, C. An improved Harris hawks optimizer for job-shop scheduling problem. J. Supercomput. 2021, 77, 14090–14129. [Google Scholar] [CrossRef]
- Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Dynamic harris hawks optimization with mutation mechanism for satellite image segmentation. Remote Sens. 2019, 11, 1421. [Google Scholar] [CrossRef]
- Yousri, D.; Allam, D.; Eteiba, M.B. Optimal photovoltaic array reconfiguration for alleviating the partial shading influence based on a modified harris hawks optimizer. Energy Convers. Manag. 2020, 206, 112470. [Google Scholar] [CrossRef]
- Yousri, D.; Rezk, H.; Fathy, A. Identifying the parameters of different configurations of photovoltaic models based on recent artificial ecosystem-based optimization approach. Int. J. Energy Res. 2020, 44, 11302–11322. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Arashpour, M.; Behnood, A. Predicting the compressive strength of green concretes using Harris hawks optimization-based data-driven methods. Constr. Build. Mater. 2022, 318, 125944. [Google Scholar] [CrossRef]
- Belge, E.; Altan, A.; Hacıoğlu, R. Metaheuristic optimization-based path planning and tracking of quadcopter for payload hold-release mission. Electronics 2022, 11, 1208. [Google Scholar] [CrossRef]
- Cai, C.; Jia, C.; Nie, Y.; Zhang, J.; Li, L. A path planning method using modified harris hawks optimization algorithm for mobile robots. PeerJ Comput. Sci. 2023, 9, e1473. [Google Scholar] [CrossRef]
- Qu, C.; He, W.; Peng, X.; Peng, X. Harris hawks optimization with information exchange. Appl. Math. Model. 2020, 84, 52–75. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Zou, L.; Zhou, S.; Li, X. An efficient improved greedy Harris Hawks optimizer and its application to feature selection. Entropy 2022, 24, 1065. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, J.; Chen, H.; Jin, M.; Ren, H. Enhanced Harris hawks optimization with multi-strategy for global optimization tasks. Expert Syst. Appl. 2021, 185, 115499. [Google Scholar] [CrossRef]
- Hussain, K.; Neggaz, N.; Zhu, W.; Houssein, E.H. An efficient hybrid sine-cosine Harris hawks optimization for low and high-dimensional feature selection. Expert Syst. Appl. 2021, 176, 114778. [Google Scholar] [CrossRef]
- Li, S.; Zhang, R.; Ding, Y.; Qin, X.; Han, Y.; Zhang, H. Multi-UAV Path Planning Algorithm Based on BINN-HHO. Sensors 2022, 22, 9786. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Fu, Q.; Tong, N. An improved Harris hawks optimization algorithm and its application in grid map path planning. Biomimetics 2023, 8, 428. [Google Scholar] [CrossRef]
- Nasr, A.A. A new cloud autonomous system as a service for multi-mobile robots. Neural Comput. Appl. 2022, 34, 21223–21235. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-based chaotic harris hawks optimizer: Algorithm and internet of vehicles application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Lou, T.S.; Yue, Z.P.; Jiao, Y.Z.; He, Z.D. A hybrid strategy-based GJO algorithm for robot path planning. Expert Syst. Appl. 2024, 238, 121975. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Xue, J.; Bo, S. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Andrew, L. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Russell, E. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA; Volume 4. [Google Scholar]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Jiang, S.; Yue, Y.; Chen, C.; Chen, Y.; Cao, L. A multi-objective optimization problem solving method based on improved golden jackal optimization algorithm and its application. Biomimetics 2024, 9, 270. [Google Scholar] [CrossRef] [PubMed]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Pfannkuch, M. Comparing box plot distributions: A teacher’s reasoning. Stat. Educ. Res. J. 2006, 5, 27–45. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Chakrabortty, R.K. Light spectrum optimizer: A novel physics-inspired metaheuristic optimization algorithm. Mathematics 2022, 10, 3466. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Wunnava, A.; Jena, B.; Abraham, A. A leader Harris hawks optimization for 2-D Masi entropy-based multilevel image thresholding. Multimed. Tools Appl. 2021, 80, 35543–35583. [Google Scholar] [CrossRef]
- Hussain, K.; Zhu, W.; Salleh, M.N.M. Long-term memory Harris’ hawk optimization for high dimensional and optimal power flow problems. IEEE Access 2019, 7, 147596–147616. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]












| Type | Function | Dim | Global Optima |
|---|---|---|---|
| Unimodal function | 30 | 0 | |
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| Multimodal function | 30 | −418.9829 × Dim | |
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| Fixed-dimension multimodal function | 2 | 1 | |
| 4 | −10.1532 | ||
| 4 | −10.4028 | ||
| 4 | −10.5363 |
| Functions | Index | GWO | SSA | WOA | PSO | GBO | SCSO | DBO | HHO | MIHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 3.9079 × 10−30 | 0 | 7.9517 × 10−87 | 0.00063606 | 3.1733 × 10−128 | 3.0221 × 10−125 | 1.6001 × 10−167 | 3.0379 × 10−113 | 0 |
| Mean | 8.8865 × 10−28 | 2.641 × 10−54 | 1.6 × 10−73 | 0.017306 | 1.8033 × 10−116 | 2.257 × 10−112 | 1.4317 × 10−101 | 1.2927 × 10−91 | 0 | |
| Std | 1.0723 × 10−27 | 1.4466 × 10−53 | 7.1291 × 10−73 | 0.034734 | 8.7403 × 10−116 | 1.1837 × 10−111 | 7.8418 × 10−101 | 7.0796 × 10−91 | 0 | |
| F2 | Best | 1.2306 × 10−8 | 1.4022 × 10−92 | 21,136.148 | 836.2801 | 1.9012 × 10−108 | 6.0921 × 10−112 | 1.8658 × 10−160 | 1.3875 × 10−98 | 0 |
| Mean | 2.8545 × 10−5 | 5.1396 × 10−27 | 43,441.7047 | 2252.6295 | 7.9774 × 10−93 | 2.5836 × 10−97 | 3.9476 × 10−78 | 2.3464 × 10−71 | 0 | |
| Std | 9.7623 × 10−5 | 2.6469 × 10−26 | 14,283.7721 | 1888.0826 | 3.8353 × 10−92 | 1.4119 × 10−96 | 2.1622 × 10−77 | 1.2415 × 10−70 | 0 | |
| F3 | Best | 5.0592 × 10−8 | 1.2812 × 10−119 | 0.00020182 | 4.4928 | 8.7515 × 10−61 | 6.9719 × 10−57 | 4.3432 × 10−78 | 1.0308 × 10−55 | 0 |
| Mean | 8.3153 × 10−7 | 4.3847 × 10−29 | 54.7644 | 6.8881 | 9.5192 × 10−54 | 2.4293 × 10−50 | 8.0166 × 10−43 | 4.9189 × 10−48 | 0 | |
| Std | 5.3132 × 10−7 | 2.0033 × 10−28 | 27.7913 | 1.652 | 3.7547 × 10−53 | 1.1926 × 10−49 | 4.3909 × 10−42 | 2.4996 × 10−47 | 0 | |
| F4 | Best | 0.00076823 | 0.00012883 | 0.00015767 | 0.023535 | 1.5371 × 10−5 | 2.8588 × 10−6 | 0.00017808 | 9.2355 × 10−7 | 7.6663 × 10−7 |
| Mean | 0.0023435 | 0.0015127 | 0.0022641 | 0.050177 | 0.00075366 | 0.00016184 | 0.0010493 | 0.00017823 | 4.1231 × 10−5 | |
| Std | 0.001236 | 0.001253 | 0.0023919 | 0.020627 | 0.00048108 | 0.00030857 | 0.00078951 | 0.00018419 | 6.5041 × 10−5 | |
| F5 | Best | −7188.2016 | −9445.9825 | −12,567.2869 | −10,062.4719 | −11,331.6109 | −8739.4336 | −12,569.4866 | −12,569.4866 | −12,569.4866 |
| Mean | −6047.4534 | −8616.5616 | −9923.8706 | −8457.1427 | −9141.0372 | −6779.157 | −12,561.848 | −12,553.3976 | −12,569.4241 | |
| Std | 753.6649 | 510.1863 | 1719.7314 | 717.7575 | 1007.4905 | 782.0046 | 39.5743 | 57.1789 | 0.11163 | |
| F6 | Best | 5.6843 × 10−14 | 0 | 0 | 33.8536 | 0 | 0 | 0 | 0 | 0 |
| Mean | 2.464 | 0 | 5.1567 | 60.6847 | 0 | 0 | 0 | 0 | 0 | |
| Std | 3.9927 | 0 | 28.2444 | 20.048 | 0 | 0 | 0 | 0 | 0 | |
| F7 | Best | 6.839 × 10−14 | 8.8818 × 10−16 | 8.8818 × 10−16 | 0.012108 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 |
| Mean | 9.7759 × 10−14 | 8.8818 × 10−16 | 4.3225 × 10−15 | 0.78959 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| Std | 1.7303 × 10−14 | 0 | 2.5523 × 10−15 | 0.7778 | 0 | 0 | 0 | 0 | 0 | |
| F8 | Best | 0 | 0 | 0 | 0.0019214 | 0 | 0 | 0 | 0 | 0 |
| Mean | 0.0054766 | 0 | 3.700 × 10−18 | 0.033218 | 0 | 0 | 0.00057474 | 0 | 0 | |
| Std | 0.0097153 | 0 | 2.027 × 10−17 | 0.028653 | 0 | 0 | 0.003148 | 0 | 0 | |
| F9 | Best | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| Mean | 5.0138 | 4.4439 | 2.9319 | 0.998 | 1.0311 | 3.5514 | 1.4558 | 1.6249 | 0.998 | |
| Std | 4.2031 | 4.9767 | 2.9653 | 7.1417 × 10−17 | 0.18148 | 3.4054 | 1.8284 | 1.2557 | 3.4985 × 10−11 | |
| F10 | Best | −10.1531 | −10.1532 | −10.1526 | −10.1532 | −10.1532 | −10.1532 | −10.1532 | −10.0896 | −10.1529 |
| Mean | −9.3149 | −7.9441 | −8.6934 | −6.5652 | −8.4539 | −5.7364 | −7.7898 | −5.1382 | −10.1479 | |
| Std | 2.2163 | 2.5694 | 2.4565 | 3.5141 | 2.4443 | 1.762 | 2.5662 | 1.0359 | 0.0046385 | |
| F11 | Best | −10.4024 | −10.4029 | −10.4012 | −10.4029 | −10.4029 | −10.4029 | −10.4029 | −10.2685 | −10.4026 |
| Mean | −10.4011 | −8.6312 | −7.1244 | −8.5207 | −8.4086 | −6.1973 | −8.2877 | −5.594 | −10.3967 | |
| Std | 0.0011786 | 2.5485 | 2.9416 | 3.2195 | 2.6768 | 2.6959 | 2.6305 | 1.5557 | 0.0061323 | |
| F12 | Best | −10.5362 | −10.5364 | −10.5349 | −10.5364 | −10.5364 | −10.5364 | −10.5364 | −5.1285 | −10.5363 |
| Mean | −10.2639 | −8.7338 | −6.2514 | −8.2255 | −7.7551 | −6.9006 | −8.0298 | −5.122 | −10.5312 | |
| Std | 1.4812 | 2.5929 | 3.1803 | 3.4083 | 2.8594 | 2.8879 | 2.7245 | 0.0096613 | 0.0054868 | |
| Estimation | Mean | 5.08 | 4.33 | 5.42 | 5.83 | 3 | 4.17 | 3.75 | 4.5 | 1.08 |
| Rank | 7 | 5 | 8 | 9 | 2 | 4 | 3 | 6 | 1 |
| Functions | GWO | SSA | WOA | PSO | GBO | SCSO | DBO | HHO |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.2118 × 10−12 | 4.5736 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F2 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F3 | 1.2118 × 10−12 | 4.5736 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F4 | 3.0199 × 10−11 | 8.891 × 10−10 | 3.4742 × 10−10 | 3.0199 × 10−11 | 4.1997 × 10−10 | 0.00055611 | 8.1014 × 10−10 | 0.00076973 |
| F5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8682 × 10−5 |
| F6 | 4.5164 × 10−12 | NaN | NaN | 1.2118 × 10−12 | NaN | NaN | 0.33371 | NaN |
| F7 | 1.1359 × 10−12 | NaN | 1.1585 × 10−8 | 1.2118 × 10−12 | NaN | NaN | NaN | NaN |
| F6 | 0.0055843 | NaN | 0.1608 | 1.2118 × 10−12 | NaN | NaN | NaN | NaN |
| F8 | 4.9752 × 10−11 | 0.075607 | 1.7769 × 10−10 | 6.3188 × 10−12 | 5.1812 × 10−12 | 2.1959 × 10−7 | 8.6748 × 10−6 | 2.0338 × 10−9 |
| F9 | 7.6588 × 10−5 | 0.0072169 | 1.3853 × 10−6 | 0.0078403 | 0.0075506 | 8.4848 × 10−9 | 1.7273 × 10−5 | 3.0199 × 10−11 |
| F10 | 4.9426 × 10−5 | 0.025536 | 3.5201 × 10−7 | 0.0015453 | 0.000267 | 9.5139 × 10−6 | 7.6152 × 10−5 | 3.0199 × 10−11 |
| F11 | 0.00022539 | 5.3435 × 10−5 | 1.85 × 10−8 | 0.0074461 | 0.0075566 | 6.765 × 10−5 | 0.0039086 | 3.0199 × 10−11 |
| F12 | 1.2118 × 10−12 | 4.5736 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| +/=/− | 12/0/0 | 8/3/1 | 10/1/1 | 12/0/0 | 9/3/0 | 9/3/0 | 9/2/1 | 9/3/0 |
| Type | Function | Descriptive | Global Optima |
|---|---|---|---|
| UF | F13(CEC1) | Shifted and Full Rotated Zakharov Function | 300 |
| BF | F14(CEC2) | Shifted and Full Rotated Rosenbrock’s Function | 400 |
| F15(CEC3) | Shifted and Full Rotated Expanded Schaffer’s f6 | 600 | |
| F16(CEC4) | Shifted and Full Rotated Non-Continuous Rastrigin’s Function | 800 | |
| F17(CEC5) | Shifted and Full Rotated Levy Function | 900 | |
| HF | F18(CEC6) | Hybrid Function 1 (N = 3) | 1800 |
| F19(CEC7) | Hybrid Function 2 (N = 6) | 2000 | |
| F20(CEC8) | Hybrid Function 3 (N = 5) | 2200 | |
| CF | F21(CEC9) | Composition Function 1 (N = 5) | 2300 |
| F22(CEC10) | Composition Function 2 (N = 4) | 2400 | |
| F23(CEC11) | Composition Function 3 (N = 5) | 2600 | |
| F24(CEC12) | Composition Function 4 (N = 6) | 2700 |
| Function | Index | GWO | SSA | WOA | PSO | GBO | SCSO | DBO | HHO | MIHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| F13 | Best | 339.7353 | 300 | 12,561.1581 | 300 | 300 | 418.1413 | 300.8018 | 358.61 | 300 |
| Mean | 2576.2897 | 303.0602 | 30,798.4928 | 300.0367 | 300.0183 | 3289.2294 | 2138.4791 | 1086.4727 | 300.0177 | |
| Std | 2333.0803 | 10.8327 | 14,457.3781 | 0.15351 | 0.22764 | 2151.6108 | 1964.0605 | 493.6898 | 0.0039427 | |
| F14 | Best | 404.1306 | 400.0093 | 404.4626 | 400.3851 | 400.1968 | 402.1813 | 404.9318 | 400.2839 | 400.0019 |
| Mean | 435.4307 | 412.865 | 467.277 | 436.4721 | 408.6839 | 431.3265 | 439.2044 | 463.4548 | 408.0651 | |
| Std | 26.413 | 23.3158 | 88.2943 | 66.9228 | 24.9756 | 28.6752 | 56.23 | 62.5455 | 12.6514 | |
| F15 | Best | 600.0776 | 600.0004 | 620.7523 | 600 | 600.0028 | 603.4417 | 601.9854 | 622.115 | 600.1547 |
| Mean | 601.8192 | 604.5389 | 639.8656 | 600.4853 | 600.86 | 617.4314 | 613.2101 | 640.0181 | 602.1263 | |
| Std | 4.5103 | 8.6267 | 13.0016 | 1.0975 | 1.289 | 11.6609 | 8.589 | 11.4329 | 0.97759 | |
| F16 | Best | 806.6137 | 806.9647 | 812.4975 | 803.9798 | 808.9546 | 807.6149 | 807.9637 | 815.1933 | 809.9519 |
| Mean | 815.9944 | 828.9864 | 839.6426 | 815.8086 | 822.6187 | 828.1278 | 832.8943 | 826.6859 | 833.3066 | |
| Std | 7.7395 | 9.968 | 17.0224 | 8.1472 | 10.5987 | 8.5899 | 13.6251 | 6.5979 | 8.9145 | |
| F17 | Best | 900.25 | 936.3489 | 1075.8395 | 900 | 900 | 906.5558 | 906.9326 | 1204.7792 | 943.4538 |
| Mean | 943.3298 | 1388.5225 | 1596.4899 | 900.4999 | 915.3015 | 1148.2269 | 1023.872 | 1462.7634 | 1319.221 | |
| Std | 86.2365 | 177.0459 | 480.2666 | 0.7359 | 26.8651 | 183.5889 | 140.3544 | 141.8046 | 184.9728 | |
| F18 | Best | 2676.966 | 1909.9082 | 2207.2638 | 1890.7644 | 1831.8326 | 2157.598 | 1996.5885 | 2365.7332 | 1874.7405 |
| Mean | 6728.5109 | 4198.761 | 5769.3454 | 5313.3755 | 3430.7368 | 5323.3402 | 5593.4363 | 7545.2141 | 3183.9722 | |
| Std | 2217.4785 | 1545.6812 | 2891.1287 | 2227.0454 | 1923.2512 | 1990.6186 | 2590.603 | 6485.6816 | 1758.3396 | |
| F19 | Best | 2021.9415 | 2005.5998 | 2046.625 | 2000.6243 | 2005.5649 | 2022.2196 | 2022.0505 | 2040.2114 | 2001.328 |
| Mean | 2031.741 | 2033.3058 | 2082.5441 | 2019.0671 | 2023.298 | 2043.1307 | 2045.0321 | 2090.901 | 2020.5375 | |
| Std | 7.1208 | 26.1242 | 27.3671 | 8.0415 | 8.4338 | 17.1861 | 30.7455 | 34.6306 | 6.2211 | |
| F20 | Best | 2207.6728 | 2220.1155 | 2226.4034 | 2200.8093 | 2206.2251 | 2221.6339 | 2221.6866 | 2223.7919 | 2204.9731 |
| Mean | 2241.2538 | 2233.7783 | 2237.3402 | 2254.3118 | 2224.2991 | 2227.9122 | 2232.9896 | 2237.8373 | 2220.9942 | |
| Std | 40.2969 | 36.4304 | 11.0016 | 55.3187 | 4.3037 | 3.8658 | 20.9083 | 9.0343 | 3.1009 | |
| F21 | Best | 2529.3391 | 2529.2844 | 2551.0113 | 2529.2844 | 2529.2844 | 2529.2989 | 2529.2844 | 2543.0909 | 2529.2863 |
| Mean | 2579.7157 | 2548.8938 | 2624.5304 | 2535.7198 | 2529.2844 | 2573.3561 | 2563.494 | 2621.089 | 2534.1854 | |
| Std | 37.2357 | 50.7938 | 50.8682 | 27.016 | 4.3879 × 10−13 | 30.7537 | 52.0602 | 38.9846 | 26.8255 | |
| F22 | Best | 2500.3161 | 2500.2153 | 2500.7107 | 2500.3665 | 2500.3319 | 2500.3769 | 2500.5935 | 2500.5952 | 2500.3736 |
| Mean | 2597.1597 | 2642.1248 | 2770.7768 | 2583.4666 | 2558.2117 | 2565.6277 | 2555.9037 | 2697.673 | 2533.1447 | |
| Std | 136.8643 | 209.9238 | 424.5043 | 79.5016 | 62.8245 | 66.5665 | 68.7745 | 303.6366 | 74.2088 | |
| F23 | Best | 2603.886 | 2600 | 2737.3267 | 2600 | 2600 | 2606.164 | 2600 | 2611.1604 | 2600 |
| Mean | 3005.905 | 2816.3805 | 3039.2047 | 2783.5197 | 2826.79 | 2899.8734 | 2771.6167 | 2866.442 | 2727.1559 | |
| Std | 168.7909 | 135.5907 | 338.7632 | 131.4767 | 129.7348 | 178.8386 | 111.1563 | 155.1139 | 127.0772 | |
| F24 | Best | 2863.5019 | 2862.5674 | 2870.2711 | 2862.4421 | 2861.4049 | 2863.7479 | 2863.6612 | 2868.8918 | 2859.6596 |
| Mean | 2873.0944 | 2880.9625 | 2915.3618 | 2874.3854 | 2871.5042 | 2873.5491 | 2882.3811 | 2944.4871 | 2872.7128 | |
| Std | 13.1856 | 31.5485 | 46.1435 | 16.813 | 20.0176 | 11.2892 | 24.5016 | 56.6887 | 12.0736 | |
| Estimation | Mean | 4.92 | 4.92 | 8.33 | 3.5 | 2.33 | 5.33 | 5.25 | 7.5 | 2.5 |
| Rank | 4 | 4 | 9 | 3 | 1 | 7 | 6 | 8 | 2 |
| Function | GWO | SSA | WOA | PSO | GBO | SCSO | DBO | HHO |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.2118 × 10−12 | 4.5736 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F2 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F3 | 1.2118 × 10−12 | 4.5736 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| F4 | 3.0199 × 10−11 | 8.891 × 10−10 | 3.4742 × 10−10 | 3.0199 × 10−11 | 4.1997 × 10−10 | 0.00055611 | 8.1014 × 10−10 | 0.00076973 |
| F5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8682 × 10−5 |
| F6 | 4.5164 × 10−12 | NaN | NaN | 1.2118 × 10−12 | NaN | NaN | 0.33371 | NaN |
| F7 | 1.1359 × 10−12 | NaN | 1.1585 × 10−8 | 1.2118 × 10−12 | NaN | NaN | NaN | NaN |
| F6 | 0.0055843 | NaN | 0.1608 | 1.2118 × 10−12 | NaN | NaN | NaN | NaN |
| F8 | 4.9752 × 10−11 | 0.075607 | 1.7769 × 10−10 | 6.3188 × 10−12 | 5.1812 × 10−12 | 2.1959 × 10−7 | 8.6748 × 10−6 | 2.0338 × 10−9 |
| F9 | 7.6588 × 10−5 | 0.0072169 | 1.385 × 10−6 | 0.0078403 | 0.0075506 | 8.4848 × 10−9 | 1.7273 × 10−5 | 3.0199 × 10−11 |
| F10 | 4.9426 × 10−5 | 0.025536 | 3.5201 × 10−7 | 0.0015453 | 0.000267 | 9.5139 × 10−6 | 7.6152 × 10−5 | 3.0199 × 10−11 |
| F11 | 0.00022539 | 5.3435 × 10−5 | 1.85 × 10−8 | 0.0074461 | 0.0075566 | 6.765 × 10−5 | 0.0039086 | 3.0199 × 10−11 |
| F12 | 1.2118 × 10−12 | 4.5736 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 | 1.2118 × 10−12 |
| +/=/− | 12/0/0 | 8/3/1 | 10/1/1 | 12/0/0 | 9/3/0 | 9/3/0 | 9/2/1 | 9/3/0 |
| Function | Index | NCHHO | LHHO | LMHHO | MIHHO |
|---|---|---|---|---|---|
| F1 | Best | 4.3835 × 10−239 | 8.3093 × 10−166 | 0 | 0 |
| Mean | 2.1917 × 10−240 | 2.8468 × 10−145 | 0 | 0 | |
| Std | 0 | 9.8053 × 10−145 | 0 | 0 | |
| F2 | Best | 2.1941 × 10−249 | 6.6287 × 10−135 | 0 | 0 |
| Mean | 1.8669 × 10−214 | 1.2616 × 10−100 | 0 | 0 | |
| Std | 0 | 6.8972 × 10−100 | 0 | 0 | |
| F3 | Best | 8.0046 × 10−131 | 1.6516 × 10−82 | 1.849 × 10−249 | 0 |
| Mean | 5.6251 × 10−119 | 8.8838 × 10−71 | 2.316 × 10−236 | 0 | |
| Std | 2.3441 × 10−118 | 4.7576 × 10−70 | 0 | 0 | |
| F4 | Best | 1.0575 × 10−7 | 9.3114 × 10−6 | 4.037 × 10−7 | 1.0246 × 10−6 |
| Mean | 0.0001236 | 9.2186 × 10−5 | 9.3295 × 10−5 | 1.8966 × 10−5 | |
| Std | 9.911 × 10−5 | 5.3666 × 10−5 | 9.2981 × 10−5 | 1.6225 × 10−5 | |
| F5 | Best | −12,569.4817 | −12,569.4865 | −12,569.487 | −12,569.4866 |
| Mean | −12,501.4776 | −12,569.4717 | −12,569.214 | −12,569.4124 | |
| Std | 177.6465 | 0.21166 | 1.0492 | 0.12898 | |
| F6 | Best | 0 | 0 | 0 | 0 |
| Mean | 0 | 0 | 0 | 0 | |
| Std | 0 | 0 | 0 | 0 | |
| F7 | Best | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 |
| Mean | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| Std | 0 | 0 | 0 | 0 | |
| F8 | Best | 0 | 0 | 0 | 0 |
| Mean | 0 | 0 | 0 | 0 | |
| Std | 0 | 0 | 0 | 0 | |
| F9 | Best | 0.998 | 0.998 | 0.998 | 0.998 |
| Mean | 1.7916 | 1.0311 | 0.998 | 0.998 | |
| Std | 1.4977 | 0.18148 | 1.44 × 10−10 | 1.33 × 10−11 | |
| F10 | Best | −10.1025 | −10.1532 | −5.0548 | −10.1532 |
| Mean | −8.2697 | −9.1315 | −4.9995 | −10.1473 | |
| Std | 2.0236 | 2.073 | 0.11759 | 0.0082563 | |
| F11 | Best | −10.3122 | −10.4026 | −5.0876 | −10.4027 |
| Mean | −7.8291 | −9.3316 | −5.0278 | −10.3978 | |
| Std | 2.453 | 2.1583 | 0.10179 | 0.0043626 | |
| F12 | Best | −10.4924 | −10.5364 | −5.1278 | −10.5363 |
| Mean | −7.2542 | −9.6282 | −5.0867 | −10.5309 | |
| Std | 2.496 | 2.0468 | 0.086013 | 0.0053248 |
| Double Adaptive Weight Strategy | DLH Search Strategy | Position Update Strategy Based on DBO Algorithm | |
|---|---|---|---|
| HHO | 0 | 0 | 0 |
| HHO1 | 1 | 0 | 0 |
| HHO2 | 0 | 1 | 0 |
| HHO3 | 0 | 0 | 1 |
| HHO12 | 1 | 1 | 0 |
| HHO13 | 1 | 0 | 1 |
| HHO23 | 0 | 1 | 1 |
| Function | Index | HHO | HHO1 | HHO2 | HHO3 | HHO12 | HHO13 | HHO23 |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 3.3253 × 10−112 | 8.9003 × 10−171 | 0 | 8.0823 × 10−227 | 0 | 2.7309 × 10−271 | 0 |
| Mean | 1.5801 × 10−96 | 5.7737 × 10−135 | 4.9407 × 10−324 | 0 | 0 | 2.112 × 10−253 | 0 | |
| Std | 8.343 × 10−96 | 1.0541 × 10−135 | 0 | 3.8473 × 10−207 | 0 | 0 | 0 | |
| F2 | Best | 1.2599 × 10−96 | 2.0311 × 10−148 | 2.0311 × 10−148 | 4.0299 × 10−239 | 0 | 4.1191 × 10−239 | 0 |
| Mean | 6.6397 × 10−66 | 1.1736 × 10−122 | 2.1428 × 10−123 | 0 | 0 | 1.5794 × 10−203 | 1.9179 × 10−282 | |
| Std | 3.6367 × 10−65 | 2.1428 × 10−123 | 1.1736 × 10−122 | 6.169 × 10−169 | 0 | 0 | 0 | |
| F3 | Best | 2.2842 × 10−57 | 3.2572 × 10−85 | 2.9095 × 10−165 | 1.1407 × 10−105 | 4.5555 × 10−222 | 1.2775 × 10−135 | 2.9634 × 10−176 |
| Mean | 7.8555 × 10−50 | 1.015 × 10−72 | 9.6934 × 10−146 | 9.1514 × 10−98 | 1.5838 × 10−202 | 7.7083 × 10−123 | 3.2638 × 10−156 | |
| Std | 2.9179 × 10−49 | 1.89 × 10−73 | 5.2825 × 10−145 | 1.6848 × 10−98 | 0 | 4.2008 × 10−122 | 1.7562 × 10−155 | |
| F6 | Best | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Std | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| F8 | Best | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Std | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| F13 | Best | 499.5464 | 451.3108 | 300.0151 | 405.3196 | 300.0091 | 300.073 | 300.0109 |
| Mean | 1054.6712 | 723.4408 | 304.8567 | 876.3008 | 302.4262 | 301.6767 | 300.0219 | |
| Std | 450.29 | 296.5269 | 13.9405 | 323.1338 | 70.5143 | 2.0059 | 0.007624 | |
| F14 | Best | 426.1614 | 412.2925 | 404.3665 | 405.4668 | 400.2645 | 400.092 | 400.0791 |
| Mean | 482.2627 | 465.128 | 473.499 | 441.9414 | 451.3182 | 414.1834 | 424.0303 | |
| Std | 46.4494 | 67.3456 | 74.5752 | 56.6134 | 55.7907 | 20.6095 | 34.091 | |
| F18 | Best | 2397.4281 | 2011.1804 | 2056.762 | 2123.1912 | 1972.6731 | 1990.5764 | 1906.2921 |
| Mean | 7016.2047 | 4514.9281 | 3871.4013 | 3963.7292 | 3275.5863 | 3392.9889 | 3280.4198 | |
| Std | 6090.2478 | 4452.2142 | 2301.3651 | 3065.6397 | 3052.8942 | 2258.0825 | 2056.7581 | |
| F21 | Best | 2585.9431 | 2529.2851 | 2540.4439 | 2552.0027 | 2529.3682 | 2529.2844 | 2533.6741 |
| Mean | 2696.4308 | 2593.1123 | 2668.2599 | 2635.4749 | 2598.81 | 2589.1342 | 2619.374 | |
| Std | 40.9474 | 49.2524 | 31.7577 | 43.6345 | 51.2598 | 37.2641 | 46.626 |
| Map Size | Algorithm | Path Length | Iterations | ||||
|---|---|---|---|---|---|---|---|
| Best | Mean | Std | Best | Mean | Std | ||
| 20 × 20 | GWO | 28.1302 | 28.99975 | 0.730980313 | 23 | 47.2 | 22.55758064 |
| SSA | 28.1749 | 29.31758 | 1.320170692 | 2 | 25.5 | 26.56752403 | |
| WOA | 29.0814 | 31.83472 | 1.953097743 | 1 | 13 | 10 | |
| PSO | 28.1302 | 32.25132 | 2.554425596 | 41 | 67.3 | 18.49954954 | |
| GBO | 28.1302 | 29.73836 | 1.201097738 | 48 | 69 | 16.91153453 | |
| SCSO | 30.3603 | 33.01106 | 1.847597231 | 1 | 14 | 19.9276469 | |
| DBO | 28.1302 | 28.92537 | 0.677979036 | 19 | 48.9 | 22.323132 | |
| HHO | 28.1302 | 28.92959 | 0.885522541 | 10 | 45.6 | 31.52142129 | |
| MIHHO | 27.8279 | 28.35375 | 0.340219678 | 9 | 17.6 | 9.570788891 | |
| 40 × 40 | GWO | 60.259 | 64.4877 | 4.299023495 | 26 | 68.6 | 22.52998003 |
| SSA | 64.9702 | 71.00163 | 2.457679449 | 7 | 40.7 | 23.73955911 | |
| WOA | 70.4079 | 75.30136 | 2.098619263 | 5 | 16.7 | 11.83262909 | |
| PSO | 73.1966 | 112.78083 | 20.932749 | 86 | 94.4 | 5.738757124 | |
| GBO | 72.5571 | 74.09069 | 1.725264679 | 6 | 41.6 | 22.30196802 | |
| SCSO | 73.5807 | 75.97282 | 1.057445971 | 2 | 7.4 | 3.306559138 | |
| DBO | 61.3757 | 67.25799 | 3.752098025 | 15 | 58.3 | 23.39539366 | |
| HHO | 69.2777 | 71.36853 | 1.445605752 | 7 | 22.1 | 16.78921612 | |
| MIHHO | 58.2233 | 61.05562 | 1.556186577 | 13 | 32.2 | 18.20134305 | |
| Map Size | Algorithm | Path Length | Iterations | ||||
|---|---|---|---|---|---|---|---|
| Best | Mean | Std | Best | Mean | Std | ||
| 20 × 20 | GWO | 28.9969 | 30.80291 | 1.187916685 | 10 | 18.1 | 5.78215646 |
| SSA | 28.8569 | 30.68388 | 1.534795537 | 21 | 42.5 | 22.62864458 | |
| WOA | 32.2587 | 34.62525 | 1.307826451 | 1 | 11.3 | 7.616502551 | |
| PSO | 30.9325 | 35.941 | 2.579778856 | 1 | 11.9 | 18.02128371 | |
| GBO | 32.0805 | 34.39496 | 1.656553955 | 1 | 47.1 | 29.69268522 | |
| SCSO | 31.964 | 34.2809 | 1.702263173 | 1 | 10.5 | 15.27707069 | |
| DBO | 30.0285 | 31.43774 | 1.423925406 | 6 | 21.1 | 16.07240561 | |
| HHO | 30.1685 | 31.10808 | 1.208440051 | 14 | 40.2 | 30.17283547 | |
| MIHHO | 28.8569 | 29.70135 | 0.793536696 | 4 | 15.5 | 8.2360994 | |
| 40 × 40 | GWO | 67.0996 | 70.99656 | 3.51914798 | 14 | 53.7 | 29.63125227 |
| SSA | 75.0711 | 75.59832 | 0.185246225 | 7 | 28.8 | 17.32563932 | |
| WOA | 76.2426 | 77.1213 | 0.497834272 | 3 | 6 | 3.771236166 | |
| PSO | 80.6919 | 85.61078 | 3.460530845 | 1 | 19.4 | 24.42312201 | |
| GBO | 74.8929 | 76.16624 | 0.784418269 | 12 | 45.2 | 22.14497686 | |
| SCSO | 75.6569 | 77.18406 | 0.563175905 | 1 | 3.4 | 2.319003617 | |
| DBO | 67.2777 | 74.28681 | 2.734354672 | 3 | 41.1 | 29.58396713 | |
| HHO | 70.5138 | 74.94902 | 1.612339986 | 6 | 26.5 | 28.43413442 | |
| MIHHO | 65.5203 | 68.06217 | 1.030074189 | 28 | 36.2 | 6.908931418 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.; Li, W.; Han, T.; Yu, L.; Cui, T. Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning. Biomimetics 2024, 9, 552. https://doi.org/10.3390/biomimetics9090552
Tang C, Li W, Han T, Yu L, Cui T. Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning. Biomimetics. 2024; 9(9):552. https://doi.org/10.3390/biomimetics9090552
Chicago/Turabian StyleTang, Chaoli, Wenyan Li, Tao Han, Lu Yu, and Tao Cui. 2024. "Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning" Biomimetics 9, no. 9: 552. https://doi.org/10.3390/biomimetics9090552
APA StyleTang, C., Li, W., Han, T., Yu, L., & Cui, T. (2024). Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning. Biomimetics, 9(9), 552. https://doi.org/10.3390/biomimetics9090552






