Human–Exoskeleton Coupling Simulation for Lifting Tasks with Shoulder, Spine, and Knee-Joint Powered Exoskeletons
Abstract
1. Introduction
2. Methods
2.1. Subject-Specific Coupled Human–Exoskeleton Model
2.2. Human–Exoskeleton Coupled Equations of Motion (EOMs)
3. Lifting Optimization Formulation
3.1. Design Variables
3.2. Objective Functions
3.3. Constraints
4. Exoskeleton Control Strategy and Experiments
4.1. Knee Exoskeleton Control Strategy
4.2. Experimental Procedure
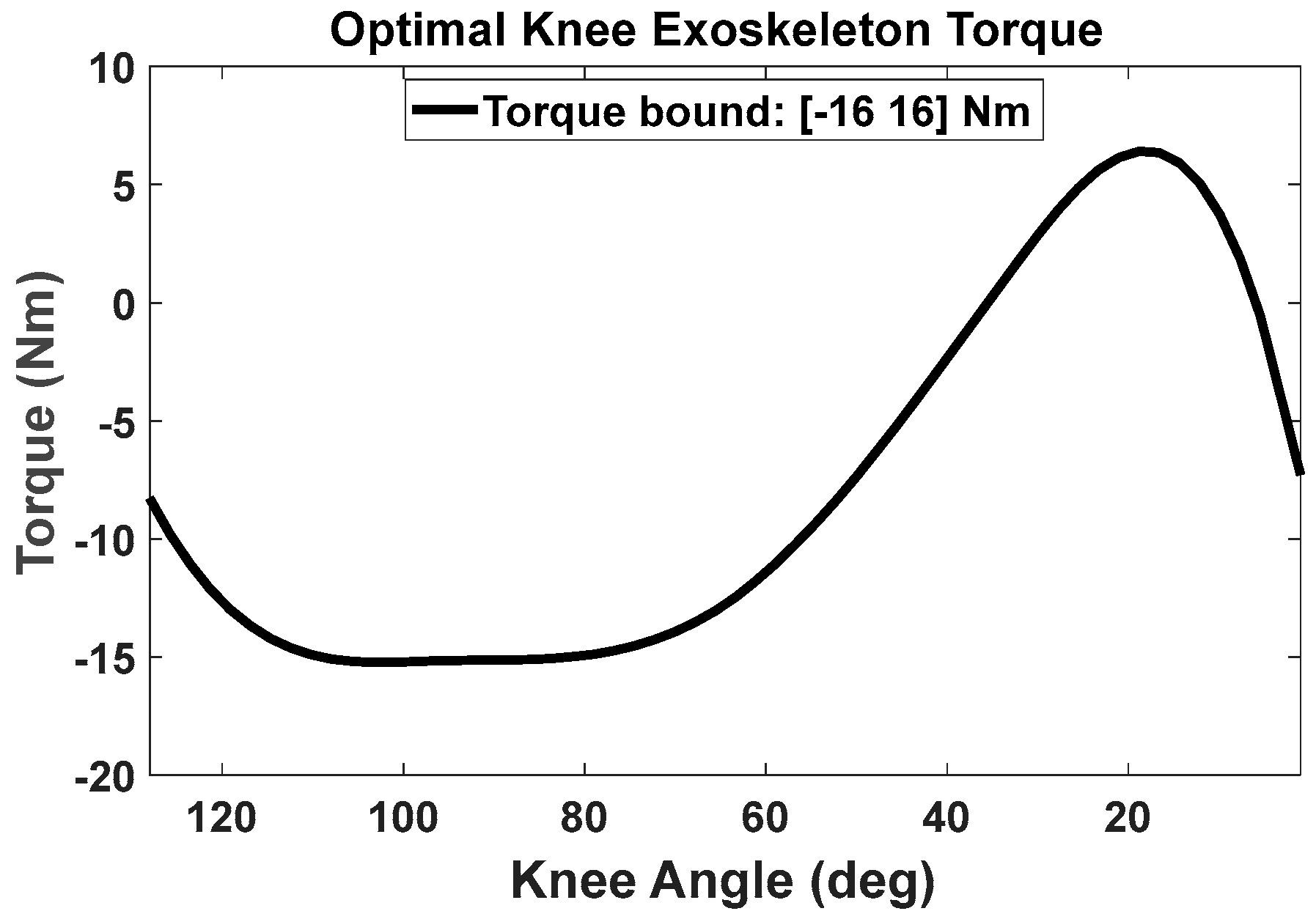
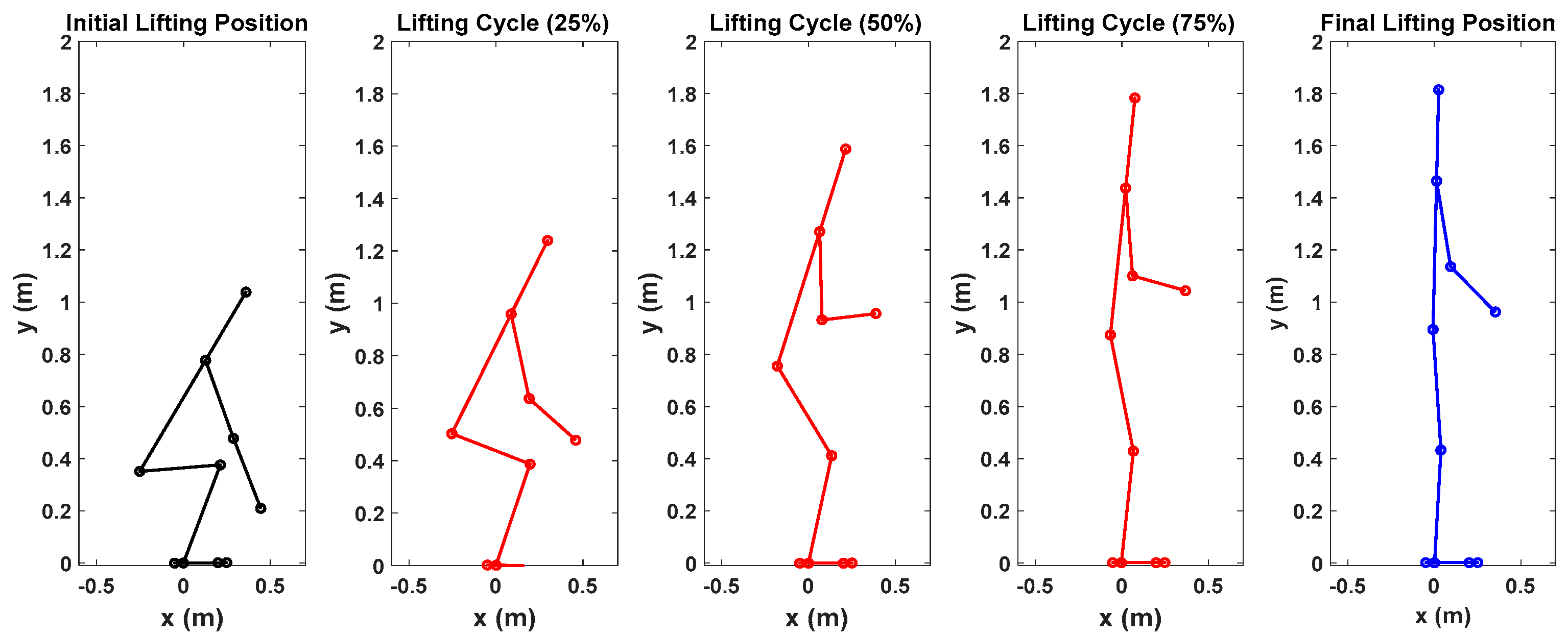
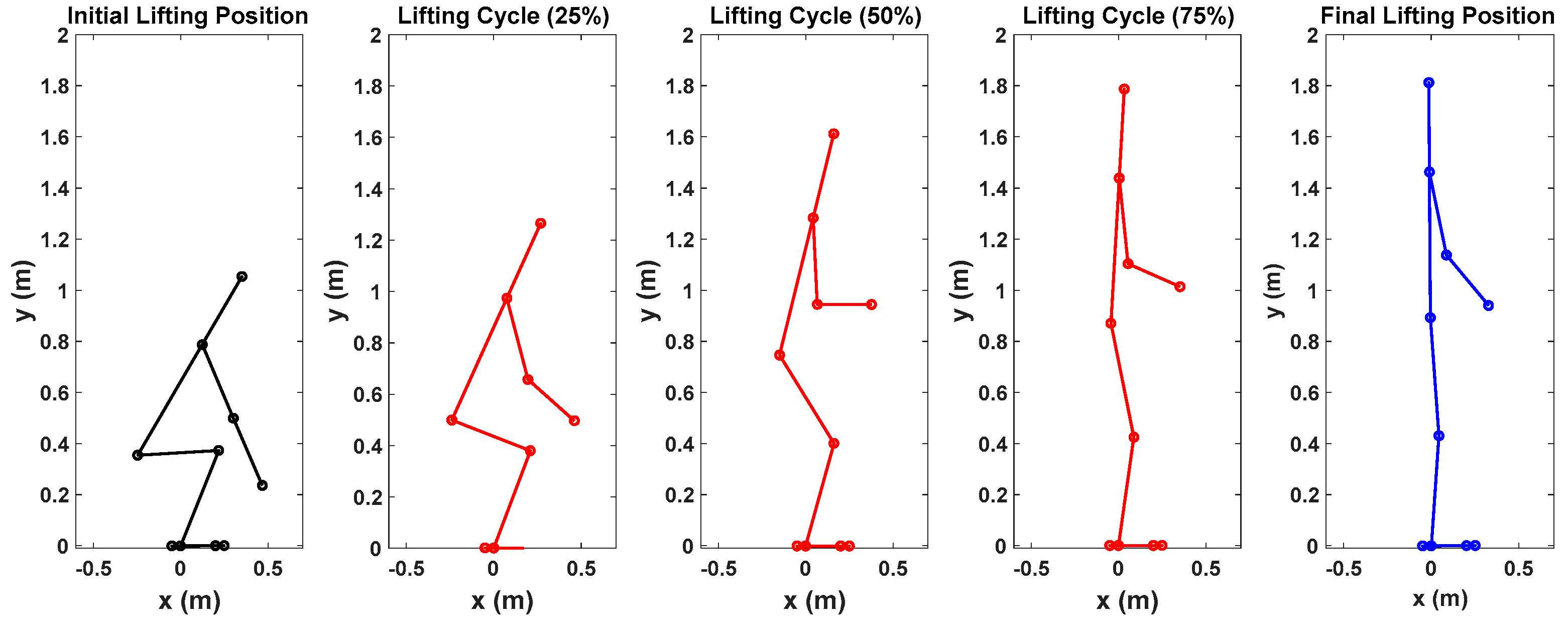
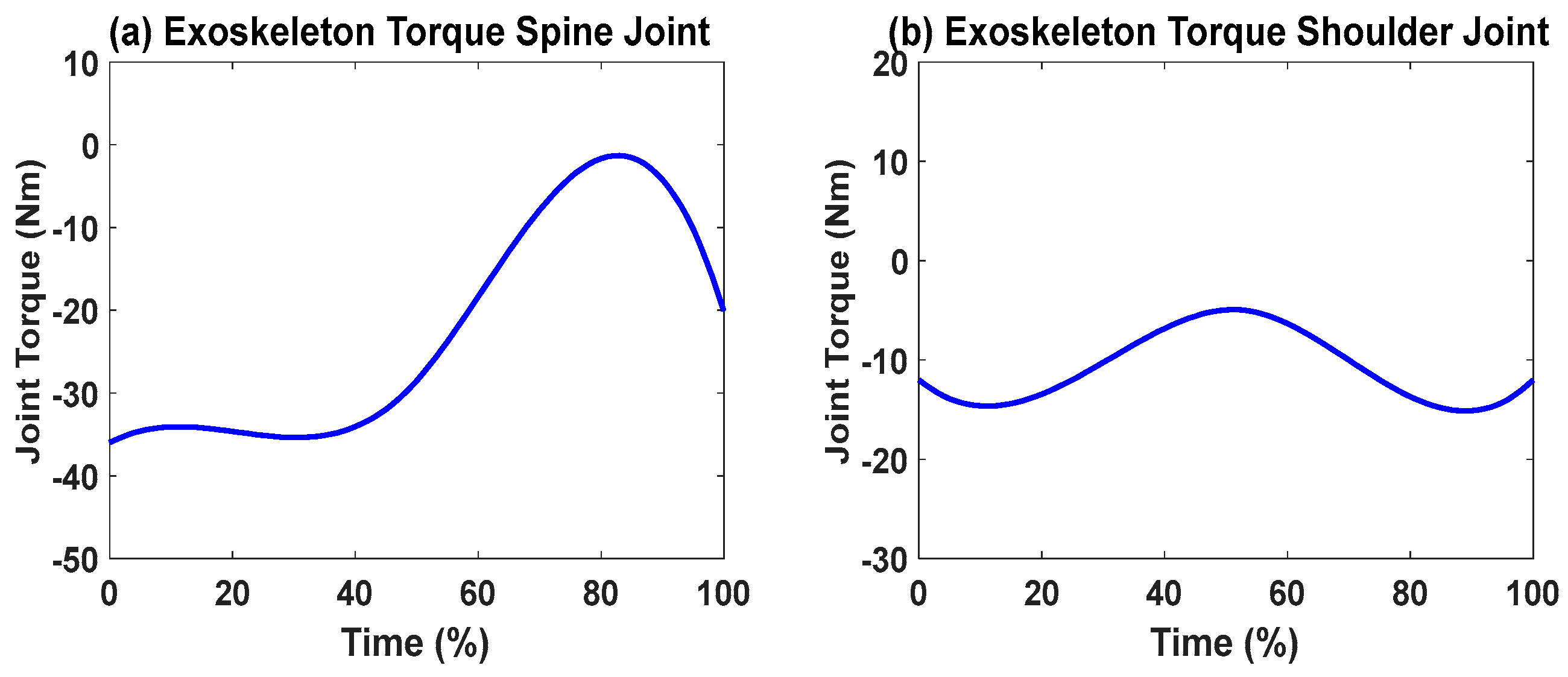
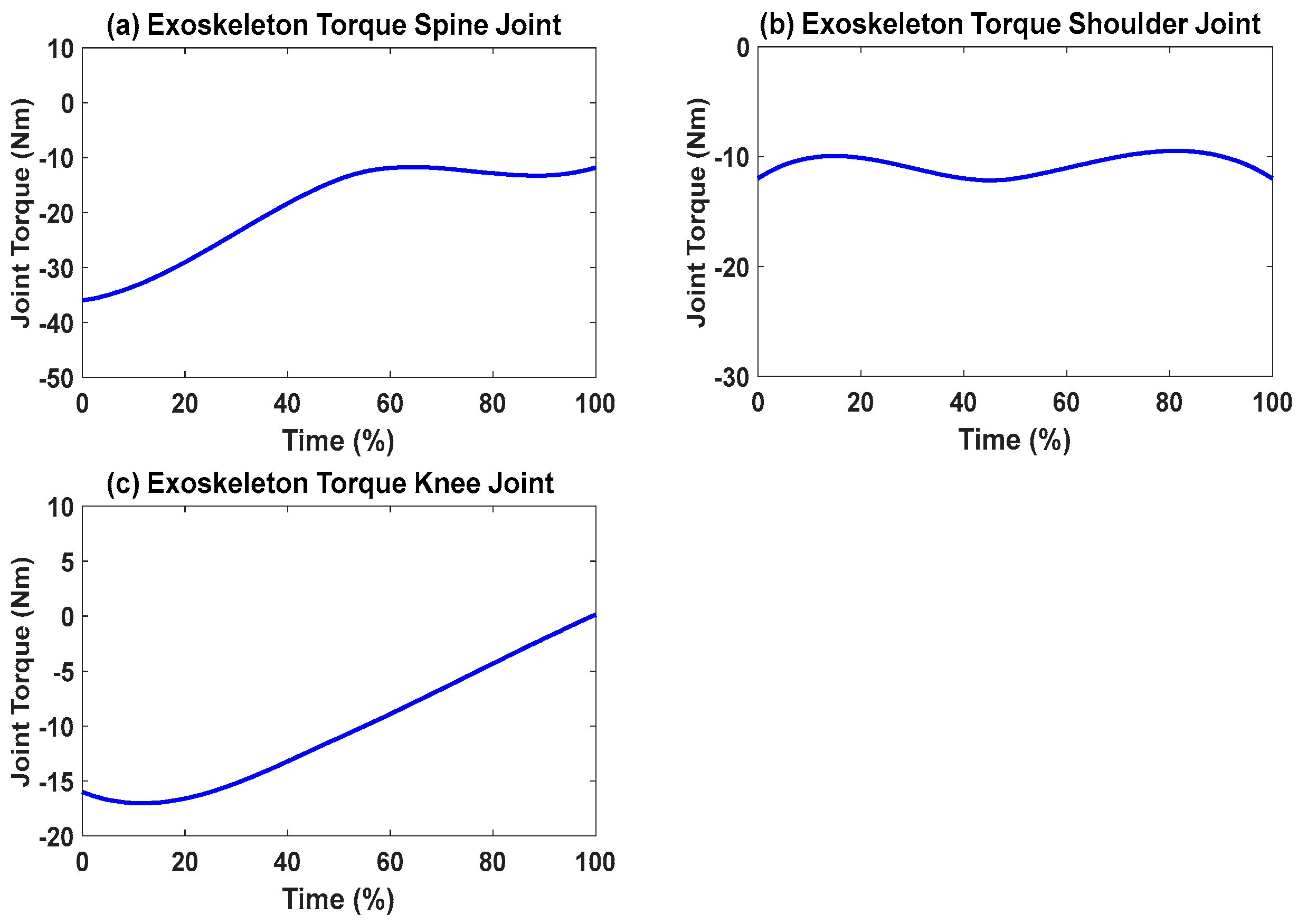
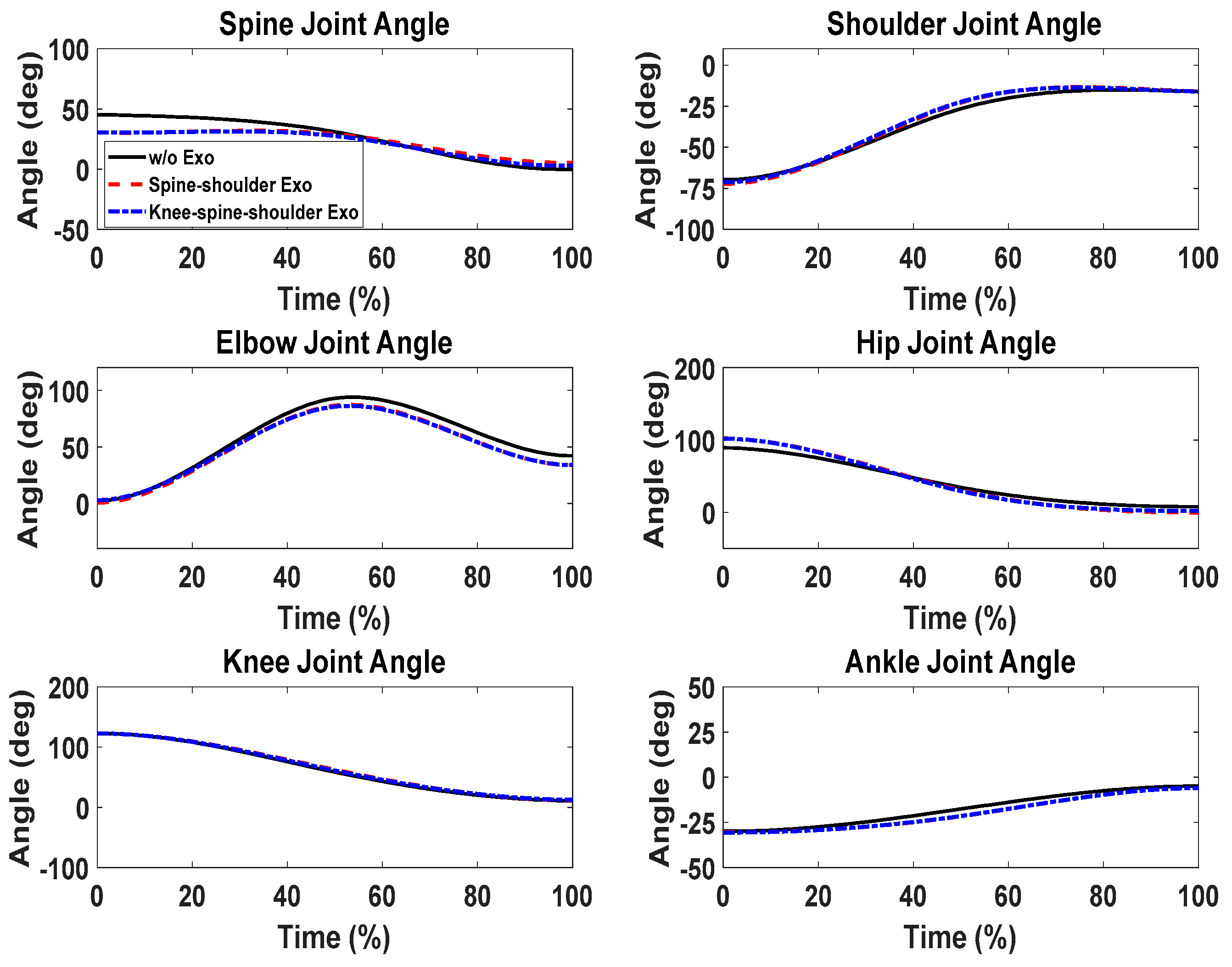
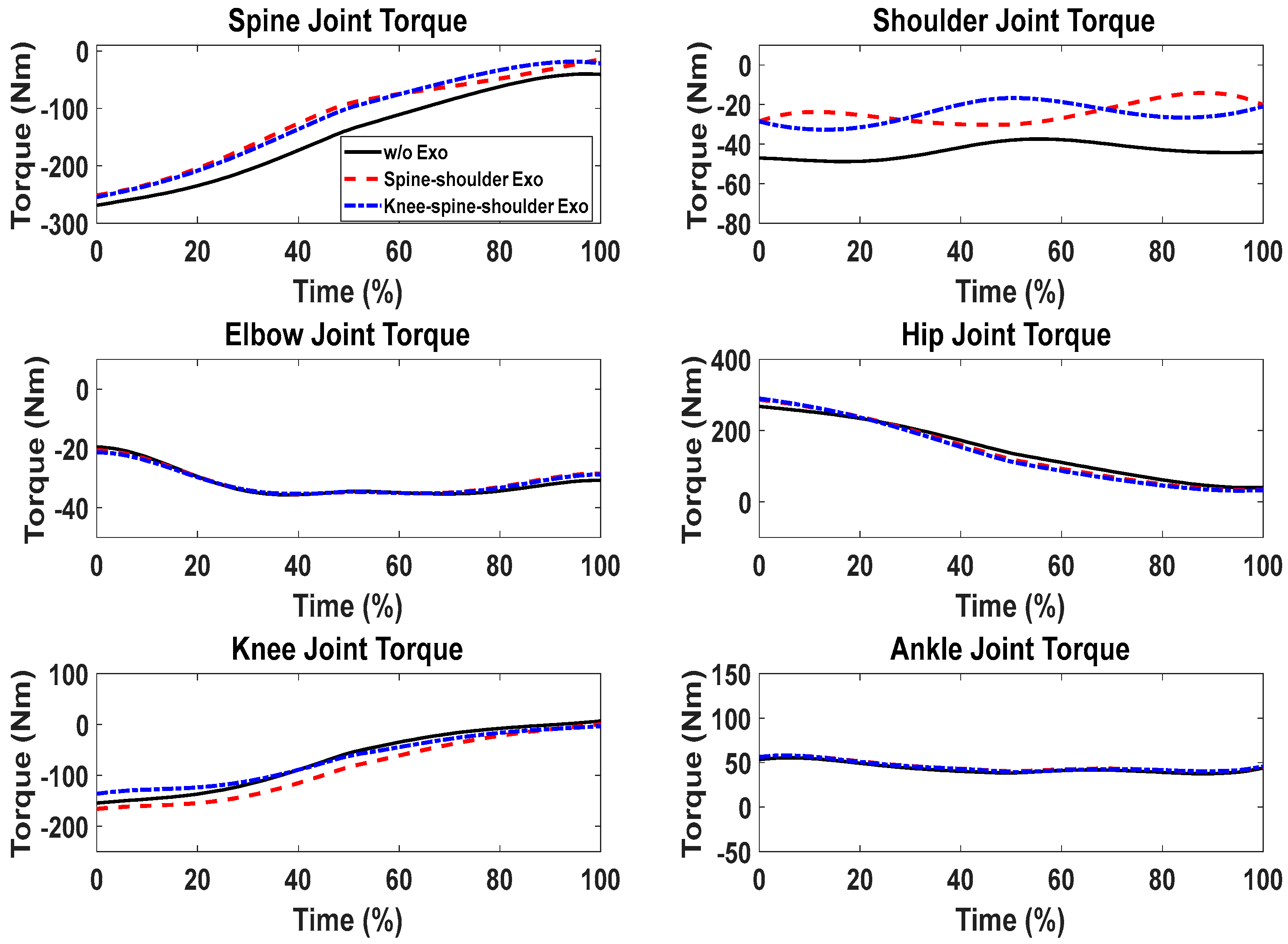
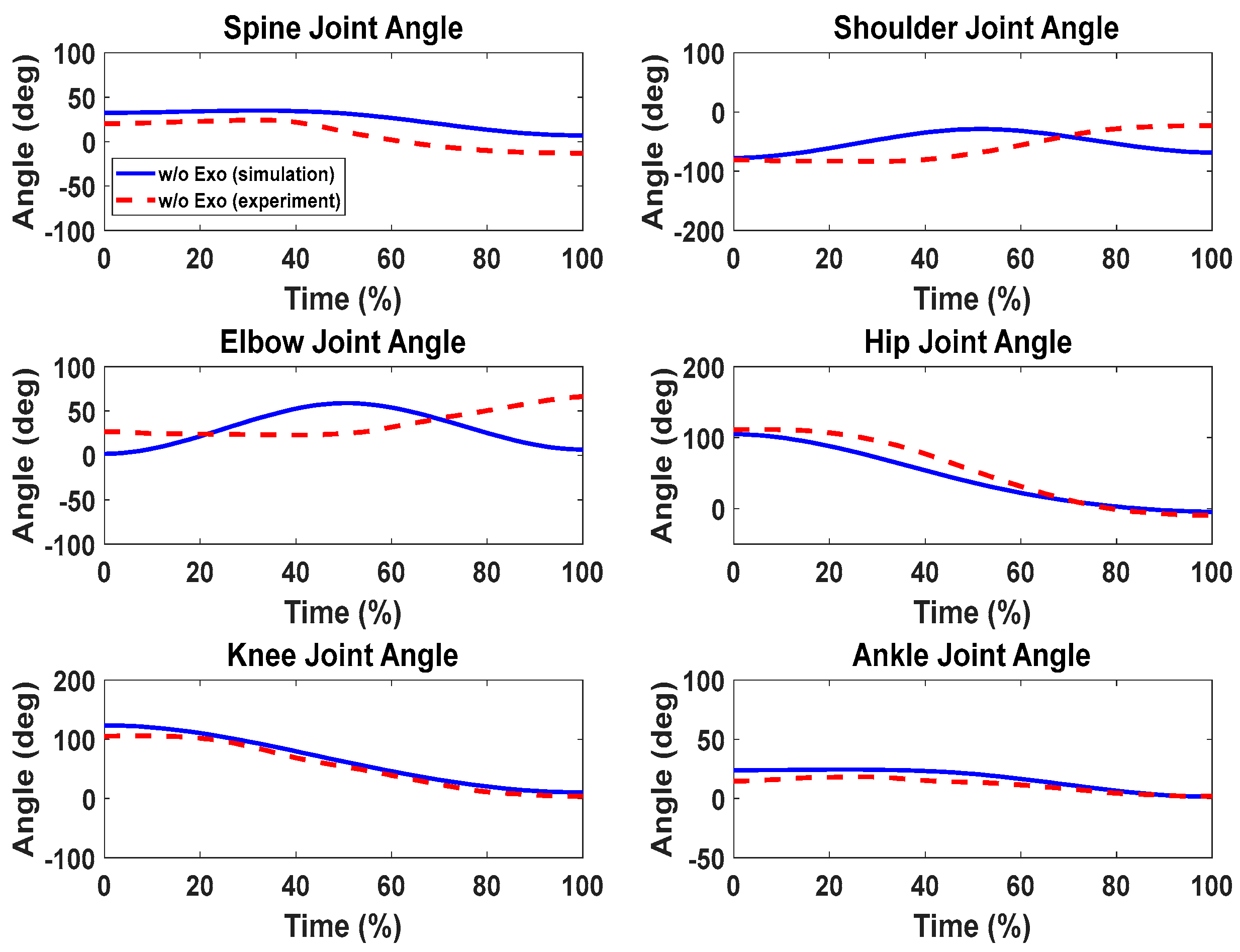
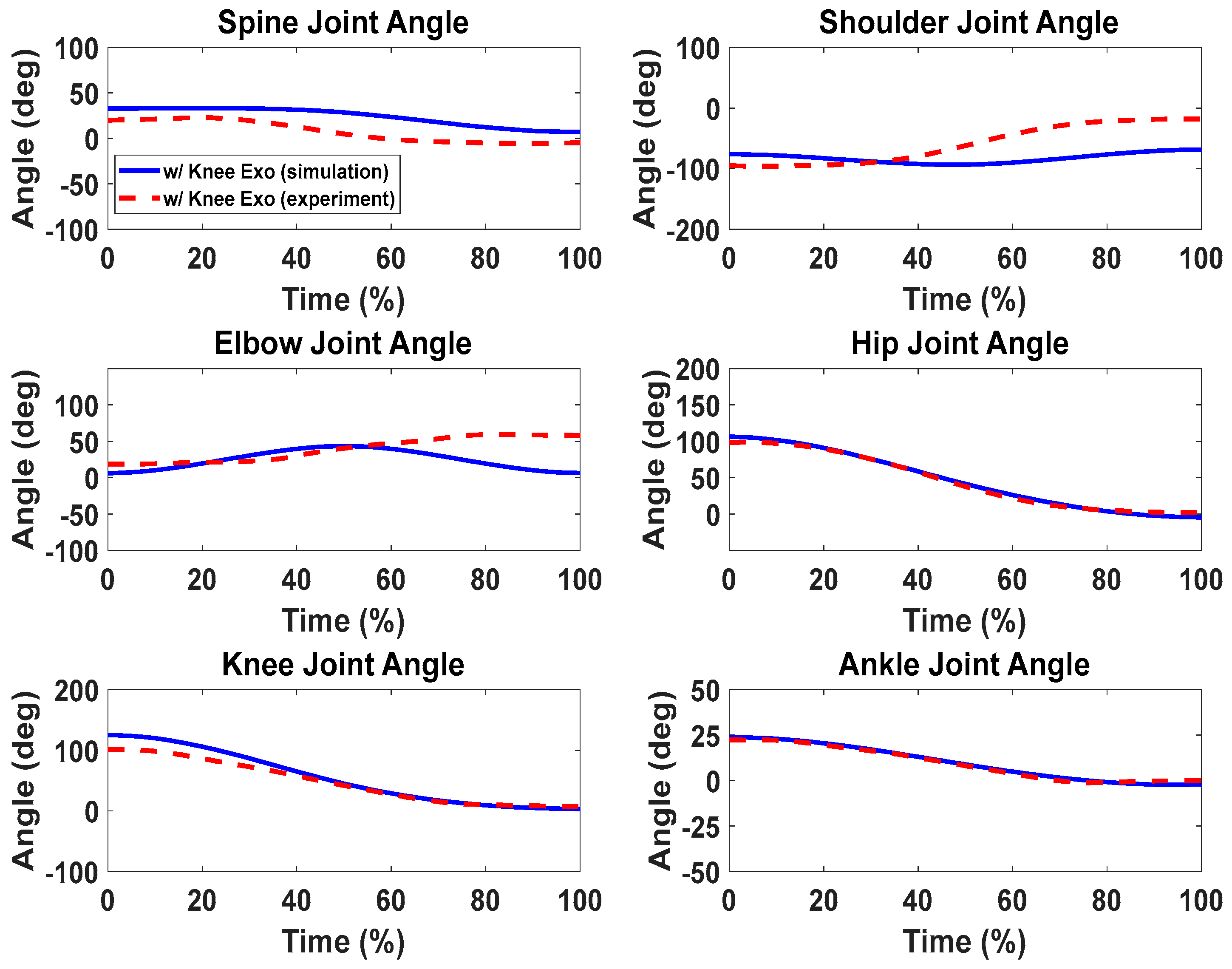
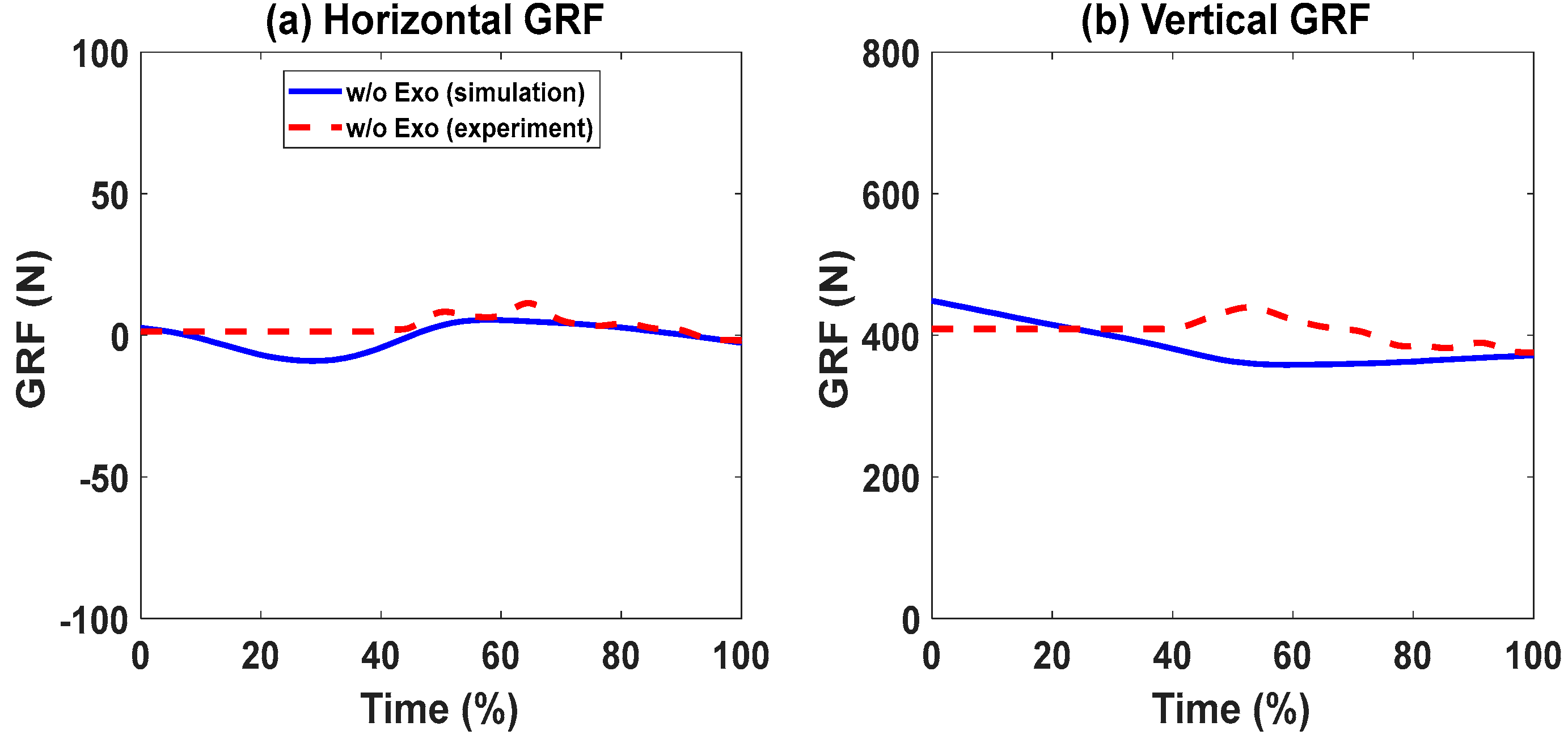
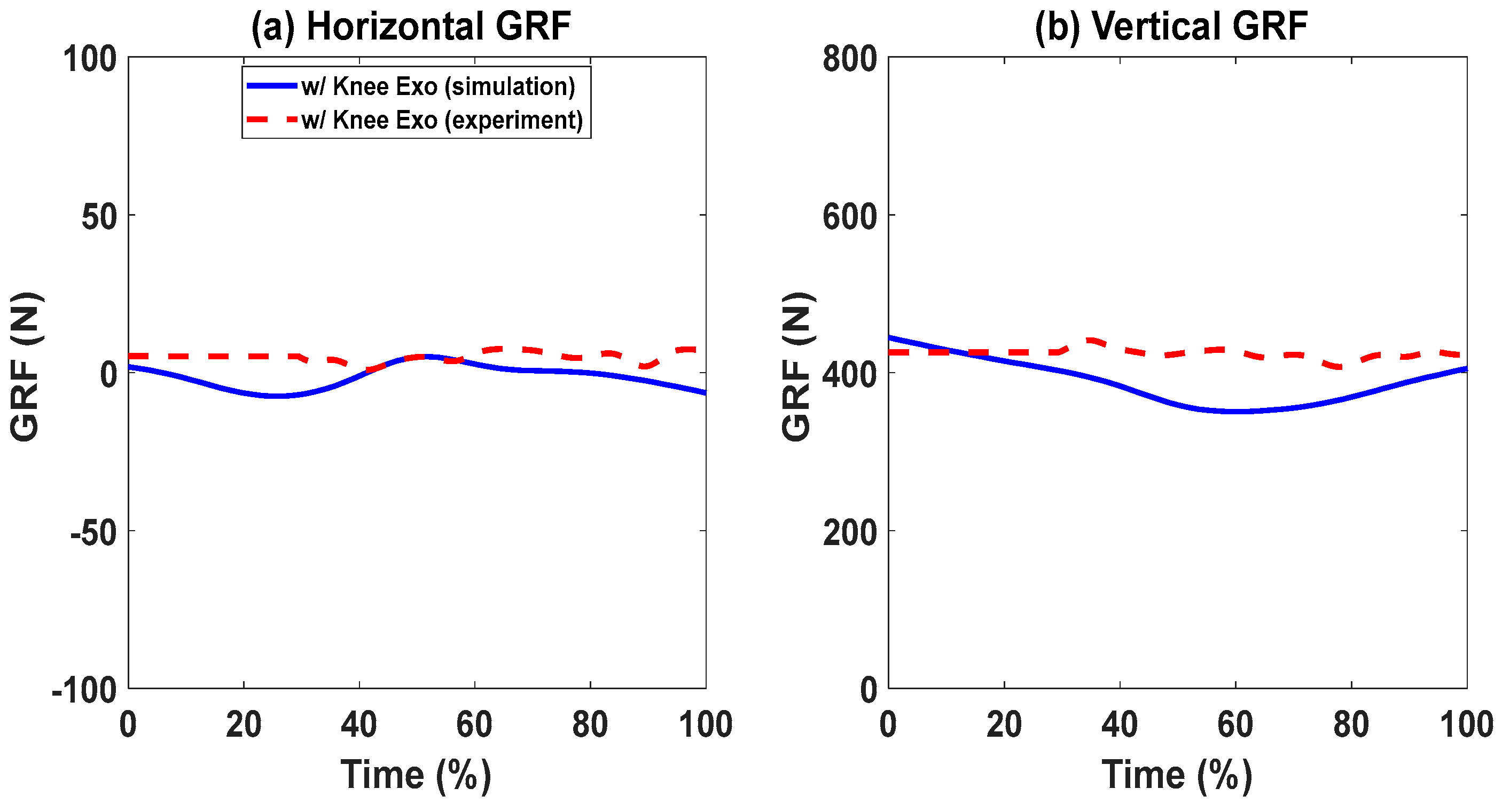
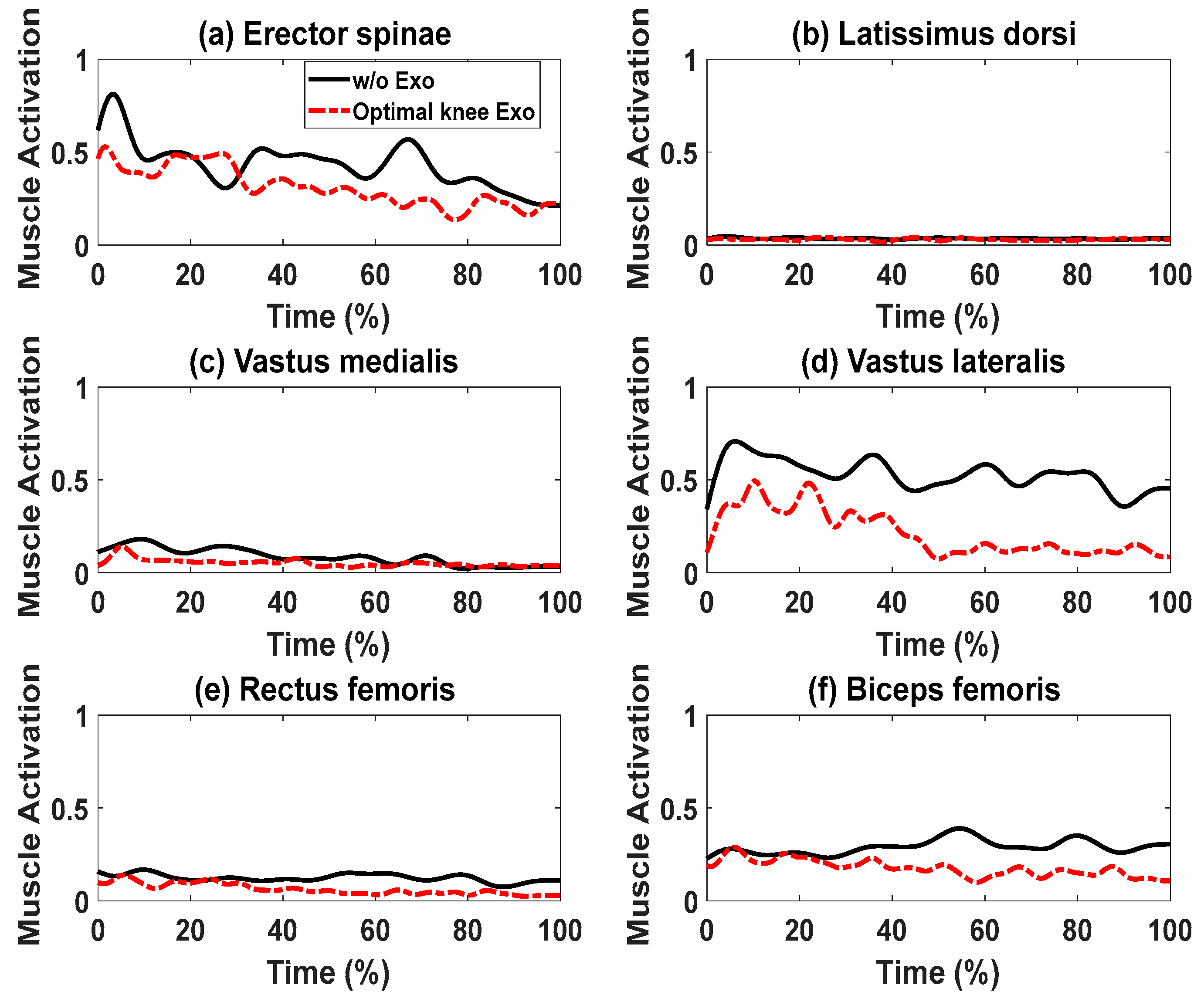
5. Results
Lifting Validation with the Knee Exoskeletons
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Houtenville, A.J.; Brucker, D.L.; Lauer, E.A. Annual Compendium of Disability Statistics: 2015; Institute on Disability: Durham, NH, USA, 2016. [Google Scholar]
- Bai, S.; Rasmussen, J. Modelling of physical human-robot interaction for exoskeleton designs. In Proceedings of the Multibody Dynamics 2011, ECCOMAS Thematic Conference, Brussels, Belgium, 4–7 July 2011. [Google Scholar]
- Agarwal, P.; Kuo, P.H.; Neptune, R.R.; Deshpande, A.D. A novel framework for virtual prototyping of rehabilitation exoskeletons. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Cho, K.; Kim, Y.; Yi, D.; Jung, M.; Lee, K. Analysis and evaluation of a combined human-exoskeleton model under two different constraints condition. In Proceedings of the International Summit on Human Simulation, St. Pete Beach, FL, USA, 23–25 May 2012. [Google Scholar]
- Ramadurai, S.; Jeong, H.; Kim, M. Predicting the metabolic cost of exoskeleton-assisted squatting using foot pressure features and machine learning. Front. Robot. AI 2023, 10, 1166248. [Google Scholar] [CrossRef] [PubMed]
- Millard, M.; Sreenivasa, M.; Mombaur, K. Predicting the motions and forces of wearable robotic systems using optimal control. Front. Robot. AI 2017, 4, 41. [Google Scholar] [CrossRef]
- Heo, U.; Kim, S.J.; Kim, J. Backdrivable and fully-portable pneumatic back support exoskeleton for lifting assistance. IEEE Robot. Autom. Lett. 2020, 5, 2047–2053. [Google Scholar] [CrossRef]
- Otten, B.M.; Weidner, R.; Argubi-Wollesen, A. Evaluation of a novel active exoskeleton for tasks at or above head level. IEEE Robot. Autom. Lett. 2018, 3, 2408–2415. [Google Scholar] [CrossRef]
- Ebrahimi, A. Stuttgart Exo-Jacket: An exoskeleton for industrial upper body applications. In Proceedings of the 2017 10th International Conference on Human System Interactions (HSI), Ulsan, Republic of Korea, 17–19 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 258–263. [Google Scholar]
- Sylla, N.; Bonnet, V.; Colledani, F.; Fraisse, P. Ergonomic contribution of ABLE exoskeleton in automotive industry. Int. J. Ind. Ergon. 2014, 44, 475–481. [Google Scholar] [CrossRef]
- Arefeen, A.; Xiang, Y. Modeling and simulation of a powered exoskeleton system to aid human-robot collaborative lifting. In Proceedings of the 7th International Digital Human Modeling Symposium (DHM 2022) and Iowa Virtual Human Summit 2022, Iowa City, IA, USA, 29–30 August 2022; Volume 7. [Google Scholar]
- Kiguchi, K.; Kado, K.; Hayashi, Y. Design of a 7DOF upper-limb power-assist exoskeleton robot with moving shoulder joint mechanism. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2937–2942. [Google Scholar]
- Rahman, M.H.; Ouimet, T.K.; Saad, M.; Kenne, J.P.; Archambault, P.S. Development and control of a wearable robot for rehabilitation of elbow and shoulder joint movements. In Proceedings of the IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1506–1511. [Google Scholar]
- Zhang, T.; Huang, H. A lower-back robotic exoskeleton: Industrial handling augmentation used to provide spinal support. IEEE Robot. Autom. Mag. 2018, 25, 95–106. [Google Scholar] [CrossRef]
- Sado, F.; Yap, H.J.; Ghazilla, R.A.R.; Ahmad, N. Design and control of a wearable lower-body exoskeleton for squatting and walking assistance in manual handling works. Mechatronics 2019, 63, 102272. [Google Scholar] [CrossRef]
- Gams, A.; Petrič, T.; Debevec, T.; Babič, J. Effects of robotic knee exoskeleton on human energy expenditure. IEEE Trans. Biomed. Eng. 2013, 60, 1636–1644. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wu, X.; Zhang, Y.; Chen, C.; Liu, S.; Liu, Y.; Ma, Y. A semi-active exoskeleton based on EMGs reduces muscle fatigue when squatting. Front. Neurorobotics 2021, 15, 625479. [Google Scholar] [CrossRef]
- Yu, S.; Huang, T.H.; Wang, D.; Lynn, B.; Sayd, D.; Silivanov, V.; Su, H. Design and control of a high-torque and highly backdrivable hybrid soft exoskeleton for knee injury prevention during squatting. IEEE Robot. Autom. Lett. 2019, 4, 4579–4586. [Google Scholar] [CrossRef]
- Arefeen, A.; Xiang, Y. Subject specific optimal control of powered knee exoskeleton to assist human lifting tasks under controlled environment. Robotica 2023, 41, 2809–2828. [Google Scholar] [CrossRef]
- Shepherd, M.K.; Rouse, E.J. Design and validation of a torque-controllable knee exoskeleton for sit-to-stand assistance. IEEE/ASME Trans. Mechatron. 2017, 22, 1695–1704. [Google Scholar] [CrossRef]
- Karavas, N.; Ajoudani, A.; Tsagarakis, N.; Saglia, J.; Bicchi, A.; Caldwell, D. Tele-impedance based stiffness and motion augmentation for a knee exoskeleton device. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2194–2200. [Google Scholar]
- Sanz-Pena, I.; Jeong, H.; Kim, M. Personalized wearable ankle robot using modular additive manufacturing design. IEEE Robot. Autom. Lett. 2023, 8, 4935–4942. [Google Scholar] [CrossRef]
- de Andrade, R.M.; Fabriz Ulhoa, P.H.; Fragoso Dias, E.A.; Filho, A.B.; Vimieiro, C.B.S. Design and testing a highly backdrivable and kinematic compatible magneto-rheological knee exoskeleton. J. Intell. Mater. Syst. Struct. 2023, 34, 653–663. [Google Scholar] [CrossRef]
- Liew, H.L.; Mizuuchi, I. Energy Regeneration System for Quasi-Direct Drive Actuated Knee Exoskeleton. In Proceedings of the 2023 IEEE/SICE International Symposium on System Integration (SII), Atlanta, GA, USA, 17–20 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Wu, Z.; Yang, M.; Xia, Y.; Wang, L. Mechanical Structural Design and Actuation Technologies of Powered Knee Exoskeletons: A Review. Appl. Sci. 2023, 13, 1064. [Google Scholar] [CrossRef]
- Luo, S.; Androwis, G.; Adamovich, S.; Su, H.; Nunez, E.; Zhou, X. Reinforcement learning and control of a lower extremity exoskeleton for squat assistance. Front. Robot. AI 2021, 8, 702845. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Androwis, G.; Adamovich, S.; Nunez, E.; Su, H.; Zhou, X. Robust walking control of a lower limb rehabilitation exoskeleton coupled with a musculoskeletal model via deep reinforcement learning. J. NeuroEngineering Rehabil. 2023, 20, 34. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Si, J.; Wen, Y.; Li, M.; Huang, H. Reinforcement learning control of robotic knee with human-in-the-loop by flexible policy iteration. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 5873–5887. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Peng, Z.; Cheng, H.; Hu, J.; Qiu, J.; Zou, C.; Chen, Q. Learning-based walking assistance control strategy for a lower limb exoskeleton with hemiplegia patients. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2280–2285. [Google Scholar]
- Liu, C.; Audu, M.L.; Triolo, R.J.; Quinn, R.D. Neural networks trained via reinforcement learning stabilize walking of a three-dimensional biped model with exoskeleton applications. Front. Robot. AI 2021, 8, 710999. [Google Scholar] [CrossRef]
- Li, W.Z.; Cao, G.Z.; Zhu, A.B. Review on control strategies for lower limb rehabilitation exoskeletons. IEEE Access 2021, 9, 123040–123060. [Google Scholar] [CrossRef]
- Masengo, G.; Zhang, X.; Dong, R.; Alhassan, A.B.; Hamza, K.; Mudaheranwa, E. Lower limb exoskeleton robot and its cooperative control: A review, trends, and challenges for future research. Front. Neurorobotics 2023, 16, 913748. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Jiang, M.; Zhang, S.; Zhu, J.; Yu, S.; Silva, I.D.; Wang, T.; Rouse, E.; Zhou, B.; Yuk, H.; et al. Experiment-free exoskeleton assistance via learning in simulation. Nature 2024, 630, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Liu, X.; Chen, Y.; Yu, L.; Yan, Z.; Yang, C.; Zhou, C.; Yang, W. Reducing the muscle activity of walking using a portable hip exoskeleton based on human-in-the-loop optimization. Front. Bioeng. Biotechnol. 2023, 11, 1006326. [Google Scholar] [CrossRef] [PubMed]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Wang, Q.; Xiang, Y.; Kim, H.J.; Arora, J.S.; Abdel-Malek, K. Alternative formulations for optimization-based digital human motion prediction. In Proceedings of the 2005 Digital Human Modeling for Design and Engineering Symposium, Iowa City, IA, USA, 14–16 June 2005. SAE Technical Paper 2005-01-2691. [Google Scholar]
- Zaman, R.; Arefeen, A.; Quarnstrom, J.; Barman, S.; Yang, J.; Xiang, Y. Optimization-based biomechanical lifting models for manual material handling: A comprehensive review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 1273–1287. [Google Scholar] [CrossRef] [PubMed]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Xiang, Y.; Arefeen, A. Two-dimensional team lifting prediction with floating-base box dynamics and grasping force coupling. Multibody Syst. Dyn. 2020, 50, 211–231. [Google Scholar] [CrossRef]
- Xiang, Y.; Arora, J.S.; Rahmatalla, S.; Abdel-Malek, K. Optimization-based dynamic human walking prediction: One step formulation. Int. J. Numer. Methods Eng. 2009, 79, 667–695. [Google Scholar] [CrossRef]
- Xiang, Y.; Arora, J.S.; Abdel-Malek, K. Optimization-based motion prediction of mechanical systems: Sensitivity analysis. Struct. Multidiscip. Optim. 2009, 37, 551–570. [Google Scholar] [CrossRef]
- Nguyen, V.Q.; LaPre, A.K.; Price, M.A.; Umberger, B.R.; Sup, F.C., IV. Inclusion of actuator dynamics in simulations of assisted human movement. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3334. [Google Scholar] [CrossRef]
- Xiang, Y.; Arora, J.S.; Chung, H.J.; Kwon, H.J.; Rahmatalla, S.; Bhatt, R.; Abdel-Malek, K. Predictive simulation of human walking transitions using an optimization formulation. Struct. Multidiscip. Optim. 2012, 45, 759–772. [Google Scholar] [CrossRef]
- Zaman, R.; Xiang, Y.; Cruz, J.; Yang, J. Two-dimensional versus three-dimensional symmetric lifting motion prediction models: A case study. ASME J. Comput. Inf. Sci. Eng. 2021, 21, 044501. [Google Scholar] [CrossRef]




| DOF | ϴ | d | a | α | Translation/Rotation | Branch |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | Global translation (GT1) | Global branch | ||
| 2 | L4 + L5 | 0 | Global translation (GT2) | |||
| 3 | 0 | 0 | 0 | 0 | Global rotation (GR1) | |
| 4 | 0 | L1 | 0 | Spine joint rotation (Q1) | Upper body branch | |
| 5 | 0 | L2 | 0 | Arm joint rotation (Q2) | ||
| 6 | 0 | 0 | L3 | 0 | Elbow joint rotation (Q3) | |
| 7 | 0 | L4 | 0 | Hip joint rotation (Q4) | Lower body branch | |
| 8 | 0 | 0 | L5 | 0 | Knee joint rotation (Q5) | |
| 9 | 0 | L6 | 0 | Ankle joint rotation (Q6) | ||
| 10 | 0 | 0 | L7 | 0 | Subtalar joint rotation (Q7) |
| Time-Dependent | Time-Independent |
|---|---|
| 1. Human joint angle limits [40] | 1. Initial and final box location |
| 2. Human joint torque limits [43] | 2. Initial and final static conditions |
| 3. Human feet contact position | |
| 4. Hand forward position | |
| 5. Collision avoidance | 3. Initial, middle, and final joint angles where , and is the experimental joint angle for the human joints. |
| 6. Stability condition | |
| 7. Exoskeleton torque limits |
| Parameters | |
|---|---|
| Box weight (kg) | 10 |
| Box height (m) | 0.15 |
| Box depth (m) | 0.65 |
| Initial hand position (x, y, z) (m) | (0.0, 0.070, 0.418) |
| Final hand position (x, y, z) (m) | (0.0, 1.088, 0.417) |
| T (s) | 1.44 |
| Cases | Joints | Peak Joint Torques (Nm) | Human Mechanical Energy (J) |
|---|---|---|---|
| Without exoskeletons | Spine | 268.60 | 622.6 |
| Shoulder | 48.78 | ||
| Knee | 154.42 | ||
| Coupled spine and shoulder exoskeletons | Spine | 251.40 | 637.7 |
| Shoulder | 30.24 | ||
| Knee | 165.73 | ||
| Coupled knee, spine, and shoulder exoskeletons | Spine | 254.35 | 586.3 |
| Shoulder | 32.65 | ||
| Knee | 135.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arefeen, A.; Xia, T.; Xiang, Y. Human–Exoskeleton Coupling Simulation for Lifting Tasks with Shoulder, Spine, and Knee-Joint Powered Exoskeletons. Biomimetics 2024, 9, 454. https://doi.org/10.3390/biomimetics9080454
Arefeen A, Xia T, Xiang Y. Human–Exoskeleton Coupling Simulation for Lifting Tasks with Shoulder, Spine, and Knee-Joint Powered Exoskeletons. Biomimetics. 2024; 9(8):454. https://doi.org/10.3390/biomimetics9080454
Chicago/Turabian StyleArefeen, Asif, Ting Xia, and Yujiang Xiang. 2024. "Human–Exoskeleton Coupling Simulation for Lifting Tasks with Shoulder, Spine, and Knee-Joint Powered Exoskeletons" Biomimetics 9, no. 8: 454. https://doi.org/10.3390/biomimetics9080454
APA StyleArefeen, A., Xia, T., & Xiang, Y. (2024). Human–Exoskeleton Coupling Simulation for Lifting Tasks with Shoulder, Spine, and Knee-Joint Powered Exoskeletons. Biomimetics, 9(8), 454. https://doi.org/10.3390/biomimetics9080454






