The Effect of Hindwing Trajectories on Wake–Wing Interactions in the Configuration of Two Flapping Wings in Tandem
Abstract
1. Introduction
2. Problem Formulation
3. Numerical Method
4. Results and Discussions
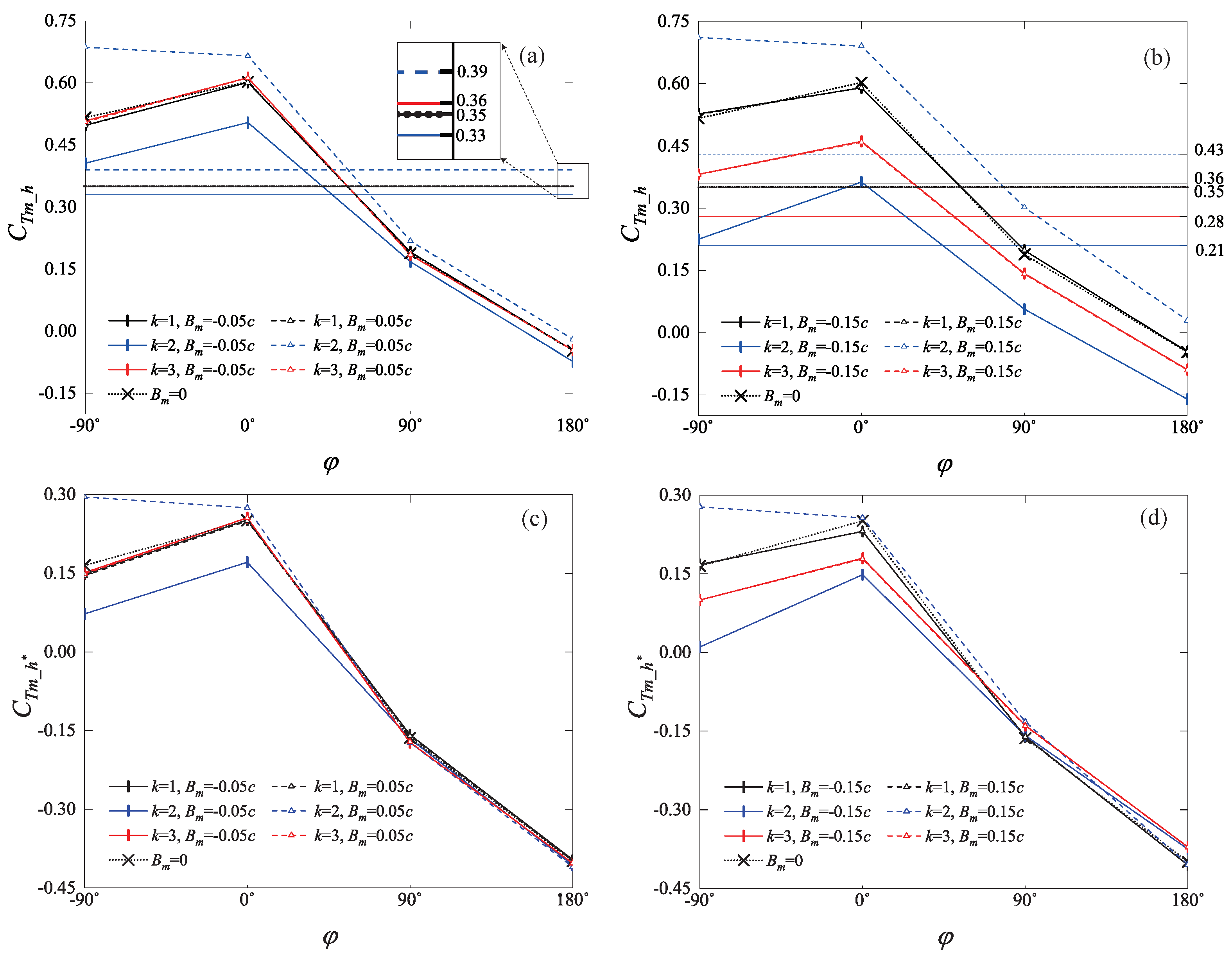
4.1. Statistics of Hindwing Thrust
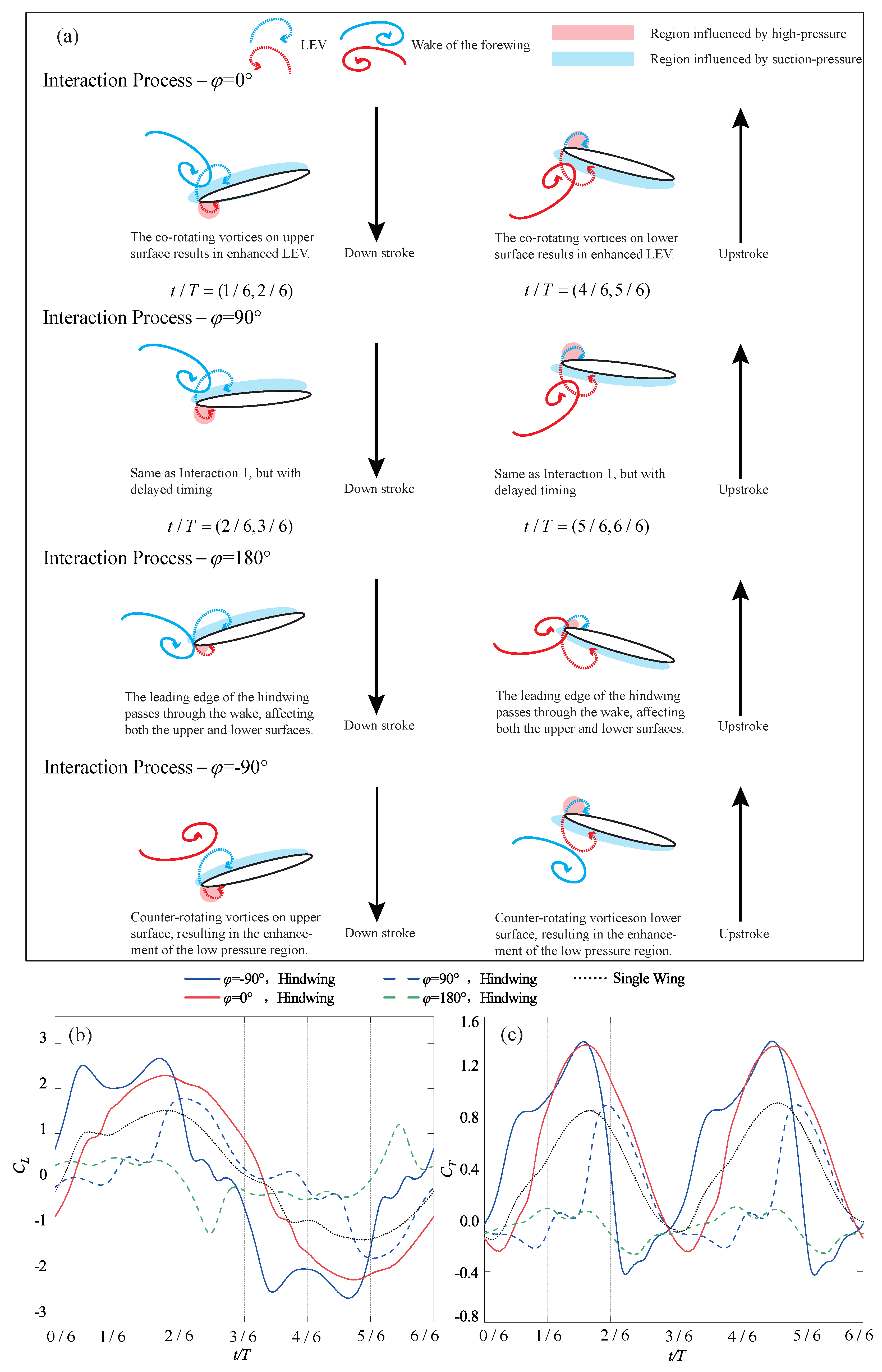
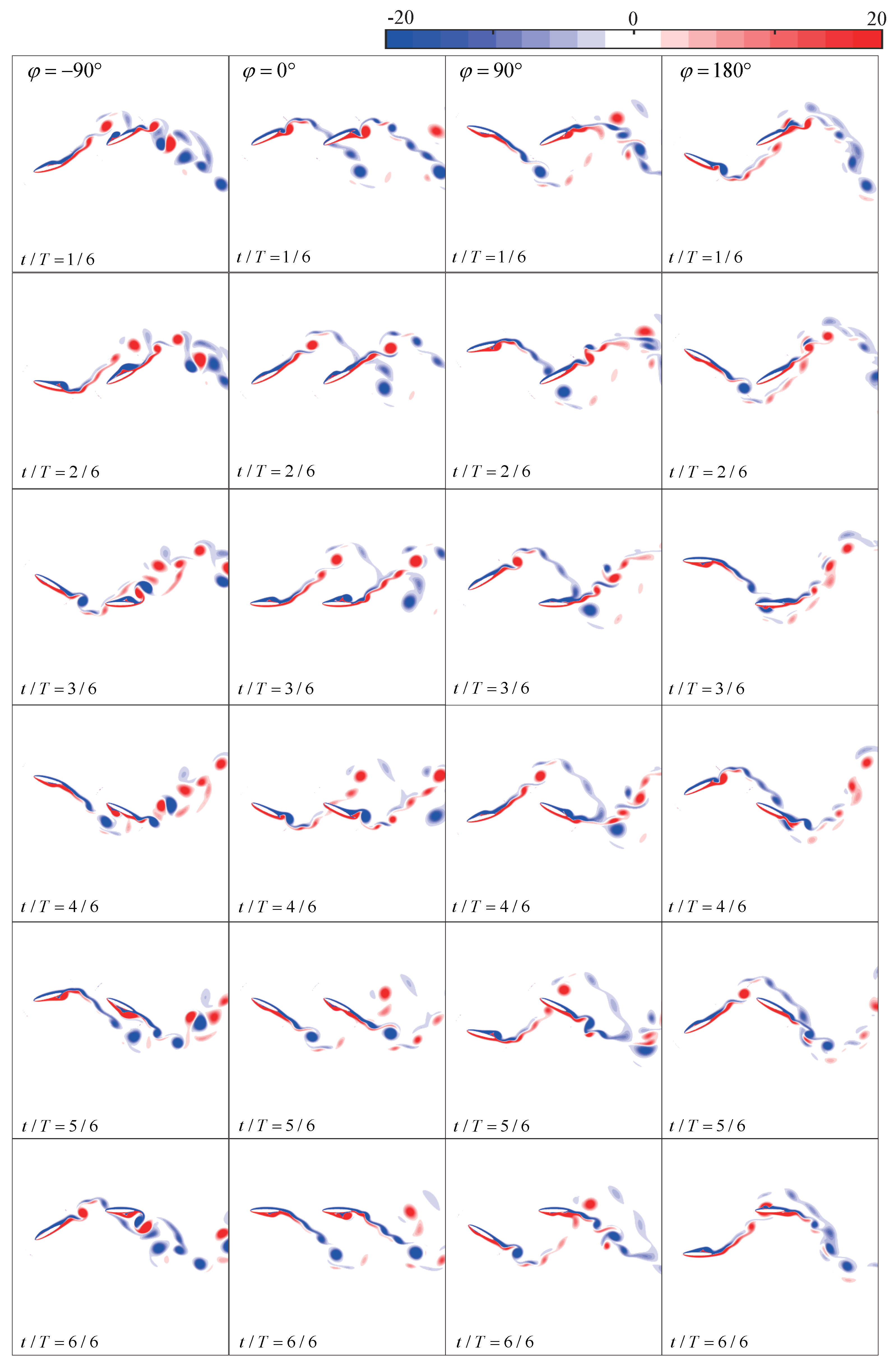
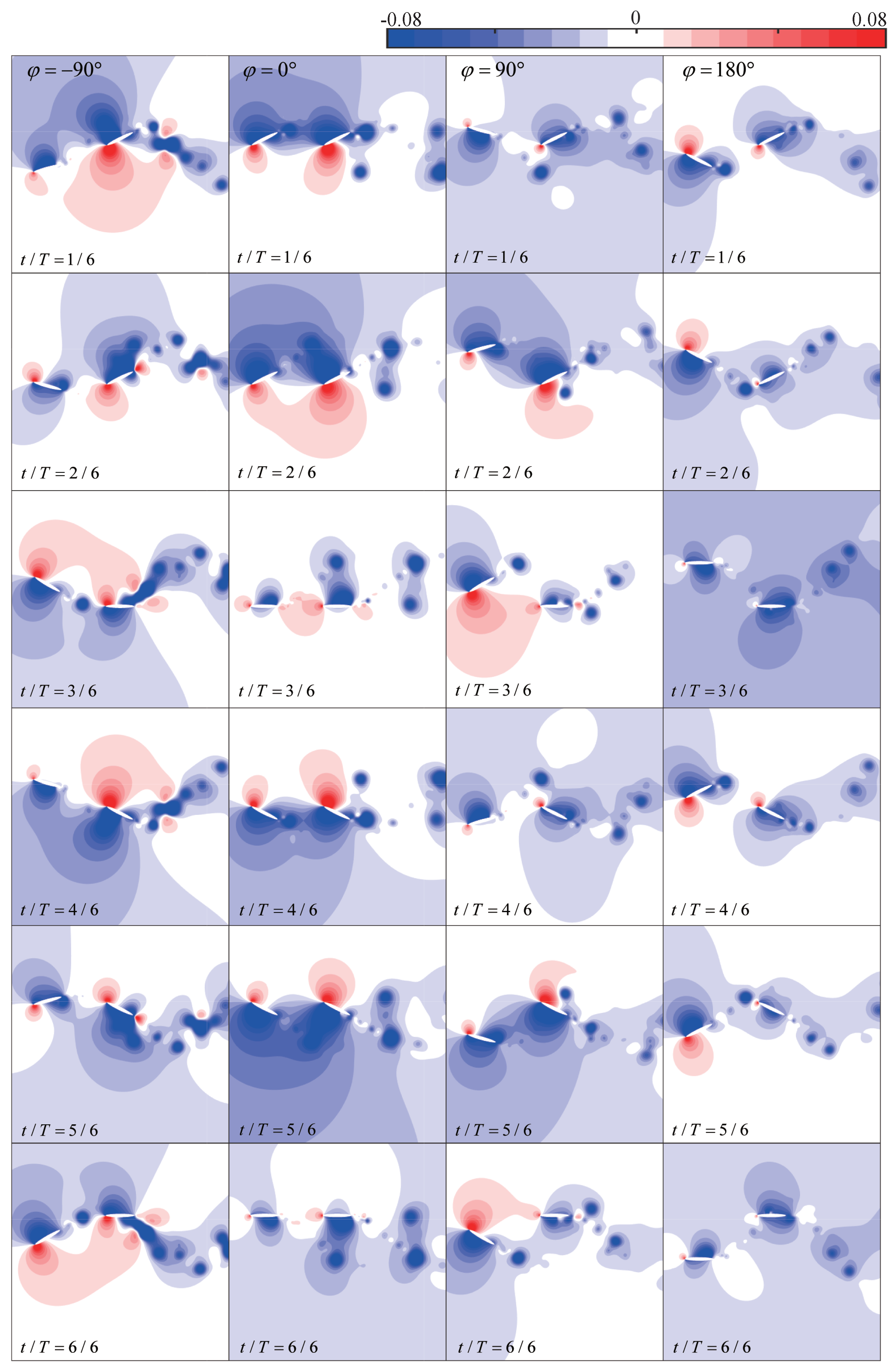
4.2. Phase Difference
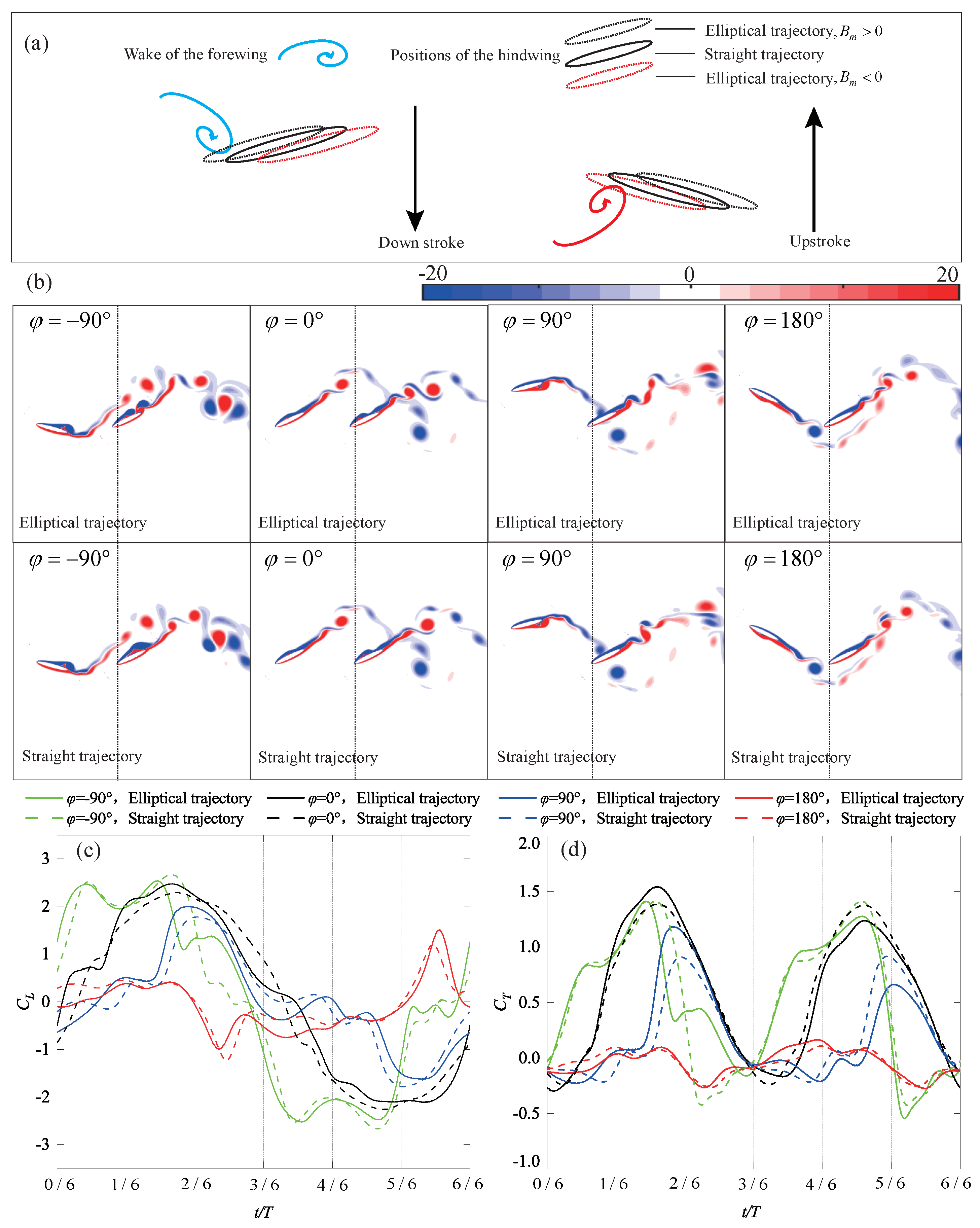
4.3. Surging Motion
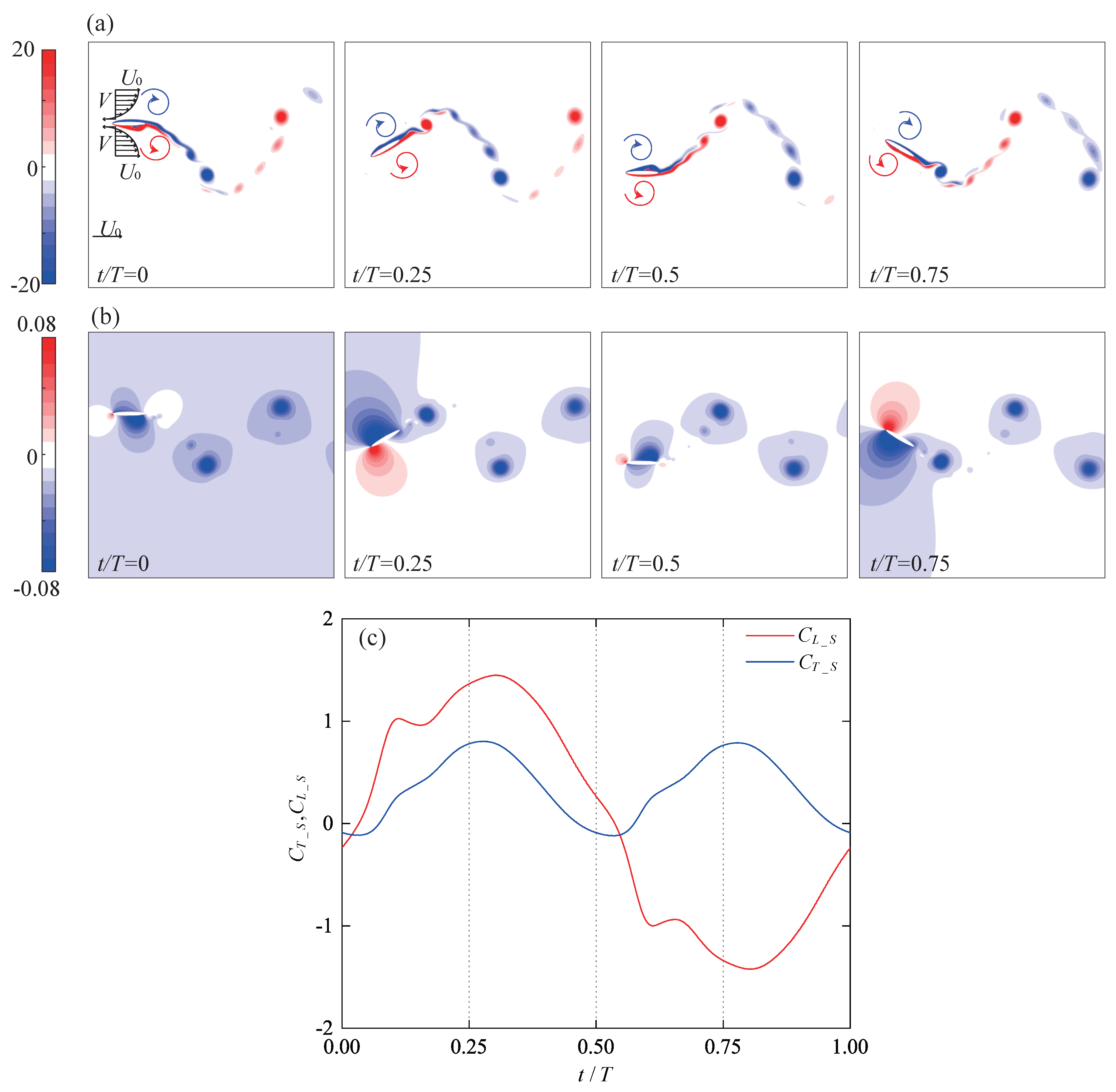
4.3.1. Elliptical Trajectory
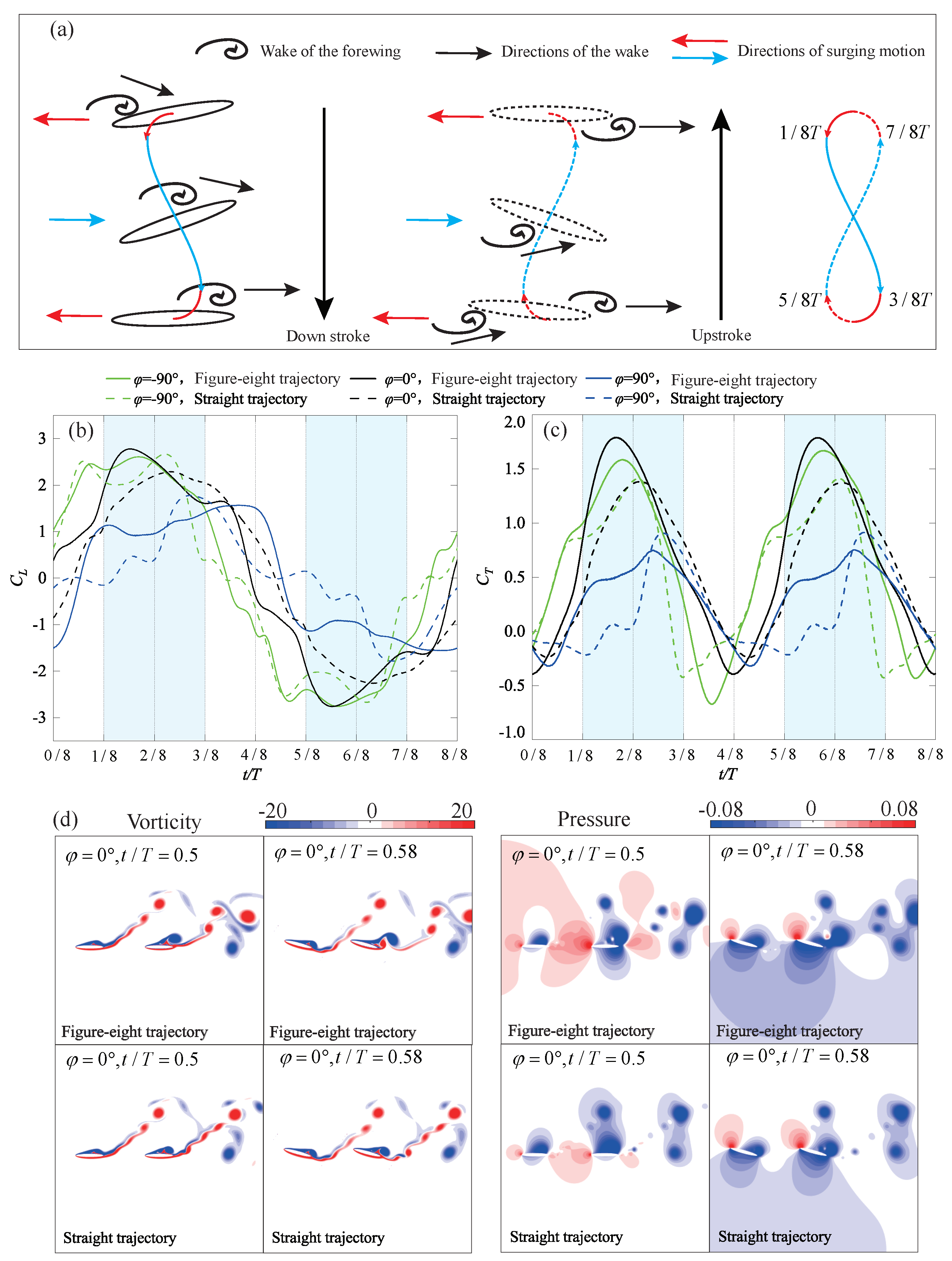
4.3.2. Figure-Eight Trajectory
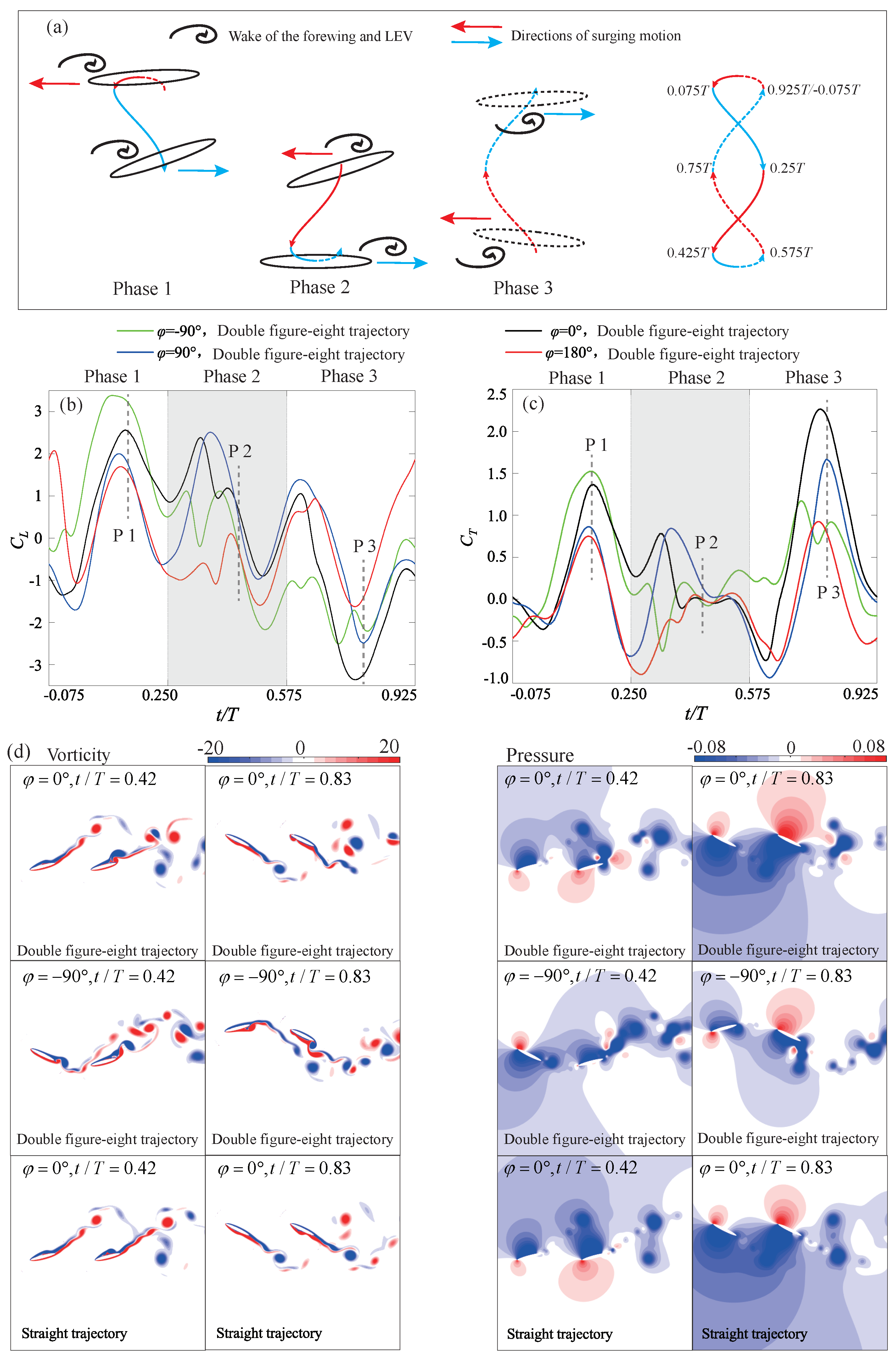
4.3.3. Double Figure-Eight Trajectory
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
- The following abbreviation is used in this manuscript:
| LEV | Leading-Edge Vortices |
Appendix A
- 1.
- When , L, and are fixed, the thrust coefficient of the hindwing and the lift coefficient of the hindwing can be considered to be functions of , and . Once the flow field reaches a quasi-steady state, it can be considered that:
- 2.
- Due to the trigonometric properties of the motion trajectory, when k is odd, the following relationship exists:
- 3.
- Assuming there is a symmetric motion as shown in Figure A1, with flow field variations identical to the original motion but observed from a different perspective.
- 4.
- Combining Equations (A2) and (A4):This means that trajectories with and actually have the same , differing only by half a period in phase. Therefore, the mean thrust coefficients are equal. Similarly, it can be concluded that their satisfy that: . The conditions for the above relations to hold are that k is an odd number.

References
- Alexander, R. Form and function of insect wings: The evolution of biological structures. Nature 2000, 405, 17–18. [Google Scholar] [CrossRef]
- Shyy, W.; Lian, Y.; Tang, J.; Viieru, D.; Liu, H. Aerodynamics of Low Reynolds Number Flyers; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Vargas, A.; Mittal, R.; Dong, H. A computational study of the aerodynamic performance of a dragonfly wing section in gliding flight. Bioinspir. Biomim. 2008, 3, 026004. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Lahooti, M.; Kim, D. Aerodynamic characteristics of unsteady gap flow in a bristled wing. Phys. Fluids 2018, 30, 071901. [Google Scholar] [CrossRef]
- Cheng, X.; Sun, M. Wing kinematics and aerodynamic forces in miniature insect Encarsia formosa in forward flight. Phys. Fluids 2021, 33, 021905. [Google Scholar] [CrossRef]
- Zheng, L.; Hedrick, T.L.; Mittal, R. Time-Varying Wing-Twist Improves Aerodynamic Efficiency of Forward Flight in Butterflies. PLoS ONE 2013, 8, e53060. [Google Scholar] [CrossRef] [PubMed]
- Noda, R.; Liu, X.; Hefler, C.; Shyy, W.; Qiu, H.H. The interplay of kinematics and aerodynamics in multiple flight modes of a dragonfly. J. Fluid Mech. 2023, 967, A31. [Google Scholar] [CrossRef]
- Li, C.; Dong, H. Wing kinematics measurement and aerodynamics of a dragonfly in turning flight. Bioinspir. Biomim. 2017, 12, 026001. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Hu, K.; Huang, B.; Deng, H.; Ding, X. A Review of Research on the Mechanical Design of Hoverable Flapping Wing Micro-Air Vehicles. J. Bionic Eng. 2021, 18, 1235–1254. [Google Scholar] [CrossRef]
- Hu, Y.; Ru, W.; Liu, Q.; Wang, Z. Design and Aerodynamic Analysis of Dragonfly-like Flapping Wing Micro Air Vehicle. J. Bionic Eng. 2022, 19, 343–354. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, H.; Xu, L.; Xie, P.; Wu, J.; Wang, C. Mechanism and Kinematics for Flapping Wing Micro Air Vehicles Maneuvering Based on Bilateral Wings. Int. J. Aerosp. Eng. 2022, 2022, 5759343. [Google Scholar] [CrossRef]
- Zhang, R.; Hu, W.; Zheng, X.; Xu, L.; Wang, C. Improvement of Flapping Mechanism and Measurement of Aerodynamic Force/Moment of Bionic Dragonfly Prototype. J. Aerosp. Power 2022, 37, 2729–2735. [Google Scholar]
- Jia, B.B.; Gong, W.Q. Force and Flow Field Measurement System for Tandem Flapping Wings. Exp. Tech. 2016, 40, 1495–1509. [Google Scholar] [CrossRef]
- Sun, X.; Gong, X.; Huang, D. A review on studies of the aerodynamics of different types of maneuvers in dragonflies. Arch. Appl. Mech. 2017, 87, 521–554. [Google Scholar] [CrossRef]
- Guyon, E.; Hulin, J.-P.; Petit, L. Hydrodynamique Physique; EDP Sciences: Paris, France, 2012. [Google Scholar]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Lua, K.B.; Lim, T.T.; Yeo, K.S.; Oo, G.Y. Wake-structure formation of a heaving two-dimensional elliptic airfoil. AIAA J. 2007, 45, 1571–1583. [Google Scholar] [CrossRef]
- Anderson, J.; Streitlien, K.; Barrett, D.; Triantafyllou, M. Oscillating foils of high propulsive efficiency. J. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Nakata, T.; Henningsson, P.; Lin, H.T. Flight of the dragonflies and damselflies. Philos. Trans. R. Soc. B-Biol. Sci. 2016, 371, 20150389. [Google Scholar] [CrossRef]
- Liu, X.; Hefler, C.; Shyy, W.; Qiu, H. The Importance of Flapping Kinematic Parameters in the Facilitation of the Different Flight Modes of Dragonflies. J. Bionic Eng. 2021, 18, 419–427. [Google Scholar] [CrossRef]
- Lian, Y.; Broering, T.; Hord, K.; Prater, R. The characterization of tandem and corrugated wings. Prog. Aeosp. Sci. 2014, 65, 41–69. [Google Scholar] [CrossRef]
- Gong, W.Q.; Jia, B.B.; Xi, G. Experimental study on instantaneous thrust and lift of two plunging wings in tandem. Exp. Fluids 2016, 57, 8. [Google Scholar] [CrossRef]
- Azuma, A.; Watanabe, T. Flight performance of a dragonfly. J. Exp. Biol. 1988, 137, 221–252. [Google Scholar] [CrossRef]
- Wang, Z.J. The role of drag in insect hovering. J. Exp. Biol. 2004, 207, 4147–4155. [Google Scholar] [CrossRef] [PubMed]
- Norberg, R.A. Hovering flight of the dragonfly Aeschna juncea L., kinematics and aerodynamics. In Swimming and Flying in Nature; Wu, T.Y., Brokaw, C.J., Brennen, C., Eds.; Plenum Press: New York, NY, USA, 1975; pp. 763–781. [Google Scholar]
- Alexander, D. Unusual Phase-Relationships between the Forewings and Hindwings in Flying Dragonflies. J. Exp. Biol. 1984, 109, 379–383. [Google Scholar] [CrossRef]
- Thomas, A.L.R.; Taylor, G.K.; Srygley, R.B.; Nudds, R.L.; Bomphrey, R.J. Dragonfly flight: Free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms, controlled primarily via angle of attack. J. Exp. Biol. 2004, 207, 4299–4323. [Google Scholar] [CrossRef] [PubMed]
- Lan, S.; Sun, M. Aerodynamic force and flow structures of two airfoils in flapping motions. Acta Mech. Sin. 2001, 17, 310–331. [Google Scholar]
- Lua, K.B.; Lu, H.; Zhang, X.H.; Lim, T.T.; Yeo, K.S. Aerodynamics of two-dimensional flapping wings in tandem configuration. Phys. Fluids 2016, 28, 121901. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Y.; Tang, H. An experimental study on the forewing-hindwing interactions in hovering and forward flights. Int. J. Heat Fluid Flow 2016, 59, 62–73. [Google Scholar] [CrossRef]
- Muscutt, L.E.; Weymouth, G.D.; Ganapathisubramani, B. Performance augmentation mechanism of in-line tandem flapping foils. J. Fluid Mech. 2017, 827, 484–505. [Google Scholar] [CrossRef]
- Peng, L.; Zheng, M.; Pan, T.; Su, G.; Li, Q. Tandem-wing interactions on aerodynamic performance inspired by dragonfly hovering. R. Soc. Open Sci. 2021, 8, 202275. [Google Scholar] [CrossRef]
- Gong, W.Q.; Jia, B.B.; Xi, G. Experimental Study on Mean Thrust of Two Plunging Wings in Tandem. AIAA J. 2015, 53, 1693–1705. [Google Scholar] [CrossRef]
- Nagai, H.; Fujita, K.; Murozono, M. Experimental Study on Forewing-Hindwing Phasing in Hovering and Forward Flapping Flight. AIAA J. 2019, 57, 3779–3790. [Google Scholar] [CrossRef]
- Boschitsch, B.M.; Dewey, P.A.; Smits, A.J. Propulsive performance of unsteady tandem hydrofoils in an in-line configuration. Phys. Fluids 2014, 26, 051901. [Google Scholar] [CrossRef]
- Heydari, S.; Kanso, E. School cohesion, speed and efficiency are modulated by the swimmers flapping motion. J. Fluid Mech. 2021, 922, A27. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Chen, L. Enhanced performance of tandem plunging airfoils with an asymmetric pitching motion. Phys. Fluids 2022, 34, 011910. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Zhang, T.; Yang, L. Flow-mediated organization of two freely flapping swimmers. J. Fluid Mech. 2021, 912, A37. [Google Scholar] [CrossRef]
- Joshi, V.; Mysa, R.C. Mechanism of wake-induced flow dynamics in tandem flapping foils: Effect of the chord and gap ratios on propulsion. Phys. Fluids 2021, 33, 087104. [Google Scholar] [CrossRef]
- Fry, S.N.; Sayaman, R.; Dickinson, M.H. The aerodynamics of hovering flight in Drosophila. J. Exp. Biol. 2005, 208, 2303–2318. [Google Scholar] [CrossRef] [PubMed]
- Willmott, A.P.; Ellington, C.P. The mechanics of flight in the hawkmoth Manduca sexta I. Kinematics of hovering and forward flight. J. Exp. Biol. 1997, 200, 2705–2722. [Google Scholar] [CrossRef] [PubMed]
- Wakeling, J.M.; Ellington, C.P. Dragonfly flight: II. Velocities, accelerations and kinematics of flapping flight. J. Exp. Biol. 1997, 200, 557–582. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.H.; Skote, M.; Zhao, Y.; Huang, W.M. Dragonfly (Sympetrum flaveolum) flight: Kinematic measurement and modelling. J. Fluids Struct. 2013, 40, 115–126. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, J. Kinematics, Deformation, and Aerodynamics of a Flexible Flapping Rotary Wing in Hovering Flight. J. Bionic Eng. 2021, 18, 197–209. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, C.; Zhu, X. Influences of flapping modes and wing kinematics on aerodynamic performance of insect hovering flight. J. Mech. Sci. Technol. 2020, 34, 1603–1612. [Google Scholar] [CrossRef]
- Amiralaei, M.R.; Alighanbari, H.; Hashemi, S.M. Flow field characteristics study of a flapping airfoil using computational fluid dynamics. J. Fluids Struct. 2011, 27, 1068–1085. [Google Scholar] [CrossRef]
- Esfahani, J.A.; Barati, E.; Karbasian, H.R. Fluid structures of flapping airfoil with elliptical motion trajectory. Comput. Fluids 2015, 108, 142–155. [Google Scholar] [CrossRef]
- Yang, S.; Liu, C.; Wu, J. Effect of motion trajectory on the aerodynamic performance of a flapping airfoil. J. Fluids Struct. 2017, 75, 213–232. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, C.; Wang, C.; Xie, P. Aerodynamic characteristics of dragonfly in asymmetric flapping. Acta Aeronaut. Astronaut. Sin. 2017, 38, 121389. [Google Scholar]
- Li, Q.; Zheng, M.; Pan, T.; Su, G. Experimental and Numerical Investigation on Dragonfly Wing and Body Motion during Voluntary Take-off. Sci. Rep. 2018, 8, 1011. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, R.; Zhou, C.; Sun, Z. Numerical Investigation on Flapping Aerodynamic Performance of Dragonfly Wings in Crosswind. Int. J. Aerosp. Eng. 2020, 2020, 7325154. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lua, K.B.; Lim, T.T.; Yeo, K.S. A quasi-steady aerodynamic model for flapping flight with improved adaptability. Bioinspir. Biomim. 2016, 11, 036005. [Google Scholar] [CrossRef] [PubMed]
- Broering, T.M.; Lian, Y.S. The effect of phase angle and wing spacing on tandem flapping wings. Acta Mech. Sin. 2012, 28, 1557–1571. [Google Scholar] [CrossRef]
- Tuncer, I.H.; Kaya, M. Thrust generation caused by flapping airfoils in a biplane configuration. J. Aircraft 2003, 40, 509–515. [Google Scholar] [CrossRef]
- Miao, J.M.; Ho, M.H. Effect of flexure on aerodynamic propulsive efficiency of flapping flexible airfoil. J. Fluids Struct. 2006, 22, 401–419. [Google Scholar] [CrossRef]

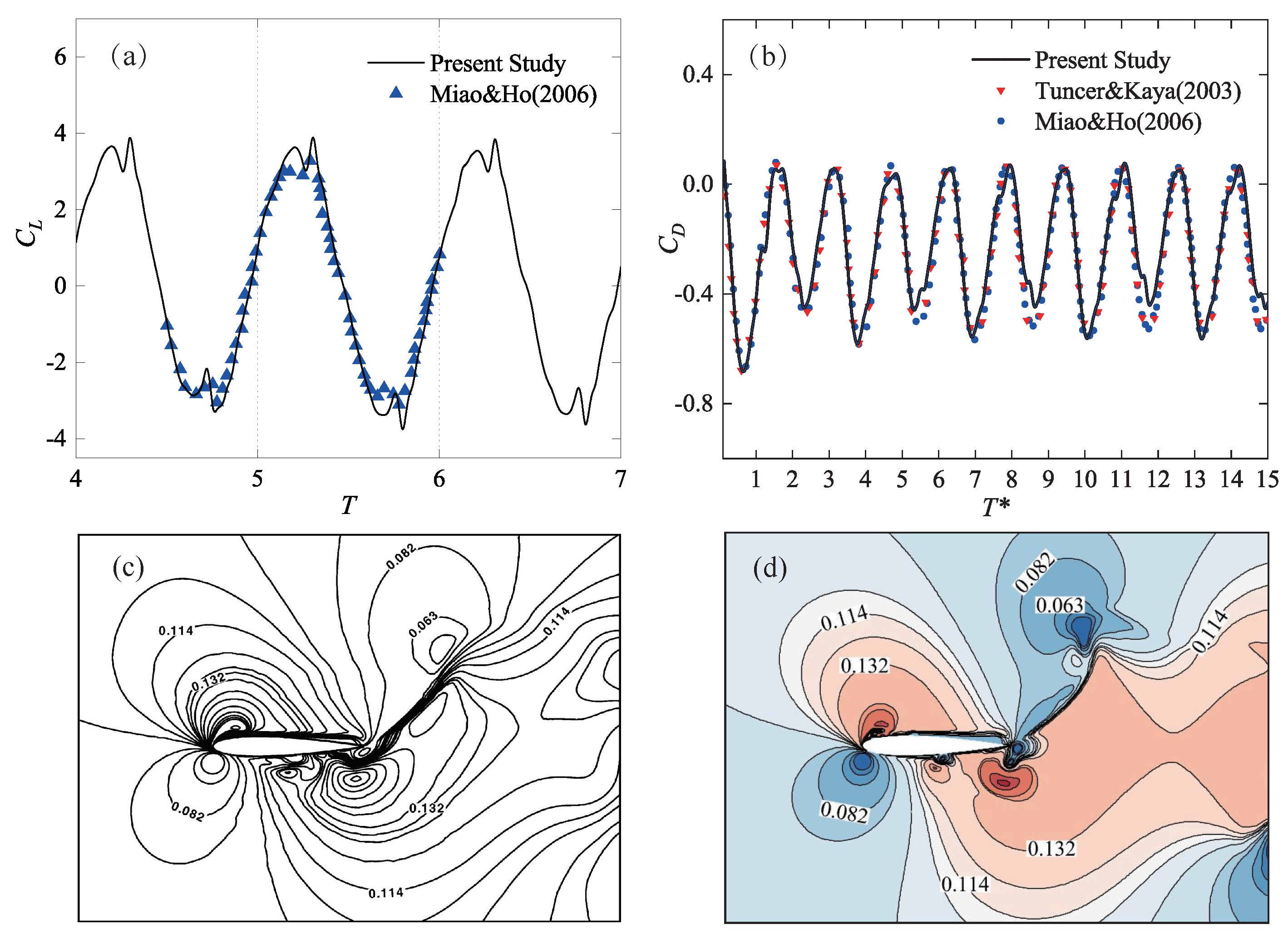
| Number | Number of Cells in the Foreground Grid | ||||
|---|---|---|---|---|---|
| Mesh 1 | 3000 | 1.546 | −2.08% | 1.224 | −2.21% |
| Mesh 2 | 12,000 | 1.580 | 0.07% | 1.242 | −0.76% |
| Mesh 3 | 27,000 | 1.574 | −0.30% | 1.242 | −0.76% |
| Mesh 4 | 48,000 | 1.579 | - | 1.251 | - |
| Number | Time Step Size | ||||
|---|---|---|---|---|---|
| Case 1 | 1.559 | −1.541% | 1.219 | −2.949% | |
| Case 2 | 1.564 | −1.210% | 1.235 | −1.650% | |
| Case 3 | 1.573 | −0.606% | 1.246 | −0.822% | |
| Case 4 | 1.583 | - | 1.256 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wang, C.; Jia, P.; Zhong, Z. The Effect of Hindwing Trajectories on Wake–Wing Interactions in the Configuration of Two Flapping Wings in Tandem. Biomimetics 2024, 9, 406. https://doi.org/10.3390/biomimetics9070406
He X, Wang C, Jia P, Zhong Z. The Effect of Hindwing Trajectories on Wake–Wing Interactions in the Configuration of Two Flapping Wings in Tandem. Biomimetics. 2024; 9(7):406. https://doi.org/10.3390/biomimetics9070406
Chicago/Turabian StyleHe, Xu, Chao Wang, Pan Jia, and Zheng Zhong. 2024. "The Effect of Hindwing Trajectories on Wake–Wing Interactions in the Configuration of Two Flapping Wings in Tandem" Biomimetics 9, no. 7: 406. https://doi.org/10.3390/biomimetics9070406
APA StyleHe, X., Wang, C., Jia, P., & Zhong, Z. (2024). The Effect of Hindwing Trajectories on Wake–Wing Interactions in the Configuration of Two Flapping Wings in Tandem. Biomimetics, 9(7), 406. https://doi.org/10.3390/biomimetics9070406






