A City Shared Bike Dispatch Approach Based on Temporal Graph Convolutional Network and Genetic Algorithm
Abstract
1. Introduction
- We employ the T-GCN to predict bike demand by capturing spatiotemporal features and conducting comparative analysis across multiple time intervals. The analysis shows that the prediction algorithm performs well at a 30-min interval, which can be considered a reasonable redistribution interval in practical applications.
- When modeling the bike redistribution problem, we fully consider the complexity of real-time redistribution scenarios. The model takes into account different types of redistribution vehicles with different capacity constraints, the requirement for vehicles to complete the delivery process within a limited time, and the possibility of a station being visited by single or multiple vehicles simultaneously and repeatedly. These considerations make the model more realistic.
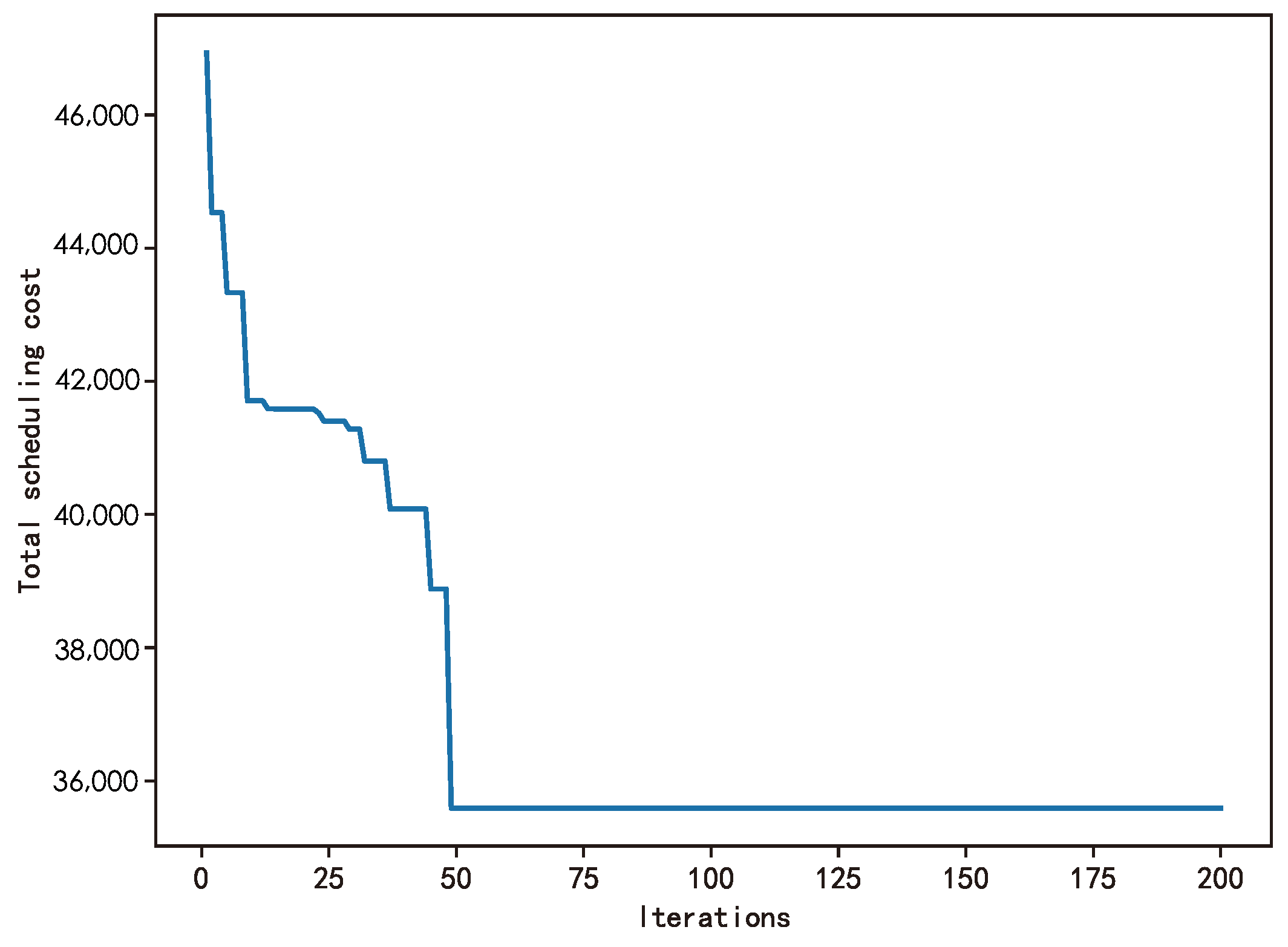
- We design a cost-minimizing solution based on a genetic algorithm and validate its efficiency and applicability through simulations. In the problem scenario, the genetic algorithm converges in approximately 50 generations, demonstrating high computational efficiency, and enabling rapid response or the handling of large-scale datasets. The algorithm shows good adaptability across different time redistribution scenarios within a day, effectively coping with dynamically changing demand and exhibiting high robustness.
2. Related Work
2.1. Bike-Sharing Rebalancing Problem
2.2. Traffic Flow Forecasting
2.3. Dispatching Optimization
3. Problem Description and Methodology
3.1. Problem Description
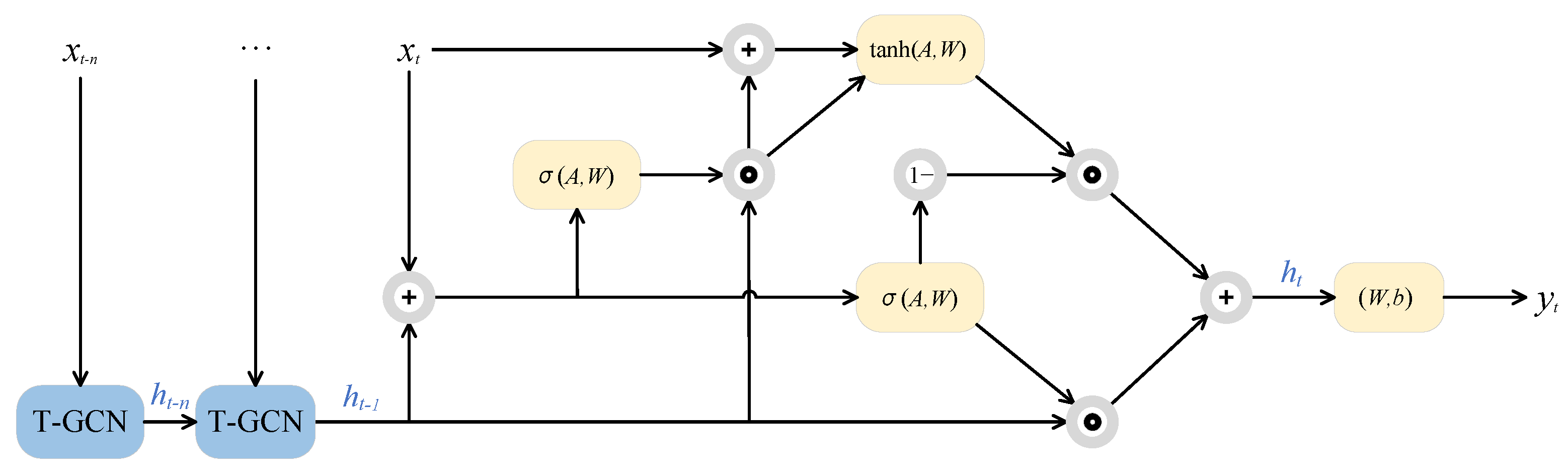
3.2. Demand Forecasting Model
3.3. Dispatching Optimization Model
3.3.1. Notation Descriptions
3.3.2. Problem Definition and Hypothesis
- Dispatching is carried out in the form of task reward release, dispatching vehicles have no fixed cost, and only dispatching vehicles within the starting point of the path node can accept tasks.
- The distance between nodes is measured by the Manhattan distance.
- There are very few orders during the dispatching period; so, the bike movement has little impact on the overall system.
- The starting point of the dispatching car must be a node with , and the endpoint must be a node with .
- In a dispatch trip, vehicles can pick up and drop bikes at multiple nodes, but all bikes must be completely dropped by the end of the dispatch trip.
- In each pick-up area, the number of bikes picked up by the vehicle should meet the pick-up requirements as much as possible without exceeding the vehicle’s load capacity.
- At each delivery area, the vehicle needs to unload the required bikes for the area or all the bikes, but the unloaded bikes cannot exceed the amount required by the area.
3.3.3. Mathematical Model
3.3.4. Problem Solving
- EncodeIn this work, we have chosen the encoding of natural numbers to be consistent with the encoding of nodes, such as , which indicates a simple dispatching path. The random full permutation generating path is used as the initial population.
- DecodeOn the dispatching path, the dispatch vehicle may exhibit one of four behaviors when passing through node i, which are as follows:
- (a)
- The vehicle will pick up all extra bikes in node i.
- (b)
- The vehicle will pick up a portion of bikes at pick-up node i, potentially reaching its full load capacity during the dispatch process.
- (c)
- The dispatch vehicle drops all its bikes at node i, yet the demand at node i remains unmet.
- (d)
- The vehicle unloads enough bikes to meet the demand at node i, but there are still excess bikes remaining on the dispatch vehicle.
To deal with these behaviors, the following decoding rules are formulated:- (a)
- Alternate dispatching: Based on bike demands, nodes are categorized into pick-up nodes and delivery nodes, representing positive and negative demands, respectively. Dispatching operations involve collecting bikes from pick-up areas to reduce excess and delivering them to delivery areas to meet demands. In each operation, the dispatch vehicle must be fully loaded first and completely unloaded by the end of the dispatch.
- (b)
- Chromosome expansion: Nodes that meet the requirements are removed from the partition list. If behaviors (b) and (c) are encountered, indicating that the requirements for node i are not met, the requirements for node i are retained and updated in the partition. The scheduler continues to dispatch based on the partition and expands the chromosome to indicate that the path can be repeated. For example, the chromosome is extended to , indicating that the dispatch vehicle did not meet the requirements of node 2 on the first visit and returns to node 2 after processing node 3.
- (c)
- Chromosome splitting: When the dispatch vehicle completes one cycle of alternate dispatching and the next cycle exceeds the maximum distance limit, the chromosome is split. For example, splitting the chromosome results in , indicating that the dispatch path for the first vehicle is , the second vehicle’s path is , and the third vehicle’s path is .
- Fitness FunctionThe fitness function is defined as the total dispatching cost of shared bikes, aligning with the objective function. A smaller fitness value indicates a better solution.
| Algorithm 1 Genetic Algorithm |
| Input: : a matrix represents the number of nodes required, P: population size, : crossover probability, : mutation probability, T: iterations |
| Output: Routes: dispatch routes. Cost: dispatching cost |
| begin |
| 1: Initialize population with randomly generated chromosomes using natural number encoding; |
| 2: ; |
| 3: while do |
| 4: for to P do |
| 5: Evaluate fitness of each chromosome in ; |
| 6: end for |
| 7: for to M do |
| 8: Select parent chromosomes for crossover from ; |
| 9: end for |
| 10: for to do |
| 11: Perform crossover operation on selected parent chromosomes; |
| 12: end for |
| 13: for to M do |
| 14: Perform mutation operation on chromosomes in ; |
| 15: end for |
| 16: for to M do |
| 17: Decode chromosomes in using the decoding rules; |
| 18: Update chromosomes in according to the decoded results; |
| 19: end for |
| 20: ; |
| 21: end while |
| 22: end |
4. Experimental Analysis
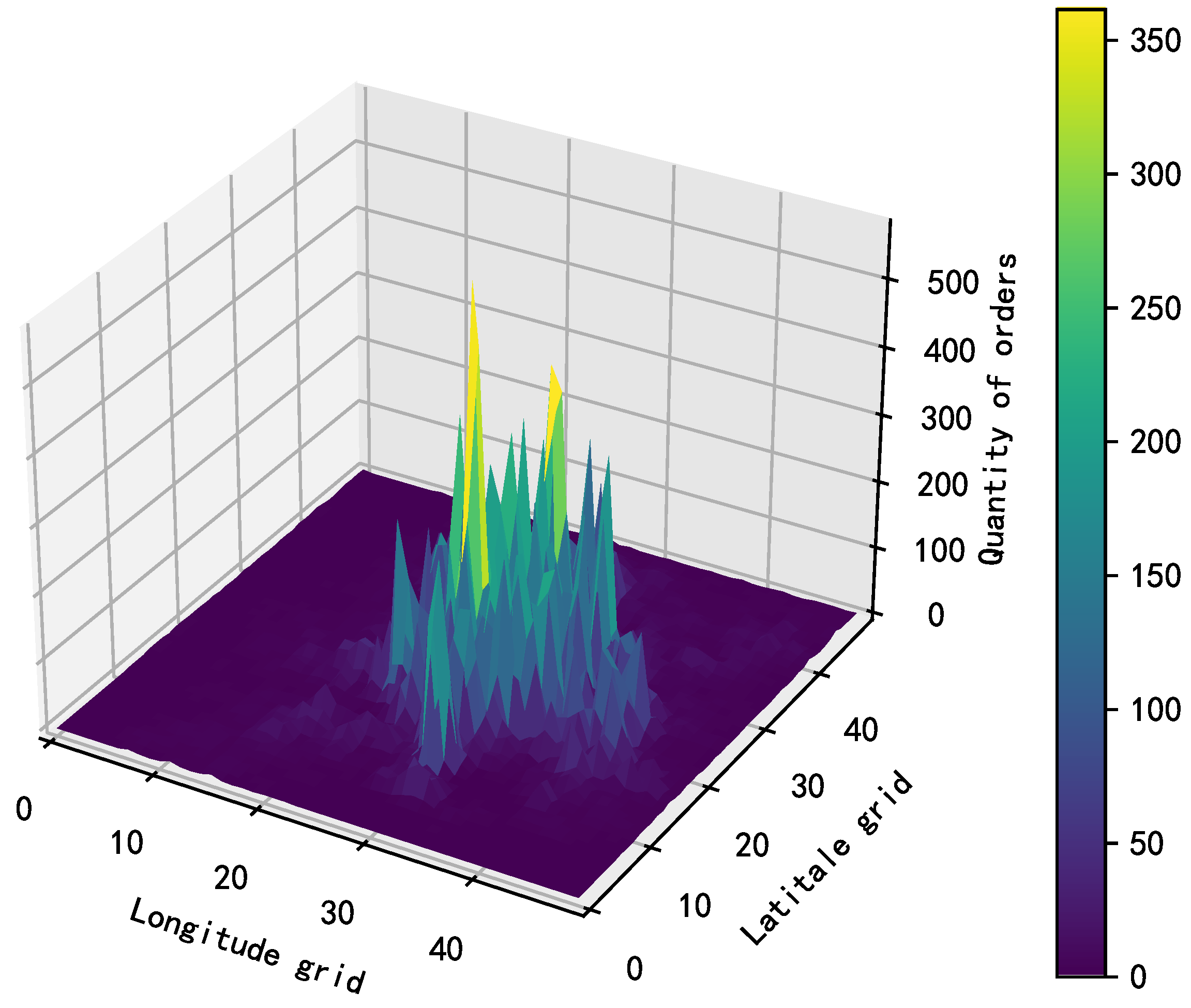
4.1. Experimental Data
4.1.1. Data Sources
4.1.2. Data Preprocessing
4.2. Performance Indicators
4.3. Demand Forecasting Experiment
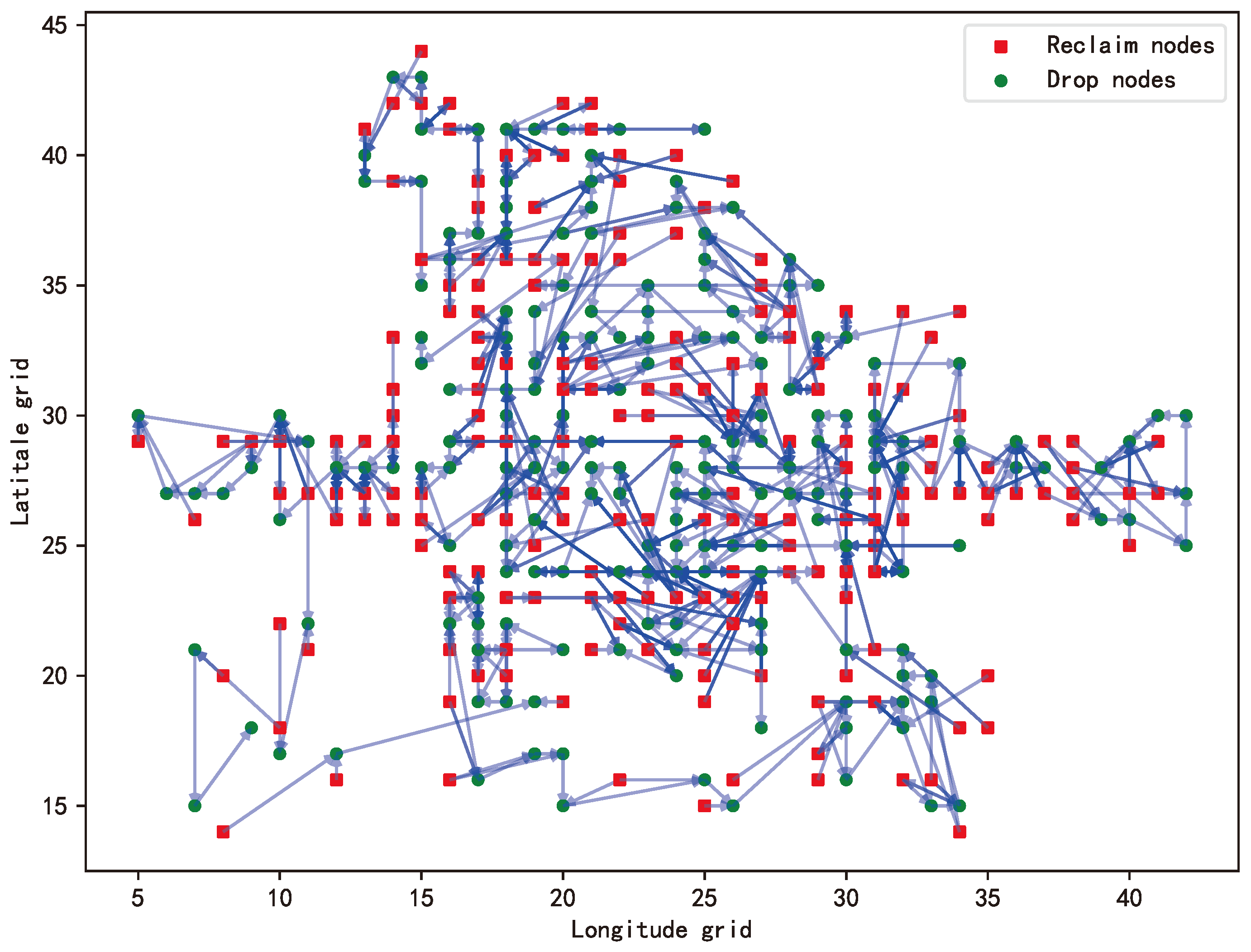
4.4. Dispatching Optimization Experiment
4.5. Results
4.5.1. Experimental Results of the Demand Prediction
4.5.2. Experimental Results of the Dispatching Optimization
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Lin, J.; Yang, Y.; Guo, J. A digital decision approach for scheduling process planning of shared bikes under Internet of Things environment. Appl. Soft Comput. 2023, 133, 109934. [Google Scholar] [CrossRef]
- Akova, H.; Hulagu, S.; Celikoglu, H. Static bike repositioning problem with heterogeneous distribution haracteristics in bike sharing systems. Transp. Res. Procedia 2022, 62, 205–212. [Google Scholar] [CrossRef]
- Bruck, B.P.; Subramanian, A. Bike-Sharing Rebalancing Problems. In Encyclopedia of Optimization; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–9. [Google Scholar]
- Dell’Amico, M.; Hadjicostantinou, E.; Iori, M.; Novellani, S. The bike sharing rebalancing problem: Mathematical formulations and benchmark instances. Omega 2014, 45, 7–19. [Google Scholar] [CrossRef]
- Kadri, A.A.; Kacem, I.; Labadi, K. A branch-and-bound algorithm for solving the static rebalancing problem in bicycle-sharing systems. Comput. Ind. Eng. 2016, 95, 41–52. [Google Scholar] [CrossRef]
- Cruz, F.; Subramanian, A.; Bruck, B.P.; Iori, M. A heuristic algorithm for a single vehicle static bike sharing rebalancing problem. Comput. Oper. Res. 2017, 79, 19–33. [Google Scholar] [CrossRef]
- Pal, A.; Zhang, Y. Free-floating bike sharing: Solving real-life large-scale static rebalancing problems. Transp. Res. Part C Emerg. Technol. 2017, 80, 92–116. [Google Scholar] [CrossRef]
- Schuijbroek, J.; Hampshire, R.C.; Van Hoeve, W.J. Inventory rebalancing and vehicle routing in bike sharing systems. Eur. J. Oper. Res. 2017, 257, 992–1004. [Google Scholar] [CrossRef]
- Guo, R.; Jiang, Z.; Huang, J.; Tao, J.; Wang, C.; Li, J.; Chen, L. BikeNet: Accurate bike demand prediction using graph neural networks for station rebalancing. In Proceedings of the 2019 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Leicester, UK, 19–23 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 686–693. [Google Scholar]
- Vincent, F.Y.; Aloina, G.; Jodiawan, P.; Gunawan, A.; Huang, T.C. The vehicle routing problem with simultaneous pickup and delivery and occasional drivers. Expert Syst. Appl. 2023, 214, 119118. [Google Scholar]
- Shi, B.; Huang, X.; Song, Z.; Xu, J. User incentive bike-sharing dispatching mechanism. J. Comput. Appl. 2022, 42, 3395–3403. [Google Scholar]
- Chandra, S.R.; Al-Deek, H. Predictions of freeway traffic speeds and volumes using vector autoregressive models. J. Intell. Transp. Syst. 2009, 13, 53–72. [Google Scholar] [CrossRef]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 21. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, S.; Tang, J.; Wang, X. Understanding characteristics in multivariate traffic flow time series from complex network structure. Phys. Stat. Mech. Appl. 2017, 477, 149–160. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Hu, Z.; Zong, F.; Han, C.; Li, L. Traffic flow prediction based on combination of support vector machine and data denoising schemes. Phys. Stat. Mech. Appl. 2019, 534, 120642. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, K.; Li, J.; Lin, X.; Yang, B. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 324–328. [Google Scholar]
- Zhao, W.; Gao, Y.; Ji, T.; Wan, X.; Ye, F.; Bai, G. Deep temporal convolutional networks for short-term traffic flow forecasting. IEEE Access 2019, 7, 114496–114507. [Google Scholar] [CrossRef]
- Qu, Z.; Li, H.; Li, Z.; Zhong, T. Short-Term Traffic Flow Forecasting Method With M-B-LSTM Hybrid Network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 225–235. [Google Scholar] [CrossRef]
- Meng, W.; Zhang, K.; Xi, G.; Ma, C.; Huang, X.; Wu, X.; Lai, Y. Application of EEMD+ BI_GRU hybrid model for intelligent service area traffic flow forecasting. Adv. Transp. Stud. 2023, 61, 195–208. [Google Scholar]
- Sadeghi-Niaraki, A.; Mirshafiei, P.; Shakeri, M.; Choi, S. Short-term traffic flow prediction using the modified Elman recurrent neural network optimized through a genetic algorithm. IEEE Access 2020, 8, 217526–217540. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Y.; Qi, Y.; Shu, F.; Wang, Y. Short-term traffic flow prediction based on spatiotemporal analysis and CNN deep learning. Transp. Transp. Sci. 2019, 15, 1688–1711. [Google Scholar]
- Du, S.; Li, T.; Gong, X.; Horng, S. A hybrid method for traffic flow forecasting using multimodal deep learning. Int. J. Comput. Intell. Syst. 2020, 13, 85–97. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Bai, J.; Zhu, J.; Song, Y.; Zhao, L.; Hou, Z.; Du, R.; Li, H. A3t-gcn: Attention temporal graph convolutional network for traffic forecasting. ISPRS Int. J. Geo-Inf. 2021, 10, 485. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Tao, C.; Deng, H.; Zhao, L.; Li, H. AST-GCN: Attribute-augmented spatiotemporal graph convolutional network for traffic forecasting. IEEE Access 2021, 9, 35973–35983. [Google Scholar] [CrossRef]
- Liu, M.; Xv, X.; Ning, J.; Cao, J. Modeling and Optimizing Method for Rebalancing the Dock-less Bicycles based on Order Data Analysis. Chin. J. Manag. Sci. 2022, 30, 275–286. [Google Scholar] [CrossRef]
- Xv, Y.; Zhou, Y.; Huang, J.; Li, Y.; Hei, L. Process planning for scheduling task in bike-sharing service. Comput. Integr. Manuf. Syst. 2022, 28, 3284. [Google Scholar]
- Wang, X.; Zheng, S.; Wang, L.; Han, S.; Liu, L. Multi-objective optimal scheduling model for shared bikes based on spatiotemporal big data. J. Clean. Prod. 2023, 421, 138362. [Google Scholar] [CrossRef]
- Cui, C.; Tian, Z.; Xu, Y. Study On Bike Repositioning Problem with Rental and Return Demand. Syst. Eng. Theory Pract. 2024, 44, 645–660. [Google Scholar] [CrossRef]
- Xu, G.; Li, Y.; Jin, D.; Li, J. A user-based method for the static bike repositioning problem. Syst. Eng. Theory Pract. 2020, 40, 426–436. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Nosouhian, S.; Nosouhian, F.; Khoshouei, A.K. A review of recurrent neural network architecture for sequence learning: Comparison between LSTM and GRU. Comput. Sci. 2021, 2021070252. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| Z | Total dispatch cost |
| Node i coordinates | |
| The number of shared-bikes departing from node i at the start of dispatching | |
| The number of shared-bikes entering node i at the end of dispatch. | |
| The number of bikes required at node i | |
| D | The maximum distance the dispatch vehicle can travel |
| The maximum loading capacity of the dispatch car m | |
| The distance between node i and node j | |
| C | The unit distance cost of dispatching vehicles |
| The number of bikes collected by vehicle m at node i | |
| The number of bikes placed by vehicle m at node i | |
| The decision variable. A binary variable with a value of 1 if vehicle m reaches node j from node i, and 0 otherwise |
| Label | Meaning |
|---|---|
| orderid | Order number |
| orderid | User number |
| bikeid | Cycle number |
| biketype | Bike type |
| starttime | Order start time |
| geohashed_start_loc | Order start location |
| geohashed_end_loc | Order end location |
| Hidden Sizes | Loss (Single-Step) | Loss (Two-Step) | Loss (Four-Step) |
|---|---|---|---|
| 8 | 3.7664 | 5.0739 | 8.5486 |
| 16 | 2.5840 | 3.6724 | 4.7292 |
| 32 | 2.0192 | 2.9346 | 4.1562 |
| 64 | 1.3971 | 1.7332 | 3.4376 |
| 128 | 1.7933 | 2.0697 | 2.7761 |
| 256 | 1.9800 | 2.5230 | 2.8487 |
| Parameters | Meaning | Value(s) |
|---|---|---|
| D | The maximum distance the dispatch vehicle can travel | 10 (KM) |
| The maximum loading capacity of the dispatching car m | 20, 15, 10 (/CAR) | |
| C | The unit distance cost of dispatching vehicles | 3 (CNY/KM) |
| Parameters | Meaning | Value(s) |
|---|---|---|
| l | Chromosome Encoding Length | 2500 |
| p | Population Size | 100 |
| Crossover Probability | 0.95 | |
| Mutation Probability | 0.05 | |
| Maximum Iteration Count | 200 |
| Metrics | 30-min | 60-min | 120-min |
|---|---|---|---|
| 0.4786 | 0.5342 | 0.8147 | |
| 2.2175 | 2.4909 | 3.7291 | |
| 0.8974 | 0.8741 | 0.7131 |
| Time Interval | Number of Iterations at Algorithm Convergence | ||
|---|---|---|---|
| Minimum | Maximum | Average | |
| half hour | 29 | 56 | 34 |
| one hour | 22 | 83 | 51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Zheng, S.; Lin, S.; Cheng, Y. A City Shared Bike Dispatch Approach Based on Temporal Graph Convolutional Network and Genetic Algorithm. Biomimetics 2024, 9, 368. https://doi.org/10.3390/biomimetics9060368
Ma J, Zheng S, Lin S, Cheng Y. A City Shared Bike Dispatch Approach Based on Temporal Graph Convolutional Network and Genetic Algorithm. Biomimetics. 2024; 9(6):368. https://doi.org/10.3390/biomimetics9060368
Chicago/Turabian StyleMa, Ji, Shenggen Zheng, Shangjing Lin, and Yonghong Cheng. 2024. "A City Shared Bike Dispatch Approach Based on Temporal Graph Convolutional Network and Genetic Algorithm" Biomimetics 9, no. 6: 368. https://doi.org/10.3390/biomimetics9060368
APA StyleMa, J., Zheng, S., Lin, S., & Cheng, Y. (2024). A City Shared Bike Dispatch Approach Based on Temporal Graph Convolutional Network and Genetic Algorithm. Biomimetics, 9(6), 368. https://doi.org/10.3390/biomimetics9060368








