A Photosensitivity-Enhanced Plant Growth Algorithm for UAV Path Planning
Abstract
1. Introduction
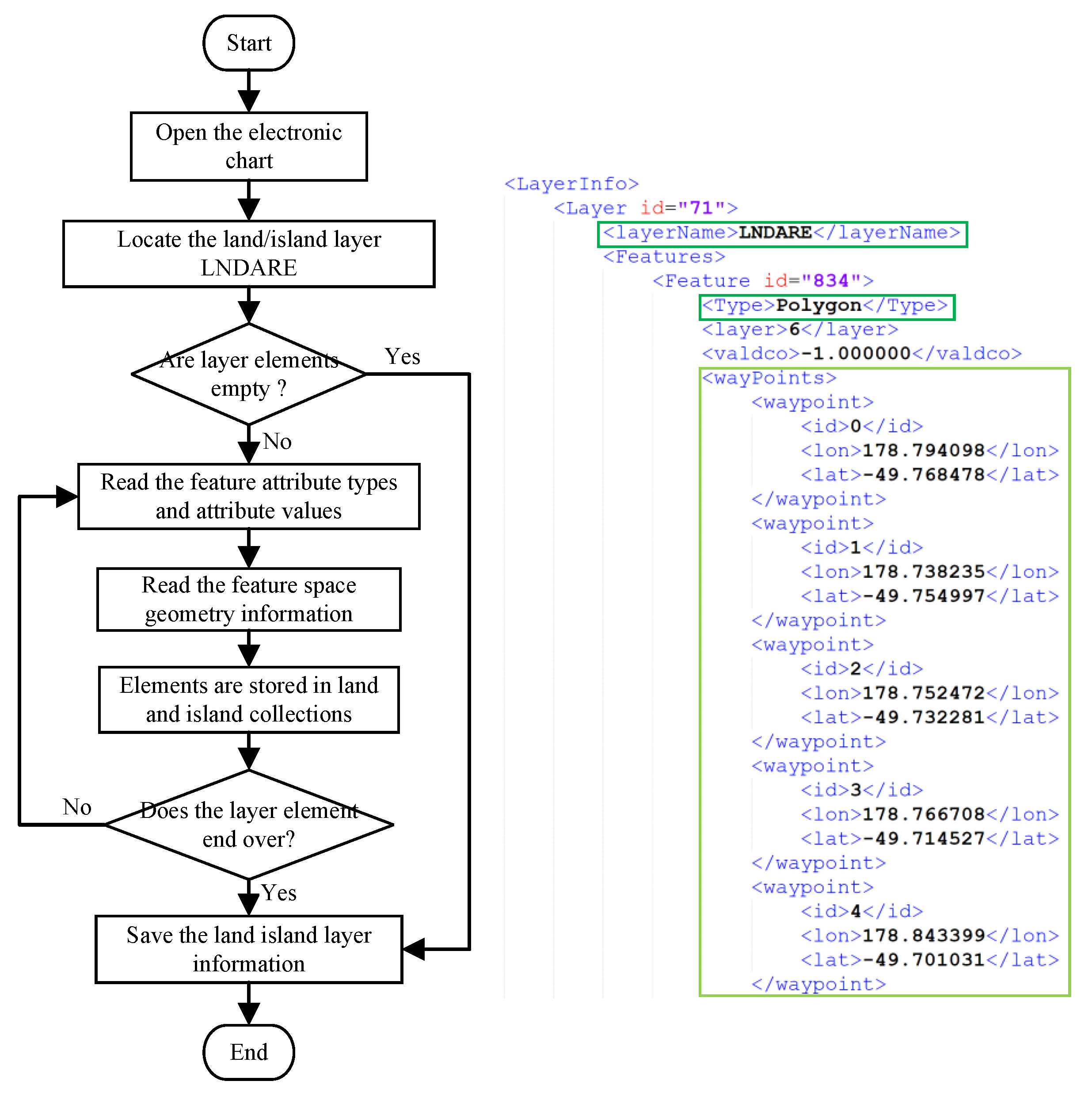
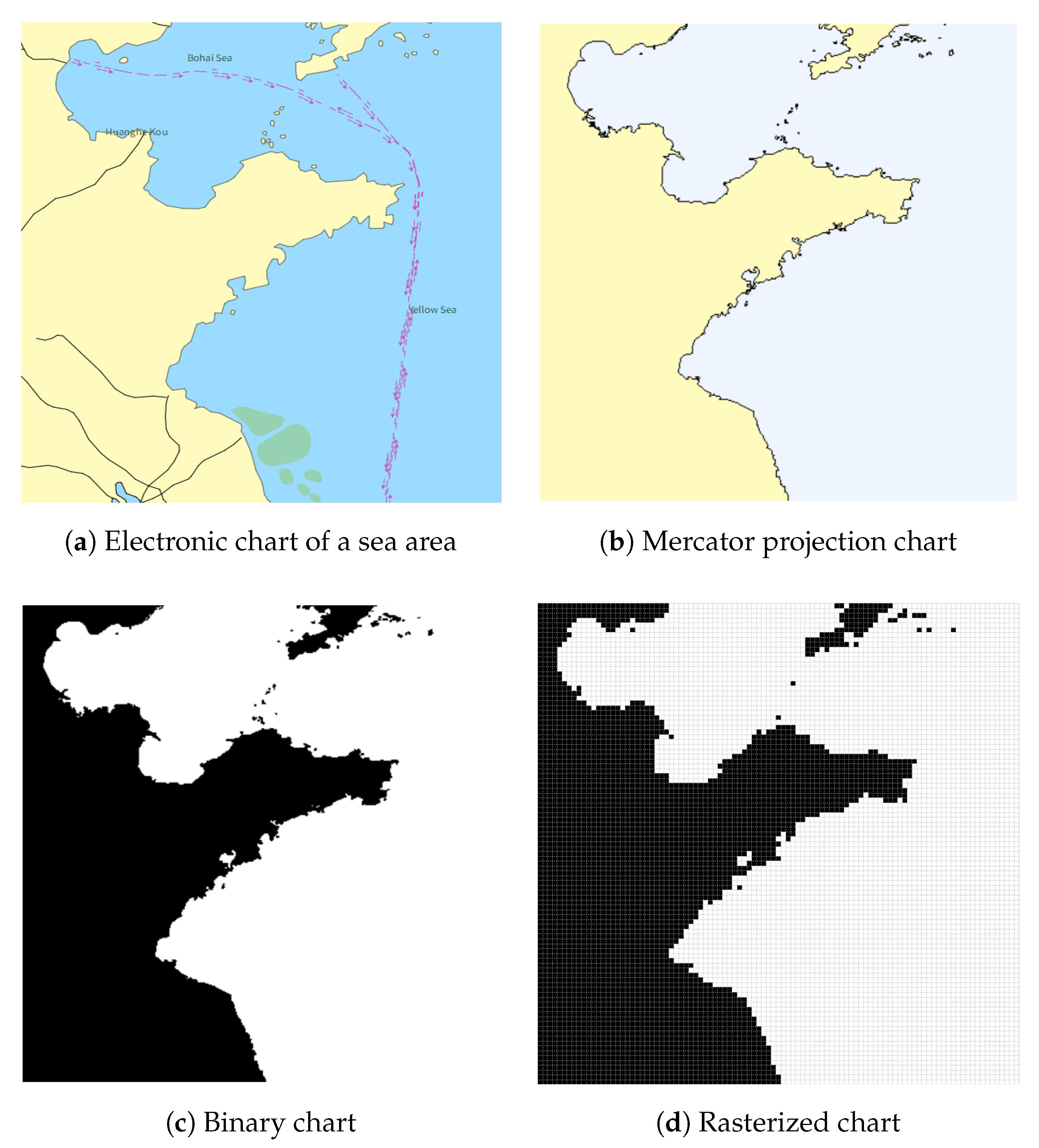
- Based on an S-57 electronic chart file and the Mercator projection, information on obstacles such as land islands is extracted, rasterized, and combined with threat information such as radar, and an accurate marine combat simulation environment is constructed.
- Aiming at a low-altitude penetration mission in the above complex concave obstacle combat environment, a PEPG algorithm based on the PGPP algorithm is proposed, which improves the light intensity preprocessing and other parts, combines with the UAV’s turning angle constraints, enhances the algorithm’s heuristic information in the path search, and the planned path is shorter and smoother.
- The three common path planning algorithms are compared and contrasted via simulation tests, and the effectiveness of the algorithm proposed in this paper is verified.
2. Complex Marine Combat Environment Construction
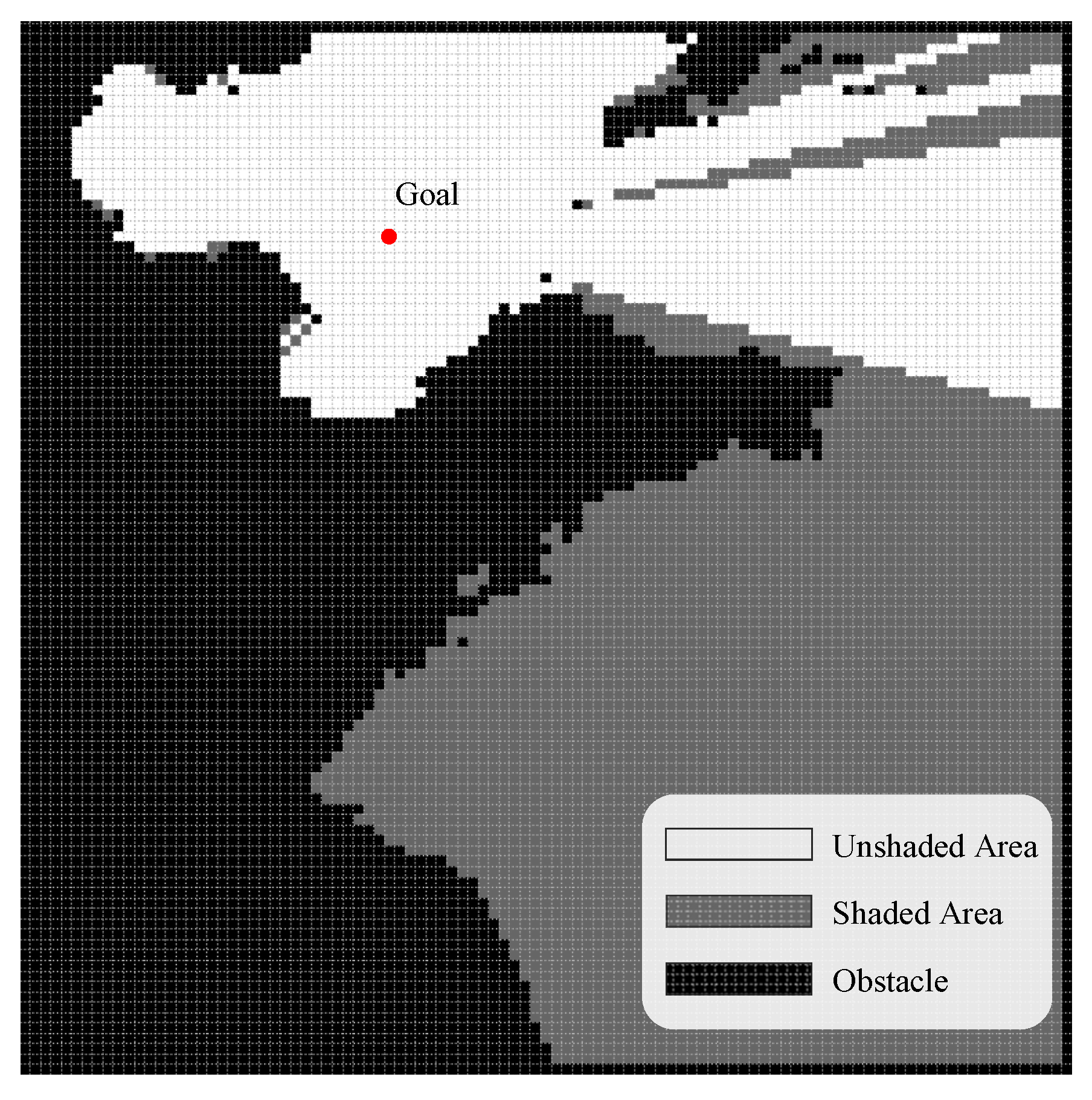
2.1. Construction of the Gridded Nautical Chart Environment
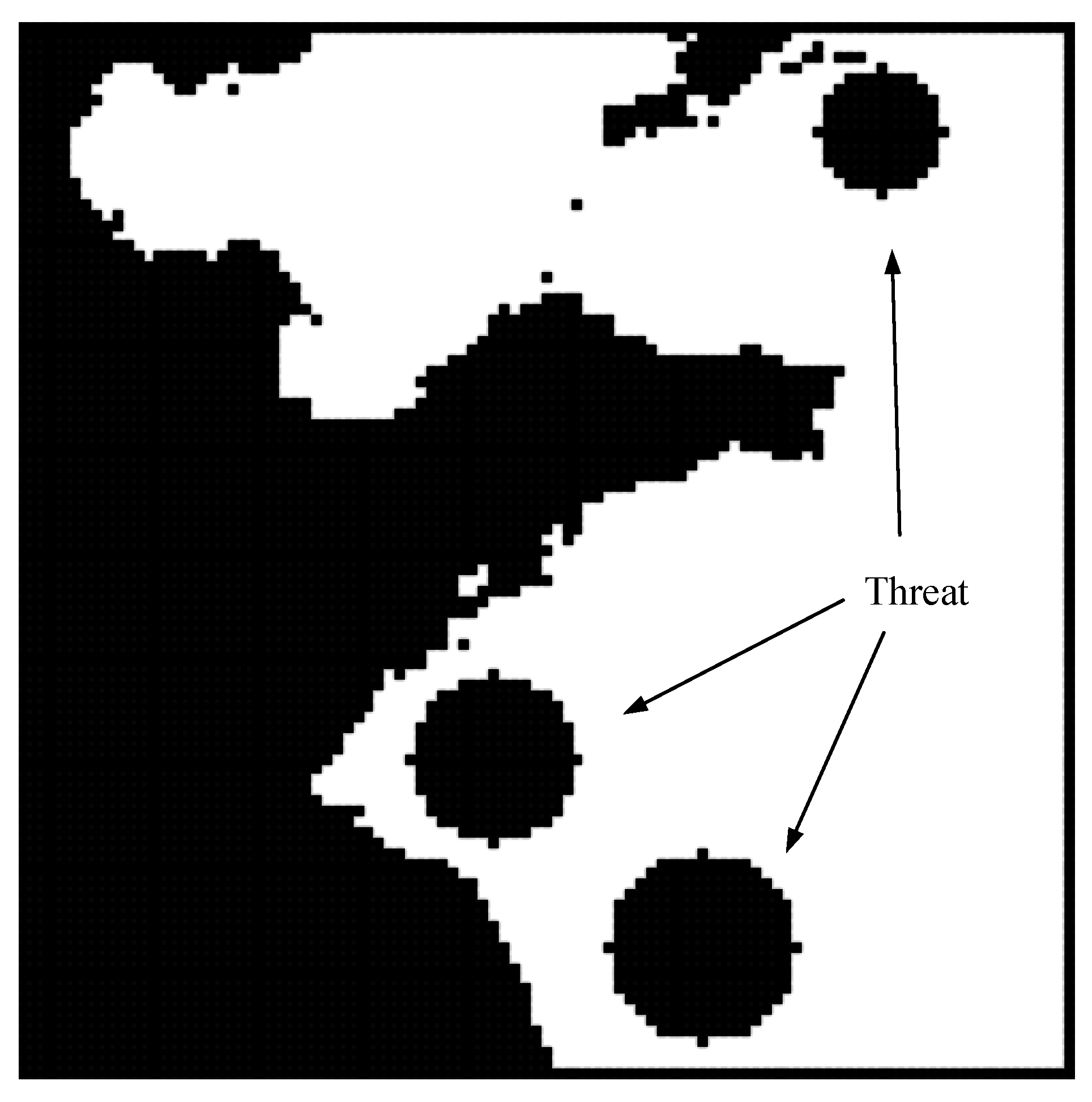
2.2. Gridding of the Threat Information
3. Photosensitivity-Enhanced Plant Growth Algorithm
3.1. Fundamentals of the PGPP Algorithm
3.2. Preprocessing of the Light Intensity Values in Complex Environments
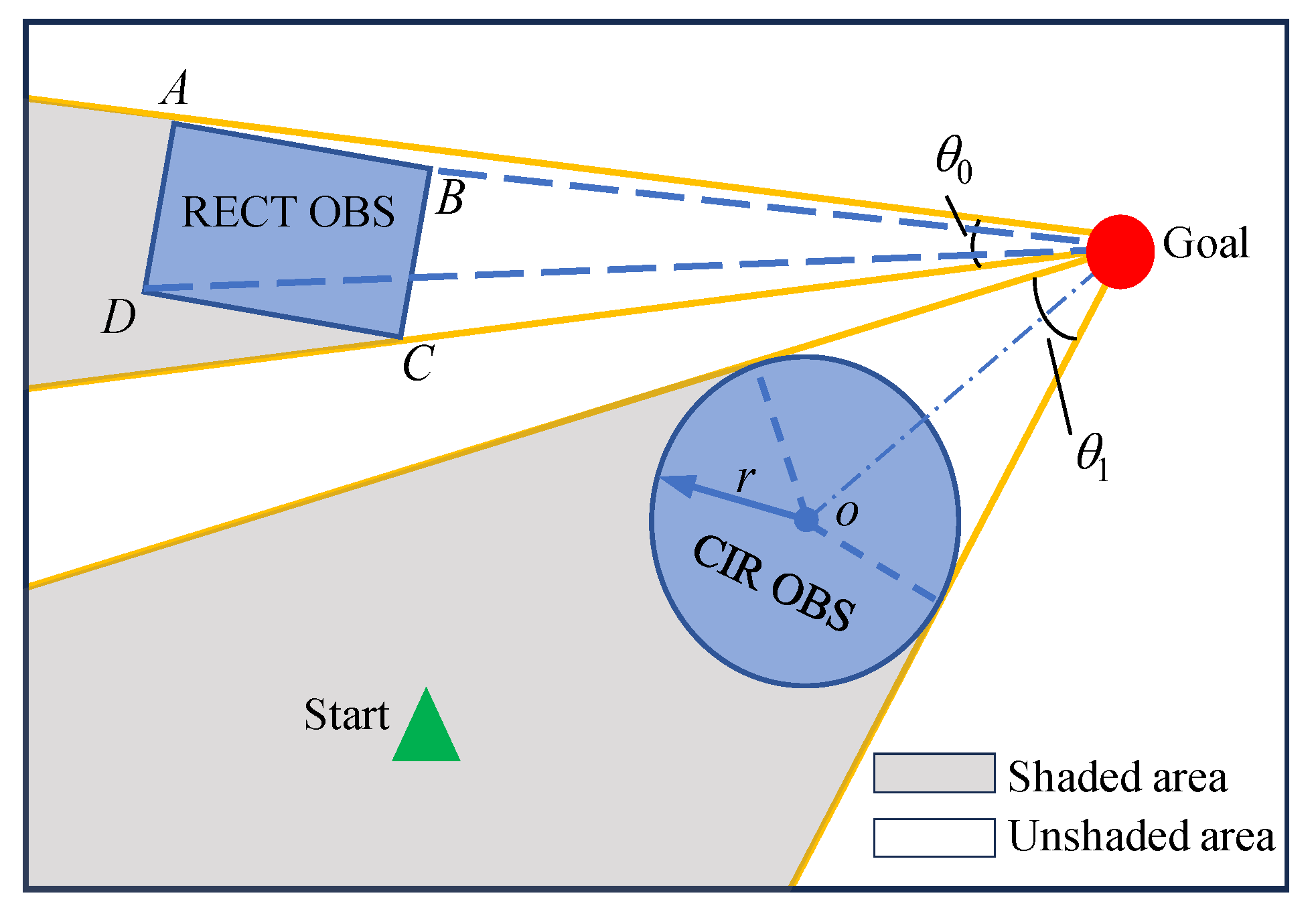
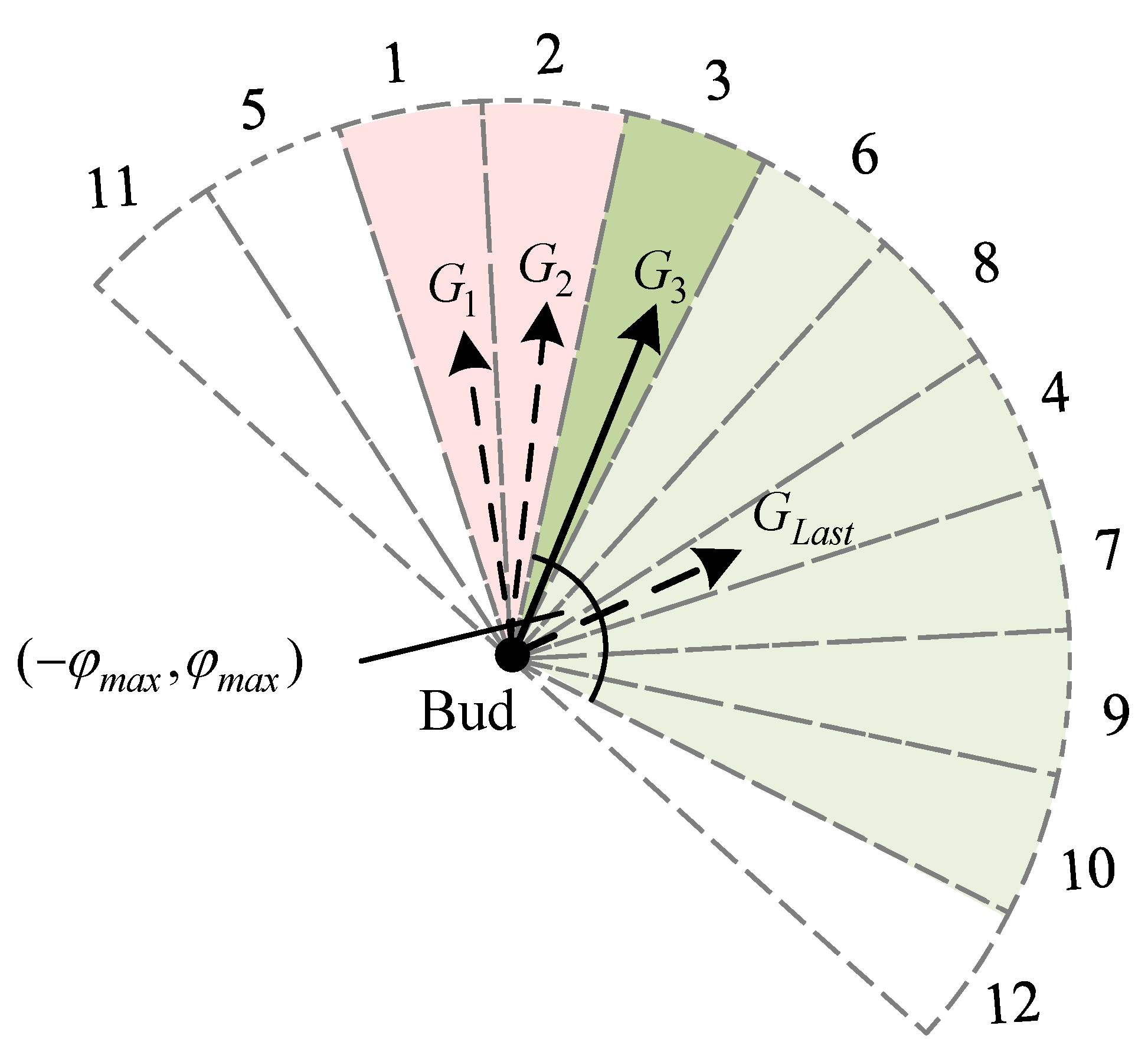
3.3. Sector Light Intensity Vector Homogenization
3.4. Growth Vector Calculations Considering Turning Angle Constraints
| Algorithm 1: PEPG |
 |
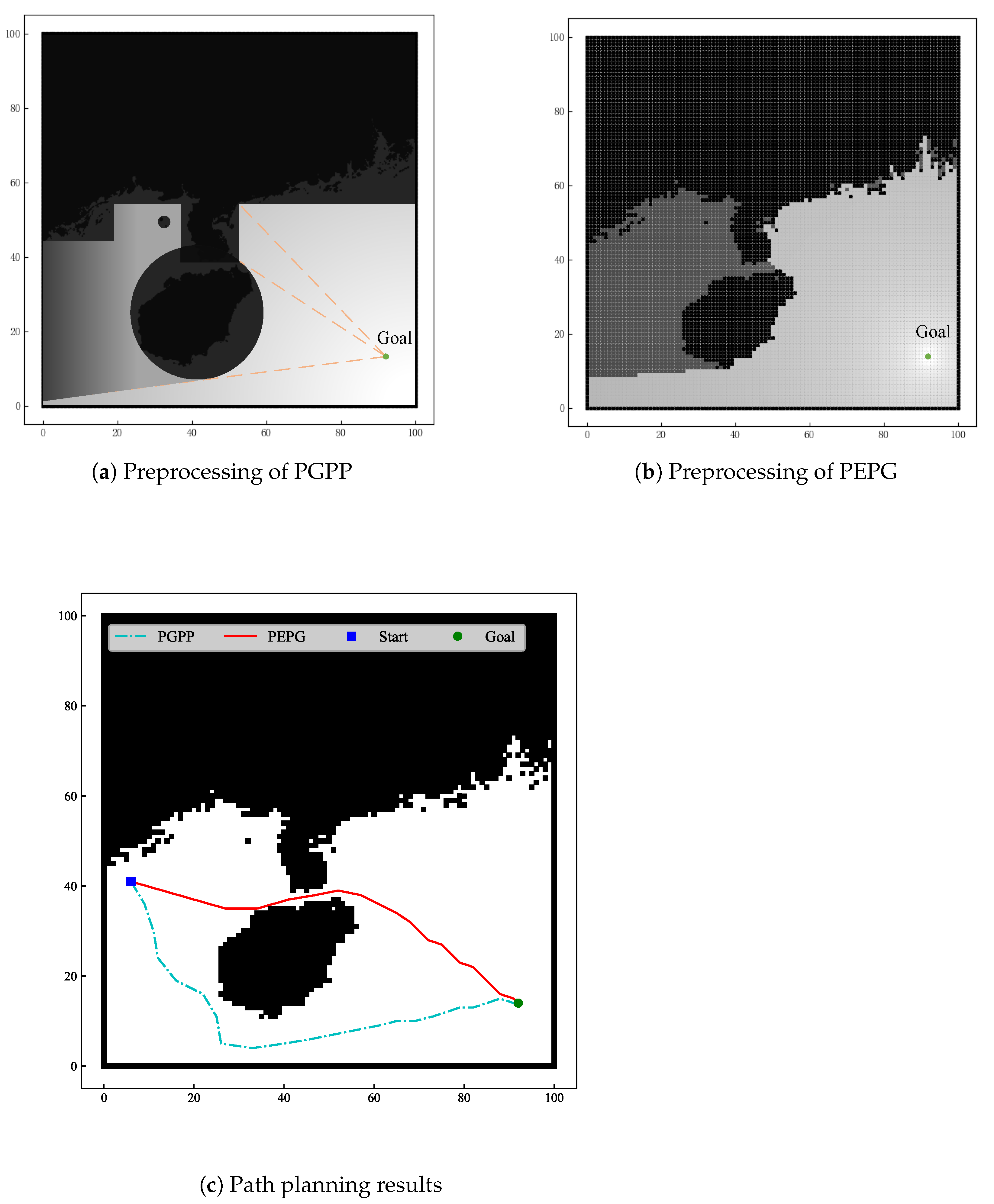
3.5. Planning Effect of the PEPG Algorithm
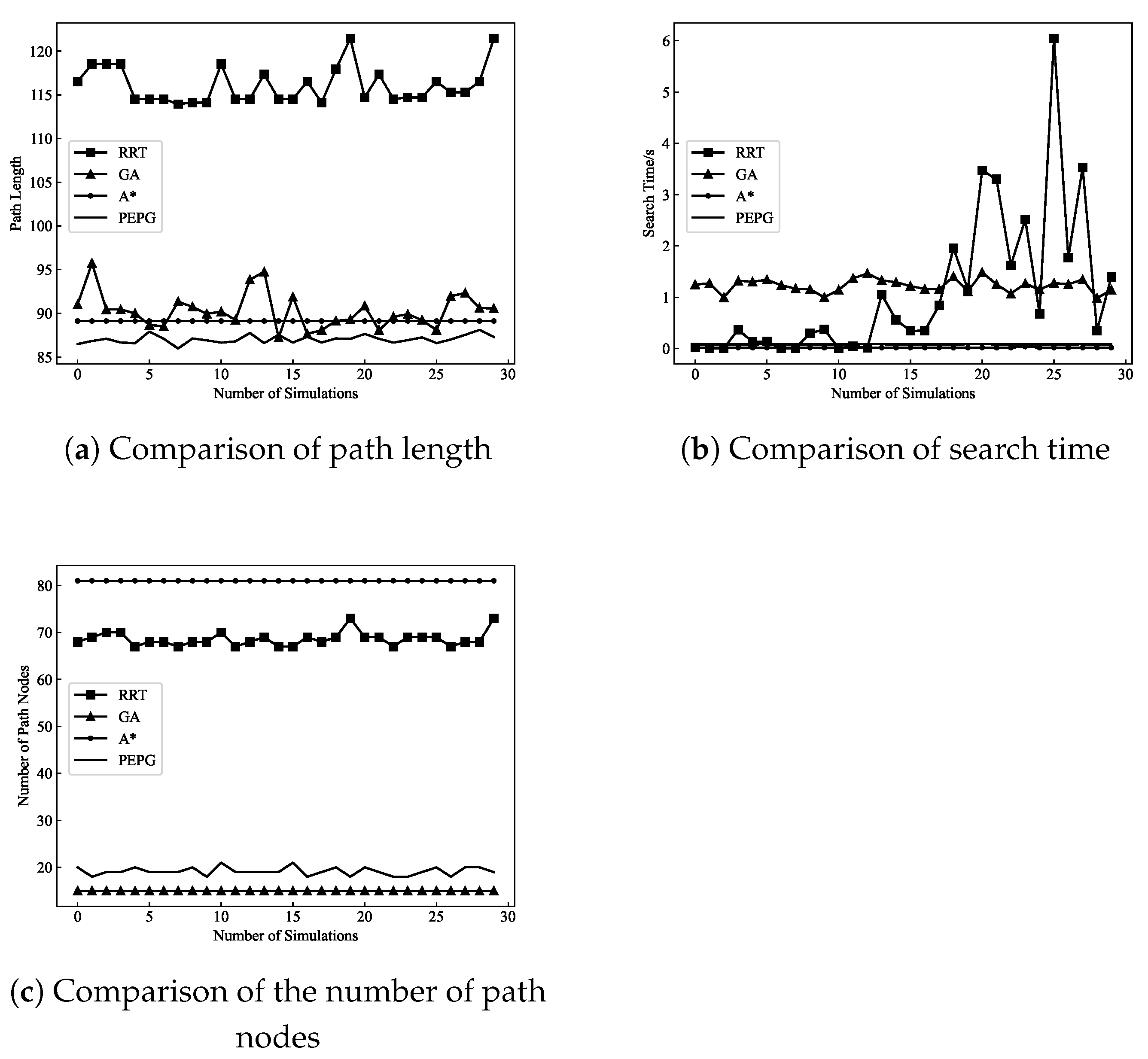
4. Simulation Test
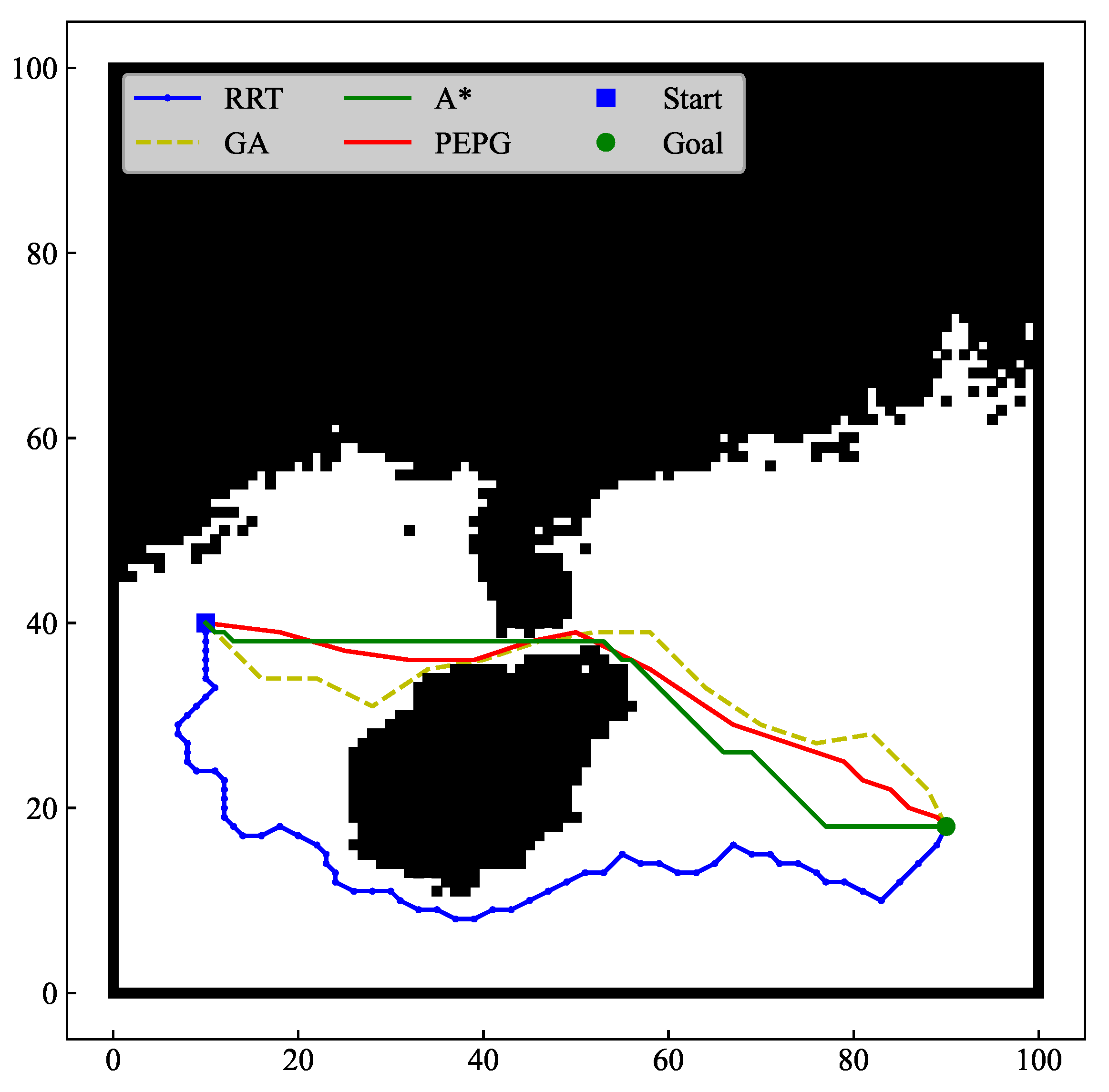
4.1. Algorithm Simulation and Comparison Verification
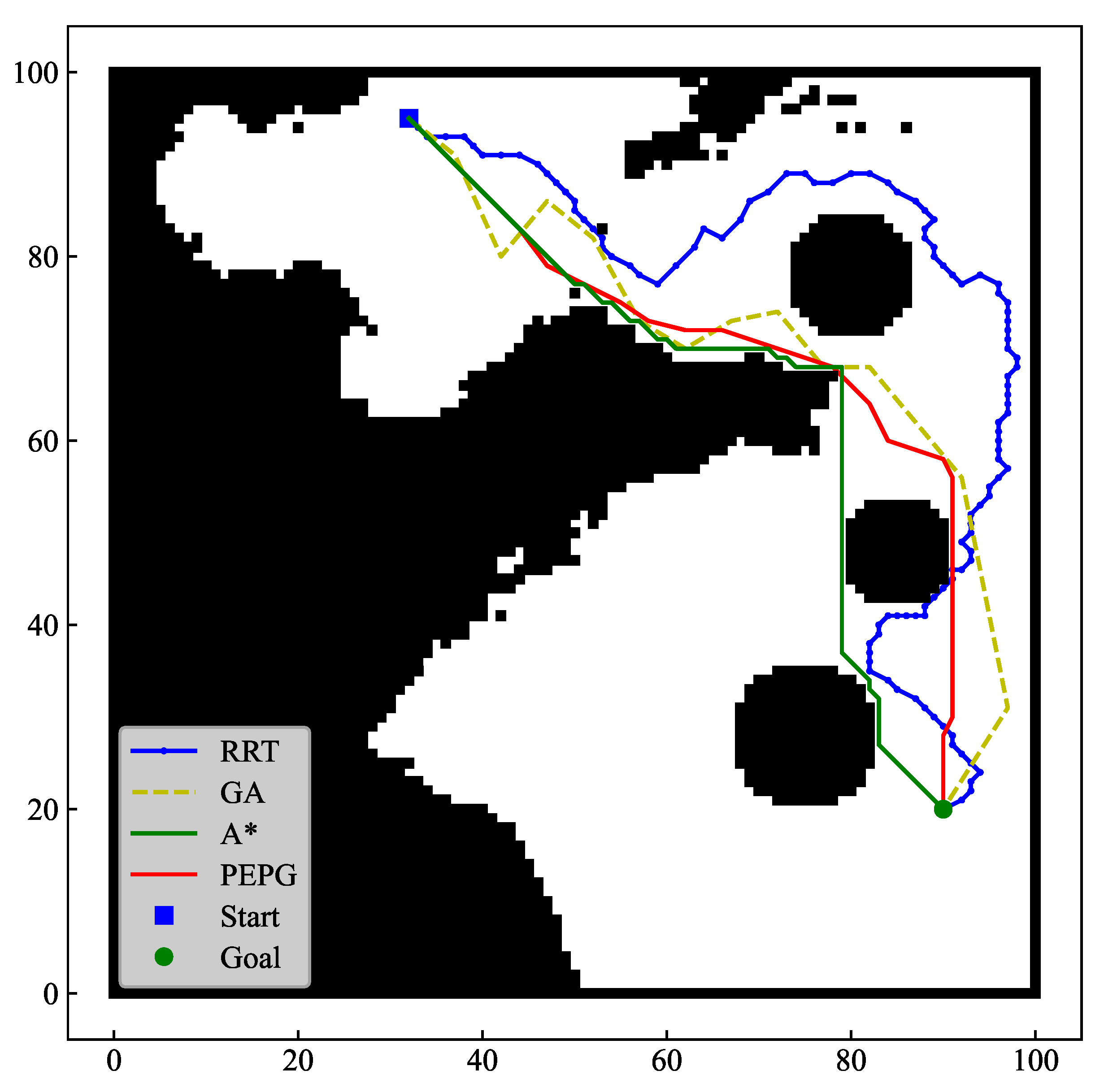
4.1.1. Complex Scenarios without Threats
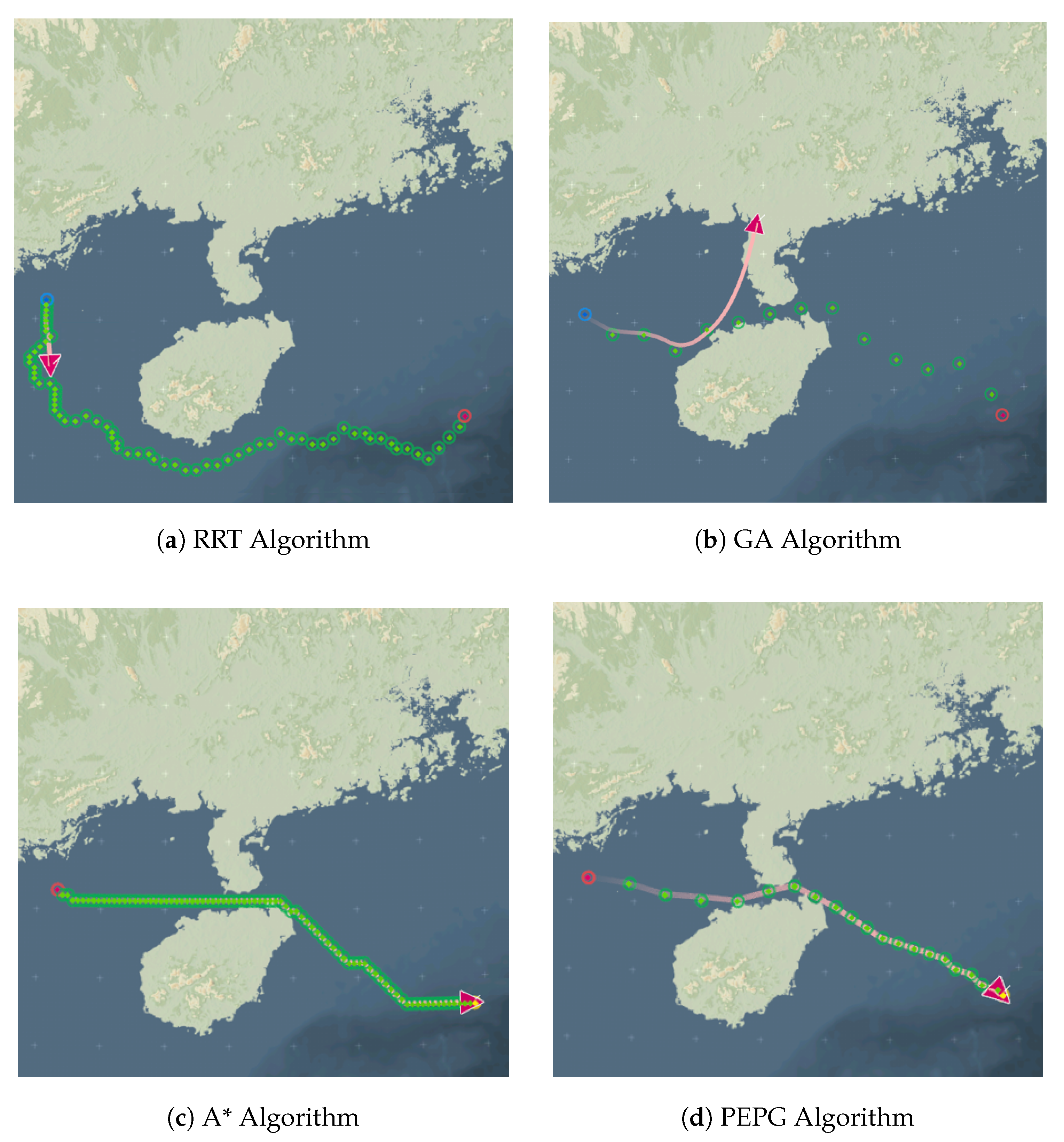
4.1.2. Complex Scenarios with Threats
4.2. Tracking Control Test
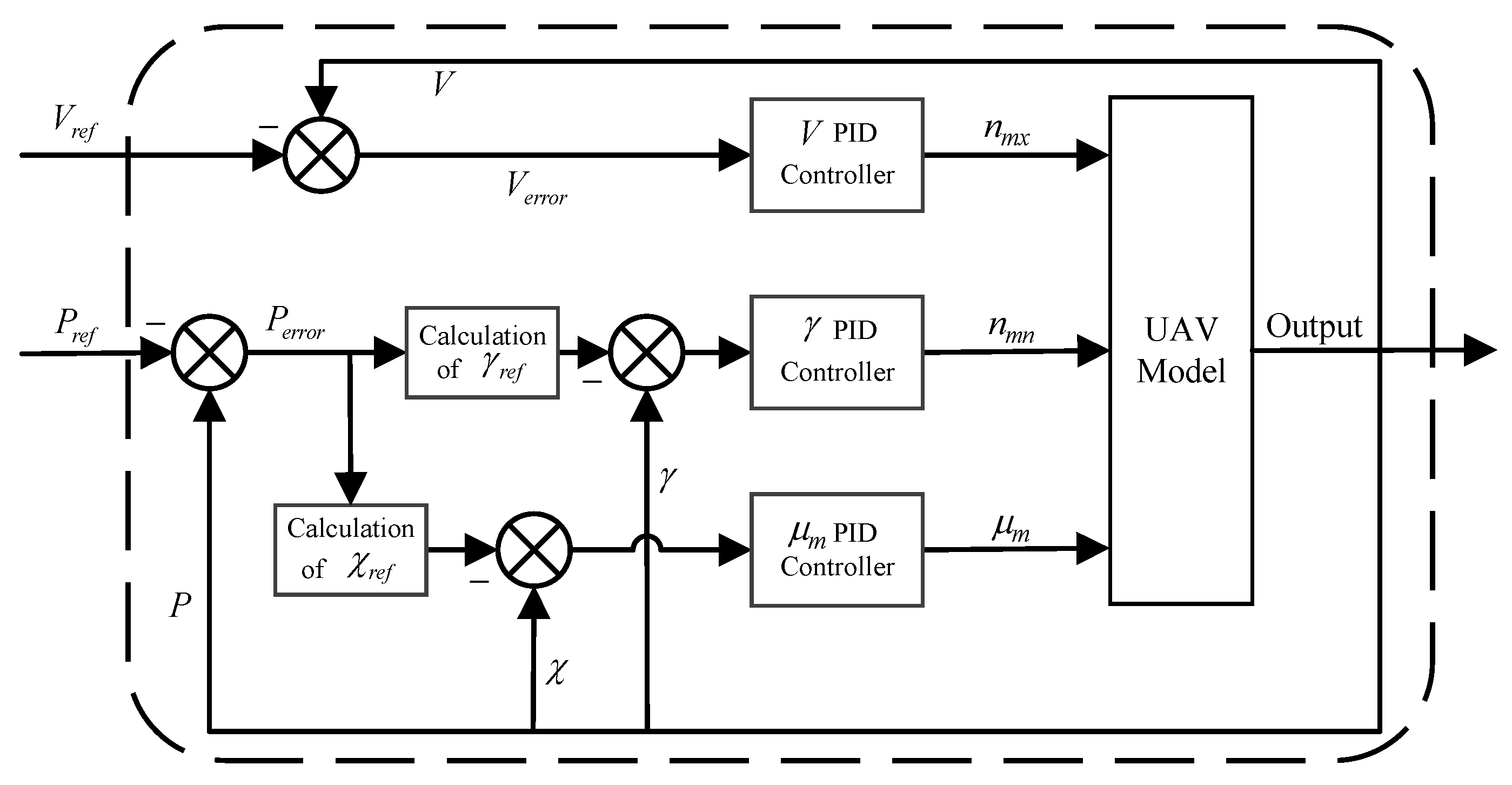
4.2.1. UAV Dynamics Model
4.2.2. Control Law Design
4.2.3. Tracking Control Effect
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Shen, D.; Tang, X.; Yu, F.; Zhang, R. Review of Route Planning for Combat Aircraft Penetration. Aero Weapon. 2022, 29, 11–19. [Google Scholar]
- Wu, M.; Zhang, A.; Gao, M.; Zhang, J. Ship Motion Planning for MASS Based on a Multi-Objective Optimization HA* Algorithm in Complex Navigation Conditions. J. Mar. Sci. Eng. 2021, 9, 1126. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Hu, C. Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm. Biomimetics 2022, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Hecht, H. The Electronic Chart: Functions, Potential and Limitations of a New Marine Navigation System; Geomares Publishing: Lemmer, The Netherlands, 2006; pp. 49–83. [Google Scholar]
- Bo, H.; Feng, L.; Yanyong, C. Research on route planning technology based on electronic charts for long-distance torpedo. Ship Sci. Technol. 2015, 37, 116–119. [Google Scholar]
- Fang, X.; Huang, L.; Fei, Q. Path Planning Based on Improved Particle Swarm Algorithm for USV. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 6918–6923. [Google Scholar]
- Naus, K.; Szymak, P.; Piskur, P.; Niedziela, M.; Nowak, A. Methodology for the Correction of the Spatial Orientation Angles of the Unmanned Aerial Vehicle Using Real Time GNSS, a Shoreline Image and an Electronic Navigational Chart. Energies 2021, 14, 2810. [Google Scholar] [CrossRef]
- Quan, L.; Han, L.; Zhou, B.; Shen, S.; Gao, F. Survey of UAV motion planning. IET Cyber Syst. Robot. 2020, 2, 14–21. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Dai, J.; Ying, J.; He, C. Fast penetration path planning for stealth UAV based on improved A-Star algorithm. Acta Aeronaut. Astronaut. Sin. 2020, 41, 254–264. [Google Scholar]
- Koenig, S.; Likhachev, M. D* lite. In Proceedings of the 18th National Conference on Artificial Intelligence; AAAI Press: Washington, DC, USA, 2002; pp. 476–483. [Google Scholar]
- Saravanakumar, A.; Kaviyarasu, A.; Ashly Jasmine, R. Sampling based path planning algorithm for UAV collision avoidance. Sādhanā 2021, 46, 112. [Google Scholar] [CrossRef]
- Zhou, Q.; Feng, H.; Liu, Y. Multigene and Improved Anti-Collision RRT* Algorithms for Unmanned Aerial Vehicle Task Allocation and Route Planning in an Urban Air Mobility Scenario. Biomimetics 2024, 9, 125. [Google Scholar] [CrossRef]
- Simeon, T.; Laumond, J.P.; Nissoux, C. Visibility-based probabilistic roadmaps for motion planning. Adv. Robot. 2000, 14, 477–493. [Google Scholar] [CrossRef]
- Na, Y.; Li, Y.; Chen, D.; Yao, Y.; Li, T.; Liu, H.; Wang, K. Optimal Energy Consumption Path Planning for Unmanned Aerial Vehicles Based on Improved Particle Swarm Optimization. Sustainability 2023, 15, 12101. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Pehlivanoglu, P. An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems. Appl. Soft Comput. 2021, 112, 107796. [Google Scholar] [CrossRef]
- Konatowski, S.; Pawłowski, P. Application of the ACO algorithm for UAV path planning. Przegląd Elektrotechniczny 2019, 1, 115–119. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Chen, X.; Zhang, L.; Wu, K. A novel path planning algorithm based on plant growth mechanism. Soft Comput. 2017, 21, 435–445. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X.; Jia, Q.; Liu, X.; Zhang, W. HPO-RRT*: A sampling-based algorithm for UAV real-time path planning in a dynamic environment. Complex Intell. Syst. 2023, 9, 7133–7153. [Google Scholar] [CrossRef]
- Lee, M.; Noh, G.; Park, J.; Lee, D. Real-time directed rapidly exploring random tree path planning for air collision avoidance. J. Aerosp. Inf. Syst. 2022, 19, 330–343. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, Z.; Lian, Y.; Chen, L.; An, Q.; Wang, L.; Ma, B. Global Optimization of UAV Area Coverage Path Planning Based on Good Point Set and Genetic Algorithm. Aerospace 2022, 9, 86. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, J.; Wu, J.; Zhou, X. Efficient and optimal penetration path planning for stealth unmanned aerial vehicle using minimal radar cross-section tactics and modified A-Star algorithm. ISA Trans. 2023, 134, 42–57. [Google Scholar] [CrossRef]
- Luo, J.; Liang, Q.; Li, H. UAV penetration mission path planning based on improved holonic particle swarm optimization. J. Syst. Eng. Electron. 2023, 34, 197–213. [Google Scholar] [CrossRef]
- Zhao, L.; Zheng, B.; Yin, Y.; Guo, H.; Chen, F.; Feng, G. Path Planning of UAV Penetration Based on Improved Particle Swarm Optimization. Electron. Opties Control. 2023, 30, 12–16+39. [Google Scholar]
- Yaoming, Z.; Yu, S.; Anhuan, X.; Lingyu, K. A newly bio-inspired path planning algorithm for autonomous obstacle avoidance of UAV. Chin. J. Aeronaut. 2021, 34, 199–209. [Google Scholar]
- Nielsen, L.D.; Sung, I.; Nielsen, P. Convex decomposition for a coverage path planning for autonomous vehicles: Interior extension of edges. Sensors 2019, 19, 4165. [Google Scholar] [CrossRef] [PubMed]
- Ling, F.; Du, C.; Chen, J.; Yuan, Z. An Improved Geometrical Path Planning Algorithm for UAV in Irregular-obstacle Environment. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 972–976. [Google Scholar]
- Prasad, B.; Dalei, D.K.; Rajesh, M.; Panigrahi, N. Modelling and Analysis of Underwater Surface using ENC Chart Visualization. In Proceedings of the 2022 4th International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 21–23 September 2022; pp. 1696–1700. [Google Scholar]
- Oh, D.; Park, D.; Lim, Y.; Park, S. Methods of GML-based representation of S-101 ENC vector data. In Proceedings of the 2015 5th International Conference on IT Convergence and Security (ICITCS), Kuala Lumpur, Malaysia, 24–27 August 2015; pp. 1–3. [Google Scholar]
- Vasilca, D.; Badea, A.C.; Iliescu-Cremeneanu, A.; Badea, G.; Badea, D. The Effects of Using Web Mercator Projection instead of the Mercator Projection for Representing Romania on Maps. Int. Multidiscip. Sci. Geoconference SGEM 2018, 18, 635–642. [Google Scholar]
- Gaol, F.L. Bresenham Algorithm: Implementation and Analysis in Raster Shape. J. Comput. 2013, 8, 69–78. [Google Scholar] [CrossRef]


| No. | Start and Goal Node | PGPP Path Length | PEPG Path Length |
|---|---|---|---|
| 1 | (12, 36), (96, 42) | 105.61 | 85.51 |
| 2 | (5, 25), (94, 20) | 121.01 | 102.33 |
| 3 | (6, 41), (92, 14) | 111.58 | 96.65 |
| 4 | (5,10), (90, 53) | 108.42 | 99.52 |
| 5 | (10, 20), (85, 40) | 99.34 | 84.04 |
| 6 | (85, 40), (10, 20) | 101.43 | 92.49 |
| 7 | (90, 53), (5,10) | 123.10 | 104.27 |
| 8 | (92, 14), (6, 41) | 114.38 | 99.78 |
| 9 | (94, 20), (5, 25) | 117.18 | 104.99 |
| 10 | (96, 42), (12, 36) | 106.32 | 85.77 |
| Algorithms | Average Time/ms | Average Path Length | Average Path Nodes |
|---|---|---|---|
| RRT | 1078 | 116.09 | 68.6 |
| GA | 1230 | 90.30 | 15 |
| A* | 19 | 89.11 | 81 |
| PEPG | 82 | 87.02 | 19.2 |
| Threat | Location | Radius/n Mile |
|---|---|---|
| Weather Threat | (122.125° E, 33.914° N) | 35 |
| Radar Threat | (122.460° E, 37.860° N) | 30 |
| Fire Threat | (122.834° E, 35.495° N) | 25 |
| Algorithms | Mean Time/ms | Mean Path Length | Mean Path Nodes |
|---|---|---|---|
| RRT | 2085 | 162.68 | 111.43 |
| GA | 1853 | 116.97 | 15 |
| A* | 101 | 110.74 | 96 |
| PEPG | 341 | 110.21 | 37.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Huang, P.; Gao, H.; Qin, Q.; Guo, T.; Wang, Y.; Zhou, Y. A Photosensitivity-Enhanced Plant Growth Algorithm for UAV Path Planning. Biomimetics 2024, 9, 212. https://doi.org/10.3390/biomimetics9040212
Yang R, Huang P, Gao H, Qin Q, Guo T, Wang Y, Zhou Y. A Photosensitivity-Enhanced Plant Growth Algorithm for UAV Path Planning. Biomimetics. 2024; 9(4):212. https://doi.org/10.3390/biomimetics9040212
Chicago/Turabian StyleYang, Renjie, Pan Huang, Hui Gao, Qingyang Qin, Tao Guo, Yongchao Wang, and Yaoming Zhou. 2024. "A Photosensitivity-Enhanced Plant Growth Algorithm for UAV Path Planning" Biomimetics 9, no. 4: 212. https://doi.org/10.3390/biomimetics9040212
APA StyleYang, R., Huang, P., Gao, H., Qin, Q., Guo, T., Wang, Y., & Zhou, Y. (2024). A Photosensitivity-Enhanced Plant Growth Algorithm for UAV Path Planning. Biomimetics, 9(4), 212. https://doi.org/10.3390/biomimetics9040212






