Stereo Camera Setup for 360° Digital Image Correlation to Reveal Smart Structures of Hakea Fruits
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Experimental Setup for 360° DIC with One Stereo Camera System
3.2. 360°-DIC Measurement
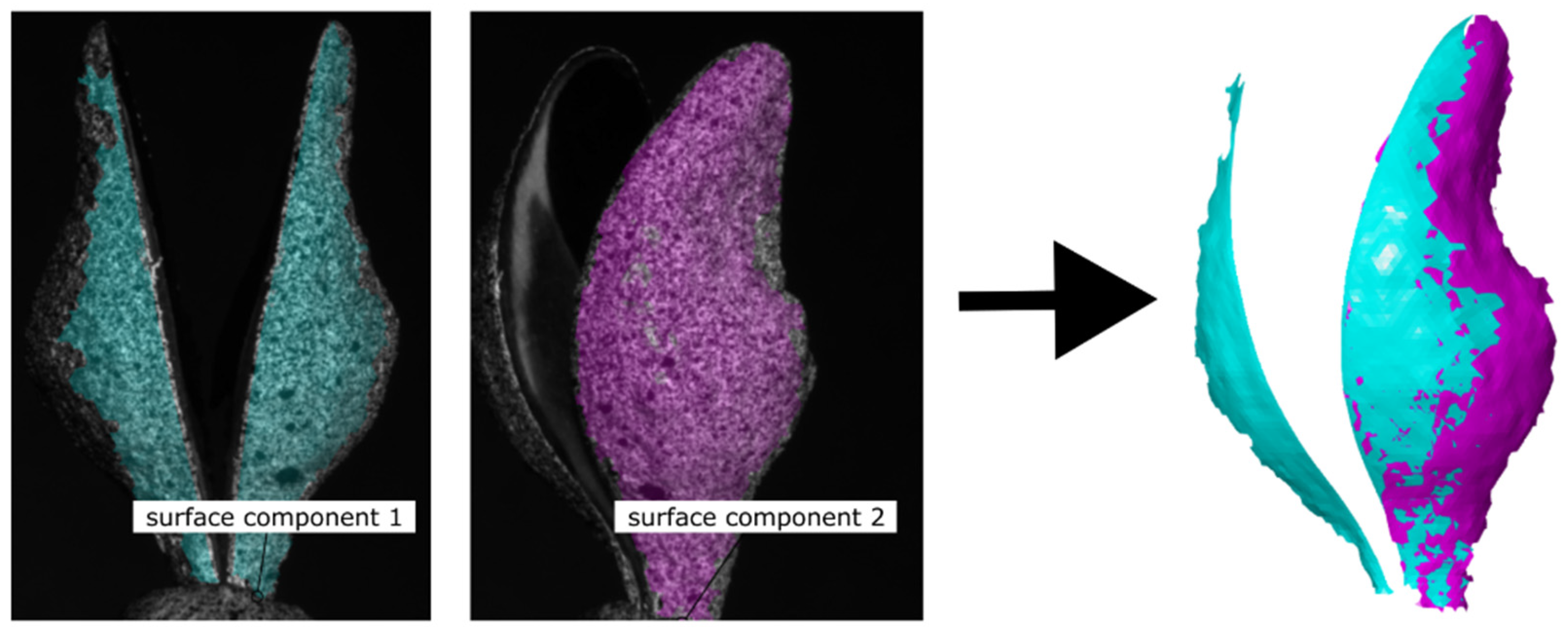
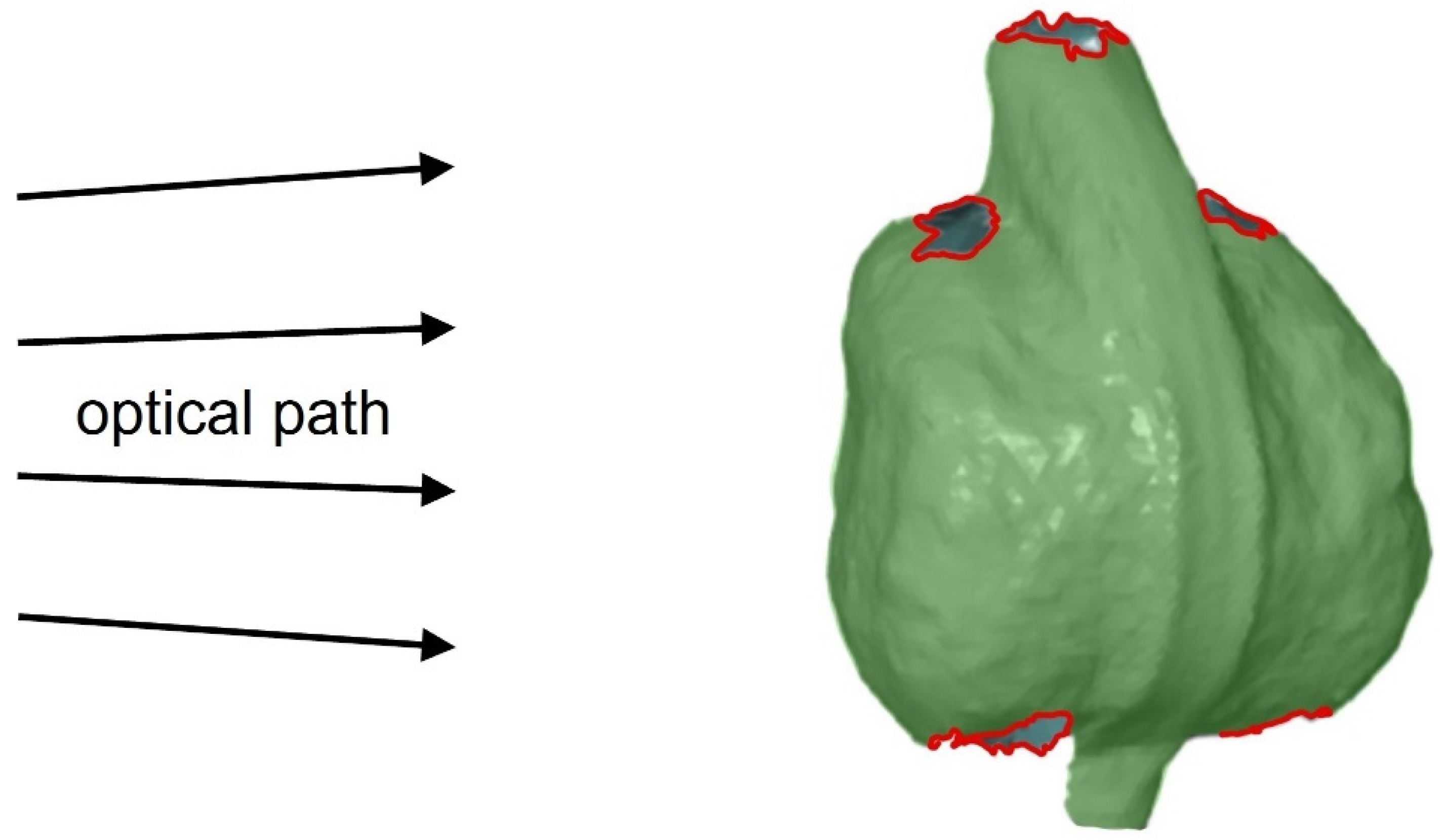
3.3. 360° DIC Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, L.A.S.; Briggs, B.G. On the Protaceae—The Evolution and Classification of a Southern Family. Bot. J. Linn. Soc. 1975, 70, 83–182. [Google Scholar] [CrossRef]
- Wilson, A. (Ed.) Protaceae 3, Hakea to Dryandra. In Flora of Australia; CSIRO: Melbourne, Australia, 1999; Volume 17B, ISBN 0643064540. [Google Scholar]
- Filla, F. Das Perikarp der Proteaceae: Ein Beitrag zur Biologie der Früchte. Flora Allg. Bot. Ztg. 1925, 120, 99–142. (In German) [Google Scholar] [CrossRef]
- Wanieck, K.; Hamann, L.; Bartz, M.; Uttich, E.; Hollermann, M.; Drack, M.; Beismann, H. Biomimetics Linked to Classical Product Development: An Interdisciplinary Endeavor to Develop a Technical Standard. Biomimetics 2022, 7, 36. [Google Scholar] [CrossRef] [PubMed]
- International Standardization Organization. Biomimetics—Terminology, Concepts and Methodology; International Standardization Organization: Geneva, Switzerland, 2015; p. 18458. [Google Scholar]
- Janeliukstis, R.; Chen, X. Review of Digital Image Correlation Application to Large-Scale Composite Structure Testing. Compos. Struct. 2021, 271, 114143. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques in Experimental Stress Analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F.; Sutton, M.A.; Chu, T.C.; Anderson, J. Application of Digital Correlation Methods to Rigid Body Mechanics. Opt. Eng. 1983, 22, 738–742. [Google Scholar] [CrossRef]
- Hild, F.; Roux, S. Digital Image Correlation: From Displacement Measurement to Identification of Elastic Properties—A Review. Strain 2006, 42, 69–80. [Google Scholar] [CrossRef]
- Pan, B. Recent Progress in Digital Image Correlation. Exp. Mech. 2011, 51, 1223–1235. [Google Scholar] [CrossRef]
- Pan, B. Digital Image Correlation for Surface Deformation Measurement: Historical Developments, Recent Advances and Future Goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Sutton, M.A.; Matta, F.; Rizos, D.; Ghorbani, R.; Rajan, S.; Mollenhauer, D.H.; Schreier, H.W.; Lasprilla, A.O. Recent Progress in Digital Image Correlation: Background and Developments since the 2013 W M Murray Lecture. Exp. Mech. 2017, 57, 1–30. [Google Scholar] [CrossRef]
- Mousa, M.A.; Yussof, M.M.; Udi, U.J.; Nazri, F.M.; Kamarudin, M.K.; Parke, G.A.R.; Assi, L.N.; Ghahari, S.A. Application of Digital Image Correlation in Structural Health Monitoring of Bridge Infrastructures: A Review. Infrastructures 2021, 6, 176. [Google Scholar] [CrossRef]
- Palanca, M.; Brugo, T.M.; Cristofolini, L. Use of Digital Image Correlation to Investigate the Biomechanics of the Vertebra. J. Mech. Med. Biol. 2015, 15, 1540004. [Google Scholar] [CrossRef]
- Palanca, M.; Tozzi, G.; Cristofolini, L. The Use of Digital Image Correlation in the Biomechanical Area: A review. Int. Biomech. 2016, 3, 1–21. [Google Scholar] [CrossRef]
- Mylo, M.D.; Poppinga, S. Digital Image Correlation Techniques for Motion Analysis and Biomechanical Characterization of Plants. Front. Plant Sci. 2024, 14, 1335445. [Google Scholar] [CrossRef]
- Mylo, M.D.; Hofmann, M.; Balle, F.; Beisel, S.; Speck, T.; Speck, O. Biomechanics of the Parasite-Host Interaction of the European Mistletoe. J. Exp. Bot. 2022, 73, 1204–1221. [Google Scholar] [CrossRef]
- Mylo, M.D.; Hoppe, A.; Pastewka, L.; Speck, T.; Speck, O. Elastic Property and Fracture Mechanics of Lateral Branch-Branch Junctions in Cacti: A case Study of Opuntia ficus-indica and Cylindropuntia bigelovii. Front. Plant Sci. 2022, 13, 950860. [Google Scholar] [CrossRef]
- Jentzsch, M.; Badstöber, M.-C.; Umlas, F.; Speck, T. Damage Protection in Fruits: Comparative Analysis of the Functional Morphology of the Fruit Peels of Five Citrus Species via quasi-static compression tests. Front. Mater. 2022, 9, 979151. [Google Scholar] [CrossRef]
- Sachse, R.; Westermeier, A.; Mylo, M.; Nadasdi, J.; Bischoff, M.; Speck, T.; Poppinga, S. Snapping Mechanics of the Venus flytrap (Dionaea muscipula). Proc. Natl. Acad. Sci. USA 2020, 117, 16035–16042. [Google Scholar] [CrossRef] [PubMed]
- Durak, G.M.; Thierer, R.; Sachse, R.; Bischoff, M.; Speck, T.; Poppinga, S. Smooth or with a Snap! Biomechanics of Trap Reopening in the Venus Flytrap (Dionaea muscipula). Adv. Sci. 2022, 9, e2201362. [Google Scholar] [CrossRef] [PubMed]
- Correa, D.; Poppinga, S.; Mylo, M.D.; Westermeier, A.S.; Bruchmann, B.; Menges, A.; Speck, T. 4D Pine Scale: Biomimetic 4D Printed Autonomous Scale and Flap Structures Capable of Multi-Phase Movement. Philos. Trans. A Math. Phys. Eng. Sci. 2020, 378, 20190445. [Google Scholar] [CrossRef] [PubMed]
- Eger, C.J.; Horstmann, M.; Poppinga, S.; Sachse, R.; Thierer, R.; Nestle, N.; Bruchmann, B.; Speck, T.; Bischoff, M.; Rühe, J. The Structural and Mechanical Basis for Passive-Hydraulic Pine Cone Actuation. Adv. Sci. 2022, 9, e2200458. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-Dimensional Digital Image Correlation for In-Plane Displacement and Strain Measurement: A Review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Sutton, M.A.; Yan, J.H.; Tiwari, V.; Schreier, H.W.; Orteu, J.J. The Effect of out-of-Plane Motion on 2D and 3D Digital Image Correlation Measurements. Opt. Lasers Eng. 2008, 46, 746–757. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.-J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements; Springer: New York, NY, USA, 2009; ISBN 978-0-387-78747-3. [Google Scholar]
- Lecompte, D.; Smits, A.; Bossuyt, S.; Sol, H.; Vantomme, J.; van Hemelrijck, D.; Habraken, A.M. Quality Assessment of Speckle Patterns for Digital Image Correlation. Opt. Lasers Eng. 2006, 44, 1132–1145. [Google Scholar] [CrossRef]
- Dong, Y.L.; Pan, B. A Review of Speckle Pattern Fabrication and Assessment for Digital Image Correlation. Exp. Mech. 2017, 57, 1161–1181. [Google Scholar] [CrossRef]
- Degenhardt, R.; Tessmer, J.; Kling, A. Collapse Behaviour of Thin-walled CFRP Structures due to Material and Geometric Nonlinearities-experiments and Simulation. In Proceedings of the ICAS 2008, 26th Congress of the International Council of the Aeronautical Science, Including 8th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Anchorage, AK, USA, 14–19 September 2008; Optimage Ltd. on behalf of the International Council of the Aeronautical Sciences (ICAS): Edinburgh, UK, 2008; pp. 1–10, ISBN 0953399192. [Google Scholar]
- Degenhardt, R.; Kling, A.; Bethge, A.; Orf, J.; Kärger, L.; Zimmermann, R.; Rohwer, K.; Calvi, A. Investigations on Imperfection Sensitivity and Deduction of Improved Knock-Down Factors for Unstiffened CFRP Cylindrical Shells. Compos. Struct. 2010, 92, 1939–1946. [Google Scholar] [CrossRef]
- Harvent, J.; Bugarin, F.; Orteu, J.-J.; Devy, M.; Barbeau, P.; Marin, G. Inspection of aeronautics parts for shape defect detection using a multi-camera system. In Proceedings of the XIth International Congress and Exposition of the Society for Experimental Mechanics, Orlando, FL, USA, 2–5 June 2008; Curran Associates, Inc.: Red Hook, NY, USA, 2008; pp. 1992–1999. [Google Scholar]
- Orteu, J.-J.; Bugarin, F.; Harvent, J.; Robert, L.; Velay, V. Multiple-Camera Instrumentation of a Single Point Incremental Forming Process Pilot for Shape and 3D Displacement Measurements: Methodology and Results. Exp. Mech. 2011, 51, 625–639. [Google Scholar] [CrossRef]
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Genovese, K.; Herr, H.M. MultiDIC: An Open-Source Toolbox for Multi-View 3D Digital Image Correlation. IEEE Access 2018, 6, 30520–30535. [Google Scholar] [CrossRef]
- Malowany, K.; Malesa, M.; Kowaluk, T.; Kujawinska, M. Multi-Camera Digital Image Correlation Method with Distributed Fields of View. Opt. Lasers Eng. 2017, 98, 198–204. [Google Scholar] [CrossRef]
- Abdel-Aziz, Y.I.; Karara, H.M. Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates in Close-Range Photogrammetry. Photogramm. Eng. Remote Sens. 2015, 81, 103–107. [Google Scholar] [CrossRef]
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Herr, H.M. A Framework for Measuring the Time-Varying Shape and Full-Field Deformation of Residual Limbs Using 3-D Digital Image Correlation. IEEE Trans. Biomed. Eng. 2019, 66, 2740–2752. [Google Scholar] [CrossRef]
- LeBlanc, B.; Niezrecki, C.; Avitabile, P.; Chen, J.; Sherwood, J. Damage Detection and Full Surface Characterization of a Wind Turbine Blade Using Three-Dimensional Digital Image Correlation. Struct. Health Monit. 2013, 12, 430–439. [Google Scholar] [CrossRef]
- Dong, S.; Yu, S.; Huang, Z.; Song, S.; Shao, X.; Kang, X.; He, X. Target-Based Calibration Method for Multifields of View Measurement Using Multiple Stereo Digital Image Correlation systems. Opt. Eng. 2017, 56, 124102. [Google Scholar] [CrossRef]
- Lane, B.A.; Lessner, S.M.; Vyavahare, N.R.; Sutton, M.A.; Eberth, J.F. Null Strain Analysis of Submerged Aneurysm Analogues Using a Novel 3D Stereomicroscopy Device. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 332–344. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Dai, Y.; Qiu, H.; He, X. Application of multi-camera digital image correlation in the stability study of the long timber column with the circular cross-section under axial compression. BioRes 2022, 17, 1717–1728. [Google Scholar] [CrossRef]
- Genovese, K.; Badel, P.; Cavinato, C.; Pierrat, B.; Bersi, M.R.; Avril, S.; Humphrey, J.D. Multi-View Digital Image Correlation Systems for in Vitro Testing of Arteries from Mice to Humans. Exp. Mech. 2021, 61, 1455–1472. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Zhao, J.; Li, X.; Xu, Z.; Chen, Z. Study on the Compressive Properties of an Elastomeric Porous Cylinder Using 360° Three-Dimensional Digital Image Correlation System. Materials 2023, 16, 4301. [Google Scholar] [CrossRef] [PubMed]
- Genovese, K.; Cortese, L.; Rossi, M.; Amodio, D. A 360-deg Digital Image Correlation System for Materials Testing. Opt. Lasers Eng. 2016, 82, 127–134. [Google Scholar] [CrossRef]
- Badel, P.; Genovese, K.; Avril, S. 3D Residual Stress Field in Arteries: Novel Inverse Method Based on Optical Full-field Measurements. Strain 2012, 48, 528–538. [Google Scholar] [CrossRef]
- Genovese, K.; Lee, Y.-U.; Lee, A.Y.; Humphrey, J.D. An Improved Panoramic Digital Image Correlation Method for Vascular Strain Analysis and Material Characterization. J. Mech. Behav. Biomed. Mater. 2013, 27, 132–142. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Pan, B. Mirror-Assisted Multi-View Digital Image Correlation: Principles, Applications and Implementations. Opt. Lasers Eng. 2022, 149, 106786. [Google Scholar] [CrossRef]
- Pan, B.; Chen, B. A Novel Mirror-Assisted Multi-View Digital Image Correlation for Dual-Surface Shape and Deformation Measurements of Sheet Samples. Opt. Lasers Eng. 2019, 121, 512–520. [Google Scholar] [CrossRef]
- Chen, B.; Pan, B. Mirror-Assisted Panoramic-Digital Image Correlation for Full-Surface 360-Deg Deformation Measurement. Measurement 2019, 132, 350–358. [Google Scholar] [CrossRef]
- Chen, B.; Pan, B. Through-Thickness Strain Field Measurement Using the Mirror-Assisted Multi-View Digital Image Correlation. Mech. Mater. 2019, 137, 103104. [Google Scholar] [CrossRef]
- Chen, B.; Zhao, J.; Pan, B. Mirror-assisted Multi-view Digital Image Correlation with Improved Spatial Resolution. Exp. Mech. 2020, 60, 283–293. [Google Scholar] [CrossRef]
- Chen, B.; Genovese, K.; Pan, B. In vivo Panoramic Human Skin Shape and Deformation Measurement Using Mirror-Assisted Multi-View Digital Image Correlation. J. Mech. Behav. Biomed. Mater. 2020, 110, 103936. [Google Scholar] [CrossRef]
- Zhu, K.; Pan, B. Reflection Transformation Calibration for Mirror-Assisted Multi-View Digital Image Correlation System Using Fluorescent Speckle Patterns. Measurement 2023, 217, 113113. [Google Scholar] [CrossRef]
- Xie, R.; Chen, B.; Pan, B. Mirror-Assisted Multi-View High-Speed Digital Image Correlation for Dual-Surface Dynamic Deformation Measurement. Sci. China Technol. Sci. 2023, 66, 807–820. [Google Scholar] [CrossRef]
- Zhu, K.; Pan, B. Panoramic/Dual-Surface Digital Image Correlation Measurement Using a Single Camera. Sensors 2022, 22, 3266. [Google Scholar] [CrossRef]
- Genovese, K.; Lee, Y.U.; Humphrey, J.D. Novel optical system for in vitro quantification of full surface strain fields in small arteries: I. Theory and design. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 213–225. [Google Scholar] [CrossRef]
- Genovese, K.; Lee, Y.U.; Humphrey, J.D. Novel optical system for in vitro quantification of full surface strain fields in small arteries: II. Correction for refraction and illustrative results. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 227–237. [Google Scholar] [CrossRef]
- Genovese, K.; Casaletto, L.; Humphrey, J.D.; Lu, J. Digital image correlation-based point-wise inverse characterization of heterogeneous material properties of gallbladder in vitro. Proc. R. Soc. A 2014, 470, 20140152. [Google Scholar] [CrossRef]
- Bersi, M.R.; Bellini, C.; Di Achille, P.; Humphrey, J.D.; Genovese, K.; Avril, S. Novel Methodology for Characterizing Regional Variations in the Material Properties of Murine Aortas. J. Biomech. Eng. 2016, 138, 710051–7100515. [Google Scholar] [CrossRef] [PubMed]
- Genovese, K. An omnidirectional DIC system for dynamic strain measurement on soft biological tissues and organs. Opt. Lasers Eng. 2019, 116, 6–18. [Google Scholar] [CrossRef]
- Ge, P.; Wang, H.; Zhang, Q.; Xie, H.; Wang, Y. Mirror-assisted multiview DIC for 360° panoramic large deformation measurement. Opt. Lasers Eng. 2021, 146, 106673. [Google Scholar] [CrossRef]
- Srivastava, V.; Baqersad, J. A multi-view optical technique to extract the operating deflection shapes of a full vehicle using digital image correlation. Thin-Walled Struct. 2019, 145, 106426. [Google Scholar] [CrossRef]
- Malesa, M.; Malowany, K.; Kujawinska, M. Multi-camera DIC system with spatial data stitching procedure for measurements of engineering objects. Photonics Lett. Pol. 2014, 6, 157–159. [Google Scholar]
- Malesa, M.; Malowany, K.; Pawlicki, J.; Kujawinska, M.; Skrzypczak, P.; Piekarczuk, A.; Lusa, T.; Zagorski, A. Non-destructive testing of industrial structures with the use of multi-camera Digital Image Correlation method. Eng. Fail. Anal. 2016, 69, 122–134. [Google Scholar] [CrossRef]
- Huss, J.C.; Schoeppler, V.; Merritt, D.J.; Best, C.; Maire, E.; Adrien, J.; Spaeker, O.; Janssen, N.; Gladisch, J.; Gierlinger, N.; et al. Climate-dependent heat-triggered opening mechanism of Banksia seed pods. Adv. Sci. 2018, 5, 1700572. [Google Scholar] [CrossRef] [PubMed]
- Hofhuis, H.; Moulton, D.; Lessinnes, T.; Routier-Kierzkowska, A.-L.; Bomphrey, R.J.; Mosca, G.; Reinhardt, H.; Sarchet, P.; Gan, X.; Tsiantis, M.; et al. Morphomechanical Innovation Drives Explosive Seed Dispersal. Cell 2016, 166, 222–233. [Google Scholar] [CrossRef]
- Elbaum, R.; Abraham, Y. Insights into the microstructures of hygroscopic movement in plant seed dispersal. Plant Sci. 2014, 223, 124–133. [Google Scholar] [CrossRef] [PubMed]
- Fischer, M.; Beismann, H. 3D Characterization of the Complex Vascular Bundle System of Hakea Fruits Based on X-ray Microtomography (µCT) for a better understanding of the opening mechanism. Flora 2022, 289, 152035. [Google Scholar] [CrossRef]
- Mylo, M.D.; Speck, O. Longevity of System Functions in Biology and Biomimetics: A Matter of Robustness and Resilience. Biomimetics 2023, 8, 173. [Google Scholar] [CrossRef] [PubMed]
- Poppinga, S.; Nestle, N.; Šandor, A.; Reible, B.; Masselter, T.; Bruchmann, B.; Speck, T. Hygroscopic motions of fossil conifer cones. Sci. Rep. 2017, 7, 40302. [Google Scholar] [CrossRef] [PubMed]
- Sahin, E.S.; Cheng, T.; Wood, D.; Tahouni, Y.; Poppinga, S.; Thielen, M.; Speck, T.; Menges, A. Cross-Sectional 4D-Printing: Upscaling Self-Shaping Structures with Differentiated Material Properties Inspired by the Large-Flowered Butterwort (Pinguicula grandiflora). Biomimetics 2023, 8, 233. [Google Scholar] [CrossRef]
- Ahmed, A.; Arya, S.; Gupta, V.; Furukawa, H.; Khosla, A. 4D Printing: Fundamentals, Materials, Applications and Challenges. Polymer 2021, 228, 123926. [Google Scholar] [CrossRef]
- Palombini, F.L.; Lautert, E.L.; Mariath, J.E.d.A.; de Oliveira, B.F. Combining numerical models and discretizing methods in the analysis of bamboo parenchyma using finite element analysis based on X-ray microtomography. Wood Sci. Technol. 2020, 54, 161–186. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, M.; Mylo, M.D.; Lorenz, L.S.; Böckenholt, L.; Beismann, H. Stereo Camera Setup for 360° Digital Image Correlation to Reveal Smart Structures of Hakea Fruits. Biomimetics 2024, 9, 191. https://doi.org/10.3390/biomimetics9030191
Fischer M, Mylo MD, Lorenz LS, Böckenholt L, Beismann H. Stereo Camera Setup for 360° Digital Image Correlation to Reveal Smart Structures of Hakea Fruits. Biomimetics. 2024; 9(3):191. https://doi.org/10.3390/biomimetics9030191
Chicago/Turabian StyleFischer, Matthias, Max D. Mylo, Leon S. Lorenz, Lars Böckenholt, and Heike Beismann. 2024. "Stereo Camera Setup for 360° Digital Image Correlation to Reveal Smart Structures of Hakea Fruits" Biomimetics 9, no. 3: 191. https://doi.org/10.3390/biomimetics9030191
APA StyleFischer, M., Mylo, M. D., Lorenz, L. S., Böckenholt, L., & Beismann, H. (2024). Stereo Camera Setup for 360° Digital Image Correlation to Reveal Smart Structures of Hakea Fruits. Biomimetics, 9(3), 191. https://doi.org/10.3390/biomimetics9030191







