Simulation Analysis of Frog-Inspired Take-Off Performance Based on Different Structural Models
Abstract
1. Introduction
2. Analysis of Frog Jumping Movement
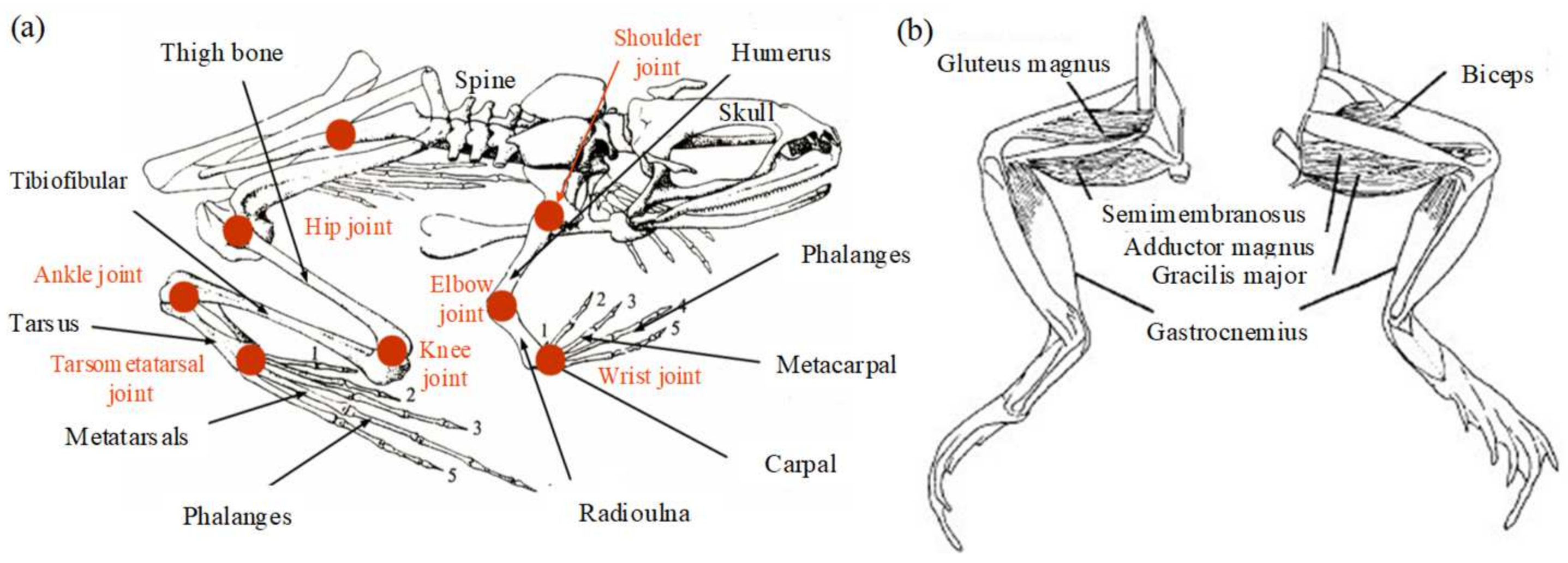
2.1. Musculoskeletal Analysis
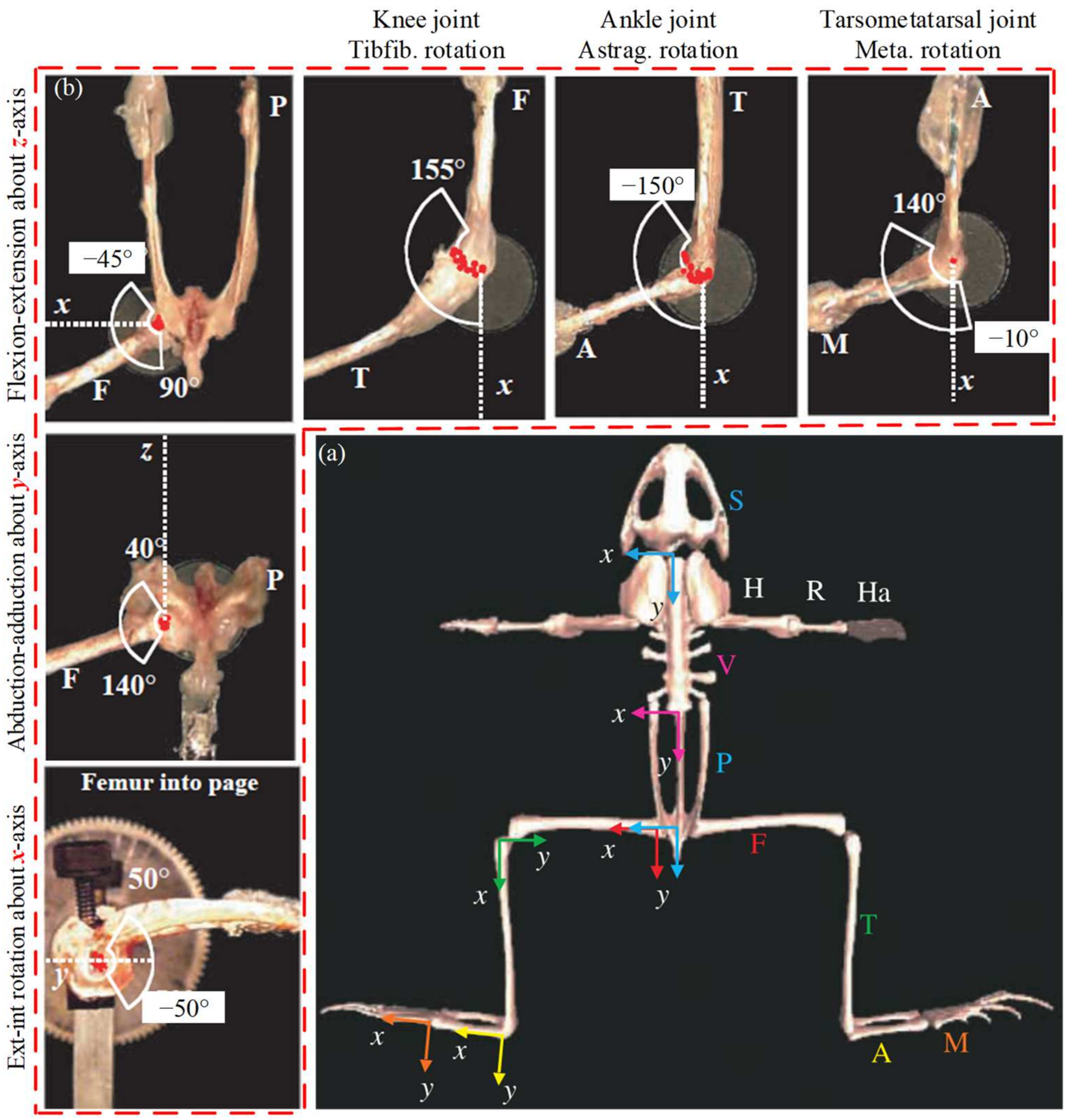
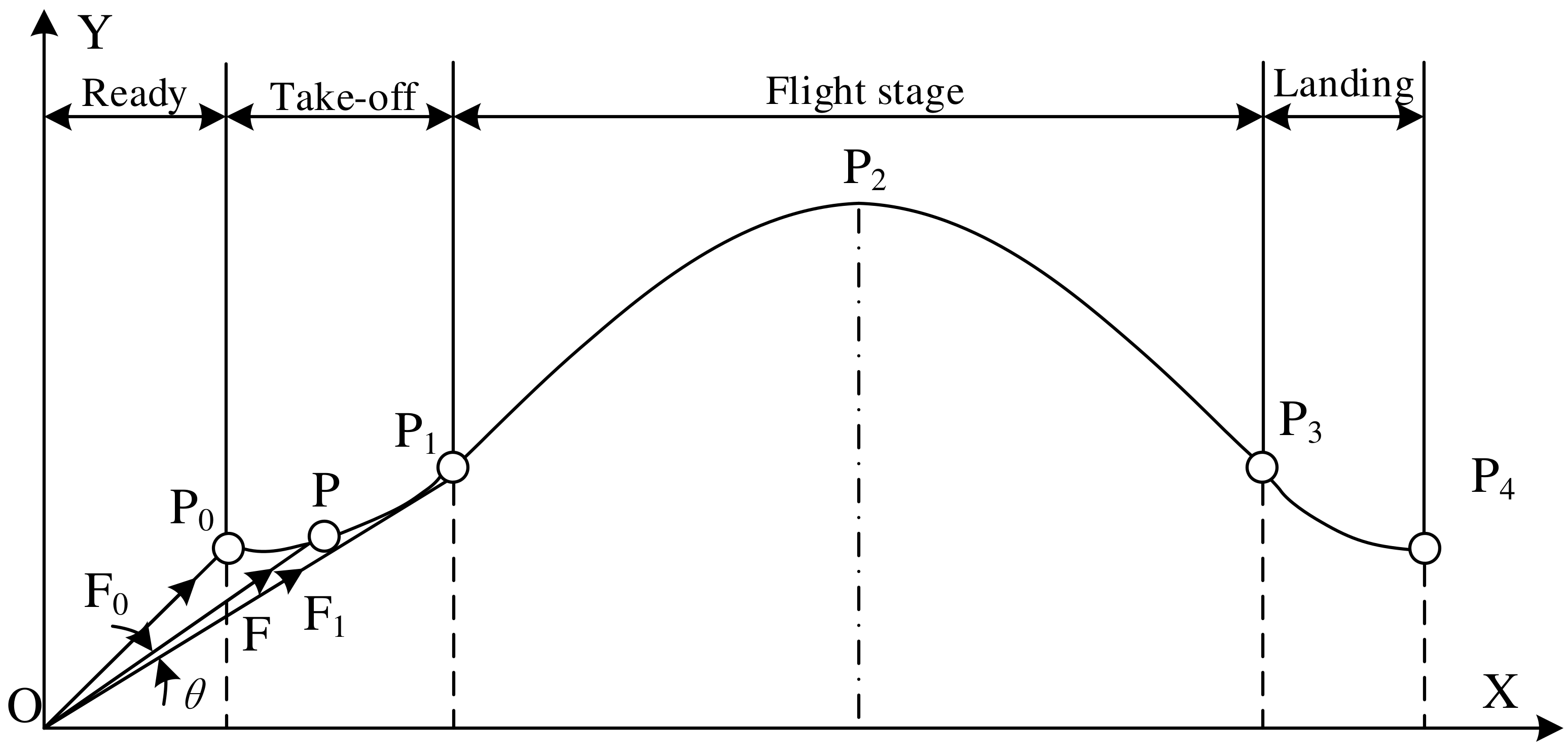
2.2. Jumping Motion Information Analysis
3. Numerical Modeling
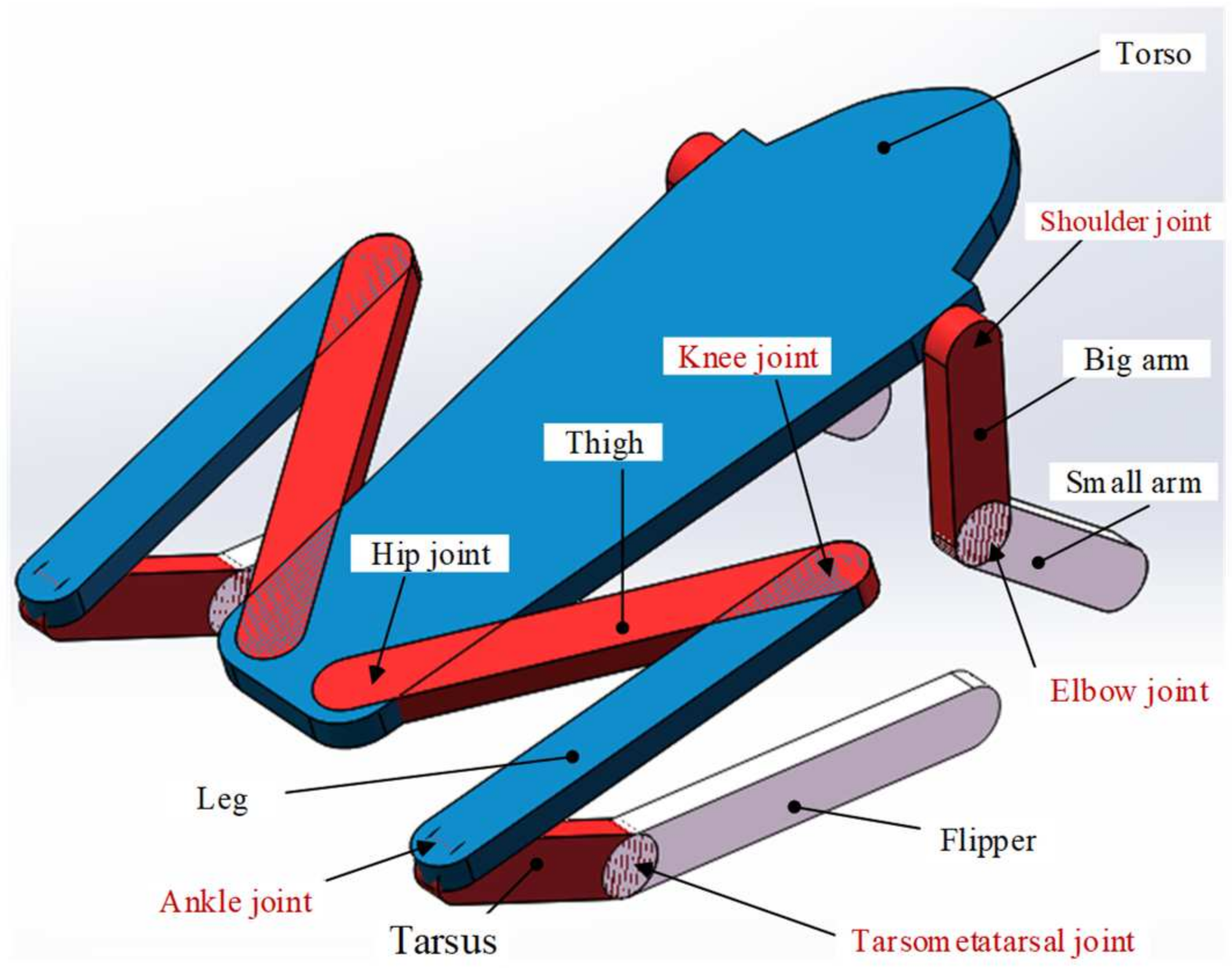
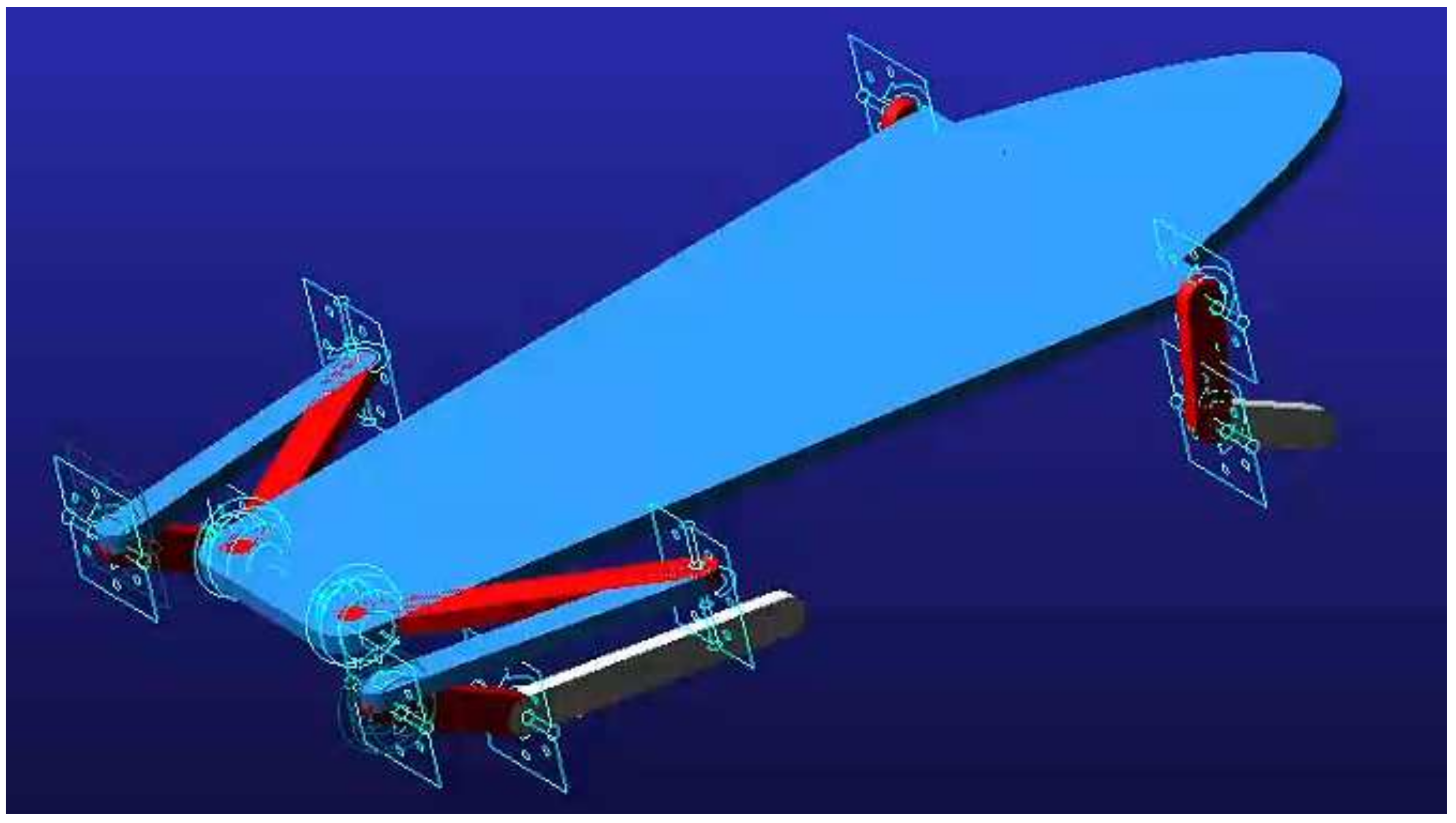
3.1. Skeleton Structure Modeling
3.2. Simulation of Multiple Structural Models
3.3. Simulation Analysis
4. Result
4.1. Ground Reaction Forces Analysis
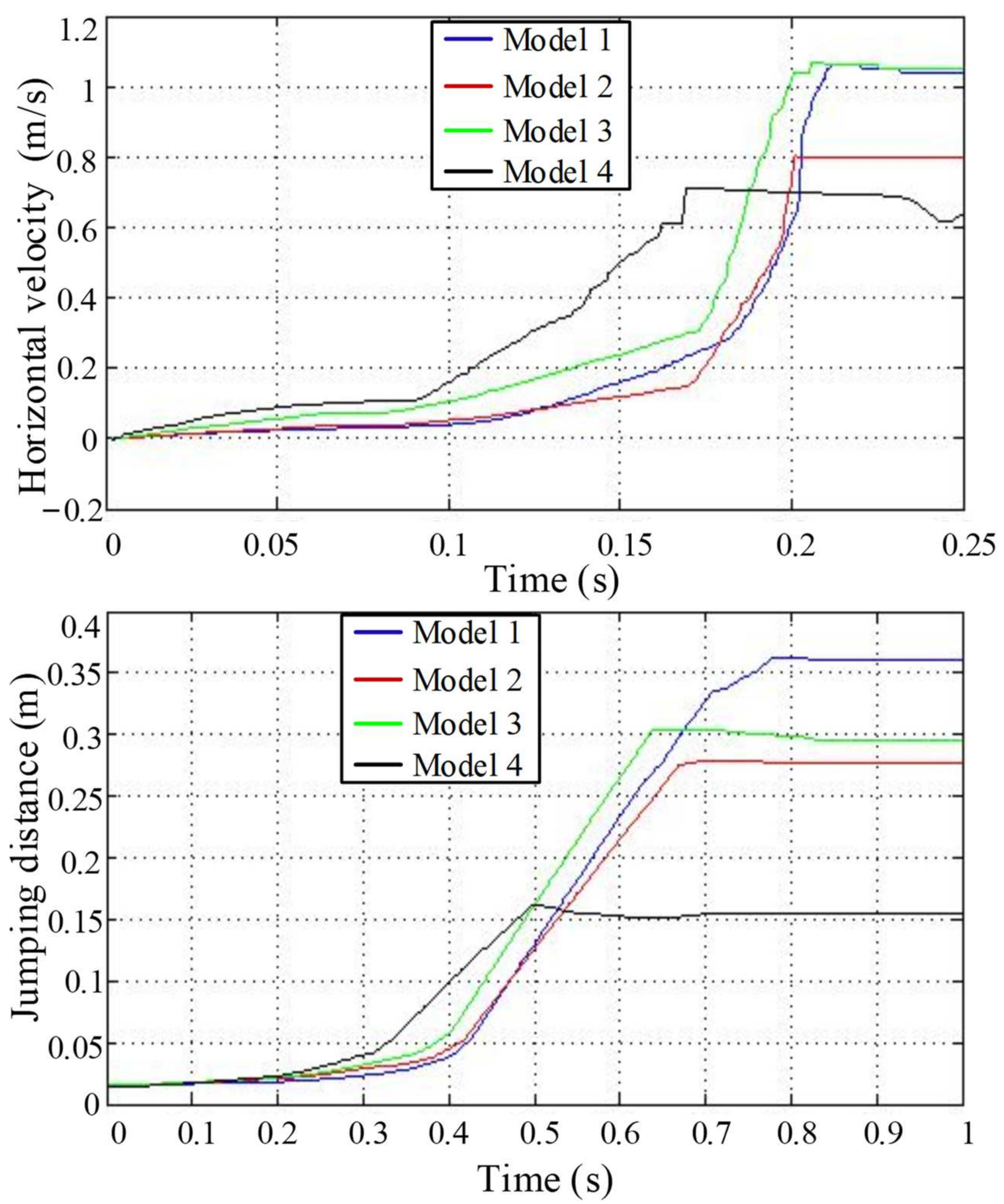
4.2. Jumping Speed and Distance Analysis
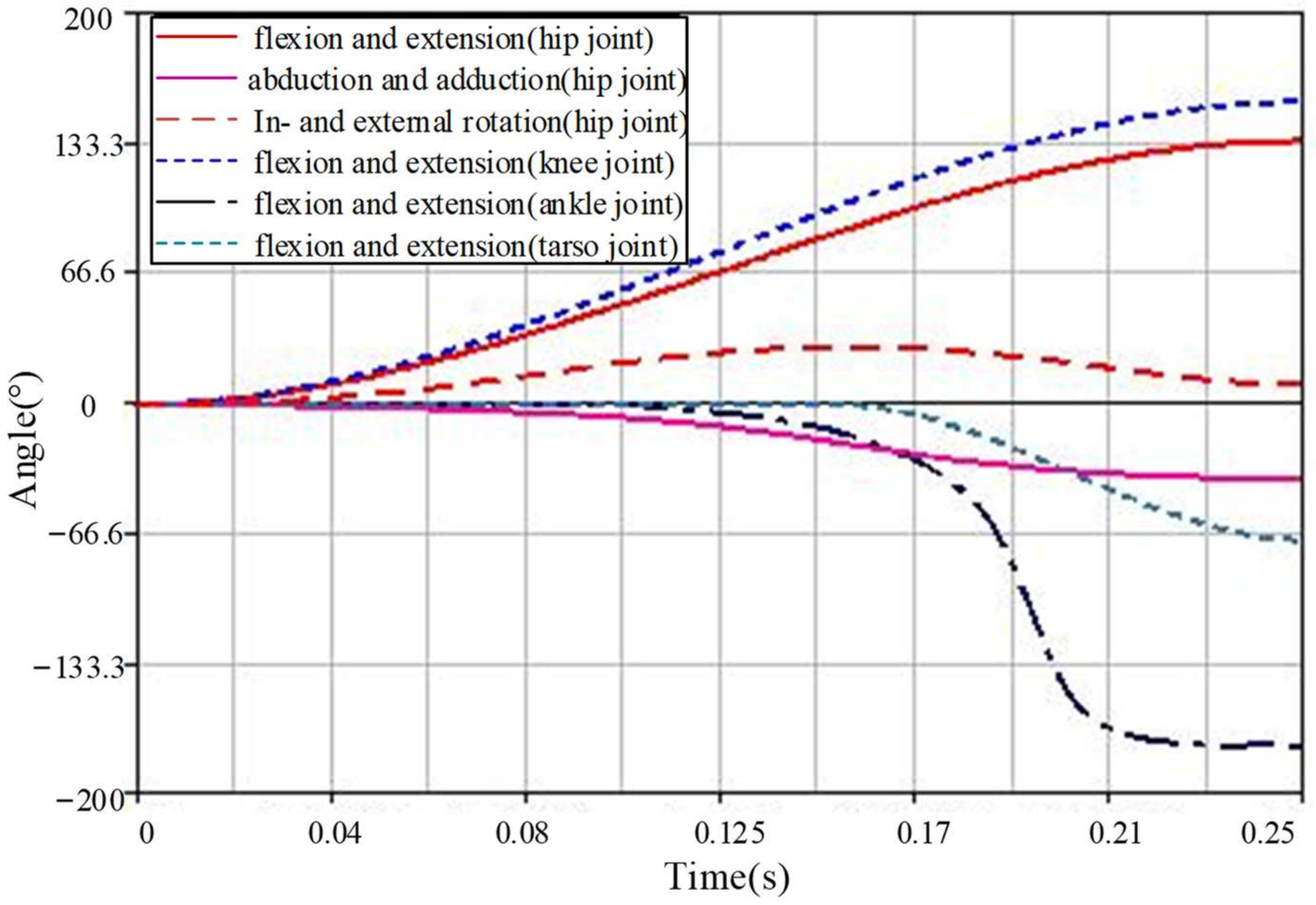
4.3. Joint Torque Analysis
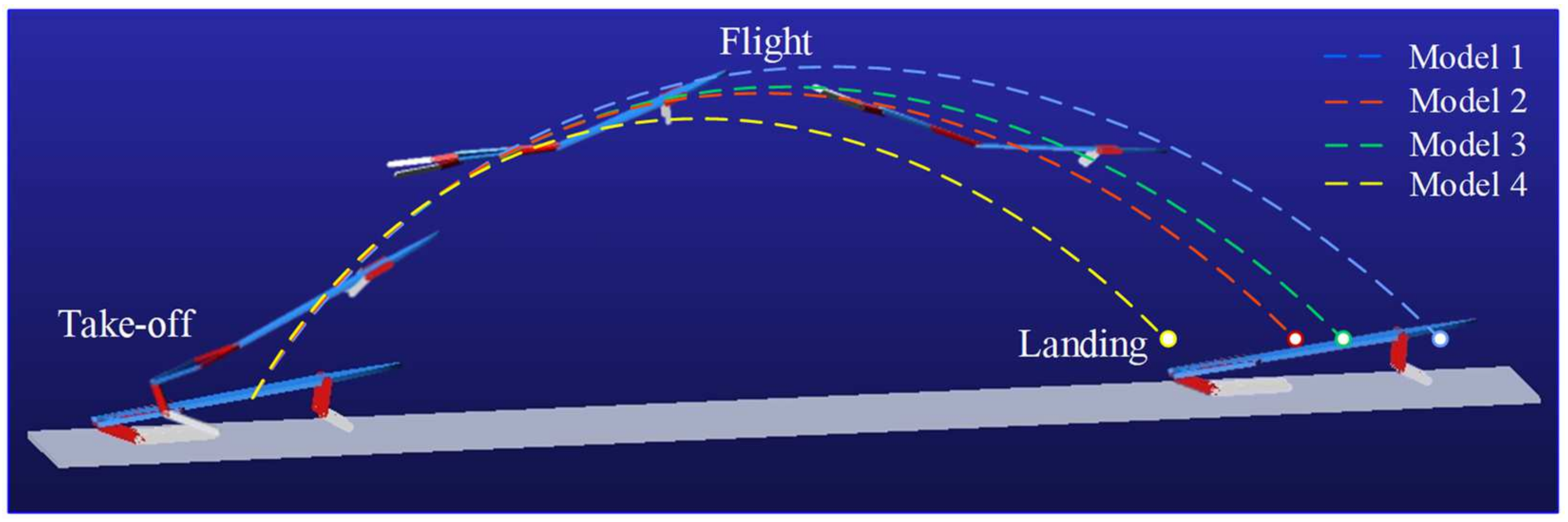
4.4. Jumping Performance Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ji, A.; Dai, Z.; Zhou, L. Research Progress of Bionic Robots. Robots 2005, 27, 284–288. [Google Scholar]
- Sinha, A.; Tan, N.; Mohan, R. Terrain perception for a reconfigurable biomimetic robot using monocular vision. Robot. Biomim. 2014, 1, 23. [Google Scholar] [CrossRef]
- Mo, X.; Ge, W.; Ren, Y.; Zhao, D.; Wei, D.; Romano, D. Locust-Inspired Jumping Mechanism Design and Improvement Based on Takeoff Stability. J. Mech. Robot. 2024, 16, 061013. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.; Yuan, S.; Jing, C. Motion mechanism and thrust characteristics of amphibious robots with long fin fluctuation for propulsion on hard level ground. Bioinspiration Biomim. 2022, 17, 056006. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Yang, J.; Zeng, L.; Huang, C. A Spider-Joint-like Bionic Actuator with an Approximately Triangular Prism Shape. Biomimetics 2023, 8, 299. [Google Scholar] [CrossRef]
- Chen, D.; Xiong, Y.; Wang, B.; Tong, R.; Meng, Y.; Yu, J. Performance Optimization for Bionic Robotic Dolphin with Active Variable Stiffness Control. Biomimetics 2023, 8, 545. [Google Scholar] [CrossRef] [PubMed]
- Mo, X.; Ge, W.; Miraglia, M.; Inglese, F.; Zhao, D.; Stefanini, C.; Romano, D. Jumping locomotion strategies: From animals to bioinspired robots. Appl. Sci. 2020, 10, 8607. [Google Scholar] [CrossRef]
- Xia, D.; Li, Y.; Li, Z.; Tian, M.; Wang, X. Development of a Variable-Configuration Bionic Robotic Fish. Biomimetics 2023, 8, 407. [Google Scholar] [CrossRef]
- Aubin, C.A.; Heisser, R.H.; Peretz, O.; Timko, J.; Lo, J.; Helbling, E.F.; Sobhani, S.; Gat, A.D.; Shepherd, R.F. Powerful, soft combustion actuators for insect-scale robots. Science 2023, 381, 1212–1217. [Google Scholar] [CrossRef]
- Phan, H.V.; Park, H.C. Mechanisms of collision recovery in flying beetles and flapping-wing robots. Science 2020, 370, 1214–1219. [Google Scholar] [CrossRef]
- Tang, Y.; Qin, L.; Li, X.; Chew, C.-M.; Zhu, J. A frog-inspired swimming robot based on dielectric elastomer actuators. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2403–2408. [Google Scholar]
- Pandey, J.; Reddy, N.; Ray, R.; Shome, S. Biological Swimming Mechanism Analysis and Design of Robotic Frog. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, IEEE (2013), Takamatsu, Japan, 4–7 August 2013; pp. 1726–1731. [Google Scholar]
- Fan, J.; Wang, S.; Yu, Q.; Zhu, Y. Swimming Performance of the Frog-Inspired Soft Robot. Soft Robot. 2020, 7, 615–626. [Google Scholar] [CrossRef]
- Ahn, J.; Park, J.; Kim, K.; Kim, S. Frog-Inspired Jumping Robot for Overcoming High Obstacles. In Proceedings of the International Symposium on Robotics, IEEE (2014), Seoul, Republic of Korea, 24–26 October 2013; pp. 1–4. [Google Scholar]
- Aerts, P.; Nauwelaerts, S. Environmentally induced mechanical feedback in locomotion: Frog performance as a model. J. Theor. Biol. 2009, 261, 372–378. [Google Scholar] [CrossRef]
- Kecai, Z.; Ting, T.; Congbin, Z.; Guo, P. A comparative study on the Microhyla skeletal system of three species of frogs in my country Amphibian: Microhylidae. Sichuan Zool. 2009, 28, 234–240. [Google Scholar]
- Kargo, W.; Nelson, F.; Rome, L. Jumping in frogs: Assessing the design of the skeletal system by anatomically realistic modeling and forward dynamic simulation. J. Exp. Biol. 2002, 205, 1683–1702. [Google Scholar] [CrossRef]
- Azizi, E.; Roberts, T. Muscle Performance during Frog Jumping: Influence of Elasticity on Muscle Operating Length. Proc. Biol. Sci. 2010, 277, 1523–1530. [Google Scholar] [CrossRef] [PubMed]
- Nauwelaerts, S. Propulsive impulse as a covarying performance measure in the comparison of the kinematics of swimming and jumping in frogs. J. Exp. Biol. 2003, 206, 4341–4351. [Google Scholar] [CrossRef] [PubMed]
- Guan, S. Research on the Hopping Principle and Simulation of Bionic Frog Hopping Robot; Harbin Institute of Technology: Harbin, China, 2007. [Google Scholar]
- Wang, M.; Zang, X.; Zhao, J. Frog jumping trajectory acquisition method for biomimetic robots. J. Beijing Univ. Posts Telecommun. 2008, 31, 37–41, 52. [Google Scholar]
- Richards, C.; Clemente, C. A bio-robotic platform for integrating internal and external mechanics during muscle-powered swimming. Bioinspiration Biomim. 2012, 7, 016010. [Google Scholar] [CrossRef]
- Stamhuis, E. Propulsive force calculations in swimming frogs II. Application of a vortex ring model to DPIV data. J. Exp. Biol. 2005, 208 Pt 8, 1445–1451. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, W.; Zhu, Y.; Zhao, J. CFD-based self-propulsion simulation for frog swimming. J. Mech. Med. Biol. 2014, 14, 1440012. [Google Scholar] [CrossRef]
- Fan, J.; Du, Q.; Dong, Z.; Zhao, J.; Xu, T. Design of the Jump Mechanism for a Biomimetic Robotic Frog. Biomimetics 2022, 7, 142. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Luo, M.; Liu, X.; Fan, J.; Zhao, J. Frog-inspired jumping robot actuated by pneumatic muscle actuators. Adv. Mech. Eng. 2018, 10, 1687814018782303. [Google Scholar] [CrossRef]
- Wang, M.; Zang, X.Z.; Fan, J.Z.; Zhao, J. Biological Jumping Mechanism Analysis and Modeling for Frog Robot. J. Bionic Eng. 2008, 5, 8. [Google Scholar] [CrossRef]
- Pearson, K.G. Common principles of motor control in vertebrates and invertebrates. Annu. Rev. Neurosci. 1993, 16, 265–297. [Google Scholar] [CrossRef] [PubMed]
- Richard, D. The springiness of the long-distance hopper. Sciences 1975, 12, 11. [Google Scholar]
- Barnes, W.J.; Goodwyn, P.J.; Nokhbatolfoghahai, M.; Gorb, S.N. Elastic modulus of tree frog adhesive toe pads. J. Comp. Physiol. A Neuroethol. Sens. Neural. Behav. Physiol. 2011, 197, 969–978. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, W.; Cai, L.; Guo, D. Friction and Wear Properties of Commercial Solid Wood Floorings. Tribology 2012, 32, 557–562. [Google Scholar]
- Meng, F.; Liu, Q.; Wang, X.; Tan, D.; Xue, L.; Barnes, W.J.P. Tree frog adhesion biomimetics: Opportunities for the development of new, smart adhesives that adhere under wet conditions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20190131. [Google Scholar] [CrossRef]
- Hanna, G.; Barnes, W.-J.P. Adhesion and detachment of the toe pads of tree frogs. J. Exp. Biol. 1991, 155, 103–125. [Google Scholar] [CrossRef]
- Langowski, J.K.A.; Dodou, D.; van Assenbergh, P.; van Leeuwen, J.L. Design of Tree-Frog-Inspired Adhesives. Integr. Comp. Biol. 2020, 60, 906–918. [Google Scholar] [CrossRef]
- Romano, D.; Bloemberg, J.; Tannous, M.; Stefanini, C. Impact of aging and cognitive mechanisms on high-speed motor activation patterns: Evidence from an orthoptera-robot interaction. IEEE Trans. Med. Robot. Bionics 2020, 2, 292–296. [Google Scholar] [CrossRef]

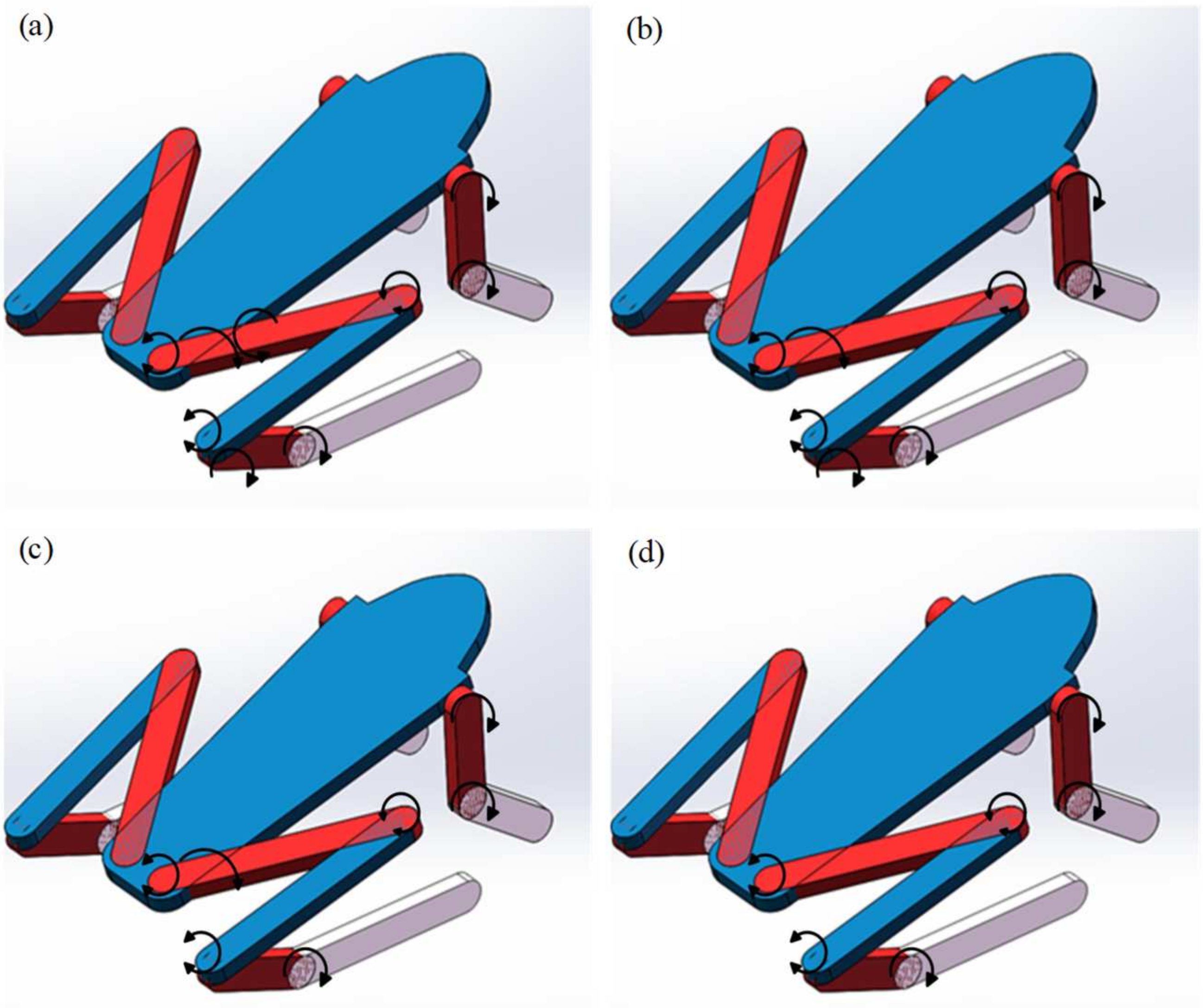

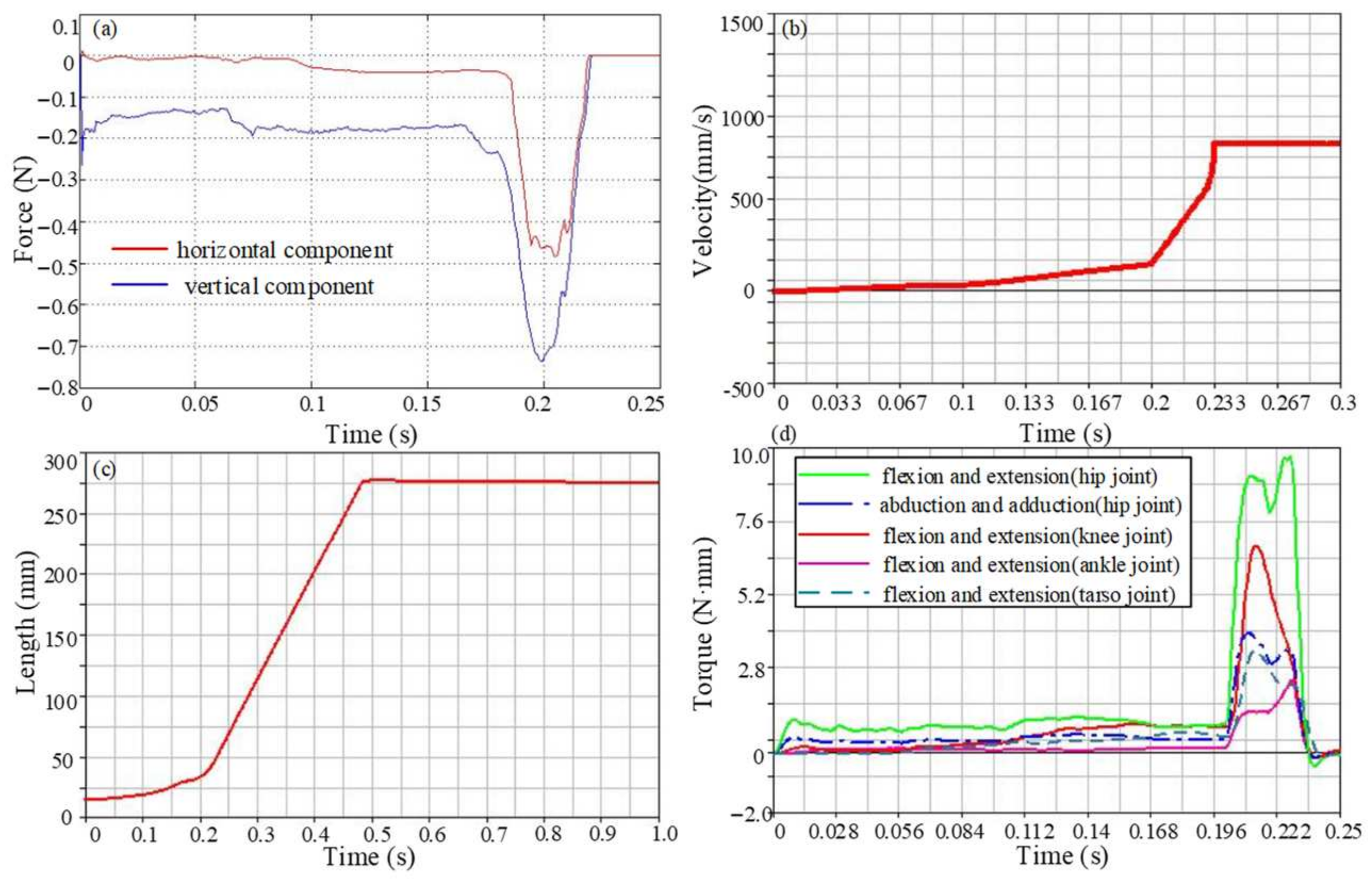
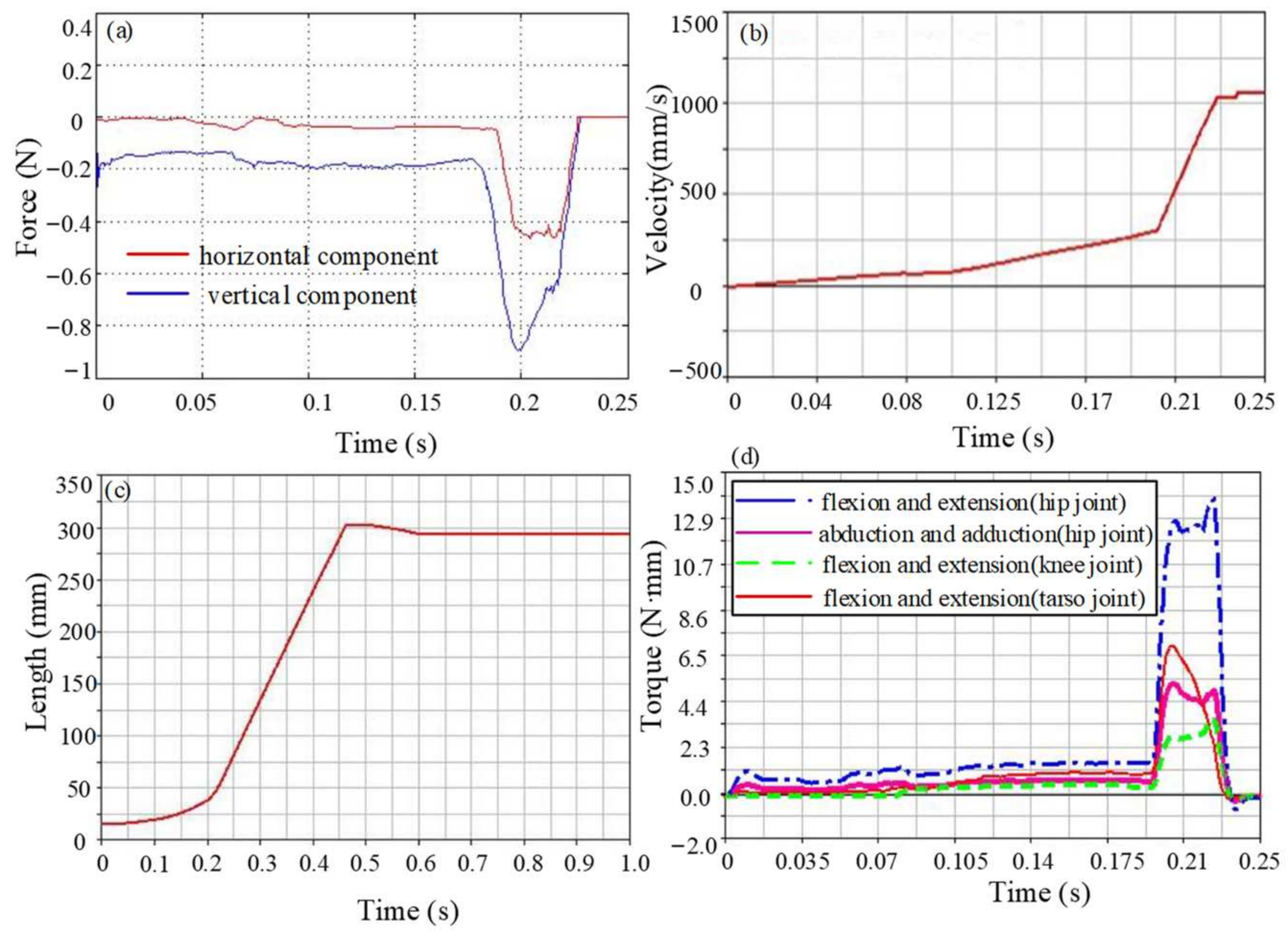
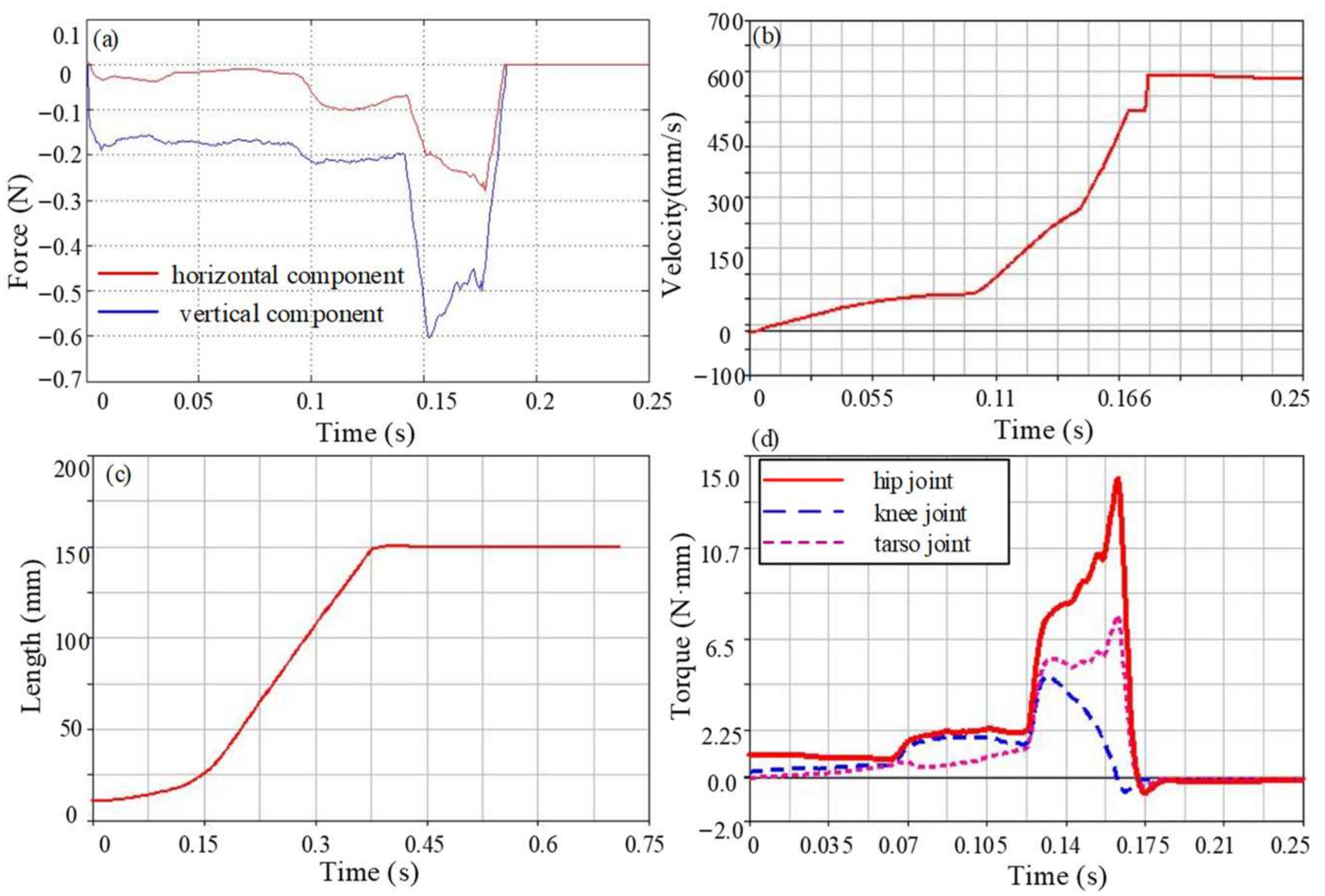
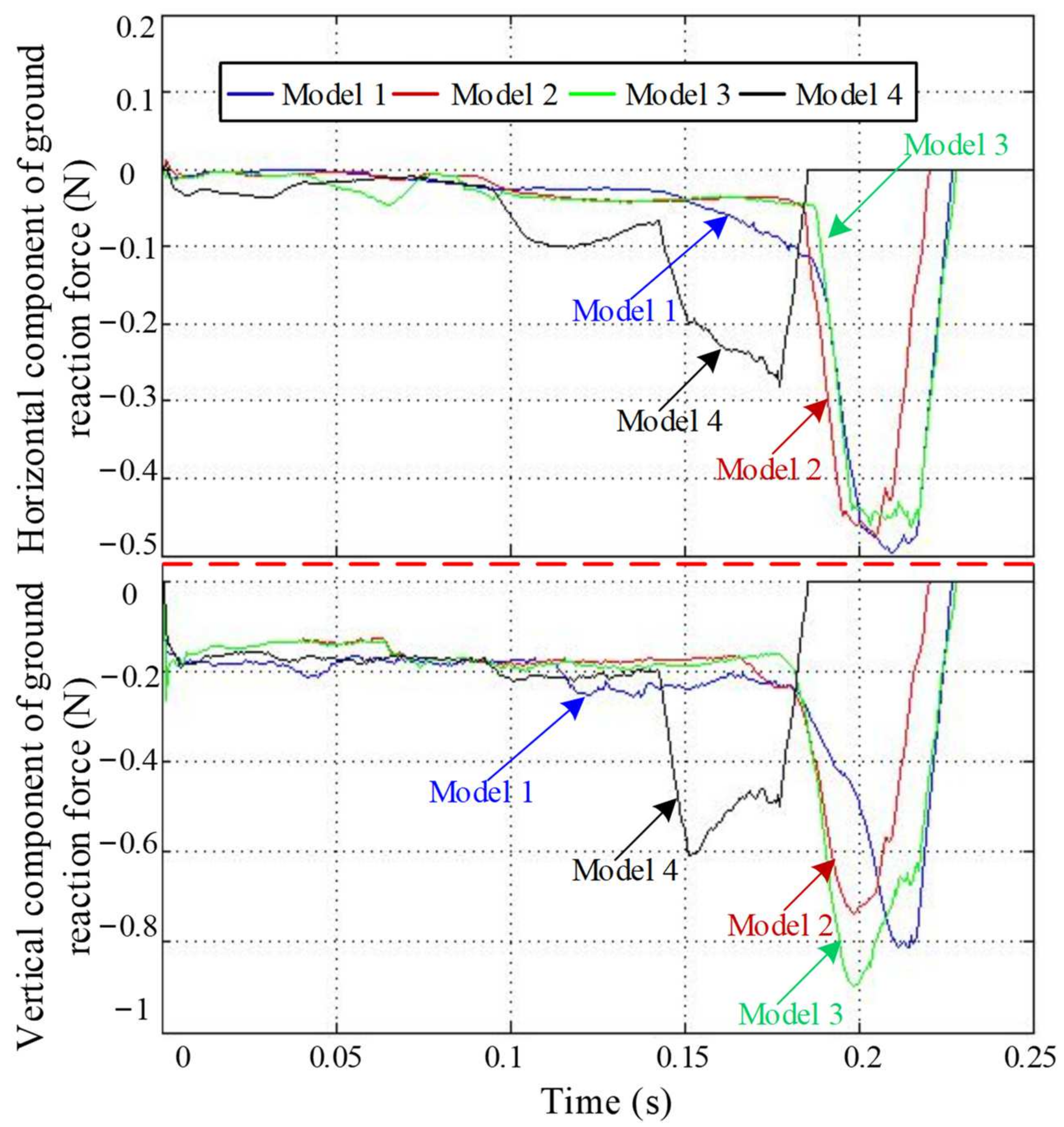
| Model | Torso | Big Arm | Small Arm | Thigh | Leg | Sole | Flipper |
|---|---|---|---|---|---|---|---|
| Dimension (mm) | 40 × 16 × 20 | 12.5 | 12 | 28 | 27.5 | 15 | 25 |
| Mass (g) | 20 | 0.5 | 0.5 | 1 | 1 | 0.5 | 0.5 |
| Inertia (kg·m2) | 5.6 × 10−6 | 1.8 × 10−9 | 1.5 × 10−9 | 2.1 × 10−8 | 2.0 × 10−8 | 3.1 × 10−9 | 8.3 × 10−9 |
| Name | Stiffness | Damping | Force Exponent | Penetration Depth | Friction Coefficient | Stiction Transition |
|---|---|---|---|---|---|---|
| Value | 1.0 × 107 N/m | 3.0 × 104 N·s/m | 2.2 | 1.0 × 10−4 m | 0.7 | 0.1 m/s |
| Model | Flexion and Extension (H) | Abduction and Adduction | Rotation | Flexion and Extension (K) | Flexion and Extension (A) | Flexion and Extension (T) |
|---|---|---|---|---|---|---|
| 1 | 13.2 | 7.7 | 1.1 | 2.4 | 2.4 | 3.2 |
| 2 | 9.0 | 4.2 | 0 | 2.4 | 2.4 | 3.4 |
| 3 | 12.5 | 5.2 | 0 | 3.3 | 0 | 6.7 |
| 4 | 13.3 | 0 | 0 | 4.8 | 0 | 7.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Fan, J.; Liu, Y. Simulation Analysis of Frog-Inspired Take-Off Performance Based on Different Structural Models. Biomimetics 2024, 9, 168. https://doi.org/10.3390/biomimetics9030168
Wang S, Fan J, Liu Y. Simulation Analysis of Frog-Inspired Take-Off Performance Based on Different Structural Models. Biomimetics. 2024; 9(3):168. https://doi.org/10.3390/biomimetics9030168
Chicago/Turabian StyleWang, Shuqi, Jizhuang Fan, and Yubin Liu. 2024. "Simulation Analysis of Frog-Inspired Take-Off Performance Based on Different Structural Models" Biomimetics 9, no. 3: 168. https://doi.org/10.3390/biomimetics9030168
APA StyleWang, S., Fan, J., & Liu, Y. (2024). Simulation Analysis of Frog-Inspired Take-Off Performance Based on Different Structural Models. Biomimetics, 9(3), 168. https://doi.org/10.3390/biomimetics9030168






